ดาวหางฮัลเลย์และกฎการเคลื่อนที่ดาวเคราะห์ของเคปเลอร์ (Kepler's laws of planetary motion)
27-08-2019 อ่าน 32,372

ดาวหางฮัลเลย์ถ่ายได้ในปี ค.ศ. 1986
ที่มา NASA/National Space Science Data Center
ดาวหางฮัลเลย์เป็นดาวหางดวงแรกที่มนุษย์สามารถใช้คณิตศาสตร์ในการทำนายการกลับมาของมันได้ โดยใน ค.ศ. 1705 นักดาราศาสตร์ชาวอังกฤษชื่อเอ็ดมันด์ แฮลลีย์ (Edmond Halley) ตีพิมพ์ผลงานของเขาแสดงการคำนวณให้เห็นว่า ดาวหางที่เห็นบนท้องฟ้าในปี ค.ศ. 1531 ค.ศ. 1607 และ ค.ศ. 1682 จริงๆแล้วเป็นดาวหางดวงเดียวกัน และเขายังทำนายว่ามันจะปรากฏตัวอีกครั้งในปี ค.ศ. 1758 และก็มันก็ปรากฏตัวเป็นตามที่ไว้จริงๆ แม้น่าเสียดายที่แฮลลีย์ได้เสียชีวิตไปก่อนหลายปี แต่เราก็ได้เรียกชื่อดาวหางนี้ในปัจจุบันตามชื่อของเขาเพื่อเป็นเกียรติแก่เขา
เราสามารถทำนายการเคลื่อนที่ของดาวหางได้อย่างไร จริงๆแล้วเราสังเกตุการณ์เคลื่อนที่ของดวงดาวและวัตถุต่างๆบนท้องฟ้ามานานแล้วตั้งแต่ในอดีต แต่มันสร้างความสับสนงุนงงให้แก่ผู้คนที่เฝ้าสังเกตมันอย่างมาก นั่นเป็นเพราะเราสังเกตสิ่งต่างๆบนท้องฟ้าจากในโลก ขณะที่โลกหมุนรอบตัวเอง โลกยังโคจรรอบดวงอาทิตย์ และดาวเคราะห์ในระบบสุริยะดวงอื่นๆต่างก็โคจรรอบดวงอาทิตย์ด้วยเช่นกัน
เช่น ในบางครั้งถ้าเราจะเห็นเส้นทางการโคจรของดาวอังคารโดยการสังเกตจากโลกนั้นมีการหมุนเป็นวงก่อนเคลื่อนที่ต่อไป สร้างความแปลกใจให้แก่ผู้สังเกต ปัจจุบันนี้เราทราบกันดีแล้วว่านี่คือ ปรากฎการณ์เคลื่อนที่ถอยหลัง (Apparent retrograde motion) เป็นสิ่งที่เกิดขึ้นกับดาวเคราะห์วงนอก (Superior Planets) เช่นดาวอังคาร เกิดขึ้นจากการที่โลกเคลื่อนที่เร็วกว่าดาวเคราะห์วงนอก ดังนั้นเมื่อเรามองจากโลกไปยังดาวเคราะห์วงนอก จะเห็นดาวเคราะห์นั้นเคลื่อนที่ถอยหลัง

เส้นทางวงโคจรของดาวอังคารที่สังเกตเห็นจากโลกมีการหมุนเป็นวง ก่อนเคลื่อนที่ต่อไป การเคลื่อนที่แบบนี้เรียกว่าปรากฎการณ์เคลื่อนที่ถอยหลัง (Apparent retrograde motion)
Resnick, R., Walker, J. and Halliday, D. (2014). Fundamentals of physics. Hoboken, N.J.: Wiley.
เมื่อโยฮันเนส เคปเลอร์ (Johannes Kepler) นักวิทยาศาสตร์ชาวเยอรมันได้ใช้เวลาเกือบจะทั้งชีวิตศึกษาการเคลื่อนที่ของดาวเคราะห์โดยอาศัยข้อมูลการสังเกตการณ์จากทีโค บรา (Tycho Brahe) ทำให้เขาสามารถสร้างกฎพื้นฐานการเคลื่อนที่ของดาวเคราะห์ได้ 3 ข้อโดยตีพิมพ์ผลงานในชื่อ Astronomia nova ในปี ค.ศ. 1609 กฎเหล่านี้ชื่อว่ากฎการเคลื่อนที่ดาวเคราะห์ของเคปเลอร์ (Kepler's laws of planetary motion) ซึ่งไม่ใช่เพียงดาวเคราะห์เท่านั้นที่สามารถใช้กฎนี้อธิบายได้ สิ่งอื่นๆเช่นดาวหางที่โคจรรอบดวงอาทิตย์ก็สามารถใช้กฎนี้มาอธิบายมันได้ด้วยเช่นกัน ซึ่งสิ่งนี้เองทำให้มนุษย์เข้าใจการเคลื่อนที่ของดวงดาวบนท้องฟ้ามากยิ่งขึ้น โดยกฎของเคปเลอร์ทั้ง 3 ข้อสามารถอธิบายได้คร่าวๆดังนี้Resnick, R., Walker, J. and Halliday, D. (2014). Fundamentals of physics. Hoboken, N.J.: Wiley.
1.กฎแห่งการโคจร ดาวเคราะห์ทุกดวงจะโคจรเป็นวงรีโดยมีดวงอาทิตย์เป็นโฟกัส และเพราะดวงอาทิตย์มีมวลมากกว่าดาวเคราะห์มาก จึงให้จุดศูนย์กลางมวลของระบบดาวเคราะห์-ดวงอาทิตย์อยู่ที่ประมาณจุดศูนย์กลางของดวงอาทิตย์ โดยแนวคิดที่ดาวเคราะห์โคจรเป็นวงรีนั้นขัดกับแนวคิดที่สอนกันมาตั้งแต่ในยุคกรีกโบราณที่เชื่อว่าวงโคจรของดาวเคราะห์นั้นเป็นวงกลม เพราะถือว่าวงกลมคือความสมบูรณ์แบบ เคปเลอร์ต้องใช้เวลาศึกษาอย่างยาวนานเพื่อลบความเชื่อเก่านี้
2.กฎของพื้นที่ ระหว่างที่ดาวเคราะห์โคจรรอบดวงอาทิตย์เมื่อลากเส้นตรงเชื่อระหว่างดาวเคราะห์กับดวงอาทิตย์ ในระยะเวลาที่เท่ากัน การเคลื่อนที่ของดาวเคราะห์จะกวาดพื้นที่เป็นขนาดที่เท่ากัน ดูภาพประกอบจะเข้าใจได้ง่ายขึ้น กฎนี้ทำให้เห็นว่าดาวเคราะห์เคลื่อนที่ด้วยความเร็วไม่คงที่ เมื่ออยู่ใกล้ดวงอาทิตย์จะเคลื่อนที่เร็วขึ้นและเมื่ออยู่ห่างจากดวงอาทิตย์จะเคลื่อนที่ช้าลง กฎนี้ขัดแย้งกับแนวคิดที่สอนกันมาตั้งแต่ยุคกรีกโบราณว่าดาวเคราะห์ต่างๆเคลื่อนที่ด้วยความเร็วคงที่

กฎการเคลื่อนที่ดาวเคราะห์ของเคปเลอร์ข้อที่ 2 กฎของพื้นที่
https://eloisechen.wordpress.com/2013/02/20/conservation-of-angular-momentum-and-keplers-second-law/
https://eloisechen.wordpress.com/2013/02/20/conservation-of-angular-momentum-and-keplers-second-law/
3.กฎของคาบ กำลังสองของคาบการโคจรของดาวเคราะห์เป็นสัดส่วนโดยตรงกับกำลังสามของกึ่งแกนเอกของวงโคจร โดยอาศัยความรู้จากสมการกฎข้อที่สาม
\(T^2=(\dfrac{4π^2}{GM})r^3\)
โดยที่ T,G,M,r คือ คาบของการเคลื่อนที่ของดาวเคราะห์, ค่าคงที่โน้มถ่วงสากล, มวลของดวงอาทิตย์ และรัศมีของการโคจร ตามลำดับ
สำหรับการโคจรในแบบวงรีเราแทน r ด้วย a หรือกึ่งแกนเอกของวงโคจร จะได้เป็นอัตราส่วนของ \(\dfrac{T^2}{a^3}\) ที่มีค่าคงที่เท่ากันในทุกดาวเคราะห์ที่โคจรรอบดวงอาทิตย์ดวงเดียวกัน
เมื่อเราเข้าใจกฎนี้แล้วเราก็สามารถนำกฎนี้ไปศึกษาการเคลื่อนที่ของสิ่งต่างๆได้ เช่นเราสนใจการเคลื่อนที่ของดาวหางฮัลเลย์ เมื่อเราดูการโคจรของสิ่งต่างๆรอบดวงอาทิตย์ จากรูปจะพบว่า \(R_P\) หรือตำแหน่งโคจรที่อยู่ใกล้ดวงอาทิตย์ที่สุด (Perihelion) กับ \(R_a\) หรือตำแหน่งโคจรที่อยู่ไกลดวงอาทิตย์ที่สุด (Aphelion) จากรูปเราจะพบความสัมพันธ์ที่ว่า
\(R_P+R_a=2a\)
โดยที่ a คือกึ่งแกนเอกของวงโคจร
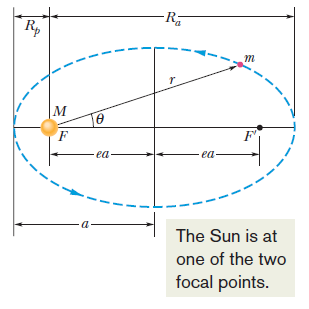
การโคจรของดาวเคราะห์รอบดวงอาทิตย์
Resnick, R., Walker, J. and Halliday, D. (2014). Fundamentals of physics. Hoboken, N.J.: Wiley.
\(T^2=(\dfrac{4π^2}{GM})r^3\)
เราเปลี่ยนจากตัวแปร r เป็น a และย้ายฝั่งเพื่อหาค่ากึ่งแกนเอกของวงโคจร (a) จะได้เป็น\(a=(\dfrac{GMT^2}{4 π^2})^\dfrac{1}{3}\)
\(=2.7*10\)12 เมตร
และจากความสัมพันธ์ที่ว่า
\(R_p+R_a=2a\)
เมื่อเราแทนค่า \(R_p\)และ \(a\) ลงไป เราก็จะสามารถคำนวณระยะตำแหน่งโคจรที่อยู่ไกลดวงอาทิตย์ที่สุด\((R_a)\)ของดาวหางฮัลเลย์ได้ก็คือ \(R_a=5.3*10\)12 เมตร
ดาวหางฮัลเลย์จะมาให้คนบนโลกเห็นกันอีกในปี ค.ศ. 2061 นับจากปี ค.ศ. 2019 ก็กว่าอีก 42 ปี ไม่รู้ว่าเราจะมีอายุยืนจะได้เห็นถึงหรือเปล่า แต่เราสามารถใช้คณิตศาสตร์คำนวณเข้าใจการเคลื่อนที่วงโคจรของมันก็นับว่าประสบความสำเร็จแล้ว
เรียบเรียงโดย
ณัฐพล โชติศรีศุภรัตน์
ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
ณัฐพล โชติศรีศุภรัตน์
ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
อ้างอิง
- Resnick, R., Walker, J. and Halliday, D. (2014). Fundamentals of physics. Hoboken, N.J.: Wiley.
- Kepler's laws of planetary motion. (2015). Encyclopædia Britannica. Encyclopædia Britannica Ultimate Reference Suite. Chicago: Encyclopædia Britannica.
- "Kepler’s Laws." Microsoft® Student 2009 [DVD]. Redmond, WA: Microsoft Corporation, 2008.
- สธน วิจารณ์วรรณลักษณ์. (2555). คู่มือประกอบสื่อการสอนวิทยาศาสตร์และคณิตศาสตร์ระดับมัธยมศึกษาตอนปลาย วิชาโลก ดาราศาสตร์ และอวกาศ เรื่อง ดาวเคราะห์วงนอก: Retrograde motion. สืบค้นเมื่อ 19 สิงหาคม 2562, จาก http://www.phukhieo.ac.th/obec-media/2555/manual/%A4%D9%E8%C1%D7%CD%E2%C5%A1%B4%D2%C3%D2%C8%D2%CA%B5%C3%EC%E1%C5%D0%CD%C7%A1%D2%C8/51_%B4%D2%C7%E0%A4%C3%D2%D0%CB%EC%C7%A7%B9%CD%A1%20Retrograde%20motion.pdf
บทความฟิสิกส์ล่าสุด
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

