ข้อสอบคัดเลือกของทีม USA 2015 (25 ข้อ)
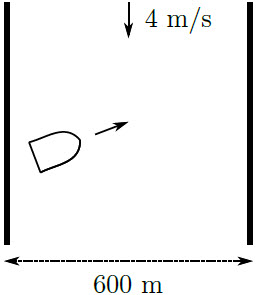
| 1. | แม่น้ำกว้าง 600 เมตร ไหลไปทางทิศใต้ด้วยอัตราเร็ว 4.0 m/s เรือยนต์เล็กมีอัตราเร็ว 5.0 m/s ในน้ำนิ่งขับข้ามฝั่งไปโดยหันหัวเรือไปในทิศทาง ดังรูป
 |
| A | 67 s |
| B | 120 s |
| C | 150 s |
| D | 200 s |
| E | 600 s |
ตอบ (D)
อัตราเร็วสัมพัทธ์ของเรือที่กำลังข้ามฝั่งจะเท่ากับ 3.0 m/s และมีเวกเตอร์ตามรูปที่โจทย์กำหนดให้
อัตราเร็วสัมพัทธ์ของเรือที่กำลังข้ามฝั่งจะเท่ากับ 3.0 m/s และมีเวกเตอร์ตามรูปที่โจทย์กำหนดให้
| 2. | ขับรถไปทางทิศเหนืออัตราเร็วคงที่ 80 km/hr เป็นระยะทาง 25 km จากนั้นขับต่อไปด้วยอัตราเร็วคงที่ 75 km/hr อีก 75 km อัตราเร็วเฉลี่ยในการเดินทางครั้งนี้เท่ากับข้อใด |
| A | 55.2 km/hr |
| B | 57.5 km/hr |
| C | 65 km/hr |
| D | 69.6 km/hr |
| E | 72.5 km/hr |
ตอบ (A)
อัตราเร็วเฉลี่ยหาจากระยะทางทั้งหมดหารด้วยเวลาทั้งหมด ในช่วงแรก ระยะทาง 25 km ใช้เวลา 0.31 ชั่วโมง ในช่วงหลัง ระยะทาง 75 km ใช้เวลา 1.5 ชั่วโมง
ดังนั้น อัตราเร็วเฉลี่ย \(=\dfrac{25+75}{1.5+0.31}\approx55.2~\rm km/hr\)
อัตราเร็วเฉลี่ยหาจากระยะทางทั้งหมดหารด้วยเวลาทั้งหมด ในช่วงแรก ระยะทาง 25 km ใช้เวลา 0.31 ชั่วโมง ในช่วงหลัง ระยะทาง 75 km ใช้เวลา 1.5 ชั่วโมง
ดังนั้น อัตราเร็วเฉลี่ย \(=\dfrac{25+75}{1.5+0.31}\approx55.2~\rm km/hr\)
| 3. | แรงต้านการเคลื่อนที่ของเครื่องบินที่ระดับความสูงหนึ่ง หาจาก Ff = kv2 , โดย k คือค่าคงที่ v คือ อัตราเร็วของเครื่องบิน ให้กำลังที่ออกมาจากเครื่องยนต์ คือ P0 เครื่องบินจะบินด้วยอัตราเร็ว v0 ถ้ากำลังที่ออกมาจากเครื่องยนต์เพิ่มขึ้น 100% เป็น 2P0 แล้วเครื่องบินจะบินได้ด้วยอัตราเร็วเท่าใด |
| A | 1.12 v0 |
| B | 1.26 v0 |
| C | 1.41 v0 |
| D | 2.82 v0 |
| E | 8 v0 |
ตอบ (B)
จาก P = Fv ดังนั้น P = kv3 จึงได้
จาก P = Fv ดังนั้น P = kv3 จึงได้
\(\rm v / v_0 = \sqrt[3]{P/P_0}\)
เมื่อแทนค่า จะได้ v = 1.26 v0| 4. | กล่องหนัก 2.0 kg อยู่นิ่งบนพื้นราบ มีค่าสัมประสิทธิ์แรงเสียดทานสถิตระหว่างกล่องและพื้น μ และค่าสัมประสิทธิ์แรงเสียดทานจลน์ระหว่างกล่องและพื้นผิว μk = 0.90 μs ถ้ามีแรงภายนอกมากระทำกับกล่องในแนวนอนขนาด P แล้วข้อใดเป็นกราฟความเร่งของกล่องเทียบกับแรงภายนอก P |
| A |  |
| B | 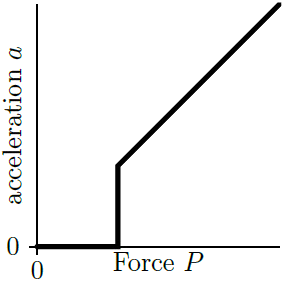 |
| C | 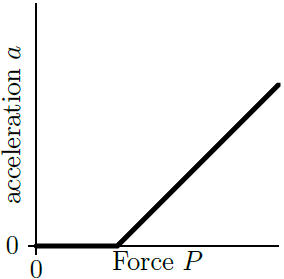 |
| D |  |
| E | 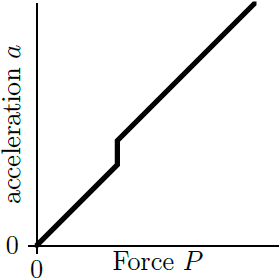 |
ตอบ (A)
กล่องจะไม่ขยับจนกว่า P > μsmg เมื่อกล่องเคลื่อนที่จะมีความเร่งเท่ากับ a = P/m – μkg สังเกตว่า กราฟจะไม่ต่อเนื่องที่ P = μsmg และกราฟจะมีความชันเท่ากับ 1/m
หรืออีกวิธีเราอาจพิจารณาว่า จะเกิดอะไรขึ้นถ้าไม่มีแรงมากระทำในแนวราบ
กล่องจะไม่ขยับจนกว่า P > μsmg เมื่อกล่องเคลื่อนที่จะมีความเร่งเท่ากับ a = P/m – μkg สังเกตว่า กราฟจะไม่ต่อเนื่องที่ P = μsmg และกราฟจะมีความชันเท่ากับ 1/m
หรืออีกวิธีเราอาจพิจารณาว่า จะเกิดอะไรขึ้นถ้าไม่มีแรงมากระทำในแนวราบ
| 5. | ยิงกระสุน 470 กรัม ทำมุมเงย 60 องศา ด้วยอัตราเร็วต้น 100 m/s ตรงไปยังเป้าหมายบนกำแพงที่อยู่ห่างออกไป 150 เมตร ดังรูป
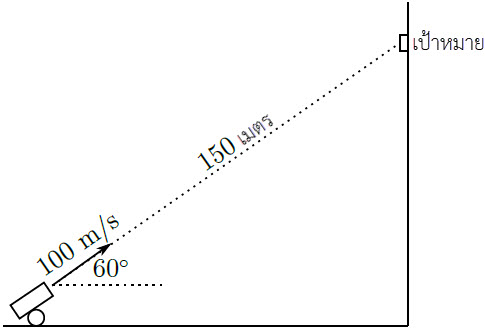 |
| A | 1.3 m |
| B | 2.2 m |
| C | 5.0 m |
| D | 7.1 m |
| E | 11 m |
ตอบ (E)
หากไม่สนแรงโน้มถ่วง เวลาที่กระสุนจะไปถึงเป้าหมายจะเท่ากับ
หากไม่สนแรงโน้มถ่วง เวลาที่กระสุนจะไปถึงเป้าหมายจะเท่ากับ
\(\rm 150~ (m) /100~ (m/s) = 1.5 ~s\)
ในช่วงเวลานั้น ระยะที่กระสุนจะเคลื่อนที่ลงในแนวตั้งจะเท่ากับ\(\rm d = \dfrac{1}{2}gt^2 = 11.25 ~m\)
| 6. | รถของเล่นสามคัน เคลื่อนที่หนึ่งมิติอย่างอิสระตามแนวนอนโดยไม่มีแรงเสียดทาน รถ A มีมวล 1.9 kg ไปทางขวาด้วยอัตราเร็วต้น 1.7 m/s รถ B มีมวล 1.1 kg ไปทางซ้ายด้วยอัตราเร็วต้น 2.5 m/s รถ C มีมวล 1.3 kg จอดอยู่นิ่งๆ ถ้าการชนระหว่างรถ A และ B ยืดหยุ่นสมบูรณ์ ส่วนการชนระหว่างรถ B และ C ไม่ยืดหยุ่นสมบูรณ์
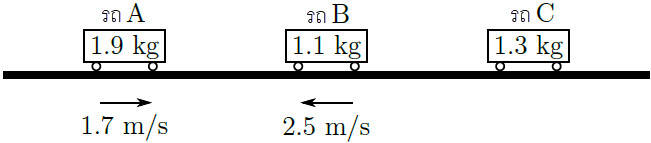 |
| A | 0.11 m/s |
| B | 0.16 m/s |
| C | 1.4 m/s |
| D | 2.0 m/s |
| E | 3.23 m/s |
ตอบ (A)
จากอัตราเร็วที่จุดศูนย์กลางมวลจะไม่เปลี่ยนไป ไม่ว่าจะเกิดการชนแบบใดก็ตาม จะได้ว่า
จากอัตราเร็วที่จุดศูนย์กลางมวลจะไม่เปลี่ยนไป ไม่ว่าจะเกิดการชนแบบใดก็ตาม จะได้ว่า
\({{\rm{v}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{{\rm{(1}}{\rm{.9 kg)(1}}{\rm{.7 m/s) + (1}}{\rm{.1 kg)( - 2}}{\rm{.5 m/s) + (1}}{\rm{.3 kg)(0 m/s)}}}}{{{\rm{(1}}{\rm{.9 kg) + (1}}{\rm{.1 kg) + (1}}{\rm{.3 kg)}}}}{\rm{ = 0}}{\rm{.11 m/s}}\)
| 7. |  รถ C จอดที่ระยะ 2.0 เมตร ณ จุดที่กำหนดตำแหน่งไว้ ส่วนรถ A อยู่ที่จุดเริ่มต้นที่ระยะศูนย์เมตร ได้เคลื่อนที่ไปทางรถ B ที่อัตราเร็ว v0 สมมุติว่าการชนกันทั้งหมดไม่ยืดหยุ่นสมบูรณ์ แล้วอัตราเร็วสุดท้ายของรถ C เท่ากับข้อใด |
| A | v0/13 |
| B | v0/10 |
| C | v0/9 |
| D | v0/3 |
| E | 2v0/5 |
ตอบ (A)
หลังเกิดการชนครั้งแรก รถทั้งสองคันจะเคลื่อนที่ด้วยอัตราเร็ว v0 / (1+3) หลังเกิดการชนครั้งที่สอง รถทั้งหมดจะเคลื่อนที่ด้วยอัตราเร็ว v0 / (1+3+9)
หลังเกิดการชนครั้งแรก รถทั้งสองคันจะเคลื่อนที่ด้วยอัตราเร็ว v0 / (1+3) หลังเกิดการชนครั้งที่สอง รถทั้งหมดจะเคลื่อนที่ด้วยอัตราเร็ว v0 / (1+3+9)
| 8. |  รถ C จอดที่ระยะ 2.0 เมตร ณ จุดที่กำหนดตำแหน่งไว้ ส่วนรถ A อยู่ที่จุดเริ่มต้นที่ระยะศูนย์เมตร ได้เคลื่อนที่ไปทางรถ B ที่อัตราเร็ว v0 สมมุติว่าการชนกันทั้งหมดยืดหยุ่นสมบูรณ์ แล้วอัตราเร็วสุดท้ายของรถ C เท่ากับข้อใด |
| A | v0/8 |
| B | v0/4 |
| C | v0/2 |
| D | v0 |
| E | 2v0 |
ตอบ (B)
โจทย์ข้อนี้หาคำตอบโดยใช้กฎการอนุรักษ์พลังงานจลน์และโมเมนตัม
สำหรับรถหนึ่งคันในกรณีที่เดิมอยู่นิ่ง และกรณีที่มีอัตราเร็วต้น จะใช้สมการ ดังนี้
เมื่อคำนวณซ้ำอีกครั้ง จะได้อัตราเร็วสุดท้ายของรถคันที่สามเท่ากับ v0/4
โจทย์ข้อนี้หาคำตอบโดยใช้กฎการอนุรักษ์พลังงานจลน์และโมเมนตัม
สำหรับรถหนึ่งคันในกรณีที่เดิมอยู่นิ่ง และกรณีที่มีอัตราเร็วต้น จะใช้สมการ ดังนี้
\({{\rm{v}}_{{\rm{1f}}}}{\rm{ = }}{{\rm{v}}_{\rm{0}}}\dfrac{{{{\rm{m}}_{\rm{1}}}{\rm{ - }}{{\rm{m}}_{\rm{2}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_2}}}\)
และ
\({{\rm{v}}_{{\rm{2f}}}}{\rm{ = }}{{\rm{v}}_{\rm{0}}}\dfrac{{{\rm{2}}{{\rm{m}}_{\rm{1}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_2}}}\)
โดยรถคันแรกจะชนกับรถคันที่สองจากทางด้านหลัง แล้วเคลื่อนที่ไปข้างหน้าด้วยอัตราเร็ว v0/2เมื่อคำนวณซ้ำอีกครั้ง จะได้อัตราเร็วสุดท้ายของรถคันที่สามเท่ากับ v0/4
| 9. | ลูกบอล 0.650 kg เคลื่อนที่ด้วยอัตราเร็ว 5.00 m/s ชนกันลูกบอล 0.750 kg ที่เดิมอยู่นิ่ง หลังการชนลูกบอล 0.750 kg เคลื่อนที่ด้วยอัตราเร็ว 4.00 m/s และลูกบอล 0.650 kg กระเด็นทำมุมฉากกับทิศที่ลูกบอล 0.750 kg เคลื่อนที่ออกไป ถ้าอัตราเร็วสุดท้ายของลูกบอล 0.650 kg เท่ากับข้อใด |
| A | 1.92 m/s |
| B | 2.32 m/s |
| C | 3.0 m/s |
| D | 4.64 m/s |
| E | 5.77 m/s |
ตอบ (A)
คำนวณจากกฎการอนุรักษ์ของโมเมนตัม ซึ่งข้อนี้การชนเป็นรูปสามเหลี่ยมมุมฉาก จะได้
และ \({{\rm{p}}_{{\rm{2f}}}}{\rm{ = (0}}{\rm{.75 kg)(4}}{\rm{.0 m/s) = 3}}{\rm{.0 kg}} \cdot {\rm{m/s}}\)
จึงได้
คำนวณจากกฎการอนุรักษ์ของโมเมนตัม ซึ่งข้อนี้การชนเป็นรูปสามเหลี่ยมมุมฉาก จะได้
\({\rm{p}}_{{\rm{2f}}}^{\rm{2}}{\rm{ + p}}_{{\rm{1f}}}^{\rm{2}}{\rm{ = p}}_{{\rm{1i}}}^{\rm{2}}\)
โดยที่ \({{\rm{p}}_{{\rm{1i}}}}{\rm{ = (0}}{\rm{.65 kg)(5}}{\rm{.0 m/s) = 3}}{\rm{.25 kg}} \cdot {\rm{m/s}}\)และ \({{\rm{p}}_{{\rm{2f}}}}{\rm{ = (0}}{\rm{.75 kg)(4}}{\rm{.0 m/s) = 3}}{\rm{.0 kg}} \cdot {\rm{m/s}}\)
จึงได้
\({{\rm{p}}_{{\rm{1f}}}}{\rm{ = 1}}{\rm{.25 kg}} \cdot {\rm{m/s}}\)
ดังนั้น
\({{\rm{v}}_{{\rm{1f}}}}{\rm{ = 1}}{\rm{.25/0}}{\rm{.65 = 25/13 = 1}}{\rm{.92 ~m/s}}\)
| 10. | ลูกบอล 0.650 kg เคลื่อนที่ด้วยอัตราเร็ว 5.00 m/s ชนกันลูกบอล 0.750 kg ที่เดิมอยู่นิ่ง หลังการชนลูกบอล 0.750 kg เคลื่อนที่ด้วยอัตราเร็ว 4.00 m/s และลูกบอล 0.650 kg กระเด็นทำมุมฉากกับทิศที่ลูกบอล 0.750 kg เคลื่อนที่ออกไป ให้การเปลี่ยนแปลงพลังงานจลน์สุทธิจากการชนครั้งนี้ หาจาก ΔK = Kf - Ki โดย Kf คือ พลังงานจลน์สุดท้ายสุทธิ และ Ki คือ พลังงานจลน์เริ่มต้นสุทธิ แล้วข้อใดต่อไปนี้ถูกต้อง |
| A | \(\rm ΔK = (K_f + K_i)/2\) |
| B | \(\rm K_f < ΔK < K_i\) |
| C | \(\rm 0 < ΔK < K_f\) |
| D | \(\rm ΔK = 0\) |
| E | \(\rm – K_i < ΔK < 0\) |
ตอบ (E)
พิจารณาจากสมการ
พิจารณาจากสมการ
\({\rm{p}}_{{\rm{2f}}}^{\rm{2}}{\rm{ + p}}_{{\rm{1f}}}^{\rm{2}}{\rm{ = p}}_{{\rm{1i}}}^{\rm{2}}\)
จะได้
\(\begin{align*}
\Delta {\rm{K}} &= \frac{1}{2}\left( {\frac{{{\rm{p}}_{{\rm{2f}}}^{\rm{2}}}}{{{{\rm{m}}_2}}} + \frac{{{\rm{p}}_{{\rm{1f}}}^{\rm{2}}}}{{{{\rm{m}}_1}}} - \frac{{{\rm{p}}_{{\rm{1i}}}^{\rm{2}}}}{{{{\rm{m}}_1}}}} \right)\\
&= \frac{1}{2}{\rm{ }}\left( {\frac{{{\rm{p}}_{{\rm{2f}}}^{\rm{2}}}}{{{{\rm{m}}_2}}} - \frac{{{\rm{p}}_{{\rm{2f}}}^{\rm{2}}}}{{{{\rm{m}}_1}}}} \right)
\end{align*}\)
ดังนั้น
\(\Delta \rm K =\dfrac{1}{2}\dfrac{{{\rm{p}}_{{\rm{2f}}}^{\rm{2}}}}{{{{\rm{m}}_1}}}\left( {\dfrac{{{{\rm{m}}_1}}}{{{{\rm{m}}_2}}} - 1} \right)\)
ชัดเจนว่า ค่าที่ได้จะเป็นลบ และมีขนาดเล็กว่า K_i| 11. | ทรงกลมลอยอยู่ในน้ำ โดย 2/3 ของปริมาตรทรงกลมจมอยู่ในน้ำ ถ้าหยิบทรงกลมไปวางในน้ำมันที่มีความหนาแน่น 3/4 ของน้ำ แล้วสัดส่วนของทรงกลมที่จมอยู่ในน้ำมันเท่ากับข้อใด |
| A | 1/12 |
| B | 1/2 |
| C | 8/9 |
| D | 17/12 |
| E | ทรงกลมจะไม่ลอย แต่จะจมในน้ำมัน |
ตอบ (C)
เนื่องจากสัดส่วนที่จมอยู่ในน้ำ เท่ากับ อัตราส่วนของความหนาแน่นของทรงกลม จากโจทย์จะได้
เนื่องจากสัดส่วนที่จมอยู่ในน้ำ เท่ากับ อัตราส่วนของความหนาแน่นของทรงกลม จากโจทย์จะได้
\(\rm {\rho _{{\rm{sphere}}}} = 2/3{\rho _{{\rm{water}}}}\)
เมื่อเปลี่ยนไปวางในน้ำมันส่วนที่จมจะเท่ากับ
\(\displaystyle\rm \frac{{{\rho _{{\rm{sphere}}}}}}{{{\rho _{oil}}}} = \frac{{2/3}}{{3/4}} = \frac{8}{9}\)
| 12. | ให้ลูกตุ้มประกอบไปด้วย ตุ้มขนาดเล็กมวล m ผูกติดกับเชือกยาว L ให้ลูกตุ้มที่เดิมอยู่นิ่งแกว่งลงมาจากจุดที่ทำมุม θmax < 90 องศา แล้วข้อใดกล่าวถูกต้องเกี่ยวกับความเร่งของลูกตุ้ม |
| A | ขนาดของความเร่งจะคงที่ สำหรับการแกว่งนี้ |
| B | ขนาดของความเร่งที่จุดต่ำสุดมีค่าเท่ากับ g ความเร่งเป็นไปตามการตกอย่างอิสระ |
| C | ขนาดของความเร่งเป็นศูนย์ ณ บางจุดของการแกว่งนี้ |
| D | ความเร่งจะชี้ไปที่จุดศูนย์กลางของวงกลมเสมอ |
| E | ความเร่งที่จุดต่ำสุดของการแกว่งจะชี้ขึ้นในแนวตั้ง |
ตอบ (E)
ให้พิจารณาแต่ละสถานการณ์
ให้พิจารณาแต่ละสถานการณ์
| 13. | ให้ลูกตุ้มประกอบไปด้วย ตุ้มขนาดเล็กมวล m ผูกติดกับเชือกยาว L ให้ลูกตุ้มที่เดิมอยู่นิ่งแกว่งลงมาจากจุดที่ทำมุม θmax < 90 องศา พิจารณา ขณะลูกตุ้มทำมุม \(\rm θ = \dfrac{1}{2} θ_{max}\) ขณะแกว่งขึ้น ( ขึ้นไปทาง θmax ) ภาพใดแสดงเวกเตอร์ทิศของความเร่งของลูกตุ้มได้ถูกต้อง |
| A | 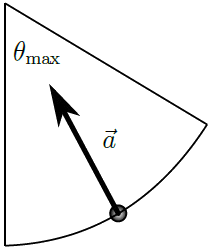 |
| B |  |
| C | 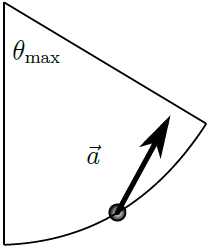 |
| D | 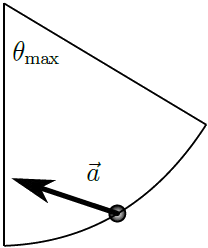 |
| E | 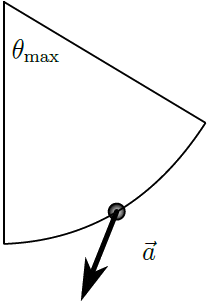 |
ตอบ (D)
การเคลื่อนที่ของลูกตุ้มจะมีความเร่งชี้ไปที่จุดศูนย์กลางการแกว่ง และมีความเร่งในแนวสัมผัสส่วนโค้งที่ชี้ไปที่ด้านล่างของเส้นทางที่ลูกตุ้มผ่าน
การเคลื่อนที่ของลูกตุ้มจะมีความเร่งชี้ไปที่จุดศูนย์กลางการแกว่ง และมีความเร่งในแนวสัมผัสส่วนโค้งที่ชี้ไปที่ด้านล่างของเส้นทางที่ลูกตุ้มผ่าน
| 14. | ให้คานเบายาว 3.0 เมตร สามารถหมุนตามแนวนอนได้อย่างอิสระรอบจุดศูนย์กลาง ที่ปลายคานมีวัตถุสองชิ้นมวล 5.0 กิโลกรัม วางอยู่ วัตถุสามารถเลื่อนได้อย่างอิสระบนคาน โดยไม่มีแรงเสียดทาน และมีเชือกเบาผูกวัตถุทั้งสองชิ้นไว้ไม่ให้หล่นออกจากคาน ให้เดิมระบบหมุน 4.0 เรเดียนต่อวินาที ถือว่าระบบไม่มีแรงเสียดทาน และไม่สนใจความไม่เสถียรของระบบ แล้วแรงตึงเชือกเดิมเท่ากับข้อใด |
| A | 60 N |
| B | 106 N |
| C | 120 N |
| D | 240 N |
| E | 480 N |
ตอบ (C)
ข้อนี้หาคำตอบตรงๆ จาก
\({\rm{F = mr}}{\omega ^{\rm{2}}}{\rm{ = (5}}{\rm{.0 kg)(1}}{\rm{.5 m)(4}}{\rm{.0 rad/s}}{{\rm{)}}^{\rm{2}}}{\rm{ = 120 N}}\)
| 15. | ให้คานเบายาว 3.0 เมตร สามารถหมุนตามแนวนอนได้อย่างอิสระรอบจุดศูนย์กลาง ที่ปลายคานมีวัตถุสองชิ้นมวล 5.0 กิโลกรัม วางอยู่ วัตถุสามารถเลื่อนได้อย่างอิสระบนคาน โดยไม่มีแรงเสียดทาน และมีเชือกเบาผูกวัตถุทั้งสองชิ้นไว้ไม่ให้หล่นออกจากคาน ให้เดิมระบบหมุน 4.0 เรเดียนต่อวินาที ถือว่าระบบไม่มีแรงเสียดทาน และไม่สนใจความไม่เสถียรของระบบ ถ้าเชือกค่อยๆ ตึงขึ้น ด้วยมอเตอร์เบาอันเล็กๆ ติดที่อยู่บนวัตถุชิ้นหนึ่ง โดยมอเตอร์จะช่วยดึงทั้งสองวัตถุให้เข้ามาใกล้จุดศูนย์กลางของแกนหมุน แล้วงานที่มอเตอร์ใช้ดึงทั้งสองวัตถุจากปลายคานมาอยู่ที่ระยะ 0.5 เมตร จากจุดศูนย์กลางของแกนหมุนเท่ากับข้อใด |
| A | 120 J |
| B | 180 J |
| C | 240 J |
| D | 1440 J |
| E | 1620 J |
ตอบ (D)
งานที่เปลี่ยนเป็นพลังงานหาจาก
แทน Ii = 22.5 kg·m2 , If = 2.5 kg·m2 และ L = 90 kg·m2 / s
งานที่เปลี่ยนเป็นพลังงานหาจาก
\(\rm W = \dfrac{1}{{2{I_f}}}{L^2} - \dfrac{1}{{2{I_i}}}{L^2}\)
โดย L มาจากกฎการอนุรักษ์โมเมนตัมเชิงมุม ซึ่ง L = Iiωi และ I คือ ความเฉื่อยในการหมุนหรือ mr2 แทน Ii = 22.5 kg·m2 , If = 2.5 kg·m2 และ L = 90 kg·m2 / s
จะได้
\(\rm W = 1440~ J\)
| 16. | พิจารณากราฟพลังงานศักย์กับตำแหน่งของวัตถุ 0.50 kg
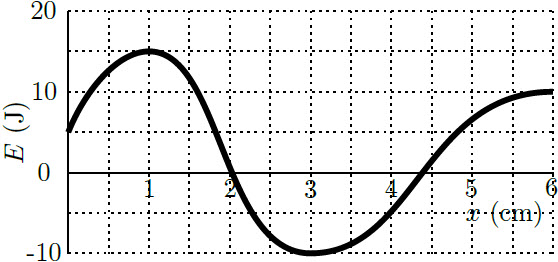 |
| A | วัตถุสมดุลที่ x = 1 cm หรือ x = 3 cm |
| B | พลังงานต่ำสุดสุทธิที่เป็นไปได้สำหรับวัตถุนี้เท่ากับ -10 J |
| C | แรงที่กระทำบนวัตถุที่ x = 4 cm มีค่าประมาณ 1000 N |
| D | ถ้าพลังงานสุทธิของวัตถุเท่ากับ 0 J แล้ววัตถุจะมีพลังงานจลน์ 10 J |
| E | ความเร่งของวัตถุที่ x = 2 cm มีค่าประมาณ 4 cm/s2 |
ตอบ (E)
ให้พิจารณาแต่ละสถานการณ์
ให้พิจารณาแต่ละสถานการณ์
| 17. | เราสามารถใช้ล้อหมุนเพื่อเก็บพลังงานจลน์ได้ ถ้าล้อมีลักษณะเป็นแผ่นกลม มีความหนาแน่น ρ ความทนต่อแรงดึง σ (ใช้หน่วยปาสคาล) รัศมี r และความหนา h และล้อสามารถหมุนที่ความเร็วเชิงมุมสูงสุดได้โดยไม่แตกหัก แล้วข้อใดคือพลังงานจลน์สูงสุดต่อกิโลกรัมที่ล้อสามารถเก็บพลังงานไว้ได้ สมมุติว่า α เป็นค่าคงที่ (ระดับเตรียมสอบ สอวน. ให้ใช้การวิเคราะห์มิติ) |
| A | \(\rm \alpha \sqrt {\rho \sigma /r}\) |
| B | \(\rm \alpha h\sqrt {\rho \sigma /r}\) |
| C | \(\rm \alpha \sqrt {(h/r)} {(\sigma /\rho )^2}\) |
| D | \(\rm \alpha (h/r)(\sigma /\rho )\) |
| E | \(\rm \alpha \sigma /r\) |
ตอบ (E)
ข้อนี้จะใช้การวิเคราะห์มิติ โดยการหาเลขชี้กำลัง a, b, c, d ใน
จะได้
เมื่อแก้สมการจะได้ b = 1, a = -1 และ c = -d แม้ว่าเราจะหาค่า d จากการวิเคราะห์มิติไม่ได้ แต่เราสามารถใช้เหตุผลอธิบายได้ว่า ถ้าแผ่นกลมหนาขึ้นเป็นสองเท่า แล้วความเร็วในการหมุนสูงสุดที่เป็นไปได้ก่อนที่ล้อจะแตกจะไม่เปลี่ยนแปลง แสดงว่า พลังงานและมวลจะต้องเกิดขึ้นสองครั้ง
ดังนั้น d = 0
ข้อนี้จะใช้การวิเคราะห์มิติ โดยการหาเลขชี้กำลัง a, b, c, d ใน
\(\rm ρ^a~ σ^b~ r^c~ h^d\)
ซึ่งมีมิติของพลังงานคิดเป็นต่อมวล จะได้
\(\rm (M / L^3) ^a (M / LT ^2)^b (L)^c (L)^d = (L^2 / T^2)\)
เมื่อแก้สมการจะได้ b = 1, a = -1 และ c = -d แม้ว่าเราจะหาค่า d จากการวิเคราะห์มิติไม่ได้ แต่เราสามารถใช้เหตุผลอธิบายได้ว่า ถ้าแผ่นกลมหนาขึ้นเป็นสองเท่า แล้วความเร็วในการหมุนสูงสุดที่เป็นไปได้ก่อนที่ล้อจะแตกจะไม่เปลี่ยนแปลง แสดงว่า พลังงานและมวลจะต้องเกิดขึ้นสองครั้ง
ดังนั้น d = 0
| 18. | พิจารณาสามกราฟ ที่มาจากข้อมูลเดียวกัน
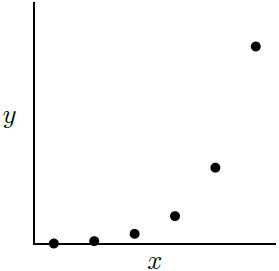 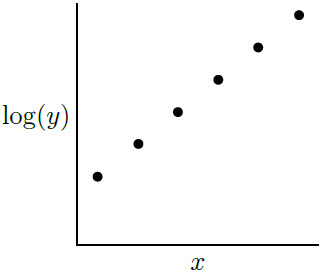 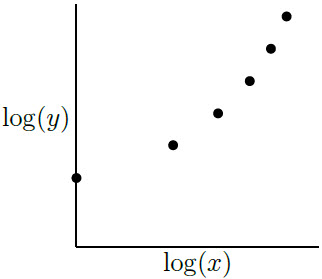 |
| A | y = ax + b |
| B | y = ax2 + b |
| C | y = axb |
| D | y = aebx |
| E | y = a log x + b |
ตอบ (D)
จากกราฟ log เชิงเส้นเป็นเส้นตรง แสดงว่าข้อมูลจะเป็นไปตามสมการ
จากกราฟ log เชิงเส้นเป็นเส้นตรง แสดงว่าข้อมูลจะเป็นไปตามสมการ
\(\rm log\, y = Ax +B\)
หรือ
\(\rm y = ae^{bx}\)
| 19. | มาโนมิเตอร์รูปตัวยู (U-tube manometer) คือ ท่อทรงกระบอกที่โค้งงอเป็นรูปตัว U มีเส้นผ่านศูนย์กลางสม่ำเสมอตลอดเส้น ภายในท่อจะมีน้ำที่มีความหนาแน่น ρw ระดับความสูงของน้ำในท่อทั้งสองฝั่งจะเท่ากับ L ในที่นี้เราจะไม่สนใจความตึงผิวและความหนืดของของเหลว ถ้าน้ำในท่อฝั่งหนึ่งขยับตัวสูงขึ้นมา x แล้วน้ำในท่ออีกฝั่งจะลดลงมา x ด้วยเช่นกัน แล้วความถี่การขึ้นลงของน้ำในท่อเท่ากับข้อใด |
| A | \(\rm \dfrac{1}{{2\pi }}\sqrt {2g/L}\) |
| B | \(\rm 2\pi \sqrt {g/L}\) |
| C | \(\rm \dfrac{1}{{2\pi }}\sqrt {2L/g}\) |
| D | \(\rm \dfrac{1}{{2\pi }}\sqrt {g/{\rho _w}}\) |
| E | \(\rm 2\pi \sqrt {{\rho _w}gL}\) |
ตอบ (A)
ความถี่ในการสั่นหาจาก
ถ้าระยะทางที่ของเหลวเคลื่อนที่ไปได้เท่ากับ x แล้วแรงดึงกลับสุทธิบนของไหลจะเท่ากับ 2xgAρ
จะได้ k = 2gAρ
ดังนั้น
ความถี่ในการสั่นหาจาก
\(\rm f = \dfrac{1}{{2\pi }}\sqrt {k/m} \)
โดย m คือ มวล ซึ่งเท่ากับ LAρ โดย L เป็นความยาวทั้งหมดของของเหลว และมี k เป็นค่านิจสปริงถ้าระยะทางที่ของเหลวเคลื่อนที่ไปได้เท่ากับ x แล้วแรงดึงกลับสุทธิบนของไหลจะเท่ากับ 2xgAρ
จะได้ k = 2gAρ
ดังนั้น
\(f = \dfrac{1}{{2\pi }}\sqrt {2g/L}\)
| 20. | มาโนมิเตอร์รูปตัวยู (U-tube manometer) คือ ท่อทรงกระบอกที่โค้งงอเป็นรูปตัว U มีเส้นผ่านศูนย์กลางสม่ำเสมอตลอดเส้น ภายในท่อจะมีน้ำที่มีความหนาแน่น ρw ระดับความสูงของน้ำในท่อทั้งสองฝั่งจะเท่ากับ L ในที่นี้เราจะไม่สนใจความตึงผิวและความหนืดของของเหลว ถ้าเติมน้ำมันที่มีความหนาแน่นครึ่งหนึ่งของน้ำลงไปในด้านหนึ่งของท่อ จนกระทั่งความยาวของลำน้ำมันเท่ากับความยาวของลำน้ำ จงหาผลต่างความสูงของน้ำและน้ำมันที่จุดสมดุล |
| A | L |
| B | L/2 |
| C | L/3 |
| D | 3L/4 |
| E | L/4 |
ตอบ (B)
ข้อนี้จะต้องหาแรงที่ทำให้เกิดสมดุล สมมุติให้ x คือ ความสูงของน้ำในหลอดฝั่งที่มีเฉพาะแต่น้ำ
จะได้
ข้อนี้จะต้องหาแรงที่ทำให้เกิดสมดุล สมมุติให้ x คือ ความสูงของน้ำในหลอดฝั่งที่มีเฉพาะแต่น้ำ
จะได้
\(\rm xρ_w = (L – x) ρ_w + Lρ_o\)
หรือ
\(\begin{array}{l}
{\rm{x = L - x + L/2}}\\
{\rm{x = 3L/4}}
\end{array}\)
ดังนั้น ผลต่างความสูงของน้ำและน้ำมันที่จุดสมดุลจะเท่ากับ
\(\rm (2 L – x) – x = 2(L – x) = L / 2\)
| 21. | ยิงวัตถุขึ้นฟ้าด้วยอัตราเร็ว 50 m/s แล้วตกกลับลงมาพื้นดินด้วยสัมประสิทธิ์การกระแทก CR = 0.9 หมายความว่า วัตถุจะมีการกระเด้งกลับด้วยอัตราเร็ว 90% ของอัตราเร็วที่ตกลงมา จงหาเวลารวมที่ใช้ ตั้งแต่เริ่มยิ่งวัตถุจนกระทั้งตกกลับลงมาถึงพื้นแล้วหยุดนิ่ง สมมุติว่าเวลาในการกระแทกเป็นศูนย์ (การกระเด้งกลับเกิดขึ้นอย่างรวดเร็ว) เหตุการณ์นี้เป็นแบบอุดมคติ และไม่สนใจผลควอนตัมใด ๆ ที่อาจเกิดขึ้นกับการกระแทก |
| A | 71 s |
| B | 100 s |
| C | 141 s |
| D | 1000 s |
| E | ∞ (วัตถุจะไม่มีวันหยุดนิ่ง) |
ตอบ (B)
ในการกระแทกพื้นจะมี CR = vf / vi และเวลาที่ลูกลอยกลางอากาศระหว่างกระแทกพื้นสองครั้งเท่ากับ t = 2v / g
โดย v คือ อัตราเร็วต้นขณะวัตถุพุ่งขึ้นจากการกระแทก เราจะได้ลำดับอนันต์ คือ
ในการกระแทกพื้นจะมี CR = vf / vi และเวลาที่ลูกลอยกลางอากาศระหว่างกระแทกพื้นสองครั้งเท่ากับ t = 2v / g
โดย v คือ อัตราเร็วต้นขณะวัตถุพุ่งขึ้นจากการกระแทก เราจะได้ลำดับอนันต์ คือ
\({{\rm{t}}_{\rm{n}}}{\rm{ = }}\dfrac{{\rm{2}}}{{\rm{g}}}{{\rm{v}}_{\rm{n}}}{\rm{ = }}\dfrac{{\rm{2}}}{{\rm{g}}}{{\rm{v}}_{\rm{0}}}{\rm{C}}_{\rm{R}}^{\rm{n}}\)
เมื่อหาผลรวม เราจะได้อนุกรมที่เป็นเวลารวมทั้งหมด คือ
\({\rm{T = }}\sum {\dfrac{{\rm{2}}}{{\rm{g}}}} {{\rm{v}}_{\rm{0}}}{\rm{C}}_{\rm{R}}^{\rm{n}}{\rm{ = }}\dfrac{{\rm{2}}}{{\rm{g}}}{{\rm{v}}_{\rm{0}}}\sum {{\rm{C}}_{\rm{R}}^{\rm{n}}} = \dfrac{{\rm{2}}}{{\rm{g}}}{{\rm{v}}_{\rm{0}}}\dfrac{1}{{1 - {{\rm{C}}_{\rm{R}}}}}\)
ดังนั้น
\({\rm{T = }}\dfrac{{\rm{2}}}{{{\rm{10 m/}}{{\rm{s}}^{\rm{2}}}}}{\rm{(50 m/s)}}\dfrac{1}{{1 - 0.9}} = {\rm{100 s}}\)
| 22. | ปล่อยลูกบอลตันกลิ้งจากจุดนิ่งไปตามพื้นเอียงที่มีมุม θ ต่างๆ แต่ความสูง h มีค่าเท่ากัน ค่าสัมประสิทธิ์ของแรงเสียดทานสถิต และแรงเสียดทานจลน์ทั้งสองมีค่าเท่ากับ μ กราฟใดแสดงพลังงานจลน์สุทธิของลูกบอลที่ด้านล่างของพื้นเอียง ที่เปลี่ยนไปตามมุม θ ต่างๆ ได้ถูกต้อง |
| A | 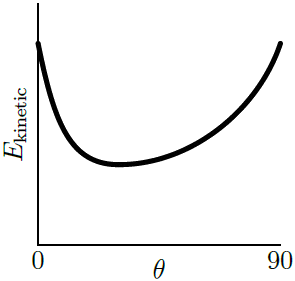 |
| B | 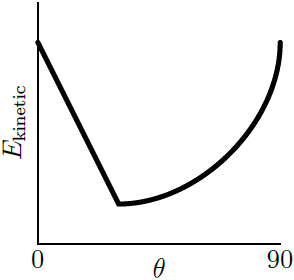 |
| C | 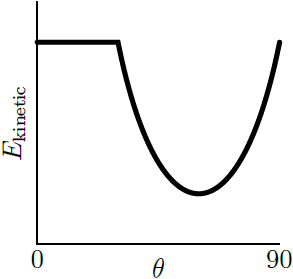 |
| D | 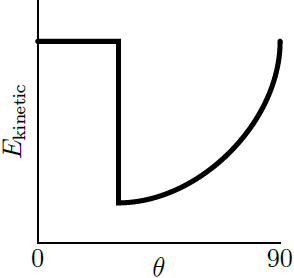 |
| E |  |
ตอบ (C)
เนื่องจากลูกบอลจะกลิ้งโดยไม่ไถล ถ้า θ มีค่าน้อยกว่ามุมวิกฤติ ดังนั้น สำหรับ θ ที่น้อยกว่ามุมวิกฤติ จึงไม่มีพลังงานที่สูญเสียไปกับแรงเสียดทาน แต่สำหรับ θ ที่มากกว่ามุมวิกฤติ ลูกบอลจะเกิดการไถลและมีพลังงานที่สูญเสียไปกับแรงเสียดทาน และถ้า θ = 90 องศา ลูกจะตกลงมาตรงๆ โดยไม่มีแรงเสียดทาน จึงไม่มีพลังงานที่สูญเสียไป
ดังนั้น กราฟจะต้องมีมุมหนึ่งที่มีการสูญเสียพลังงานไปกับแรงเสียดทานมากที่สุด
เนื่องจากลูกบอลจะกลิ้งโดยไม่ไถล ถ้า θ มีค่าน้อยกว่ามุมวิกฤติ ดังนั้น สำหรับ θ ที่น้อยกว่ามุมวิกฤติ จึงไม่มีพลังงานที่สูญเสียไปกับแรงเสียดทาน แต่สำหรับ θ ที่มากกว่ามุมวิกฤติ ลูกบอลจะเกิดการไถลและมีพลังงานที่สูญเสียไปกับแรงเสียดทาน และถ้า θ = 90 องศา ลูกจะตกลงมาตรงๆ โดยไม่มีแรงเสียดทาน จึงไม่มีพลังงานที่สูญเสียไป
ดังนั้น กราฟจะต้องมีมุมหนึ่งที่มีการสูญเสียพลังงานไปกับแรงเสียดทานมากที่สุด
| 23. | วัตถุ 2.0 kg เดิมหยุดนิ่งตกลงมาจากความสูง 5.0 เมตร ไปโดนวัตถุ 6.0 kg ที่ตั้งอยู่บนสปริงเบาที่มีค่านิจสปริง k = 72 N / m จากการกระแทก ทำให้วัตถุทั้งสองติดไปด้วยกันและทำให้สปริงเกิดการสั่น จงหาว่าวัตถุ 6.0 kg จะเคลื่อนที่ไปได้ไกลเท่าไรจากจุดเริ่มต้น |
| A | 0.27 m |
| B | 1.1 m |
| C | 2.5 m |
| D | 2.8 m |
| E | 3.1 m |
ตอบ (B)
ใช้กฎการอนุรักษ์พลังงานหาอัตราเร็วของวัตถุ 2.0 kg ขณะก่อนเกิดการชน จะได้
พิจารณา
ดังนั้น วัตถุจะเคลื่อนไปได้ไกล 1.1 m ( จริงๆ ควรปัดเป็น 1.2 m )
ใช้กฎการอนุรักษ์พลังงานหาอัตราเร็วของวัตถุ 2.0 kg ขณะก่อนเกิดการชน จะได้
\(\rm {{\rm{m}}_1}{\rm{gy}} = (2.0kg)(10m/s)(5.0m) = 100J\)
ซึ่งมีค่าเท่ากับพลังงานจลน์ จะได้
\({\rm{v = }}\sqrt {{\rm{2}}{{\rm{K}}_{\rm{1}}}{\rm{/}}{{\rm{m}}_{\rm{1}}}} {\rm{ = 10}}{\rm{.0 m/s}}\)
เนื่องจากการชนนั้นไม่ยืดหยุ่น จึงได้
\({{\rm{v}}_{\rm{f}}}{\rm{ = }}{{\rm{v}}_{\rm{1}}}{\rm{ }}\dfrac{{{{\rm{m}}_{\rm{1}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}}}{\rm{ = 2}}{\rm{.5 m/s}}\)
ใช้กฎการอนุรักษ์พลังงานอีกครั้ง
\({{\rm{K}}_{\rm{f}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{m}}_{\rm{t}}}{{\rm{v}}^{\rm{2}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{(8}}{\rm{.0kg)(2}}{\rm{.5m/s}}{{\rm{)}}^{\rm{2}}}{\rm{ = 25~J}}\)
ขณะสปริงถูกบีบจะมีการเปลี่ยนแปลงพลังงานศักย์โน้มถ่วง เราจึงต้องแก้สมการเพื่อหาค่า x พิจารณา
\(\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{{\rm{x}}^2}{\rm{ + }}{{\rm{m}}_{\rm{t}}}{\rm{gx = }}{{\rm{K}}_{\rm{f}}}\)
หรือ
\({\rm{36}}{{\rm{x}}^2}{\rm{ + 20x}}-25{\rm{ = 0}}\)
จะได้ค่า x = – 1.15 และ x = 0.6 mดังนั้น วัตถุจะเคลื่อนไปได้ไกล 1.1 m ( จริงๆ ควรปัดเป็น 1.2 m )
| 24. | อัตราเร็วของคลื่นตามขวางในเส้นลวดเหล็ก หาจาก
\(\rm v = \sqrt {\dfrac{T}{{M/L}}}\)
โดย T คือ แรงตึงในเส้นลวด M คือ มวล และ L คือ ความยาวลวด สมมุติว่าไม่มีการยืดจากแรงตึง ถ้าลวดเหล็กสองอันที่ยาวเท่ากัน แต่เส้นแรกมีรัศมี r1 เส้นที่สองรัศมี r2 = 4r1 แต่ละสายถูกดึงให้ตึงที่สุดเท่าที่จะตึงได้โดยไม่ขาดออก แล้วอัตราส่วนความถี่มูลฐานของการสั่น ของลวดทั้งสองเส้น f1/f2 เท่ากับข้อใด |
| A | \(1\) |
| B | \(\sqrt2\) |
| C | \(2\) |
| D | \(2\sqrt2\) |
| E | \(4\) |
ตอบ (A)
ลวดจะขาดเมื่อ T > σA โดยที่ σ คือความต้านทานแรงดึง และ A เป็นพื้นที่หน้าตัด จะได้
เนื่องจากสมการนี้ไม่ขึ้นอยู่กับความยาวของสตริง ดังนั้น อัตราเร็วของคลื่นในลวดทั้งสองเส้นจะเท่ากัน และจาก v = fλ และลวดมีความยาวเท่ากัน
ดังนั้น ความถี่มูลฐานของการสั่นของทั้งสองจะเท่ากัน
ลวดจะขาดเมื่อ T > σA โดยที่ σ คือความต้านทานแรงดึง และ A เป็นพื้นที่หน้าตัด จะได้
\({\rm{v = }}\sqrt {\dfrac{{\rm{T}}}{{{\rm{M/L}}}}} = \sqrt {\dfrac{{\sigma {\rm{AL}}}}{{\rm{M}}}} = \sqrt {\dfrac{\sigma }{\rho }}\)
โดย ρ คือ ความหนาแน่น เนื่องจากสมการนี้ไม่ขึ้นอยู่กับความยาวของสตริง ดังนั้น อัตราเร็วของคลื่นในลวดทั้งสองเส้นจะเท่ากัน และจาก v = fλ และลวดมีความยาวเท่ากัน
ดังนั้น ความถี่มูลฐานของการสั่นของทั้งสองจะเท่ากัน
| 25. | รถกระป๋อง A และ B เหมือนกันทุกประการ แต่ละคันมีมวล m ทั้งสองคันเชื่อมกันด้วยสปริงที่มีค่านิจสปริง k และมีสปริงอีกสองเส้นเชื่อมรถทั้งสองกับกำแพง ดังรูป รถสามารถขยับตามการสั่นของสปริงได้อย่างอิสระ และมีทิศทางเดียวโดยไม่มีความฝืด
 \(\rm {x_{\rm{A}}}(t) = {x_0}sin{\omega _1}t = {x_{\rm{B}}}(t)\)
โดย \(\rm x_{_A}\) และ \(\rm x_{_B}\) คือ ระยะของรถเทียบกับตำแหน่งสมดุลของรถแต่ละคัน ภายใต้เงื่อนไขเริ่มต้นอีกแบบ รถสองคันจะมีเฟสการแกว่ง คือ \(\rm {x_{\rm{A}}}(t) = {x_0}sin{\omega _2}t = - {x_{\rm{B}}}(t)\)
อัตราส่วน \(\rm {\omega _2}/{\omega _1}\) จะมีค่าเท่ากับข้อใด |
| A | \(\sqrt3\) |
| B | \(2\) |
| C | \(2\sqrt2\) |
| D | \(3\) |
| E | \(5\) |
ตอบ (A)
( ข้อนี้เราอาจใช้เมทริกซ์ช่วยในการหาคำตอบ แต่ก็ต้องระมัดระวังการแยกพิจารณาด้วย )
กรณีที่พิจารณาแต่ละช่วง เราจะต้องแยกพิจารณาสองมวลที่เป็นค่าคงที่ ดังนั้น แรงของ A ที่กระทำบน B จะเป็นค่าคงที่ ในกรณีนี้มีสปริงเดียวเท่านั้นที่ให้แรงต่างออกไป ดังนั้น ความถี่เชิงมุมจะเท่ากับ
อีกกรณีหนึ่ง เราจะใช้จุดกึ่งกลางของสปริงอันกลางเป็นจุดอ้างอิง
ดังนั้น วัตถุเหมือนเคลื่อนที่อยู่ภายใต้สปริงสองอันที่ขนานกัน โดยเส้นหนึ่งยาว L อีกเส้นยาว L / 2 เนื่องจากสปริงมีค่านิจสปริง k เท่ากันและขนานกัน จะได้ค่านิจสปริงเท่ากับ 2k ดังนั้น ค่านิจสปริงสุทธิจะเท่ากับ k + 2k = 3k จึงมีความถี่ตามสมการ
( ข้อนี้เราอาจใช้เมทริกซ์ช่วยในการหาคำตอบ แต่ก็ต้องระมัดระวังการแยกพิจารณาด้วย )
กรณีที่พิจารณาแต่ละช่วง เราจะต้องแยกพิจารณาสองมวลที่เป็นค่าคงที่ ดังนั้น แรงของ A ที่กระทำบน B จะเป็นค่าคงที่ ในกรณีนี้มีสปริงเดียวเท่านั้นที่ให้แรงต่างออกไป ดังนั้น ความถี่เชิงมุมจะเท่ากับ
\(\rm {\omega _1} = \sqrt {k{\rm{ }}/{\rm{ }}m}\)
อีกกรณีหนึ่ง เราจะใช้จุดกึ่งกลางของสปริงอันกลางเป็นจุดอ้างอิง
ดังนั้น วัตถุเหมือนเคลื่อนที่อยู่ภายใต้สปริงสองอันที่ขนานกัน โดยเส้นหนึ่งยาว L อีกเส้นยาว L / 2 เนื่องจากสปริงมีค่านิจสปริง k เท่ากันและขนานกัน จะได้ค่านิจสปริงเท่ากับ 2k ดังนั้น ค่านิจสปริงสุทธิจะเท่ากับ k + 2k = 3k จึงมีความถี่ตามสมการ
\(\rm {\omega _2} = \sqrt {3k{\rm{ }}/{\rm{ }}m} = \sqrt 3 = {\omega _1}\)
ดังนั้น \(\rm {\omega _2}/{\omega _1} = \sqrt 3\)
