ข้อสอบคัดเลือกของทีม USA 2016 (25 ข้อ)
| 1. | รถขับทวนเข็มนาฬิกาบนถนนโค้งเรียบ ด้วยอัตราเร็วคงที่ ถ้าล้อหน้าซ้ายเคลื่อนที่เป็นวงกลมรัศมี R = 9.60 เมตร และรถกว้าง 1.74 m แล้วอัตราส่วนความเร็วเชิงมุมของการหมุนของเพลาล้อหน้าซ้าย ต่อเพลาล้อหน้าขวาของรถ ขณะเข้าโค้งเท่ากับข้อใด สมมติว่าล้อหมุนโดยไม่ไถล |
| A | 0.331 |
| B | 0.630 |
| C | 0.708 |
| D | 0.815 |
| E | 0.847 |
ตอบ (E)
เนื่องจากความเร็วคงที่ เราจึงใช้ความเร็วเชิงมุมเฉลี่ย ω = Δθ / Δt ได้
โดยทั้งสองล้อจะมี Δt เดียวกัน ส่วน Δθ จะหาจาก
ดังนั้น Δθ ของล้อซ้ายเท่ากับ
เนื่องจากความเร็วคงที่ เราจึงใช้ความเร็วเชิงมุมเฉลี่ย ω = Δθ / Δt ได้
โดยทั้งสองล้อจะมี Δt เดียวกัน ส่วน Δθ จะหาจาก
\(\rm Δθ = S / C\)
โดยที่ S คือ ความยาวส่วนโค้งที่ล้อกวาดไป และ C คือ เส้นรอบวงของล้อ ให้พิจารความยาวส่วนโค้งในหน่วย \(\pi\) เรเดียน จะได้ S = \(\pi\) R ดังนั้น Δθ ของล้อซ้ายเท่ากับ
\(\Delta {\theta _l} = \dfrac{{\pi {\rm{R}}}}{{2\pi {\rm{r}}}}\)
และ Δθ ของล้อขวาเท่ากับ
\(\Delta {\theta _r} = \dfrac{{\pi ({\rm{R + dR)}}}}{{2\pi {\rm{r}}}}\)
จากล้อทั้งสองมีรัศมี r เท่ากัน เมื่อเทียบสัดส่วนจะได้
\(\dfrac{{{\omega _l}}}{{{\omega _r}}} = \dfrac{{\dfrac{{\pi {\rm{R}}}}{{2\pi {\rm{r}}\Delta {\rm{t}}}}}}{{\dfrac{{\pi ({\rm{R + dR)}}}}{{2\pi {\rm{r}}\Delta {\rm{t}}}}}} = \dfrac{{\rm{R}}}{{{\rm{R + dR}}}} = \dfrac{1}{{1 + \dfrac{{{\rm{dR}}}}{{\rm{R}}}}}\)
แทนค่าลงไปจะได้
\(\dfrac{{{\omega _l}}}{{{\omega _r}}} = \frac{1}{{1 + \dfrac{{{\rm{1}}{\rm{.74m}}}}{{{\rm{9}}{\rm{.60m}}}}}} = 0.847\)
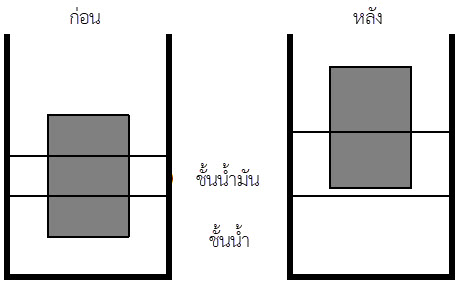
| 2. | ชั้นน้ำมันหนา 3.0 cm มีความหนาแน่น ρo = 800 kg / m3 ลอยเหนือน้ำที่มีความหนาแน่น ρw = 1000 kg / m3 กำหนดให้เดิม 1/3 ของทรงกระบอกตันลอยอยู่ในน้ำ อีก 1/3 ลอยอยู่ในน้ำมัน และอีก 1/3 อยู่ในอากาศ ถ้าเติมน้ำมันเพิ่มจนกว่าทรงกระบอกจะลอยในชั้นน้ำมันเท่านั้น แล้วสัดส่วนของทรงกระบอกที่ลอยอยู่ในชั้นน้ำมันเท่ากับข้อใด
 |
| A | 3/5 |
| B | 3/4 |
| C | 2/3 |
| D | 8/9 |
| E | 4/5 |
ตอบ (B)
สมมุติว่า ทรงกระบอกมีปริมาตร 3 ลูกบาศก์เมตร แสดงว่ามวลเข้ามาแทนที่น้ำ 1000 kg และเข้ามาแทนที่น้ำมัน 800 kg โดยไม่ต้องพิจารณาการแทนที่ในอากาศ จะได้มวลที่เข้ามาแทนที่ทั้งหมด 1800 kg ถ้าต้องการให้ทรงกระบอกลอยอยู่ในชั้นน้ำมันเท่านั้น หมายความว่าน้ำมันจะต้องถูกแทนที่ด้วยมวล 1800 kg คิดเป็นปริมาณน้ำมันได้
สมมุติว่า ทรงกระบอกมีปริมาตร 3 ลูกบาศก์เมตร แสดงว่ามวลเข้ามาแทนที่น้ำ 1000 kg และเข้ามาแทนที่น้ำมัน 800 kg โดยไม่ต้องพิจารณาการแทนที่ในอากาศ จะได้มวลที่เข้ามาแทนที่ทั้งหมด 1800 kg ถ้าต้องการให้ทรงกระบอกลอยอยู่ในชั้นน้ำมันเท่านั้น หมายความว่าน้ำมันจะต้องถูกแทนที่ด้วยมวล 1800 kg คิดเป็นปริมาณน้ำมันได้
\({{\rm{V}}_{\rm{o}}}{\rm{ = }}\left( {{\rm{1800 kg}}} \right){\rm{ / }}\left( {{\rm{800 kg/}}{{\rm{m}}^{\rm{3}}}} \right){\rm{ = }}\dfrac{9}{4}{{\rm{m}}^{\rm{3}}}\)
เทียบสัดส่วนที่ลอยอยู่ในชั้นน้ำมันจะเท่ากับ
\(\left( {\dfrac{{\rm{9}}}{{\rm{4}}}{\rm{}}{{\rm{m}}^{\rm{3}}}} \right){\rm{/}}\left( {{\rm{3}}{{\rm{m}}^{\rm{3}}}} \right){\rm{ = }}\dfrac{{\rm{3}}}{{\rm{4}}}{\rm{}}\)
| 3. | นักเรียนวิชาฟิสิกส์เบื้องต้น ฉลองเกรดเทอมแรกของเขาด้วยการทิ้งหนังสือลงมาจากระเบียงลงยังไปกองหิมะด้านล่างสูง 3.00 m ถ้าหนังสือเล่มนี้จมลงไปในหิมะประมาณ 1.00 m และหนังสือมีมวล 5 kg แล้วแรงเฉลี่ยที่หิมะกระทำกับหนังสือเท่ากับข้อใด |
| A | 85 N |
| B | 100 N |
| C | 120 N |
| D | 150 N |
| E | 200 N |
ตอบ (E)
กำหนดตัวแปร H = 3.00 m , h = 1.00 m และ v เป็นอัตราเร็วที่หนังสือตกลงไปถึงพื้น จากหลักจลน์ศาสตร์จะได้
เนื่องจาก a = 3g
ดังนั้น แรงที่หิมะกระทำกลับมาจะเท่ากับ 4mg
หรือคิดจากพลังงานศักย์ที่สูญเสียจากแรงเสียดทาน
กำหนดตัวแปร H = 3.00 m , h = 1.00 m และ v เป็นอัตราเร็วที่หนังสือตกลงไปถึงพื้น จากหลักจลน์ศาสตร์จะได้
\(\rm 2gH = v^2 =2ah\)
โดย a คือ ความเร่งบนหิมะเนื่องจาก a = 3g
ดังนั้น แรงที่หิมะกระทำกลับมาจะเท่ากับ 4mg
หรือคิดจากพลังงานศักย์ที่สูญเสียจากแรงเสียดทาน
\(\rm mg × 4\) เมตร \(\rm = F × 1\) เมตร
ดังนั้น F = 4mg นิวตัน| 4. | ปล่อยลูกปัดให้ไถลไปตามลวดที่ขดเหมือนสปริงในแนวตั้ง ข้อใดคือกราฟขนาดความเร่งลัพธ์ a ต่อเวลา t ของเหตุการณ์ดังกล่าว |
| A |  |
| B | 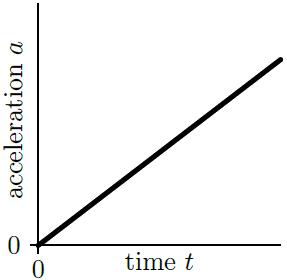 |
| C |  |
| D |  |
| E |  |
ตอบ (D)
ความเร่งในแนวสัมผัสกับเกลียวลวดจะเท่ากับ
ความเร่งในแนวสัมผัสกับเกลียวลวดจะเท่ากับ
\(\rm a_t = g~ sin θ\)
โดย θ คือ ขนาดมุมเอียงของเกลียวลวด ถ้าความเร่งมาก ลูกปัดก็จะเคลื่อนที่เร็วขึ้น ตามสมการ
\(\rm v = a_t t\)
เนื่องจากลูกปัดเคลื่อนที่เป็นวงกลม ความเร่งตามเรเดียนจะเท่ากับ
\({\rm{a = }}\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{r}}}{\rm{ = }}\dfrac{{{\rm{a}}_{\rm{t}}^{\rm{2}}}}{{\rm{r}}}{{\rm{t}}^{\rm{2}}}\)
ดังนั้น ความเร่งของลูกปัดจะเท่ากับ
\({\rm{a}} = \sqrt {{{\rm{a}}_{\rm{r}}}^2 + {{\rm{a}}_{\rm{t}}}^2} = {{\rm{a}}_{\rm{t}}}\sqrt {{{\rm{a}}_{\rm{t}}}^2\dfrac{{{{\rm{t}}^4}}}{{{{\rm{r}}^2}}} + 1} \)
| 5. | พิจารณาวัตถุในกล่องที่มีแรงโน้มถ่วงในทิศลง ดังรูป
 แล้วภาพในข้อใด แสดงทิศทางการเคลื่อนที่ของวัตถุภายในกล่องได้ถูกต้อง |
| A | 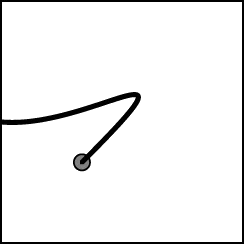 |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (C)
โดยปกติแล้ว การเคลื่อนที่ที่มีความเร่งจะเคลื่อนที่แบบพาราโบลา ซึ่งตรงกับข้อ (C) และ (E)
แต่ (E) ผิด เพราะ การเคลื่อนที่นั้นจะเกิดในกรณีที่ไม่มีความเร่งในแนวนอน
โดยปกติแล้ว การเคลื่อนที่ที่มีความเร่งจะเคลื่อนที่แบบพาราโบลา ซึ่งตรงกับข้อ (C) และ (E)
แต่ (E) ผิด เพราะ การเคลื่อนที่นั้นจะเกิดในกรณีที่ไม่มีความเร่งในแนวนอน
| 6. | พิจารณาวัตถุในกล่องที่มีแรงโน้มถ่วงในทิศลง ดังรูป
 หากเลือกขนาดความเร่งของกล่องได้ถูกต้อง วัตถุสามารถเคลื่อนที่กลับมายังจุดเริ่มได้อีกครั้ง ภาพในข้อใด แสดงทิศทางการเคลื่อนที่ของวัตถุภายในกล่องได้ถูกต้อง |
| A |  |
| B | 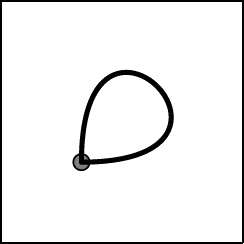 |
| C |  |
| D |  |
| E |  |
ตอบ (A)
โดยปกติแล้ว การเคลื่อนที่ที่มีความเร่งจะเคลื่อนที่แบบพาราโบลา
ดังนั้น ทิศทางการเคลื่อนที่ของวัตถุภายในกล่องจะเป็นไปตามข้อ (A)
โดยปกติแล้ว การเคลื่อนที่ที่มีความเร่งจะเคลื่อนที่แบบพาราโบลา
ดังนั้น ทิศทางการเคลื่อนที่ของวัตถุภายในกล่องจะเป็นไปตามข้อ (A)
| 7. | (เกินหลักสูตรการสอบเข้า สอวน.) มวลติดกับสปริงที่ยังไม่ถูกยืดออกและตรึงปลายด้านหนึ่งไว้ ถูกวางบนโต๊ะลื่น ถ้าขยับมวลออกมาด้วยระยะ A ขนานกับโต๊ะ แต่ตั้งฉากกับสปริงจนเกิดการสั่น แล้วคาบของการสั่น T จะเปลี่ยนไปอย่างไร |
| A | คาบของการสั่นไม่ได้ขึ้นกับระยะ A |
| B | เพิ่มขึ้น เมื่อ A เพิ่มขึ้น และเข้าใกล้ค่าคงที่ค่าหนึ่ง |
| C | ลดลง เมื่อ A เพิ่มขึ้น และเข้าใกล้ค่าคงที่ค่าหนึ่ง |
| D | หาค่าประมาณเป็นค่าคงที่ได้ เมื่อ A มีค่าเล็กๆ จากนั้นจะเพิ่มขึ้นโดยไม่มีขอบเขต |
| E | หาค่าประมาณเป็นค่าคงที่ได้ เมื่อ A มีค่าเล็กๆ จากนั้นจะลดลงโดยไม่มีขอบเขต |
ตอบ (C)
| 8. | จากกฎของเคปเลอร์ ( Kepler's Laws ) ระบุว่า I. วงโคจรของดาวเคราะห์จะเป็นวงรี โดยมีดวงอาทิตย์เป็นจุดโฟกัส II. เส้นตรงที่เชื่อมระหว่างดาวเคราะห์กับดวงอาทิตย์จะกวาดพื้นที่ได้เท่ากัน ในระยะเวลาที่เท่ากัน III. กำลังสองของคาบการโคจรของดาวเคราะห์ เป็นสัดส่วนโดยตรงกับกำลังสามของกึ่งแกนเอก (semimajor axis) ของวงโคจร กฎข้อใดจะเป็นจริง ถ้าแรงโน้มถ่วงมีสัดส่วนเป็น 1/r3 แทนที่จะเป็น 1/r2 |
| A | เฉพาะข้อ I. |
| B | เฉพาะข้อ II. |
| C | เฉพาะข้อ III. |
| D | ข้อ I. และ II. |
| E | ไม่มีข้อใดเป็นจริง |
ตอบ (B)
เพราะกฎข้อที่สองเป็นไปตามกฎการอนุรักษ์โมเมนตัมเชิงมุม จึงเป็นจริงสำหรับ central potential ใดๆ
ส่วนอีกสองข้อจำเป็นจะต้องแปรผันกับ 1/r2
เพราะกฎข้อที่สองเป็นไปตามกฎการอนุรักษ์โมเมนตัมเชิงมุม จึงเป็นจริงสำหรับ central potential ใดๆ
ส่วนอีกสองข้อจำเป็นจะต้องแปรผันกับ 1/r2
| 9. | ลูกปัดขนาดเล็กวางอยู่บนลูกแก้วกลมลื่นที่มีเส้นผ่านศูนย์กลาง D ดังรูป ถ้าสะกิดให้ลูกปัดลื่นไปตามลูกแก้ว แล้วอัตราเร็ว v ของลูกปัด ขณะไหลตกจากลูกแก้วเท่ากับข้อใด
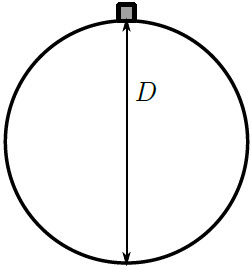 |
| A | \(\rm v = \sqrt {gD}\) |
| B | \(\rm v = \sqrt {4gD/5}\) |
| C | \(\rm v = \sqrt {2gD/3}\) |
| D | \(\rm v = \sqrt {gD/2}\) |
| E | \(\rm v = \sqrt {gD/3}\) |
ตอบ (E)
หาคำตอบจากสมการ
หาคำตอบจากสมการ
\(\begin{align*} \rm mgh &=\frac{1}{2}\rm mv^2\\ \rm{mg ~sin}\theta &= \rm m\frac{v^2}{\rm R} \end{align*}\)
| 10. | กล่องสองใบ ถูกผูกติดกันด้วยเชือกเบาสองเส้น และนำไปแขวนไว้บนเพนดาน ดังรูป มวลของกล่องบนและล่างหนัก m1 = 2 kg และ m2 = 4 kg ตามลำดับ ถ้าตัดเชือกที่แขวนกับเพดานแล้วความเร่งของกล่องทั้งสองใบ ขณะกล่องใบบนสุดเริ่มร่วงลงจะเท่ากับข้อใด
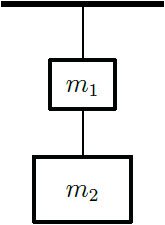 |
| A | กล่องบน: 10 m/s2, กล่องล่าง: 0 |
| B | กล่องบน: 10 m/s2, กล่องล่าง: 10m/s2 |
| C | กล่องบน: 20 m/s2, กล่องล่าง: 10 m/s2 |
| D | กล่องบน: 30 m/s2, กล่องล่าง: 0 |
| E | กล่องบน: 30 m/s2, กล่องล่าง: 10 m/s2 |
ตอบ (D)
แผนภาพของกล่องใบที่ 1 และ 2 ก่อนตัดเชือก สามารถใช้พิจารณาขณะเชือกถูกตัดทันทีได้ เพราะเวลาที่เชือกถูกตัดนั้นสั้นมาก และไม่ก่อให้เกิดแรงที่กระทำต่อกล่องใบที่ 1 ลองใช้ผลที่ได้จากแผนภาพหาความเร่งของกล่องทั้งสองใบดู
แผนภาพของกล่องใบที่ 1 และ 2 ก่อนตัดเชือก สามารถใช้พิจารณาขณะเชือกถูกตัดทันทีได้ เพราะเวลาที่เชือกถูกตัดนั้นสั้นมาก และไม่ก่อให้เกิดแรงที่กระทำต่อกล่องใบที่ 1 ลองใช้ผลที่ได้จากแผนภาพหาความเร่งของกล่องทั้งสองใบดู
| 11. | พลังงานที่ออกมาจากรถทดลองรุ่นทรงลูกบาศก์ จะแปรผันตามมวล m ของรถ และแรงต้านอากาศต่อรถจะแปรผันตาม Av2 โดย v คือ อัตราเร็วของรถ และ A คือ พื้นที่ตัดขวาง เมื่ออยู่บนถนนเรียบรถจะมีอัตราเร็วสูงสุดเป็น vmax สมมุติว่า รถรุ่นนี้มีความหนาแน่นเท่ากันทุกคัน แล้วข้อใดต่อไปนี้เป็นจริง |
| A | \(\rm {v_{\max }} \propto {{\rm{m}}^{1/9}}\) |
| B | \(\rm {v_{\max }} \propto {{\rm{m}}^{1/7}}\) |
| C | \(\rm {v_{\max }} \propto {{\rm{m}}^{1/3}}\) |
| D | \(\rm {v_{\max }} \propto {{\rm{m}}^{2/3}}\) |
| E | \(\rm {v_{\max }} \propto {{\rm{m}}^{3/4}}\) |
ตอบ (A)
จากปริมาตรของลูกบาศก์ L ∝ m1/3 ดังนั้น A ∝ m2/3 และโจทย์ให้ความหนาแน่นเป็นค่าคงที่
จะหาความเร็วได้ ดังนี้
จากปริมาตรของลูกบาศก์ L ∝ m1/3 ดังนั้น A ∝ m2/3 และโจทย์ให้ความหนาแน่นเป็นค่าคงที่
จะหาความเร็วได้ ดังนี้
\(\rm m ∝ P = Fv ∝ Av^3 ∝ m^{2/3} v^3\)
ดังนั้น
\(\rm m ∝ v^9\)
| 12. | ให้ภาชนะที่บรรจุของเหลว มีบล็อกก้อนหนึ่งลอยแบบจมบางส่วนอยู่ ถ้าเราเพิ่มความเร่งให้ทั้งภาชนะ แล้วผลลัพธ์จะเป็นอย่างไร สมมุติว่า ทั้งบล็อกและของเหลวไม่สามารถบีบอัดได้ |
| A | บล็อกจะจมลงไปในของเหลว |
| B | บล็อกในของเหลวจะลอยสูงขึ้น |
| C | บล็อกจะไม่ลอยหรือจมไปจากเดิม |
| D | คำตอบขึ้นอยู่กับทิศทางการเคลื่อนที่ของภาชนะ |
| E | คำตอบขึ้นอยู่กับอัตราการเปลี่ยนแปลงของความเร่ง |
ตอบ (C)
ส่วนที่จมหรือลอยไม่ขึ้นกับค่าความโน้มถ่วง g กล่าวคือ
ส่วนที่จมหรือลอยไม่ขึ้นกับค่าความโน้มถ่วง g กล่าวคือ
ρวัตถุgVวัตถุ = ρเหลวgVแทนที่
Vแทนที่ = (ρวัตถุ Vวัตถุ)/ρเหลว
ดังนั้น บล็อกจะไม่ลอยหรือจมไปจากเดิมVแทนที่ = (ρวัตถุ Vวัตถุ)/ρเหลว
| 13. | วัตถุมวล m1 เริ่มเคลื่อนที่ด้วยอัตราเร็ว v0 แล้วชนกับวัตถุที่เดิมหยุดนิ่ง มวล m2 = αm1 โดยที่ α < 1 การชนกันอาจจะยืดหยุ่นสมบูรณ์ ไม่สมบูรณ์ หรือยืดหยุ่นบางส่วนก็ได้ หลังการชน วัตถุทั้งสองจะเคลื่อนที่ด้วยอัตราเร็ว v1 และ v2 สมมุติว่า เป็นการชนกันหนึ่งมิติ และวัตถุแรกไม่สามารถทะลุผ่านวัตถุสองได้ แล้วอัตราส่วนอัตราเร็วของวัตถุที่สองหลังการชน r2 = v2 / v0 จะอยู่ในช่วงใด |
| A | (1 – α) / (1 + α) ≤ r2 ≤ 1 |
| B | (1 – α) / (1 + α) ≤ r2 ≤ 1 / (1 + α) |
| C | α / (1 + α) ≤ r2 ≤ 1 |
| D | 0 ≤ r2 ≤ 2 α / (1 + α) |
| E | 1 / (1 + α) ≤ r2 ≤ 2 / (1 + α) |
ตอบ (E)
จากกฎการอนุรักษ์โมเมนตัม และพลังงานจลน์ ในกรณีที่การชนนั้นยืดหยุ่นสมบูรณ์ จะได้ว่า
จากกฏการอนุรักษ์โมเมนตัม ในกรณีที่การชนนั้นไม่ยืดหยุ่นสมบูรณ์ จะได้ว่า
ดังนั้น
จากกฎการอนุรักษ์โมเมนตัม และพลังงานจลน์ ในกรณีที่การชนนั้นยืดหยุ่นสมบูรณ์ จะได้ว่า
\(\begin{array}{l}
\rm{r_1} = \dfrac{{{v_1}}}{{{v_0}}} = \dfrac{{1 - \alpha }}{{1 + \alpha }}\\
\rm{r_2} = \dfrac{{{v_2}}}{{{v_0}}} = \dfrac{2}{{1 + \alpha }}
\end{array}\)
เนื่องจาก \(\rm \alpha < 1\) วัตถุ m1 จะมีอิทธิพลมากกว่าวัตถุ m2 ดังนั้น การเคลื่อนที่จะยังคงไปข้างหน้า จากกฏการอนุรักษ์โมเมนตัม ในกรณีที่การชนนั้นไม่ยืดหยุ่นสมบูรณ์ จะได้ว่า
\(\rm {r_1} = {r_2} = \dfrac{1}{{1 + \alpha }}\)
จากที่วัตถุ m2 เคลื่อนที่ไปข้างหน้าเสมอ และวัตถุ m1 ไม่สามารถทะลุผ่านวัตถุ m2 ได้ ดังนั้น วัตถุ m2 จะต้องเคลื่อนที่ด้วยความเร็วที่เป็นบวกมากกว่า (หรือเท่ากับ) วัตถุ m1 ดังนั้น
\(\rm 1/(1 + \alpha ) \le {r_2} \le 2/(1 + \alpha )\)
การหาช่วงคำตอบของ วัตถุ m1 อาจจะยากกว่าเล็กน้อย เพราะสถานการณ์นี้อาจจะมีการกระดอนกลับเกิดขึ้น แต่ในกรณีนี้ \(\rm \alpha < 1\) ทำให้ความเร็วหลังการชนเคลื่อนที่ไปข้างหน้า จึงได้ว่า
\(\rm (1 - \alpha )/(1 + \alpha ) \le {r_1} \le 1/(1 + \alpha )\)
| 14. | (เกินหลักสูตรการสอบเข้า สอวน.) กำหนดคานยาว l วางบนระนาบพื้นลื่น ปลายด้านหนึ่งถูกยึดให้หมุนรอบแกนได้ และปลายอีกด้านติดสปริงยาว L >> l ขณะยังไม่ยืดออก สปริงถูกวางอยู่บนพื้นและตั้งฉากกับคาน และสปริงฝั่งที่ติดกับคานสามารถขยับได้ และปลายอีกข้างเป็นจุดตรึง เมื่อขยับคานหมุนรอบแกนเล็กน้อย สปริงจะสั่นด้วยความถี่ f  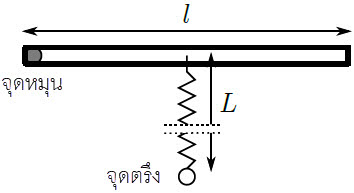 |
| A | \(\rm f/2\) |
| B | \(\rm f/\sqrt{2}\) |
| C | \(\rm f\) |
| D | \(\rm \sqrt{2}f\) |
| E | \(\rm 2f\) |
ตอบ (A)
สังเกตว่า สปริงยังคงตั้งฉากกับคานเหมือนเดิม
สมมุติว่า โมเมนต์ความเฉื่อยของคานรอบจุดหมุนคือ I ระยะจากจุดหมุนถึงสปริงคือ r และค่านิจสปริงคือ k เมื่อขยับคานทำมุม θ สปริงจะยืดออก θr และแรงที่กระทำโดยสปริงจะเท่ากับ kθr มีระยะห่างจากจุดหมุน r จะได้สมการการเคลื่อนที่ ดังนี้
สังเกตว่า สปริงยังคงตั้งฉากกับคานเหมือนเดิม
สมมุติว่า โมเมนต์ความเฉื่อยของคานรอบจุดหมุนคือ I ระยะจากจุดหมุนถึงสปริงคือ r และค่านิจสปริงคือ k เมื่อขยับคานทำมุม θ สปริงจะยืดออก θr และแรงที่กระทำโดยสปริงจะเท่ากับ kθr มีระยะห่างจากจุดหมุน r จะได้สมการการเคลื่อนที่ ดังนี้
\(\begin{align*} \rm \tau &= \rm I\alpha \\ \rm - k{r^2}\theta &=\rm I\ddot \theta \end{align*}\)
พิจารณา สูตรความถี่ของการสั่นแบบฮาร์มอนิกอย่างง่าย
\({\rm{f = }}\dfrac{{\rm{1}}}{{{\rm{2}}\pi }}\omega {\rm{ = }}\dfrac{{\rm{1}}}{{{\rm{2}}\pi }}\sqrt {\dfrac{{{\rm{k}}{{\rm{r}}^{\rm{2}}}}}{{\rm{I}}}} \)
จะเห็นว่า ความถี่แปรผันตรงกับระยะห่าง r เมื่อระยะห่างลดลงครึ่งหนึ่ง ความถี่ก็จะลดลงครึ่งหนึ่งเช่นกัน| 15. | (เกินหลักสูตรการสอบเข้า สอวน.) กำหนดคานยาว l วางบนระนาบพื้นลื่น ปลายด้านหนึ่งถูกยึดให้หมุนรอบแกนได้ และปลายอีกด้านติดสปริงยาว L >> l ขณะยังไม่ยืดออก สปริงถูกวางอยู่บนพื้นและตั้งฉากกับคาน และสปริงฝั่งที่ติดกับคานสามารถขยับได้ และปลายอีกข้างเป็นจุดตรึง เมื่อขยับคานหมุนรอบแกนเล็กน้อย สปริงจะสั่นด้วยความถี่ f  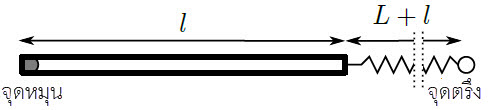 |
| A | \(\rm f/3\) |
| B | \(\rm f/\sqrt3\) |
| C | \(\rm f\) |
| D | \(\rm \sqrt3 f\) |
| E | \(\rm 3f\) |
ตอบ (C)
สมมุติว่า โมเมนต์ความเฉื่อยของคานรอบจุดหมุนคือ I ระยะจากจุดหมุนถึงสปริงคือ r และค่านิจสปริงคือ k เมื่อขยับคานทำมุม θ สปริงจะยืดออก θr และแรงที่กระทำโดยสปริงจะเท่ากับ kθr มีระยะห่างจากจุดหมุน r จะได้สมการการเคลื่อนที่ ดังนี้
พิจารณา แรงที่กระทำโดยสปริง คือ kl และระยะห่างจากจุดหมุนคือ lθ จะได้สมการการเคลื่อนที่ ดังนี้
สมมุติว่า โมเมนต์ความเฉื่อยของคานรอบจุดหมุนคือ I ระยะจากจุดหมุนถึงสปริงคือ r และค่านิจสปริงคือ k เมื่อขยับคานทำมุม θ สปริงจะยืดออก θr และแรงที่กระทำโดยสปริงจะเท่ากับ kθr มีระยะห่างจากจุดหมุน r จะได้สมการการเคลื่อนที่ ดังนี้
\(\rm \tau = \rm I\alpha\)
\(\rm - k{r^2}\theta =\rm I\ddot \theta\) --- (1)
สังเกตว่า แรงตึงในสปริงสามารถแทนด้วยค่าคงที่\(\rm - k{r^2}\theta =\rm I\ddot \theta\) --- (1)
พิจารณา แรงที่กระทำโดยสปริง คือ kl และระยะห่างจากจุดหมุนคือ lθ จะได้สมการการเคลื่อนที่ ดังนี้
\(- {\rm{k}}{l^2}\theta = {\rm{I}}\ddot \theta\)
ซึ่งตรงกับสมการการเคลื่อนที่ (1) (โดย r = l) ดังนั้น ความถี่ต้องมีค่า f เท่าเดิม| 16. | ลูกบอลกลิ้งลงมาจากรถบรรทุกที่วิ่งไปทิศขวาด้วยอัตราเร็ว 10.0 m/s ส่วนลูกบอลกลิ้งตามแนวราบด้วยอัตราเร็ว 8.0 m/s ในทิศซ้ายมือของผู้สังเกตบนรถบรรทุก ถ้าลูกบอลตกลงบนพื้นถนนจากความสูง 1.25 m แล้วจุดที่ลูกบอลตกกระทบพื้นขณะนั้น จะห่างจากด้านหลังของรถบรรทุกเท่าใด |
| A | 0.50 m |
| B | 1.0 m |
| C | 4.0 m |
| D | 5.0 m |
| E | 9.0 m |
ตอบ (C)
ใช้สูตร
ดังนั้น ระยะห่างจากรถบรรทุกเท่ากับ (8.0m/s)(0.5s) = 4.0 m
ใช้สูตร
\(\rm d = \dfrac{1}{2}a{t^2}\)
จะได้เวลาในการตกถึงพื้น 0.5s เทียบกับอัตราเร็วรถบรรทุก ดังนั้น ระยะห่างจากรถบรรทุกเท่ากับ (8.0m/s)(0.5s) = 4.0 m
| 17. | (เกินหลักสูตรการสอบเข้า สอวน.) จากรูป ลูกปิงปองมวล m กลิ้งอยู่บนพื้นด้วยความเร็วต้นในแนวนอน v และความเร็วเชิงมุม ω เนื่องจากพื้นมีแรงเสียดทาน ทำให้ความเร็วและความเร็วเชิงมุมของลูกปิงปองเปลี่ยนแปลงไป จงหาความเร็ววิกฤติ vc ที่ทำให้ลูกปิงปองหยุดนิ่ง อย่าลืมว่าลูกปิงปองเป็นทรงกลมกลวง
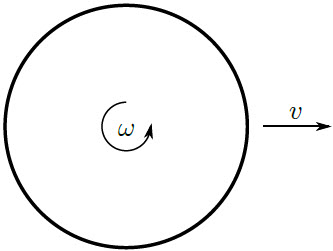 |
| A | \(\rm v = \dfrac{2}{3}R\omega \) |
| B | \(\rm v = \dfrac{2}{5}R\omega \) |
| C | \(\rm v = R\omega \) |
| D | \(\rm v = \dfrac{3}{5}R\omega \) |
| E | \(\rm v = \dfrac{5}{3}R\omega \) |
ตอบ (A)
โมเมนตัมเริ่มต้นของลูกปิงปองเท่ากับ mv และโมเมนตัมเชิงมุมรอบจุดศูนย์กลางเร่มต้น เท่ากับ \(\rm I\omega = \dfrac{2}{3}m{R^2}\omega\)
เมื่อลูกปิงปองสัมผัสกับพื้นที่มีแรงเสียดทาน จะเกิดแรงดล \(\rm F\delta t\) และเกิดทอร์ก \(\rm FR\delta t\)
ดังนั้นเราจะได้
โมเมนตัมเริ่มต้นของลูกปิงปองเท่ากับ mv และโมเมนตัมเชิงมุมรอบจุดศูนย์กลางเร่มต้น เท่ากับ \(\rm I\omega = \dfrac{2}{3}m{R^2}\omega\)
เมื่อลูกปิงปองสัมผัสกับพื้นที่มีแรงเสียดทาน จะเกิดแรงดล \(\rm F\delta t\) และเกิดทอร์ก \(\rm FR\delta t\)
ดังนั้นเราจะได้
\(\rm F\delta t = mv\) --- (1)
และ
\(\rm Fr\delta t = \dfrac{2}{3}m{r^2}\omega\) --- (2)
นำ (2) ÷ (1) จะได้
\(\rm R = \dfrac{2}{3}m{R^2}\dfrac{\omega }{v}\)
| 18. | วัตถุที่เดิมหยุดนิ่ง ถูกหมุนและเร่งความเร็วจนมีความเร็วเชิงมุม \(\rm ω = π /15~ rad / s\) และความเร่งเชิงมุม \(\rm α = π / 75~ rad / s^2\) ถ้าวัตถุยังคงหมุนต่อด้วยความเร็วเชิงมุมคงที่ และหยุดด้วยความเร่งเชิงมุมที่มีขนาดเท่ากับความเร่งก่อนหน้านี้ แล้วระยะเวลาที่วัตถุจะหมุนวนครบ 3 รอบเท่ากับข้อใด |
| A | 75 s |
| B | 80 s |
| C | 85 s |
| D | 90 s |
| E | 95 s |
ตอบ (E)
การหมุนทั้งสามแบบ คือ การหมุนด้วยอัตราเร็วเพิ่มขึ้น คงที่ และลดลง ช่วงของการเปลี่ยนความเร็วจะสมมาตรกัน โดยมีระยะห่าง \(\rm \theta = 6\pi\) จึงได้ว่า
แต่ \(\rm \omega = \alpha {t_1}\) ดังนั้น
เมื่อแก้สมการจะได้ t2 = 85 s และ t1 = 5 s เนื่องจาก t1 เกิดขึ้นสองครั้ง
ดังนั้น คำตอบ คือ 95 s
การหมุนทั้งสามแบบ คือ การหมุนด้วยอัตราเร็วเพิ่มขึ้น คงที่ และลดลง ช่วงของการเปลี่ยนความเร็วจะสมมาตรกัน โดยมีระยะห่าง \(\rm \theta = 6\pi\) จึงได้ว่า
\(\rm \theta = \alpha t_1^2 + \omega {t_2}\)
แต่ \(\rm \omega = \alpha {t_1}\) ดังนั้น
\(\rm \theta = \alpha {\left( {\dfrac{\omega }{\alpha }} \right)^2} + \omega {t_2}\)
เมื่อแก้สมการจะได้ t2 = 85 s และ t1 = 5 s เนื่องจาก t1 เกิดขึ้นสองครั้ง
ดังนั้น คำตอบ คือ 95 s
| 19. | ลวดรูปครึ่งวงกลมมีรัศมี R ถูกจับตั้ง ดังรูป ถ้าปล่อยลูกปัดให้ลื่นลงมาจากด้านบนของลวด โดยไม่มีแรงเสียดทานตามแรงโน้มถ่วง แล้วพุ่งออกจากปลายลวดลงไปยังพื้นดินที่ระดับความสูง H อยู่ไกลจากปลายลวดในแนวนอน D
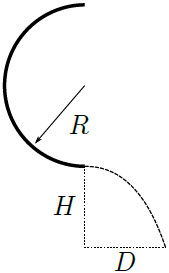 |
| A |  |
| B |  |
| C | 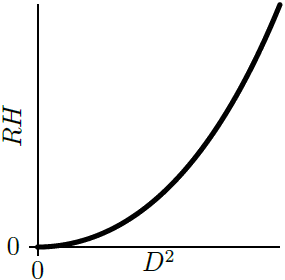 |
| D |  |
| E |  |
ตอบ (D)
ให้ v เป็นอัตราเร็วขณะลูกปัดหล่นออกจากปลายลวด จากกฎการอนุรักษ์พลังงาน จะได้
ให้ v เป็นอัตราเร็วขณะลูกปัดหล่นออกจากปลายลวด จากกฎการอนุรักษ์พลังงาน จะได้
\(\rm\dfrac{1}{2}{v^2} = 2gR\)
ให้ t เป็นเวลาที่ลูกปัดเคลื่อนที่แบบโพรเจกไทล์ จะได้ D = vt และ
\(\rm H = \dfrac{1}{2}g{t^2} = \dfrac{1}{2}g{\left( {\dfrac{D}{v}} \right)^2}\)
รวมสมการจะได้
\(\rm H = \dfrac{1}{8}\dfrac{{{D^2}}}{R}\)
ดังนั้น กราฟ RH เทียบกับ D2 จะเป็นเส้นตรง| 20. | ปริซึมมุมฉาก มีหน้าตัดเป็นรูปสามเหลี่ยมมุมฉาก สูง h ด้านตรงข้ามมุมฉากยาว w = 2h วางอยู่บนพื้นเอียงที่ทำมุมกับแนวนอน θ ข้อใดคือสัมประสิทธิ์ต่ำสุดของแรงเสียดทานสถิตที่ทำให้ปริซึมหมุนกลิ้งลงมา (โดยมีจุดยอดหนึ่งเป็นจุดหมุน) และไม่ไถล
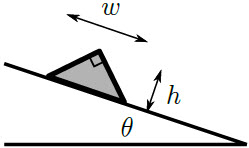 |
| A | 0.71 |
| B | 1.41 |
| C | 1.50 |
| D | 1.73 |
| E | 3.00 |
ตอบ (E)
ปริซึมจะหมุนกลิ้งลงมา เมื่อจุดศูนย์กลางมวลของปริซึมอยู่สูงกว่ามุมขวาของด้านที่วางบนพื้นเอียง หากอธิบายด้วยตรีโกณมิติ จะกล่าวได้ว่า ปริซึมจะหมุนกลิ้งลงมา เมื่อ
ปริซึมจะหมุนกลิ้งลงมา เมื่อจุดศูนย์กลางมวลของปริซึมอยู่สูงกว่ามุมขวาของด้านที่วางบนพื้นเอียง หากอธิบายด้วยตรีโกณมิติ จะกล่าวได้ว่า ปริซึมจะหมุนกลิ้งลงมา เมื่อ
\(\rm \tan \theta > \mu\)
จะเห็นว่าค่าที่สอดคล้อง คือ ข้อ (E)| 21. | คานเบายาว L ที่วางตัวในแนวดิ่งและปลายบนติดกับมวล m ปลายล่างสัมผัสกับพื้นและติดกับมวล 3m กำหนดให้ไม่มีแรงเสียดทาน และสมมุติว่าทุกอย่างเคลื่อนที่ในระนาบเดียว ถ้า x เป็นระยะกระจัดในแนวนอนของมวล m เมื่อกระทบพื้น แล้วค่า x มีค่าเท่ากับข้อใด |
| A | \(\rm x=\dfrac{3}{4}L\) |
| B | \(\rm x=\dfrac{3}{5}L\) |
| C | \(\rm x=\dfrac{1}{4}L\) |
| D | \(\rm x=\dfrac{1}{3}L\) |
| E | \(\rm x=\dfrac{2}{5}L\) |
ตอบ (A)
เนื่องจากจุดศูนย์กลางมวลของระบบไม่สามารถเคลื่อนที่ในแนวนราบได้ จึงไม่แรงที่กระทำกับในแนวนอน
ดังนั้น \(\rm x=\dfrac{3}{4}L\)
เนื่องจากจุดศูนย์กลางมวลของระบบไม่สามารถเคลื่อนที่ในแนวนราบได้ จึงไม่แรงที่กระทำกับในแนวนอน
ดังนั้น \(\rm x=\dfrac{3}{4}L\)
| 22. | คานเบายาว L ที่วางตัวในแนวดิ่งและปลายบนติดกับมวล m ปลายล่างสัมผัสกับพื้นและติดกับมวล 3m กำหนดให้ไม่มีแรงเสียดทาน และสมมุติว่าทุกอย่างเคลื่อนที่ในระนาบเดียว ถ้า v เป็นอัตราเร็วของมวล m เมื่อกระทบพื้น แล้วค่า v มีค่าเท่ากับข้อใด |
| A | \(\rm v = \sqrt {2gL}\) |
| B | \(\rm v = \sqrt {gL}\) |
| C | \(\rm v = \sqrt {2gL/3}\) |
| D | \(\rm v = \sqrt {3gL/2}\) |
| E | \(\rm v = \sqrt {gL/4}\) |
ตอบ (A)
มวล m จะเคลื่อนที่เฉพาะในแนวตั้งก่อนตกถึงพื้น และในขณะนั้นมวล 3m จะถูกทำให้เคลื่อนที่ แต่ตอนนี้มวล 3m จะยังอยู่นิ่งก่อน และพลังงานจะถูกสงวนไว้ ดังนั้น ทุกพลังงานศักย์ที่จุดศูนย์กลางมวลของระบบจะอยู่ในมวล m จะได้ว่า
ดังนั้น
มวล m จะเคลื่อนที่เฉพาะในแนวตั้งก่อนตกถึงพื้น และในขณะนั้นมวล 3m จะถูกทำให้เคลื่อนที่ แต่ตอนนี้มวล 3m จะยังอยู่นิ่งก่อน และพลังงานจะถูกสงวนไว้ ดังนั้น ทุกพลังงานศักย์ที่จุดศูนย์กลางมวลของระบบจะอยู่ในมวล m จะได้ว่า
\(\rm U = 4mgh\)
เมื่อ h คือ ความสูงของจุดศูนย์กลางมวล โดยที่ \(\rm h = \dfrac{1}{4}L\)ดังนั้น
\(\rm U = mgL\)
และแน่นอนว่า เราต้องแปลงเป็นพลังงานศักย์ของมวล m ก่อนจะได้
\(\rm mgL = \dfrac{1}{2}m{v^2}\)
ดังนั้น \(\rm v = \sqrt {2gL} \)| 23. | หนังยางสม่ำเสมอมวล M และมีค่านิจสปริง k มีรัศมีเดิม R ถ้าขว้างหนังยางออกไปในอากาศ โดยสมมุติว่า หนังยางยังคงเป็นวงกลม และหมุนด้วยอัตราเร็วเชิงมุม ω รอบจุดศูนย์กลางวงแล้วข้อใด คือ รัศมีใหม่ของหนังยาง |
| A | \(\rm ( 2πkR ) / ( 2πk - Mω^2 )\) |
| B | \(\rm( 4πkR ) / ( 4πk - Mω^2 )\) |
| C | \(\rm ( 8π^2 kR ) / ( 8π^2 k - Mω^2 )\) |
| D | \(\rm ( 4π^2 kR ) / ( 4π2 k - Mω^2 )\) |
| E | \(\rm ( 4πkR ) / ( 2πk - Mω^2 )\) |
ตอบ (D)
สำหรับองค์ประกอบของมวล \(\rm\Delta M\)ให้พิจารณา
สำหรับองค์ประกอบของมวล \(\rm\Delta M\)ให้พิจารณา
\(\rm 2T\sin \dfrac{{\Delta \theta }}{2} = \Delta m{\omega ^2}R'\)
จาก \(\sin \dfrac{{\Delta \theta }}{2} \approx \dfrac{{\Delta \theta }}{2}\) จะได้ว่า
\(\rm T = \dfrac{M}{{2\pi }}{\omega ^2}R'\)
ในขณะที่
\(\rm T = k2\pi (R' - R)\)
เทียบ T ทั้งสองสมการ แล้วจัดรูปจะได้
\(\rm R' = \dfrac{{4{\pi ^2}kR}}{{4{\pi ^2}k - M{\omega ^2}}}\)
| 24. | โมเมนต์ความเฉื่อยของรูปสามเหลี่ยมด้านเท่าสม่ำเสมอมวล m แต่ละด้านยาว a แกนที่ผ่านด้านใดด้านหนึ่งและขนานกับด้านนั้นเท่ากับ (1/8)ma2 แล้วโมเมนต์ความเฉื่อยของรูปหกเหลี่ยมด้านเท่ามวล m แต่ละด้านยาว a แกนที่ผ่านสองจุดที่อยู่ฝั่งตรงข้าม เท่ากับข้อใด |
| A | (1/8)ma2 |
| B | (5/24)ma2 |
| C | (17/72)ma2 |
| D | (19/72)ma2 |
| E | (9/32)ma2 |
ตอบ (B)
เราสามารถแบ่งรูปหกเหลี่ยมมวล m เป็นรูปสามเหลี่ยมด้านเท่าได้หกอัน โดยรูปสามเหลี่ยมด้านเท่าสี่อันจะรวมกันได้ (1/8)(m/6)a2 ส่วนอีกสองอันจะรวมกันได้ ((1/24+1/3)a2)(m/6) ตามทฤษฎีบทของแกนขนาน
เมื่อรวมทั้งหมดจะได้ (5/4)(m/6)a2 = (5/24)ma2
เราสามารถแบ่งรูปหกเหลี่ยมมวล m เป็นรูปสามเหลี่ยมด้านเท่าได้หกอัน โดยรูปสามเหลี่ยมด้านเท่าสี่อันจะรวมกันได้ (1/8)(m/6)a2 ส่วนอีกสองอันจะรวมกันได้ ((1/24+1/3)a2)(m/6) ตามทฤษฎีบทของแกนขนาน
เมื่อรวมทั้งหมดจะได้ (5/4)(m/6)a2 = (5/24)ma2
| 25. | นักเรียนสามคน วัดความยาวคานยาว 1.50 เมตร แต่ละคนรายงานความคลาดเคลื่อนในการประมาณค่า เพื่อให้ทราบข้อผิดพลาดที่เกิดขึ้นจากการวัด ดังนี้
ก : วัดครั้งเดียว โดยใช้ตลับเมตรความยาว 2.0 เมตร มีความคลาดเคลื่อน ± 2 มิลลิเมตร
ข : วัดสองครั้ง โดยใช้ไม้เมตร แต่ละครั้งมีความคลาดเคลื่อน ± 2 มิลลิเมตร ซึ่งเขารวมความคลาดเคลื่อนเข้าด้วยกัน
ค : วัดสองครั้ง โดยใช้ไม้บรรทัดสเกลละเอียดสำหรับงานช่าง แต่ละครั้งมีความคลาดเคลื่อน ± 1 มิลลิเมตร ซึ่งเขารวมความคลาดเคลื่อนเข้าด้วยกัน
จากข้อมูล ครูต้องเลือกข้อมูลที่มีความผิดพลาดน้อยที่สุด ข้อใดจัดลำดับความน่าเชื่อถือได้ถูกต้อง |

