ข้อสอบคัดเลือกของทีม USA 2017 (25 ข้อ)
| 1. | ขี่มอเตอร์ไซค์ไต่รอบถังทรงกลมขนาดใหญ่ ถ้าสัมประสิทธิ์แรงเสียดทานระหว่างยางมอเตอร์ไซค์กับผนัง คือ μ แล้ว μ น้อยสุดที่ทำให้มอเตอร์ไซค์ไม่หล่นลงไปเท่ากับข้อใด ตอบในรูป μ ที่แปรผันกับอัตราเร็ว s ของมอเตอร์ไซค์ |
| A | \(\rm\mu \propto {s^0}\) |
| B | \(\rm\mu \propto {s^{ - 1/2}}\) |
| C | \(\rm\mu \propto {s^{ - 1}}\) |
| D | \(\rm\mu \propto {s^{ - 2}}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
| 2. | มวล m ถูกแขวนด้วยสปริงเบาที่ติดอยู่เพดานภายในของกล่องมวล M ขณะกล่องอยู่นิ่งระบบสปริงจะสั่นในแนวตั้งด้วยความถี่เชิงมุม ω ถ้าปล่อยกล่องให้ตกลงอย่างอิสระภายใต้แรงโน้มถ่วง แล้วความถี่เชิงมุมจะเปลี่ยนแปลงอย่างไร |
| A | ω จะไม่เปลี่ยนแปลง |
| B | ω จะเพิ่มขึ้น |
| C | ω จะลดลง |
| D | การสั่นจะไม่เกิดขึ้น ภายใต้เงื่อนไขดังกล่าว |
| E | ω จะเปลี่ยนแปลง โดยขึ้นกับมวล M และ m |
ตอบ (B)
| 3. | ลูกบอลเล็กรัศมี R มวล m ถูกใส่เข้าไปในบอลใหญ่เปลือกบางที่มีมวลเท่ากัน แต่มีรัศมี 2R ให้ตอนแรกลูกบอลเล็กอยู่ที่ผิวด้านข้างของลูกบอลใหญ่ และยังไม่เสียดสีกับพื้นในแนวนอน จากนั้นปล่อยลูกบอลเล็กให้กลิ้งภายในบอลใหญ่ จนหยุดที่ด้านล่างของลูกบอลใหญ่ แล้วลูกบอลใหญ่จะกลิ้งไปได้เท่าไร จากจุดเริ่มต้นที่สัมผัสพื้น
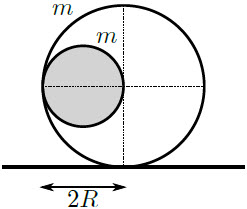 |
| 4. | รถแบบเดียวกันหลายคันกำลังติดไฟแดงบนถนนหนึ่งเลน ซึ่งจอดต่อกันเป็นแถวเดียว และมีระยะหว่างระหว่างคันเท่ากัน เมื่อขึ้นไฟเขียว รถคันแรกไปทิศขวาด้วยความเร่งคงที่ แล้วรถคันที่สองก็วิ่งแบบเดียวกันใน 0.2 วินาที ให้หลัง และรถคันถัดไปก็จะวิ่งอย่างเดียวกัน ถ้ารถทุกคันเร่งความเร็ว จนมีอัตราเร็ว 45 km/hr จากนั้นวิ่งไปทิศขวาด้วยอัตราเร็วคงที่ พิจารณาการเรียงแถวของรถยนต์ ตามรูป
 |
| A | เปลี่ยนจาก I ไป II ไป III |
| B | เปลี่ยนจาก I ไป II ไป IV |
| C | เปลี่ยนจาก I ไป IV ไม่มี II และ III |
| D | เปลี่ยนจาก I ไป II |
| E | เปลี่ยนจาก I ไป III |
ตอบ (B)
| 5. | ยิงปืนด้วยอัตราเร็ว v0 ออกจากขอบหน้าผาสูง h ทำมุม θ กับแนวนอน โดยไม่คำนึงถึงแรงต้านอากาศ จงหา θ ที่ทำให้กระสุนพุ่งออกไปในแนวราบได้ไกลที่สุด |
| A | 45° < θ < 90° |
| B | θ = 45° |
| C | 0° < θ < 45° |
| D | θ = 0° |
| E | θ < 45° หรือ 45° < θ ขึ้นกับค่า h และ v0 |
ตอบ (C)
| 6. | กำหนดคานสองคาน มีเชือกเบา 7 เส้น ผูกอยู่ในตำแหน่งต่างๆ ดังรูป ถ้ามวลของวัตถุ M1 = 400 g, M2 = 200 g และ M4 = 500 กรัม แล้วมวล M3 มีค่าเท่าใด เมื่อคานอยู่ในสภาวะสมดุล
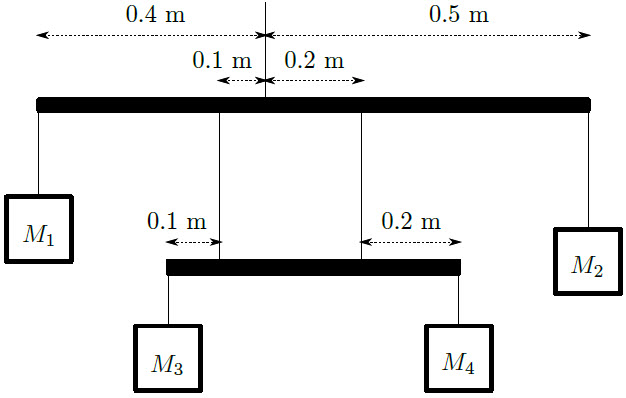 |
| 7. | รถไฟเดิมมีมวล M เคลื่อนที่ไปตามแนวราบโดยไม่มีแรงเสียดทาน และมีอัตราเร็วคงที่ เมื่อหิมะเริ่มตกลงมาเกาะรถไฟด้วยอัตรา ρ โดย ρ มีหน่วย kg/s ซึ่งรถไฟจะต้องรักษาระดับอัตราเร็ว v ให้คงที่ แม้จะมีหิมะเกาะสะสมอยู่บนรถไฟ แล้วพลังงานจลน์ของรถไฟและหิมะเพิ่มขึ้นในอัตราเท่าใด |
| A | \(0\) |
| B | \(\rm Mgv\) |
| C | \(\rm \dfrac{1}{2}Mv^2\) |
| D | \(\rm \dfrac{1}{2}\rho v^2\) |
| E | \(\rm \rho v^2\) |
ตอบ (D)
| 8. | รถไฟเดิมมีมวล M เคลื่อนที่ไปตามแนวราบโดยไม่มีแรงเสียดทาน และมีอัตราเร็วคงที่ เมื่อหิมะเริ่มตกลงมาเกาะรถไฟด้วยอัตรา ρ โดย ρ มีหน่วย kg/s ซึ่งรถไฟจะต้องรักษาระดับอัตราเร็ว v ให้คงที่ แม้จะมีหิมะเกาะสะสมอยู่บนรถไฟ กำลังต่ำสุดที่รถไฟต้องใช้รักษาระดับอัตราเร็ว v ให้คงที่ เท่ากับข้อใด |
| A | \(0\) |
| B | \(\rm Mgv\) |
| C | \(\rm \dfrac{1}{2}Mv^2\) |
| D | \(\rm \dfrac{1}{2}\rho v^2\) |
| E | \(\rm \rho v^2\) |
ตอบ (E)
| 9. | ขวด A, B และ C มีฐานเป็นวงกลมรัศมี 2 cm เหมือนกัน ถ้าเทน้ำที่มีปริมาณเท่ากัน ลงในขวดแต่ละใบ โดยไม่ให้มีน้ำล้นออกมา จงเรียงลำดับ แรง F ที่น้ำกระทำกับฐานของขวดจากมากไปหาน้อย 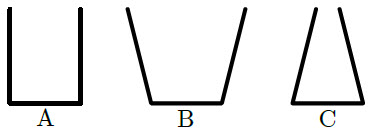 |
| 10. | หูจับแกลลอนนม มี Plug อุดอยู่เนื่องจากข้อผิดพลาดในการผลิต หลังจากเปิดฝา แล้วเทนมบางส่วนออกมา นมที่อยู่ในแกลลอนจะอยู่ต่ำกว่านมที่อยู่ในหูจับ ตามรูป ข้อใดเป็นจริงเกี่ยวกับความดันเกจ P ของนมที่ฐานด้านล่างของแกลลอน เมื่อ ρ คือ ความหนาแน่นของนม  |
| 11. | ทรงกลมตันขนาดเล็กมวล m รัศมีเล็กมาก เชื่อมกับคานบางยาว L มีมวล 2m และทรงกลมตันขนาดเล็กอันที่สองมวล M มีรัศมีเล็กมาก ถูกยิงในแนวตั้งฉากกับคานบางเหนือทรงกลมตันแรกเป็นระยะ h ดังรูป
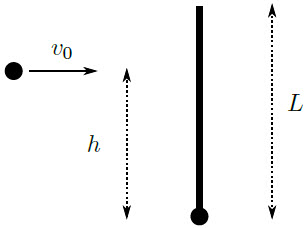 |
| 12. | ทรงกลมตันขนาดเล็กมวล m รัศมีเล็กมาก เชื่อมกับคานบางยาว L มีมวล 2m และทรงกลมตันขนาดเล็กอันที่สองมวล M มีรัศมีเล็กมาก ถูกยิงในแนวตั้งฉากกับคานบางเหนือทรงกลมตันแรกเป็นระยะ h ดังรูป
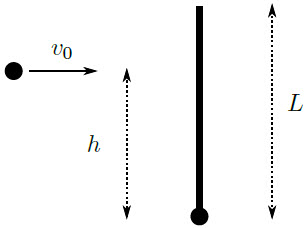 |
| 13. | เชือกเบาคล้องผ่านรอกที่ไม่มีความฝืด วัตถุมวล M และ M + m ถูกแขวนที่ปลายเชือกแต่ละด้าน ถ้า m = 0 แล้วแรงตึงเชือก T เท่ากับ Mg แล้วกรณีที่เพิ่มค่า m ถึงอนันต์ แรงตึงเชือกจะเปลี่ยนไปอย่างไร |
| A | คงที่ |
| B | ลดลง และเข้าใกล้ค่าคงที่ ที่ไม่ใช่ศูนย์ |
| C | ลดลง และเข้าใกล้ 0 |
| D | เพิ่มขึ้น และเข้าใกล้ค่าคงที่ค่าหนึ่ง |
| E | เพิ่มขึ้น และมีค่าเป็นอนันต์ |
ตอบ (D)
| 14. | กำหนดให้ วัตถุจากจุดนิ่งกลิ้งลงบนพื้นลาดเอียงโดยไม่ไถล ถ้าวัตถุในแต่ละข้อมีมวล M รัศมี R เหมือนกัน แล้วข้อใดมีอัตราเร่งมากสุด ขณะกลิ้งลงมา |
| 15. | กำหนดให้ วัตถุจากจุดนิ่งกลิ้งลงบนพื้นลาดเอียงโดยไม่ไถล ถ้าวัตถุในแต่ละข้อเป็นทรงกลมสม่ำเสมอ ที่เดิมอยู่นิ่งและถูกปล่อยออกเหมือนกัน แล้วข้อใดจะมีอัตราเร็วมากที่สุด หลังจุดศูนย์กลางมวลเคลื่อนที่ตามแนวตั้งไปได้ระยะ h แล้ว |
| A | ทรงกลมมวล M รัศมี R |
| B | ทรงกลมมวล 2M รัศมี \(\frac{1}{2}\) R |
| C | ทรงกลมมวล M/2 รัศมี 2R |
| D | ทรงกลมมวล 3M รัศมี 3R |
| E | ทุกข้อมีอัตราเร็วเท่ากัน |
ตอบ (E)
| 16. | ไม้ท่อนหนึ่งถูกวางพาดกับผนังเอียง ดังรูป ถ้าส่วนปลายของไม้ที่สัมผัสพื้นเคลื่อนที่ด้วยความเร็ว v แล้วอัตราเร็วส่วนปลายที่สัมผัสกับผนังจะมีค่าเท่ากับข้อใด
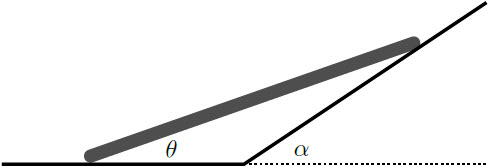 |
| A | \(\rm v\dfrac{{\sin \theta }}{{\cos (\alpha - \theta )}}\) |
| B | \(\rm v\dfrac{{\sin (\alpha - \theta )}}{{\cos (\alpha + \theta )}}\) |
| C | \(\rm v\dfrac{{\cos (\alpha - \theta )}}{{\sin (\alpha + \theta )}}\) |
| D | \(\rm v\dfrac{{\cos \theta }}{{\cos (\alpha - \theta )}}\) |
| E | \(\rm v\dfrac{{\sin \theta }}{{\cos (\alpha + \theta )}}\) |
ตอบ (D)
| 17. | วัตถุถูกขว้างลงมาในแนวดิ่งจากอาคารสูง 180 เมตร ถ้าผ่านไป 1.0 วินาที วัตถุเคลื่อนที่ได้ 60 เมตร แล้วอัตราเร็วต้นของวัตถุที่ขว้างลงมาเท่ากับข้อใด |
| 18. | แผ่นกลมถูกดึงด้วยแรง F ผ่านเชือกที่ยึดกับจุดศูนย์กลางมวล ดังรูป สมมุติว่า แผ่นกลมกลิ้งโดยไม่มีการไถล ในช่วงเวลาหนึ่ง ๆ พื้นที่ใดที่มีความเร่งเป็นศูนย์ (ถ้ามี)
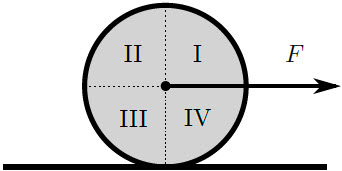 |
| 19. | ลูกฮอกกี้ถูกตีขึ้นทางลาดที่ทำมุม 30◦ กับแนวนอน ได้กราฟอัตราเร็วของลูกฮอกกี้กับเวลา ดังรูป แล้วค่าสัมประสิทธิ์แรงเสียดทานระหว่างลูกฮอกกี้กับทางลาดเท่ากับข้อใด
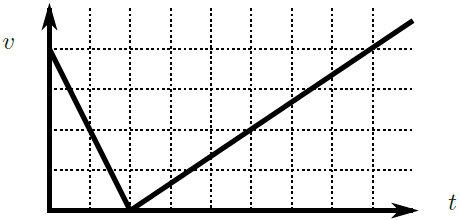 |
| 20. | วัตถุมวล m เคลื่อนที่ด้วยอัตราเร็ว v0 ชนกับวัตถุมวล M ซึ่งเดิมอยู่นิ่ง จะได้สัดส่วนการถ่ายโอนโมเมนตัม f คือ ค่าสัมบูรณ์ของโมเมนตัมสุดท้ายของ M หารด้วยโมเมนตัมเริ่มต้นของ m ถ้าการชนนั้นไม่ยืดหยุ่นสมบูรณ์ แล้วเงื่อนไขในข้อใด ที่ทำให้สัดส่วนการถ่ายโอนโมเมนตัมของสองวัตถุ มีค่ามากสุด |
| 21. | วัตถุมวล m เคลื่อนที่ด้วยอัตราเร็ว v0 ชนกับวัตถุมวล M ซึ่งเดิมอยู่นิ่ง จะได้สัดส่วนการถ่ายโอนโมเมนตัม f คือ ค่าสัมบูรณ์ของโมเมนตัมสุดท้ายของ M หารด้วยโมเมนตัมเริ่มต้นของ m ถ้าการชนนั้นยืดหยุ่นสมบูรณ์ แล้วสัดส่วนการถ่ายโอนโมเมนตัมที่มีค่ามากสุด ที่เป็นไปได้ fmax มีค่าเท่าใด |
| A | \(\rm 0 < f_{max} < \dfrac{1}{2}\) |
| B | \(\rm f_{max} = \dfrac{1}{2}\) |
| C | \(\rm \dfrac{1}{2} < f_{max} < \dfrac{3}{2}\) |
| D | \(\rm f_{max} = 2\) |
| E | \(\rm f_{max}\ge 3\) |
ตอบ (D)
| 22. | วัตถุมวล m เคลื่อนที่ด้วยอัตราเร็ว v0 ชนกับวัตถุมวล M ซึ่งเดิมอยู่นิ่ง จะได้สัดส่วนการถ่ายโอนโมเมนตัม f คือ ค่าสัมบูรณ์ของโมเมนตัมสุดท้ายของ M หารด้วยโมเมนตัมเริ่มต้นของ m สัดส่วนการถ่ายโอนพลังงาน คือ ค่าสัมบูรณ์ของพลังงานจลน์สุดท้ายของ M หารด้วยพลังงานจลน์เริ่มต้นของ m ถ้าการชนนั้นยืดหยุ่นสมบูรณ์ แล้วเงื่อนไขในข้อใด ที่ทำให้สัดส่วนการถ่ายโอนพลังงานของสองวัตถุ มีค่ามากสุด |
| 23. | สปริงขณะยังไม่ถูกดึงยาว 1.0 เมตร เมื่อยืดสปริงให้ยาว 10 เมตร การสั่นของคลื่นจากปลายหนึ่งไปสู่อีกปลายใช้เวลา 1.0 วินาที ถ้ายืดสปริงให้ยาว 20 เมตร แล้วเวลาที่ใช้ในการสั่นของคลื่นจากปลายหนึ่งไปสู่อีกปลาย จะมีค่าใกล้เคียงกับข้อใด |
| 24. | บอลมวล m เคลื่อนที่ด้วยอัตราเร็ว v ชนกับสปริงเบาที่มีค่านิจสปริง k โดยสปริงติดอยู่กับกล่องนิ่งมวล M ในอวกาศ ถ้าการชนไม่มีการสูญเสียพลังงานเชิงกล และระบบไม่เกิดการหมุน แล้วระยะหดมากสุดของสปริง x มีค่าเท่ากับข้อใด |
| A | \(\rm x = v\sqrt {\dfrac{{mM}}{{(m + M)k}}}\) |
| B | \(x = v\sqrt {\dfrac{m}{k}}\) |
| C | \(\rm x = v\sqrt {\dfrac{M}{k}}\) |
| D | \(x = v\sqrt {\dfrac{{m + M}}{k}}\) |
| E | \(\rm x = v\sqrt {\dfrac{{{{(m + M)}^3}}}{{mMk}}}\) |
ตอบ (A)
| 25. | ดาวเคราะห์ดวงหนึ่งโคจรรอบดาวฤกษ์ S ดังรูป ให้ระยะครึ่งแกนเอกถึงวงโคจร เท่ากับ a และ ระยะที่สั้นที่สุดระหว่างดาวเคราะห์กับดาวฤกษ์ มีค่าเท่า 0.5a ถ้าดาวเคราะห์เคลื่อนผ่านไป จุด P (จุดบนเส้นตรงที่ผ่านดาวฤกษ์ S และตั้งฉากกับแกนเอก) ด้วยอัตราเร็ว v1 แล้วอัตราเร็ว v2 ขณะผ่านจุด perigee มีค่าเท่ากับข้อใด
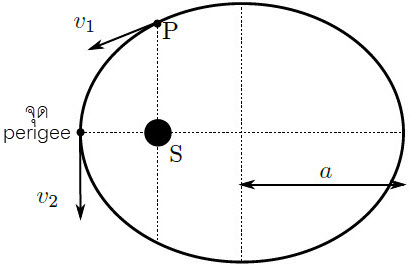 |
| A | \(\rm {v_2} = \dfrac{3}{{\sqrt 5 }}{v_1}\) |
| B | \(\rm {v_2} = \dfrac{3}{{\sqrt 7 }}{v_1}\) |
| C | \(\rm{v_2} = \dfrac{2}{{\sqrt 3 }}{v_1}\) |
| D | \(\rm {v_2} = \dfrac{{\sqrt 7 }}{{\sqrt 3 }}{v_1}\) |
| E | \(\rm {v_2} = 4{v_1}\) |
ตอบ (A)

