ข้อสอบคัดเลือกของทีม USA 2018 (ชุด B) (25 ข้อ)
| 1. | ถ้าก้อนดินขนาดใหญ่หล่นออกจากกำแพงลงสู่พื้นดิน แล้วกราฟข้อใด แสดงความเร่งที่จุดศูนย์กลางมวลของก้อนดินกับเวลา ได้ดีที่สุด |
| A |  |
| B |  |
| C | 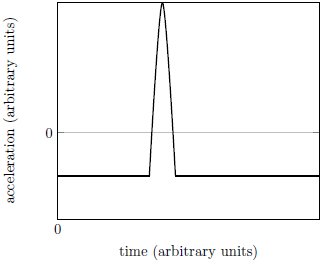 |
| D | 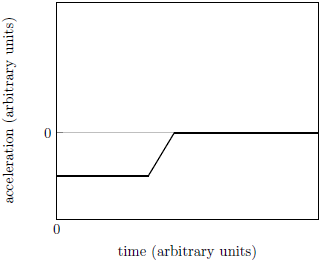 |
| E |  |
ตอบ (B)
ในการตกอย่างอิสระ ความเร่งจะเป็นค่าคงที่และมีค่าประมาณ
-10 m/s2 ทิศลง หลังจากนั้นจะมีแรงดันจากพื้น ทำให้มีความเร่งในทิศขึ้น แรงดันจะมีค่าสูงสุดค่าหนึ่ง แล้วลดลงจนเป็นศูนย์ เมื่อก้อนดินหยุดนิ่ง
ในการตกอย่างอิสระ ความเร่งจะเป็นค่าคงที่และมีค่าประมาณ
-10 m/s2 ทิศลง หลังจากนั้นจะมีแรงดันจากพื้น ทำให้มีความเร่งในทิศขึ้น แรงดันจะมีค่าสูงสุดค่าหนึ่ง แล้วลดลงจนเป็นศูนย์ เมื่อก้อนดินหยุดนิ่ง
| 2. | บล็อกสม่ำเสมอมวล 10 kg เดิมอยู่นิ่งถูกปล่อยลงมาจากพื้นเอียงที่มีความยาว 10 m เอียง 30◦ และเคลื่อนที่ลงมาจนถึงด้านล่าง ถ้าสัมประสิทธิ์แรงเสียดทานสถิตและแรงเสียดทานจลน์เท่ากับ μs = μk = 0.1 พลังงานที่สูญเสียไปกับแรงเสียดทานเท่ากับข้อใด |
| A | 0 J |
| B | 22 J |
| C | 43 J |
| D | 87 J |
| E | 164 J |
ตอบ (D)
แรงตั้งฉากที่เกิดขึ้นจะเท่ากับ \(100 (\sqrt3/2) \rm ~N\) ดังนั้น แรงเสียดทานจะเท่ากับ \(5\sqrt 3 \rm~ N\) เมื่อกระทำเป็นระยะ \(10\rm~ m\) พลังงานจะสูญเสียไปจะเท่ากับ \(50\sqrt 3 \rm ~J\) มีค่าประมาณ \(87 \rm~J\)
แรงตั้งฉากที่เกิดขึ้นจะเท่ากับ \(100 (\sqrt3/2) \rm ~N\) ดังนั้น แรงเสียดทานจะเท่ากับ \(5\sqrt 3 \rm~ N\) เมื่อกระทำเป็นระยะ \(10\rm~ m\) พลังงานจะสูญเสียไปจะเท่ากับ \(50\sqrt 3 \rm ~J\) มีค่าประมาณ \(87 \rm~J\)
| 3. | มวล 3.0 kg เคลื่อนที่ 40 m/s ไปทางขวาเกิดการพุ่งชนแล้วติดไปกับมวล 2.0 kg ที่กำลังเคลื่อนที่ไปทางขวา 20 m/s หลังเกิดการชน พลังงานจลน์ของระบบเท่ากับข้อใด หลังการชน |
| A | 600 J |
| B | 1200 J |
| C | 2600 J |
| D | 2800 J |
| E | 3400 J |
ตอบ (C)
ใช้กฎการอนุรักษ์โมเมนตัม จะได้ความเร็วต้นที่จุดศูนย์กลางมวลเท่ากับ \((3·40+2·20)/5 = 32 ~\rm m/s\) หลังการชน
ดังนั้น พลังงานจลน์จะเท่ากับ \(\dfrac{{{{\rm{m}}_{{\rm{tot}}}}{{\rm{V}}^2}}}{2} ≈ 2600\rm~ J\)
ใช้กฎการอนุรักษ์โมเมนตัม จะได้ความเร็วต้นที่จุดศูนย์กลางมวลเท่ากับ \((3·40+2·20)/5 = 32 ~\rm m/s\) หลังการชน
ดังนั้น พลังงานจลน์จะเท่ากับ \(\dfrac{{{{\rm{m}}_{{\rm{tot}}}}{{\rm{V}}^2}}}{2} ≈ 2600\rm~ J\)
| 4. | ให้ลูกบาสที่เดิมอยู่นิ่งถูกปล่อยลงมากระแทกพื้น ถ้าพิจารณาเฉพาะลูกบาสในช่วงก่อนและหลังกระแทกพื้น แล้วข้อความใดต่อไปนี้เป็นจริง |
| A | โมเมนตัม และพลังงานสุทธิของลูกบาสจะถูกอนุรักษ์ไว้ |
| B | โมเมนตัมของลูกบาสจะถูกอนุรักษ์ไว้ แต่พลังงานจลน์ไม่ถูกอนุรักษ์ไว้ |
| C | พลังงานสุทธิของลูกบาสจะถูกอนุรักษ์ไว้ แต่โมเมนตัมไม่ถูกอนุรักษ์ไว้ |
| D | พลังงานจลน์ของลูกบาสจะถูกอนุรักษ์ไว้ แต่โมเมนตัมไม่ถูกอนุรักษ์ไว้ |
| E | พลังงานจลน์ และโมเมนตัมของลูกบาสไม่ได้ถูกอนุรักษ์ไว้ |
ตอบ (E)
โมเมนตัมของลูกบาสไม่ถูกอนุรักษ์ไว้ เพราะมีแรงภายนอกจากพื้นดินมากระทำ
พลังงานจลน์ไม่ถูกอนุรักษ์ไว้ เพราะมีการเปลี่ยนพลังงานบางส่วนเป็นคลื่นเสียง เป็นการสั่นสะเทือนกับพื้น ฯลฯ
โมเมนตัมของลูกบาสไม่ถูกอนุรักษ์ไว้ เพราะมีแรงภายนอกจากพื้นดินมากระทำ
พลังงานจลน์ไม่ถูกอนุรักษ์ไว้ เพราะมีการเปลี่ยนพลังงานบางส่วนเป็นคลื่นเสียง เป็นการสั่นสะเทือนกับพื้น ฯลฯ
| 5. | ฮาร์ดดิสก์ในคอมพิวเตอร์จะหมุนถึงอัตราเร็วที่ต้องการภายใน 10 รอบ แต่เมื่อปิดเครื่องมันจะหมุนได้ถึง 50 รอบ ก่อนหยุดลง สมมุติว่า ฮาร์ดดิสก์มีความเร่งเชิงมุม α1 ในช่วงแรก และช่วงการชะลอมีความเร่งเชิงมุม α2 แล้วอัตราส่วน α1 / α2 เท่ากับข้อใด |
| A | \(\dfrac{1}{5}\) |
| B | \(\dfrac{1}{\sqrt5}\) |
| C | \(\sqrt5\) |
| D | \(5\) |
| E | \(25\) |
ตอบ (D)
ให้ ω0 คือ ความเร็วที่ต้องการ
เมื่อ ωf2 – ωi2 = 2αθ โดยในช่วงแรก ωi = 0, ωf = ω0 และในช่วงหลัง ωi = ω0, ωf = 0
แล้วค่าของ αθ จะเท่ากันทั้งสองกรณี ดังนั้น ความเร่งที่ได้จะมีค่าเป็นสัดส่วนห้าเท่า
ให้ ω0 คือ ความเร็วที่ต้องการ
เมื่อ ωf2 – ωi2 = 2αθ โดยในช่วงแรก ωi = 0, ωf = ω0 และในช่วงหลัง ωi = ω0, ωf = 0
แล้วค่าของ αθ จะเท่ากันทั้งสองกรณี ดังนั้น ความเร่งที่ได้จะมีค่าเป็นสัดส่วนห้าเท่า
| 6. | คานเบายาว L ถูกตรึงด้านหนึ่งไว้ และมีแรงกด F กระทำที่ปลายคานด้านที่ไม่ถูกตรึง จนคานยุบลงไปเป็นระยะ x โดยที่ระยะที่ยุบลงไปเป็น x นี้แปรผันตรงกับขนาดของ F และเป็นสัดส่วนผกผันกับโมเมนตัดขวาง I ซึ่งมีหน่วย m4 การยุบนี้ยังขึ้นอยู่กับมอดุลัสของยัง E ซึ่งมีหน่วย N / m2 แล้ว x จะแปรผันตรงกับ L อย่างไร |
| A | \(\rm x ∝ \sqrt L\) |
| B | \(\rm x ∝ L\) |
| C | \(\rm x ∝ L^2\) |
| D | \(\rm x ∝ L^3\) |
| E | \(\rm x ∝ L^4\) |
ตอบ (D)
ใช้การวิเคราะห์หน่วย โดยสมมุติว่า x ∝ FaEbIcLd
จะได้ a = 1, b = – 1, c = – 1 และ d = 3 ซึ่งจะทำให้ x มีหน่วยเป็น m
ดังนั้น x ∝ L3
ใช้การวิเคราะห์หน่วย โดยสมมุติว่า x ∝ FaEbIcLd
จะได้ a = 1, b = – 1, c = – 1 และ d = 3 ซึ่งจะทำให้ x มีหน่วยเป็น m
ดังนั้น x ∝ L3
| 7. | ให้ลูกตุ้มยาว L แกว่งอยู่ภายในกล่องใบหนึ่ง หากมีคนยกกล่องขึ้นมาแล้วค่อยๆ เขย่าในแนวตั้งด้วยความถี่ ω และให้แอมพลิจูดคงที่ตามช่วงเวลาหนึ่งที่กำหนด แล้วแอมพลิจูดสุดท้ายของลูกตุ้มจะมีค่ามากที่สุด เมื่อ ω เท่ากับข้อใด |
| A | \(\rm ω = \sqrt{4g/L}\) |
| B | \(\rm ω = \sqrt{2g/L}\) |
| C | \(\rm ω = \sqrt{g/L}\) |
| D | \(\rm ω = \sqrt{g/4L}\) |
| E | \(ω\) ไม่มีผลต่อแอมพลิจูดของลูกตุ้มอย่างมีนัยสำคัญ |
ตอบ (A)
ภายในกล่อง การสั่นตามแนวตั้งจะเท่ากับ g และมีความถี่ในการสั้น ω ในการเพิ่มแอมพลิจูด แรงโน้มถ่วงจะต้องเพิ่มขึ้นขณะลูกตุ้มเคลื่อนที่ลง และน้อยลงขณะลูกตุ้มเคลื่อนที่ขึ้น จึงทำให้เกิดเรโซแนนซ์ (resonance)
ดังนั้น การสั่นของลูกตุ้มแต่ละรอบจะต้องเกิดการสั่นของกล่อง 2 รอบ จึงได้ว่า \(\rm ω = \sqrt{2g/L}\)
ภายในกล่อง การสั่นตามแนวตั้งจะเท่ากับ g และมีความถี่ในการสั้น ω ในการเพิ่มแอมพลิจูด แรงโน้มถ่วงจะต้องเพิ่มขึ้นขณะลูกตุ้มเคลื่อนที่ลง และน้อยลงขณะลูกตุ้มเคลื่อนที่ขึ้น จึงทำให้เกิดเรโซแนนซ์ (resonance)
ดังนั้น การสั่นของลูกตุ้มแต่ละรอบจะต้องเกิดการสั่นของกล่อง 2 รอบ จึงได้ว่า \(\rm ω = \sqrt{2g/L}\)
| 8. | ให้สัมประสิทธิ์แรงเสียดทานสถิตและแรงเสียดทานจลน์ระหว่างลูกบอลและพื้นเท่ากับ μs = μk = μ ถ้าตอนเริ่มต้นบอลได้รับอัตราเร็วในแนวนอน โดยไม่มีความเร็วเชิงมุมรอบจุดศูนย์กลางมวล แล้วกราฟในข้อใด แสดงความเร็วเชิงมุมของลูกบอลรอบจุดศูนย์กลางมวลเทียบกับเวลา ได้ดีที่สุด |
| A |  |
| B | 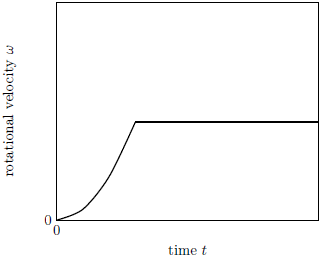 |
| C | 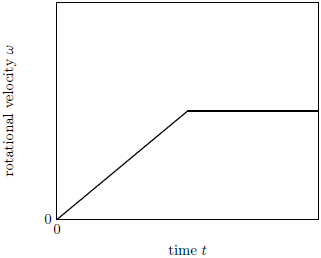 |
| D |  |
| E |  |
ตอบ (C)
แรงเสียดทานจลน์ μN จะกระทำด้วยทอร์กคงที่ ขณะที่ลูกบอลไถลไปกับพื้น
ดังนั้น ความเร็วเชิงมุมต้นจะเพิ่มขึ้นแบบเป็นเส้นตรง และความเร็วเชิงมุมจะคงที่หลังเกิดการหมุนโดยไม่ไถล
แรงเสียดทานจลน์ μN จะกระทำด้วยทอร์กคงที่ ขณะที่ลูกบอลไถลไปกับพื้น
ดังนั้น ความเร็วเชิงมุมต้นจะเพิ่มขึ้นแบบเป็นเส้นตรง และความเร็วเชิงมุมจะคงที่หลังเกิดการหมุนโดยไม่ไถล
| 9. | บอลมวล 3.0 kg เคลื่อนที่ไปทางทิศตะวันออก 10 m/s แล้วชนแบบยืดหยุ่นกับบอลมวล 2.0 kg ที่กำลังเคลื่อนที่ไปทางทิศตะวันตก 15 m/s แล้วข้อความใดต่อไปนี้ถูกต้อง หลังเกิดการชน |
| A | บอลทั้งสองจะพุ่งไปทางทิศตะวันออก |
| B | บอลมวล 3.0 kg เคลื่อนที่ไปทางทิศตะวันตก 15 m/s |
| C | บอลมวล 2.0 kg เคลื่อนที่ไปทางทิศเหนือ 10 m/s |
| D | บอลมวล 3.0 kg หยุดนิ่ง |
| E | บอลมวล 2.0 kg เคลื่อนที่ไปทางทิศใต้ 15 m/s |
ตอบ (E)
เนื่องจากโมเมนตัมสุทธิที่จุดศูนย์กลางมวลต้องมีค่าเป็นศูนย์ ทำให้โมเมนตัมสุดท้ายจะต้องมีค่าเท่ากัน และมีทิศตรงข้าม และเพื่ออนุรักษ์พลังงาน ความเร็วสุดท้ายของแต่ละลูกจะต้องเท่ากับความเร็วต้น ซึ่งข้อที่ครอบคลุมทั้งหมดคือ (E) ( ส่วนบอลมวล 3.0 kg จะเคลื่อนที่ไปทางทิศเหนือ 10 m/s หลังการชน )
เนื่องจากโมเมนตัมสุทธิที่จุดศูนย์กลางมวลต้องมีค่าเป็นศูนย์ ทำให้โมเมนตัมสุดท้ายจะต้องมีค่าเท่ากัน และมีทิศตรงข้าม และเพื่ออนุรักษ์พลังงาน ความเร็วสุดท้ายของแต่ละลูกจะต้องเท่ากับความเร็วต้น ซึ่งข้อที่ครอบคลุมทั้งหมดคือ (E) ( ส่วนบอลมวล 3.0 kg จะเคลื่อนที่ไปทางทิศเหนือ 10 m/s หลังการชน )
| 10. | ให้ลูกโป่งที่มีอากาศบรรจุไว้จมลงในน้ำที่ความลึก h และมีแรงลอยตัว B0 เมื่อลูกโป่งจมลงที่ความลึก 2h จะมี แรงลอยตัว B สมมุติว่า น้ำไม่สามารถบีบอัดได้ แต่ลูกโป่งและอากาศสามารถบีบอัดได้ แล้วแรงลอยตัว B จะเป็นไปตามข้อใด |
| A | B ≥ 2B0 |
| B | B0 < B < 2B0 |
| C | B = B0 |
| D | B < B0 |
| E | คำตอบขึ้นกับแรงบีบอัดของลูกโป่งและอากาศ |
ตอบ (D)
แรงลอยตัวคือ ρV โดย ρ คือความหนาแน่นของน้ำ และ V คือปริมาตรน้ำจะถูกแทนที่ เนื่องจากน้ำไม่สามารถบีบอัดตัวได้ แสดงว่า ρ จะคงที่ ส่วน V จะลดลง ส่วนลูกโป่งและอากาศนั้นสามารถบีบอัดได้
แรงลอยตัวคือ ρV โดย ρ คือความหนาแน่นของน้ำ และ V คือปริมาตรน้ำจะถูกแทนที่ เนื่องจากน้ำไม่สามารถบีบอัดตัวได้ แสดงว่า ρ จะคงที่ ส่วน V จะลดลง ส่วนลูกโป่งและอากาศนั้นสามารถบีบอัดได้
| 11. | วงเชือกถูกหมุนด้วยความเร็วเชิงมุม ω0 ในอวกาศคลื่นตามขวางในเส้นเชือกมีอัตราเร็วเชิงมุม v0 เมื่อวัดในกรอบอ้างอิงที่หมุนไปพร้อมกับเชือก (เห็นเชือกอยู่นิ่งในกรอบอ้างอิงนี้) ถ้าเพิ่มความเร็วเชิงมุมของเชือกเป็นสองเท่า แล้วอัตราเร็วใหม่ของคลื่นตามขวางที่วัดในกรอบอ้างอิงที่หมุนไปพร้อมกับเชือก (เห็นเชือกอยู่นิ่งในกรอบอ้างอิงนี้) จะเท่ากับข้อใด |
| A | \(\rm v_0\) |
| B | \(\sqrt 2 \rm v_0\) |
| C | \(2\rm v_0\) |
| D | \(4\rm v_0\) |
| E | \(8 \rm v_0\) |
ตอบ (C)
พิจารณาที่ส่วนเล็ก ๆ ของเชือก แรงตึงที่ปลายแต่ละด้านของเชือกจะเข้าสู่ศูนย์กลาง ดังนั้น \(\rm T ∝ ω^2\) ทำให้อัตราเร็วคลื่นเท่ากับ \(\rm v = \sqrt{T/μ}∝ ω\) ซึ่งตรงกับข้อ (C)
พิจารณาที่ส่วนเล็ก ๆ ของเชือก แรงตึงที่ปลายแต่ละด้านของเชือกจะเข้าสู่ศูนย์กลาง ดังนั้น \(\rm T ∝ ω^2\) ทำให้อัตราเร็วคลื่นเท่ากับ \(\rm v = \sqrt{T/μ}∝ ω\) ซึ่งตรงกับข้อ (C)
| 12. | ให้เด็กคนหนึ่งยืนอยู่ในสถานีอวกาศวงกลมที่กำลังหมุนอยู่ ถ้าเขาโยนลูกบอลไปในทิศทางหนึ่งขณะสถานีอวกาศกำลังหมุน แล้วลูกบอลย้อนกลับมาหาเขาหลังสถานีอวการหมุนไปได้ครึ่งรอบ แล้ววิถีของลูกบอลจากจุดที่เด็กคนนั้นเห็นจะเป็นไปตามข้อใด ให้เด็กยืนอยู่ที่ด้านล่างของสถานีอวกาศ แต่รูปจะแสดงเฉพาะตำแหน่งเริ่มต้นของลูกบอลเท่านั้น |
| A | 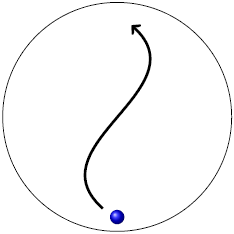 |
| B | 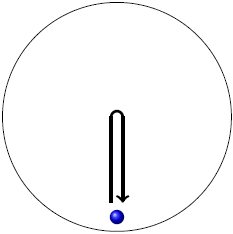 |
| C | 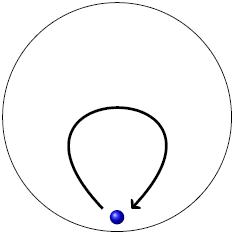 |
| D | 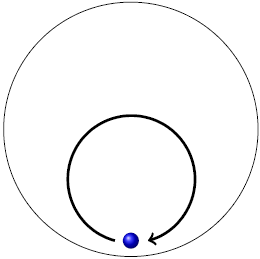 |
| E | 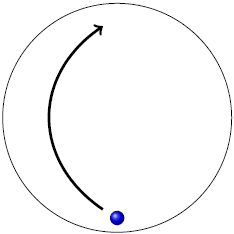 |
ตอบ (C)
โจทย์บอกว่าเด็กรับลูกบอลได้ ดังนั้นวิถีของลูกบอลจะต้องเริ่มและสิ้นสุดที่เด็กคนนั้น ทำให้ข้อ A และ E ไม่ใช่คำตอบ เหลือ B, C, D พิจารณาที่ความเร็วของเด็กขณะขว้างลูกบอลออกไป ขณะที่ลูกบอลจะเคลื่อนที่ไปข้างหน้า ตัวเด็กก็จะเคลื่อนที่ไปทางขวา ดังนั้น ในมุมมองของเด็ก ความเร็วสัมพัทธ์จะมีการเคลื่อนที่สองทิศทาง คือ ไปข้างหน้าและไปทางซ้าย จึงตอบข้อ C
โจทย์บอกว่าเด็กรับลูกบอลได้ ดังนั้นวิถีของลูกบอลจะต้องเริ่มและสิ้นสุดที่เด็กคนนั้น ทำให้ข้อ A และ E ไม่ใช่คำตอบ เหลือ B, C, D พิจารณาที่ความเร็วของเด็กขณะขว้างลูกบอลออกไป ขณะที่ลูกบอลจะเคลื่อนที่ไปข้างหน้า ตัวเด็กก็จะเคลื่อนที่ไปทางขวา ดังนั้น ในมุมมองของเด็ก ความเร็วสัมพัทธ์จะมีการเคลื่อนที่สองทิศทาง คือ ไปข้างหน้าและไปทางซ้าย จึงตอบข้อ C
| 13. | ให้กล่องสองอัน มีมวล m1 = 2.0 และ m2 = 1.0 วางซ้อนกันบนโต๊ะลื่น ดังรูป ถ้าสัมประสิทธิ์แรงเสียดทานสถิตระหว่างกล่องทั้งสองเท่ากับ μs = 0.20 แล้วแรงในแนวนอนน้อยสุดที่กระทำกับกล่องด้านบน เพื่อให้กล่องด้านบนไถลไปบนกล่องล่างเท่ากับข้อใด
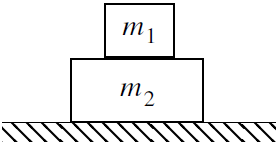 |
| A | 4.0 N |
| B | 6.0 N |
| C | 8.0 N |
| D | 12.0 N |
| E | กล่องบนจะไม่มีทางไถลไปบนกล่องล่าง |
ตอบ (D)
สมมุติว่า มวล m1 กำลังจะขยับ แล้วแรงเสียดทานมากสุดที่เป็นไปได้จะเท่ากับ 4 N ในขณะที่ m1 และ m2 มีความเร่งเท่ากัน จะได้ F – 4 N = 8 N
ดังนั้น F = 12 N
สมมุติว่า มวล m1 กำลังจะขยับ แล้วแรงเสียดทานมากสุดที่เป็นไปได้จะเท่ากับ 4 N ในขณะที่ m1 และ m2 มีความเร่งเท่ากัน จะได้ F – 4 N = 8 N
ดังนั้น F = 12 N
| 14. | หลอดด้ายทำจากทรงกระบอกและมีแผ่นวงกลมบางๆ ติดหัวท้ายกระบอก ดังรูป ให้ทรงกระบอกมีรัศมี r = 0.75 cm แผ่นวงกลมแต่ละวงมีรัศมี R = 1.00 cm และมีเชือกพันรอบแกนหลอดด้ายสองสามรอบ แล้วขนาดของ θ ที่ดึงเชือกแล้วหลอดด้ายจะเคลื่อนที่โดยไม่หมุนเท่ากับข้อใด
 |
| A | 31.2° |
| B | 41.4° |
| C | 54.0° |
| D | 60.8° |
| E | 81.5° |
ตอบ (B)
หากไม่ต้องการให้หลอดด้ายกลิ้ง ต้องมีทอร์กเป็นศูนย์ ณ จุดที่หลอดด้ายสัมผัสกับพื้น กรณีนั้นจะเกิดขึ้นเมื่อด้ายอยู่ในแนวที่ตัดกับจุดที่สัมผัสพื้น เมื่อวาดสามเหลี่ยมมุมฉากจะได้ sin(90° - θ) = r / R เมื่อแทนค่าจะได้ θ = 41.4
สังเกตว่า การเลือกจุดสัมผัสพื้นเป็นจุดอ้างอิง ทำให้ไม่ต้องคำนึงถึงแรงเสียดทาน
หากไม่ต้องการให้หลอดด้ายกลิ้ง ต้องมีทอร์กเป็นศูนย์ ณ จุดที่หลอดด้ายสัมผัสกับพื้น กรณีนั้นจะเกิดขึ้นเมื่อด้ายอยู่ในแนวที่ตัดกับจุดที่สัมผัสพื้น เมื่อวาดสามเหลี่ยมมุมฉากจะได้ sin(90° - θ) = r / R เมื่อแทนค่าจะได้ θ = 41.4
สังเกตว่า การเลือกจุดสัมผัสพื้นเป็นจุดอ้างอิง ทำให้ไม่ต้องคำนึงถึงแรงเสียดทาน
| 15. | ถ้าคุณยืนถือหนังสือฟิสิกส์เล่มใหญ่อยู่บนเครื่องชั่ง แล้วอ่านน้ำหนักได้ 700 นิวตัน ขณะยืนนิ่งอยู่ และที่เวลา t = 1 s คุณเริ่มยกหนังสือขึ้น จน t = 2 s หนังสืออยู่สูงขึ้นไปครึ่งเมตรแล้วหยุดนิ่งอีกครั้ง แล้วกราฟในข้อใด แสดงน้ำหนักที่อ่านได้เทียบกับเวลาได้ดีที่สุด |
| A | 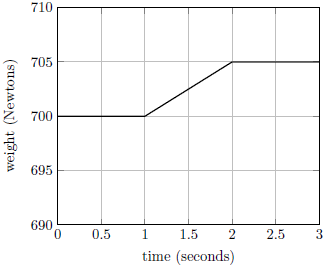 |
| B |  |
| C | 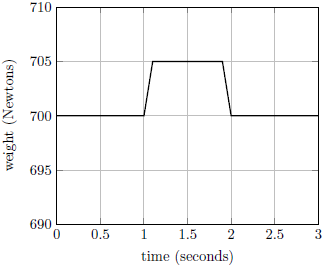 |
| D | 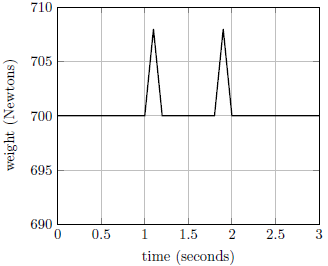 |
| E | 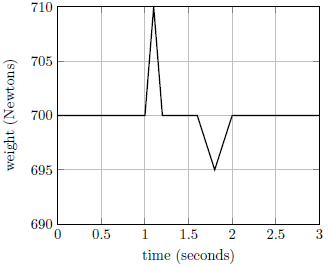 |
ตอบ (E)
ความเร็วที่จุดศูนย์กลางมวลของคุณและหนังสือไม่ว่าจะก่อนหรือหลังก็จะเท่ากับศูนย์เสมอ
ดังนั้น ค่าเฉลี่ยที่อ่านสเกลได้จะต้องเท่ากับ 700 N (ซึ่งรวมกับน้ำหนักด้วย) โดยช่วงต้นค่าจะเพิ่มขึ้น เพราะมีการใส่แรงอย่างฉบับพลันบนหนังสือ ทำให้มีแรงจากหนังสือกดลงมา และในช่วงท้ายค่าก็จะลดต่ำลง เพราะ ความเร็วของหนังสือลดลง
ความเร็วที่จุดศูนย์กลางมวลของคุณและหนังสือไม่ว่าจะก่อนหรือหลังก็จะเท่ากับศูนย์เสมอ
ดังนั้น ค่าเฉลี่ยที่อ่านสเกลได้จะต้องเท่ากับ 700 N (ซึ่งรวมกับน้ำหนักด้วย) โดยช่วงต้นค่าจะเพิ่มขึ้น เพราะมีการใส่แรงอย่างฉบับพลันบนหนังสือ ทำให้มีแรงจากหนังสือกดลงมา และในช่วงท้ายค่าก็จะลดต่ำลง เพราะ ความเร็วของหนังสือลดลง
| 16. | เครื่องบินจะบินโดยใช้การเอียงบริเวณขอบส่วนปลายปีกของเครื่องลงด้วยมุมเล็ก ๆ θ เรียกว่า มุมที่สร้างแรงยกตัว ขณะออกบิน ถ้าเครื่องบินมีอัตราเร็วบนพื้นดิน v แล้วแรงยกตัวจะแปรผันตาม v2θ และแรงฉุดเพื่อเอาชนะแรงต้านอากาศจะแปรผันตาม v2 พิจารณาเครื่องบินที่อยู่บนระดับความสูงหนึ่ง และมีอัตราเร็วคงที่ตอนอยู่บนพื้นดิน v ถ้ามีลมพัดจากหางไปยังหัวเครื่องบินด้วยความเร็ว w < v (ขนาดของ w วัดเทียบกับพื้นดิน) ( อากาศจะช่วยดันเครื่องบิน ให้บินไปยังทิศที่เราต้องการ ) แล้วกำลังของเครื่องยนต์ และมุมที่สร้างแรงยกตัวจะเปลี่ยนไปอย่างไร เพื่อให้ความเร็วของเครื่องบินยังคงบินในแนวระดับด้วยอัตราเร็วเท่าเดิม |
| A | กำลังของเครื่องยนต์จะลดลง และมุมที่สร้างแรงยกตัวจะลดลง |
| B | กำลังของเครื่องยนต์จะลดลง และมุมที่สร้างแรงยกตัวจะเท่าเดิม |
| C | กำลังของเครื่องยนต์จะลดลง และมุมที่สร้างแรงยกตัวจะเพิ่มขึ้น |
| D | กำลังของเครื่องยนต์จะเพิ่มขึ้น และมุมที่สร้างแรงยกตัวจะลดลง |
| E | กำลังของเครื่องยนต์จะเพิ่มขึ้น และมุมที่สร้างแรงยกตัวจะเพิ่มขึ้น |
ตอบ (C)
ให้ u เป็นความเร็วสัมพัทธ์ระหว่างเครื่องบินกับอากาศ หากต้องคงแรงยกไว้ ในกรณีที่ u ลดลง θ ต้องเพิ่มขึ้น
ส่วนแรงฉุดนั้นแปรผันกับ u2 ทำให้กำลังของเครื่องยนต์ที่แปรผันกับ u3 ต้องลดลง
ให้ u เป็นความเร็วสัมพัทธ์ระหว่างเครื่องบินกับอากาศ หากต้องคงแรงยกไว้ ในกรณีที่ u ลดลง θ ต้องเพิ่มขึ้น
ส่วนแรงฉุดนั้นแปรผันกับ u2 ทำให้กำลังของเครื่องยนต์ที่แปรผันกับ u3 ต้องลดลง
| 17. | ไม้กระโดดจำลองประกอบด้วยสปริงเบามีค่านิจสปริง k ติดที่ด้านล่างของบล็อกมวล m ให้ไม้กระโดดถูกปล่อยลง โดยสปริงจะกระแทกพื้นด้วยอัตราเร็ว v หลังจากการกระแทกแล้ว ส่วนปลายด้านล่างของสปริงจะถูกยึดติดกับพื้น
 |
| A | \(\rm v\) |
| B | \(\rm v + 2mg^2/kv\) |
| C | \(\rm v + mg^2/kv\) |
| D | \(\rm \sqrt{v + 2mg^2/kv}\) |
| E | \(\rm \sqrt{v + mg^2/kv}\) |
ตอบ (E)
จุดสมดุลอยู่ต่ำกว่าตำแหน่งที่สปริงไม่ยืดไม่หดเท่ากับ Δy
ดังนั้น พลังงานเริ่มต้นจะเท่ากับ \(\rm E = mv^2/2 + K (Δy)^2/2\) ความเร็วสูงสุดหาจาก \(\rm mv_{max}^ 2 / 2 = E\)
จะได้ \(\rm v_{max} = \sqrt{(v^2 +mg^2/k)}\) และมวลจะสั่นรอบจุดสมดุล
จุดสมดุลอยู่ต่ำกว่าตำแหน่งที่สปริงไม่ยืดไม่หดเท่ากับ Δy
ดังนั้น พลังงานเริ่มต้นจะเท่ากับ \(\rm E = mv^2/2 + K (Δy)^2/2\) ความเร็วสูงสุดหาจาก \(\rm mv_{max}^ 2 / 2 = E\)
จะได้ \(\rm v_{max} = \sqrt{(v^2 +mg^2/k)}\) และมวลจะสั่นรอบจุดสมดุล
| 18. | ให้สปริงที่มีความยาวตามปกติ l1 มีค่านิจสปริง k1 วางขนานกับสปริงที่มีความยาวตามปกติ l2 และมีค่านิจสปริง k2 และมีแรง F กระทำในแต่ละด้าน
 |
| A | k = k1 + k2 และ l = l1l2/(l1 + l2) |
| B | k = k1 + k2 และ l = ( l1 k1 + l2 k2 )/( k1 + k2 ) |
| C | k = k1 + k2 และ l = ( l1 k2 + l2 k1 )/( k1 + k2 ) |
| D | k = ( l1 k1 + l2 k2 )/ (l1+l2) และ l = ( l1 k1 + l2 k2 )/( k1 + k2 ) |
| E | k = ( l2 k1 + l1 k2 )/ (l1+l2) และ l = ( l1 k2 + l2 k1 )/( k1 + k2 ) |
ตอบ (B)
แรงในการคงสภาพเท่ากับ F = k1 (x - l1) + k2 (x - l2) = k (x - l) จากนั้นหาคำตอบด้วยพีชคณิต
แรงในการคงสภาพเท่ากับ F = k1 (x - l1) + k2 (x - l2) = k (x - l) จากนั้นหาคำตอบด้วยพีชคณิต
| 19. | (เกินหลักสูตรสอบเข้า สอวน.) ในการทดสอบอัตราเร็วเสียง นักเรียนคนหนึ่งวัดระยะทางที่คลื่นเสียงเดินทางไปได้ 75.0 ± 2.0 cm และใช้เวลาในการเดินทาง 2.15 ± 0.10 ms สมมุติว่าความคลาดเคลื่อนมีการกระจายตัวแบบ Gaussian (มีการแจกแจงแบบปกติ) แล้วอัตราเร็วที่คำนวณได้ควรเท่ากับข้อใด |
| A | 348.8 ± 0.5 m/s |
| B | 348.8 ± 0.8 m/s |
| C | 349 ± 8 m/s |
| D | 349 ± 15 m/s |
| E | 349 ± 19 m/s |
ตอบ (E)
คำตอบข้อนี้เราจะใช้เศษส่วนความคลาดเคลื่อน ( ถ้าต้องการคำอธิบายเพิ่มให้ดูการหา F = ma ) จาก v ∝ d / t เศษส่วนความคลาดเคลื่อนของการวัด หาจาก
คำตอบข้อนี้เราจะใช้เศษส่วนความคลาดเคลื่อน ( ถ้าต้องการคำอธิบายเพิ่มให้ดูการหา F = ma ) จาก v ∝ d / t เศษส่วนความคลาดเคลื่อนของการวัด หาจาก
\(\sqrt{ \left(\dfrac{2.0}{75.0}\right)^2 + \left(\dfrac{0.10}{2.15} \right)^2} = 5.4%\)
แปลงเป็นค่าคลาดเคลื่อนได้ (0.054)(349 m/s) =19 m/s| 20. | ให้เชือกที่แข็งแรงและสม่ำเสมอยาว L วางราบบนโต๊ะที่มีความยาว L/3 และมีสัมประสิทธิ์แรงเสียดทาน μs = 1/7 โดยทั้งสองด้านของโต๊ะจะมีเชือกยาว L/3 เลยออกมาจากโต๊ะเท่ากัน ให้เชือกพาดผ่านขอบโต๊ะที่โค้งและมีความลื่น และไร้แรงเสียดทาน สมมุติว่า เราดึงปลายเชือกด้านหนึ่งที่ห้อยอยู่เป็นระยะ x แล้วปล่อยไว้นิ่งๆ โดยปลายเชือกทั้งสองด้านยังไม่แตะพื้น แล้วค่า x มากสุดที่เชือกจะไม่หล่นลงมาเท่ากับข้อใด |
| A | L/42 |
| B | L/21 |
| C | L/14 |
| D | 2L/21 |
| E | 3L/14 |
ตอบ (A)
มีแค่เชือกส่วนที่อยู่บนโต๊ะเท่านั้นที่เกิดแรงเสียดทาน และมวลของเชือกบนโต๊ะเท่ากับเป็น M / 3 ดังนั้น แรงเสียดทานที่ต้องเอาชนะเท่ากับ
ผลต่างระหว่างแรงของเชือกสองด้านที่เลยออกมาจึงเท่ากับ
ดังนั้น เงื่อนไขในการลื่นหล่นลงมา คือ Δf > f หรือ x > L / 42
มีแค่เชือกส่วนที่อยู่บนโต๊ะเท่านั้นที่เกิดแรงเสียดทาน และมวลของเชือกบนโต๊ะเท่ากับเป็น M / 3 ดังนั้น แรงเสียดทานที่ต้องเอาชนะเท่ากับ
f = μmg = 1/7(mg/3)
ผลต่างระหว่างแรงของเชือกสองด้านที่เลยออกมาจึงเท่ากับ
ΔF = 2x (mg/L)
ดังนั้น เงื่อนไขในการลื่นหล่นลงมา คือ Δf > f หรือ x > L / 42
| 21. | คานสม่ำเสมอยาว L มวล M มีจุดหมุนอยู่ที่ระยะ x ห่างจากศูนย์กลางคาน ถ้าคานที่เดิมอยู่นิ่งถูกปล่อยลงมาจากตำแหน่งในแนวนอน แล้วคาบของการแกว่งจะน้อยสุดเมื่อ x เท่ากับข้อใด |
| A | \(\rm x = L/2\) |
| B | \(\rm x = L/2\sqrt3\) |
| C | \(\rm x = L/4\) |
| D | \(\rm x = L/4\sqrt3\) |
| E | \(\rm x = L/12\) |
ตอบ (B)
คานในที่นี้เสมือนเป็นลูกตุ้ม และมีคาบเป็นสัดส่วนกับ \(\rm \sqrt{I/Mgx}\) โดย \(\rm I = ML^2/12 + Mx^2\) โดยทฤษฎีบทแกนขนาน เราควรจะเลือก x ที่ทำให้ \(\rm (L^2/12 + x^2)/x\) ต่ำสุด เราสามารถหาโดยใช้แคลคูลัสหรือใช้กรณีการเท่ากันใน AM-GM inequality ซึ่งทั้งสองวิธีจะได้ \(\rm x = L/2\sqrt3\)
สำหรับ AM-GM inequality
ให้ \(\rm a = L^2/12x ,~ b = x\) จะได้ว่า
ซึ่งเป็นจุดที่ \(\dfrac{{{{\rm{L}}^2}}}{{12{\rm{x}}}}{\rm{ + }}\,\,{\rm{x}}\) มีค่าน้อยสุด
คานในที่นี้เสมือนเป็นลูกตุ้ม และมีคาบเป็นสัดส่วนกับ \(\rm \sqrt{I/Mgx}\) โดย \(\rm I = ML^2/12 + Mx^2\) โดยทฤษฎีบทแกนขนาน เราควรจะเลือก x ที่ทำให้ \(\rm (L^2/12 + x^2)/x\) ต่ำสุด เราสามารถหาโดยใช้แคลคูลัสหรือใช้กรณีการเท่ากันใน AM-GM inequality ซึ่งทั้งสองวิธีจะได้ \(\rm x = L/2\sqrt3\)
สำหรับ AM-GM inequality
ให้ \(\rm a = L^2/12x ,~ b = x\) จะได้ว่า
\(\begin{align*} \frac{{(a + b)}}{2}\,\, &\ge \,\,\sqrt {{\rm{ab}}} \\ \frac{{{{\rm{L}}^2}}}{{12{\rm{x}}}}\,\, + \,\,{\rm{x}}\,\, &\ge \,\,2\sqrt {\frac{{{{\rm{L}}^2}}}{{12}}} \end{align*}\)
และทั้งสองข้างจะเท่ากัน เมื่อ a = b หรือ \({\rm{x}} = \sqrt {\dfrac{{{{\rm{L}}^2}}}{{12}}} \)ซึ่งเป็นจุดที่ \(\dfrac{{{{\rm{L}}^2}}}{{12{\rm{x}}}}{\rm{ + }}\,\,{\rm{x}}\) มีค่าน้อยสุด
| 22. | ให้มวล m สองอัน เชื่อมติดกันบนรอก ดังรูป
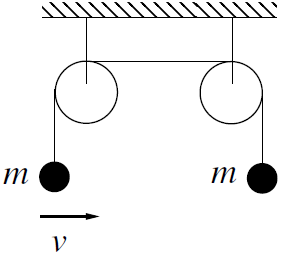 |
| A | ยังคงอยู่นิ่ง |
| B | จะสั่นในแนวตั้ง และมีการเคลื่อนที่สุทธิในทิศขึ้น |
| C | จะสั่นในแนวตั้ง และมีการเคลื่อนที่สุทธิในทิศลง |
| D | จะสั่นในแนวตั้ง โดยไม่มีการเคลื่อนที่สุทธิ |
| E | จะสั่นในแนวนอน โดยไม่มีการเคลื่อนที่สุทธิ |
ตอบ (B)
มวลที่อยู่ด้านขวาจะสั่นเพราะแรงตึงในเส้นเชือกเกิดการสั่น แต่มันจะไม่สั่นในแนวนอน เพราะ ไม่ทอร์กในแนวนั้น สมมุติว่าการสั่นเกิดขึ้นในแนวนอนโดยไม่มีแรงลัพธ์ แล้วค่าเฉลี่ยแรงตึงในแกน y ที่กระทำบนมวลทางด้านซ้ายจะเท่ากับ mg แต่ในทางตรงข้ามแรงตึงบนแกน x จะไม่เท่ากับศูนย์ ทำให้ค่าเฉลี่ยของแรงตึงมีค่ามากกว่า mg ดังนั้น มวลทางขวาจึงสั่นและเคลื่อนที่ขึ้นไปข้างบน
มวลที่อยู่ด้านขวาจะสั่นเพราะแรงตึงในเส้นเชือกเกิดการสั่น แต่มันจะไม่สั่นในแนวนอน เพราะ ไม่ทอร์กในแนวนั้น สมมุติว่าการสั่นเกิดขึ้นในแนวนอนโดยไม่มีแรงลัพธ์ แล้วค่าเฉลี่ยแรงตึงในแกน y ที่กระทำบนมวลทางด้านซ้ายจะเท่ากับ mg แต่ในทางตรงข้ามแรงตึงบนแกน x จะไม่เท่ากับศูนย์ ทำให้ค่าเฉลี่ยของแรงตึงมีค่ามากกว่า mg ดังนั้น มวลทางขวาจึงสั่นและเคลื่อนที่ขึ้นไปข้างบน
| 23. | ให้มวล m1 และ m2 เชื่อมกันด้วยคานแข็งเบายาว L วางราบบนโต๊ะลื่น ที่เวลา t = 0 มวลก้อนแรกได้รับแรงดลในทิศตั้งฉากกับคาน จนมีอัตราเร็ว v ในขณะนั้นมวลก้อนที่สองยังคงอยู่นิ่ง แล้วมวลก้อนที่สองจะหยุดนิ่งอีกครั้งตอน t เท่ากับข้อใด |
| A | \(\rm t = 2πL / v\) |
| B | \(\rm t = π ( m_1 + m_2 )L / m_2v \) |
| C | \(\rm t = 2πm_2L / ( m_1 + m_2 )v\) |
| D | \(\rm t = 2πm_1m_2L / ( m_1 + m_2 )^2v\) |
| E | \(\rm t = 2πm_1L / ( m_1 + m_2 )v \) |
ตอบ (A)
ข้อนี้มีสองการเคลื่อนที่ซ้อนทับกันอยู่ มวลทั้งสองเคลื่อนที่ด้วยอัตราเร็ว \(\rm m_1v / (m_1 + m_2)\) และการเคลื่อนที่เป็นวงกลมรอบจุดศูนย์กลางมวล โดยอัตราเร็วของมวลก้อนแรกเท่ากับ \(\rm m_2v / (m_1 + m_2)\) แล้วมวลก้อนสองหยุดนิ่งอีกครั้งหลังวนเป็นวงกลมครบหนึ่งรอบ รัศมีวงกลมของมวลก้อนแรก (เมื่อมองจากจุดศูนย์กลางมวล) เท่ากับ \(\rm Lm_2 / (m_1 + m_2)\) จะมีคาบ \(\rm t = 2πL / v\) หรือคิดจากรัศมีและมีมวลของก้อนที่สองก็ได้เช่นกัน
ข้อนี้มีสองการเคลื่อนที่ซ้อนทับกันอยู่ มวลทั้งสองเคลื่อนที่ด้วยอัตราเร็ว \(\rm m_1v / (m_1 + m_2)\) และการเคลื่อนที่เป็นวงกลมรอบจุดศูนย์กลางมวล โดยอัตราเร็วของมวลก้อนแรกเท่ากับ \(\rm m_2v / (m_1 + m_2)\) แล้วมวลก้อนสองหยุดนิ่งอีกครั้งหลังวนเป็นวงกลมครบหนึ่งรอบ รัศมีวงกลมของมวลก้อนแรก (เมื่อมองจากจุดศูนย์กลางมวล) เท่ากับ \(\rm Lm_2 / (m_1 + m_2)\) จะมีคาบ \(\rm t = 2πL / v\) หรือคิดจากรัศมีและมีมวลของก้อนที่สองก็ได้เช่นกัน
| 24. | มวล m ถูกวางที่จุดศูนย์กลางของครึ่งทรงกลมบางที่มีรัศมี R และมีมวลหนาแน่น σ โดย σ มีหน่วย kg/m2
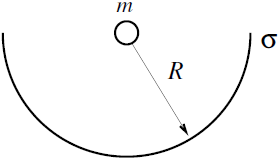 |
| A | \(\rm (1/3) (πGmσ)\) |
| B | \(\rm (2/3) (πGmσ) \) |
| C | \(\rm (1/\sqrt2) (πGmσ) \) |
| D | \(\rm (3/4) (πGmσ)\) |
| E | \(\rm πGmσ\) |
ตอบ (E)
เราจะใช้กฏข้อที่สามของนิวตันในการหาแรง โดยแรงจากทรงกลมต่อ m จะเท่ากับแรงจาก m ที่กระทำต่อทรงกลม พิจารณาส่วนเล็กๆ ของทรงกลม เนื่องจากความดันจากแรงที่กระทำบนพื้นที่เล็กๆ เท่ากับ \(\rm P = Gmσ / R^2\) ซึ่งเท่ากันทุกส่วนของทรงกลม เราจึงสามารถพิจารณาเสมือนทรงกลมบรรจุแก๊สที่มีความดัน P เนื่องจากครึ่งวงกลมไม่สามารถขยับเองได้ แรงลัพธ์บนทรงกลมจึงเท่ากับ \(\rm πR2P\) ( คิดจากprojected area ) ดังนั้นแรงที่กระทำบนมวล m เท่ากับ \(\rm π (Gmσ)\)
เราจะใช้กฏข้อที่สามของนิวตันในการหาแรง โดยแรงจากทรงกลมต่อ m จะเท่ากับแรงจาก m ที่กระทำต่อทรงกลม พิจารณาส่วนเล็กๆ ของทรงกลม เนื่องจากความดันจากแรงที่กระทำบนพื้นที่เล็กๆ เท่ากับ \(\rm P = Gmσ / R^2\) ซึ่งเท่ากันทุกส่วนของทรงกลม เราจึงสามารถพิจารณาเสมือนทรงกลมบรรจุแก๊สที่มีความดัน P เนื่องจากครึ่งวงกลมไม่สามารถขยับเองได้ แรงลัพธ์บนทรงกลมจึงเท่ากับ \(\rm πR2P\) ( คิดจากprojected area ) ดังนั้นแรงที่กระทำบนมวล m เท่ากับ \(\rm π (Gmσ)\)
| 25. | ไม้บรรทัด และวัดความยาวท่อได้ 1.00 ± 0.01 m โดยใช้ไม้เมตร หากต้องการให้ผลลัพธ์แม่นยำขึ้น เราสามารถทำได้หลายวิธี ดังนี้
วิธีที่ 1 : เปลี่ยนจากไม้บรรทัด เป็น คาลิปเปอร์ ที่มีความคลาดเคลื่อน 0.01 cm
วิธีที่ 2 : เปลี่ยนจากไม้เมตร เป็น ตลับเมตร ที่มีความคลาดเคลื่อน 0.001 m
วิธีที่ 3 : วัดใหม่ โดยแยกเป็นสิบครั้งแล้วหาค่าเฉลี่ยของผลลัพธ์
ข้อใดเปรียบเทียบความคลาดเคลื่อนของแต่ละวิธีได้ถูกต้องที่สุด |
| A | วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด ในขณะที่วิธีที่ 1 และ 2 มีความคลาดเคลื่อนเท่ากัน |
| B | วิธีที่ 3 มีความคลาดเคลื่อนสูงที่สุด ในขณะที่วิธีที่ 1 และ 2 มีความคลาดเคลื่อนเท่ากัน |
| C | วิธีที่ 1 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 2 มีความคลาดเคลื่อนต่ำที่สุด |
| D | วิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด |
| E | วิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด |
ตอบ (D)
คำตอบข้อนี้เราจะใช้เศษส่วนความคลาดเคลื่อน ( ถ้าต้องการคำอธิบายเพิ่มให้ดูการหา F = ma ) ตามกฎที่อธิบายไว้ที่ เศษส่วนความคลาดเคลื่อนของค่าเฉลี่ยของการทดลอง N ที่เป็นอิสระ คือ จะถูกลดลงโดย \(\rm 1 / \sqrt N\) พื้นที่ผิวหาจากรัศมีคูณความยาว ดังนั้น เศษส่วนความคลาดเคลื่อนที่จะถูกเพิ่มเข้าไปในแต่ละวิธีจะได้ดังนี้
ดังนั้น วิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด
คำตอบข้อนี้เราจะใช้เศษส่วนความคลาดเคลื่อน ( ถ้าต้องการคำอธิบายเพิ่มให้ดูการหา F = ma ) ตามกฎที่อธิบายไว้ที่ เศษส่วนความคลาดเคลื่อนของค่าเฉลี่ยของการทดลอง N ที่เป็นอิสระ คือ จะถูกลดลงโดย \(\rm 1 / \sqrt N\) พื้นที่ผิวหาจากรัศมีคูณความยาว ดังนั้น เศษส่วนความคลาดเคลื่อนที่จะถูกเพิ่มเข้าไปในแต่ละวิธีจะได้ดังนี้
วิธีที่ 1: \(\sqrt{ (1\%)^2 + (1\%)^2 }≈ 1.4\% \)
วิธีที่ 2: \(\sqrt{(0.1\%)^2 +(10\%)^2} ≈ 10\% \)
วิธีที่ 3: \(\sqrt{(1\%)^2 +(10\%)^2}/10≈ 3.3\% \)
ดังนั้น วิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด

