ข้อสอบคัดเลือกของทีม USA 2007 (38 ข้อ)
| 1. | ให้การเคลื่อนที่ของวัตถุหนึ่งในสองมิติ เป็นไปตามสมการ
\(\rm \vec r(t) = (4.0t^2-9.0)\hat i + (2.0t - 5.0)\hat j \)
โดย r มีหน่วย เมตร และ t มีหน่วย วินาที แล้ววัตถุจะตัดแกน x ที่วินาทีใด |
| A | 0.0 s |
| B | 0.4 s |
| C | 0.6 s |
| D | 1.5 s |
| E | 2.5 s |
ตอบ (E)
จาก
จาก
\(\rm \vec r(t) = x(t)\hat i + y(t)\hat j \)
วัตถุตัดแกน x เมื่อ y(t) = 0
\(\begin{align*}\rm 2.0(t) -5.0 &= 0\\ \therefore \rm t &= 2.5 ~\rm s \end{align*}\)
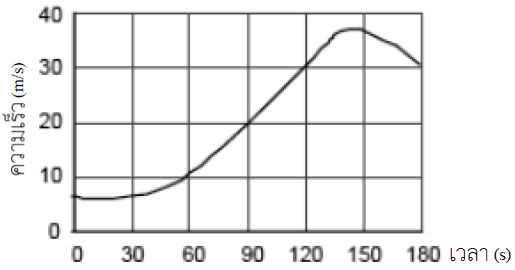
| 2. | กำหนดกราฟความเร็วเทียบกับเวลาของรถคันหนึ่ง อยากทราบว่า ความเร่งที่วินาทีที่ 90 เท่ากับข้อใด
 |
| A | 0.22 m/s2 |
| B | 0.33 m/s2 |
| C | 1.0 m/s2 |
| D | 9.8 m/s2 |
| E | 30 m/s2 |
ตอบ (B)
จากโจทย์เป็นกราฟ v-t ความเร่งที่ t ใดๆ จึงหาจากความชันของกราฟที่ t นั้นๆ
ประมาณช่วง t = 60 – 120 s เป็นเส้นตรง เลือกพิกัด (60,10) และ (120,30) จะได้
จากโจทย์เป็นกราฟ v-t ความเร่งที่ t ใดๆ จึงหาจากความชันของกราฟที่ t นั้นๆ
ประมาณช่วง t = 60 – 120 s เป็นเส้นตรง เลือกพิกัด (60,10) และ (120,30) จะได้
\(\begin{align*} {{\rm{a}}_{t\, = \,90}} &= \frac{{\Delta {\rm{v}}}}{{\Delta {\rm{t}}}}\\ &= \frac{{30 - 10}}{{120 - 60}}\\ &= \frac{{20}}{{60}}\\ &= 0.33\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}} \end{align*}\)
| 3. | ให้ตำแหน่งของวัตถุกำหนดจากฟังก์ชันของเวลา x = 8t – 3t2 โดย x มีหน่วยเมตร และ t ในหน่วยวินาที แล้วความเร็วเฉลี่ยในช่วง t = 1 ถึง t = 2 s เท่ากับข้อใด |
| A | - 2 m/s |
| B | - 1 m/s |
| C | - 0.5 m/s |
| D | 0.5 m/s |
| E | 1 m/s |
ตอบ (B)
ข้อนี้ถามความเร็วเฉลี่ย จะได้
ความเร็วเฉลี่ย = \(\dfrac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}} = \dfrac{{{{\rm{x}}_2} - {{\rm{x}}_1}}}{{{{\rm{t}}_2} - {{\rm{t}}_1}}}\)
( ส่วนความเร็ว ณ ขณะใดๆ \(= \rm v(t)=\dfrac{{{\rm{dx}}}}{{{\rm{dt}}}} = \mathop {{\rm{lim}}}\limits_{\Delta {\rm{t}} \to 0} = \dfrac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}}\) )ข้อนี้ถามความเร็วเฉลี่ย จะได้
\(\begin{align*} \frac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}} &= \frac{{{{\rm{x}}_{{\rm{t = 2}}}} - {{\rm{x}}_{{\rm{t = 1}}}}}}{{2 - 1}}\\ &= \frac{{(8(2) - 3{{(2)}^2}) - (8(1) - 3{{(1)}^2})}}{{2 - 1}}\\ &= - 1\,\,{\rm{m/s}} \end{align*}\)
| 4. | วัตถุถูกปล่อยจากหยุดนิ่ง และเคลื่อนที่ได้ระยะทาง h ในวินาทีแรก จงหาระยะที่วัตถุเคลื่อนที่ได้ในวินาทีที่สอง |
| A | h |
| B | 2h |
| C | 3h |
| D | 4h |
| E | h2 |
ตอบ (C)
ถ้าปล่อยวัตถุจากหยุดนิ่ง แล้วเกิดการเคลื่อนที่แสดงว่ามีความเร่ง a เกิดขึ้น
จาก v(t) = at จะได้
ถ้าปล่อยวัตถุจากหยุดนิ่ง แล้วเกิดการเคลื่อนที่แสดงว่ามีความเร่ง a เกิดขึ้น
จาก v(t) = at จะได้
\({\rm{x(t)}} = \int {{\rm{v dt}} = \dfrac{1}{2}} {\rm{a}}{{\rm{t}}^{\rm{2}}}\)
สมมุติให้ x(0) = 0 จากโจทย์จะได้
\(\begin{array}{l} {\rm{x(t = 1)}} = \dfrac{1}{2}{\rm{a(1}}{{\rm{)}}^{\rm{2}}} = {\rm{h}}\\ {\rm{x(t = 2)}} = \dfrac{1}{2}{\rm{a(2}}{{\rm{)}}^{\rm{2}}} = 4{\rm{h}} \end{array}\)
ดังนั้น ในวินาทีที่ 2 วัตถุเคลื่อนที่ไปได้ \(\rm x(t = 2) – x(t = 1) = 4h – h =3h\)| 5. | มีลังใส่ของเล่นถูกวางนิ่งไว้บนรถเลื่อนหิมะคันหนึ่ง ขณะเดียวกันมีแรงดึงรถเลื่อนขึ้นเนินเขาด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ โดยลังไม่ได้ถูกยึดกับรถเลื่อนไว้ แล้วข้อใดคือแรงที่จะต้องรองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา |
| A | แรงเสียดทานสถิตของรถเลื่อนที่กระทำกับลังของเล่น |
| B | แรงตั้งฉากของพื้นหิมะที่กระทำกับรถเลื่อน |
| C | แรงตั้งฉากของรถเลื่อนที่กระทำกับลังของเล่น |
| D | แรงโน้มถ่วงที่กระทำต่อรถเลื่อน |
| E | ไม่มีแรงใดรองรับ |
ตอบ (A)
จากโจทย์ให้ลังใส่ของมีความเร่ง แสดงว่าต้องมีแรงที่กระทำกับลังเกิดขึ้น
เมื่อเขียนแผนภาพจะได้ 
สังเกตว่า มีแรงเสียดทานระหว่างลังกับเลื่อนหิมะ f เพียงแรงเดียวที่มีทิศเดียวกับ a (และทำให้ a เป็นบวก)
ดังนั้น มีแรงเสียดทานที่รองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา
จากโจทย์ให้ลังใส่ของมีความเร่ง แสดงว่าต้องมีแรงที่กระทำกับลังเกิดขึ้น
เมื่อเขียนแผนภาพจะได้
ดังนั้น มีแรงเสียดทานที่รองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา
| 6. | ในเวลา t = 0 รถลาก เริ่มเคลื่อนที่จากหยุดนิ่งในแนวเส้นตรง ด้วยความเร็วตามฟังก์ชัน v = 5t2 , โดย v มีหน่วย m / s และ t มีหน่วย s ข้อใดแสดงการเคลื่อนที่ของรถจาก t = 0 ถึง t ได้ถูกต้องที่สุด |
| A | 5t3 |
| B | 5t3/3 |
| C | 10t |
| D | 15t2 |
| E | 5t/2 |
ตอบ (B)
จาก
จากเงื่อนไขเริ่มต้นให้ x(t = 0) = 0 จะได้
จาก
\(\begin{align*} {\rm{x}} &= \int {{\rm{v dt}}} \\ {\rm{x(t)}} &= \int\limits_{{\rm{t = 0}}}^{\rm{t}} {{\rm{5}}{{\rm{t}}^{\rm{2}}}{\rm{dt}}} \\ &= \dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}{\rm{ + c}} \end{align*}\)
( c เป็นค่าคงที่ )จากเงื่อนไขเริ่มต้นให้ x(t = 0) = 0 จะได้
\(\begin{array}{l} {\rm{0 = }}\dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}{\rm{ + c }}\\ {\rm{c = 0}} \end{array}\)
ดังนั้น \(\rm x(t) = \dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}\)| 7. | พลังงานศักย์ทางเคมีที่ถูกเก็บไว้ในแบตเตอรี่จะถูกแปลงเป็นพลังงานจลน์ที่ช่วยเพิ่มอัตราเร็วของรถของเล่นจาก 0 เป็น 2 ไมล์ต่อชั่วโมง แล้วเพิ่มจาก 2 เป็น 4 ไมล์ต่อชั่วโมง ถ้าไม่คำนึงถึงพลังงานที่กลายเป็นพลังงานความร้อนเนื่องจากแรงเสียดทาน และแรงต้านอากาศ แล้วข้อใดเปรียบเทียบพลังงานที่ต้องใช้ในการขับเคลื่อนจาก 2 เป็น 4 ไมล์ต่อชั่วโมงกับพลังงานที่ต้องใช้จาก 0 เป็น 2 ไมล์ต่อชั่วโมงได้ถูกต้องที่สุด |
| A | ใช้พลังงานเป็นครึ่งหนึ่ง |
| B | ใช้พลังงานเท่ากัน |
| C | ใช้พลังงานเป็นสองเท่า |
| D | ใช้พลังงานเป็นสามเท่า |
| E | ใช้พลังงานเป็นสี่เท่า |
ตอบ (D)
จากสูตรพลังงานจลน์
จะได้ Ek ที่ใช้เปลี่ยน v จาก 0 เป็น 2 ไมล์ต่อชั่วโมง เท่ากับ
จากสูตรพลังงานจลน์
\({{\rm{E}}_{\rm{k}}} = \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2}\)
เมื่อ m = มวลวัตถุ , v = ความเร็ววัตถุจะได้ Ek ที่ใช้เปลี่ยน v จาก 0 เป็น 2 ไมล์ต่อชั่วโมง เท่ากับ
\({{\rm{E}}_{{\rm{k(0}} \to 2)}} = \dfrac{1}{2}{\rm{m(2}}{{\rm{)}}^2} - \dfrac{1}{2}{\rm{m(0}}{{\rm{)}}^2} = 2{\rm{m}}\)
และ Ek ที่ใช้เปลี่ยน v จาก 2 เป็น 4 ไมล์ต่อชั่วโมง เท่ากับ
\({{\rm{E}}_{{\rm{k(2}} \to 4)}} = \dfrac{1}{2}{\rm{m(4}}{{\rm{)}}^2} - \dfrac{1}{2}{\rm{m(2}}{{\rm{)}}^2} = 6{\rm{m}}\)
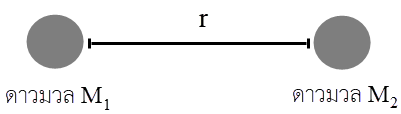
ดังนั้น \(\dfrac{{{{\rm{E}}_{{\rm{k(2}} \to 4)}}}}{{{{\rm{E}}_{{\rm{k(0}} \to 2)}}}} = \dfrac{{6{\rm{m}}}}{{2{\rm{m}}}} = 3\)| 8. | ถ้าดาวฤกษ์สองดวงอยู่ห่างกันมาก แล้วพลังงานศักย์โน้มถ่วงของทั้งสองเท่ากับศูนย์ ถ้าดาวทั้งสองดวงห่างกัน d พลังงานศักย์โน้มถ่วงของระบบจะเท่ากับ U แล้วดาวที่ห่างกัน 2d พลังงานศักย์โน้มถ่วงของระบบจะเท่ากับข้อใด |
| A | U/4 |
| B | U/2 |
| C | U |
| D | 2U |
| E | 4U |
ตอบ (B)
จาก
จะได้ว่า
ดังนั้น
\({\rm{U}} = \dfrac{{ - {\rm{G}}{{\rm{M}}_{\rm{1}}}{{\rm{M}}_{\rm{2}}}}}{{\rm{r}}}\)
ดังนั้น \({\rm{U}} \propto \dfrac{1}{{\rm{r}}}\)จะได้ว่า
\(\dfrac{{{{\rm{U}}_{\rm{1}}}}}{{{{\rm{U}}_{\rm{2}}}}}{\rm{ = }}\dfrac{{{{\rm{r}}_{\rm{2}}}}}{{{{\rm{r}}_{\rm{1}}}}}\)
ให้ U1 = U, r1 = d และ r2 = 2dดังนั้น
\(\begin{array}{l} \dfrac{{\rm{U}}}{{{{\rm{U}}_{\rm{2}}}}}{\rm{ = }}\dfrac{{{\rm{2d}}}}{{\rm{d}}}\\ {{\rm{U}}_{\rm{2}}} = \dfrac{{\rm{U}}}{2} \end{array}\)
| 9. | ให้พื้นเอียงถูกวางอยู่บนพื้นลื่น และมีกล่องที่เดิมอยู่นิ่งค่อยๆ เลื่อนลงมาจากพื้นเอียงที่มีความขรุขระ แล้วการเคลื่อนที่ของจุดศูนย์กลางมวลของระบบกล่องและพื้นเอียงจะเป็นไปตามข้อใด |
| A | จะไม่มีการเคลื่อนที่เกิดขึ้น |
| B | มีการเคลื่อนที่ตามแนวนอนด้วยอัตราเร็วคงที่ |
| C | มีการเคลื่อนที่ตามแนวนอนด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ |
| D | มีการเคลื่อนที่ตามแนวตั้งด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ |
| E | มีการเคลื่อนที่ทั้งในแนวตั้ง และแนวนอน |
ตอบ (D)
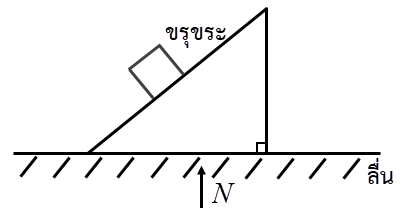หลักการ คือ จุดศูนย์กลางมวลจะเคลื่อนที่ได้เมื่อมีแรงภายนอกมากระทำ
พิจารณาแกน X : พื้นลื่นจึงไม่มีแรงเสียดทาน
ดังนั้น จุดศูนย์กลางมวลในแนวแกน X ไม่เคลื่อนที่
พิจารณาแกน Y : มีแรง N จากพื้นในทิศขึ้น
จาก
(เพิ่มเติม แรงเสียดทานระหว่างพื้นเอียงกับกล่องเป็นแรงภายใน จึงไม่ส่งผลต่อจุดศูนย์กลางมวลของทั้งระบบ)
พิจารณาแกน X : พื้นลื่นจึงไม่มีแรงเสียดทาน
ดังนั้น จุดศูนย์กลางมวลในแนวแกน X ไม่เคลื่อนที่
พิจารณาแกน Y : มีแรง N จากพื้นในทิศขึ้น
จาก
\(\begin{align*} \sum \rm F_y &= \rm ma_y\\ \rm a_y &> 0 \end{align*} \)
ดังนั้น จุดศูนย์กลางมวลจะเคลื่อนที่ในแนวแกน Y ด้วยความเร่ง(เพิ่มเติม แรงเสียดทานระหว่างพื้นเอียงกับกล่องเป็นแรงภายใน จึงไม่ส่งผลต่อจุดศูนย์กลางมวลของทั้งระบบ)
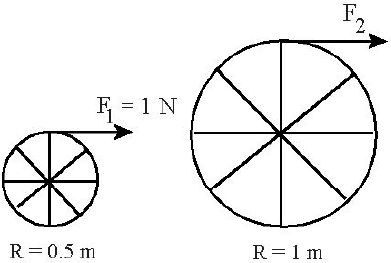
| 10. | ล้อมวล 1 kg สองวง มีแกนล้อคงที่ จากที่เดิมอยู่นิ่งมีแรงมากระทำ ดังรูป สมมุติว่า แกนล้อและซี่ล้อมีมวลเบามาก และความเฉื่อยในการหมุนเท่ากับ I = mR2 ถ้าต้องการให้ความเร่งเชิงมุมของทั้งสองล้อมีค่าเท่ากัน แล้วแรง F2 ที่กระทำบนแกนล้อควรเท่ากับข้อใด
 |
| A | 0.25 N |
| B | 0.5 N |
| C | 1 N |
| D | 2 N |
| E | 4 N |
ตอบ (D)
จาก
พิจารณาล้อ 1 (R = 0.5 m)
ดังนั้น
จาก
\(\sum {\tau = {\rm{I}}\alpha } \)
พิจารณาล้อ 1 (R = 0.5 m)
\(\begin{align*} \rm F_1R &= \rm m_1^2\alpha \\ \rm{F}_1&= \rm mR_1\alpha \end{align*}\)
พิจารณาล้อ 2 (R = 1 m)
\({{\rm{F}}_{\rm{2}}}{\rm{ = m}}{{\rm{R}}_2}\alpha \)
ดังนั้น
\(\begin{array}{c} \dfrac{{{{\rm{F}}_{\rm{2}}}}}{{{{\rm{F}}_{\rm{1}}}}}{\rm{ = }}\dfrac{{{{\rm{R}}_{\rm{2}}}}}{{{{\rm{R}}_{\rm{1}}}}}\\ \dfrac{{{{\rm{F}}_{\rm{2}}}}}{1}{\rm{ = }}\dfrac{1}{{0.5}}\\ {{\rm{F}}_{\rm{2}}} = 2{\rm{N}} \end{array}\)
| 11. | ให้แผ่นกลม, ห่วง และทรงกลม มีมวล และรัศมีเท่ากัน และจะหมุนอย่างอิสระรอบแกนที่ผ่านจุดศูนย์กลางของวัตถุ โดยสมมุติว่าห่วงเชื่อมกับแกนหมุนด้วยซี่ล้อรถ ถ้าวัตถุที่เดิมอยู่นิ่ง ถูกกระทำที่วงด้านนอกด้วยแรงเดียวกัน ในเวลาเดียวกัน แล้วข้อใดจัดอันดับพลังงานจลน์ของวัตถุจากน้อยไปมาก หลังเวลาผ่านไป t ได้ถูกต้อง
 |
| A | แผ่นกลม, ห่วง, ทรงกลม |
| B | ทรงกลม, แผ่นกลม, ห่วง |
| C | ห่วง, ทรงกลม, แผ่นกลม |
| D | แผ่นกลม, ทรงกลม, ห่วง |
| E | ห่วง, แผ่นกลม, ทรงกลม |
ตอบ (E)
จากโจทย์ให้ทุกวัตถุถูกหมุนด้วย F เท่ากัน รัศมีเท่ากัน ดังนั้น ทอร์กต้องเท่ากัน
เนื่องจาก วัตถุที่มีโมเมนต์ความเฉื่อย (I) มาก จะหมุนช้า ทำให้พลังงานจลน์มีค่าน้อย
ดังนั้น การเรียงลำดับพลังงานจลน์จากน้อยไปมาก ต้องเรียงลำดับ I จากมากไปน้อย ดังนี้
จากโจทย์ให้ทุกวัตถุถูกหมุนด้วย F เท่ากัน รัศมีเท่ากัน ดังนั้น ทอร์กต้องเท่ากัน
เนื่องจาก วัตถุที่มีโมเมนต์ความเฉื่อย (I) มาก จะหมุนช้า ทำให้พลังงานจลน์มีค่าน้อย
ดังนั้น การเรียงลำดับพลังงานจลน์จากน้อยไปมาก ต้องเรียงลำดับ I จากมากไปน้อย ดังนี้
ห่วง (\({\rm{M}}{{\rm{R}}^{\rm{2}}}\)) , แผ่นกลม (\(\dfrac{1}{2}{\rm{M}}{{\rm{R}}^{\rm{2}}}\)) , ทรงกลม (\(\dfrac{2}{5}{\rm{M}}{{\rm{R}}^{\rm{2}}}\))
| 12. | หินหนัก 2 kg แขวนที่ปลายไม้เมตรสม่ำเสมอยาว 1 เมตร ด้วยเชือกเบา ถ้าไม้เมตรเกิดสมดุลเมื่อหินที่แขวนอยู่ อยู่ห่างจากจุดหมุนไป 0.20 m แล้วไม้เมตรมีมวลเท่าใด  |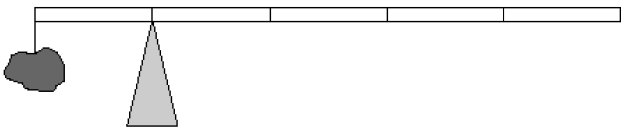
| A | 0.20 kg |
| B | 1.00 kg |
| C | 1.33 kg |
| D | 2.00 kg |
| E | 3.00 kg |
ตอบ (C)
ให้หินมีมวล m และไม้เมตรมีมวล M
จากไม้เมตรเกิดสมดุลแสดงว่า
ให้หินมีมวล m และไม้เมตรมีมวล M
โมเมนต์ตาม \(=\) โมเมนต์ทวน
\(\begin{align*} \dfrac{4}{5}{\rm{Mg}}(0.40) &= \rm mg(0.20) + \dfrac{1}{5}{\rm{Mg}}(0.10)\\ \left( {\dfrac{4}{5}(0.40) - \dfrac{1}{5}(0.10)} \right)\rm M &= (0.20)(2)\\ \rm M &= \dfrac{4}{3} \end{align*}\)
ดังนั้น ไม้เมตรมีมวล \(\dfrac{4}{3} = 1.33 \rm ~~kg\)| 13. | ถ้าวัตถุหนึ่งเคลื่อนที่ไปตามแกน x พุ่งชนแบบยืดหยุ่นกับวัตถุแบบเดียวกันที่เดิมอยู่นิ่ง แล้วกราฟในข้อใดแสดงโมเมนตัม P เทียบกับเวลา t ของแต่ละวัตถุได้ถูกต้อง |
| A |  |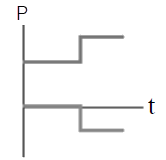
| B |  |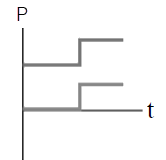
| C |  |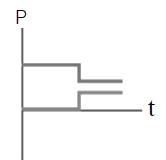
| D |  |
| E |  |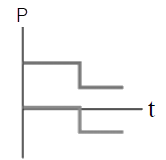
ตอบ (D)
โจทย์ให้เป็นการชนแบบยืดหยุ่นแสดงว่า
1) อนุรักษ์โมเมนตัม \(\sum \rm P\) ก่อนชน = \(\sum \rm P\)หลังชน
2) อนุรักษ์พลังงาน \(\rm E\)ก่อน = \(\rm E\)หลัง
พิจารณาจากเงื่อนไข 1)
จากกราฟจะเห็นว่า กราฟ (B), (E) มีการเปลี่ยนแปลงหลังชนไปในทำนองเดียวกัน (เพิ่มขึ้นเหมือนกัน หรือลดลงเหมือนกัน) ซึ่งขัดกับการอนุรักษ์โมเมนตัม
ดังนั้น กราฟ (B), (E) ไม่ใช่คำตอบ
และเมื่อวาดรูปจากกราฟ (A) จะได้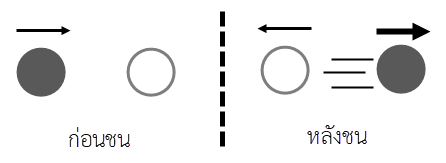
สังเกตว่า วัตถุที่อยู่นิ่งไม่ควรเด้งกลับหลังถูกชน
ดังนั้น กราฟ (A) ไม่ใช่คำตอบ
พิจารณาจากเงื่อนไข 2)
จากกราฟ (C)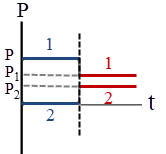
จากกราฟ (D)
ดังนั้น กราฟ (D) ถูกต้อง
โจทย์ให้เป็นการชนแบบยืดหยุ่นแสดงว่า
1) อนุรักษ์โมเมนตัม \(\sum \rm P\) ก่อนชน = \(\sum \rm P\)หลังชน
2) อนุรักษ์พลังงาน \(\rm E\)ก่อน = \(\rm E\)หลัง
พิจารณาจากเงื่อนไข 1)
จากกราฟจะเห็นว่า กราฟ (B), (E) มีการเปลี่ยนแปลงหลังชนไปในทำนองเดียวกัน (เพิ่มขึ้นเหมือนกัน หรือลดลงเหมือนกัน) ซึ่งขัดกับการอนุรักษ์โมเมนตัม
ดังนั้น กราฟ (B), (E) ไม่ใช่คำตอบ
และเมื่อวาดรูปจากกราฟ (A) จะได้
ดังนั้น กราฟ (A) ไม่ใช่คำตอบ
พิจารณาจากเงื่อนไข 2)
จากกราฟ (C)
\(\rm E\)ก่อน \(=\dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} + 0 = \dfrac{1}{2}\dfrac{{{{\rm{m}}^2}{{\rm{v}}^2}}}{{\rm{m}}} = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
\(\rm E\)หลัง \(=\dfrac{1}{2}{\rm{mv}}_1^2 + \dfrac{1}{2}{\rm{mv}}_2^2 = \dfrac{1}{2}\dfrac{{{\rm{P}}_1^{^2}}}{{\rm{m}}} + \dfrac{1}{2}\dfrac{{{\rm{P}}_2^{^2}}}{{\rm{m}}} = \dfrac{1}{{2{\rm{m}}}}\left( {{\rm{P}}_1^{^2} + {\rm{P}}_2^{^2}} \right)\)
จากกราฟสังเกตว่า \(\rm P_1 + P_2 \approx P\) แสดงว่า
\(\rm E\)ก่อน \(\approx \dfrac{1}{{2{\rm{m}}}}{\left( {{{\rm{P}}_1} + {{\rm{P}}_2}} \right)^2} = \dfrac{1}{{2{\rm{m}}}}({\rm{P}}_1^2 + {\rm{P}}_2^2 + 2{{\rm{P}}_1}{{\rm{P}}_2}) > \) \(\rm E\)หลัง
ซึ่งขัดกับการอนุรักษ์พลังงาน ดังนั้น กราฟ (C) ไม่ใช่คำตอบจากกราฟ (D)
\(\rm E\)ก่อน \(= \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} + 0 = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
\(\rm E\)หลัง \(= 0 + \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
ซึ่ง \(\rm E\)ก่อน = \(\rm E\)หลังดังนั้น กราฟ (D) ถูกต้อง
| 14. | ให้อัตราเร็วของรถยนต์ที่มีระบบขับเคลื่อนล้อหลังมีขนาดเพิ่มขึ้น แล้วทิศทางของแรงเสียดทานบนยางรถยนต์จะเป็นไปตามข้อใด |
| A | ที่ล้อหน้ามีทิศถอยหลัง ที่ล้อหลังมีทิศไปข้างหน้า |
| B | ที่ล้อหน้ามีทิศไปข้างหน้า ที่ล้อหลังมีทิศถอยหลัง |
| C | ทุกล้อมีทิศไปข้างหน้า |
| D | ทุกล้อมีทิศถอยหลัง |
| E | แรงเสียดทานเป็นศูนย์ |
ตอบ (A)
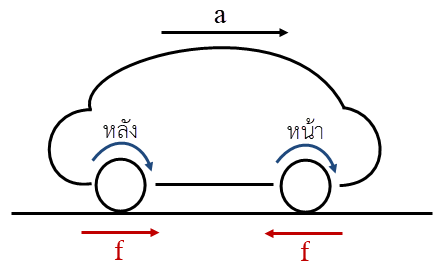ล้อหลัง : จะตะกุยพื้นเพื่อดันรถไปข้างหน้า ทำให้ล้อที่สัมผัสพื้นเคลื่อนที่ไปด้านหลัง \((\leftarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหลังจะมีทิศไปข้างหน้า \((\rightarrow)\)
ล้อหน้า : เพลาของล้อหน้าจะเคลื่อนที่ไปข้างหน้า \((\rightarrow)\) ทำให้ล้อส่วนที่สัมผัสพื้นเคลื่อนที่ตามเพลา คือ ไปข้างหน้า \((\rightarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหน้าจะมีทิศไปข้างหลัง \((\leftarrow)\)
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหลังจะมีทิศไปข้างหน้า \((\rightarrow)\)
ล้อหน้า : เพลาของล้อหน้าจะเคลื่อนที่ไปข้างหน้า \((\rightarrow)\) ทำให้ล้อส่วนที่สัมผัสพื้นเคลื่อนที่ตามเพลา คือ ไปข้างหน้า \((\rightarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหน้าจะมีทิศไปข้างหลัง \((\leftarrow)\)
| 15. | ให้แผ่นกลมสม่ำเสมอ (I = \(\dfrac{1}{2}\)MR2) มีมวล 8.0 kg สามารถหมุนรอบแกนโดยไม่มีแรงเสียดทาน และมีเชือกคล้องผ่านแผ่นกลมนั้น และแขวนมวล 6.0 kg เอาไว้ ดังรูป ถ้าเชือกไม่มีการไถล แล้วแรงตึงเชือกขณะมวลหย่อนลงมาเท่ากับข้อใด
 |
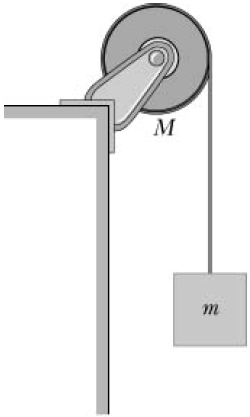| A | 20.0 N |
| B | 24.0 N |
| C | 34.3 N |
| D | 60.0 N |
| E | 80.0 N |
ตอบ (B)
โจทย์ให้ \(\rm M = 8.0 kg ,~ m = 6.0 kg\) ให้เชือกมีแรงตึง \(\rm T\)
พิจารณามวล \(\rm M\)
จาก \(\sum {\tau = {\rm{I}}\alpha }\)
จาก \(\sum {{\rm{F = ma}}}\)
พิจารณามวล \(\rm M\)
จาก \(\sum {\tau = {\rm{I}}\alpha }\)
\(\begin{align*} \rm TR &= \dfrac{{\rm{1}}}{{\rm{2}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}\alpha \\ \alpha &= \dfrac{{{\rm{2T}}}}{{{\rm{MR}}}} \end{align*}\)
จากเงื่อนไขเชือกไม่ไถลทำให้
\(\rm a = \alpha \rm R = \left( {\dfrac{{{\rm{2T}}}}{{{\rm{MR}}}}} \right){\rm{R}} = \dfrac{{{\rm{2T}}}}{{\rm{M}}}\)
พิจารณามวล \(\rm m\)จาก \(\sum {{\rm{F = ma}}}\)
\({\rm{mg}} - {\rm{T = ma}}\)
แทน \({\rm{a = }}\dfrac{{{\rm{2T}}}}{{\rm{M}}}\) จะได้
\(\begin{align*} \rm mg - T &= m \dfrac{{{\rm{2T}}}}{{\rm{M}}}\\ \rm T &=\dfrac{{{\rm{mg}}}}{{1 + \dfrac{{{\rm{2m}}}}{{\rm{M}}}}}\\ &= \dfrac{{{\rm{6}}{\rm{.0(10)}}}}{{1 + \dfrac{{{\rm{2(6}}{\rm{.0)}}}}{{8.0}}}}\\ &= 24\,\,{\rm{N}} \end{align*}\)
ดังนั้น \(\rm T = 24 ~~N\)| 16. | ให้ลูกเบสบอลตกใส่ด้านบนของลูกบาส ขณะที่ลูกบาสกระแทกพื้นแล้วกระเด้งกลับด้วยอัตราเร็ว 4.0 m/s และพุ่งชนกับลูกเบสบอลที่ตกลงมาด้วยอัตราเร็ว 4.0 m/s หลังการชนลูกเบสบอลพุ่งกลับขึ้นไป ดังรูป และลูกบาสกลับมาอยู่นิ่งทันทีหลังการชน ถ้าลูกเบสบอลมวล 0.2 kg และลูกบาสมวล 0.5 kg และไม่สนแรงต้านอากาศ ไม่สนการดลเนื่องจากแรงโน้มถ่วง เพราะช่วงเวลาในการชนนั้นสั้นมาก แล้วอัตราเร็วของลูกเบสบอลหลังการชนกับลูกบาสที่พุ่งขึ้นมาเท่ากับข้อใด
 |
| A | 4.0 m/s |
| B | 6.0 m/s |
| C | 8.0 m/s |
| D | 12.0 m/s |
| E | 16.0 m/s |
ตอบ (B)
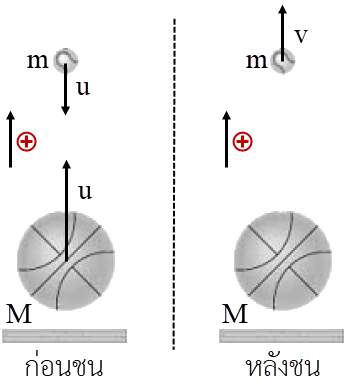โจทย์ให้ M = 0.5 kg, m = 0.2 kg, u = 4.0 m/s
ใช้หลักการอนุรักษ์โมเมนตัม (ในแนวดิ่ง)
ใช้หลักการอนุรักษ์โมเมนตัม (ในแนวดิ่ง)
ก่อนชน = หลังชน
\(\begin{align*} {\rm{Mu}} - {\rm{mu}} &= \rm M(0) + mv\\ {\rm{Mu}} - {\rm{mu}} &= \rm mv\\ v &= \left( {\frac{{{\rm{M}} - {\rm{m}}}}{{\rm{m}}}} \right){\rm{u}}\\ &= \left( {\frac{{0.5 - 0.2}}{{0.2}}} \right)4.0\\ &= 6.0\,\,{\rm{m/s}} \end{align*}\)
\(\begin{align*} {\rm{Mu}} - {\rm{mu}} &= \rm M(0) + mv\\ {\rm{Mu}} - {\rm{mu}} &= \rm mv\\ v &= \left( {\frac{{{\rm{M}} - {\rm{m}}}}{{\rm{m}}}} \right){\rm{u}}\\ &= \left( {\frac{{0.5 - 0.2}}{{0.2}}} \right)4.0\\ &= 6.0\,\,{\rm{m/s}} \end{align*}\)
| 17. | ให้วัตถุเล็กๆ ถูกขว้างไปออกจากตึกสูง 50.0 m ตามแนวนนอนด้วยอัตราเร็วต้น 10.0 m/s ตามแนววิถีที่วัตถุเคลื่อนที่ไปจะมีองค์ประกอบที่เป็นความเร่งที่สัมผัสกับแนววิถีการเคลื่อนที่ และความเร่งที่ตั้งฉากกับแนววิถี แล้วความเร่งของวัตถุในแนวสัมผัสกับแนวตั้งฉากจะมีค่าเท่ากัน หลังวัตถุถูกโยนออกไปกี่วินาที ไม่ต้องคำนึงถึงแรงต้านอากาศ |
| A | 2.00 s |
| B | 1.50 s |
| C | 1.00 s |
| D | 0.50 s |
| E | ที่ความสูงนั้นยังไม่สามารถทำให้เกิดเหตุการณ์นั้นได้ |
ตอบ (A)
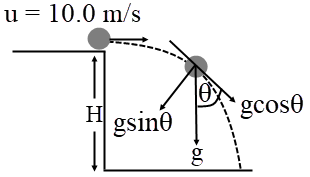จากรูป ความเร่งในแนวตั้งฉาก \(= \rm g\sin\theta\) และ ความเร่งในแนวสัมผัส \(=\rm g\cos\theta\)
โดยความเร่งในแนวตั้งฉาก \(=\) ความเร่งในแนวสัมผัส เมื่อ \(\rm g\sin\theta = g\cos\theta\)
ดังนั้น \(\tan\theta = 1\)
แสดงว่า \(\dfrac{{\rm{u}}}{{\rm{v}}} = \tan {\rm{\theta }} = 1\) ด้วย เมื่อ \(v\) เป็นความเร็วในแนวดิ่งของวัตถุ
จาก \(\rm v = gt\)
จาก
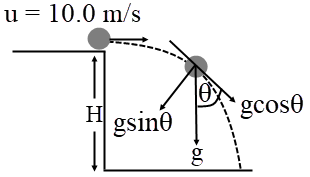
โดยความเร่งในแนวตั้งฉาก \(=\) ความเร่งในแนวสัมผัส เมื่อ \(\rm g\sin\theta = g\cos\theta\)
ดังนั้น \(\tan\theta = 1\)
แสดงว่า \(\dfrac{{\rm{u}}}{{\rm{v}}} = \tan {\rm{\theta }} = 1\) ด้วย เมื่อ \(v\) เป็นความเร็วในแนวดิ่งของวัตถุ
จาก \(\rm v = gt\)
\({\rm{t = }}\dfrac{{\rm{v}}}{{\rm{g}}}{\rm{ = }}\dfrac{{\rm{u}}}{{\rm{g}}} \approx \dfrac{{10.0}}{{10.0}} = 1.00\,\,{\rm{s}}\)
ตรวจสอบระยะทางที่ตก (s) จาก
\({\rm{s = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{{\rm{t}}^{\rm{2}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{ \times 10 \times }}{{\rm{1}}^{\rm{2}}}{\rm{ = 5m < 50}}{\rm{.0m}}\)
ดังนั้น ความสูงเพียงพอที่จะทำให้เกิดเหตุการณ์นั้นได้| 18. | ก้อนน้ำแข็งเล็กๆ ที่เดิมอยู่นิ่ง ไหลลงมาตามแผ่นน้ำแข็งโค้งที่ไม่มีแรงเสียดทาน ดังรูป แล้วที่จุด A จะเป็นจุดเชื่อมแผ่นน้ำแข็งกับพื้นเอียงที่ยกขึ้นมา 30° จากแนวระดับ และมีสัมประสิทธิ์เสียดทาน μk ความยาวทางลาดยาว \(\dfrac{3}{2}\rm h\) ถ้าก้อนน้ำแข็งนิ่งสนิทที่ปลายด้านล่างของพื้นเอียง แล้ว μk เท่ากับข้อใด
 |
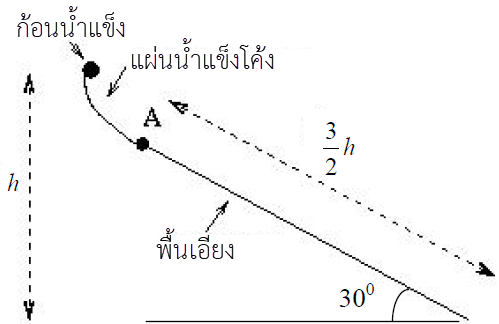| A | 0.866 |
| B | 0.770 |
| C | 0.667 |
| D | 0.385 |
| E | 0.333 |
ตอบ (B)
จากงานและพลังงาน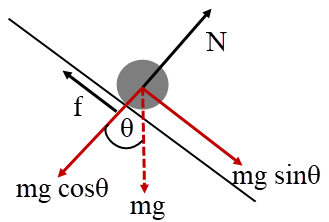
โดย \({\rm{f}} = {{\rm{\mu }}_{\rm{k}}}{\rm{N}} = {{\rm{\mu }}_{\rm{k}}}{\rm{mg}}\cos \theta \) จะได้ว่า
จากงานและพลังงาน
พลังงานศักย์โน้มถ่วง \(+\) งานที่แรงเสียดทานทำ (ติดลบ) \(= 0\) (น้ำแข็งหยุดนิ่งที่ปลายราง)
\(\rm mgh + \left( – f\left( {\dfrac{3}{2}{\rm{h}}} \right) \right)= 0\)
วาดรูปจากโจทย์
\(\rm mgh + \left( – f\left( {\dfrac{3}{2}{\rm{h}}} \right) \right)= 0\)
\(\begin{align*} \rm mgh &=\dfrac{{\rm{3}}}{{\rm{2}}}{\rm{fh}}\\ \rm mg &= \dfrac{{\rm{3}}}{{\rm{2}}}{\rm{(}}{{\rm{\mu }}_{\rm{k}}}{\rm{mg ~cos}}\theta {\rm{)}}\\ {{\rm{\mu }}_{\rm{k}}} &= \dfrac{{\rm{2}}}{{\rm{3}}}\dfrac{1}{{{\rm{cos30}}^\circ }}\\ &= \dfrac{4}{{3\sqrt 3 }}\\ &\approx 0.770 \end{align*}\)
| 19. | ให้สปริงที่ไม่ได้เป็นไปตาม กฎของฮุค มีแรง F = – kx2 โดย k เป็นค่านิจสปริง x เป็นระยะสปริงที่ยังไม่ถูกยืดจากระบบที่แสดง ดังรูป ถ้านำวัตถุมวล m ติดกับสปริงที่เดิมอยู่นิ่ง แล้วระยะยืดของสปริงจนระบบหยุดนิ่งชั่วขณะเท่ากับข้อใด สมมุติว่า ทุกพื้นผิวและรอกไม่มีแรงเสียดทาน
 |
| A | \(\rm \left(\dfrac{3mg}{2k}\right)^{1/2}\) |
| B | \(\rm \left(\dfrac{mg}{k}\right)^{1/2}\) |
| C | \(\rm \left(\dfrac{2mg}{k}\right)^{1/2}\) |
| D | \(\rm \left(\dfrac{\sqrt3mg}{2k}\right)^{1/2}\) |
| E | \(\rm \left(\dfrac{3\sqrt3mg}{2k}\right)^{1/2}\) |
ตอบ (A)
จากโจทย์บอกระบบหยุดนิ่งชั่วขณะ แสดงว่าตอนนั้นระบบต้องไม่มีพลังงานจลน์
สมมุติให้วัตถุเคลื่อนที่ไปได้ระยะทาง x
ตอนสุดท้าย
เพิ่มเติม ข้อนี้ใช้สมดุลแรงไม่ได้ เพราะ ตรงจุดนี้วัตถุยังมีความเร็วอยู่ (Ek ≠ 0)
จากโจทย์บอกระบบหยุดนิ่งชั่วขณะ แสดงว่าตอนนั้นระบบต้องไม่มีพลังงานจลน์
สมมุติให้วัตถุเคลื่อนที่ไปได้ระยะทาง x
ตอนสุดท้าย
Eสปริง \(\displaystyle = - \int {{\rm{Fdx}} = - \left( { - \int {{\rm{k}}{{\rm{x}}^{\rm{2}}}{\rm{dx}}} } \right){\rm{ = }}\dfrac{{\rm{1}}}{{\rm{3}}}{\rm{k}}{{\rm{x}}^{\rm{3}}}} \)
ตอนแรก
Eศักย์ \(= {\rm{mg ~x}}\sin 30^\circ = \dfrac{1}{2}{\rm{mg ~x}}\)
จากกฎอนุรักษ์พลังงาน
\(\begin{align*} \dfrac{1}{3}{\rm{k}}{{\rm{x}}^3} &= \dfrac{1}{2}{\rm{mgx}}\\ \rm x &= \sqrt {\dfrac{3}{2}\dfrac{{{\rm{mg}}}}{{\rm{k}}}} \end{align*}\)
ดังนั้น ระยะยืดเท่ากับ \({\left( {\dfrac{{3{\rm{mg}}}}{{2{\rm{k}}}}} \right)^{\frac{1}{2}}}\) เพิ่มเติม ข้อนี้ใช้สมดุลแรงไม่ได้ เพราะ ตรงจุดนี้วัตถุยังมีความเร็วอยู่ (Ek ≠ 0)
Ek = Eศักย์ – Eสปริง = \(\dfrac{1}{2}{\rm{mg x}} - \dfrac{{\rm{1}}}{{\rm{3}}}{\rm{k}}{{\rm{x}}^{\rm{3}}} = \sqrt {\dfrac{1}{8}\dfrac{{{{\rm{m}}^{\rm{3}}}{{\rm{g}}^{\rm{3}}}}}{{\rm{k}}}} - \sqrt {\dfrac{1}{{24}}\dfrac{{{{\rm{m}}^{\rm{3}}}{{\rm{g}}^{\rm{3}}}}}{{\rm{k}}}} \ne 0\)
เพราะ สมดุลแรงบอกแค่ว่า a = 0 ไม่ได้บอกว่า v = 0 หรือไม่| 20. | จุดมวลเล็กๆ เคลื่อนที่ไปตามแนวนอนระหว่างผนังสองด้านที่ไม่มีแรงเสียดทาน ด้วยพลังงานจลน์เริ่มต้น E ทุกครั้งที่ชนกับผนัง มวลจะสูญเสียพลังงานจลน์ไป \(\dfrac{1}{2}\) ไปเป็นพลังงานความร้อน แล้ววัตถุจะชนกับผนังได้กี่ครั้ง ก่อนที่ความเร็วของมวลจะลดลงจนเหลือ \(\dfrac{1}{8}\) เท่าของของเดิม |
| A | 3 |
| B | 4 |
| C | 6 |
| D | 8 |
| E | 16 |
ตอบ (C)
จาก
v2, E2 เป็นความเร็ว (ที่ลดลงไป 8 เท่า) และพลังงาน ณ ขณะนั้น
จะได้
ดังนั้น ต้องชน 6 ครั้ง
\(\begin{array}{l} {{\rm{E}}_{\rm{k}}} = \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2}\\ {{\rm{E}}_{\rm{k}}} \propto {{\rm{v}}^2} \end{array}\)
ให้ v1, E1 เป็นความเร็วและพลังงานตอนแรกv2, E2 เป็นความเร็ว (ที่ลดลงไป 8 เท่า) และพลังงาน ณ ขณะนั้น
จะได้
\(\rm \displaystyle \frac{{{E_2}}}{{{E_1}}} = \frac{{v_2^2}}{{v_1^2}} = {\left( {\frac{1}{8}} \right)^2} = {\left( {\frac{1}{2}} \right)^6}\)
| 21. | ถ้าความเฉื่อยในการหมุนรอบแกนที่ผ่านจุดศูนย์กลางของทรงกลมตันคือ I แล้วความเฉื่อยในการหมุนรอบทรงกลมที่มีความหนาแน่นเท่ากัน แต่มีรัศมีเป็นสองเท่าจะเท่ากับข้อใด |
| A | 2I |
| B | 4I |
| C | 8I |
| D | 16I |
| E | 32I |
ตอบ (E)
จาก
และ
จาก
\({\rm{I}} \propto {\rm{m}}{{\rm{R}}^{\rm{2}}}\)
เมื่อ m = มวลวัตถุ , R = รัศมีวัตถุและ
\({\rm{m}} \propto \rho {{\rm{R}}^3}\)
ดังนั้น
\({\rm{I}} \propto \rho {{\rm{R}}^{\rm{5}}}\)
จากโจทย์ให้ R เป็น 2 เท่า จะได้ I เป็น 25 = 32 เท่า| 22. | จรวดสองลำอยู่ในอวกาศที่มีสนามโน้มถ่วงน้อยมาก ให้ผู้สังเกตอยู่ในกรอบอ้างอิงที่จรวดทั้งสองเดิมอยู่นิ่ง มวลของจรวดเป็น m และ 9m เมื่อมีแรงคงที่ F มากระทำกับจรวดมวล m เป็นระยะทาง d จะทำให้จรวดได้รับโมเมนตัม p ถ้ามีแรง F เท่าเดิม มากระทำกับจรวดมวล 9m เป็นระยะทางเท่ากัน d แล้วโมเมนตัมที่จรวดมวล 9m จะได้รับเท่ากับข้อใด |
| A | p/9 |
| B | p/3 |
| C | p |
| D | 3p |
| E | 9p |
ตอบ (D)
พิจารณาจรวดมวล m ใดๆ
จาก \(a = \dfrac{F}{m}\) จะได้
จากโจทย์ ถ้าเปลี่ยน \(m\) เป็น \(9m\) แล้ว p จะเป็น \(\sqrt {\rm{9}} {\rm{p = 3p}}\)
พิจารณาจรวดมวล m ใดๆ
\(\begin{align*} \rm v(t) &=\dfrac{{\rm{F}}}{{\rm{m}}}{\rm{t}}\\ \rm x(t) &=\dfrac{{\rm{1}}}{{\rm{2}}}\frac{{\rm{F}}}{{\rm{m}}}{{\rm{t}}^{\rm{2}}}= \frac{{\rm{1}}}{{\rm{2}}}\frac{{\rm{m}}}{{\rm{F}}}{{\rm{v}}^{\rm{2}}} = \frac{{\rm{1}}}{{\rm{2}}}\frac{{{{\rm{p}}^{\rm{2}}}}}{{{\rm{Fm}}}} \end{align*}\)
ที่ \(x = d\) จะได้
\(\begin{align*} \dfrac{{\rm{1}}}{{\rm{2}}}\frac{{{{\rm{p}}^{\rm{2}}}}}{{{\rm{Fm}}}} &= {\rm{d}}\\ {\rm{p}} &= \sqrt {{\rm{2Fmd}}} \end{align*}\)
ดังนั้น \({\rm{p}} \propto \sqrt {\rm{m}}\)จากโจทย์ ถ้าเปลี่ยน \(m\) เป็น \(9m\) แล้ว p จะเป็น \(\sqrt {\rm{9}} {\rm{p = 3p}}\)
| 23. | ถ้าดาวรัศมี R หมุนด้วยอัตราเร็วเชิงมุม ω รอบแกนที่ผ่านขั้วโลกเหนือ แล้วอัตราส่วนของแรงตั้งฉากที่พื้นกระทำกับคนคนหนึ่งที่เส้นศูนย์สูตร กับคนที่ขั้วโลกเหนือเท่ากับข้อใด สมมุติว่ามีสนามโน้มถ่วงคงที่ g และทั้งสองคนอยู่นิ่งเทียบเมื่อกับดาวเคราะห์ และอยู่ที่ระดับน้ำทะเล |
| A | g/Rω2 |
| B | Rω2/g |
| C | 1 – Rω2/g |
| D | 1 + g /Rω2 |
| E | 1 + Rω2/g |
ตอบ (C)
ให้ N1 เป็นแรงตั้งฉากที่พื้นกระทำกับคนที่อยู่ที่ขั้วโลกเหนือ
และ N2 เป็นแรงตั้งฉากที่พื้นกระทำกับคนที่อยู่ที่เส้นศูนย์สูตร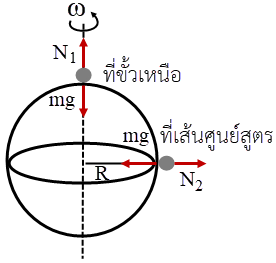
ที่ขั้วเหนือ
ดังนั้น \(\dfrac{{{{\rm{N}}_{\rm{2}}}}}{{{{\rm{N}}_{\rm{1}}}}} = \dfrac{{{\rm{g}} - {\rm{R}}{{\rm{\omega }}^2}}}{{\rm{g}}} = 1 - \dfrac{{{\rm{R}}{{\rm{\omega }}^{\rm{2}}}}}{{\rm{g}}}\)
ให้ N1 เป็นแรงตั้งฉากที่พื้นกระทำกับคนที่อยู่ที่ขั้วโลกเหนือ
และ N2 เป็นแรงตั้งฉากที่พื้นกระทำกับคนที่อยู่ที่เส้นศูนย์สูตร
\(\rm N_1 = mg\)
ที่เส้นศูนย์สูตร มีความเร่งสู่ศูนย์กลาง
\(\begin{align*} \rm mg – N_2 &=\rm mRω^2\\ \rm N_2 &=\rm m(g –Rω^2) \end{align*}\)
ดังนั้น \(\dfrac{{{{\rm{N}}_{\rm{2}}}}}{{{{\rm{N}}_{\rm{1}}}}} = \dfrac{{{\rm{g}} - {\rm{R}}{{\rm{\omega }}^2}}}{{\rm{g}}} = 1 - \dfrac{{{\rm{R}}{{\rm{\omega }}^{\rm{2}}}}}{{\rm{g}}}\)
| 24. | ถ้าเตะบอลมวล m ออกไปกลางอากาศ โดยไม่สนแรงต้านอากาศ แต่สมมุติว่า มีลมที่มีแรงคงที่ F0 กระทำในทิศทาง – x แล้วขนาดมุมเหนือแกน x ในทิศบวก ที่เตะบอลแล้วบอลจะถูกพัดกลับมาที่จุดเดิมเท่ากับข้อใด ให้แสดงในเทอมของ F0 และความเร่งโน้มถ่วง g |
| A | tan-1 (F0/mg) |
| B | tan-1 (mg/F0) |
| C | sin-1 (F0/mg) |
| D | ขนาดของมุมจะขึ้นกับแรงที่เตะ |
| E | ไม่มีมุมใดที่ทำให้เกิดเหตุการณ์ดังกล่าว |
ตอบ (B)
จากโจทย์หา effective gravity (geff) (รวมความเร่ง)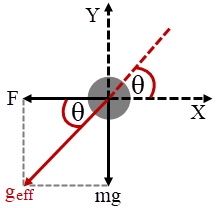
จะพบว่า geff ทำมุม \({\rm{\theta }} = {\tan ^{ - 1}}\left( {\dfrac{{{\rm{mg}}}}{{{{\rm{F}}_{\rm{0}}}}}} \right)\) กับแกน X
หากมองในมุมมองของโลกที่มี geff เป็นสนามโน้มถ่วง และต้องการให้วัตถุกลับมาที่เดิม ก็ต้องโยนวัตถุขึ้นในแนวดิ่ง แต่ถ้ามองในมุมมองปกติก็ต้องโยนลูกบอลทำมุม \({\rm{\theta }} = {\tan ^{ - 1}}\left( {\dfrac{{{\rm{mg}}}}{{{{\rm{F}}_{\rm{0}}}}}} \right)\) เท่ากับมุมของ geff ลูกบอลจึงจะกลับมาที่เดิม
จากโจทย์หา effective gravity (geff) (รวมความเร่ง)
หากมองในมุมมองของโลกที่มี geff เป็นสนามโน้มถ่วง และต้องการให้วัตถุกลับมาที่เดิม ก็ต้องโยนวัตถุขึ้นในแนวดิ่ง แต่ถ้ามองในมุมมองปกติก็ต้องโยนลูกบอลทำมุม \({\rm{\theta }} = {\tan ^{ - 1}}\left( {\dfrac{{{\rm{mg}}}}{{{{\rm{F}}_{\rm{0}}}}}} \right)\) เท่ากับมุมของ geff ลูกบอลจึงจะกลับมาที่เดิม
| 25. | จงหาคาบของการสั่นเล็ก ๆ ของ เครื่องเล่นทางน้ำที่เรียกว่า water pogo ที่มีลักษณะเป็นแท่งมวล m คล้ายกล่อง (รูปสี่เหลี่ยมด้านขนาน) มีความยาว L , กว้าง w และ สูง h และสั่นขึ้นลงในน้ำที่มีความหนาแน่น ρ สมมุติว่า water pogo มีความยาว L และกว้าง w และอยู่ในแนวนอนตลอดเวลา คำแนะนำ : แรงลอยตัวบนวัตถุหาจาก FB = ρVg โดย V คือ ปริมาตรของของเหลวที่ถูกแทนที่ และ ρ คือ ความหนาแน่นของของเหลว สมมุติว่าที่สมดุล water pogo จะลอย (ไม่จม) |
| A | \(\rm 2\pi\sqrt{\dfrac{L}{g}}\) |
| B | \(\rm \pi\sqrt{\dfrac{\rho w^2L^2g}{mh^2}}\) |
| C | \(\rm 2\pi\sqrt{\dfrac{mh^2}{\rho w^2L^2g}}\) |
| D | \(\rm 2\pi\sqrt{\dfrac{m}{\rho wLg}}\) |
| E | \(\rm \pi\sqrt{\dfrac{m}{\rho wLg}}\) |
ตอบ (D)
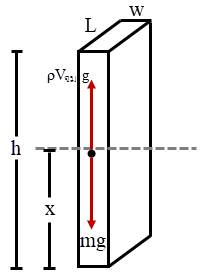เขียนสมการนิวตัน
จาก \({\rm{w = }}\sqrt {\dfrac{{{\rm{\rho Lwg}}}}{{\rm{m}}}} \) จะได้ว่า
\(\begin{align*} \rm mg ~– ρV_{จม}g &= {\rm{m}}\frac{{{{\rm{d}}^{\rm{2}}}{\rm{x}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\\ {\rm{mg }}-\rm\rho (xLw) &= \rm m\dfrac{{{{\rm{d}}^{\rm{2}}}{\rm{x}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\\ \frac{{{\rm{\rho Lwg}}}}{{\rm{m}}}{\rm{ }}\left( {\frac{{\rm{m}}}{{{\rm{\rho Lw}}}}--{\rm{x}}} \right) &= \dfrac{{{{\rm{d}}^{\rm{2}}}{\rm{x}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\\ - \frac{{{\rm{\rho Lwg}}}}{{\rm{m}}}{\rm{ }}\left( {{\rm{x}}-\frac{{\rm{m}}}{{{\rm{\rho Lw}}}}} \right) &= \dfrac{{{{\rm{d}}^{\rm{2}}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\left( {{\rm{x}}-\frac{{\rm{m}}}{{{\rm{\rho Lw}}}}} \right) \end{align*}\)
เป็นสมการ simple harmonic ( อยู่ในรูปของ \(-{{\rm{w}}^2}{\rm{x = }}\dfrac{{{{\rm{d}}^{\rm{2}}}{\rm{x}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\) )จาก \({\rm{w = }}\sqrt {\dfrac{{{\rm{\rho Lwg}}}}{{\rm{m}}}} \) จะได้ว่า
\(\therefore {\rm{T = }}\dfrac{{{\rm{2\pi }}}}{{\rm{w}}}{\rm{ = 2\pi }}\sqrt {\dfrac{{\rm{m}}}{{{\rm{\rho Lwg}}}}} \)
| 26. | มีเด็ก ๆ อยู่บนรถลากเลื่อน และรถลากเลื่อนที่เดิมอยู่นิ่งจะเคลื่อนที่ลงมาจากเนินหิมะที่ทำมุม 25° (เทียบกับแนวนอน) ซึ่งเคลื่อนที่ไป 85 เมตร ใน 17 วินาที ถ้าไม่สนแรงต้านอากาศ แล้วสัมประสิทธิ์แรงเสียดทานจลน์ระหว่างรถเลื่อนกับเนินหิมะเท่ากับข้อใด |
| A | 0.36 |
| B | 0.40 |
| C | 0.43 |
| D | 1.00 |
| E | 2.01 |
ตอบ (B)
เมื่อความเร่งมีค่าคงที่ และรถลากเลื่อนเดิมอยู่นิ่ง จะได้ว่า
พิจารณาแกน y ที่ตั้งฉากกับเนินเอียง จะมี ay = 0 ดังนั้น แรงตั้งฉากจะเท่ากับ
เมื่อความเร่งมีค่าคงที่ และรถลากเลื่อนเดิมอยู่นิ่ง จะได้ว่า
\({\rm{\Delta x = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{a}}{{\rm{t}}^{\rm{2}}}\)
ดังนั้น a = 0.588 m/s2พิจารณาแกน y ที่ตั้งฉากกับเนินเอียง จะมี ay = 0 ดังนั้น แรงตั้งฉากจะเท่ากับ
\(\rm N = mg~ cosθ \) --- (1)
จากกฎข้อที่สองของนิวตัน แรงที่ขนานกับพื้นเอียง คือ f = แรงเสียดทานจลน์ จะได้
\(\rm mg~ sinθ − f = ma\) --- (2)
ใช้ f = μN แทนในสมการ (1) และ (2) จะได้
\(\begin{align*} \mu &= \tan \theta - \dfrac{{\rm{a}}}{{{\rm{g~ cos \theta }}}}\\ &= \tan 25 - \dfrac{{{\rm{0}}{\rm{.588 ~m/}}{{\rm{s}}^2}}}{{{\rm{(10 ~m/}}{{\rm{s}}^{\rm{2}}}{\rm{ ) ~cos 25}}}}\\ &= 0.40 \end{align*}\)
| 27. | ให้สถานีอวกาศประกอบด้วย สองห้องนั่งเล่นที่เชื่อมกับอาคารศูนย์กลาง และอยู่ตรงข้าม กัน โดยทางเชื่อมทั้งสองยาวเท่ากัน แต่ละห้องนั่งเล่นจะมีนักบินอวกาศที่มีมวลเท่ากัน N คน ส่วนมวลของสถานีอวกาศถือว่าน้อยมากเมื่อเทียบกับมวลของนักบินอวกาศ และขนาดของอาคารศูนย์กลางกับห้องนั่งเล่นจะเล็กมากเมื่อเทียบกับความยาวของทางเชื่อม ในช่วงแรกๆ สถานีอวกาศจะหมุนเพื่อให้นักบินอวกาศรู้สึกว่ายังอยู่ในสนามโน้มถ่วง g ถ้านักบินอวกาศสองคน จากแต่ละห้องนั่งเล่นมายังอาคารศูนย์กลาง และนักบินอวกาศเริ่มรู้สึกถึงสนามแรงโน้มถ่วง g' แล้วอัตราส่วน g'/g เท่ากับข้อใดในเทอมของ N
 |
| A | \(\rm 2N/(N – 1)\) |
| B | \(\rm N/(N – 1)\) |
| C | \(\rm \sqrt{(N – 1)/N}\) |
| D | \(\rm \sqrt{N/(N – 1)}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (E)
กรอบอ้างอิงนี้ ความเร่งจะมีค่าเท่ากับสนามโน้มถ่วง และเราจะแทนปริมาณต่างๆ ที่เปลี่ยนแปลงหลังนักบินอวกาศมาที่อาคารศูนย์กลางด้วยการเติม ไพร์ม เข้าไป เนื่องจาก v = r ω และการเคลื่อนที่เป็นวงกลม และรัศมีคงที่
จะได้
กรอบอ้างอิงนี้ ความเร่งจะมีค่าเท่ากับสนามโน้มถ่วง และเราจะแทนปริมาณต่างๆ ที่เปลี่ยนแปลงหลังนักบินอวกาศมาที่อาคารศูนย์กลางด้วยการเติม ไพร์ม เข้าไป เนื่องจาก v = r ω และการเคลื่อนที่เป็นวงกลม และรัศมีคงที่
จะได้
\(\dfrac{{{\rm{g'}}}}{{\rm{g}}}{\rm{ = }}\dfrac{{{{{\rm{v'}}}^{\rm{2}}}}}{{{{\rm{v}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{{{{\rm{\omega '}}}^{\rm{2}}}}}{{{{\rm{\omega }}^{\rm{2}}}}}\) --- (1)
โดยโมเมนตัมเชิงมุมจะถูกอนุรักษ์ไว้ เพราะไม่มีทอร์กภายนอกมากระทำในระบบ จึงได้
\({\rm{I\omega = I'\omega '}}\) --- (2)
เพราะทางเชื่อมยาวมาก เราจึงถือว่านักบินอวกาศเป็นจุดมวลหนึ่ง สมมุติให้ r เป็นระยะห่างจากอาคารศูนย์กลางถึงห้องนั่งเล่น และ m เป็นมวลของนักบินอวกาศหนึ่งคน จากที่แต่ละห้องนั่งเล่นมีนักบินอวกาศ N คน จะได้ว่าความเฉื่อยในการหมุนก่อนนักบินอวกาศจะเคลื่อนที่เท่ากับ
\({\rm{I = 2Nm}}{{\rm{r}}^{\rm{2}}}\) --- (3)
หลังนักบินอวกาศสองคนไปถึงอาคารศูนย์กลาง จะได้
\({\rm{I' = 2(N}}-1){\rm{m}}{{\rm{r}}^{\rm{2}}}\) --- (4)
เมื่อแทน (3) และ (4) ใน (2) เราจะได้
\(\begin{align*} {\rm{2Nm}}{{\rm{r}}^{\rm{2}}}\rm \omega &= \rm 2(N -1){\rm{m}}{{\rm{r}}^{\rm{2}}}{\rm{\omega '}}\\ \frac{{{\rm{\omega '}}}}{{\rm{\omega }}} &= \frac{{\rm{N}}}{{{\rm{N}}-1}} \end{align*}\)
เมื่อนำ \(\dfrac{{{\rm{\omega '}}}}{{\rm{\omega }}} = \dfrac{{\rm{N}}}{{{\rm{N}}-1}}\) ไปแทนใน (1) จะได้
\(\dfrac{{{\rm{g'}}}}{{\rm{g}}} = \dfrac{{{\rm{\omega '}}}}{{\rm{\omega }}} = \dfrac{{\rm{N}}}{{{\rm{N}}-1}}\)
สังเกตว่า ไม่มีตัวเลือกใดถูกเลยจึงตอบข้อ (E)| 28. | แบบจำลองอย่างง่ายของจักรยานมวล M สองล้อ แต่ละล้อสัมผัสพื้นที่จุดหนึ่ง และระยะฐานล้อ (ระยะจากจุดสัมผัสกับพื้นของล้อหนึ่งถึงอีกล้อหนึ่ง) เท่ากับ w มีจุดศูนย์กลางมวลของจักรยานอยู่กึ่งกลางระหว่างล้อและอยู่สูง h เหนือพื้นดิน สมมุติให้จักรยานกำลังเคลื่อนที่ไป ทางขวา แต่มีการชะลอตัวในอัตราคงที่ มีความเร่ง a และในที่นี้จะไม่สนแรงต้านอากาศ
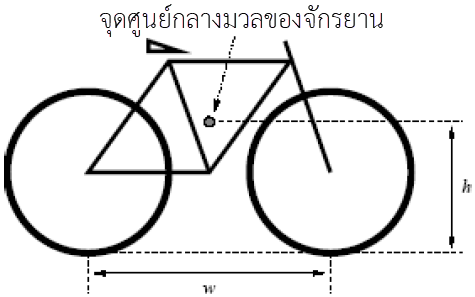 ค่า μ สูงสุดที่ล้อทั้งสองยังคงสัมผัสกับพื้นดิน เท่ากับข้อใด |
| A | \(\rm \dfrac{w}{2h}\) |
| B | \(\rm \dfrac{h}{2w}\) |
| C | \(\rm \dfrac{2h}{w}\) |
| D | \(\rm \dfrac{w}{h}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (A)
จากสมดุลสถิตในกรอบอ้างอิงที่กำหนดให้ เราต้องหาทอร์กที่จุดศูนย์กลางมวลก่อน ให้ N1 เป็นแรงตั้งฉากบนล้อหน้า, N2 เป็นแรงตั้งฉากบนล้อหลัง, f1 เป็นแรงเสียดทานที่ล้อหน้า และ f2 แรงเสียดเสียดทานที่ล้อหลัง ถ้าล้อหน้ายังไม่สัมผัสกับพื้นดิน แล้ว N1 = f1 = 0
จากทอร์กของแรงเสียดทานที่ล้อหลังในทิศทวนเข็มนาฬิกา = ทอร์กจากแรงตั้งฉากที่ล้อหลังในทิศตามเข็มนาฬิกา จะได้
จากสมดุลสถิตในกรอบอ้างอิงที่กำหนดให้ เราต้องหาทอร์กที่จุดศูนย์กลางมวลก่อน ให้ N1 เป็นแรงตั้งฉากบนล้อหน้า, N2 เป็นแรงตั้งฉากบนล้อหลัง, f1 เป็นแรงเสียดทานที่ล้อหน้า และ f2 แรงเสียดเสียดทานที่ล้อหลัง ถ้าล้อหน้ายังไม่สัมผัสกับพื้นดิน แล้ว N1 = f1 = 0
จากทอร์กของแรงเสียดทานที่ล้อหลังในทิศทวนเข็มนาฬิกา = ทอร์กจากแรงตั้งฉากที่ล้อหลังในทิศตามเข็มนาฬิกา จะได้
\({{\rm{f}}_2}{\rm{h = }}{{\rm{N}}_2}\dfrac{{\rm{w}}}{2}\)
แทน f2 = μN2 จะได้
\(\begin{align*} {\rm{\mu }}{{\rm{N}}_2}\rm h &={{\rm{N}}_2}\dfrac{{\rm{w}}}{2}\\ \rm\mu &= \dfrac{{\rm{w}}}{{2{\rm{h}}}} \end{align*}\)
| 29. | แบบจำลองอย่างง่ายของจักรยานมวล M สองล้อ แต่ละล้อสัมผัสพื้นที่จุดหนึ่ง และระยะฐานล้อ (ระยะจากจุดสัมผัสกับพื้นของล้อหนึ่งถึงอีกล้อหนึ่ง) เท่ากับ w มีจุดศูนย์กลางมวลของจักรยานอยู่กึ่งกลางระหว่างล้อและอยู่สูง h เหนือพื้นดิน สมมุติให้จักรยานกำลังเคลื่อนที่ไป ทางขวา แต่มีการชะลอตัวในอัตราคงที่ มีความเร่ง a และในที่นี้จะไม่สนแรงต้านอากาศ
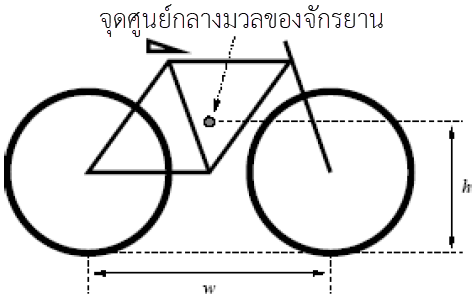 ค่า a สูงสุดที่ล้อทั้งสองยังคงสัมผัสกับพื้นดิน เท่ากับข้อใด |
| A | \(\rm \dfrac{wg}{h}\) |
| B | \(\rm \dfrac{wg}{2h}\) |
| C | \(\rm \dfrac{hg}{2w}\) |
| D | \(\rm \dfrac{h}{2wg}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (B)
จากกฎข้อที่สองของนิวตัน สำหรับการเคลื่อนในแนวนอน จะได้
จากกฎข้อที่สองของนิวตัน สำหรับการเคลื่อนในแนวนอน จะได้
\(\rm f_1 + f_2 = Ma\) --- (1)
จากทอร์กตามเข็มเท่ากับทอร์กทวนเข็ม จะได้
\(\rm \dfrac{{{{\rm{N}}_2}{\rm{w}}}}{2} = \dfrac{{{{\rm{N}}_1}{\rm{w}}}}{2} + ({f_1} + {f_2})h\) --- (2)
แทน (1) ใน (2) จะได้
\(\begin{align*} {\rm{Mah}} &= \dfrac{{\rm{w}}}{2}{\rm{(}}{{\rm{N}}_2}-{{\rm{N}}_1})\\ {\rm{a}} &= \dfrac{{\rm{w}}}{2}\dfrac{{{\rm{(}}{{\rm{N}}_2}-{{\rm{N}}_1})}}{{{\rm{Mh}}}} \end{align*}\)
ชัดเจนว่า จะเกิดค่า \(a\) สูงสุด เมื่อ N1 = 0 และ N2 = Mg จึงได้
\({\rm{a}} = \dfrac{{{\rm{w}}g}}{{2{\rm{h}}}}\)
| 30. | แบบจำลองอย่างง่ายของจักรยานมวล M สองล้อ แต่ละล้อสัมผัสพื้นที่จุดหนึ่ง และระยะฐานล้อ (ระยะจากจุดสัมผัสกับพื้นของล้อหนึ่งถึงอีกล้อหนึ่ง) เท่ากับ w มีจุดศูนย์กลางมวลของจักรยานอยู่กึ่งกลางระหว่างล้อและอยู่สูง h เหนือพื้นดิน สมมุติให้จักรยานกำลังเคลื่อนที่ไป ทางขวา แต่มีการชะลอตัวในอัตราคงที่ มีความเร่ง a และในที่นี้จะไม่สนแรงต้านอากาศ
 ถ้าทั้งสองล้อมีการลื่นไถล (หมายถึง มีการลื่นออกไปโดยไม่หมุน) แล้วค่า a สูงสุดที่ล้อทั้งสองยังคงสัมผัสกับพื้นดิน เท่ากับข้อใด |
| A | \(\rm \dfrac{wg}{h}\) |
| B | \(\rm \dfrac{wg}{3h}\) |
| C | \(\rm \dfrac{2wg}{3h}\) |
| D | \(\rm \dfrac{hg}{2w}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (E)
จากกฎข้อที่สองของนิวตัน สำหรับการเคลื่อนในแนวนอน จะได้
จากกฎข้อที่สองของนิวตัน สำหรับการเคลื่อนในแนวนอน จะได้
\(\rm f_1 + f_2 = Ma\) --- (1)
จากทอร์กตามเข็มเท่ากับทอร์กทวนเข็ม จะได้
\(\rm \dfrac{{{{\rm{N}}_2}{\rm{w}}}}{2} = \dfrac{{{{\rm{N}}_1}{\rm{w}}}}{2} + ({f_1} + {f_2})h\) --- (2)
แทน (1) ใน (2) จะได้
\(\begin{align*} {\rm{Mah}} &= \dfrac{{\rm{w}}}{2}{\rm{(}}{{\rm{N}}_2}-{{\rm{N}}_1})\\ {\rm{a}} &= \dfrac{{\rm{w}}}{2}\dfrac{{{\rm{(}}{{\rm{N}}_2}-{{\rm{N}}_1})}}{{{\rm{Mh}}}} \end{align*}\)
ชัดเจนว่า จะเกิดค่า \(a\) สูงสุด เมื่อ N1 = 0 และ N2 = Mg จึงได้
\({\rm{a}} = \dfrac{{{\rm{w}}g}}{{2{\rm{h}}}}\)
จะเห็นว่าคำตอบไม่ได้ขึ้นสัมประสิทธิ์ของแรงเสียดทานของแต่ละล้อ และไม่สนว่าพื้นเป็นอย่างไร ดังนั้น การลื่นไถลจึงไม่มีผลใด ๆ และคำตอบคือ \({\rm{a}} = \dfrac{{{\rm{w}}g}}{{2{\rm{h}}}}\) เหมือนเดิม
ซึ่งไม่มีในตัวเลือก จึงตอบข้อ (E)
ซึ่งไม่มีในตัวเลือก จึงตอบข้อ (E)
| 31. | ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 แล้วอัตราส่วน L/d เท่ากับข้อใด |
| A | \(3\sqrt2\) |
| B | \(3\) |
| C | \(12\) |
| D | \(2\sqrt3\) |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
พิจารณาความเฉื่อยในการหมุนรอบจุดศูนย์กลางของคานบางสม่ำเสมอ จะได้
พิจารณาความเฉื่อยในการหมุนรอบจุดศูนย์กลางของคานบางสม่ำเสมอ จะได้
\({{\rm{I}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{\rm{1}}}{{{\rm{12}}}}{\rm{m}}{{\rm{L}}^{\rm{2}}}\)
จากโจทย์ให้ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 เมื่อแทนที่ Icm จะได้
\(\begin{align*}{\rm{m}}{{\rm{d}}^{\rm{2}}} &= \dfrac{{\rm{1}}}{{{\rm{12}}}}{\rm{m}}{{\rm{L}}^{\rm{2}}}\\ {{\rm{L}}^{\rm{2}}} &= {\rm{12}}{{\rm{d}}^{\rm{2}}}\\ \dfrac{{\rm{L}}}{{\rm{d}}} &= \sqrt {12} \end{align*}\)
ดังนั้น \(\rm L/d = 2\sqrt3\)| 32. | ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 ถ้าคานถูกแขวน ณ ตำแหน่งที่ห่างจากจุดศูนย์กลางไป kd และถูกสั่นเบาๆ ด้วยความถี่เชิงมุม β\(\sqrt{ \rm \dfrac{g}{d}}\) แล้วค่าของ β ในเทอมของ k เท่ากับข้อใด |
| A | \(\rm 1+k^2\) |
| B | \(\rm \sqrt{1+k^2}\) |
| C | \(\rm \sqrt{\dfrac{k}{1+k}}\) |
| D | \(\rm \sqrt{\dfrac{k^2}{1+k}}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (E)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
เราจะได้
ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
\({\tau _{\rm{p}}}=\rm - mg~k~d ~sin \theta\) --- (1)
ให้ p ที่ห้อยอยู่หมายถึง จุดหมุน จากนั้นเราจะใช้ทฤษฎีบทของแกนขนานหาความเฉื่อยในการหมุนรอบจุดหมุน จะได้ว่า\(\rm I_p = I_{cm} + mh^2 = md^2 + m (kd)^2\)
\(\rm I_p = md^2 (1+k^2) \) --- (2)
จากนั้นใช้กฎข้อที่สองของนิวตันหาการหมุนของแกนที่ผ่านจุดหมุน สังเกตว่าแรงที่จุดหมุนไม่ได้ทำให้เกิดทอร์กกับแกนที่ผ่านจุดหมุนเลย เมื่อใช้สมการที่ (1) และ (2) จะได้ว่า
\(\begin{align*} {\tau _{\rm{p}}} &=\rm I{{\rm{ }}_{\rm{p}}}{\rm{\alpha }}\\ \rm - mg~k~d ~sin \theta &= \rm m{{\rm{d}}^{\rm{2}}}\left( {{\rm{1 + }}{{\rm{k}}^{\rm{2}}}} \right)\frac{{{{\rm{d}}^{\rm{2}}}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}} \end{align*}\)
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - \dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}{\rm{\theta }}\)
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - {{\rm{\omega }}^2}{\rm{\theta }}\)
เราจะได้
\({\rm{\omega = }}\sqrt {\dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}} \)
จากโจทย์ให้ \({\rm{\omega }} = \beta \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}}\)ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)
| 33. | (เกินหลักสูตรการสอบเข้า สอวน. 1) ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 ถ้าคานถูกแขวน ณ ตำแหน่งที่ห่างจากจุดศูนย์กลางไป kd และถูกสั่นเบาๆ ด้วยความถี่เชิงมุม β\(\sqrt{ \rm \dfrac{g}{d}}\) ค่าของ β สูงสุด จะเท่ากับข้อใด |
| A | \(1\) |
| B | \(\sqrt2\) |
| C | \(1/\sqrt2\) |
| D | ไม่สามารถหาค่า β สูงสุดได้ |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
เราจะได้
เราจะต้องหาค่า k ที่ทำให้ β มีค่าสูงสุด โดยการหาอนุพันธ์เทียบ k ทั้งสองข้างจะได้
สังเกตว่า \(\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = 0}}\) เมื่อ k = 1
แทน k = 1 ใน \({\rm{\beta = }}\sqrt {\dfrac{{\rm{k}}}{{{\rm{1 + }}{{\rm{k}}^{\rm{2}}}}}} \) จะได้ \({\rm{\beta = }}\sqrt {\dfrac{{\rm{1}}}{{\rm{2}}}} \)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
\({\tau _{\rm{p}}}=\rm - mg~k~d ~sin \theta\) --- (1)
ให้ p ที่ห้อยอยู่หมายถึง จุดหมุน จากนั้นเราจะใช้ทฤษฎีบทของแกนขนานหาความเฉื่อยในการหมุนรอบจุดหมุน จะได้ว่า\(\rm I_p = I_{cm} + mh^2 = md^2 + m (kd)^2\)
\(\rm I_p = md^2 (1+k^2) \) --- (2)
จากนั้นใช้กฎข้อที่สองของนิวตันหาการหมุนของแกนที่ผ่านจุดหมุน สังเกตว่าแรงที่จุดหมุนไม่ได้ทำให้เกิดทอร์กกับแกนที่ผ่านจุดหมุนเลย เมื่อใช้สมการที่ (1) และ (2) จะได้ว่า
\(\begin{align*} {\tau _{\rm{p}}} &=\rm I{{\rm{ }}_{\rm{p}}}{\rm{\alpha }}\\ \rm - mg~k~d ~sin \theta &= \rm m{{\rm{d}}^{\rm{2}}}\left( {{\rm{1 + }}{{\rm{k}}^{\rm{2}}}} \right)\frac{{{{\rm{d}}^{\rm{2}}}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}} \end{align*}\)
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - \dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}{\rm{\theta }}\)
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - {{\rm{\omega }}^2}{\rm{\theta }}\)
เราจะได้
\({\rm{\omega = }}\sqrt {\dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}} \)
จากโจทย์ให้ \({\rm{\omega }} = \beta \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}}\) ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)เราจะต้องหาค่า k ที่ทำให้ β มีค่าสูงสุด โดยการหาอนุพันธ์เทียบ k ทั้งสองข้างจะได้
\({\rm{2\beta }}\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = }}\dfrac{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}} - {\rm{k(2k)}}}}{{{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{{\rm{1}} - {{\rm{k}}^{\rm{2}}}}}{{{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}^{\rm{2}}}}}\)
สังเกตว่า \(\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = 0}}\) เมื่อ k = 1
แทน k = 1 ใน \({\rm{\beta = }}\sqrt {\dfrac{{\rm{k}}}{{{\rm{1 + }}{{\rm{k}}^{\rm{2}}}}}} \) จะได้ \({\rm{\beta = }}\sqrt {\dfrac{{\rm{1}}}{{\rm{2}}}} \)
| 34. | วัตถุมวล m ผูกติดกับทรงกระบอก รัศมี R ด้วยเชือกเบา ที่เวลา t = 0 วัตถุมีความเร็วต้น v0 ในทิศตั้งฉากกับเชือกที่มีความยาวเชือก L0 และแรงตึงในเส้นเชือกไม่เท่ากับศูนย์ ให้ทุกการเคลื่อนที่เกิดขึ้นบนพื้นที่ไม่มีแรงเสียดทานในแนวนอน ทรงกระบอกยังคงนิ่งอยู่บนพื้นและไม่มีการหมุน โดยวัตถุจะเคลื่อนหมุนวนไปรอบ ๆ ทรงกระบอก ซึ่งเชือกจะขาดเมื่อแรงตึงเชือกเกิน Tmax จงตอบคำถามในรูปของ Tmax , m, L0 , R , และ v0  |
| A | \(\rm mv_0R\) |
| B | \(\rm \dfrac{m^2v_0^3}{T_{max}}\) |
| C | \(\rm mv_0L_0\) |
| D | \(\rm \dfrac{T_{max}R^2}{v_0}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (B)
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ
โดย r คือ รัศมีของวงแกว่งรอบทรงกระบอก (เชือกที่ยังไม่พันรอบทรงกระบอก)
ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ
\({\rm{K = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{2}}}\)
ดังนั้น อัตราเร็วของวัตถุจะเท่ากับ v0 เสมอ และโมเมนตัมเชิงมุมของวัตถุที่กระทำกับแกนของทรงกระบอกจะเท่ากับ\(\rm L = mv_0r\) --- (1)
โดย r คือ รัศมีของวงแกว่งรอบทรงกระบอก (เชือกที่ยังไม่พันรอบทรงกระบอก)
ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
\({{\rm{T}}_{{\rm{max}}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{r}}}\)
หรือ \({\rm{r = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{{{\rm{T}}_{{\rm{max}}}}}}\) เมื่อนำไปแทนใน (1) จะได้
\({\rm{L = }}\dfrac{{{{\rm{m}}^2}{\rm{v}}_{\rm{0}}^{\rm{3}}}}{{{{\rm{T}}_{{\rm{max}}}}}}\)
| 35. | วัตถุมวล m ผูกติดกับทรงกระบอก รัศมี R ด้วยเชือกเบา ที่เวลา t = 0 วัตถุมีความเร็วต้น v0 ในทิศตั้งฉากกับเชือกที่มีความยาวเชือก L0 และแรงตึงในเส้นเชือกไม่เท่ากับศูนย์ ให้ทุกการเคลื่อนที่เกิดขึ้นบนพื้นที่ไม่มีแรงเสียดทานในแนวนอน ทรงกระบอกยังคงนิ่งอยู่บนพื้นและไม่มีการหมุน โดยวัตถุจะเคลื่อนหมุนวนไปรอบ ๆ ทรงกระบอก ซึ่งเชือกจะขาดเมื่อแรงตึงเชือกเกิน Tmax จงตอบคำถามในรูปของ Tmax , m, L0 , R , และ v0  |
| A | \(\rm \dfrac{mv^2_0}{2}\) |
| B | \(\rm \dfrac{mv^2_0R}{2L_0}\) |
| C | \(\rm \dfrac{mv^2_0R^2}{2L^2_0}\) |
| D | \(\rm \dfrac{mv^2_0L_0^2}{2R^2}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (A)
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ จึงได้
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ จึงได้
\({\rm{K = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{2}}}\)
| 36. | วัตถุมวล m ผูกติดกับทรงกระบอก รัศมี R ด้วยเชือกเบา ที่เวลา t = 0 วัตถุมีความเร็วต้น v0 ในทิศตั้งฉากกับเชือกที่มีความยาวเชือก L0 และแรงตึงในเส้นเชือกไม่เท่ากับศูนย์ ให้ทุกการเคลื่อนที่เกิดขึ้นบนพื้นที่ไม่มีแรงเสียดทานในแนวนอน ทรงกระบอกยังคงนิ่งอยู่บนพื้นและไม่มีการหมุน โดยวัตถุจะเคลื่อนหมุนวนไปรอบ ๆ ทรงกระบอก ซึ่งเชือกจะขาดเมื่อแรงตึงเชือกเกิน Tmax จงตอบคำถามในรูปของ Tmax , m, L0 , R , และ v0  |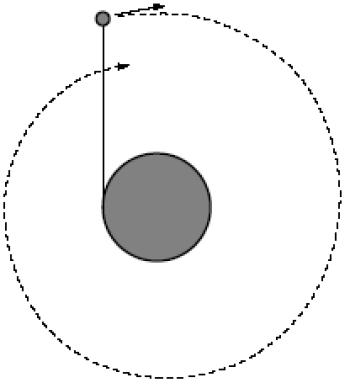
| A | \(\rm L_0 – πR\) |
| B | \(\rm L_0 –2 πR\) |
| C | \(\rm L_0 – \sqrt{18}πR\) |
| D | \(\rm \dfrac{mv^2_0}{T_{max}}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
จากอัตราเร็วของวัตถุจะเท่ากับ v0 เสมอ โมเมนตัมเชิงมุมของวัตถุที่กระทำกับแกนของทรงกระบอกจะเท่ากับ
ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
จากอัตราเร็วของวัตถุจะเท่ากับ v0 เสมอ โมเมนตัมเชิงมุมของวัตถุที่กระทำกับแกนของทรงกระบอกจะเท่ากับ
\(\rm L = mv_0r\)
โดย r คือ รัศมีของวงแกว่งรอบทรงกระบอก (เชือกที่ยังไม่พันรอบทรงกระบอก)ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
\({{\rm{T}}_{{\rm{max}}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{r}}}\)
ดังนั้น \({\rm{ r = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{{{\rm{T}}_{{\rm{max}}}}}}\)| 37. | ให้เชือกเบาที่มีความยืดหยุ่นตามกฎของฮุค จะขาดเมื่อมีแรงตึง Tmax หากนำเชือกมาตรึงปลายด้านหนึ่งไว้ ส่วนปลายอีกด้านผูกกับมวล 3m และมวลที่สองขนาด m ซึ่งเล็กกว่า และมีอัตราเร็วต้น v0 พุ่งเข้าชนกับมวลแรก แล้วติดไปด้วยกัน จึงทำให้เชือกถูกดึงจนขาดออก โดยพลังงานจลน์สุดท้ายของมวลทั้งสองจะเท่ากับศูนย์ ถ้าการชนนั้นเกิดขึ้นในหนึ่งมิติ และยืดหยุ่นสมบูรณ์ แล้วขณะเชือกขาดมวลแรกจะหลุดออกไปด้วยอัตราเร็วสุดท้าย vf สมมุติให้ทุกการเคลื่อนที่เกิดขึ้นในแนวนอนและพื้นไม่มีแรงเสียดทาน แล้วค่า vf / v0 เท่ากับข้อใด |
| A | \(1/\sqrt{12}\) |
| B | \(1/\sqrt{2}\) |
| C | \(1/\sqrt{6}\) |
| D | \(1/\sqrt{3}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
โจทย์ให้เชือกขาดเมื่อถึงแรงตึงค่าหนึ่ง และเมื่อเชือกขาดก็จะเกิดพลังงานศักย์ U0 ขึ้น ในการชนที่ไม่ยืดหยุ่น (ขณะเชือกยังไม่ขาด) เราจะใช้กฎอนุรักษ์โมเมนตัม จึงได้ว่า
เนื่องจากทุกพลังงานศักย์ที่เกิดขึ้นจะถูกเปลี่ยนเป็นพลังงานจลน์ ทำให้ทราบว่าเชือกจะขาดเมื่อ
ต่อไปพิจารณา การชนแบบยืดหยุ่น เริ่มจากหาความเร็วต้นของมวลแต่ละอันหลังเกิดการชน (ขณะเชือกยังไม่ขาด)
วิธีที่ง่ายที่สุดคือหาจากจุดศูนย์กลางมวล จะได้
ในกรอบอ้างอิงนี้ ที่จุดศูนย์กลางมวลก่อนเกิดการชน m จะมีความเร็วเท่ากับ และ 3m มีความเร็วเท่ากับ \(\dfrac{{ - {{\rm{v}}_0}}}{4}\) สำหรับการชนแบบยืดหยุ่นในหนึ่งมิติ และจุดศูนย์กลางมวลแต่ละอันจะมีความเร็วหลังการชนเท่ากับก่อนชน แต่มีทิศทางตรงข้ามกับความเร็วก่อนชน ดังนั้น ความเร็วของ 3m หลังเกิดการชนจะไปทางขวาด้วย \(\dfrac{{ + {{\rm{v}}_0}}}{4}\)
เมื่อแปลง (2) กลับไปเราจะได้อัตราเร็วของ 3m หลังเกิดการชนเท่ากับ \(\dfrac{{ {{\rm{v}}_0}}}{2}\) และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) จะเท่ากับ
โจทย์ให้เชือกขาดเมื่อถึงแรงตึงค่าหนึ่ง และเมื่อเชือกขาดก็จะเกิดพลังงานศักย์ U0 ขึ้น ในการชนที่ไม่ยืดหยุ่น (ขณะเชือกยังไม่ขาด) เราจะใช้กฎอนุรักษ์โมเมนตัม จึงได้ว่า
\(\begin{align*} {\rm{m}}{{\rm{v}}_{\rm{0}}} &=\rm 4mv'\\ \rm v' &=\dfrac{{{{\rm{v}}_{\rm{0}}}}}{{\rm{4}}} \end{align*}\)
และพลังงานศักย์ของมวลทั้งสองหลังเกิดการชนจะเท่ากับ
\({{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
เนื่องจากทุกพลังงานศักย์ที่เกิดขึ้นจะถูกเปลี่ยนเป็นพลังงานจลน์ ทำให้ทราบว่าเชือกจะขาดเมื่อ
\({{\rm{U}}_{\rm{0}}}{\rm{ = }}{{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (1)
ต่อไปพิจารณา การชนแบบยืดหยุ่น เริ่มจากหาความเร็วต้นของมวลแต่ละอันหลังเกิดการชน (ขณะเชือกยังไม่ขาด)
วิธีที่ง่ายที่สุดคือหาจากจุดศูนย์กลางมวล จะได้
\({{\rm{v}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{{{\rm{v}}_0}}}{{\rm{4}}}\) --- (2)
ในกรอบอ้างอิงนี้ ที่จุดศูนย์กลางมวลก่อนเกิดการชน m จะมีความเร็วเท่ากับ และ 3m มีความเร็วเท่ากับ \(\dfrac{{ - {{\rm{v}}_0}}}{4}\) สำหรับการชนแบบยืดหยุ่นในหนึ่งมิติ และจุดศูนย์กลางมวลแต่ละอันจะมีความเร็วหลังการชนเท่ากับก่อนชน แต่มีทิศทางตรงข้ามกับความเร็วก่อนชน ดังนั้น ความเร็วของ 3m หลังเกิดการชนจะไปทางขวาด้วย \(\dfrac{{ + {{\rm{v}}_0}}}{4}\)
เมื่อแปลง (2) กลับไปเราจะได้อัตราเร็วของ 3m หลังเกิดการชนเท่ากับ \(\dfrac{{ {{\rm{v}}_0}}}{2}\) และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) จะเท่ากับ
\({{\rm{K}}_{\rm{2}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (3)
แต่โจทย์กำหนดให้เชือกต้องขาด จากที่เราทราบว่า U0 ของพลังงานจนล์ของ 3m จะถูกส่งไปที่เชือก เราจะใช้กฎอนุรักษ์พลังงานร่วมกับสมการที่ (1) และ (3) จะได้
\({{\rm{K}}_{\rm{3}}}{\rm{ = }}{{\rm{K}}_{\rm{2}}} - {{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}} - \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\)
หาค่า vf / v0 จาก K3 ดังนี้
\(\begin{align*} {{\rm{K}}_{\rm{3}}}&= \dfrac{{{\rm{3mv}}_f^{\rm{2}}}}{{\rm{2}}} =\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\\ \frac{{{{\rm{v}}_{\rm{f}}}}}{{{{\rm{v}}_{\rm{0}}}}} &= \sqrt {\frac{1}{6}} \end{align*}\)
| 38. | ให้เชือกเบาที่มีความยืดหยุ่นตามกฎของฮุค จะขาดเมื่อมีแรงตึง Tmax หากนำเชือกมาตรึงปลายด้านหนึ่งไว้ ส่วนปลายอีกด้านผูกกับมวล 3m และมวลที่สองขนาด m ซึ่งเล็กกว่า และมีอัตราเร็วต้น v0 พุ่งเข้าชนกับมวลแรก แล้วติดไปด้วยกัน จึงทำให้เชือกถูกดึงจนขาดออก โดยพลังงานจลน์สุดท้ายของมวลทั้งสองจะเท่ากับศูนย์ ถ้าการชนนั้นเกิดขึ้นในหนึ่งมิติ และยืดหยุ่นสมบูรณ์ แล้วขณะเชือกขาดมวลแรกจะหลุดออกไปด้วยอัตราเร็วสุดท้าย vf สมมุติให้ทุกการเคลื่อนที่เกิดขึ้นในแนวนอนและพื้นไม่มีแรงเสียดทาน แล้วอัตราส่วนของพลังงานจลน์สุทธิของระบบของมวลทั้งสองหลังการชนแบบยืดยุ่นสมบูรณ์และเชือกได้ขาดออก กับ พลังงานจลน์เริ่มต้นของมวลที่สองก่อนเกิดการชน เท่ากับข้อใด |
| A | 1/4 |
| B | 1/3 |
| C | 1/2 |
| D | 3/4 |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
พลังงานศักย์ของมวลทั้งสองหลังเกิดการชนเท่ากับ
และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) เท่ากับ
จากในกรอบอ้างอิง ที่จุดศูนย์กลางมวลหลังเกิดการชน m จะมีความเร็วเท่ากับ \(\dfrac{{ - 3{{\rm{v}}_0}}}{4}\) เมื่อแปลงกลับไปเราจะหาความเร็วของ m หลังชนกับมวลที่มี \(\dfrac{{{{\rm{v}}_0}}}{2}\) ได้ ดังนั้น พลังงานจลน์ของมวล m หลังเกิดการชนแบบยืดหยุ่นเท่ากับ
ใช้สมการ (1) และค่า K3 หาพลังงานจลน์รวมของระบบหลังเกิดการชนแบบยืดหยุ่นจะได้
ดังนั้น อัตราส่วนของพลังงานจลน์สุทธิของระบบหลังเกิดการชนแบบยืดหยุ่นกับพลังงานจลน์เริ่มต้นของมวล m ก่อนชนและทำให้เชือกขาดจะเท่ากับ
พลังงานศักย์ของมวลทั้งสองหลังเกิดการชนเท่ากับ
\({{\rm{K}}_{\rm{1}}} = \dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) เท่ากับ
\({{\rm{K}}_{\rm{2}}} = \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
จากโจทย์กำหนดให้เชือกต้องขาด และเราทราบว่า U0 ของพลังงานจนล์ของ 3m จะถูกส่งไปที่เชือก เราจะใช้กฎอนุรักษ์พลังงานร่วมกับ K1 และ K2 จะได้
\({{\rm{K}}_{\rm{3}}}{\rm{ = }}{{\rm{K}}_{\rm{2}}} - {{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}} - \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\)
จากในกรอบอ้างอิง ที่จุดศูนย์กลางมวลหลังเกิดการชน m จะมีความเร็วเท่ากับ \(\dfrac{{ - 3{{\rm{v}}_0}}}{4}\) เมื่อแปลงกลับไปเราจะหาความเร็วของ m หลังชนกับมวลที่มี \(\dfrac{{{{\rm{v}}_0}}}{2}\) ได้ ดังนั้น พลังงานจลน์ของมวล m หลังเกิดการชนแบบยืดหยุ่นเท่ากับ
\({{\rm{K}}_{\rm{4}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (1)
ใช้สมการ (1) และค่า K3 หาพลังงานจลน์รวมของระบบหลังเกิดการชนแบบยืดหยุ่นจะได้
\({{\rm{K}}_4}{\rm{ + }}{{\rm{K}}_{\rm{3}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{8} + \dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}} = \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{8}\)
ดังนั้น อัตราส่วนของพลังงานจลน์สุทธิของระบบหลังเกิดการชนแบบยืดหยุ่นกับพลังงานจลน์เริ่มต้นของมวล m ก่อนชนและทำให้เชือกขาดจะเท่ากับ
\(\dfrac{{\frac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{8}}}{{\frac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{2}}} = \dfrac{3}{4}\)
