ฮาร์มอนิคอย่างง่าย ชุดที่ 2 (9 ข้อ)
| 1. | คาบการแกว่งของนาฬิกาลูกตุ้มอย่างง่ายที่ลวดแขวนยาวขึ้นเพราะอุณหภูมิเพิ่มขึ้น กำหนด ก. คาบ T ของนาฬิกาลูกตุม้ อย่างง่ายเป็นไปตามสูตร \(\text{T} = 2π \sqrt{l/\text{g}}\) เมื่อ l เป็นความยาวของลวดแขวนลูกตุ้มและ g เป็นขนาดความเร่งเนื่องจากแรงโน้มถ่วงของโลก
ข. สัมประสิทธิ์การขยายตัวเชิงเส้นเนื่องจากความร้อน α คือ อัตราส่วนความยาวที่เปลี่ยนไป Δl ต่อความยาวเดิม l เมื่ออุณหภูมิเปลี่ยนไปหนึ่งหน่วย
ค. นักเรียนสามารถใช้การประมาณ \(\rm \sqrt{1+x}≈1 + x/2\) เมื่อ x มีขนาดน้อย 1 กว่ามาก ๆ
นาฬิกาลูกตุ้ม อย่างง่ายเรือนหนึ่งมีลวดแขวนที่มีสัมประสิทธิ์การขยายตัว เชิงเส้นเนื่องจากความร้อนเท่ากับ α และมีคาบแกว่ง T ที่ความยาว l1 เมื่ออุณหภูมิเพิ่มขึ้น Δθ น้อยมาก ๆ เมื่อ เทียบกับอุณหภูมิเดิม และคาบการแกว่งเปลี่ยนไปเป็น T + ΔT จงหาค่าอัตราส่วน ΔT/T ในรูปของตัวแปรที่กำหนดมา(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 2. | มวล M กับ m เชื่อมกันด้วยสปริงเบา ๆ กำลังสั่น "อยู่กับที่" เทียบกับระบบอ้างอิงเฉื่อย โดยที่ m สั่นด้วยแอมพลิจูด A จงหาค่าของแอมพลิจูดของการสั่นของ M (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555) 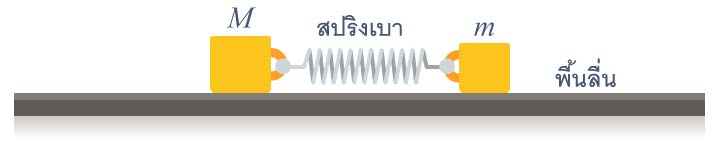 |
| 3. |  (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557) |
| 4. | การเคลื่อนที่ของระบบนี้บรรยายได้ด้วยการเคลื่อนที่ 3 สมการ
\(\rm m\ddot x_1 = +k(x_2 − x_1 − ℓ)\) . . . (1)
จงเขียนอีก 2 สมการให้ครบแล้วแก้สมการเพื่อหาความถี่ของการสั่นพื้นฐานซึ่งมีอยู่ 2 ค่า(ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 26 มี.ค. 2556) 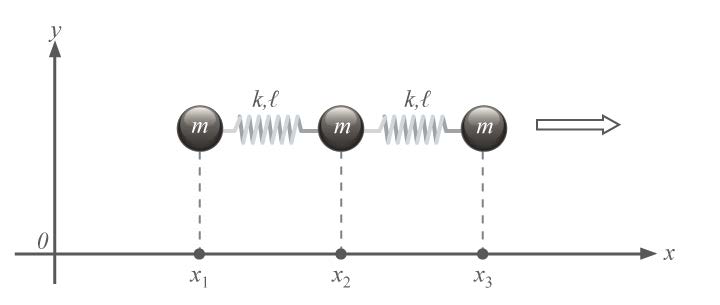 |
ตอบ
\(\rm m\ddot x_2 = +k(x_3-x_2 − ℓ)-k(x_2-x_1 − ℓ)\) . . . (2)
\(\rm m\ddot x_3 = -k(x_3-x_2 − ℓ)\) . . . (3)
\(\rm ω_2=\sqrt{\dfrac{3k}{m}}\)
\(\rm f_2 = \dfrac{1}{2\pi}\sqrt{\dfrac{3k}{m}}\)
\(\rm m\ddot x_2 = +k(x_3-x_2 − ℓ)-k(x_2-x_1 − ℓ)\) . . . (2)
\(\rm m\ddot x_3 = -k(x_3-x_2 − ℓ)\) . . . (3)
\(\rm ω_2=\sqrt{\dfrac{3k}{m}}\)
\(\rm f_2 = \dfrac{1}{2\pi}\sqrt{\dfrac{3k}{m}}\)
| 5. | ล้อทรงกระบอกตันมวล M รัศมี R สามารถหมุนได้คล่องรอบจุด O มีปลายหนึ่งของสปริง k ยึดไว้และอีกปลายของสปริงยึดกับเพดาน มวล m ซึ่งถ่วงขอบของทรงกระบอกทำให้นิ่งและ OA อยู่ในแนวระดับพอดี ต่อมาดึง m ลงนิดหน่อยแล้วปล่อย m จะเคลื่อนขึ้นลงๆ ด้วยคาบของการสั่นเป็นเท่าไร (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2553) 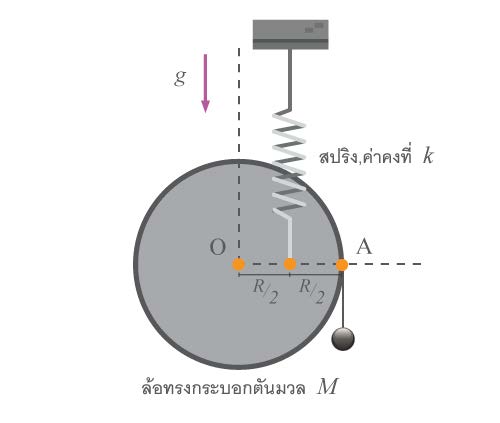 |
| 6. | ลูกกลมโลหะขนาดเล็กมาก 2 ลูกที่เหมือนกันทุกประการ (แต่ละลูกมีมวล m และประจุ q) ถูกแขวนจากเชือกที่ทำจากฉนวนยาว L จงหาค่า x เมื่อระบบอยู่ในสมดุล โดยมุม θ มีขนาดเล็กมากจนประมาณได้ว่า tan θ ≈ sin θ (ตอบในรูปของตัวแปร m, q, L และค่าคงที่มาตรฐานต่างๆ เช่น g) (ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 18 ต.ค. 2554) 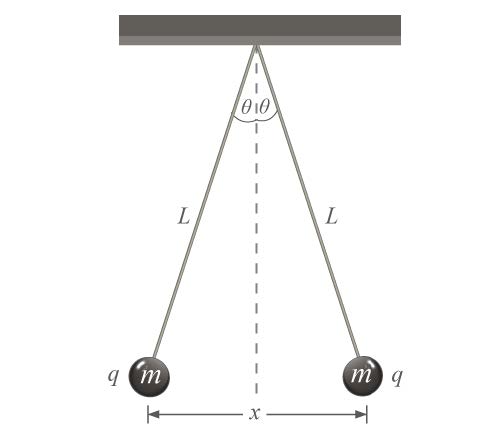 |
| 7. | แผ่นกลมแบนแกว่งได้คล่องในระนาบของแผ่นรอบจุด O ระยะทางจาก O ถึงจุด CM ต้องมีค่าเท่าไร คาบของการแกว่งด้วยแอมพลิจูดเล็ก ๆ จึงจะมีค่าเล็กที่สุด และค่านี้เป็นเท่าไรในรูปของ g , R (ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 24 มี.ค. 2552) 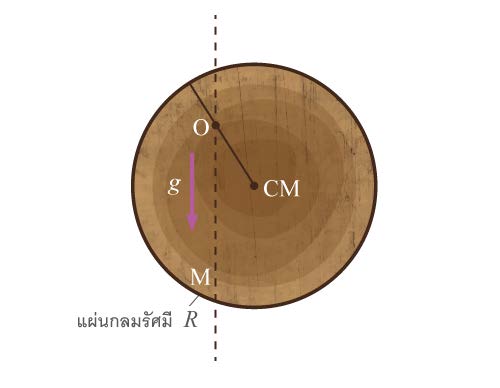 |
| 8. | ภาพนี้แสดงระบบในสภาวะสมดุลเชิงกล l เป็นระยะทางระหว่างรอกทั้งสอง ขณะที่เชือกส่วนนี้ทำมุม θ0 กับแนวดิ่งถ้าดึง M ลงนิดหน่อยแล้วปล่อยระบบจะสั่น ( M และ m เคลื่อนที่ขึ้นลงสลับกัน) จงวิเคราะห์หาคาบของการสั่นด้วยแอมพลิจูดเล็ก ๆ นี้ในเทอมของ m , M , l , g , sin θo (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557) หมายเหตุ \(\dfrac{1}{1+a} ≈ 1-a\) สำหรับ \(|a| ≪ 1\) \(Δ(\cos θ) ≈ −\sin θ ⋅ Δθ\) ถ้ารู้แคลคูลัส... (ไม่รู้ก็ทำได้อยู่แล้ว) |
| 9. | สปริงไร้มวล ความยาวธรรมชาติ l ค่าคงตัวสปริง k ขดหนึ่งวางตั้งตรงอยู่ในแนวดิ่ง ปลายล่างของสปริงถูกยึดไว้กับพื้น ส่วนปลายบนเคลื่อนที่ได้อย่าอิสระ ปล่อยวัตถุมวล m จากที่สูง h จากปลายบนของสปริงให้ตกในแนวดิ่ง ลงมาบนสปริงกำหนดว่าเมื่อวัตถุชนกับสปริง แล้วจะถูกยึดติดกับปลายของสปริงตลอดเวลา สมมุติด้วยว่าความสูงที่ปล่อยวัตถุลงมาไม่สูงมากพอให้สปริงหดสั้นจนถึงพื้นได ้
1) สปริงหดสั้นที่สุดเท่าใด
2) ตำแหน่งสมดุลของวัตถุอยู่สองจากพื้นเท่าใด
3) วัตถุจะกระดอนกลับขึ้นไปสูงสุดจากพื้นเท่าใด
4) วัตถุมีอัตราเร็วสูงสุดเท่าใด
5) ให้ y เป็นตำแหน่งของวัตถุจากตำแหน่งสมดุล โดยให้ y มีค่าเป็นบวกเมื่อวัดขึ้นในแนวดิ่ง ที่ตำแหน่งใด ๆ นี้วัตถุมีความเร่งเท่าใด
จงใหเ้หตุผลแสดงว่าวัตถุจะสั่นขึ้นลงแบบฮาร์มอนิกอย่างง่าย แล้วให้หาว่าตำแหน่ง y ของวัตถุจากตำแหน่งสมดุลที่เวลา t ใด ๆหลังติดกับสปริงเป็นฟังก์ชันอย่างใดของเวลา t
6) การสั่นนี้มีคาบเท่าใด
(ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 24 ต.ค. 2552) |
ตอบ
1) \(\rm x =\dfrac{mg}{k}+\dfrac{\sqrt{m^2g^2 + 2mghk}}{k}\)
2) \(l-\dfrac{\text{mg}}{\text{k}}\)
3) \(\text H =l -\dfrac{\text{mg}}{\text{k}}+\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\)
4) \(\rm v_{max} = \sqrt{\dfrac{mg^2}{k}+2gh}\)
5) \(\rm \dfrac{d^2}{dt^2}y=-\left(\dfrac{k}{m}\right)y\) และ \(\rm y(t)=\left[\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\right]\sin\left[\sqrt{\dfrac{k}{m}}t+arcsin\left(\dfrac{mg}{\sqrt{\rm m^2g^2 + 2mghk}}\right)\right]\)
6) \(\rm T=2\pi\sqrt{\dfrac{m}{k}}\)
1) \(\rm x =\dfrac{mg}{k}+\dfrac{\sqrt{m^2g^2 + 2mghk}}{k}\)
2) \(l-\dfrac{\text{mg}}{\text{k}}\)
3) \(\text H =l -\dfrac{\text{mg}}{\text{k}}+\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\)
4) \(\rm v_{max} = \sqrt{\dfrac{mg^2}{k}+2gh}\)
5) \(\rm \dfrac{d^2}{dt^2}y=-\left(\dfrac{k}{m}\right)y\) และ \(\rm y(t)=\left[\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\right]\sin\left[\sqrt{\dfrac{k}{m}}t+arcsin\left(\dfrac{mg}{\sqrt{\rm m^2g^2 + 2mghk}}\right)\right]\)
6) \(\rm T=2\pi\sqrt{\dfrac{m}{k}}\)

