งาน พลังงาน โมเมนตัม ชุดที่ 2 (17 ข้อ)
| 1. | ลูกตุ้มมวล m ยาว ℓ เริ่มแกว่งจากหยุดนิ่งในแนวระดับลงไปชนมวล M แล้วติดไปด้วยกัน หลังการชนมวล m จะแกว่งขึ้นไปได้ระยะทางสูงสุดเท่าใดจากพื้น (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |
| 2. | มวล M ตั้งต้นเคลื่อนที่เข้าหากำแพงจากระยะห่าง D ด้วยความเร็วคงที่ v ที่จังหวะเดียวกันกับที่ลูกบอลเล็กๆ มวล m << M กระดอนจาก M แล้วด้วยความเร็ว u > v เทียบกับพื้นไปชนและกระดอนอย่างยืดหยุ่นจากกำแพงแข็งกลับมาชนกับ M อีก ที่จังหวะนี้ m ได้เคลื่อนที่ไปแล้วเป็นระยะทางรวมเท่าใดนับจากเมื่อชน M ครั้งแรก (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |
| 3. | สปริงมีความยาวธรรมชาติ ℓ ปลายหนึ่งยึดติดกำแพง อีกปลายหนึ่งยึดกับมวล m ถูกอัดไว้เป็นระยะทาง \(\dfrac{ℓ}{2}\) แล้วปล่อยให้ดันมวล m ไปชนมวล m เท่ากันอีกก้อนที่แค่เดิมอยู่นิ่งที่ B แล้วติดกันไป จะไปได้ไกลสุดเท่าใดจากจุด B (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 3 ก.ย. 2549)  |
| 4. | จงแปลงค่าของพลังงานจลน์ \(\rm \dfrac{1}{2}mv^2=5\) จูล ไปอยู่ในหน่วยกรัม (มิลลิเมตรต่อวินาที)2 (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 6 ก.ย. 2546) |
| 5. | มวล M อยู่นิ่งบนพื้นระดับลื่นและมีสปริงเบาติดอยู่ด้านซ้าย ค่าคงที่สปริงเท่ากับ k มวล m เคลื่อนที่ด้วยความเร็วต้น u เข้าชน สปริงจะหดเข้าไปมากที่สุดเป็นระยะทางเท่าไร (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 6 ก.ย. 2546)  |
| 6. | โปรเจคไทล์ตั้งต้นจากจุด O เมื่อขึ้นไปถึงจุดสูงสุดก็ระเบิดออกเป็นสองชิ้นมวลเท่ากัน ชิ้นหน้าคือ A ชิ้นหลังคือ B ทันทีหลังระเบิด B มีความเร็วเป็นศูนย์เทียบกับพื้น ชิ้น A จะตกบนพื้นเลยจุดตกของ B ไปเป็นระยะทางกี่เท่าของระยะทาง OC (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |
| 7. | ปล่อยลูกบอลมวล m จากจุดหยุดนิ่งจากที่สูง H จากพื้นทุกครั้งที่ลูกบอลกระทบพื้นจะกระดอนขึ้นด้วยอัตราเร็ว e(< 1) เท่าของอัตราเร็วก่อนกระทบพื้นพอดี ตอนที่ลูกบอลกระดอนขึ้นครั้งที่ n ลูกบอลมีพลังงานจลน์เท่าใด และจะกระดอนขึ้นไปได้สูงเท่าใดก่อนตกกลับลงมาอีก (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 29 ส.ค. 2553) |
| 8. | ลูกปืนตะกั่วลูกหนึ่งเคลื่อนที่ด้วยอัตราเร็ว 200 m/s เข้าใส่เป้าและหยุดนิ่งอยู่ในเป้า สมมุติว่าพลังงานจลน์ทั้งหมดของลูกปืนเปลี่ยนเป็นความร้อนหมด และความร้อนนี้แบ่งไปให้ลูกปืนกับเป้าอย่างละเท่ากัน ลูกปืนมีอุณหภูมิเพิ่มขึ้นเท่าใด ความจุความร้อนจำเพาะของตะกั่วมีค่าเป็น 0.032 เท่าของน้ำ ความจุความร้อนจำเพาะของน้ำมีค่าเท่ากับ 1.00 cal/(g ⋅∘C) และ 1.00 cal มีค่าเท่ากับ 4.186 J (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 30 ส.ค. 2552) |
| 9. | A กับ B เป็นมวลทรงกลมผิวเกลี้ยงรัศมีเท่ากัน A กำลังเคลื่อนที่ในแนว OX เข้าชน B ซึ่งอยู่นิ่งก่อนชนหลังการชนกันอย่างยืดหยุ่น แล้ว B จะกระเด็นทำมุมกี่องศากับแนว OX (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2551) 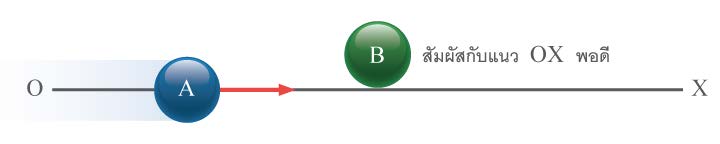 |
| 10. | ปล่อยมวลเล็ก ๆ ให้ไถลจากจุดหยุดนิ่งที่จุด A เข้าสู่รางวงกลม OB อย่างนุ่มนวล (ไม่มีการสะดุด, กระแทก) จะต้องให้จุด A อยู่สูงจากพื้นระดับเป็นกี่เท่าของรัศมีของราง OB จึงจะทำให้มวลนั้นขึ้นถึงจุด B ได้พอดีโดยไม่แยกตัวจากรางก่อน (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2551) 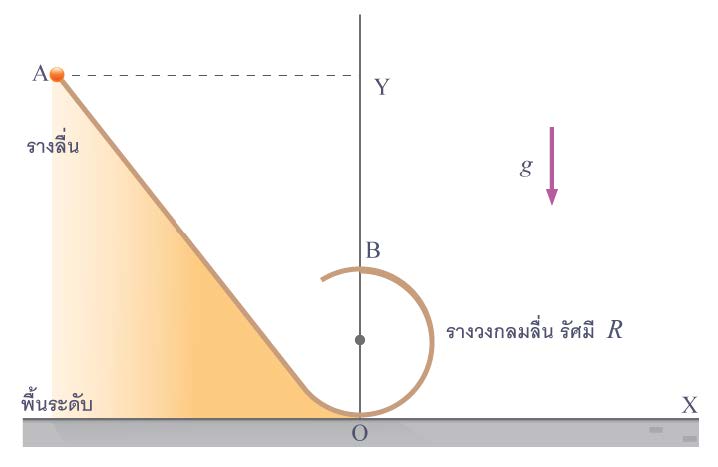 |
| 11. | ลูกบอลลูกหนึ่งตกลงมาจากที่สูง 10 m กระดอนกับพื้น และลอยกลับขึ้นไปได้สูง 2.5 m ถ้าลูกบอลกระทบพื้นนาน 0.10 s ความเร่งเฉลี่ยของลูกบอลระหว่างที่แตะพื้นมีขนาดเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 31 ส.ค. 2551) |
| 12. | M กับ m ผูกโยงกันด้วยเส้นยางยืดหย่อนๆ อยู่บนผืนระดับรอบเเละลื่นต่อมาดีด M ไปทางขวาด้วยความเร็ว v∘ อึดใจต่อมาขณะที่เส้นยางยืดตึงที่สุดนั้น M มีความเร็วเป็นเท่าไรและพลังงานศักย์ของระบบขณะเดียวกันนั้นมีค่าเท่าไร (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 1 ก.ย. 2556)  |
ตอบ \(\rm v_{_M} = \dfrac{M}{M +m}v_0\) และ \(\rm PE = \dfrac{1}{2}\left(\dfrac{mM}{M +m}\right) v^2_0\)
| 13. | ลูกตุ้ม M ห้อยอยู่นิ่ง ๆ มวล m เคลื่อนที่ด้วยความเร็ว u เข้าชนแล้วติดกันไปจะขึ้นไปได้สูงจากเดิมเป็นระยะทางเท่าไร (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 31 ส.ค. 2557)  |
| 14. | มวล M รูปทรงกลมรัศมี R วางไว้ที่พื้นในห้องที่อุณหภูมิ t∘ จะมีพลังงานศักย์เพิ่มขึ้นหรือลดลงเท่าใด เมื่ออุณหภูมิห้องสูงขึ้นเป็น t1 (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 12 ก.ย. 2547) 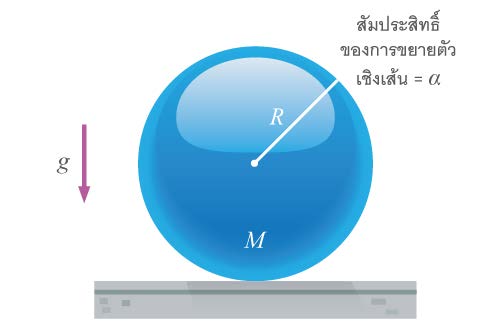 |
| 15. | มวล m1 กับ m2 ผูกติดกันด้วยเชือกยาว l และถูกเหวี่ยงให้หมุนอย่างอิสระบนโต๊ะระดับด้วยอัตราเร็วเชิงมุม ω ผู้สังเกตในระบบอ้างอิงเฉื่อยจะพบความเร็วสัมพันธ์ระหว่าง m2 กับ m1 มีขนาดเป็นเท่าใด (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 3 ก.ย. 2549)  |
| 16. | จงตอบคำถามต่อไปนี้
1) จงพิสูจน์ว่าในกรอบอ้างอิงจุดศูนย์กลางมวลของระบบ โมเมนตัมของระบบมีค่ารวมกันเป็นศูนย์
2) จงแสดงว่าพลังงานจลน์ทั้งหมดของระบบมีค่าเท่ากับพลังงานจลน์ของจุดศูนย์กลางมวลของระบบบวกกับพลังงานจลน์รอบจุดศูนย์กลางมวลของระบบ
(ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 24 ต.ค. 2552) |
ตอบ
1) จาก นิยามของ \(\rm v_{cm}\)จะได้
2) พลังงานจลน์ของระบบคือ
1) จาก นิยามของ \(\rm v_{cm}\)จะได้
\(\rm v_{cm}=\dfrac{\sum\limits_{i = 1}^{i = n} {m_iv_i} }{\sum\limits_{i = 1}^{i = n} {m_1}}\)
โมเมนตัมรวมของระบบเทียบจุดศูนย์กลางมวล คือ
\(\rm \sum\limits_{i = 1}^{i = n} {m_i{(v-v_{cm})}}i\)
จึงได้ว่า
\(\rm \sum\limits_{i = 1}^{i = n} {m_iv_i} - \sum\limits_{i = 1}^{i = n} {m_iv_{cm}} = 0\)
2) พลังงานจลน์ของระบบคือ
\(\rm \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_i} = \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_i(v_{cm}+v_{i,cm})^2} = \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_{cm}} + \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_{i,cm}}\)
ใช้ผลจากข้อที่แล้วร่วมด้วย เพื่อตัดพจน์ตรงกลางทิ้งไป
\(\rm ∴ KE_{system} = KE_{cm} +KE_{around \,cm}\)
| 17. | 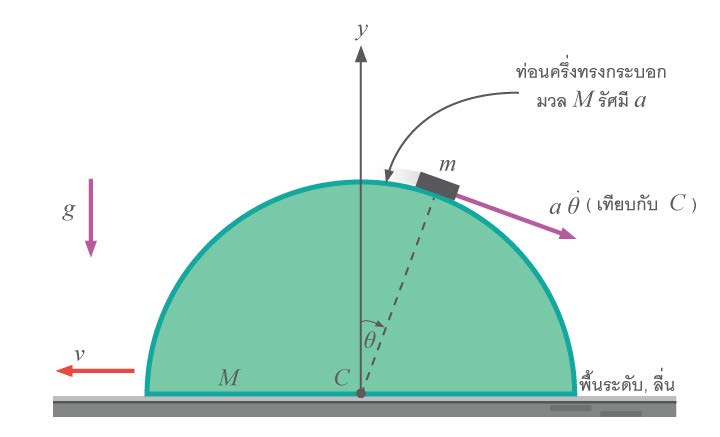 (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 25 ต.ค. 2551) |
ตอบ
1) \(\rm V=\dfrac{m\dotθRcos}{M+m}\)
2) \(\rm 2g(1-\cos\theta) = \left[\dfrac{M+m(1-\cos\theta)^2}{M+m}\right]a\dot\theta^2\)
3) \(\rm \theta=arccos\left[\dfrac{2(M+m)}{2(M+m)+M}\right]\)
1) \(\rm V=\dfrac{m\dotθRcos}{M+m}\)
2) \(\rm 2g(1-\cos\theta) = \left[\dfrac{M+m(1-\cos\theta)^2}{M+m}\right]a\dot\theta^2\)
3) \(\rm \theta=arccos\left[\dfrac{2(M+m)}{2(M+m)+M}\right]\)

