กฎการเคลื่อนที่ของนิวตัน ชุดที่ 2 (12 ข้อ)
| 1. | มวล M กับ m เชื่อมกันด้วยสปริงเบา ๆ กำลังสั่น "อยู่กับที่" เทียบกับระบบอ้างอิงเฉื่อย โดยที่ m สั่นด้วยแอมพลิจูด A จงหาค่าของแอมพลิจูดของการสั่นของ M (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555) 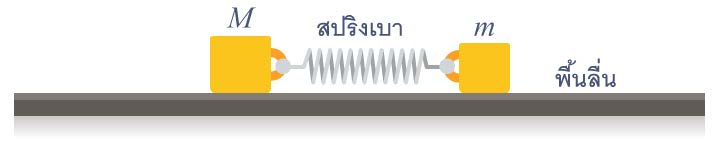 |
| 2. | ถ้าคุณดันหนังสือกับผนังแนวดิ่งด้วยแรงมากพอหนังสือจะไม่ไถลตกลงมา ถ้าสัมประสิทธิ์ของความเสียดทานสถิตระหว่างหนังสือกับผนังมีค่าเท่ากับ 0.7
1) คุณจะตองออกแรงดันตั้งฉากกับผนังด้วยขนาดอย่างน้อยเท่าใด หนังสือมวล 2.0 kg จึงจะไม่ไถลตกลงมากำหนดว่าความเร่งเนื่องจากแรงโน้มถ่วงโลกมีขนาด 9.8 m/s2
2) ถ้าคุณออกแรงดันขนาด 35N แรงเสียดทานสถิตที่ผนังกระทำต่อหนังสือมีขนาดเท่าใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2548) |
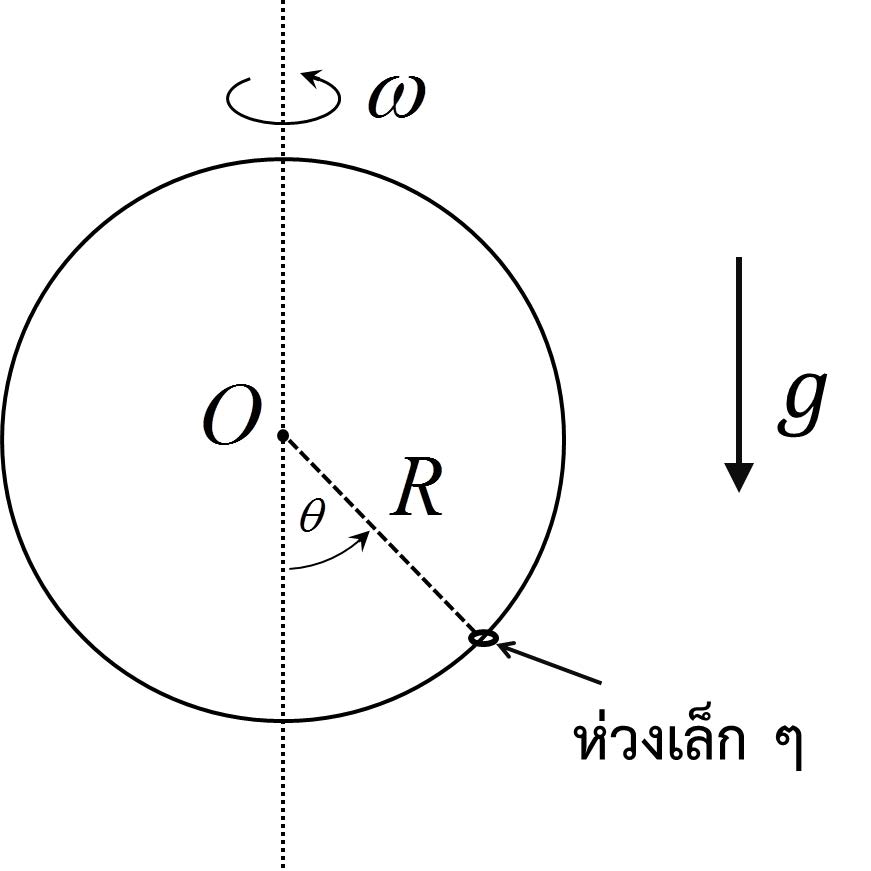
| 3. | ห่วงเล็ก ๆ คล้องอยู่ในห่วงใหญ่ดังรูป โดยที่ห่วงใหญ่มีรัศมี R ถ้าสัมประสิทธิ์ความเสียดทานของทั้งสองห่วงเท่ากับศูนย์ จงหาค่าของมุม θ ที่จุดสมดุลเมื่อห่วงใหญ่หมุนรอบตัวเองด้วยความเร็วเชิงมุม ω สูงมาก ๆ
 |
| 4. | ดีดวัตถุมวล m ก้อนหนึ่งด้วยอัตราเร็วต้น u ให้ไถลขึ้นไปตามพื้นเอียงซึ่งทำมุม θ กับแนวระดับ เมื่อวัตถุขึ้นไปไดสู้งสุดก็ตกกลับมาตามพื้นเอียง ถ้าสัมประสิทธิ์ของความเสียดทานจลน์ระหว่างวัตถุกับผิวพื้นเอียงมีค่า μk อัตราเร็วของวัตถุขณะที่กลับมาถึงที่ปลายพื้นเอียงมีค่าเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) |
| 5. | ตาชั่งสปริงอันหนึ่งแขวนไว้กับเพดานลิฟต์ที่กำลังเคลื่อนที่ ถ้าปลายล่างของตาชั่งมีวัตถุมวล 10 kg แขวนอยู่และตาชั่งอ่านค่าได ้125 N
1) จงหาความเร่ง (ทิศเเละขนาด) ของลิฟต์
2) ถ้าที่แขวนตาชั่งหลุดจากเพดาน ตาชั่งอ่านค่าเท่าใด
กำหนดว่าขนาดสนามโน้มถ่วงของโลกที่บริเวณนั้นมีค่าเท่ากับ 9.8 N/kg(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) |
| 6. | ในระบบดาวฤกษ์สองดวง m1 กับ m2 ซึ่งโคจรรอบกันและกัน m1 โคจรตามแนววงกลมรัศมี R1 นั้น m2 จะมีอัตราเร็วเชิงเส้นเป็นเท่าใด (ใช้กฎการโน้มถ่วง \(\rm F =\dfrac{Gm_1m_2}{r^2} ,~ r =\) ระยะห่าง) (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555) |
| 7. | ดีดวัตถุมวล m ด้วยอัตราเร็วต้นไปในทางทิศขวามือให้ไถลไปบนผิวแผ่นไม้มวล M แผ่นไม้วางอยู่บนพื้นลื่นอีกทีหนึ่ง ให้ μk และ μs เป็นสัมประสิทธิ์ความเสียดทานจลน์และสัมประสิทธความเสียดทานสถิตระหว่างวัตถุและแผ่นไม้ตามลำดับ
1) แรงเสียดทานที่แผ่นไม้ทำต่อวัตถุมีทิศทางใด และมีขนาดเท่าใด
2) ความเร่งของแผ่นไม้มีทิศทางใด และมีขนาดเท่าใด
3) แผ่นไม้เคลื่อนที่ไปเท่าใด เมื่อวัตถุและแผ่นไม้มีความเร็วเท่ากัน
4) วัตถุไถลไปบนแผ่นไม้เป็นระยะทางเท่าใด (วัดเทียบกับแผ่นไม ้ และวัดตั้งแต่ต้นจนวัตถุเริ่มหยุดไถลบนแผ่นไม้)
5) เมื่อวัตถุหยุดไถล แรงเสียดทานที่แผ่นไม้ทำต่อวัตถุมีขนาดเท่าใด และมีทิศทางใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 29 ส.ค. 2553) |
ตอบ
1) ทิศไปทางซ้าย และ \(\rm f_k = μ_kmg\)
2) ทิศไปทางขวา และ \(\rm a = \dfrac{\mu_kmg}{M}\)
3) แผ่นไม้เคลื่อนที่ไปได้ \(\rm \dfrac{mMu^2}{2\mu_kg(m+M)^2}\)
4) วัตถุไถลไปได้ \(\rm \dfrac{Mu^2}{2\mu_k g(M+m)}\)
5) ไม่เกิดทิศ และแรงเสียดทานจลน์เท่ากับศูนย์
1) ทิศไปทางซ้าย และ \(\rm f_k = μ_kmg\)
2) ทิศไปทางขวา และ \(\rm a = \dfrac{\mu_kmg}{M}\)
3) แผ่นไม้เคลื่อนที่ไปได้ \(\rm \dfrac{mMu^2}{2\mu_kg(m+M)^2}\)
4) วัตถุไถลไปได้ \(\rm \dfrac{Mu^2}{2\mu_k g(M+m)}\)
5) ไม่เกิดทิศ และแรงเสียดทานจลน์เท่ากับศูนย์
| 8. | ท่อนผอม, ตรง, ยาว, มวล M ความยาว L กำลังล้มจากหยุดนิ่งจากแนวดิ่งบนพื้นฝืด จงวิเคราะห์หาแรงเสียดทานที่พื้นกระทำต่อปลายล่างของท่อนทำให้ท่อนไม่ไถลไปทางซ้าย หาแรงปฏิกิริยาที่พื้นกระทำต่อปลายล่าง แล้วหาเงื่อนไขเกี่ยวกับค่าสัมประสิทธิ์ความเสียดทาน (μ) ที่จะทำให้ปลายล่างไม่ไถลไปทางซ้ายเลย [ถึงแม้ว่าในที่สุดจะไปทางขวา] (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 18 ธ.ค. 2554)  |
ตอบ
\(\rm f=\dfrac{3mg}{4}(3\cos\theta-2)\sin\theta\)
\(\rm N = \dfrac{3mg}{4}\left[3\cos^2\theta-2\cos\theta-1+\dfrac{4}{3}\right]\)
\(\rm \mu \approx 0.3706\) โดย \(\rm \mu \ge \dfrac{f}{N}\) ทุกๆ θ
\(\rm f=\dfrac{3mg}{4}(3\cos\theta-2)\sin\theta\)
\(\rm N = \dfrac{3mg}{4}\left[3\cos^2\theta-2\cos\theta-1+\dfrac{4}{3}\right]\)
\(\rm \mu \approx 0.3706\) โดย \(\rm \mu \ge \dfrac{f}{N}\) ทุกๆ θ
| 9. | มวล m1 , m2 โยงกันด้วยเชือกยาว ℓ กำลังตกเข้าหาโลกมวล M ในแนวเข้าสู่ O โดยไม่มีการหมุน จงหาความตึงในเส้นเชือกในเทอมของ r , m1 , m2 , M , ℓ และ G ซึ่งเป็นค่า Gravitational constant และถ้า ℓ ≪ r ความตึงนี้จะมีค่าประมาณเท่าใด (ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 24 มี.ค. 2552) 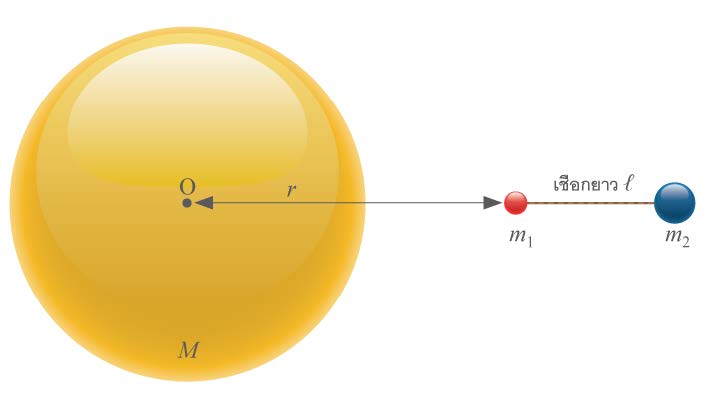 |
| 10. | ค่อย ๆ วางวัตถุมวล m อย่างช้าๆ ลงบนทางเลื่อน (มวลมากกว่า m มาก ๆ) ในสนามบินสุวรรณภูมิซึ่ง กำลังเลื่อนด้วยอัตราเร็ว u คงตัว ถ้าสัมประสิทธิ์ของความเสียดทานจลน์ระหว่างวัตถุและทางเลื่อนเท่ากับ μk
1) จงหา นานเท่าใดหลังจากวางวัตถุ วัตถุจึงจะหยุดไถล และ
2) วัตถุเคลื่อนที่ไปได้ระยะทางเท่าใด (เทียบกับคนที่ยืนอยู่นอกทางเลื่อน) ในระหว่างช่วงเวลาในข้อ 1)
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 11. | วัตถุเล็ก ๆ ตกจากหยุดนิ่งตามแนวรางลื่นจาก A ไป C แล้วไป B จะใช้เวลาเป็นกี่เท่าของการตกตามแนวรางลื่น A ตรงไป B (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2554)  |
| 12. | M ถูกดีดด้วยความเร็วต้น vo ให้กระตุกโซ่ออกไปจากกองที่ origin O ของระบบอ้างอิงเฉื่อย XOY โซ่มีมวลต่อหน่วยความยาวเป็น λ สัมประสิทธิ์ความเสียดทานระหว่างโซ่และ M กับพื้นเป็น μ จงวิเคราะห์หา:
 ก. สมการเคลื่อนที่ equation of motion ของ M
ข. ความเร็ว v ที่ขณะใดๆ ในรูปของ vo,M, g, μ, λ และ x
ค. ความเร่ง \(\rm\dfrac{d}{dt}v\) ในรูปของ vo,M, g, μ, λ และ x
ง. ความเร่ง \(\rm\dfrac{d}{dt}v\) ที่จังหวะที่ x = 0 เป็นเท่าใด
(ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2548) |
ตอบ
ก. \(\rm (M + λx)\ddot{x}= −μ(M + λx)g − λv^2\)
ข. \(\rm v(x) =\sqrt{\dfrac{3λ M^2v_0^2− 2μg[(M + λx )^3- M^3]}{3λ(M + λx)^2}}\)
ค. \(\rm a = -\mu g-\dfrac{1}{3(M + λx)^3}(3λ M^2v_0^2− 2μg[(M + λx )^3- M^3])\)
ง. \(\rm a = -\mu g-\dfrac{λ}{M}v^2_0\)
ก. \(\rm (M + λx)\ddot{x}= −μ(M + λx)g − λv^2\)
ข. \(\rm v(x) =\sqrt{\dfrac{3λ M^2v_0^2− 2μg[(M + λx )^3- M^3]}{3λ(M + λx)^2}}\)
ค. \(\rm a = -\mu g-\dfrac{1}{3(M + λx)^3}(3λ M^2v_0^2− 2μg[(M + λx )^3- M^3])\)
ง. \(\rm a = -\mu g-\dfrac{λ}{M}v^2_0\)

