จลศาสตร์ในหนึ่งมิติและสองมิติ ชุดที่ 2 (15 ข้อ)
| 1. | ปล่อยวัตถุ A จากหยุดนิ่งลงมาจากที่สูง H ที่เวลา \(\rm\sqrt{\dfrac{H}{2g}}\) หลังจากนั้นก็ปาวัตถุ B ตามลงมา จงหาว่าจะต้องปา B ด้วยอัตราเร็วเท่าใด จึงจะให้ทัน A ที่พื้นพอดี (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
ตอบ \(\rm \dfrac{1}{4}\sqrt{\dfrac{2gH}{3}}\)
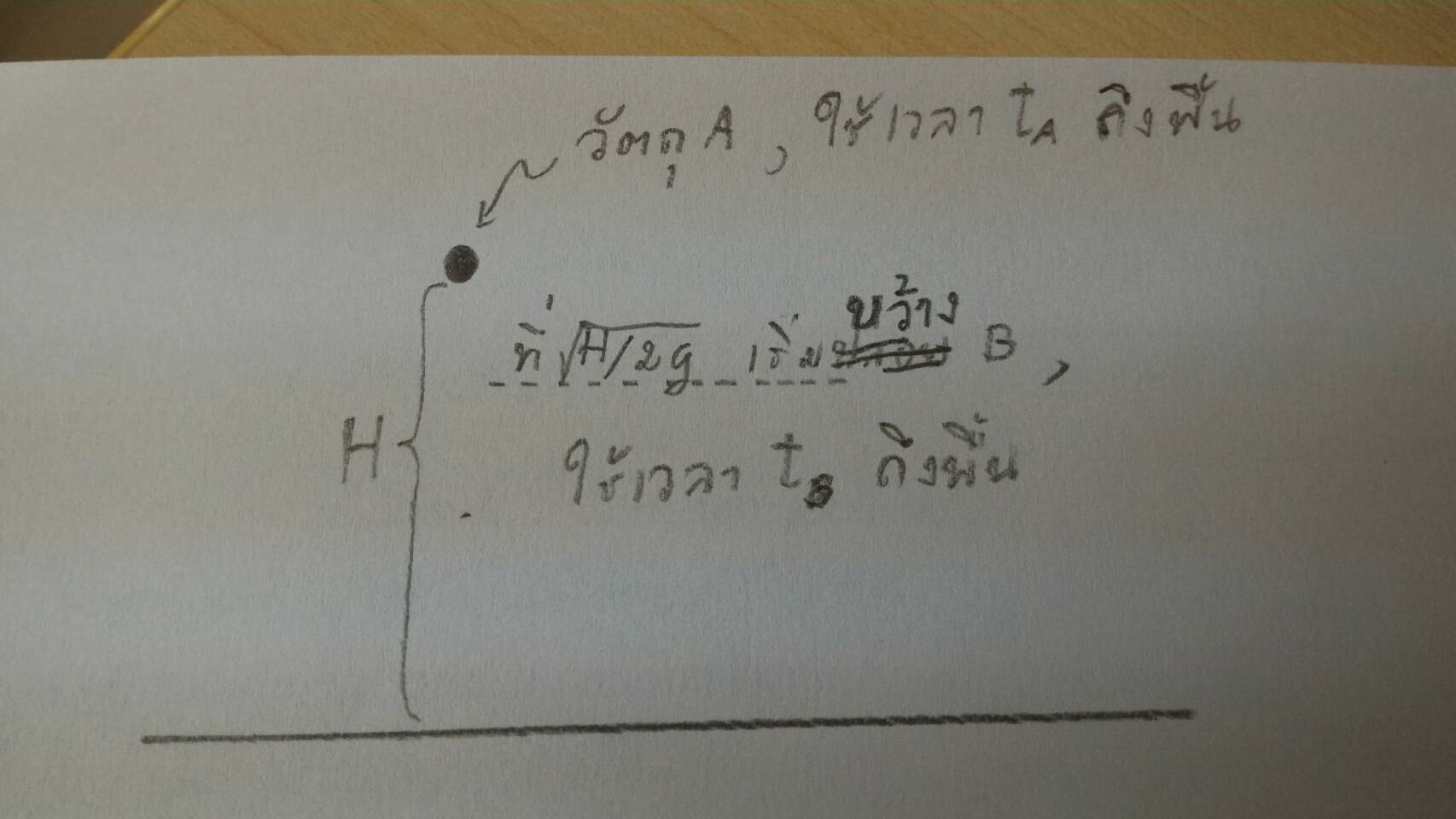(จากรูป) เวลาที่วัตถุ A ใช้ในการเคลื่อนที่ถึงพื้นหาได้จาก
หลังจากเวลา \(\rm\sqrt{\dfrac{H}{2g}}\) ขว้าง B ตามลงไปด้วยอัตราเร็วต้น \(\rm u_B\) และสามารถหาอัตราเร็วของ B ได้จาก
กำหนดให้ \(\rm t_A\)เป็นเวลาที่ A ใช้เคลื่อนที่จนถึงพื้น มีค่าเท่ากับ
ดังนั้น สามารถหาอัตราเร็วของ B ได้จาก
\(\begin{align*} \rm H&=\rm0+\dfrac{1}{2}g(t_A)^2\\ \rm t_A &=\rm\sqrt{\dfrac{2H}{g}} \end{align*}\)
หลังจากที่เวลาผ่านไป \(\rm\sqrt{\dfrac{H}{2g}}\) เริ่มขว้าง B และใช้เวลา \(\rm t_B\) เคลื่อนที่จนถึงพื้นพร้อม A ดังนั้น เขียนสมการได้ว่า
\(\begin{align*} \rm\sqrt{\dfrac{H}{2g}} + t_B&=\rm t_A\\ \rm t_B&=\rm t_A-\sqrt{\dfrac{H}{2g}}\\ \rm t_B&=\rm\sqrt{\dfrac{3H}{2g}} \end{align*}\)
\(\begin{align*} \rm H&= \rm u_B\cdot t_B +\dfrac{1}{2}g(t_B)^2\\ \rm H&=\rm u_B\cdot \sqrt{\dfrac{3H}{2g}}+\dfrac{1}{2}g\dfrac{3H}{2g}\\ \rm u_B&=\rm\dfrac{1}{4}\sqrt{\dfrac {2gH}{3}} \end{align*}\)
\(\rm t_A =\sqrt{\dfrac{H}{2g}}+T\)
สามารถหา T จากการเคลื่อนที่ของ B ด้วยอัตราเร็ว \(\rm v_B\)
\(\begin{align*} \rm H&=\rm u_B \cdot T+\dfrac{1}{2}gT^2\\ 0&=\rm T^2+\sqrt{\dfrac{2H}{g}}T -\dfrac{3H}{2g}\\ \rm T&=\rm+\sqrt{\dfrac{3H}{2g}} \end{align*}\)
หมายเหตุ เลือกค่าเวลาเป็นบวกดังนั้น สามารถหาอัตราเร็วของ B ได้จาก
\(\begin{align*} \rm H&=\rm u_B \cdot \sqrt{\dfrac{3H}{2g}}+\dfrac{1}{2}g\dfrac{3H}{2g}\\ \rm u_B &= \rm \dfrac{1}{4}\sqrt{\dfrac{2gH}{3}} \end{align*}\)
| 2. | รถไฟ A และ B สองขบวนแล่นบนรางตรงเดียวกันมาในทิศทางตรงกันข้ามพนักงานขับรถต่างเห็นรถไฟอีกขบวนหนึ่งอยู่ข้างหน้า จึงดึงห้ามล้อพร้อมกันเมื่อรถไฟทั้งสองอยู่ห่างกัน D และมีอัตราเร็วตอนนั้น uA และ uB สมมุติว่ารถไฟทั้งสองขบวนเคลื่อนที่ช้าลงด้วยความหน่วงคงตัว และรถไฟหยุดพร้อมกันที่ระยะห่างกัน d
1) จงหาอัตราส่วนขนาดความหน่วงของรถไฟ B ต่อขนาดความหน่วงของรถไฟ A
2) จงหาขนาดความหน่วงของรถไฟ A
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
ตอบ
1) \(\rm \dfrac{a_{_B}}{a_{_A}} = \dfrac{u_{_B}}{u_{_A}}\)
2) \(\rm a_{_A}=\dfrac{u_{_A}}{2(D-d)}(u_{_A}+u_{_B})\)
1) \(\rm \dfrac{a_{_B}}{a_{_A}} = \dfrac{u_{_B}}{u_{_A}}\)
2) \(\rm a_{_A}=\dfrac{u_{_A}}{2(D-d)}(u_{_A}+u_{_B})\)
| 3. | รางลื่นรูปวงกลมรัศมี R อยู่ในระนาบดิ่งมวล m ถูกดีดจากจุดล่างสุดให้ไถลขึ้นด้านในของราง พอถึงจุด A มวล m ก็แยกตัวจากรางเเล้วเคลื่อนที่โค้งวกลงมาตัดเเนวระดับเดียวกันกับ A ที่จุด B จงหาค่าของระยะทาง AB ในเทอมของ R กับ θ (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 1 ก.ย. 2556)  |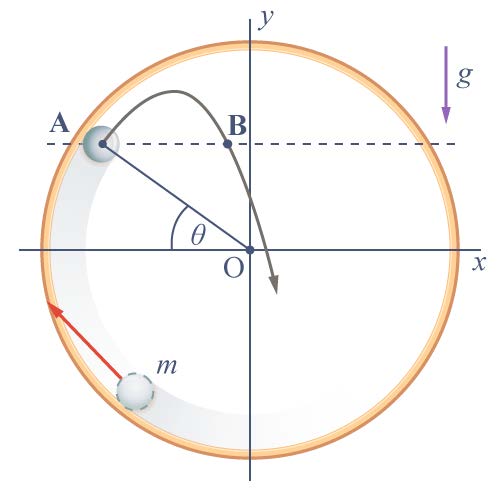
| 4. | นาย A และ นาย B แรกอยู่ห่างกันเป็นระยะทาง d นาย A กับ B ตั้งต้นออกวิ่งเข้าหากันที่จังหวะเดียวกัน A และ B มีอัตราเร็วคงที่เท่ากับ v1 และ v2 ตามลำดับ ทั้งคู่จะชนกันเมื่อ A เคลื่อนที่ได้ระยะทางเท่าไหร่ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2554)  |
| 5. | นักบิน T และ C ขณะที่กำลังบินด้วยความเร็ว \(\rm \vec v_c\) และ \(\rm \vec v_T\) ตามลำดับเทียบกับพื้นโลกนััน นักบิน T จะพบว่า C กำลังเคลื่อนที่หนีจากเขาด้วยความเร็ว(สัมพันธ์) ขนาดเท่าไร (ตอบในรูป vc vT และ θ)
 |
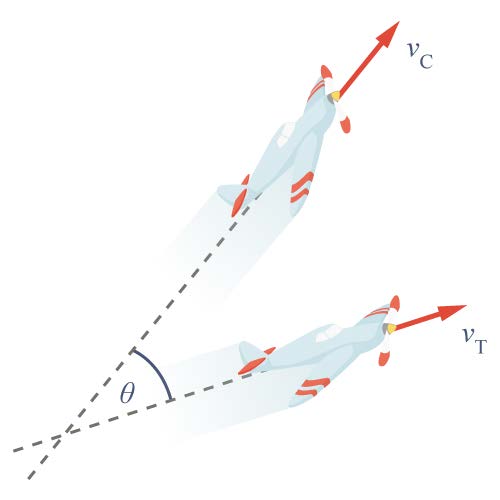| 6. | ระยะทาง AB = D เป็นรางรถไฟตรง เมื่อนกออกบินจาก A พร้อมกันกับที่รถไฟออกจาก B นกบินได้เร็ว รถไฟเคลื่อนที่เร็ว เมื่อนกบินถึงรถไฟก็บินกลับทันทีด้วยความเร็วขนาดเท่าเดิม เมื่อนกบินถึง A รถไฟจะอยู่ห่าง B เท่าไร (กำหนดว่า v > u นกจะได้ไม่ถูกชน)
 |
| 7. | โจ๊กเกอร์วางแผนปล่อยหนูปีศาจออกมาอาละวาดในเมือง เขาเอาหนูปีศาจใส่รถบรรทุกแล่นด้วยอัตราเร็ว 10 m/s ไปตามถนนตรงเเละปล่อยหนูปีศาจออกมาทีละตัว โดยปล่อยหนึ่งตัวต่อวินาที หนูปีศาจเมื่อหลุดจากรถก็วิ่งไปข้างหน้าทันทีด้วยอัตราเร็ว 20 m/s (อัตราเร็วของหนูปีศาจบนถนนไม่ขึ้นกับอัตราเร็วของรถบรรทุก) แบทแมนรู้ข่าวนี้ล่วงหน้าจึงรีบมาจัดการเก็บหนูปีศาจ เขาขับรถค้างคาวแล่นสวนเข้ามาด้วยอัตราเร็ว 20 m/s ในทิศตรงข้ามกับทิศที่หนูวิ่งรถค้างคาวมีเครื่องมือเก็บหนูปีศาจทันทีที่หนูถึงรถ จงหาว่าแบทแมนจะเก็บหนูปีศาจไปทำหนูสะเต๊ะได้กี่ตัวต่อหนึ่งนาที |
| 8. | ปล่อยวัตถุหนึ่งจากหยุดนิ่งจากที่สูงขนาดหนึ่งลงมาในแนวดิ่ง พบว่าในวินาทีสุดท้ายก่อนกระทบพื้น วัตถุเคลื่อนที่ได้ระยะทางหนึ่งในสี่ของความสูงทั้งหมดที่ตกลงมา จงหาว่าวัตถุใช้เวลาทั้งหมดเท่าใดในการตกลงมาก่อนถึงพื้น |
| 9. | รถไฟขบวนหนึ่งกำลังแล่นด้วยอัตราเร็ว vA ไปตามตารางตรง ทันใดนั้น พนักงานขับรถก็สังเกตเห็นรถไฟอีกขบวนหนึ่งที่ระยะห่าง d กำลังแล่นอยู่ข้างหน้าไปในทิศทางเดียวกันด้วยอัตราเร็ว vB เขาจึงดึงห้ามล้อทันที ถ้ารถไฟแล่นต่อด้วยความหน่วงคงตัว เเละรถไฟขบวนหน้าแล่นด้วยความเร็วเท่าเดิมไปเรื่อย ๆ จงหาความหน่วงที่น้อยที่สุดที่จะทำให้หลีกเลี่ยงการชนกับรถไฟขบวนหน้าได้พอดี |
| 10. | โยงวัตถุ A ขึ้นในแนวดิ่งด้วยอัตราเร็ว u และที่เวลา u/g ต่อมาก็โยงวัตถุ B ตามขึ้นไปด้วยอัตราเร็ว u เท่ากัน ถ้าวัตถุทั้งสองชนกันเหนือพื้น จงหาความสูงของตำเเหน่งที่วัตถุทั้งสองชนกัน ในที่นี้ g คือ ขนาดความเร่งสนามโน้มถ่วงโลกที่บริเวณนั้น |
| 11. | ล้อรัศมี R กำลังหมุนอยู่กับที่รอบแกน C ด้วยอัตราเร็ว f รอบต่อวินาที หยดน้ำที่ถูกสลัดออกไปจากจุด A ในแนวระดับจะตกกระทบพื้นระดับห่างจากจุด O เป็นระยะทางเท่าไร
 |
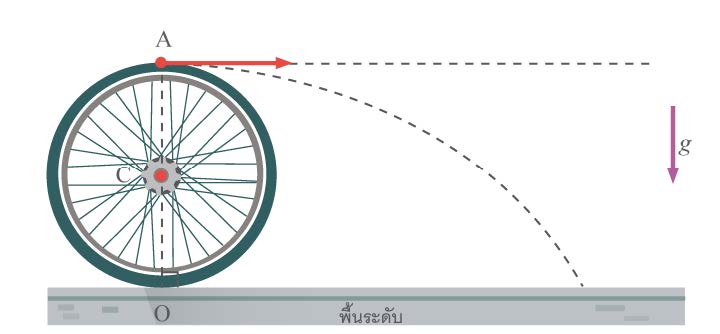| 12. | ยิงกระสุนปืนออกไปในแนวราบ (บนผิวดวงจันทร์) กระสุนกระทบเป้าที่ระยะห่าง 25 เมตร ที่ตำแหน่ง 5 mm ใต้แนวการยิง แต่ถ้าเลื่อนเป้าให้ห่างจากจุดที่ยิงเป็น 50 เมตร ลูกปืนจะกระทบเป้าใต้แนวการยิงกี่มิลลิเมตร |
| 13. | ยิงโปรเจคไทล์อันแรกขึ้นจากพื้นในแนวดิ่งด้วยความเร็วต้น vo ยิงอันที่สองในแนวดิ่งตามขึ้นไปจากจุดเดียวกันด้วยความเร็วต้น \(\rm\dfrac{v_o}{2}\) ในจังหวะที่อันแรกขึ้นถึงจุดสูงสุดพอดี ทั้งคู่จะทันกันที่ตำแหน่งสูงจากพื้นเท่าไร |
| 14. | วัตถุเคลื่อนที่เป็นวงกลมด้วยอัตราเร็วไม่คงตัว นอกจากมีส่วนประกอบความเร่งเข้าสู่ศูนย์กลางแล้วยังมีส่วนประกอบความเร่งในแนว สัมผัสด้วยรถยนต์คันหนึ่งซึ่งเดิมอยู่นิ่งเคลื่อนที่ไปตามเส้นทางวงกลมรัศมี 40.0 m ด้วยส่วนประกอบความเร่งในแนวสัมผัสขนาดคงตัว 2.00 m/s2 ตอนตั้งต้นรถยนต์อยู่ที่ตำแหน่งตะวันตกสุดของวงกลมและกำลังจะแล่นไปในทิศเหนือ 1) หลังจากที่รถยนต์แล่นไปได้ระยะทาง 1/4 ของเส้นรอบวง รถยนต์มีอัตราเร็วเท่าใด และกำลังแล่นไปทางทิศใด
2) ที่จุดนี้ส่วนประกอบความเร่งในแนวเข้าสู่ศูนย์กลางของรถยนต์มีขนาดเท่าใด
3) ที่จุดเดียวกันนี้ความเร่งสุทธิของรถยนต์มีขนาดเท่าใด
|
| 15. |  กำหนดให้ นำไปใช้ได ้\(\left(\dfrac{1.50}{9.8}\right)^{\frac{1}{2}}=0.391\) |
