จลศาสตร์ในหนึ่งมิติและสองมิติ ชุดที่ 1 (15 ข้อ)
| 1. | รถเคลื่อนที่ไปทางทิศตะวันออกจากจุด A ไปยังจุด B ในเวลา 20 วินาที ได้ระยะทาง 200 เมตร หรือการกระจัด 200 เมตร ไปทางทิศตะวันออก รถคันนี้มีอัตราเร็วเฉลี่ยและความเร็วเฉลี่ยเป็นเท่าใด
 |
ตอบ อัตราเร็วเฉลี่ยและความเร็วเฉลี่ย เท่ากับ 10 m/s มีทิศไปทางทิศตะวันออก
อัตราเร็วเฉลี่ย \(=\) ระยะทาง / เวลา \(\rm= \dfrac{200~m}{20~s} = 10~m/s\)
ความเร็วเฉลี่ย \(=\) การกระจัด / เวลา \(\rm= \dfrac{200~m}{20~s} = 10~m/s\)
ดังนั้น อัตราเร็วเฉลี่ยและความเร็วเฉลี่ย เท่ากับ 10 m/s มีทิศไปทางทิศตะวันออก| 2. | เด็กคนหนึ่งเดินไปทางทิศเหนือได้ระยะทาง 300 เมตร จากนั้นเดินไปทางทิศตะวันออกได้ระยะทาง 400 เมตร ใช้เวลาเดินทางทั้งหมด 500 วินาที เด็กคนนี้เดินด้วยอัตราเร็วเฉลี่ยกี่เมตรต่อวินาที |
ตอบ 1.4 m/s
เรื่อง การเคลื่อนที่แนวตรง
อัตราเร็วเฉลี่ย คือ ระยะทางทั้งหมดในช่วงเวลาที่ใช้ เราสามารถหาอัตราเร็วเฉลี่ยของเด็กคนนี้ได้ ดังนี้
เรื่อง การเคลื่อนที่แนวตรง
อัตราเร็วเฉลี่ย คือ ระยะทางทั้งหมดในช่วงเวลาที่ใช้ เราสามารถหาอัตราเร็วเฉลี่ยของเด็กคนนี้ได้ ดังนี้
\(\rm v =\dfrac{s}{t} = \dfrac{300+400~m}{500~s} = 1.4 ~m/s\)
ดังนั้น เด็กคนนี้เดินด้วยอัตราเร็วเฉลี่ย 1.4 เมตรต่อวินาที| 3. | ถ้าการเคลื่อนที่ของวัตถุที่ลากแถบกระดาษ ซึ่งเครื่องเคาะสัญญาณเวลาที่เคาะทุกๆ \(\dfrac{1}{50}\)วินาที ทำให้เกิดจุดดังรูป จากการสังเกตจุดเหล่านี้จะบอกได้คร่าวๆ ว่าความเร่งเป็นอย่างไร
 |
ตอบ สม่ำเสมอ
จากสมการ
แต่ระยะทางของจุดที่บันทึกได้เพิ่มขึ้นเรื่อยๆ แสดงว่าค่าความเร็วเพิ่มขึ้น นั้นคือจะต้องมีความเร่ง และสังเกตจากรูปพบว่าระยะมีการเพิ่มค่อนข้างสม่ำเสมอ
จึงสรุปว่า เป็นการบันทึกการเคลื่อนที่ที่มีความเร่งสม่ำเสมอ
จากสมการ
v = u + at
เนื่องจาก ความเร็วเริ่มต้นในการเคลื่อนที่คงที่ และโจทย์กำหนดให้บันทึกทุกๆ \(\dfrac{1}{50}\) วินาที นั้นคือ เวลาที่ใช้ในการเคลื่อนที่คงที่แต่ระยะทางของจุดที่บันทึกได้เพิ่มขึ้นเรื่อยๆ แสดงว่าค่าความเร็วเพิ่มขึ้น นั้นคือจะต้องมีความเร่ง และสังเกตจากรูปพบว่าระยะมีการเพิ่มค่อนข้างสม่ำเสมอ
จึงสรุปว่า เป็นการบันทึกการเคลื่อนที่ที่มีความเร่งสม่ำเสมอ
| 4. | กราฟของตำแหน่งวัตถุบนแนวแกน x กับเวลา t เป็นดังรูป ช่วงเวลาใดหรือที่ตำแหน่งใดที่วัตถุไม่มีความเร่ง
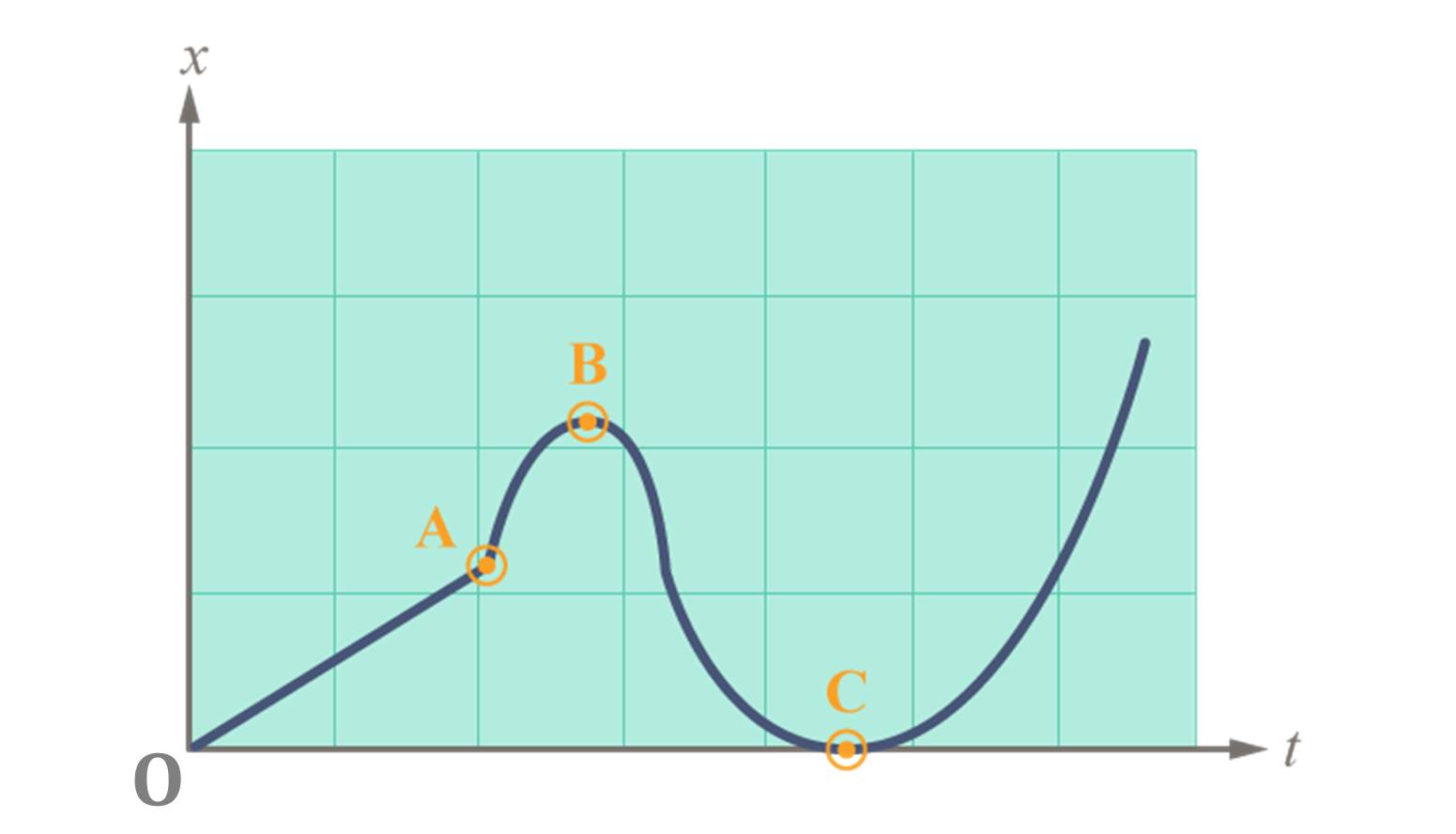 |
ตอบ ช่วง OA
ช่วงที่วัตถุไม่มีความเร่ง คือช่วงที่ความเร็วต้องมีค่าคงที่ จากกราฟแสดงความสัมพันธ์ระหว่างตำแหน่งในแนวแกน x กับ
เวลา t ความชันกราฟซึ่งก็คือ ความเร็วของการเคลื่อนที่ตามสมการ
ช่วงที่วัตถุไม่มีความเร่ง คือช่วงที่ความเร็วต้องมีค่าคงที่ จากกราฟแสดงความสัมพันธ์ระหว่างตำแหน่งในแนวแกน x กับ
เวลา t ความชันกราฟซึ่งก็คือ ความเร็วของการเคลื่อนที่ตามสมการ
\(\rm slope =\dfrac{Δy}{Δx} = \dfrac{Δx}{Δt}= v\)
และช่วงที่กราฟมีความชันคงที่ หรือมีความเร็วคงที่ คือ ช่วง OA| 5. | ลูกบอลลูกหนึ่งถูกปล่อยลงมาจากหน้าต่างถึงพื้น กราฟระหว่างความเร็ว-เวลาของการเคลื่อนที่เป็นดังภาพ อยากทราบว่า ที่จุด A ลูกบอลอยู่ที่ใด และความสูงจากหน้าต่างถึงพื้นเท่ากับเท่าไร
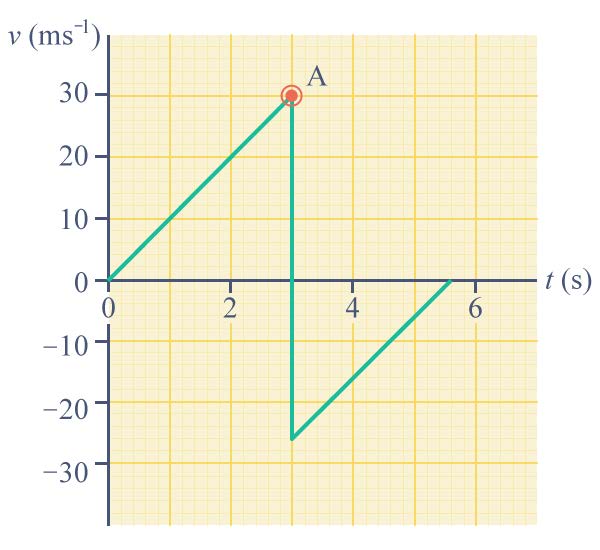 |
ตอบ หน้าต่างอยู่สูงจากพื้น 45 เมตร
ที่จุด A เป็นจุดที่มีความเร็วสูงสุด นั้นคือ จุดที่ลูกบอลกระทบพื้น
ซึ่งตอนนั้นลูกบอลมีความเร็ว 30 m/s
ดังนั้น จากหน้าต่างถึงพื้นลูกบอลใช้เวลา 3 วินาที
ระยะทางจากหน้าต่างถึงพื้น จึงหาได้จาก พื้นที่ใต้กราฟจากเวลา 0 - 3 วินาที
จะได ้
ที่จุด A เป็นจุดที่มีความเร็วสูงสุด นั้นคือ จุดที่ลูกบอลกระทบพื้น
ซึ่งตอนนั้นลูกบอลมีความเร็ว 30 m/s
ดังนั้น จากหน้าต่างถึงพื้นลูกบอลใช้เวลา 3 วินาที
ระยะทางจากหน้าต่างถึงพื้น จึงหาได้จาก พื้นที่ใต้กราฟจากเวลา 0 - 3 วินาที
จะได ้
พื้นที่ใต้กราฟ \(=\dfrac{1}{2}\times30\times3=45\)
ดังนั้น หน้าต่างอยู่สูงจากพื้น 45 เมตร| 6. | รถยนต์คันหนึ่งเคลื่อนที่ในแนวตรงโดยมีความเร็ว 20 เมตรต่อวินาที ต่อมาคนขับได้เร่งเครื่องยนต์ทำให้รถยนต์มีความเร่ง 3 เมตรต่อวินาที2 เป็นเวลา 5 วินาที จงหาความเร็วที่เวลา 5 วินาที |
ตอบ 35 เมตรต่อวินาที มีทิศทางเดียวกับความเร็วเดิม
เดิมรถยนต์มีความเร็ว \(\rm \vec{v_1}\) ต่อมามีความเร่งทำให้ความเร็วเปลี่ยนไป
ดังนั้น ความเร็วที่สิ้นสุดเวลา 5 วินาที คือ \(\rm \vec{v_2} = \vec{v_1}+Δ \vec{v}\)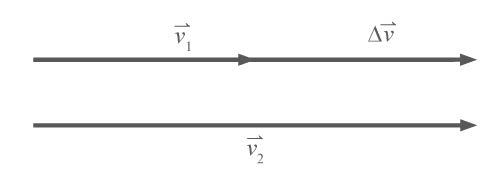 จาก
จาก
เดิมรถยนต์มีความเร็ว \(\rm \vec{v_1}\) ต่อมามีความเร่งทำให้ความเร็วเปลี่ยนไป
ดังนั้น ความเร็วที่สิ้นสุดเวลา 5 วินาที คือ \(\rm \vec{v_2} = \vec{v_1}+Δ \vec{v}\)

\(a = \rm\dfrac{v_2-v_1}{Δt}\)
ดังนั้น
\(\begin{align*} \rm v_2 − v_1 &= a(Δt)\\ \rm v_2 &= v_1 + a(Δt)\\ &=20 \rm ~m/s + (3~m/s^2)(5~s)\\ &=35\rm~m/s \end{align*}\)
ดังนั้น ความเร็วสุดท้ายเท่ากับ 35 เมตรต่อวินาที มีทิศทางเดียวกับความเร็วเดิม| 7. | วัตถุชนิดหนึ่งเคลื่อนที่จากจุด A ไปจุด B ด้วยอัตราเร็ว 6.0 m/s ใช้เวลา 20 วินาที หลังจากนั้นเคลื่อนที่จากจุด B ไปจุด C ด้วยอัตราเร็ว 4.0 m/s ใช้เวลา 10 วินาที จงหาอัตราเร็วเฉลี่ยของวัตถุนี้ในการเคลื่อนที่จากจุด A ไปจุด C
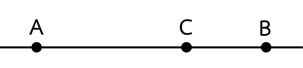 |
ตอบ 5.3 m/s
จากจุด A ไป B เคลื่อนที่ไปได้ระยะทางเท่ากับ
จากจุด A ไป B เคลื่อนที่ไปได้ระยะทางเท่ากับ
\(\rm S_{AB} = 6.0 × 20 = 120~m\)
จากจุด B ไป C เคลื่อนที่ไปได้ระยะทางเท่ากับ
\(\rm S_{BC} = 4.0 × 10 = 40~m\)
ดังนั้น อัตราเร็วเฉลี่ยจากจุด A ไป C มีค่าเท่ากับ
\(\rm \dfrac{120+40}{20+10}=5.3~m/s\)
| 8. | วัตถุหนึ่งเคลื่อนที่เป็นวงกลมรัศมี 21 เมตร ครบหนึ่งรอบ การกระจัดมีค่าเท่าใด |
ตอบ 0 เมตร
การกระจัดเป็นปริมาณเวกเตอร์ ขนาดของการกระจัดสามารถหาได้จาก ระยะที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดสุดท้ายของการเปลี่ยนตำแหน่งของวัตถุ
จากโจทย์ วัตถุเคลื่อนที่เป็นวงกลมรัศมี เมตร ครบหนึ่งรอบ แสดงว่า วัตถุเคลื่อนที่กลับมายังจุดเริ่มต้น
ดังนั้น การกระจัดของวัตถุจึงมีค่าเป็น 0
การกระจัดเป็นปริมาณเวกเตอร์ ขนาดของการกระจัดสามารถหาได้จาก ระยะที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดสุดท้ายของการเปลี่ยนตำแหน่งของวัตถุ
จากโจทย์ วัตถุเคลื่อนที่เป็นวงกลมรัศมี เมตร ครบหนึ่งรอบ แสดงว่า วัตถุเคลื่อนที่กลับมายังจุดเริ่มต้น
ดังนั้น การกระจัดของวัตถุจึงมีค่าเป็น 0
| 9. | จงเขียนเส้นทางการเคลื่อนที่ของโพรเจกไทล์ที่ยิงด้วยอัตราเร็วต้นและมุมเท่ากันบนดวงจันทร์และบนโลก |
ตอบ
หากคำนึงถึงแรงโน้มถ่วงระหว่างดวงจันทร์และโลกที่มีค่าต่างกันอยู่ประมาณ 6 เท่า ดังนั้น ถ้ายิงโปรเจคไทล์ด้วยมุมและความเร็วต้นเท่ากัน เส้นทางการเคลื่อนที่จะเป็นดังรูป
เมื่อ เส้นสีน้ำเงินแทนการเคลื่อนที่บนโลก
และ เส้นสีส้มแทนการเคลื่อนที่บนดวงจันทร์
หากคำนึงถึงแรงโน้มถ่วงระหว่างดวงจันทร์และโลกที่มีค่าต่างกันอยู่ประมาณ 6 เท่า ดังนั้น ถ้ายิงโปรเจคไทล์ด้วยมุมและความเร็วต้นเท่ากัน เส้นทางการเคลื่อนที่จะเป็นดังรูป
เมื่อ เส้นสีน้ำเงินแทนการเคลื่อนที่บนโลก
และ เส้นสีส้มแทนการเคลื่อนที่บนดวงจันทร์

| 10. | ถ้าต้องการยิงปืนใหญ่ให้ได้ระยะทางในแนวดิ่ง เป็น \(\dfrac{1}{2}\) เท่าของระยะทางในแนวระดับ จะต้องปรับปากกระบอกปืนใหญ่ให้ทำมุมเท่าไรกับแนวระดับ
 |
ตอบ \(\theta = \tan^{-1}2\)
จากสมการหาระยะในแนวระดับ
ดังนั้น \(\rm \theta=\tan^{-1}2\)
จากสมการหาระยะในแนวระดับ
\(\rm S_x=\dfrac{u^2\sin2\theta}{g}=\dfrac{u^2(2\sin\theta\cos\theta)}{g}\)
และจากสมการหาระยะในแนวระดิ่ง
\(\rm S_y = \dfrac{u^2\sin^2\theta}{2g}\)
เราสามารถหามุม θ ที่ทำให้ \(\rm S_y =\dfrac{1}{2}S_x\)ได้ดังนี้ดังนั้น \(\rm \theta=\tan^{-1}2\)
| 11. | ในการทดลองเรื่องการเคลื่อนแนววงกลมในระนาบระดับ ขณะที่กำลังแกว่งให้จุกยางหมุนอยู่นั้นเชือกที่ผูกกับจุกยางขาดออกจากกัน จงอธิบายถึงแรงที่เกี่ยวข้องก่อนและหลังการขาดของเชือก การเคลื่อนที่ของจุกยางเป็นเช่นไรหลังจากที่เชือกขาดไปแล้ว |
ตอบ
ก่อนเชือกขาด มีแรงตึงเชือก(เป็นแรงเข้าสู่ศูนย์กลาง)และแรงโนม้ ถ่วงที่จุกยาง
หลังเชือกขาด มีแค่แรงโน้มถ่วงและจุกยางเคลื่อนที่แบบโพรเจคไทล์
ก่อนเชือกขาด มีแรงตึงเชือก(เป็นแรงเข้าสู่ศูนย์กลาง)และแรงโนม้ ถ่วงที่จุกยาง
หลังเชือกขาด มีแค่แรงโน้มถ่วงและจุกยางเคลื่อนที่แบบโพรเจคไทล์
| 12. | จงอธิบายถึงเงื่อนไขที่ทำให้วัตถุเคลื่อนที่เป็นวงกลม |
| 13. | ผูกวัตถุที่ปลายล่างของเชือกเส้นหนึ่งยาว 1 เมตร ตรึงปลายบนไว้แล้วแกว่งวัตถุให้เป็นวงกลมในระนาบระดับ ถ้าเชือกทำมุม θ กับแนวดิ่งวัตถุจะแกว่งครบรอบในเวลา T วินาที ความเร่งสู่ศูนย์กลางของวัตถุมีค่า |
ตอบ \(\rm \dfrac{4\pi^2\sin\theta}{T^2}\)
เรื่อง การเคลื่อนที่วงกลม
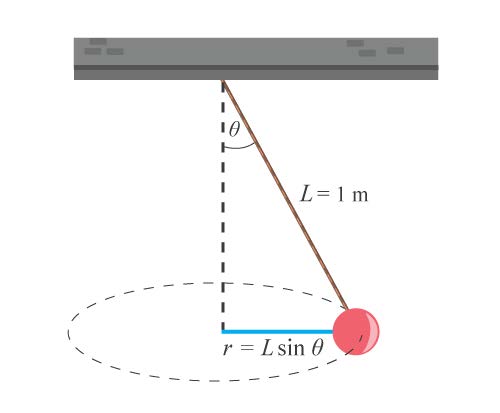
\(\rm \displaystyle ΣF_c = \dfrac{mv^2}{r} = mrω^2=ma_c\)
และจากความสัมพันธ์ระหว่างความเร็วเชิงมุม และคาบ ที่ใช้ในการเคลื่อนที่
\(\rm ω =\dfrac{2\pi}{T} \)
ดังนั้น ความเร่งสู่ศูนย์กลางของวัตถุ สามารถคำนวณได้จาก
\(\begin{align*}
\rm mrω^2 &= \rm ma_c\\
\rm (L~sin θ)\left(\dfrac{2\pi}{T}\right)^2 &= \rm a_c\\
\rm a_c &=\rm\dfrac{4\pi^2\sin\theta}{T^2}~m/s^2
\end{align*}\)
| 14. | ดาวเทียมที่วงโคจรใกล้กับไกลจากโลก จะมีอัตราเร็วในการโคจรต่างกันอย่างไร
 |
ตอบ
โดยปกติดาวเทียมจะโคจรรอบโลกโดยจะอยู่ในบริเวณที่อยู่เหนือบริเวณหนึ่งของโลกเสมอ ทั้งนี้ก็เพื่อรับสัญญาณให้กับพื้นที่ที่กำหนด ดังนั้น ดาวเทียมจึงต้องเคลื่อนที่ด้วยอัตราเร็วเท่ากับการหมุนรอบตัวเองของโลก ดาวเทียมที่อยู่ไกลจากโลกมาก จึงต้องเคลื่อนที่เร็วกว่าดาวเทียมที่อยู่ใกล้ เพราะระยะทางโคจรครบ 1 รอบของดาวเทียมที่อยู่ไกลจากโลก มีค่ามากกว่าระยะทางโคจรครบ 1 รอบของดาวเทียมที่อยู่ใกล้โลกนั้นเอง
โดยปกติดาวเทียมจะโคจรรอบโลกโดยจะอยู่ในบริเวณที่อยู่เหนือบริเวณหนึ่งของโลกเสมอ ทั้งนี้ก็เพื่อรับสัญญาณให้กับพื้นที่ที่กำหนด ดังนั้น ดาวเทียมจึงต้องเคลื่อนที่ด้วยอัตราเร็วเท่ากับการหมุนรอบตัวเองของโลก ดาวเทียมที่อยู่ไกลจากโลกมาก จึงต้องเคลื่อนที่เร็วกว่าดาวเทียมที่อยู่ใกล้ เพราะระยะทางโคจรครบ 1 รอบของดาวเทียมที่อยู่ไกลจากโลก มีค่ามากกว่าระยะทางโคจรครบ 1 รอบของดาวเทียมที่อยู่ใกล้โลกนั้นเอง
| 15. | เด็ก 4 คนนั่งอยู่ริมตลิ่งและขว้างก้อนหินพร้อมกันลงในน้ำคนละก้อน ถ้าแต่ละก้อนตกน้ำที่ตำแหน่งต่างกันคือ A B C และ D โดยมีทางเดินของก้อนหินดังรูป จงพิจารณาว่าก้อนหินที่ตกตรงตำแหน่งใดเป็นก้อนที่ถึงพื้นน้ำก่อน
 |
ตอบ C
ก้อนหินที่ถึงพื้นน้ำก่อน คือก้อนที่ใช้เวลาในการเคลื่อนที่น้อยที่สุด จากรูปเราพบว่าก้อนหินทั้งก้อน ต่างกันที่ความสูงที่ขึ้นไปได้และระยะไกลสุดที่ไปตก โดยความสัมพันธ์
ก้อนหินที่ถึงพื้นน้ำก่อน คือก้อนที่ใช้เวลาในการเคลื่อนที่น้อยที่สุด จากรูปเราพบว่าก้อนหินทั้งก้อน ต่างกันที่ความสูงที่ขึ้นไปได้และระยะไกลสุดที่ไปตก โดยความสัมพันธ์
\(\begin{align*} \rm S_y &=\rm u_yt+\dfrac{1}{2}a_yt^2\\ 0&=\rm u_yt+\dfrac{1}{2}a_yt^2\\ \rm t&=\rm \dfrac{2u_y}{g} \end{align*}\)
ระยะสูงสุด H เราหาอัตราเร็วต้น uy จาก
\(\begin{align*} \rm v^2_y &=\rm u^2_y+2a_yS_y\\ 0&=\rm u^2_y-2gH\\ \rm u_y&=\rm \sqrt{2gH} \end{align*}\)
แทนในสมการข้างต้น เพื่อหาเวลาที่ใช้ในการเคลื่อนที่ จะได ้
\(\rm t=\dfrac{2\sqrt{2gH}}{g}=\dfrac{8H}{g}\)
จากสมการจะเห็นว่า ก้อนหินที่ตกถึงพื้นก่อน จะใช้เวลาในการเคลื่อนที่น้อยสุด นั่นคือก้อนที่ขึ้นไปได้น้อยที่สุดจะตกถึงพื้นก่อน ซึ่งคือ ก้อน C
