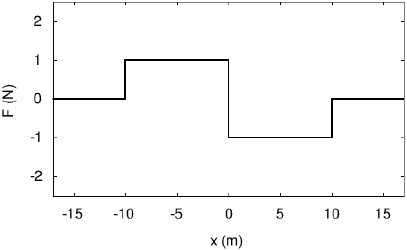
ข้อสอบคัดเลือกของทีม USA 2010 (25 ข้อ)
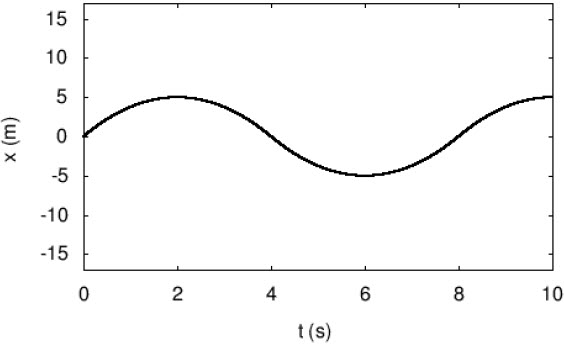
| 1. | กำหนดกราฟแสดงการเคลื่อนที่ของกระรอกที่วิ่งไปตามสายโทรศัพท์เส้นหนึ่ง และตัวอักษร A ถึง E ใช้อ้างอิงเวลาต่างๆ ดังรูป
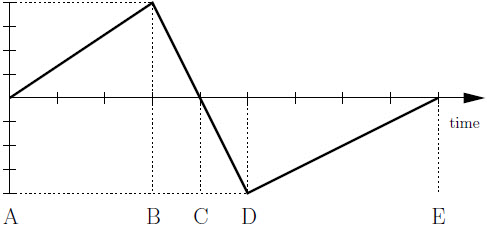 |
| A | จาก A ถึง B |
| B | จาก B ถึง C เท่านั้น |
| C | จาก B ถึง D |
| D | จาก C ถึง D เท่านั้น |
| E | จาก D ถึง E |
ตอบ (C)
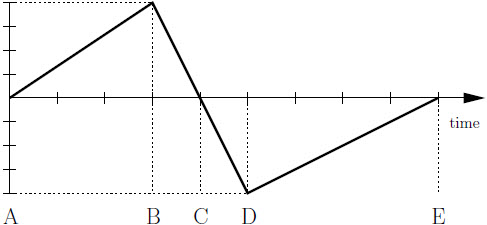
| 2. | กำหนดกราฟแสดงการเคลื่อนที่ของกระรอกที่วิ่งไปตามสายโทรศัพท์เส้นหนึ่ง และตัวอักษร A ถึง E ใช้อ้างอิงเวลาต่างๆ ดังรูป
 |
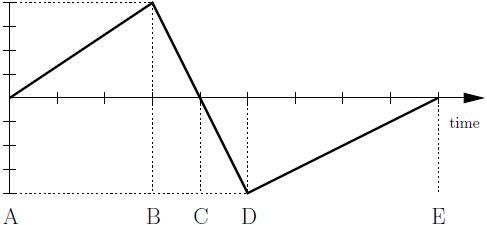
| 3. | กำหนดกราฟแสดงการเคลื่อนที่ของกระรอกที่วิ่งไปตามสายโทรศัพท์เส้นหนึ่ง และตัวอักษร A ถึง E ใช้อ้างอิงเวลาต่างๆ ดังรูป
 |
| 4. | คนขนของสองทีม ช่วยกันย้ายเปียโนลงมาจากหน้าต่างชั้น 10 ของอพาร์ตเมนต์แห่งหนึ่ง ถ้าเชือกขาดขณะเปียโนอยู่สูงจากพื้นดิน 30 เมตร และทีมขนของบนพื้นดินได้เสียงตะโกนจากทีมด้านบนครั้งแรก ขณะเปียโนอยู่สูงจากพื้นดิน 14 เมตร แล้วพวกเขามีเวลาหนีก่อนเปียโนจะตกใส่เท่าใด |
| 5. | ให้การเคลื่อนที่แบบโพลเจกไทล์ทั้งสองแบบ ถูกยิงจากความสูง 35 เมตร ดังรูป ถ้าแบบแรกถูกยิงด้วยมุมเงย 37° แบบที่สองถูกยิงด้วยมุมก้ม 37° และทั้งสองมีอัตราเร็วต้น v0 = 50 m/s
 |
| 6. | กระสุนปืนถูกยิงทำมุม θ กับแนวนอน และเคลื่อนที่โดยไม่มีแรงต้านอากาศ จะขึ้นไปได้สูงสุด H และระยะตกกลับอยู่ไกลออกไป R แล้วอัตราส่วน H / R เท่ากับข้อใด |
| A | \(\tan \theta\) |
| B | \(2\tan \theta\) |
| C | \(\dfrac{2}{\tan \theta}\) |
| D | \(\dfrac{1}{2}\tan \theta\) |
| E | \(\dfrac{1}{4}\tan \theta\) |
ตอบ (E)
| 7. | แฮร์รี่ นั่งอยู่บนม้าหมุนที่ห่างจากจุดศูนย์กลางไป 2 เมตร มัลฟอย เสกให้แฮร์รี่นั่งอยู่กับที่แล้วเดินเครื่องม้าหมุน ให้เริ่มหมุนรอบแกน ถ้าแฮร์รี่มีมวล 50.0 kg และทนต่อความเร่งได้ 5.0 g’s ก่อนสลบไป แล้วโมเมนตัมเชิงมุมของแฮร์รี่ขณะสลบไปเท่ากับข้อใด |
| 8. | รถพยายามใช้ความเร่งปีนขึ้นเนินที่ทำมุม θ กับแนวนอน สัมประสิทธิ์แรงเสียดทานสถิตระหว่างยางล้อกับเนินเท่ากับ μ > tan θ แล้วความเร่งสูงสุด (ในทิศขึ้นไปตามเนิน) เท่ากับข้อใด ไม่คิดความเฉื่อยในการหมุนของล้อ |
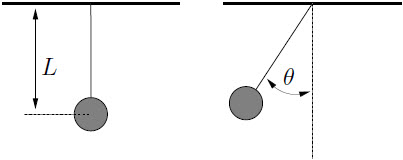
| 9. | ลูกตุ้มมวล M แขวนบนเพดานของรถด้วยเชือกเบายาว L จากรถที่เดิมอยู่นิ่ง เมื่อเร่งรถออกไป ลูกตุ้มจะแกว่งทำมุม θ กับแนวตั้ง ข้อใดคือความเร่งของรถในเทอมของ θ, M, L และ g
 |
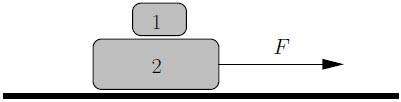
| 10. | ให้มวล m1 อยู่บนมวล m2 โดยมวลก้อนล่างวางอยู่บนพื้นราบ และมีเชือกที่ใช้ลากไปตามแนวนอนได้ และมีสัมประสิทธิ์แรงเสียดทานของการเคลื่อนที่ในทุกพื้นผิวเท่ากับ μ ถ้ามีแรง F มากระทำกับเชือก แล้วความเร่งของมวลก้อนล่างเท่ากับข้อใด ให้สมมุติว่า F มีขนาดใหญ่พอที่ทำให้มวลก้อนบนไถลบนก้อนล่าง
 |
| A | a2 = (F – μg (2 m1 + m2)) / m2 |
| B | a2 = (F – μg (m1 + m2)) / m2 |
| C | a2 = (F – μg (m1 + 2 m2)) / m2 |
| D | a2 = (F + μg (m1 + m2)) / m2 |
| E | a2 = (F – μg (m2 – m1)) / m2 |
ตอบ (A)
| 11. | วัตถุสามชิ้นที่มีมวลเท่ากันถูกแขวนไว้บนรอกเล็กๆ ด้วยเชือกเบา ดังรูป ถ้าไม่คำนึงถึงแรงเสียดทาน และสมมุติว่าระบบอยู่ในภาวะสมดุล แล้วอัตราส่วนของ a / b เท่ากับข้อใด ( สเกลของรูปประกอบไม่ใช่ขนาดจริง )
 |
| 12. | ลูกบอลมวล m กลิ้งจนหล่นจากขอบโต๊ะด้วยพลังงานจลน์เริ่มต้น K ที่เวลา t หลังจากลูกบอลหล่นจากขอบโต๊ะจะมีพลังงานจลน์ 3K แล้ว t มีค่าเท่ากับข้อใด ไม่ต้องคำนึงถึงแรงต้านอากาศ |
| A | \(\rm (3/g)\sqrt{K/m}\) |
| B | \(\rm (2/g)\sqrt{K/m}\) |
| C | \(\rm (1/g)\sqrt{8K/m}\) |
| D | \(\rm (K/g)\sqrt{6/m}\) |
| E | \(\rm (2K/g)\sqrt{1/m}\) |
ตอบ (B)
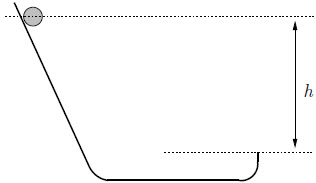
| 13. | ลูกบอลมวล M รัศมี R มีโมเมนต์ความเฉื่อย I = \(\frac{2}{5}\)MR2 ให้เดิมอยู่นิ่งแล้วกลิ้งลงมาจากพื้นเอียง โดยไม่สูญเสียพลังงานจากการเสียดสี จากนั้นกลิ้งไปตามแนวราบจนกระทั่งหลุดออกจากพื้นเอียงไปและพุ่งขึ้นไปในแนวตั้ง ดังรูป แล้วความสูงสูงสุด ymax ของลูกบอลเท่ากับข้อใด ให้ความสูงสูงสุดที่หลุดออกจากปลายพื้นเอียง ymax แสดงในเทอมของ h
 |
| A | \(\rm h\) |
| B | \(\rm \dfrac{25}{49}h\) |
| C | \(\rm \dfrac{2}{5}h\) |
| D | \(\rm \dfrac{5}{7}h\) |
| E | \(\rm \dfrac{7}{5}h\) |
ตอบ (D)
| 14. | วัตถุ 5.0 kg มีอัตราเร็ว 8.0 m / s ไปตามพื้นราบ 2.0 m จนกระทั่งพุ่งชนแบบยืดหยุ่นสมบูรณ์กับวัตถุ 15.0 kg ที่เดิมอยู่นิ่ง ถ้าสัมประสิทธิ์แรงเสียดทานจลน์ระหว่างวัตถุทั้งสองกับพื้นเท่ากับ 0.35 แล้ววัตถุ 15.0 kg จะเคลื่อนที่ไปได้ไกลเท่าใด |
| 15. | 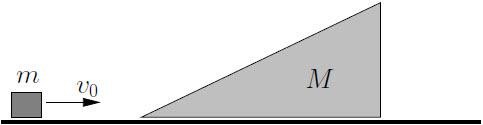 ถ้าบล็อกมวล m มีอัตราเร็วต้น v0 พุ่งขึ้นพื้นเอียงมวล M ไปโดยไม่มีแรงเสียดทาน แล้วขึ้นไปสูง h ตามพื้นเอียง จากนั้นไหลกลับลงมา จงหาความสูง h |
| A | \(\rm h=\dfrac{v^2_0}{2g}\) |
| B | \(\rm h=\dfrac{1}{g}\dfrac{Mv^2_0}{m+M}\) |
| C | \(\rm h=\dfrac{1}{2g}\dfrac{Mv^2_0}{m+M}\) |
| D | \(\rm h=\dfrac{1}{2g}\dfrac{mv^2_0}{m+M}\) |
| E | \(\rm h=\dfrac{v^2_0}{g}\) |
ตอบ (C)
| 16. | 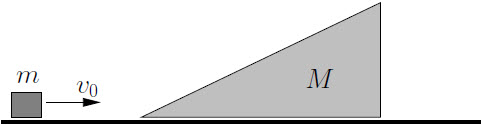 ถ้าบล็อกมวล m มีอัตราเร็วต้น v0 พุ่งขึ้นพื้นเอียงมวล M ไปโดยไม่มีแรงเสียดทาน แล้วขึ้นไปสูง h ตามพื้นเอียง จากนั้นไหลกลับลงมา จงหาอัตราเร็ว v ของมวล m หลังลื่นกลับออกมาจากทางลาด |
| A | \(\rm v=v_0\) |
| B | \(\rm v= \dfrac{m}{m+M}v_0\) |
| C | \(\rm v= \dfrac{M}{m+M}v_0\) |
| D | \(\rm v= \dfrac{M-m}{m}v_0\) |
| E | \(\rm v= \dfrac{M-m}{m+M}v_0\) |
ตอบ (E)
| 17. | ถ้ามวล m สี่อัน ถูกวางไว้ที่จุดยอดของทรงสี่หน้าที่มีความยาวด้าน a แล้วพลังงานศักย์โน้มถ่วงของการจัดวางนี้เท่ากับข้อใด |
| A | \(\rm -2\dfrac{Gm^2}{a}\) |
| B | \(\rm -3\dfrac{Gm^2}{a}\) |
| C | \(\rm -4\dfrac{Gm^2}{a}\) |
| D | \(\rm -6\dfrac{Gm^2}{a}\) |
| E | \(\rm -12\dfrac{Gm^2}{a}\) |
ตอบ (D)
| 18. | ใช้กราฟของพลังงานศักย์ต่อไปนี้ ในการตอบคำถาม
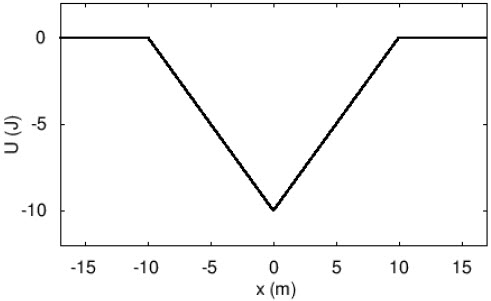 |
| 19. | ใช้กราฟของพลังงานศักย์ต่อไปนี้ ในการตอบคำถาม
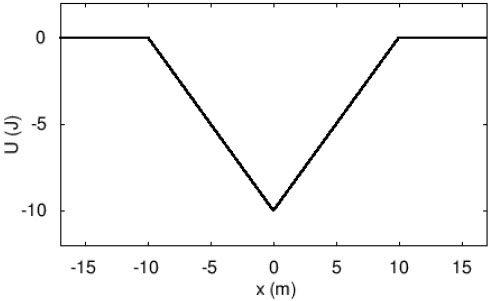  |
| 20. | ใช้กราฟของพลังงานศักย์ต่อไปนี้ ในการตอบคำถาม
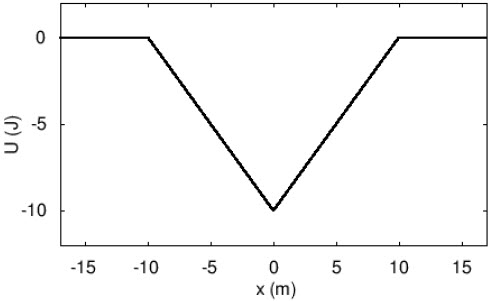  |
| 21. | พลังงานศักย์โน้มถ่วงของลูกบอลตันที่มีความหนาแน่น ρ รัศมี R เท่ากับ E แล้วพลังงานศักย์โน้มถ่วงของลูกบอลตันที่มีความหนาแน่น ρ รัศมี 2R เท่ากับข้อใด |
| 22. | ลูกโป่งบรรจุแก๊สฮีเลียมถูกผูกติดกับพื้นรถด้วยเชือกเส้นหนึ่ง เนื่องจากรถถูกปิดแน่นหนาจึงไม่มีอากาศจากภายนอกมากระทำกับลูกโป่ง ถ้ารถวิ่งเป็นวงกลมด้วยอัตราเร็วคงที่ แล้วข้อใด คือทิศทางของลูกโป่งที่ถูกผูกเอาไว้
 |
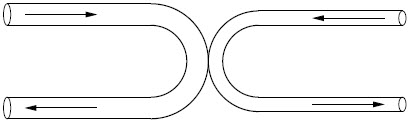
| 23. | กำหนดท่อรูปตัว U สองอัน ให้ท่อด้านซ้าย มีพื้นที่หน้าตัด A มีอัตราเร็วของน้ำที่ไหลผ่าน v ส่วนท่อด้านขวามีพื้นที่หน้าตัด A´ = A/2 ถ้าแรงลัพธ์ที่ท่อสัมผัสกันเป็นศูนย์ แล้วอัตราเร็ว v´ ของน้ำที่ไหลผ่านท่อทางด้านขวาเท่ากับข้อใด โดยไม่ต้องสนใจแรงโน้มถ่วง และสมมุติว่า อัตราเร็วของน้ำ ขาเข้า-ขาออก ในแต่ละท่อมีค่าเท่ากัน
 |
| 24. | (เกินหลักสูตรการสอบเข้า สอวน.) แผ่นวงกลมสม่ำเสมอ รัศมี R เดิมมีมวล M แกนหมุนที่จุดศูนย์กลาง ซึ่งตั้งฉากกับแผ่นวงกลมมีโมเมนต์ความเฉื่อย I0 = \(\frac{1}{2}\) MR2 ถ้าเจาะรูบนแผ่นวงกลม ดังรูป แล้วโมเมนต์ความเฉื่อยใหม่ที่แกนหมุนจะเท่ากับข้อใด ให้แสดงในเทอมของรัศมี R มวล M ของแผ่นวงกลมเดิม
 |
| 25. | ยานอวกาศ (ซึ่งมีมวลน้อยมาก) อยู่ในวงโคจรวงรีของดาวเคราะห์ดวงหนึ่ง ระยะใกล้สุดระหว่างยานอวกาศกับดาวเคราะห์เท่ากับ R และระยะไกลสุดเท่ากับ 2R ถ้าที่ระยะไกลสุดยานอวกาศเคลื่อนที่ด้วยอัตราเร็ว v0 จากนั้นเดินเครื่องเข้าสู่วงโคจรวงกลมที่มีรัศมี 2R อัตราเร็วใหม่ที่ได้จะเท่ากับข้อใด
 |
| A | \(\rm \sqrt{3/2}v_0\) |
| B | \(\rm \sqrt{5}v_0\) |
| C | \(\rm \sqrt{3/5}v_0\) |
| D | \(\rm \sqrt2 v_0\) |
| E | \(\rm 2v_0\) |
ตอบ (A)