ข้อสอบคัดเลือกของทีม USA 2014 (25 ข้อ)
| 1. | รถเลี้ยวขวาด้วยอัตราเร็วคงที่เป็นวงกลม ให้ X เป็นเวกเตอร์โมเมนตัมเชิงมุมรอบศูนย์กลางของวงกลม และ Y เป็นเวกเตอร์ความเร่งของรถ จากมุมมองของคนขับข้อใดต่อไปนี้ถูกต้อง |
| A | X ไปทางซ้าย และ Y ไปทางซ้าย |
| B | X ไปข้างหน้า และ Y ไปทางขวา |
| C | X พุ่งลง และ Y ไปข้างหน้า |
| D | X ไปทางซ้าย และ Y ไปทางขวา |
| E | X พุ่งลง และ Y ไปทางขวา |
ตอบ (E)
ใช้กฎมือขวาในการหาโมเมนตัมเชิงมุม โดยความเร่งมีทิศพุ่งเข้าจุดศูนย์กลางของการเคลื่อนที่แบบวงกลม
ใช้กฎมือขวาในการหาโมเมนตัมเชิงมุม โดยความเร่งมีทิศพุ่งเข้าจุดศูนย์กลางของการเคลื่อนที่แบบวงกลม
| 2. | ลูกบอลกลิ้งลงมาจากพื้นเอียงโดยไม่ไถล ดังรูป
 |
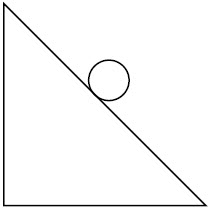| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (E)
ข้อที่ถูกต้อง คือ ข้อที่มีแรงกระทำทั้งในทิศตั้งฉาก และขนานกับพื้นเอียง สังเกตว่า ถ้าลูกบอลกลิ้งลงมาโดยมีความเร่ง แล้วแรงเสียดทานจะต้องน้อยกว่าแรงโน้มถ่วงในทิศขนานกับพื้นเอียง
ข้อที่ถูกต้อง คือ ข้อที่มีแรงกระทำทั้งในทิศตั้งฉาก และขนานกับพื้นเอียง สังเกตว่า ถ้าลูกบอลกลิ้งลงมาโดยมีความเร่ง แล้วแรงเสียดทานจะต้องน้อยกว่าแรงโน้มถ่วงในทิศขนานกับพื้นเอียง
| 3. | วัตถุที่มีความหนาแน่นสม่ำเสมอ มีส่วนที่ลอยพ้นน้ำอยู่ 20% ของวัตถุ ถ้าออกแรงกดที่ด้านบนของวัตถุ 3 N จะทำให้วัตถุจมทั้งชิ้น แล้ววัตถุมีปริมาตรเท่าใด ให้ความหนาแน่นของน้ำเท่ากับ ρน้ำ = 1000 kg/m3 |
| A | Vวัตถุ = 0.3 ลิตร |
| B | Vวัตถุ = 0.67 ลิตร |
| C | Vวัตถุ = 1.2 ลิตร |
| D | Vวัตถุ = 1.5 ลิตร |
| E | Vวัตถุ = 3.0 ลิตร |
ตอบ (D)
วัตถุที่จมลงไปในน้ำจะต้องมีแรงต้านมากระทำกับแรงลอยตัวที่เพิ่มขึ้น 0.2 ρน้ำ Vg
ดังนั้น Vวัตถุ = 1.5 ลิตร
วัตถุที่จมลงไปในน้ำจะต้องมีแรงต้านมากระทำกับแรงลอยตัวที่เพิ่มขึ้น 0.2 ρน้ำ Vg
ดังนั้น Vวัตถุ = 1.5 ลิตร
| 4. | จากข้อความที่กำหนด จงหาจำนวนชิ้นส่วน N1 , N2 และ N3 ให้ถูกต้อง ให้สมมุติว่าไม่มีแรงภายนอกมากระทำ และ ในกรณีที่ไม่สามารถสรุปจำนวนชิ้นส่วนได้ให้ใช้ N = 1 • ถ้าวัตถุระเบิดเป็น N1 ชิ้น (หรือจำนวนชิ้นน้อยกว่านี้) โดยที่ทราบมวลของแต่ละชิ้นและทราบพลังงานจลน์รวม แล้วเราจะสามารถหาพลังงานจลน์ของแต่ละชิ้นได้ • ถ้าวัตถุระเบิดเป็น N2 ชิ้น (หรือจำนวนชิ้นน้อยกว่านี้) ความเร็วของวัตถุแต่ละชิ้นจะต้องอยู่บนเส้นตรงเดียวกัน • ถ้าวัตถุระเบิดเป็น N3 ชิ้น (หรือจำนวนชิ้นน้อยกว่านี้) ความเร็วของวัตถุแต่ละชิ้นจะต้องอยู่บนระนาบ |
| A | N1 = 2, N2 = 1, N3 = 1 |
| B | N1 = 1, N2 = 2, N3 = 3 |
| C | N1 = 2, N2 = 2, N3 = 3 |
| D | N1 = 3, N2 = 2, N3 = 3 |
| E | N1 = 2, N2 = 3, N3 = 4 |
ตอบ (C)
จากโจทย์จะได้ว่า
N1 = 2
เพราะ จากกฎการอนุรักษ์โมเมนตัม เมื่อเรารู้พลังงานจลน์รวม เราก็สามารถหาพลังงานของแต่ละก้อนได้ (2 สมการ 2 ตัวแปร)
N2 = 2
เพราะ ถ้ามากกว่านี้แล้ว ความเร็วของวัตถุแต่ละชิ้นไม่จำเป็นต้องอยู่บนเส้นตรงเดียวกัน
N3 = 3
ลองวาดเวกเตอร์ 2 อันก่อน การเพิ่มอันที่ 3 เข้าไปแล้วทำให้ผลรวมเป็นศูนย์นั้น เวกเตอร์ที่ 3 ต้องอยู่บนระนาบเดียวกัน (หากมี 4 เวกเตอร์แล้ว ไม่จำเป็นต้องอยู่ในระนาบเดียวกันก็รวมเป็นศูนย์ได้)
จากโจทย์จะได้ว่า
N1 = 2
เพราะ จากกฎการอนุรักษ์โมเมนตัม เมื่อเรารู้พลังงานจลน์รวม เราก็สามารถหาพลังงานของแต่ละก้อนได้ (2 สมการ 2 ตัวแปร)
N2 = 2
เพราะ ถ้ามากกว่านี้แล้ว ความเร็วของวัตถุแต่ละชิ้นไม่จำเป็นต้องอยู่บนเส้นตรงเดียวกัน
N3 = 3
ลองวาดเวกเตอร์ 2 อันก่อน การเพิ่มอันที่ 3 เข้าไปแล้วทำให้ผลรวมเป็นศูนย์นั้น เวกเตอร์ที่ 3 ต้องอยู่บนระนาบเดียวกัน (หากมี 4 เวกเตอร์แล้ว ไม่จำเป็นต้องอยู่ในระนาบเดียวกันก็รวมเป็นศูนย์ได้)
| 5. | ขี่จักรยานตามรางที่เป็นวงกลมรัศมี 30 m ด้วยอัตราเร็วคงที่ 10 m / s (เร็วมาก!) แล้วขนาดของมุมในการเข้าโค้งของผู้ขี่จักรยานเทียบกับแนวตั้ง ที่ไม่ทำให้จักรยานล้มเท่ากับข้อใด สมมุติว่า ความสูงของคนขี่จักรยานเตี้ยกว่าความยาวรัศมีของราง |
| A | 9.46° |
| B | 9.59° |
| C | 18.4° |
| D | 19.5° |
| E | 70.5° |
ตอบ (C)
แรงที่พุ่งเข้าหาจุดศูนย์กลาง เท่ากับ mv2/r และแรงที่พุ่งไปที่พื้น เท่ากับ mg โดยแรงที่พุ่งเข้าหาจุดศูนย์กลางมาจากแรงเสียดทานและแรงจากจุดที่กระทำกับพื้น ส่วนแรงตั้งฉากเท่ากับแรงโน้มถ่วงและแรงจากจุดที่กระทำกับพื้น ดังนั้น การหาขนาดของมุมจะหาจาก tan θ โดย
แรงที่พุ่งเข้าหาจุดศูนย์กลาง เท่ากับ mv2/r และแรงที่พุ่งไปที่พื้น เท่ากับ mg โดยแรงที่พุ่งเข้าหาจุดศูนย์กลางมาจากแรงเสียดทานและแรงจากจุดที่กระทำกับพื้น ส่วนแรงตั้งฉากเท่ากับแรงโน้มถ่วงและแรงจากจุดที่กระทำกับพื้น ดังนั้น การหาขนาดของมุมจะหาจาก tan θ โดย
\(\rm \tan \theta = \dfrac{{{v^2}}}{{gr}}\)
| 6. | ลูกบาศก์มวล 10 kg แต่ละด้านยาว 5 m สามารถขยับไปตามพื้นราบได้อย่างอิสระโดยไม่มีแรงเสียดทาน ภายในลูกบาศก์มีกล่องเล็กๆ มวล 2 kg ซึ่งเคลื่อนที่ภายในลูกบาศก์ โดยไม่มีแรงเสียดทาน ที่เวลา t = 0 ถ้ากล่องเล็กๆ เคลื่อนที่ด้วยความเร็ว 5 m / s ไปยังด้านหนึ่งของกล่อง โดยลูกบาศก์ยังคงหยุดนิ่ง และสัมประสิทธิ์การกระแทกสำหรับการชนกันระหว่างลูกบาศก์กับกล่องเท่ากับ 90% หมายความว่าอัตราเร็วสัมพัทธ์ระหว่างลูกบาศก์กับกล่อง หลังการชนจะเท่ากับ 90% ของอัตราเร็วสัมพัทธ์ระหว่างลูกบาศก์กับกล่อง ก่อนการชน
 |
| A | 0 m |
| B | 50 m |
| C | 100 m |
| D | 200 m |
| E | 300 m |
ตอบ (B)
วิธีที่ง่ายที่สุดคือ พิจารณาจากการเคลื่อนที่ที่จุดศูนย์กลางมวลของระบบ โดยใช้กฎการอนุรักษ์โมเมนตัม จะได้อัตราเร็วเท่ากับ
เนื่องจาก จุดศูนย์กลางมวลอยู่ภายในกล่องลูกบาศก์ ดังนั้น ตำแหน่งของกล่องเล็กจะเคลื่อนที่จากตำแหน่งเดิมไปราวๆ 50 m เช่นกัน (คำตอบอื่นอยู่ภายนอกกล่องลูกบาศก์)
วิธีที่ง่ายที่สุดคือ พิจารณาจากการเคลื่อนที่ที่จุดศูนย์กลางมวลของระบบ โดยใช้กฎการอนุรักษ์โมเมนตัม จะได้อัตราเร็วเท่ากับ
\({{\rm{v}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{{\rm{(2kg)(5m/s)}}}}{{{\rm{(2kg) + (10kg)}}}}{\rm{ = }}\dfrac{{\rm{5}}}{{\rm{6}}}{\rm{m/s}}\)
หลังผ่านไปหนึ่งนาที จุดศูนย์กลางมวลจะเคลื่อนที่ไปได้ \(\rm \left( {\dfrac{{\rm{5}}}{{\rm{6}}}{\rm{m/s}}} \right)(60s) = 50m\)เนื่องจาก จุดศูนย์กลางมวลอยู่ภายในกล่องลูกบาศก์ ดังนั้น ตำแหน่งของกล่องเล็กจะเคลื่อนที่จากตำแหน่งเดิมไปราวๆ 50 m เช่นกัน (คำตอบอื่นอยู่ภายนอกกล่องลูกบาศก์)
| 7. | คานยาว 1.00 m มีความหนาแน่นสม่ำเสมอ มีจุดหมุนห่างจากปลายคาน 30 cm ถ้าคานเกิดสมดุลเมื่อวางวัตถุมวล 50.0 g ให้ห่างจากปลายคาน 20 cm (อ้างอิงปลายเดิม) แล้วคานมีมวลเท่าไร |
| 8. | นำวัตถุมวล M ไปแขวนกับสปริงที่มีค่านิจสปริง k และปล่อยให้แขวนลงมาในแนวตั้ง โดยคาบของการสั่นเท่ากับ T0 ถ้าตัดสปริงให้เหลือครึ่งเดียวแต่ยังใช้มวลเท่าเดิม แล้วนำไปวางบนพื้นลื่นที่เอียง θ กับแนวนอน แล้วคาบของการสั่นบนพื้นเอียงในเทอมของ T0 เท่ากับข้อใด |
| A | \(\rm T_0\) |
| B | \(\rm T_0/2\) |
| C | \(\rm 2T_0\sin θ\) |
| D | \(\rm T_0/\sqrt2\) |
| E | \(\rm T_0\sin θ / \sqrt2\) |
ตอบ (D)
ค่านิจสปริงจะแปรผกผันกับความยาวตามธรรมชาติของสปริง จากโจทย์ เมื่อตัดสปริงให้เหลือครึ่งเดียว แล้วค่านิจสปริงก็จะเพิ่มขึ้นเป็นสองเท่า ส่วนการนำสปริงไปวางบนพื้นเอียงแม้ว่าจะทำให้ตำแหน่งสมดุลของมวลเปลี่ยนไป แต่จะไม่ส่งผลใดๆ ต่อคาบของการสั่นของสปริง ดังนั้น คาบของการสั่นใหม่จะเท่ากับ
ค่านิจสปริงจะแปรผกผันกับความยาวตามธรรมชาติของสปริง จากโจทย์ เมื่อตัดสปริงให้เหลือครึ่งเดียว แล้วค่านิจสปริงก็จะเพิ่มขึ้นเป็นสองเท่า ส่วนการนำสปริงไปวางบนพื้นเอียงแม้ว่าจะทำให้ตำแหน่งสมดุลของมวลเปลี่ยนไป แต่จะไม่ส่งผลใดๆ ต่อคาบของการสั่นของสปริง ดังนั้น คาบของการสั่นใหม่จะเท่ากับ
\({\rm{T = 2}}\pi \sqrt {\dfrac{{\rm{m}}}{{{\rm{2k}}}}} {\rm{ = }}\dfrac{{\rm{1}}}{{\sqrt {\rm{2}} }}{\rm{2}}\pi \sqrt {\dfrac{{\rm{m}}}{{\rm{k}}}} {\rm{ = }}\dfrac{{{{\rm{T}}_{\rm{0}}}}}{{\sqrt {\rm{2}} }}\)
| 9. | กำหนด กราฟแรงที่กระทำกับวัตถุหนัก 5.00 ตามเวลาที่เปลี่ยนแปลงไป ดังรูป ถ้าความเร็วที่ t = 0.0 s คือ +1.0 m / s แล้วความเร็วของวัตถุที่ t = 7 s คือข้อใด  |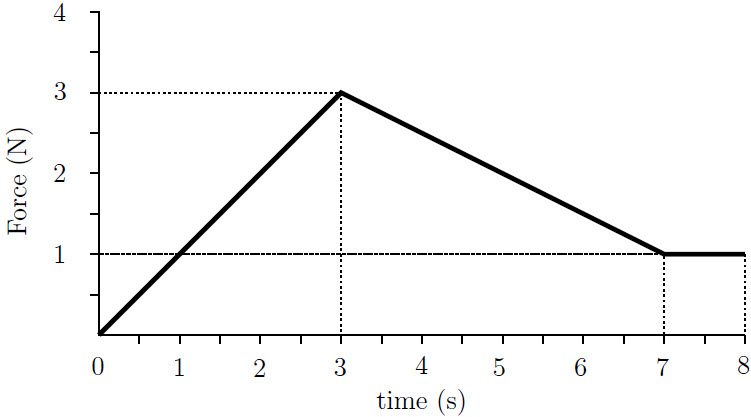
| A | 2.45 m/s |
| B | 2.50 m/s |
| C | 3.50 m/s |
| D | 12.5 m/s |
| E | 15.0 m/s |
ตอบ (C)
จากพื้นที่ใต้กราฟเท่ากับโมเมนตัมที่เปลี่ยนไป จะได้ว่า
ดังนั้น ความเร็วของวัตถุที่ t = 7 s คือ 1.0 + 2.5 = 3.5 m/s
จากพื้นที่ใต้กราฟเท่ากับโมเมนตัมที่เปลี่ยนไป จะได้ว่า
\(\Delta {\rm{p = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{(3~s)(3~N) + }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{(4 ~s)(3~N + 1~N) = 12/5 ~N}} \cdot {\rm{s}}\)
แสดงว่าจะมีอัตราเร็วเพิ่มขึ้นมาอีก \(\rm \Delta v{\rm{ = 2}}{\rm{.5~ m/s}}\)ดังนั้น ความเร็วของวัตถุที่ t = 7 s คือ 1.0 + 2.5 = 3.5 m/s
| 10. | รถบังคับวิทยุถูกผูกติดกับเสาด้วยเชือกยาว 3.00 m และถูกบังคับให้วิ่งเป็นวงกลม ด้วยความเร็วเชิงมุมเริ่มต้น 1.00 rad / s และเร่งความเร็วต่อเนื่องด้วยอัตรา 4.00 rad / s2 ถ้าเชือกขาดเมื่อความเร่งสู่ศูนย์กลางเกิน 2.43×102 m / s2 แล้วเราสามารถเร่งความเร็วรถได้นานแค่ไหนก่อนเชือกขาด |
| A | 0.25 s |
| B | 0.50 s |
| C | 1.00 s |
| D | 1.50 s |
| E | 2.00 s |
ตอบ (E)
เชือกจะขาดเมื่อ ac มีค่าสูงกว่าแรงตึงสูงสุด นั่นคือ
เชือกจะขาดเมื่อ ac มีค่าสูงกว่าแรงตึงสูงสุด นั่นคือ
\({{\rm{a}}_{\rm{c}}}{\rm{ = r}}{{\rm{\omega }}^{\rm{2}}}{\rm{ = r}}{\left( {\frac{1}{2}\alpha {{\rm{t}}^{\rm{2}}}{\rm{ + \omega }}_0^2} \right)^2}\)
จัดให้อยู่ในรูปของ t
\({\rm{t = }}\sqrt {\dfrac{2}{\alpha }\left( {\sqrt {\dfrac{{{{\rm{a}}_{\rm{c}}}}}{{\rm{r}}} - {{\rm{\omega }}_0}} } \right)} {\rm{ }}\)
ดังนั้น t = 2s| 11. | มวล m ติดสปริงในอุดมคติ ถูกนำไปวางในแนวนอนบนพื้นลื่น จากนั้นดึงมวลเล็กน้อย แล้วปล่อยออก ข้อใดแสดงกราฟพลังงานจลน์กับฟังก์ชันของพลังงานศักย์ได้ถูกต้องที่สุด |
| A |  |
| B |  |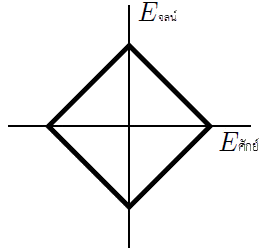
| C |  |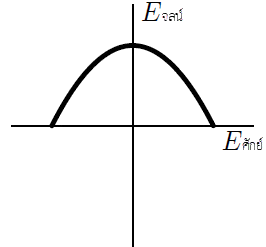
| D |  |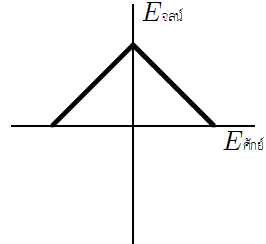
| E |  |
ตอบ (E)
เนื่องจากพลังงานจะถูกอนุรักษ์ไว้ ดังนั้น ผลรวมจะต้องเป็นค่าคงที่ค่าหนึ่ง
ดังนั้น กราฟจะต้องเป็นเส้นตรงที่ลาดลงมา และมีความชันคงที่
เนื่องจากพลังงานจะถูกอนุรักษ์ไว้ ดังนั้น ผลรวมจะต้องเป็นค่าคงที่ค่าหนึ่ง
ดังนั้น กราฟจะต้องเป็นเส้นตรงที่ลาดลงมา และมีความชันคงที่
| 12. | เฮลิคอปเตอร์กระดาษ มีรัศมีใบพัด r มีน้ำหนัก W ถูกปล่อยที่ความสูง h กลางอากาศที่มีความหนาแน่น ρ
 \(\rm T = kh^α r^βρ^δ W^ω\)
โดยที่ k เป็นค่าคงที่ที่ไม่มีมิติ (ค่าแท้จริงคือ 1.164) α, β, δ, และ ω เป็นค่าคงตัวของเลขชี้กำลังที่ต้องหาแล้วค่า α เท่ากับข้อใด |
| A | α = -1 |
| B | α = -1/2 |
| C | α = 0 |
| D | α = 1/2 |
| E | α = 1 |
ตอบ (E)
เมื่อเฮลิคอปเตอร์ไปถึงความเร็วสุดท้าย มันก็จะตกลงมาด้วยอัตราเร็วคงที่ ตาม h = vT โดย v เป็นความเร็วปลาย ในกรณีนี้ α = 1
เมื่อเฮลิคอปเตอร์ไปถึงความเร็วสุดท้าย มันก็จะตกลงมาด้วยอัตราเร็วคงที่ ตาม h = vT โดย v เป็นความเร็วปลาย ในกรณีนี้ α = 1
| 13. | เฮลิคอปเตอร์กระดาษ มีรัศมีใบพัด r มีน้ำหนัก W ถูกปล่อยที่ความสูง h กลางอากาศที่มีความหนาแน่น ρ สมมุติว่า เฮลิคอปเตอร์ไปถึง
 \(\rm T = kh^α r^βρ^δ W^ω\)
โดยที่ k เป็นค่าคงที่ที่ไม่มีมิติ (ค่าแท้จริงคือ 1.164) α, β, δ, และ ω เป็นค่าคงตัวของเลขชี้กำลังที่ต้องหาแล้วค่า β เท่ากับข้อใด |
| A | β = 1/3 |
| B | β = 1/2 |
| C | β = 2/3 |
| D | β = 1 |
| E | ข้อมูลไม่เพียงพอสำหรับการหาค่า β |
ตอบ (D)
เมื่อเฮลิคอปเตอร์ไปถึงความเร็วสุดท้าย มันก็จะตกลงมาด้วยอัตราเร็วคงที่ ตาม h = vT โดย v เป็นความเร็วปลาย ในกรณีนี้ α = 1
จากนั้นใช้การวิเคราะห์มิติกับมวลที่เราสนใจ
สังเกตว่า δ = – ω มีเฉพาะ W ที่เป็นหน่วยของเวลา (ส่วนกลับของกำลังสอง) โดย ω = –1/2 แต่ \(\rm \sqrt {\rho /W}\) มีหน่วยเป็นความยาว–2เวลา–1 และเรารู้ว่า α = 1 ดังนั้น β = 1
เมื่อเฮลิคอปเตอร์ไปถึงความเร็วสุดท้าย มันก็จะตกลงมาด้วยอัตราเร็วคงที่ ตาม h = vT โดย v เป็นความเร็วปลาย ในกรณีนี้ α = 1
จากนั้นใช้การวิเคราะห์มิติกับมวลที่เราสนใจ
สังเกตว่า δ = – ω มีเฉพาะ W ที่เป็นหน่วยของเวลา (ส่วนกลับของกำลังสอง) โดย ω = –1/2 แต่ \(\rm \sqrt {\rho /W}\) มีหน่วยเป็นความยาว–2เวลา–1 และเรารู้ว่า α = 1 ดังนั้น β = 1
| 14. | (เกินหลักสูตรการสอบเข้า สอวน.) แผ่นกลมมวล M มีโมเมนต์ความเฉื่อย I รัศมี R มีเชือกพันรอบแผ่นกลมไว้ ดังรูป แผ่นกลมกลิ้งอย่างอิสระไปตามทิศทางที่แสดงดังรูป มีแรงคงที่ T กระทำที่ปลายเชือก และทำให้แผ่นกลมมีความเร่งบนพื้นลื่น  |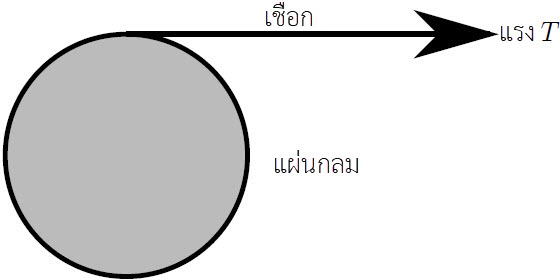
| A | \(\rm \dfrac{I}{{M{R^2}}}\) |
| B | \(\rm \dfrac{{M{R^2}}}{I}\) |
| C | \(\rm \dfrac{I}{{3M{R^2}}}\) |
| D | \(\rm \dfrac{I}{{M{R^2} + I}}\) |
| E | \(\rm \dfrac{{M{R^2}}}{{M{R^2} + I}}\) |
ตอบ (D)
แรง T จะทำให้เกิดความเร่งที่จุดศูนย์กลางมวลของแผ่นกลมในอัตรา a = T / M และทำให้เกิดทอร์กบนแผ่นกลมที่จุดศูนย์กลางมวลตาม τ = RT ดังนั้น ความเร่งเชิงมุม α จะเท่ากับ RT / I
หลังผ่านไป t ความเร็วของแผ่นกลมจะเท่ากับ v = at และความเร็วเชิงมุมจะเท่ากับ ω = αt จะได้
แรง T จะทำให้เกิดความเร่งที่จุดศูนย์กลางมวลของแผ่นกลมในอัตรา a = T / M และทำให้เกิดทอร์กบนแผ่นกลมที่จุดศูนย์กลางมวลตาม τ = RT ดังนั้น ความเร่งเชิงมุม α จะเท่ากับ RT / I
หลังผ่านไป t ความเร็วของแผ่นกลมจะเท่ากับ v = at และความเร็วเชิงมุมจะเท่ากับ ω = αt จะได้
KEการเลื่อนที่ = \(\dfrac{1}{2}{\rm{M}}{\left( {\dfrac{{\rm{T}}}{{\rm{M}}}} \right)^2}{{\rm{t}}^2}\)
และ
KEการหมุน = \(\dfrac{1}{2}{\rm{I}}{\left( {\dfrac{{{\rm{RT}}}}{{\rm{I}}}} \right)^2}{{\rm{t}}^2}\)
เมื่อหาอัตราส่วนของทั้งสองจะได้
KEการเลื่อนที่ / KEสุทธิ
\(\begin{align*} &= \frac{{\frac{1}{2}{\rm{M}}{{\left( {\frac{{\rm{T}}}{{\rm{M}}}} \right)}^2}{{\rm{t}}^2}}}{{\frac{1}{2}{\rm{M}}{{\left( {\frac{{\rm{T}}}{{\rm{M}}}} \right)}^2}{{\rm{t}}^2} + \frac{1}{2}{\rm{I}}{{\left( {\frac{{{\rm{RT}}}}{{\rm{I}}}} \right)}^2}{{\rm{t}}^2}}}\\ &= \frac{{\frac{1}{{\rm{M}}}}}{{\frac{1}{{\rm{M}}} + \frac{{{{\rm{R}}^{\rm{2}}}}}{{\rm{I}}}}}\\ &= \frac{{\rm{I}}}{{{\rm{M}}{{\rm{R}}^{\rm{2}}}{\rm{ + I}}}} \end{align*}\)
\(\begin{align*} &= \frac{{\frac{1}{2}{\rm{M}}{{\left( {\frac{{\rm{T}}}{{\rm{M}}}} \right)}^2}{{\rm{t}}^2}}}{{\frac{1}{2}{\rm{M}}{{\left( {\frac{{\rm{T}}}{{\rm{M}}}} \right)}^2}{{\rm{t}}^2} + \frac{1}{2}{\rm{I}}{{\left( {\frac{{{\rm{RT}}}}{{\rm{I}}}} \right)}^2}{{\rm{t}}^2}}}\\ &= \frac{{\frac{1}{{\rm{M}}}}}{{\frac{1}{{\rm{M}}} + \frac{{{{\rm{R}}^{\rm{2}}}}}{{\rm{I}}}}}\\ &= \frac{{\rm{I}}}{{{\rm{M}}{{\rm{R}}^{\rm{2}}}{\rm{ + I}}}} \end{align*}\)
| 15. | ให้ทอร์กสูงสุดที่ออกมาจากเครื่องยนต์ของรถทดลองมวล m คือ τ อัตราเร็วเชิงมุมสูงสุดของเครื่องยนต์คือ ω เครื่องยนต์มีกำลังที่ออกมาคงที่ P และเครื่องยนต์เชื่อมต่อกับล้ออย่างไม่มีการสูญเสียพลังงาน ถ้าล้อมีรัศมี R และสัมประสิทธิ์ของแรงเสียดทานสถิตระหว่างล้อกับถนนคือ μ แล้วอัตราเร็วสูงสุดที่รถสามารถวิ่งบนพื้นเอียง 30 องศา ได้เท่ากับข้อใด สมมุติว่า ไม่มีการสูญเสียจากแรงเสียดทาน และ μ มีขนาดใหญ่พอที่จะทำให้ยางไม่ไถลขณะวิ่ง |
| A | \(\rm v = 2P/(mg)\) |
| B | \(\rm v = 2P/(\sqrt3mg)\) |
| C | \(\rm v = 2P/( μmg)\) |
| D | \(\rm v = τω /(mg)\) |
| E | \(\rm v = τω /( μmg)\) |
ตอบ (A)
จากหลักพื้นฐาน P = Fv เมื่อ F แรงของน้ำหนักที่ขนานกับพื้นเอียง จะได้
ดังนั้น v = 2P/(mg)
จากหลักพื้นฐาน P = Fv เมื่อ F แรงของน้ำหนักที่ขนานกับพื้นเอียง จะได้
\(\rm v = P/mg sin θ\)
โจทย์ให้ θ = 30°ดังนั้น v = 2P/(mg)
| 16. | วัตถุมวล m1 เคลื่อนที่ด้วยอัตราเร็ว v0 ชนกับวัตถุมวล m2 = αm1 โดย α < 1 จากเดิมหยุดนิ่ง การชนนี้อาจยืดหยุ่นสมบูรณ์ ไม่ยืดหยุ่นสมบูรณ์ หรือ ไม่ยืดหยุ่นบางส่วนก็ได้ หลังการชนวัตถุทั้งสองเคลื่อนที่ด้วยอัตราเร็ว v1 และ v2 สมมุติว่า การชนเกิดขึ้นในหนึ่งมิติและวัตถุแรกไม่สามารถพุ่งผ่านวัตถุสองได้ หลังการชน อัตราส่วนอัตราเร็ว r1 = v1 / v0 ของวัตถุแรกจะอยู่ในช่วงใด |
| A | (1 – α) / (1 + α) ≤ r1 ≤ 1 |
| B | (1 – α) / (1 + α) ≤ r1 ≤ 1 / (1 + α) |
| C | α / (1 + α) ≤ r1 ≤ 1 |
| D | 0 ≤ r1 ≤ 2α / (1 + α) |
| E | 1 / (1 + α) ≤ r1 ≤ 2 / (1 + α) |
ตอบ (B)
จากกฎการอนุรักษ์โมเมนตัมและพลังงานจลน์ในการชนแบบยืดหนุ่ยสมบูรณ์ จะได้
จากกฏการอนุรักษ์โมเมนตัม ในกรณีที่การชนนั้นไม่ยืดหยุ่นสมบูรณ์ จะได้ว่า
ดังนั้น
จากกฎการอนุรักษ์โมเมนตัมและพลังงานจลน์ในการชนแบบยืดหนุ่ยสมบูรณ์ จะได้
\(\begin{array}{c}
{{\rm{r}}_1} = \dfrac{{{{\rm{v}}_{\rm{1}}}}}{{{{\rm{v}}_{\rm{0}}}}} = \dfrac{{1 - {\rm{\alpha }}}}{{1 + {\rm{\alpha }}}}\\
{{\rm{r}}_2} = \dfrac{{{{\rm{v}}_2}}}{{{{\rm{v}}_{\rm{0}}}}} = \dfrac{2}{{1 + {\rm{\alpha }}}}
\end{array}\)
เนื่องจาก α < 1 วัตถุ m1 จะมีอิทธิพลมากกว่าวัตถุ m2 ดังนั้น การเคลื่อนที่จะยังคงไปข้างหน้า จากกฏการอนุรักษ์โมเมนตัม ในกรณีที่การชนนั้นไม่ยืดหยุ่นสมบูรณ์ จะได้ว่า
\({{\rm{r}}_{\rm{1}}}{\rm{ = }}{{\rm{r}}_{\rm{2}}} = \dfrac{1}{{1 + {\rm{\alpha }}}}\)
จากที่วัตถุ m2 เคลื่อนที่ไปข้างหน้าเสมอ และวัตถุ m1 ไม่สามารถทะลุผ่านวัตถุ m2 ได้ ดังนั้น วัตถุ m2 จะต้องเคลื่อนที่ด้วยความเร็วที่เป็นบวกมากกว่า (หรือเท่ากับ) วัตถุ m1 ดังนั้น
\(1/(1 + {\rm{\alpha }}) \le {{\rm{r}}_2} \le 2/(1 + {\rm{\alpha }})\)
การหาช่วงคำตอบของ วัตถุ m1 อาจจะยากกว่าเล็กน้อย เพราะสถานการณ์นี้อาจจะมีการกระดอนกลับเกิดขึ้น แต่ในกรณีนี้ α < 1 ทำให้ความเร็วหลังการชนเคลื่อนที่ไปข้างหน้า จึงได้ว่า
\((1 - {\rm{\alpha }})/(1 + {\rm{\alpha }}) \le {{\rm{r}}_1} \le 1/(1 + {\rm{\alpha }})\)
| 17. | เมฆละอองฝุ่นทรงกลมในอวกาศ มีความหนาแน่นสม่ำเสมอ ρ0 มีรัศมี R0 และมีความเร่งโน้มถ่วงที่ผิวเมฆเป็น g0 ถ้าการเกิดก้อนเมฆ (การขยายตัวเนื่องจากความร้อน) ทำให้รัศมีของเมฆเป็น 2R0 และละอองฝุ่นยังคงกระจายตัวอย่างสม่ำเสมอ แล้วความเร่งโน้มถ่วงปัจจุบันที่ระยะ R0 จากศูนย์กลางของก้อนเมฆ เท่ากับข้อใด |
| A | g0 / 32 |
| B | g0 / 16 |
| C | g0 / 8 |
| D | g0 / 4 |
| E | g0 / 2 |
ตอบ (C)
จากกฎของนิวตัน แรงโน้มถ่วงสำหรับวัตถุที่เป็นทรงกลมจะขึ้นกับมวลที่อยู่ภายในระยะจากศูนย์กลางมวลถึงตำแหน่งที่วัดเท่านั้น
ในทางกลับกันความหนาแน่นจะลดขนาดลง 1/8
จากกฎของนิวตัน แรงโน้มถ่วงสำหรับวัตถุที่เป็นทรงกลมจะขึ้นกับมวลที่อยู่ภายในระยะจากศูนย์กลางมวลถึงตำแหน่งที่วัดเท่านั้น
\({\rm{g = }}\dfrac{{{\rm{GM}}}}{{{{\rm{r}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{{\rm{4\pi }}}}{{\rm{3}}}{\rm{G\rho r}}\)
ซึ่งค่าสุดท้ายนั้นจะเป็นจริง เมื่อความหนาแน่นนั้นสม่ำเสมอในทางกลับกันความหนาแน่นจะลดขนาดลง 1/8
| 18. | พิจารณกล่องและเครื่องชั่งสองอัน ดังรูป ให้เครื่องชั่ง A รับน้ำหนักกล่องผ่านเชือกเบา ภายในกล่องมีรอกแขวนลงมาจากด้านบน และมีเชือกเบาอีกเส้นคล้องผ่านรอก ให้ปลายด้านหนึ่งยึดกับพื้นกล่อง และปลายอีกด้านหนึ่งผูกกับเครื่องชั่ง B ความตึงในเส้นเชือกที่อ่านจากเครื่องชั่งทั้งสองคือ TA และ TB ให้เดิมเครื่องชั่ง A อ่านได้ 30 นิวตัน และเครื่องชั่ง B อ่านได้ 20 นิวตัน
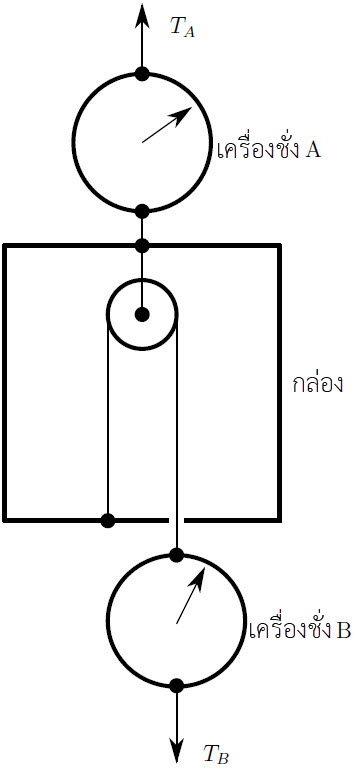 ( ดัดแปลงมาจากการสาธิตของ Richard Berg ) |
| A | 35 นิวตัน |
| B | 40 นิวตัน |
| C | 45 นิวตัน |
| D | 50 นิวตัน |
| E | 60 นิวตัน |
ตอบ (B)
จากกล่องใบดังกล่าว สิ่งที่เราควรทราบคือ เมื่อเครื่องชั่ง B ถูกดึงด้วยแรง 10 นิวตัน แล้วเครื่องชั่ง A ก็จะถูกแรงดึงด้วยแรง 10 นิวตัน เพื่อให้ระบบเกิดสมดุล
ดังนั้น เครื่องชั่ง A จะอ่านค่าได้ 40 นิวตัน
จากกล่องใบดังกล่าว สิ่งที่เราควรทราบคือ เมื่อเครื่องชั่ง B ถูกดึงด้วยแรง 10 นิวตัน แล้วเครื่องชั่ง A ก็จะถูกแรงดึงด้วยแรง 10 นิวตัน เพื่อให้ระบบเกิดสมดุล
ดังนั้น เครื่องชั่ง A จะอ่านค่าได้ 40 นิวตัน
| 19. | เฮลิคอปเตอร์บินตามแนวนอนด้วยอัตราเร็วคงที่ มีสายเคเบิลที่ยืดหยุ่นสมบูรณ์ตลอดเส้นผูกติดไว้ที่ใต้เฮลิคอปเตอร์ และมีแรงต้านอากาศกระทำกับสายเคเบิลอยู่พอสมควร แล้วข้อใดแสดงลักษณะของสายเคเบิลขณะที่เฮลิคอปเตอร์บินไปทางขวาได้ถูกต้องที่สุด |
| A |  |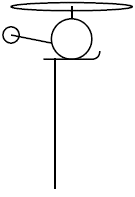
| B |  |
| C |  |
| D |  |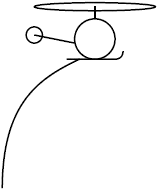
| E |  |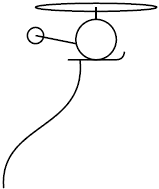
ตอบ (B)
เมื่อมีแรงต้านอากาศกระทำกับสายเคเบิล ก็จะเกิดแรงที่กระทำในแนวนอนกับสายเคเบิลที่ผูกติดอยู่ใต้เฮลิคอปเตอร์ เนื่องจากแรงต้านอากาศแปรผันตามความยาวของสายเคเบิลที่ห้อยลงมาที่จุดใดก็ได้ ดังนั้น สายเคเบิลจะเอียงเป็นเส้นทแยงมุมตามข้อ (B)
(หากมีมวลแขวนอยู่ที่ปลายสายเคเบิลจะตอบข้อ (D))
เมื่อมีแรงต้านอากาศกระทำกับสายเคเบิล ก็จะเกิดแรงที่กระทำในแนวนอนกับสายเคเบิลที่ผูกติดอยู่ใต้เฮลิคอปเตอร์ เนื่องจากแรงต้านอากาศแปรผันตามความยาวของสายเคเบิลที่ห้อยลงมาที่จุดใดก็ได้ ดังนั้น สายเคเบิลจะเอียงเป็นเส้นทแยงมุมตามข้อ (B)
(หากมีมวลแขวนอยู่ที่ปลายสายเคเบิลจะตอบข้อ (D))
| 20. | (เกินหลักสูตรการสอบเข้า สอวน.) นักวิทยาศาสตร์ได้สร้างสถานีอวกาศแห่งใหม่ที่มีรูปร่างคล้ายล้อรถ มีรัศมี R โครงสร้างทั้งหมดมีมวล M อยู่ที่ส่วนขอบ เมื่อนักบินอวกาศมาถึงสถานี สถานีจะหมุนในอัตราที่ทำให้วัตถุที่ขอบของสถานีมีความเร่งสู่ศูนย์กลางเป็น g ให้ใกล้เคียงกับแรงโน้มถ่วงของโลก โดยสภาวะนั้นต้องพึ่งจรวดเล็กสองลำ แต่ละลำมีแรงดัน T นิวตัน ให้ติดตั้งบนขอบของสถานี แล้วจรวดต้องใช้เวลาเดินเครื่อง t เท่าใด จึงจะทำให้เกิดสภาวะที่ต้องการ (ดัดแปลงมาจาก Physics for Scientists and Engineers โดย Richard Wolfson) |
| A | \(\rm t = \sqrt{gR^3} M / (2T)\) |
| B | \(\rm t = \sqrt{gR} M / (2T)\) |
| C | \(\rm t = \sqrt{gR} M / T\) |
| D | \(\rm t = \sqrt{gR/\pi} M / T\) |
| E | \(\rm t = \sqrt{gR} M / (\pi T)\) |
ตอบ (B)
ความเร่งที่เราต้องการ คือ
ความเร่งที่เราต้องการ คือ
\({\rm{g = }}{{\rm{\omega }}^{\rm{2}}}{\rm{R}} \to {\rm{\omega = }}\sqrt {{\rm{g/R}}}\)
แรงที่จรวดสองลำ เท่ากับ
\({\rm{2TR = M}}{{\rm{R}}^{\rm{2}}}{\rm{\alpha }} \to {\rm{\alpha = 2T/MR}}\)
ดังนั้น เวลาที่ใช้เท่ากับ
\({\rm{t = \omega /\alpha = }}\frac{{\sqrt {{\rm{gR}}} {\rm{M}}}}{{{\rm{2T}}}}\)
| 21. | (เกินหลักสูตรการสอบเข้า สอวน.) ให้รอกสองอัน ทำจากโลหะชนิดเดียวกันมีความหนาแน่น ρ (แสดงดังรูป) รอก A เป็นแบบแผ่นกลมสม่ำเสมอมีรัศมี R รอก B เป็นแบบวงแหวน ส่วนที่กลวงมีรัศมี R/2 นำกล่องสองใบมวล M = αm (α > 1) แขวนกับรอกผ่านเชือกเบา และหมุนโดยไม่ไถล แล้วอัตราส่วนความเร่งในระบบ A กับ B เท่ากับข้อใด ถ้ามวลของรอก A เท่ากับ M + m
 |
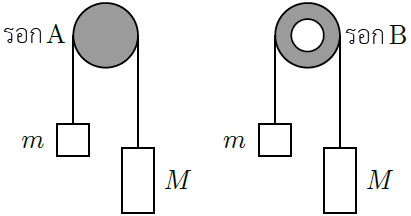| A | aA / aB = 47 / 48 |
| B | aA / aB = 31 / 32 |
| C | aA / aB = 15 / 16 |
| D | aA / aB = 9 / 6 |
| E | aA / aB = 3 / 4 |
ตอบ (A)
โจทย์ข้อนี้ เป็นโจทย์ปัญหาความสมดุลของแรงในเครื่องกลทั่วไป
สำหรับมวล M จะมีค่าตามสมการ
สำหรับมวล m จะมีค่าตามสมการ
เมื่อรวมสมการจะได้
และ βB = 1/2(1 – (1/4)(1/4)) = 15/32 เพราะรอกเป็นวงแหวนจึงต้องลบส่วนที่กลวงออกไป
ดังนั้น อัตราส่วนความเร่งจะเท่ากับ \(\dfrac{{{{\rm{a}}_{\rm{A}}}}}{{{{\rm{a}}_{\rm{B}}}}}{\rm{ = }}\dfrac{{47}}{{48}}\)
โจทย์ข้อนี้ เป็นโจทย์ปัญหาความสมดุลของแรงในเครื่องกลทั่วไป
สำหรับมวล M จะมีค่าตามสมการ
\({\rm{Ma = Mg}} - {{\rm{T}}_{\rm{M}}}\)
โดย TM คือ แรงตึงเชือกที่แขวนมวล Mสำหรับมวล m จะมีค่าตามสมการ
\({\rm{ma = }}{{\rm{T}}_{\rm{M}}} - {\rm{mg}}\)
สำหรับรอก จะมีค่าตามสมการ
\({\rm{I\alpha = R (}}{{\rm{T}}_{\rm{M}}} - {{\rm{t}}_{\rm{m}}}{\rm{)}}\)
โดย α = a / R และ I คือ โมเมนต์ความเฉื่อยเมื่อรวมสมการจะได้
\({\rm{Ia/}}{{\rm{R}}^{\rm{2}}}{\rm{ = (Mg }} - {\rm{Ma)}} - {\rm{(ma + mg)}}\)
หรือ
\({\rm{a = g}}\dfrac{{{\rm{M}} - {\rm{m}}}}{{{\rm{I/}}{{\rm{R}}^{\rm{2}}}{\rm{ + M + m}}}}\)
ให้โมเมนต์ความเฉื่อยของรอกทั้งสองอัน คือ I = β (M + m) R2 แล้วอัตราส่วนความเร่งจะเท่ากับ
\(\dfrac{{{{\rm{a}}_{\rm{A}}}}}{{{{\rm{a}}_{\rm{B}}}}}{\rm{ = }}\dfrac{{{{\rm{\beta }}_{\rm{B}}}{\rm{ + 1}}}}{{{{\rm{\beta }}_{\rm{A}}}{\rm{ + 1}}}}\)
โดย βA = 1/2 เพราะเป็นแผ่นกลมสม่ำเสมอและ βB = 1/2(1 – (1/4)(1/4)) = 15/32 เพราะรอกเป็นวงแหวนจึงต้องลบส่วนที่กลวงออกไป
ดังนั้น อัตราส่วนความเร่งจะเท่ากับ \(\dfrac{{{{\rm{a}}_{\rm{A}}}}}{{{{\rm{a}}_{\rm{B}}}}}{\rm{ = }}\dfrac{{47}}{{48}}\)
| 22. | ดาวเคราะห์มวล M และ m << M อยู่ในวงโคจรรอบจุดศูนย์กลางมวล ภายใต้แรงดึงดูดซึ่งกันและกัน และดาวทั้งสองอยู่ห่างกัน R ซึ่งมีขนาดใหญ่กว่าดาวทั้งสองดวง ถ้าชิ้นส่วนเล็ก ๆ ขนาด δm << m จากดาวมวล m ถูกดูดไปยังดาวมวล M โดยการถ่ายโอนนี้เกิดขึ้นในขณะที่วงโคจรของดาวทั้งสองยังเป็นวงกลม และยังคงห่างกัน R แล้วข้อความใดต่อไปนี้ถูกต้อง |
| A | แรงดึงดูดระหว่างดาวทั้งสองจะเพิ่มขึ้น |
| B | แรงดึงดูดระหว่างดาวทั้งสองจะยังคงที่ |
| C | โมเมนตัมเชิงมุมสุทธิของระบบจะเพิ่มขึ้น |
| D | โมเมนตัมเชิงมุมสุทธิของระบบจะยังคงที่ |
| E | คาบของวงโคจรของดาวเคราะห์ทั้งสองจะยังคงเป็นค่าคงที่ |
ตอบ (E)
แรงระหว่างดาวเคราะห์ทั้งสองดวง คือ
ขั้นตอนสุดท้าย หาคาบของการเคลื่อนที่จากสมการ v = 2πr / T จะได้
ดังนั้น ข้อ (E) คือ คำตอบที่ถูกต้อง (นักเรียนสามารถใช้กฎของเคปเลอร์ตอบได้เลยเช่นกัน)
แรงระหว่างดาวเคราะห์ทั้งสองดวง คือ
\({\rm{F = G}}\dfrac{{{\rm{Mm}}}}{{{{\rm{R}}^{\rm{2}}}}}\)
แรงใหม่ F´ จะเท่ากับ
\(\begin{align*}
\rm{F'} &= \rm G\frac{{{\rm{(M + }}\delta {\rm{m)(m}}--\delta {\rm{m)}}}}{{{{\rm{r}}^{\rm{2}}}}}\\
&= \rm G\frac{{{\rm{Mm}}--{\rm{(M}}--{\rm{m)}}\delta {\rm{m}}--{{(\delta {\rm{m}})}^2}}}{{{{\rm{R}}^{\rm{2}}}}}
\end{align*}\)
เราสามารถประมาณกับสมการแรกได้
\({\rm{F' = }}\left( {{\rm{1}}-\dfrac{{\delta {\rm{m}}}}{{\rm{m}}}} \right){\rm{F}}\)
การเคลื่อนที่สู่ศูนย์กลางจะเท่ากับ
\(\rm mv^2/r = F\)
โดย r คือระยะทางจาก m ถึงจุดศูนย์กลางมวล โดย
\({\rm{r = }}\dfrac{{\rm{M}}}{{{\rm{M + m}}}}{\rm{R}}\)
เมื่อแสดงในเทอมของโมเมนตัมเชิงมุม จะได้
\({{\rm{L}}_{\rm{m}}}{\rm{ = mvr = }}\sqrt {{\rm{m(m}}{{\rm{v}}^{\rm{2}}}{\rm{/r)}}{{\rm{r}}^{\rm{3}}}} {\rm{ = }}\sqrt {{\rm{m}}{{\rm{r}}^{\rm{3}}}{\rm{F}}} \)
หรือ
\({{\rm{L}}_{\rm{m}}}{\rm{ = }}\sqrt {\dfrac{{{\rm{m}}{{\rm{M}}^{\rm{3}}}{\rm{RGmM}}}}{{{{{\rm{(m + M)}}}^{\rm{3}}}}}} = {\rm{m}}{{\rm{M}}^{\rm{2}}}\sqrt {\dfrac{{{\rm{GR}}}}{{{{{\rm{(m + M)}}}^{\rm{3}}}}}} \)
จากความสมมาตร จะได้
\({{\rm{L}}_{\rm{M}}}{\rm{ = }}{{\rm{m}}^{\rm{2}}}{\rm{M}}\sqrt {\dfrac{{{\rm{GR}}}}{{{{{\rm{(m + M)}}}^{\rm{3}}}}}}\)
ดังนั้น ผลรวมเท่ากับ
\({\rm{L = }}{{\rm{L}}_{\rm{m}}}{\rm{ + }}{{\rm{L}}_{\rm{M}}}{\rm{ = mM}}\sqrt {\dfrac{{{\rm{GR}}}}{{{\rm{m + M}}}}}\)
จะเห็นว่า Mm จะลดลง เมื่อ δm ถูกถ่ายจาก m ไปสู่ M แสดงว่ามีทอร์กจากภายนอกมากระทำขั้นตอนสุดท้าย หาคาบของการเคลื่อนที่จากสมการ v = 2πr / T จะได้
\({\rm{T = }}\dfrac{{{\rm{2\pi r}}}}{{\rm{v}}}{\rm{ = 2\pi }}\sqrt {\dfrac{{{\rm{mr}}}}{{\rm{F}}}}\)
เมื่อรวมกับสมการด้านบน จะได้
\({\rm{T = 2\pi }}\sqrt {\dfrac{{{\rm{mMR}}}}{{{\rm{m + M}}}}\dfrac{{{{\rm{R}}^{\rm{2}}}}}{{{\rm{GmM}}}}} = {\rm{2\pi }}\sqrt {\dfrac{{{{\rm{R}}^{\rm{3}}}}}{{{\rm{G(m + M)}}}}}\)
จะเห็นว่าค่าที่ได้เป็นค่าคงที่ดังนั้น ข้อ (E) คือ คำตอบที่ถูกต้อง (นักเรียนสามารถใช้กฎของเคปเลอร์ตอบได้เลยเช่นกัน)
| 23. | นักบินอวกาศมวล 100 kg พกปืนที่บรรจุกระสุนขนาดใหญ่ไว้ 10 kg ตัวปืนและชุดนักบินมีมวลน้อยมาก เมื่อเหนี่ยวไกกระสุนจะพุ่งออกด้วยอัตราเร็วสัมพัทธ์ 50 m/s เทียบกับนักบิน แล้วขณะเหนี่ยวไก นักบินอวกาศจะได้รับแรงดลจากปืนเท่าใด |
| A | 455 Ns |
| B | 500 Ns |
| C | 550 Ns |
| D | 5000 Ns |
| E | 5500 Ns |
ตอบ (A)
พิจารณาที่จุดศูนย์กลางมวล เนื่องจากกระสุนมีมวลมากเมื่อเทียบกับนักบิน จึงต้องคิดด้วยความระมัดระวัง
เนื่องจากแรงดลที่ส่งออกมาคือ โมเมนตัมสุดท้ายของนักบิน
ให้นักบินมีมวล m1 มีความเร็วสุดท้ายเป็น v1 และตัวปืนมีมวล m2 มีความเร็วสุดท้ายเป็น v2
จากกฎการอนุรักษ์โมเมนตั้มจะได้
พิจารณาที่จุดศูนย์กลางมวล เนื่องจากกระสุนมีมวลมากเมื่อเทียบกับนักบิน จึงต้องคิดด้วยความระมัดระวัง
เนื่องจากแรงดลที่ส่งออกมาคือ โมเมนตัมสุดท้ายของนักบิน
ให้นักบินมีมวล m1 มีความเร็วสุดท้ายเป็น v1 และตัวปืนมีมวล m2 มีความเร็วสุดท้ายเป็น v2
จากกฎการอนุรักษ์โมเมนตั้มจะได้
\(\rm m_1v_1 + m_2v_2 = 0\)
และความเร็วสัมพัทธ์เท่ากับ ( สมมุติให้ v1 > 0 )
\(\rm v_r = v_1 – v_2\)
นำไปแทนค่าจะได้
\(\begin{align*}
{{\rm{m}}_{\rm{1}}}{{\rm{v}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{(}}{{\rm{v}}_{\rm{1}}}-{{\rm{v}}_{\rm{r}}}) &= 0\\
{{\rm{m}}_{\rm{1}}}{{\rm{v}}_{\rm{1}}} &= \frac{{{{\rm{m}}_{\rm{1}}}{{\rm{m}}_{\rm{2}}}}}{{{{\rm{m}}_{\rm{1}}} + {{\rm{m}}_{\rm{2}}}}}{{\rm{v}}_{\rm{r}}}
\end{align*}\)
ดังนั้น J = m1v1 = 455 Ns| 24. | นักบินอวกาศมวล 100 kg พกปืนที่บรรจุกระสุนขนาดใหญ่ไว้ 10 kg ตัวปืนและชุดนักบินมีมวลน้อยมาก เมื่อเหนี่ยวไกกระสุนจะพุ่งออกด้วยอัตราเร็วสัมพัทธ์ 50 m/s เทียบกับนักบิน หากก่อนหน้านี้นักบินอวกาศมาด้วยความเร็ว 10 m/s (วัดในกรอบอ้างอิงหนึ่ง) แล้วเขาต้องการยิงปืน เพื่อให้ความเร็วของเขาเปลี่ยนไปจากเดิมเป็นมุมที่มากที่สุดเมื่อเทียบกับทิศเดิม (วัดในกรอบอ้างอิงเดียวกัน) แล้วขนาดของมุมที่มากที่สุดเท่ากับข้อใด (คำแนะนำ: ลองวาดภาพประกอบดู) |
| A | 24.4° |
| B | 26.6° |
| C | 27.0° |
| D | 30.0° |
| E | 180.0° |
ตอบ (C)
โมเมนตัมสุดท้ายของนักบินจะเท่ากับผลรวมของโมเมนตัมเริ่มต้นกับแรงดลที่กระทำกับนักบิน
โดยโมเมนตัมเริ่มต้นของนักบินเท่ากับ
θ จะมากที่สุด เมื่อเวกเตอร์ \(\overrightarrow {{{\rm{p}}_{\rm{f}}}}\) สัมผัสกับวงกลม
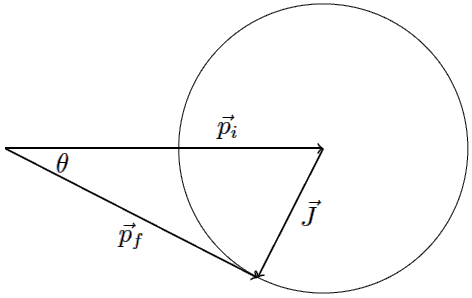ดังนั้น ค่า θ มากสุดเท่ากับ
โมเมนตัมสุดท้ายของนักบินจะเท่ากับผลรวมของโมเมนตัมเริ่มต้นกับแรงดลที่กระทำกับนักบิน
โดยโมเมนตัมเริ่มต้นของนักบินเท่ากับ
\(\rm P_i = (100 ~kg)(10 ~m/s) = 1000 ~kg\cdot m/s\)
และแรงดลที่เกิดขึ้นจะเป็นค่าค่าหนึ่งที่มีขนาดเล็กกว่าแรงดลที่นักบินอวกาศได้รับจากปืน (455 Ns) (สังเกตว่า แรงดลจะเท่ากับทุกแรงเฉื่อยในกรอบอ้างอิงต่างๆ) และโมเมนตัมสุดท้ายของนักบินจะถูกจำกัดอยู่ภายในวงกลมด้านล่าง
\({\rm{\theta = arcsin}}\dfrac{{\rm{J}}}{{{{\rm{p}}_{\rm{i}}}}}{\rm{ = 27}}{\rm{.}}{{\rm{0}}^ \circ }\)
| 25. | ปล่อยกล่องมวล m จากหยุดนิ่ง ให้ลงมาตามทางลาดโดยไม่มีแรงเสียดทาน ที่ความสูง h1 จากฐานของทางลาด เมื่อเลื่อนมาถึงฐานทางลาดแรกมันจะเลื่อนขึ้นทางลาดที่สอง โดยสัมประสิทธิ์แรงเสียดทานของกล่องกับทางลาดที่สองเท่ากับ μk ถ้าทั้งสองทางลาดทำมุม θ กับแนวนอน แล้วความสูง h2 ที่วัดจากฐานของทางลาดที่สองที่ทำให้กล่องขึ้นไปได้ เท่ากับข้อใด |
| A | h2 = (h1 sinθ) / (μk cosθ + sinθ) |
| B | h2 = (h1 sinθ) / (μk + sinθ) |
| C | h2 = (h1 sinθ) / (μk cos2 θ + sinθ) |
| D | h2 = (h1 sinθ) / (μk cos2 θ + sin2 θ) |
| E | h2 = (h1 cosθ) / (μk sinθ + cosθ) |
ตอบ (A)
ใช้หลักการของงานและพลังงาน
ใช้หลักการของงานและพลังงาน
