หัวข้อฟิสิกส์ทั้งหมด
| 1. | เลนส์เว้าความยาวโฟกัสขนาด 20 cm วางชิดกันกับกระจกราบ ลำแสงขนานตกกระทบจากทางซ้าย จะให้ภาพสุดท้ายอยู่ที่ใด (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 12 ส.ค. 2547)  |
ตอบ 20
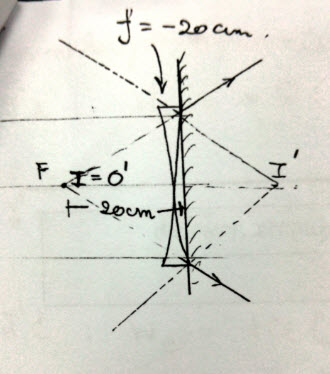เนื่องจาก แสงจะกระจายออกเมื่อผ่านเลนส์เว้า หากนำกระจกราบมาวางชิดเลนส์อีกด้านแสงจะถูกกระจกสะท้อนกลับไปในลักษณะดังภาพ จึงทำให้เสมือนกับมีแนวแสงตัดกันที่ I′ เป็นระยะ 20 cm หลังกระจกราบ
| 2. | มองวัตถุ O ผ่านแผ่นแก้วดรรชนีหักเห µ หนา t ในแนว θ องศากับเส้นตั้งฉากผิวแก้วเห็นภาพ I อยู่ที่ผิวล่างของแผ่นแก้วพอดีวัตถุอยู่ใต้ผิ้วแก้วเป็นระยะทางเท่าไร (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 8 ก.ย. 2545)  |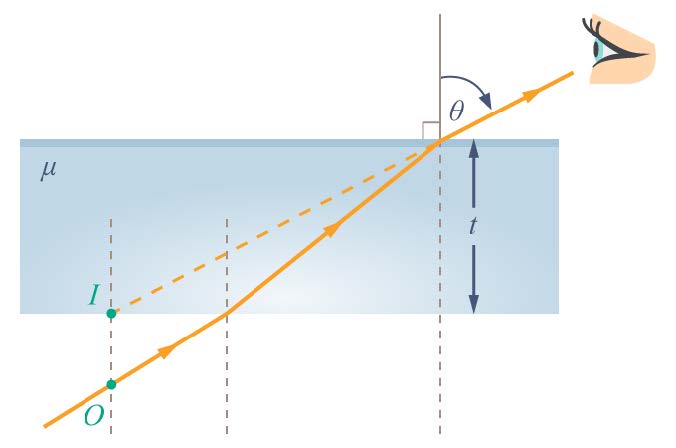
ตอบ \(t\left[1-\dfrac{\tan\left(\sin^{-1}\times\dfrac{\sin\theta}{\mu}\right)}{\tan\theta}\right]\)
| 3. | จงหาค่าของมุม ϕ ที่แนวแสงออกทำกับแนวแสงเข้า (ในเรื่องรุ้งปฐมภูมิ) ตอบติดสัญลักษณ์ θ และดรรชนีหักเห μ ของน้ำ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2554)  |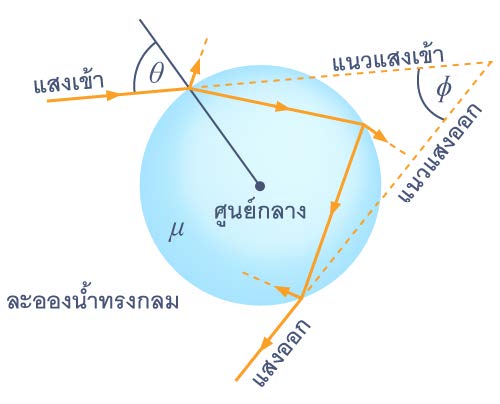
| 4. | พิจารณาทรงกลมโปร่งใสรัศมี R ลูกหนึ่ง เมื่อฉายลำรังสีขนานใกล้แกน (ขนานกับเส้นผ่านศูนย์กลางทรงกลมเส้นหนึ่ง และอยู่ใกล้กับเส้นผ่านศูนย์กลางนั้นมาก ๆ ปรากฎว่าแสงถูกโฟกัสไปผ่านที่จุด P ซึ่งเป็นจุดบนผิวทรงกลมที่ฝั่งตรงข้ามกับที่แสงเข้าพอดี จงหาว่าวัสดุที่ใช้ทำทรงกลมนี้มีดรรชนีหักเหของแสงเท่าใด กำหนดว่าสำหรับมุม θ เล็ก ๆ ในหน่วยเรีเดียน sinθ ≈ θ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550)  |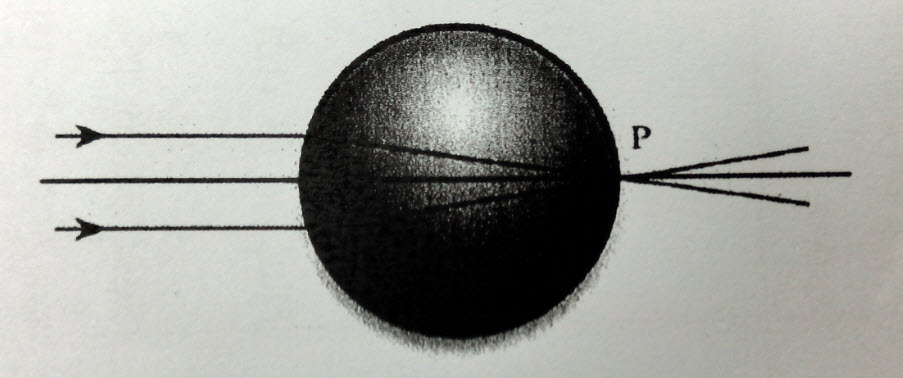
| 5. | เลนส์นูนความยาวโฟกัสขนาด 12 cm และเลนส์เว้าความยาวโฟกัสขนาด 10 cm วางอยู่บนแกนเดียวกัน โดยที่เลนส์นูนอยู่ทางซ้ายมือของเลนส์เว้าและอยู่ห่างกัน 10 cm วางวัตถุไว้ทางซ้ายมือของเลนส์นูนที่ระยะห่าง 48 cm จงหาตำแหน่ง กำลังขยาย ลักษณะภาพ (หัวตั้งหรือหัวกลับ จริงหรือเสมือน) ของภาพสุดท้ายของวัตถุสว่างนี้ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 6. | f1 , f2 เป็นขนาดของความยาวโฟกัสของเลนส์นูนเเละเลนส์เว้าตามลำดับ จะต้องวางเลนส์เว้าห่างจากเลนส์นูนเป็นระยะเท่าไหร่ (จึงจะทำให้ลำแสงออกขนานด้วย) ลำแสงออกมีความเข้มของแสงเป็นกี่เท่าของลำแสงเข้า (ก่อนเข้าเลนส์นูน, ไม่คำนึงถึงการดูดกลืนแสงในเนื้อสารของเลนส์) ต่อไปยกเลิกเงื่อนไขที่ว่าลำแสงออกเป็นลำขนาน, เลื่อนเลนส์เว้ามาประกบชิดเลนส์นูน แสงจะตัดกันบนแกนมุขสำคัญที่จุดห่างจากเลนส์คู่เป็นระยะทางเท่าไร และบอกด้วยว่าตัดทางด้านซ้ายหรือขวาของเลนส์คู่ (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 1 ก.ย. 2556)  |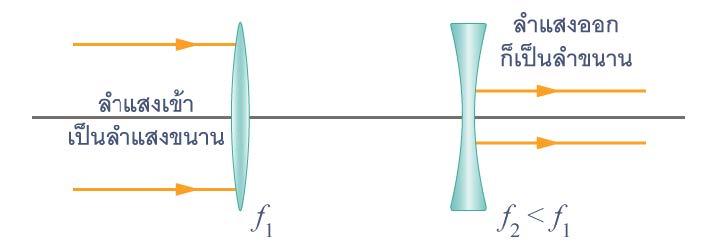
ตอบ
1) วางเลนส์เว้าห่างเลนส์นูนเป็นระยะ \(\rm f_1 − f_2\)
2) ลำแสงออกมีความเข้มของแสงเป็น \(\rm \left(\dfrac{f_2}{f_1}\right)^2\) เท่าของลำแสงเข้า
3) แสงจะตัดกันที่ระยะ \(\rm \left(\dfrac{f_1f_2}{f_1-f_2}\right)\) ทางซ้ายของเลนส์นูน
1) วางเลนส์เว้าห่างเลนส์นูนเป็นระยะ \(\rm f_1 − f_2\)
2) ลำแสงออกมีความเข้มของแสงเป็น \(\rm \left(\dfrac{f_2}{f_1}\right)^2\) เท่าของลำแสงเข้า
3) แสงจะตัดกันที่ระยะ \(\rm \left(\dfrac{f_1f_2}{f_1-f_2}\right)\) ทางซ้ายของเลนส์นูน
| 7. | ปริซึมทำด้วยวัสดุโปร่งใสทีมค่าดรรชนีหักเห n = \(\sqrt3\) จงหาค่าของ θ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2554)  |
| 8. | เมื่อวางวัตถุที่ระยะห่าง a จากเลนส์ (รูป ก.) จะได้ภาพขนาดเป็นสองเท่าของเมื่อวางวัตถุเดียวกันที่ระยะห่าง b (รูป ข.) เลนส์มีความยาวโฟกัสเป็นเท่าใด (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555)  |
| 9. | กำหนดว่าปริซึมทำด้วยแก้วดรรชนีหักเห n มุม θ จะต้องมีค่าอย่างน้อยที่สุดเท่าใด ลำแสงจึงจะไม่ทะลุด้าน AC ออกไป สำหรับค่า θ เล็กที่สุดนี้แนวแสงที่ทะลุด้าน BC ออกมาทำมุมเท่าใดกับแนว \(\rm\overline{PQ}\) (นั้นคือหามุม ϕ ในรูป ϕ = 90° + ฟังก์ชันของ n) (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555)  |
| 10. | จัดกระจกเว้าความยาวโฟคัส + f ให้ห่างจากวัตถุเหมาะ ๆ เพื่อให้ได้ภาพเสมือนหลังกระจกเป็นระยะทาง 17 cm พอดี จะได้กำลังขยายเท่าไร (ตอบติดตัว f ไว้) (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557)  |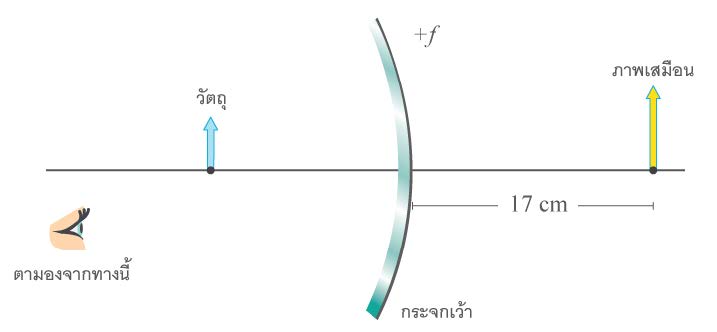
| 11. | จากรูป ถ้าลดระยะวัตถุลงนิดหน่อย (δu เป็นลบ) ระยะภาพจะเพิ่มขึ้นนิดหน่อย (δ เป็นบวก) จงหาความสัมพันธ์ระหว่าง u กับ v เท่านั้นที่จะทำให้ −δu = 4δv (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 6 ก.ย. 2546)  |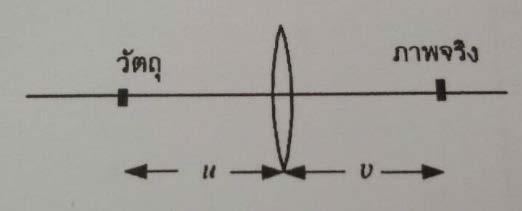
| 12. | ปริซึมรูปสามเหลี่ยมหน้าจั่วมีมุมยอดเป็น α มีลำแสงหักเหผ่านอย่างสมมาตรดังรูป จงหาค่าดรรชนีหักเหของแก้ว ปริซึมในรูปของมุม α, β (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 6 ก.ย. 2546)  |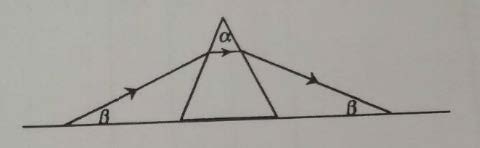
| 13. | ABCD เป็นแท่งแก้วสี่เหลี่ยมผืนผ้ายาว L กว้าง 1 มิลลิเมตร ดรรชนี 1.5 ถ้าให้แสงตกกระทบด้าน AB ที่ตำแหน่งกึ่งกลางพอดีด้วยมุมตกกระทบ θ = arcsin(3/4) พบว่ามีการสะท้อนที่ด้าน AD 3 ครั้งเเละที่ด้าน BC 2 ครั้งแล้วแสงหักเหไปทางด้าน CD ที่ตำแหน่งกึ่งกลางด้านพอดี จงหาระยะทางในแก้วที่แสงเดินทางจากด้าน AB ไปถึงด้าน CD (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 6 ก.ย. 2546)  |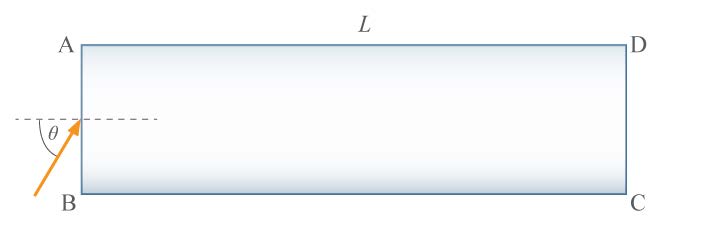
| 14. | P เป็นจุดกึ่งกลางกระจกเว้า O เป็นจุดศูนย์กลางความโค้ง ถ้าหมุนกระจกไปเป็นมุม θ รอบจุด P แสงสะท้อนจะเบนจากแนวเดิมไปเป็นมุมเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 12 ก.ย. 2547)  |
| 15. | 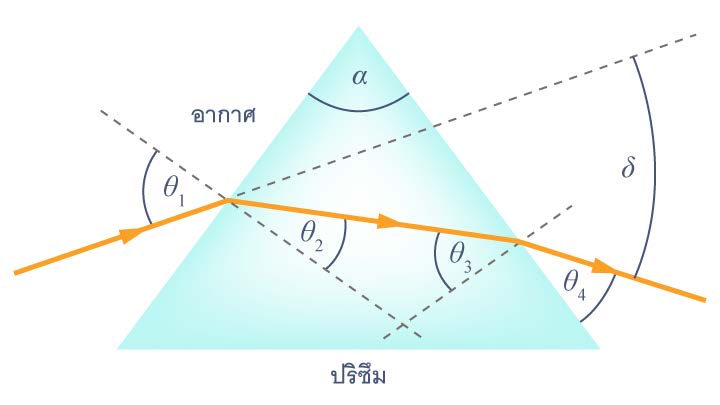 1. จงเขียนความสัมพันธ์ระหว่าง θ2, θ3 เเละมุมยอด α
2. จงเขียนความสัมพันธ์ระหว่าง θ1 , θ4 , δ และ α
3. หากคำนวณถูกต้อง จะได้ δ = θ1 − α + sin−1 (X) โดยที่ sin−1 (X) คือ มุมที่ทำให้ค่า sin ของมุมนั้นเท่ากับ X
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2548)จงหาค่าของ X ในรูปของ n , α และ θ1 |
ตอบ
1) \(\rm α = θ_2 + θ_3\)
2) \(δ = \dfrac{\pi}{2} + \theta_1− \theta_4− α\)
3) \(\rm X= n \sin\left[α − sin^{−1}(\dfrac{1}{n} sin \theta_1)\right]\)
1) \(\rm α = θ_2 + θ_3\)
2) \(δ = \dfrac{\pi}{2} + \theta_1− \theta_4− α\)
3) \(\rm X= n \sin\left[α − sin^{−1}(\dfrac{1}{n} sin \theta_1)\right]\)
| 16. | หลอดไฟเล็กสว่างสองดวงอยู่ห่างกันเป็นระยะ s และทั้งคู่อยู่ห่าง 1.0 m จากฉาก เมื่อเอาเลนส์หนึ่งวงที่ตำแหน่งหนึ่งระหว่างหลอดไฟทั้งสองเเละฉาก ปรากฏว่าเกิดภาพของหลอดไฟคมชัดบนฉากอยู่ห่างกัน 40 mm เมื่อเลนส์ไปมาระหว่างหลอดไฟและฉาก ปรากฏว่าเกิดภาพชัดบนฉากอีกครั้งเมื่อเลนส์อยู่อีกตำเเหน่งหนึ่งที่ตำแหน่ง นี้ภาพหลอดไฟสว่างบนฉากอยู่ห่างกัน 2.5 mm
1. ระยะ s มีค่าเท่าใด
2. เลนส์มีความยาวโฟกัสเท่าใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2548) |
| 17. | ต้องวางเลนส์นูน (L2) ห่างจากเลนส์เว้า (L1) เท่าไร ภาพของวัตถุ O จึงจะเกิดที่อนันต์ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 8 ก.ย. 2545)  |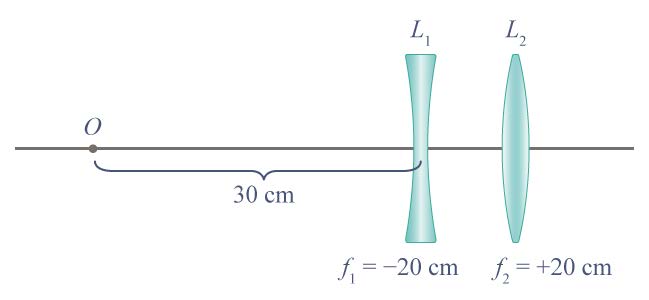
| 18. | 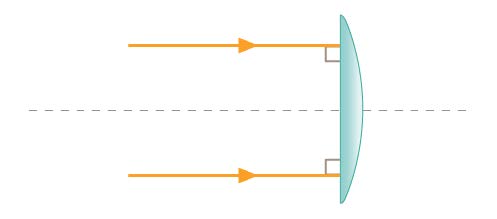 ด้านราบเข้าไป จะเกิดภาพสุดท้ายที่ระยะห่างจากเลนส์ไปทางซ้ายเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) คำแนะนำ สูตรของช่างทำเลนส์บางคือ \(\rm\dfrac{1}{f}=(\mu-1)\left(\dfrac{1}{R_1}+\dfrac{1}{R_2}\right)\)
โดย μ เป็นค่าดรรชนีหักเหของแก้ว และ R1, R2 เป็นรัศมีความโค้ง |
| 19. | รังสีแสงลำหนึ่งตกกระทบกระจกเงาราบบานหนึ่งและสะท้อนไปตกบนฉากซึ่งวางตั้งฉากกับรังสีสะท้อน และอยู่ห่างจากจุดที่แสงตกกระทบกระจกเป็นระยะ 5.00 m เมื่อเบนกระจกไปจากแนวเดิมเป็นมุม α เล็ก ๆ ปรากฏว่าจุดบนฉากเลื่อนไปเป็นระยะ 0.175 m จงหาว่ามุม α มีค่าเท่าใดในหน่วยองศา กำหนดว่าถ้ามุม θ มีค่าน้อย ๆ tan θ ≈ θ ในหน่วยเรเดียน และ π เรเดียน = 180 องศา (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 31 ส.ค. 2551) |
| 20. | แสงในตัวกลาง A ซึ่งมีค่าดรรชนีหักเห 1.50 มีความยาวคลื่นเป็น 500 นาโนเมตร เมื่อเดินทางในตัวกลาง B มีความยาวคลื่นเป็น 450 นาโนเมตร จงหาค่าดรรชนีหักเหของตัวกลาง B |
| 21. | ต้องวางวัตถุที่ตำแหน่งใดหน้ากระจกเว้าจึงจะทำให้ไม่เกิดภาพ |
| 22. | ชายคนหนึ่งมองวัตถุในน้ำตามแนวดิ่ง เห็นภาพของวัตถุสูงจากตำแหน่งของวัตถุ 10 เซนติเมตร ตำแหน่งภาพที่เขามองเห็นอยู่ห่างจากผิวน้ำกี่เซนติเมตร กำหนดให้ดัชนีหักเหของน้ำเท่ากับ \(\frac{4}{3}\) และดัชนีหักเหของอากาศเท่ากับ 1 |
| 23. | รังสีขนานตกกระทบกระจกเงาราบสองแผ่นซึ่งทำมุม θ ต่อกัน ถ้ารังสีสะท้อนทำมุม 30∘ และ 40∘ กับแนวรังสีเดิมดังรูป มุม θ เป็นเท่าใด
 |
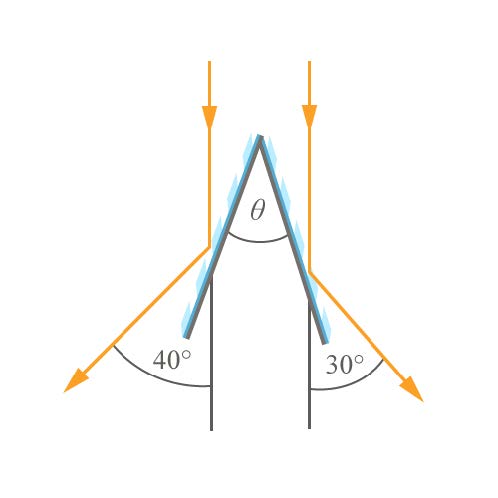| 24. | หากแสงมีมุมตกกระทบในอากาศเท่ากับ 60∘ จะเกิดมุมหักเหในของเหลวชนิด a เท่ากับ 30∘ หากเปลี่ยนตัวกลางเป็นของเหลวชนิด b แล้วให้มุมตกกระทบในอากาศเป็น 45∘ พบว่าได้มุมหักเหเท่าเดิมกับของเหลวชนิด a จงหาว่าค่าดัชนีหักเหในของเหลวชนิด b มีค่าเป็นกี่เท่าของค่าดัชนีหักเหในของเหลวชนิด a |
| 25. | เลนส์นูนมีความยาวโฟกัส 30 cm วางบนแท่งพลาสติกรูปสี่เหลี่ยมที่มีดัชนีหักเหเท่ากับ 1.5 จุดตัดใหม่ของแสงจะอยู่ลึกจากผิวแท่งเป็นระยะเท่าไร (แสงที่ส่องไปนั้นเป็นแสงในแนวตั้งฉากกับผิวแท่งพลาสติก)
 |
| 26. | มุมวิกฤตต่อแสงในของเหลวชนิดหนึ่งมีค่าเท่ากับ 60∘ ความยาวคลื่นของแสงนั้นในของเหลวจะเป็นกี่เท่าของความยาวคลื่นในอากาศ |
| 27. | ฉายแสงสีเขียวความยาวคลื่น 550 นาโนเมตร ให้ตกกระทบตั้งฉากกับด้านหนึ่งของปริซึมสามเหลี่ยมมุมฉากซึ่งวางอยู่ในอากาศ ดังรูป ถ้าลำแสงที่ออกจากปริซึมเบนออกไปจากแนวเดิม 30 องศา จงหาดรรชนีหักเหของปริซึมนี
 |
| 28. | ริ้วแสงสีต่างๆ ที่เห็นบนฟองสบู่เกิดจากปรากฏการณ์ใดเป็นส่วนสำคัญ |
| 29. | ในการส่งพลังงานในรูปคลื่นแม่เหล็กไฟฟ้าโดยใช้แสงเป็นคลื่นพาหะไปตามเส้นใยนำแสง ควรมีเงื่อนไขของมุม θ อย่างไร
 |
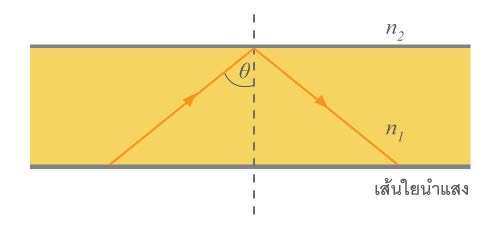| 30. | เลนส์เว้าความยาวโฟกัส 10 เซนติเมตร 2 อัน และเลนส์นูนความยาวโฟกัส 20 เซนติเมตร หนึ่งอันวางรับแสงอาทิตย์ดังรูป ถ้าลำแสงสุดท้ายหลังจากผ่านเลนส์ทั้งสามเป็นลำแสงขนาน a จะมีค่าเท่าใด
 |
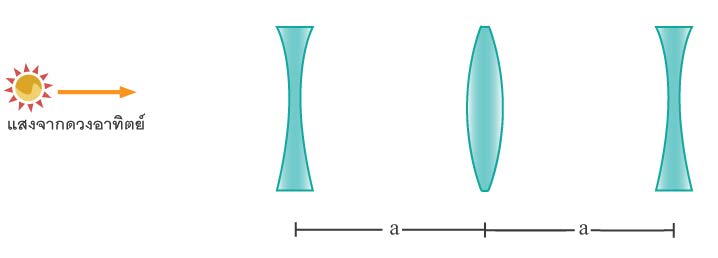| 31. | วัตถุอยู่ห่างจากเลนส์เว้า (ความยาวโฟกัส 10 เซนติเมตร) เป็นระยะทาง 10 เซนติเมตรทางซ้ายมือ และมีกระจกเวา้ (ความยาวโฟกัสเซนติเมตร) อยู่ห่างจากเลนส์เว้า 15 เซนติเมตรทางด้านขวามือแล้วภาพจะอยู่ที่เดียวกับวัตถุ ความยาวโฟกัสของเลนส์เว้ามีค่าเท่าไร
 |
| 32. | ในปรากฏการณ์กระจายของแสง เมื่อแสงขาวจากดวงอาทิตย์ผ่านปริซึม แสงสีใดจะมีมุมหักเหน้อยที่สุด |
| 33. | แว่นขยายอันหนึ่งมีความยาวโฟกัส 4 เซนติเมตร ถ้าต้องการให้แว่นขยายส่องตัวอักษรในหนังสือใหเ้ห็นภาพชัดที่สุดต้องวางหนังสือห่างจากแว่นขยายเท่าไร |
| 34. | ดอกไม้ดอกหนึ่งส่องด้วยแสงสีขาว เมื่อมองผ่านแผ่นกรองแสงสีแดงจะเห็นดอกไม้เป็นสีแดง ถ้ามองผ่านแผ่นกรองแสงสีเขียวจะเห็น เป็นสีเขียวถ้ามองผ่านแผ่นกรองแสงสี เหลืองจะเห็นเป็นสีเหลืองดอกไม้ดอกนี้มีสีอะไร |
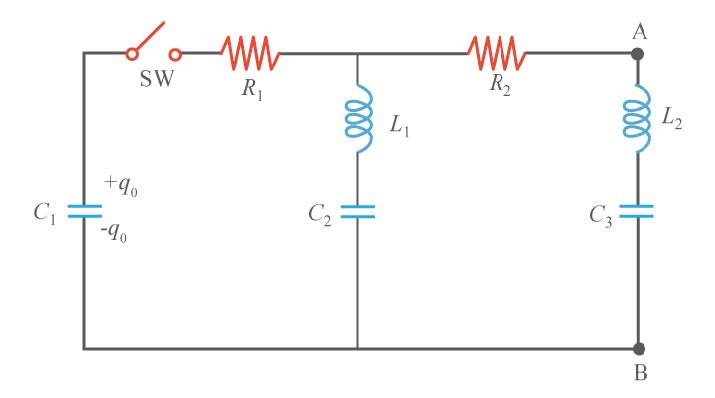
| 35. | หลังจากสับสวิทช์ SW ลงนานแล้ว ความต่างศักย์ระหว่างจุด A กับจุด B มีค่าเป็นเท่าไร ให้เหตุผลอย่างชัดเจน
 |
ตอบ
หลังจากสับ SW ลงนานแล้วกระแสมีค่าเป็นศูนย์และอัตราการเปลี่ยนแปลงของกระแสจึงมีค่าเป็น ศูนย์ด้วย ความต่างศักย์ระหว่าง 2 ปลายของ R และ L จึงเท่ากับศูนย์
ทำให้ได้ว่า
หลังจากสับ SW ลงนานแล้วกระแสมีค่าเป็นศูนย์และอัตราการเปลี่ยนแปลงของกระแสจึงมีค่าเป็น ศูนย์ด้วย ความต่างศักย์ระหว่าง 2 ปลายของ R และ L จึงเท่ากับศูนย์
ทำให้ได้ว่า
\(\rm V_{AB} = V_{C_1} = V_{C_2} = V_{C_3}\)
ดังนั้น
\(\rm V_{AB} = \dfrac{q_2}{C_2}=\dfrac{q_0}{C_1+C_2+C_3}\)
| 36. | จงหาค่าของอัตราส่วนระหว่างประจุใน C เมื่อสวิทช์อยู่ที่ตำแหน่ง ต่อประจุใน C เมื่อสับสวิทช์ไปทที่ตำแหน่ง
 |
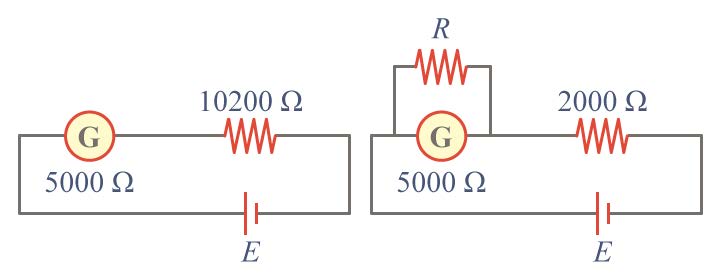
| 37. | พิจารณาวงจรทั้งสองรูปข้างล่าง G เป็นแกลแวนอมิเตอร์ตัวเดียวกันในทั้ง สองรูป E เป็นเซลล์ไฟฟ้าเดียวกันด้วย ความต้านทานภายใต้ของเซลล์ไฟฟ้ามีขนาดน้อยมาก จะต้องใช้ค่าความต้านทาน R เท่าใด จึงจะทำให้แกลแวนอมิเตอร์ชที่เดิมในทั้งสองกรณี
 |
| 38. | พิจารณาวงจรดังรูป
 2) ถ้าสวิตซ์ S ถูกปิดทิ้งไว้นานมากตัวเก็บประจุได้รับการประจุจนเต็ม ก. จงหากระแสไฟฟ้าที่ผ่านตัวต้านทานแต่ละตัว และค่าประจุบนตัวเก็บประจุแต่ละตัว
ข. จากนั้น ณ เวลา t′ = 0 ยกสวิตซ์ขึ้น จงหาค่ากระแสไฟฟ้า (I3kΩ) ที่ผ่านตัวต้านทาน 3.00 kΩ ณ เวลา t′ ใดๆ พร้อมทั้งเขียนกราฟแสดงความสัมพันธ์ระหว่าง I3kΩ นี้และเวลา t′
ค. จงหาเวลา t′ ที่ต้องใช้ในการที่ตัวเก็บประจุจะคายประจุจนเหลือประจุรวมเพียง 1/5 ของค่าเริ่มต้น
(ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 18 ธ.ค. 2554) |
ตอบ
1) \(\displaystyle\rm \dfrac{1}{20μF}\int^t_0i_2dt + (3.0~ kΩ)i_2= (15.0~ kΩ)i_3\)โดย \(\rm i_1 = i_2 + i_3\)
2) ก. \(\rm i_1=i_3=3.3\times10^{-4}~A\)และ \(\rm i_2=0\) และประจุบนตัวเก็บประจุแต่ละตัวเท่ากับ \(4.95\times10^{-5}\)
ข. \(\rm I_{3kΩ} = (2.78 × 10^{-4})e^{\frac{-t}{0.36}s}~ A\) ส่วนกราฟเป็นแบบ exponential decay ธรรมดา
ค. \(\rm t′=0.579~s\)
1) \(\displaystyle\rm \dfrac{1}{20μF}\int^t_0i_2dt + (3.0~ kΩ)i_2= (15.0~ kΩ)i_3\)โดย \(\rm i_1 = i_2 + i_3\)
2) ก. \(\rm i_1=i_3=3.3\times10^{-4}~A\)และ \(\rm i_2=0\) และประจุบนตัวเก็บประจุแต่ละตัวเท่ากับ \(4.95\times10^{-5}\)
ข. \(\rm I_{3kΩ} = (2.78 × 10^{-4})e^{\frac{-t}{0.36}s}~ A\) ส่วนกราฟเป็นแบบ exponential decay ธรรมดา
ค. \(\rm t′=0.579~s\)
| 39. | ในวงจรรูปขวามือ ถ้าต่อ A และ B เท่ากับแหล่งโวลเตจภายนอก ความสัมพันธ์ระหว่าง R1, R2, C1 และ C2 ต้องเป็นอย่างไรกัน จึงจะทำให้จุด a และจุด b มีศักย์เท่ากัน (ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 24 ต.ค. 2552)  |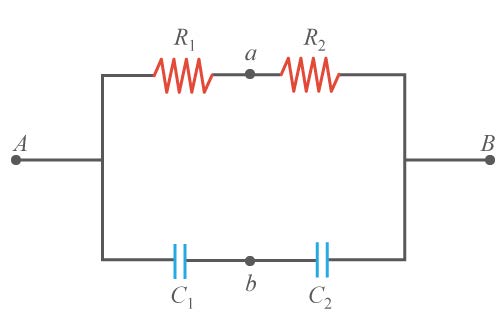
| 40. | จงหาความต่างศักย์ระหว่างจุด a กับจุด b (กำหนดให้ ε1 > ε2)
 |
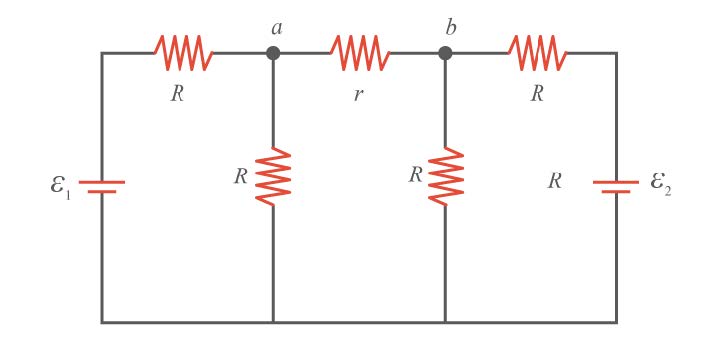| 41. | กำหนดให้ RAB, RBC, RAC แทนค่าความต้านทานสมมูลระหว่างปลาย A กับ B , B กับ C และ A กับ C ตามลำดับ จงหาค่าของอัตราส่วน RAB, RBC, RAC (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 9 ก.ย. 2544)  |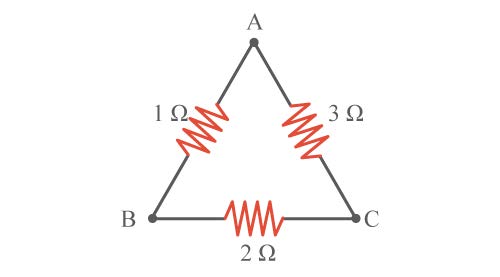
| 42. | In มีค่ากี่แอมแปร์ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)
 |
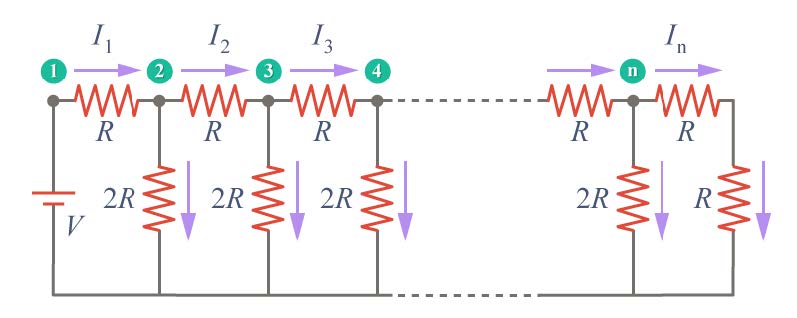| 43. | ลวดตัวนำเส้นหนึ่งมีขนาดไม่เท่ากันตลอดเส้นตอนที่มีขนาดเล็กมีพื้นที่หน้าตัด a และตอนที่มีขนาดใหญ่ มีพื้นที่หน้าตัด A ดังรูป มีกระแสไฟฟ้าไหลผ่านลวดตอนเล็ก i แอมแปร์ กระแสไฟฟ้าที่ไหลผ่านลวดตอนใหญ่จะเป็นเท่าใด
 |
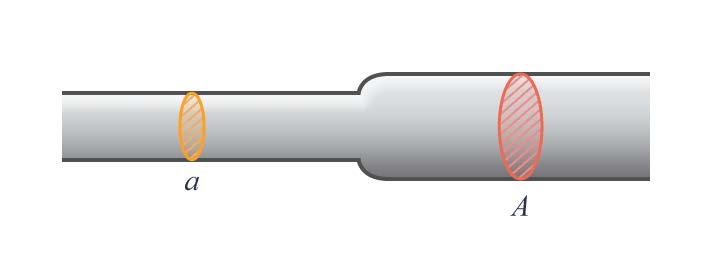| 44. | ในเส้นลวดโลหะขนาดสม่ำเสมอเส้นหนึ่งภายในเวลา t วินาทีมีประจุ +Q1 คูลอมบ์และ −Q2 คูลอมบ์เคลื่อนที่สวนทางกันผ่านพื้นที่หน้าตัดขนาด A ตารางเมตรของเส้น ลวด กระแสไฟฟ้าในเส้น ลวดโลหะนี้คือข้อใด
|
| 45. | กระแสไฟฟ้า I ที่ผ่านเส้นลวดโลหะเส้นหนึ่งสัมพันธ์กับเวลา t ดังกราฟ จงหาปริมาณประจุไฟฟ้าทั้งหมดที่ผ่านพื้นที่หน้าตัดของเส้นลวดโลหะนี้ในช่วง เวลา 0 ถึง 10 วินาที
 |
| 46. | ลวดเส้นหนึ่งยาว ℓ รัศมี r อีกเส้นหนึ่งยาว 2ℓ รัศมี \(\rm\dfrac{r}{2}\)เส้นที่มีความต้านทานสูง มีค่าความต้านทานเป็นกี่เท่าของอีกเส้นหนึ่ง ลวดทั้งคู่ทำจากวัสดุชนิดเดียวกัน |
| 47. | นำลวดโลหะเส้นหนึ่งต่อเข้ากับเซลล์ไฟฟ้าดังรูป พบว่าอัตราการสูญเสียพลังงานในลวดเป็นค่าหนึ่งถ้านำลวดเส้นนี้ไปรีดให้ยาวเพิ่มขึ้นเป็นสองเท่าโดยไม่ตัดเนื้อโลหะออกเลย แล้วนำไปต่อกับเซลล์ไฟฟ้าเซลล์เดิม อัตราการสูญเสียพลังงานไฟฟ้าในลวดเส้นใหม่นี้จะเปลี่ยนแปลงอย่างไร
 |
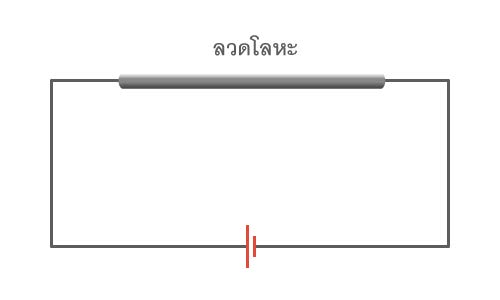| 48. | แบตเตอรี่รถยนต์ลูกหนึ่งมีขนาดเป็น 80 A ⋅ h แล้วหน่วยแอมแปร์-ชั่วโมงนี้เป็นหน่วยของอะไร |
| 49. | ถ้าต้องการนำทองแดงมวล m สภาพต้านทาน ρ มีความหนาแน่น D มาดึงเป็นเส้นลวดขนาดสม่ำเสมอใหมี้ความต้านทาน R จะได้ความยาวของลวดทองแดงมีค่าเท่าใด |
| 50. | ลวดทำความร้อนต่อกับความต่างศักย์ 220 โวลต์จุ่มอยู่ในถ้วยกาแฟที่ทำด้วยฉนวน ถ้วยนี้บรรจุนํ้า 200 กรัม พบว่าทำใหอุ้ณหภูมิของนํ้าเปลี่ยนจาก 20 องศาเซลเซียสไปเป็น 70 องศาเซลเซียสในเวลาครึ่งนาที จงหากระแสไฟฟ้าที่ผ่านลวดนี้ (ความจุความร้อนจำเพาะของนํ้าเป็น 4.2 กิโลจูลต่อกิโลกรัม-เคลวิน) |
| 51. | จากรูป กระแสไฟฟ้า I มีค่าเท่าใด
 |
| 52. | จากวงจรไฟฟ้ากระแสตรงดังแสดงในรูปด้านล่าง จงคำนวณหาค่าความต้านทาน R1 ว่ามีค่าเท่าไหร่ที่ทำให้แรงดันที่จุด AB มีค่าเท่ากับศูนย์โวลต์
 |
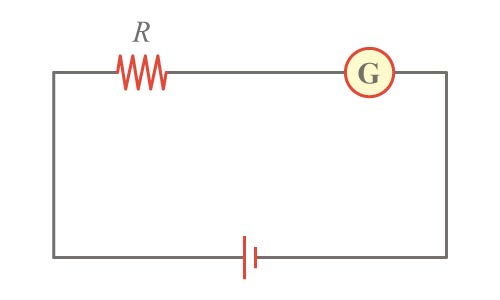
| 53. | แกลแวนอมิเตอร์เครื่องหนึ่ง ขณะที่ต่ออยู่กับวงจรตามรูปพบว่าเข็มชี้เต็มสเกลพอดี เมื่อนำตัวต้านทานอีกหนึ่งตัวค่า 1, 500 โอห์มมาต่อแบบอนุกรมให้กับวงจรพบว่า เข็มของมิเตอร์ชี้ที่ \(\dfrac{1}{4}\)ของสเกล ถ้าแรงเคลื่อนไฟฟ้าเกิดจากเซลล์ที่มีความต้านทานภายในต่ำมากและความต้า้ นทาน ของแกลแวนอมิเตอร์น้อยมาก ตัวต้านทาน R มีค่าความต้านทานเท่าไร
 |
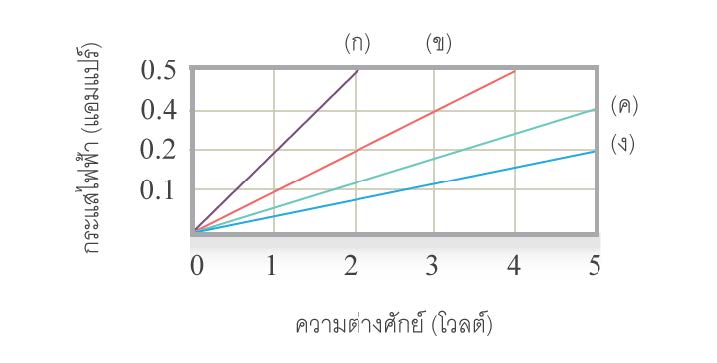
| 54. | กราฟข้างล่างนี้ แสดงถึงความสัมพันธ์ระหว่างความต่างศักย์ระหว่างปลายและกระแสไฟฟ้าที่ไหล ผ่านตัวต้านทาน 4 ตัว คือ ก, ข, ค, งตัวต้านทานที่มีค่าความต้านทานสูงสุดคือ
 |
| 55. |  |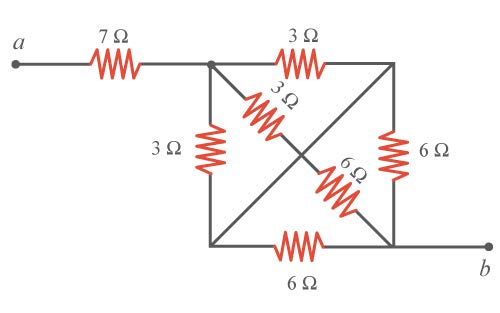
| 56. | กัลวานอมิเตอร์ตัวหนึ่งมีความต้านทาน 200 โอห์ม รับกระแสได้สูงสุด 10 มิลลิแอมแปร์นำกัลป์วานอมิเตอร์ดังกล่าวมาดัดแปลงเป็นโอห์มมิเตอร์ดังรูป ก่อนการใช้งานต้องนำปลาย X และ Y มาแตะกันและปรับค่า R0 เป็นกี่โอห์ม
 |
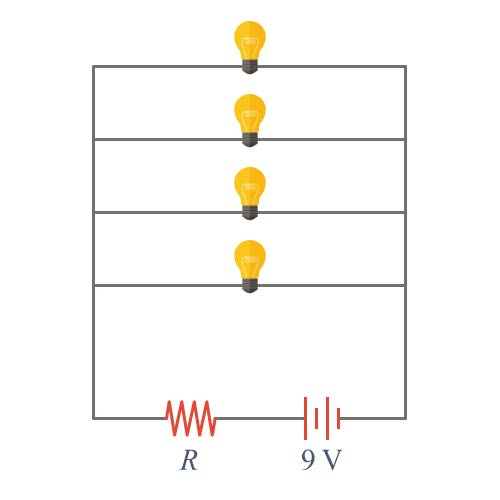
| 57. | ถ้านำหลอดไฟขนาด 0.5 แอมแปร์ 2 โวลต์จำนวน 4 ดวงมาต่อขนานกันแล้วนำไปต่อเข้ากับแรงเคลื่อน 9 โวลต์และความต้านทาน R ดังรูป R จะต้องมีค่าเท่าใดที่ทำให้หลอดไฟทั้ง 4 เปล่งสว่างปกติ (ในหน่วยโอห์ม)
 |
| 58. | วางประจุบนผิวของทรงกลมตัวนำที่อยู่โดดเดี่ยวรัศมี 2.7 cm ความหนาแน่นประจุเชิงผิวมีค่าสม่ำเสมอและมีค่าเป็น 6.9 × 10−6 C/m2 แล้วทรงกลมนี้มีประจุทั้งหมดเท่าไร |
| 59. | โลหะทรงกระบอกยาวปลายมนเป็นกลางทางไฟฟ้า ตั้งอยู่บนฐานที่เป็นฉนวน ถ้านำประจุบวกขนาดเท่ากันมาใกล้ปลายทั้งสองข้างพร้อมกัน โดยมีระยะจากปลายเท่าๆ กัน ตามลำดับ การกระจายของประจุบนส่วน A ส่วน B และส่วน C ของทรงกระบอกเป็นอย่างไร
 |
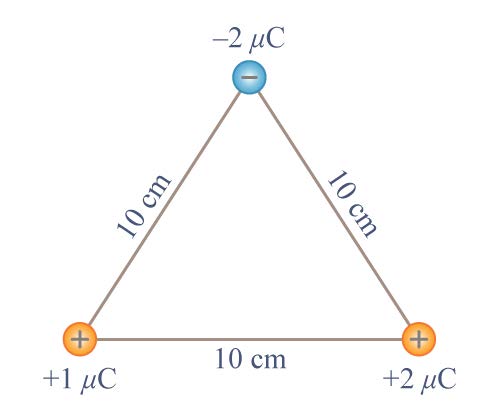
| 60. | สามเหลี่ยมด้านเท่า ยาวด้านละ 10 cm ที่จุดยอดของสามเหลี่ยมมีประจุ +1 μC, − 2 μC และ +2 μC ดังรูป จงหาแรงลัพธ์ที่กระทำต่อประจุ +2 μC
 |
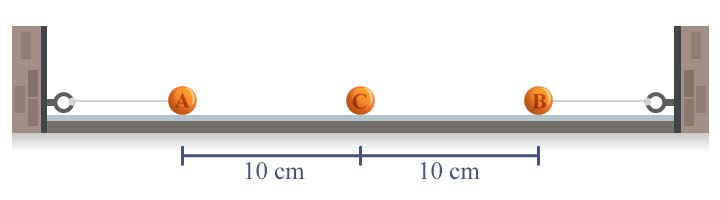
| 61. | ลูกพิท A และ B ซึ่งมีประจุ 0.8 ไมโครคูลอมบ์ เท่ากัน ผูกติดกับด้ายเบาซึ่งติดอยู่กับผนังคนละฝั่ง และวางอยู่บนพื้นราบลื่น ที่เป็นฉนวน ต่อมานำลูกพิท C ซึ่งมีประจุเป็น 1.6 ไมโครคูลอมบ์ วางระหว่างลูกพิท A และ B ปรากฎว่าด้ายที่ผูกลูกพิททั้งสองตึง และลูกพิท C วางนิ่งอยู่ วัดระยะระหว่างลูกพิท A กับ C และ B กับ C ได้ 10 เซนติเมตร ดังรูป อยากทราบว่าแรงตึงเชือกของด้ายทีผูกติดกับลูกพิท A มีค่าเท่าไร
 |
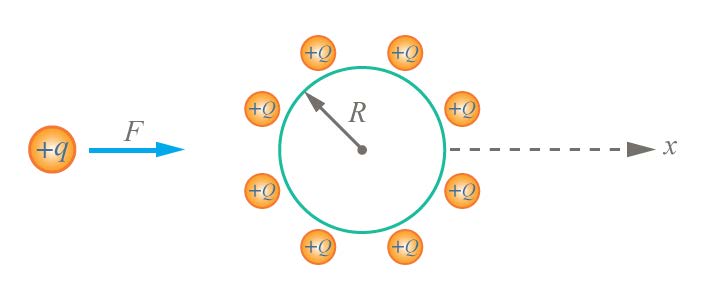
| 62. | ประจุ +Q กระจายสม่ำเสมออยู่บนผิวทรงกลมรัศมี R สมมติมีแรงภายนอกกระทำบนประจุ +q เพื่อให้ประจุ +q เคลื่อนที่เป็นเส้นตรงในแนวแกน x ด้วยความเร็วคงที่ผ่านจุดศูนย์กลางทรงกลมถ้ากำหนดให้ทิศทางของแรงไปทาง +x เป็นบวก และทิศไปทาง – x เป็นลบ กราฟระหว่างแรงภายนอกกับระยะ x จะเป็นแบบใด
 |
| 63. | อนุภาคมวล m ประจุเป็นบวกเคลื่อนที่ภายใต้แรงโน้มถ่วงและแรงไฟฟ้าจากสนามไฟฟ้า E ซึ่งชี้ขึ้นในแนวดิ่งถ้าอนุภาคตกด้วยความเร่ง a จงหาค่าของประจุของอนุภาค |
| 64. | ยิงอิเล็กตรอนมวล me ประจุ −e ในแนวระดับเข้ากึ่งกลางระหว่างแผ่นประจุไฟฟ้าคู่ขนานความต่างศักย์ 4 โวลต์ แต่ละแผ่นยาว 60 เซนติเมตร และวางห่างกัน 30 เซนติเมตร ดังรูป อิเล็กตรอนต้องมีพลังงานจลน์กี่อิเล็กตรอนโวลต์ (eV) จึงจะชนที่ปลายขอบแผ่นประจุไฟฟ้าด้านบนพอดี (ไม่คิดผลของแรงโน้มถ่วงของโลก)
 |
| 65. | อนุภาคแอลฟา อนุภาคบีตา รังสีแกมมา เมื่อเคลื่อนที่ในสนามแม่เหล็ก ข้อใดไม่เกิดการเบน |
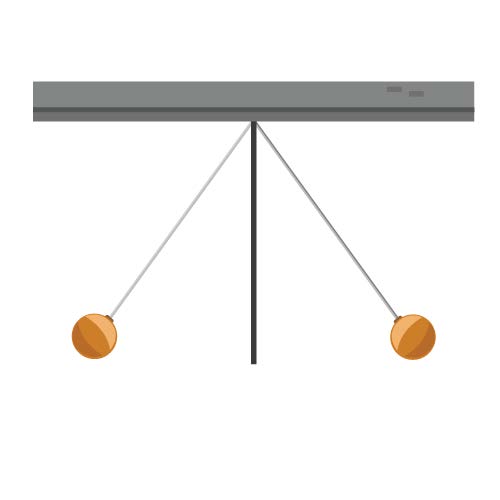
| 66. | ลูกพิธ 2 ลูก มีมวลเท่ากัน และแต่ละลูกมีประจุไฟฟ้าเท่ากันทั้งคู่ แขวนจากจุดเดียวกันด้วยเอ็นที่เป็นฉนวนยาว 10 เซนติเมตร ลูกพิธทั้งสองกางออกทำมุม 37 องศากับแนวดิ่งแรงระหว่างประจุไฟฟ้าที่กระทำต่อลูกพิธแต่ละลูกเป็นกี่เท่าของแรงโน้มถ่วง ที่กระทำต่อลูกพิธนั้น (กำหนดให้ \(\sin37°=\dfrac{3}{5}\))
 |
| 67. | ในการทดลองเรื่องหยดน้ำมันของมิลลิแกน ถ้าใช้ความต่างศักย์ไฟฟ้า 100 โวลต์ หยดน้ำมันมีมวล 8 × 10-16 กิโลกรัม ระยะห่างระหว่างแผ่นขั้วโลหะเท่ากับ 0.8 เซนติเมตร ทำให้หยดน้ำมันอยู่นิ่ง หยดน้ำมันได้รับอิเล็กตรอนกี่ตัว |
| 68. | มีประจุ +q วางอยู่บนแกน x ณ ตำแหน่ง x = 0 และประจุ −2q วางอยู่ ณ ตำแหน่ง x = +d ต้องการทราบว่า ณ ตำแหน่ง x มีค่าเท่าใดที่ศักย์ไฟฟ้าเป็นศูนย์
 |
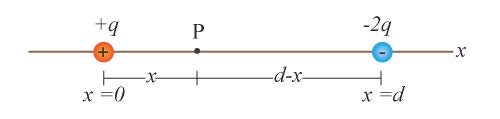| 69. | แผ่นโลหะขนาน 2 แผ่นวางห่างกันเป็นระยะ d และมีประจุไฟฟ้าชนิดตรงข้าม อิเล็กตรอนที่หลุดจากแผ่นลบจะวิ่งด้วยความเร่ง a ไปยังแผ่นบวก ถ้าให้ m และ e เป็นมวลและประจุอิเล็กตรอนตามลำดับ แผ่นโลหะทั้งสองมีความต่างศักย์เป็นเท่าไร |
| 70. | ถ้าศักย์ไฟฟ้าที่ผิวโลหะทรงกลมรัศมี R มีค่าเท่ากับ Vo จงหาสนามไฟฟ้าที่ระยะ 2R จากจุดศูนย์กลางของทรงกลม |
| 71. | เป็นแผ่นไม้ซึ่งลอยน้ำได้ (รูป ก.) M เป็นก้อนวัตถุซึ่ง หนักกว่าน้ำ เมื่อนำ M ไปห้อยติดใต้ B ทำให้ B จมลงไปจากเดิมเป็นระยะทาง d (รูป ข.) แต่ถ้านำ M วางทับ B จะทำให้ B จมลงไปอีกเป็นระยะทาง h (รูป ค.) จงหาค่าความถ่วงจำเพาะของ M (นั่นคือ หาว่า M มีความหนาแน่นเป็นกี่เท่าของความหนาแน่นของน้ำ) (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2551)  |
| 72. | ถังน้ำทรงกระบอกรัศมี R ความสูง H ใส่น้ำจนเต็มเมื่อตั้งดิ่งจากนั้นจึงจับเอียงทำมุม θ กับแนวดิ่งจะเหลือน้ำในถังเป็นปริมาตรเท่าใด (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2551)  |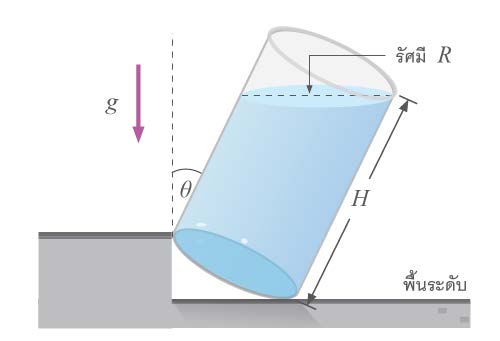
| 73. | ถังทรงกระบอกพื้นที่ภาคตัดขวาง A ตั้งดิ่งมีนํ้าบรรจุ m เป็นวัตถุที่มีความหนาแน่นครึ่งหนึ่งของน้ำ ระดับน้ำในถังจะสูงขึ้น จากเดิมเท่าใดเมื่อนำ m ไปลอยอิสระที่ผิวน้ำ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 31 ส.ค. 2555)  |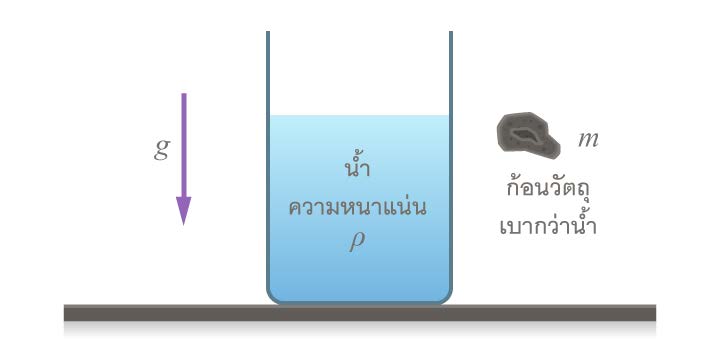
| 74. | หลอดรูปตัวยูขนาดใหญ่ปลายเปิดฐานยาว l ใส่น้ำและตรึงติดรถที่กำลังเคลื่อนที่ด้วยความเร่ง a ระดับน้ำในแขนซ้ายของหลอดจะสูงกว่าในแขนขวาอยู่เท่าใด (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 3 ก.ย. 2549)  |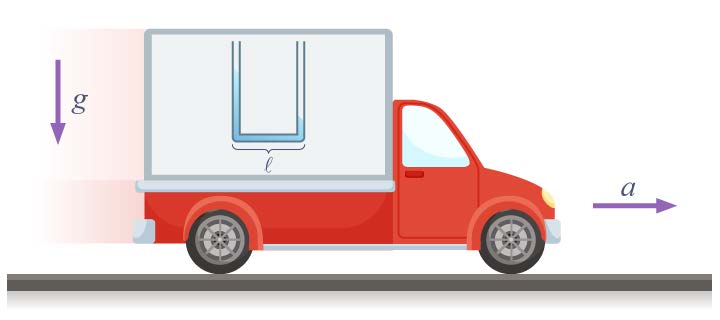
| 75. | ความดันเลือดสูงสุดของคน ๆ หนึ่งเมื่อวัดด้วยเครื่องมือที่ใช้ความสูงของปรอทวัด พบว่าลำปรอทสูง 120 มิลลิเมตร ถ้าเปลี่ยนไปใช้น้ำแทนปรอท น้ำจะขึ้นไปสูงเท่าใด กำหนดว่าความหนาแน่นของปรอทและน้ำมีค่า 13600 kg/m3 และ 1000 kg/m3 ตามลำดับ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2548) |
| 76. | ท่อพื้นที่ภาคตัดขวาง A พ่นลำน้ำสวยงามขึ้นในแนวดิ่ง กระทบลูกบอลใหญ่มวล m ทำให้ลอยอยู่ในสมดุลที่ความสูง h จากปากท่อโดยที่น้ำลอยอยู่ในสมดุลที่ความสูง h จากปากท่อโดยที่น้ำที่กระทบลูกบอลแผ่ออกจากใต้บอลตั้งฉากกับแนวเดิม จะต้องเพิ่มความเร็วต้นของลำน้ำเป็นกี่เท่าค่าเดิมจึงจะทำให้ลูกบอลเลื่อนสูงขึ้นจากปากท่อเป็น 2h (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2553)  |
ตอบ \(\rm\sqrt{\dfrac{2+\sqrt{4+\left(\dfrac{m}{\rho Ah}\right)^2}}{1+\sqrt{1+\left(\dfrac{m}{\rho Ah}\right)^2}}}\) เท่าจากเดิม
| 77. | ในรูปซ้ายมือ ท่อใหญ่มีพื้นที่ตัดขวางเป็น 2 เท่าของท่อเล็กหลอดรูปตัวยูบรรจุของเหลว ที่มีความหนาแน่น ρ2 ของไหล (คนละชนิดกับในหลอดตัวยู) ในท่อมีความหนาแน่น ρ1 ความเร็วของมันในท่อใหญ่เป็น v ค่าผลต่าง h ของระดับของเหลวในหลอดตัวยูเป็นเท่าใดให้ตอบในรูปของ ρ1, ρ2, g และ v (ข้อสอบปลายค่าย 1 ศูนย์เตรียม 28 ต.ค. 2543)  |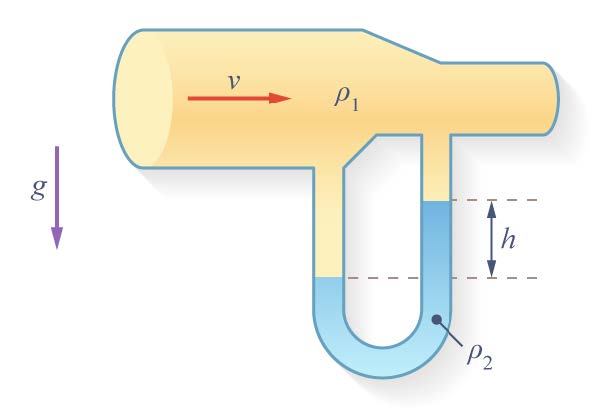
| 78. | จงประมาณกำลัง (พลังงานที่ใช้ต่อเวลา) ที่จำเป็นซึ่งจะทำให้เฮลิคอปเตอร์ มวล 500 kg ที่มีใบพัดยาว 2.5 m ลอยนิ่งอยู่ในอากาศได ้ให้ใช้ความหนาแน่นอากาศ = 1.29 kg/m3 แนะ: เฮลิคอปเตอร์ใช้กำลังในการเป่าอากาศใต้ปีกลงมา และให้สมมติว่าใบพัดเป่าอากาศซึ่งเดิมอยู่นิ่งให้เคลื่อนที่ลงมาด้วยอัตราเร็วคงที่เท่ากันหมด (ข้อสอบปลายค่าย 1 ศูนย์เตรียม 28 ต.ค. 2543) |
| 79. | ภาชนะพื้นที่ตัดขวางสม่ำเสมอ A มีน้ำความหนาแน่น ρw บรรจุอยู่ภายใน มีวัตถุรูปลูกบาศก์ด้านยาวด้านละ d ความหนาแน่น ρ(< ρw) จมอยู่ใต้น้ำ โดยมีเชือกผูกติดกับก้นภาชนะดึงไว้ ถ้าเชือกขาดและวัตถุลูกบาศก์ลอยขึ้นสู่ผิวน้ำโดยมีหน้าลูกบาศก์ขนานกับผิวน้ำในแนวระดับ จงหาว่าระดับน้ำในภาชนะลดลงหรือเพิ่มขึ้น เท่าใดจากตอนที่เชือกยังไม่ขาด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 80. | แผ่นโลหะบางรูปสี่เหลี่ยมจัตุรัสซึ่งแต่ละด้านยาว 5 เซนติเมตร เมื่อนำแผ่นโลหะไปลอยบนผิวน้ำพบว่าแผ่นโลหะสามารถลอยอยู่บนน้ำได้ ้ถ้าเหตุการณ์ดังกล่าวเป็นผลมาจากแรงตึงผิวเพียงอย่างเดียว จงคำนวณหามวลที่มากที่สุดที่เป็นไปได้ของแผ่นโลหะนี้ กำหนดให้ความตึงผิวของน้ำมีค่า 0.070 นิวตันต่อเมตร |
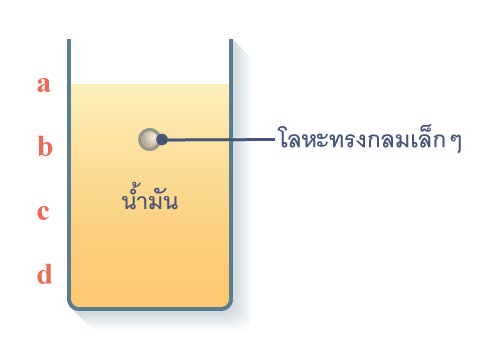
| 81. | เมื่อหย่อนลูกโลหะทรงกลมเล็ก ๆ ลงในทรงกระบอกที่ทำด้วยแก้วโดยมีน้ำมันบรรจุอยู่ ถ้าระยะ ab = bc = cd แล้วการเคลื่อนที่ของลูกโลหะในช่วงใดที่น่าจะมีความเร่ง และมีความเร็วคงตัว
 |
ตอบ
สำหรับมวลน้อยหน่อย : ช่วง a ถึง b จะมีความเร่ง แล้วต่อจากนั้นความเร็วจะคงตัว
สำหรับมวลมากหน่อย : ช่วง a ถึง c จะมีความเร่ง แล้วต่อจากนั้นความเร็วจะคงตัว
สำหรับมวลน้อยหน่อย : ช่วง a ถึง b จะมีความเร่ง แล้วต่อจากนั้นความเร็วจะคงตัว
สำหรับมวลมากหน่อย : ช่วง a ถึง c จะมีความเร่ง แล้วต่อจากนั้นความเร็วจะคงตัว
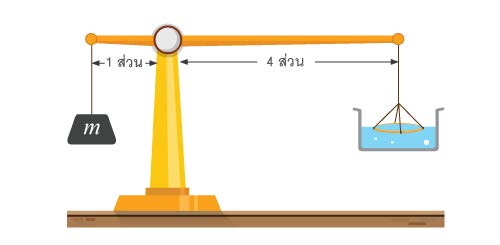
| 82. | ในการทดลองหาความตึงผิวของของเหลวอย่างหนึ่งถ้าวงแหวนที่ใช้มีเส้นรอบวงยาว 25 ซม. จะต้องแขวนมวล 50 กรัม เพื่อทำให้คานอยู่ในสมดุล ขณะที่ห่วงวงแหวนยังสัมผัสผิวของเหลว และเมื่อค่อยๆ เพิ่มมวลจนห่วงวงแหวนหลุดจากผิวของเหลวพบว่าต้องใช้มวล m ทั้งหมด 62.6 กรัม ความตึงผิวของของเหลวที่ใช้ทดลองมีค่าเท่าใด
 |
| 83. | ลูกปิงปองกำลังลอยขึ้นจากก้นสระน้ำในขณะที่ลูกปิงปองมีอัตราเร็วไม่คงที่ผลของความหนืดของน้ำจะทำให้อัตราเร็วและอัตราเร่งของลูกปิงปองมีการเปลี่ยนแปลงอย่างไร |
| 84. | เครื่องอัดไฮโดรริกใช้สำหรับยกรถยนต์เครื่องหนึ่งใช้น้ำมันที่มีความหนาแน่น 1000 กิโลกรัมต่อลูกบาศก์เมตร พื้นที่ของลูกสูบใหญ่และลูกสูบเล็กมีค่า 1200 ตารางเซนติเมตร และ 30 ตารางเซนติเมตรตามลำดับ ต้องการยกรถยนต์หนัก 1500 กิโลกรัม โดยใช้แรงกด 300 N อยากทราบว่าขณะที่กดลูกสูบเล็กระดับน้ำมันในลูกสูบเล็กอยู่สูงกว่าระดับ น้ำมันในลูกสูบใหญ่เท่าใด |
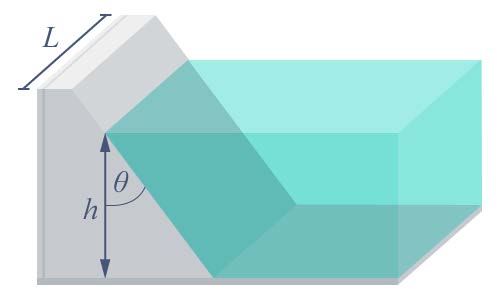
| 85. | เขื่อนแห่งหนึ่งกว้าง ℓ โดยผนังเขื่อนที่รับน้ำเอียงทำมุม θ กับแนวดิ่ง และน้ำมีความหนาแน่นเป็น ρ ถ้าแรงดันเนื่องจากน้ำหนักของน้ำที่กระทำต่อเขื่อนมีค่าเป็น F ระดับน้ำในเขื่อนจะสูงเท่าไรจากพื้นเขื่อน
 |
| 86. | เนื่องจากฝนตกทำให้ระดับน้ำเหนือเขื่อนเพิ่มขึ้นจาก 8 เมตร เป็น 10 เมตร แรงดันที่น้ำกระทำต่อเขื่อนจะเพิ่มขึ้นจากเดิมกี่เปอร์เซ็นต์ ถ้าความกว้างของเขื่อนคงตัว |
| 87. | ของเหลว 3 ชนิด มีความหนาแน่น D1, D2, D3 บรรจุในภาชนะดังรูป ถ้า D2 = 2D1 จงหาว่า D3 เป็นกี่เท่าของ D1
 |
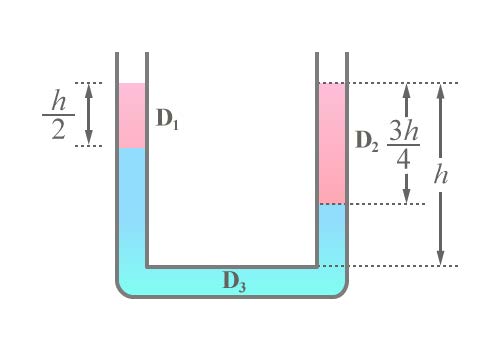| 88. | เมื่อใช้แมนอมิเตอร์แบบปรอทวัดความดันของแก๊สในถัง พบว่าปรอทสูงขึ้น 10 เซนติเมตรดังรูป จงหาความดันของแก๊สดังกล่าว
 |
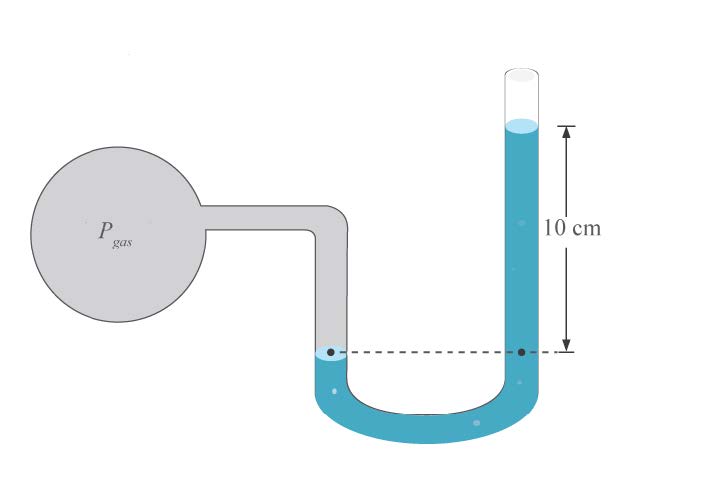| 89. | การขึ้นรูปโลหะวิธีการหนึ่งที่เป็นที่นิยมคือการ กด (Press) โดยใชเ้ครื่องกดไฮดรอลิกส์ ถ้าหากว่าที่เราต้องการแรงกดเท่ากับ 1,000 กิโลนิวตัน ซึ่งพื้นที่หน้าตัดของกระบอกสูบหัวกดมีค่าเท่ากับ A ส่วนด้านกระบอกสูบให้แรงลูกสูบมีพื้นที่หน้าตัด \(\rm\dfrac{A}{10}\) จงหาว่าต้องการออกแรง F ที่ด้านกระบอกสูบให้แรงเท่าใด
 |
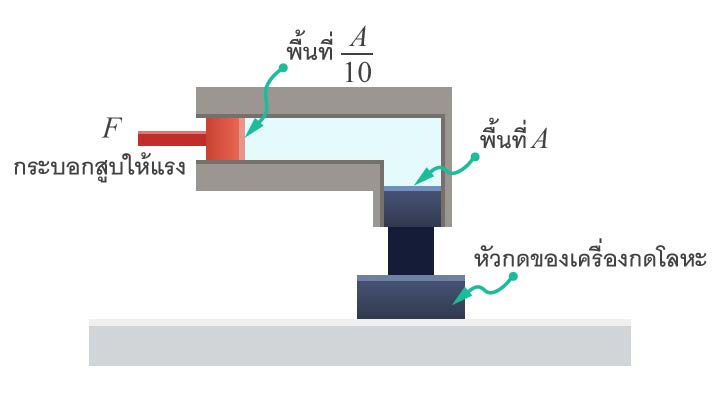| 90. | จากกราฟความสัมพันธ์ระหว่างความดัน (P) และความลึก (h) ดังรูป อยากทราบว่าความหนาแน่นของของเหลวมีค่าเท่าไร
 |
| 91. | จากรูป ระบบซึ่งประกอบด้วยกระบอกสูบและลูกสูบ 3 ชุดภายในบรรจุด้วยของเหลวมีพื้นที่หน้าตัดของกระบอกสูบเป็น A, 2A และ 3A ซึ่งมีมวล M1, M2 และ M3 วางอยู่บนลูกสูบของแต่ละชุดตามลำดับ ถ้าถือได้ว่าลูกสูบทุกอันมีน้ำหนักเบามากและไม่มีแรงเสียดทานระหว่างผิวของกระบอกสูบและลูกสูบเมื่อระบบอยู่ในภาวะสมดุล จงหาความสัมพันธ์ระหว่าง M1, M2 และ M3
 |
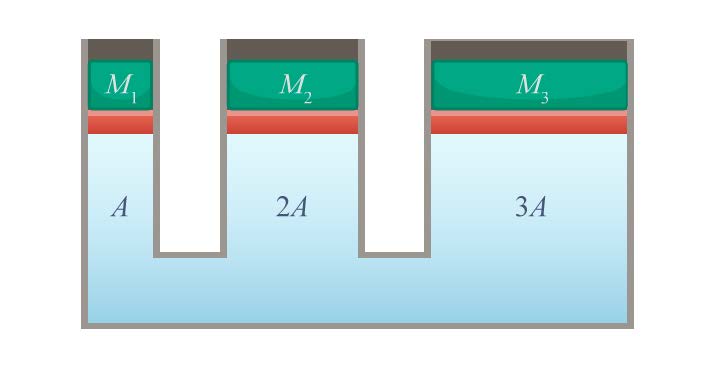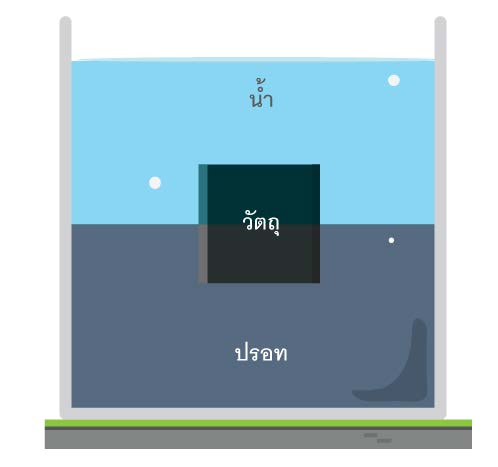
| 92. | วัตถุทรงลูกบาศก์ที่ทำจากเหล็กซึ่งมีความหนาแน่น 7.7 × 103 กิโลกรัมต่อลูกบาศก์เมตร และมีความยาวแต่ละด้านเป็น 1 เซนติเมตรเมื่อนำวัตถุนี้ไปใส่ในภาชนะที่บรรจุน้ำและปรอทพบว่าวัตถุลอยอยู่ระหว่าง ชั้น ของน้ำและปรอทดังรูป จงหาว่าวัตถุนี้จมลงไปในปรอทเป็นระยะเท่าใด ถ้ากำหนดให้น้ำและปรอทมีความหนาแน่น 103 กิโลกรัมต่อลูกบาศก์เมตร และ 13.6 × 103 กิโลกรัมต่อลูกบาศก์เมตร ตามลำดับ
 |
| 93. | ถาดน้ำกับน้ำมีมวลรวมกันเท่ากับ M วางอยู่แล้วบนตาชั่ง นำก้อนวัตถุมวล m ปริมาตร V มาใส่ลงในถาดและจมลงในน้ำนั้น อยากทราบว่าตาชั่งจะชี้น้ำหนักเท่าไหร่ กำหนดให้ว่าน้ำมีความหนาแน่น ρ และค่าความโน้มถ่วงของโลกเป็น g |
| 94. | ลูกบอลลูนทำด้วยวัสดุที่มีมวล 2M มีปริมาตร V ภายในบอลลูนบรรจุอากาศร้อนที่มีความหนาแน่น ρ อากาศภายนอกบอลลูนมีความหนาแน่น ρair ถ้าลูกบอลลูนลอยได้พอดี อากาศร้อนต้องมีความหนาแน่นเท่าใด (ทุกปริมาณใช้หน่วย SI) |
| 95. | คาบการแกว่งของนาฬิกาลูกตุ้มอย่างง่ายที่ลวดแขวนยาวขึ้นเพราะอุณหภูมิเพิ่มขึ้น กำหนด ก. คาบ T ของนาฬิกาลูกตุม้ อย่างง่ายเป็นไปตามสูตร \(\text{T} = 2π \sqrt{l/\text{g}}\) เมื่อ l เป็นความยาวของลวดแขวนลูกตุ้มและ g เป็นขนาดความเร่งเนื่องจากแรงโน้มถ่วงของโลก
ข. สัมประสิทธิ์การขยายตัวเชิงเส้นเนื่องจากความร้อน α คือ อัตราส่วนความยาวที่เปลี่ยนไป Δl ต่อความยาวเดิม l เมื่ออุณหภูมิเปลี่ยนไปหนึ่งหน่วย
ค. นักเรียนสามารถใช้การประมาณ \(\rm \sqrt{1+x}≈1 + x/2\) เมื่อ x มีขนาดน้อย 1 กว่ามาก ๆ
นาฬิกาลูกตุ้ม อย่างง่ายเรือนหนึ่งมีลวดแขวนที่มีสัมประสิทธิ์การขยายตัว เชิงเส้นเนื่องจากความร้อนเท่ากับ α และมีคาบแกว่ง T ที่ความยาว l1 เมื่ออุณหภูมิเพิ่มขึ้น Δθ น้อยมาก ๆ เมื่อ เทียบกับอุณหภูมิเดิม และคาบการแกว่งเปลี่ยนไปเป็น T + ΔT จงหาค่าอัตราส่วน ΔT/T ในรูปของตัวแปรที่กำหนดมา(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 96. | มวล M กับ m เชื่อมกันด้วยสปริงเบา ๆ กำลังสั่น "อยู่กับที่" เทียบกับระบบอ้างอิงเฉื่อย โดยที่ m สั่นด้วยแอมพลิจูด A จงหาค่าของแอมพลิจูดของการสั่นของ M (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555)  |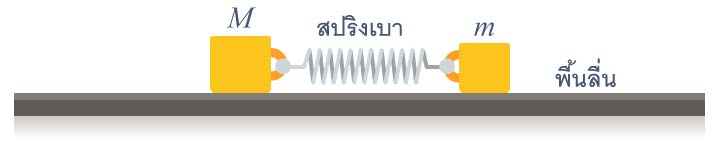
| 97. |  (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557) |
| 98. | การเคลื่อนที่ของระบบนี้บรรยายได้ด้วยการเคลื่อนที่ 3 สมการ
\(\rm m\ddot x_1 = +k(x_2 − x_1 − ℓ)\) . . . (1)
จงเขียนอีก 2 สมการให้ครบแล้วแก้สมการเพื่อหาความถี่ของการสั่นพื้นฐานซึ่งมีอยู่ 2 ค่า(ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 26 มี.ค. 2556)  |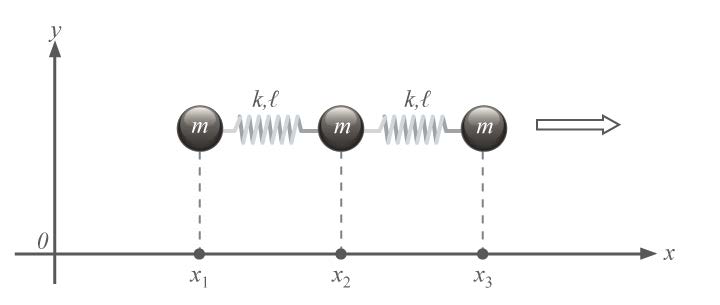
ตอบ
\(\rm m\ddot x_2 = +k(x_3-x_2 − ℓ)-k(x_2-x_1 − ℓ)\) . . . (2)
\(\rm m\ddot x_3 = -k(x_3-x_2 − ℓ)\) . . . (3)
\(\rm ω_2=\sqrt{\dfrac{3k}{m}}\)
\(\rm f_2 = \dfrac{1}{2\pi}\sqrt{\dfrac{3k}{m}}\)
\(\rm m\ddot x_2 = +k(x_3-x_2 − ℓ)-k(x_2-x_1 − ℓ)\) . . . (2)
\(\rm m\ddot x_3 = -k(x_3-x_2 − ℓ)\) . . . (3)
\(\rm ω_2=\sqrt{\dfrac{3k}{m}}\)
\(\rm f_2 = \dfrac{1}{2\pi}\sqrt{\dfrac{3k}{m}}\)
| 99. | ล้อทรงกระบอกตันมวล M รัศมี R สามารถหมุนได้คล่องรอบจุด O มีปลายหนึ่งของสปริง k ยึดไว้และอีกปลายของสปริงยึดกับเพดาน มวล m ซึ่งถ่วงขอบของทรงกระบอกทำให้นิ่งและ OA อยู่ในแนวระดับพอดี ต่อมาดึง m ลงนิดหน่อยแล้วปล่อย m จะเคลื่อนขึ้นลงๆ ด้วยคาบของการสั่นเป็นเท่าไร (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2553)  |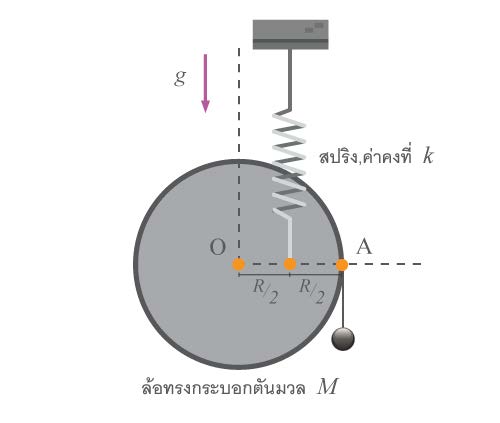
| 100. | ลูกกลมโลหะขนาดเล็กมาก 2 ลูกที่เหมือนกันทุกประการ (แต่ละลูกมีมวล m และประจุ q) ถูกแขวนจากเชือกที่ทำจากฉนวนยาว L จงหาค่า x เมื่อระบบอยู่ในสมดุล โดยมุม θ มีขนาดเล็กมากจนประมาณได้ว่า tan θ ≈ sin θ (ตอบในรูปของตัวแปร m, q, L และค่าคงที่มาตรฐานต่างๆ เช่น g) (ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 18 ต.ค. 2554)  |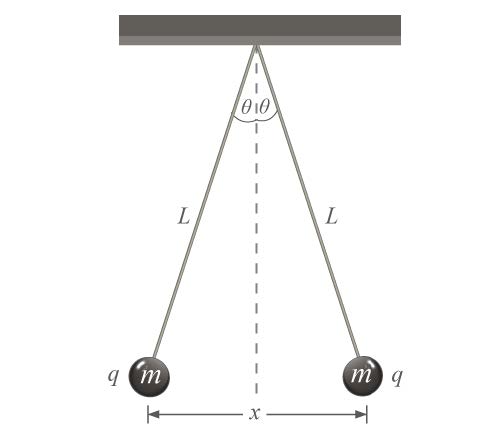
| 101. | แผ่นกลมแบนแกว่งได้คล่องในระนาบของแผ่นรอบจุด O ระยะทางจาก O ถึงจุด CM ต้องมีค่าเท่าไร คาบของการแกว่งด้วยแอมพลิจูดเล็ก ๆ จึงจะมีค่าเล็กที่สุด และค่านี้เป็นเท่าไรในรูปของ g , R (ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 24 มี.ค. 2552)  |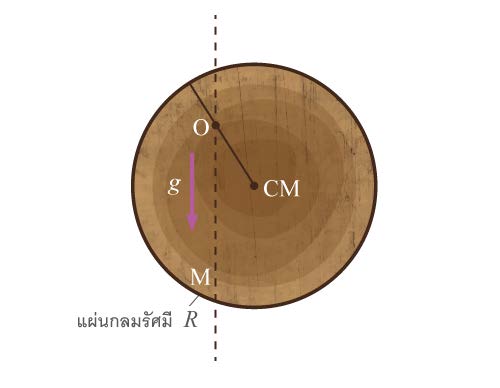
| 102. | ภาพนี้แสดงระบบในสภาวะสมดุลเชิงกล l เป็นระยะทางระหว่างรอกทั้งสอง ขณะที่เชือกส่วนนี้ทำมุม θ0 กับแนวดิ่งถ้าดึง M ลงนิดหน่อยแล้วปล่อยระบบจะสั่น ( M และ m เคลื่อนที่ขึ้นลงสลับกัน) จงวิเคราะห์หาคาบของการสั่นด้วยแอมพลิจูดเล็ก ๆ นี้ในเทอมของ m , M , l , g , sin θo (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557) หมายเหตุ \(\dfrac{1}{1+a} ≈ 1-a\) สำหรับ \(|a| ≪ 1\) \(Δ(\cos θ) ≈ −\sin θ ⋅ Δθ\) ถ้ารู้แคลคูลัส... (ไม่รู้ก็ทำได้อยู่แล้ว) |
| 103. | สปริงไร้มวล ความยาวธรรมชาติ l ค่าคงตัวสปริง k ขดหนึ่งวางตั้งตรงอยู่ในแนวดิ่ง ปลายล่างของสปริงถูกยึดไว้กับพื้น ส่วนปลายบนเคลื่อนที่ได้อย่าอิสระ ปล่อยวัตถุมวล m จากที่สูง h จากปลายบนของสปริงให้ตกในแนวดิ่ง ลงมาบนสปริงกำหนดว่าเมื่อวัตถุชนกับสปริง แล้วจะถูกยึดติดกับปลายของสปริงตลอดเวลา สมมุติด้วยว่าความสูงที่ปล่อยวัตถุลงมาไม่สูงมากพอให้สปริงหดสั้นจนถึงพื้นได ้
1) สปริงหดสั้นที่สุดเท่าใด
2) ตำแหน่งสมดุลของวัตถุอยู่สองจากพื้นเท่าใด
3) วัตถุจะกระดอนกลับขึ้นไปสูงสุดจากพื้นเท่าใด
4) วัตถุมีอัตราเร็วสูงสุดเท่าใด
5) ให้ y เป็นตำแหน่งของวัตถุจากตำแหน่งสมดุล โดยให้ y มีค่าเป็นบวกเมื่อวัดขึ้นในแนวดิ่ง ที่ตำแหน่งใด ๆ นี้วัตถุมีความเร่งเท่าใด
จงใหเ้หตุผลแสดงว่าวัตถุจะสั่นขึ้นลงแบบฮาร์มอนิกอย่างง่าย แล้วให้หาว่าตำแหน่ง y ของวัตถุจากตำแหน่งสมดุลที่เวลา t ใด ๆหลังติดกับสปริงเป็นฟังก์ชันอย่างใดของเวลา t
6) การสั่นนี้มีคาบเท่าใด
(ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 24 ต.ค. 2552) |
ตอบ
1) \(\rm x =\dfrac{mg}{k}+\dfrac{\sqrt{m^2g^2 + 2mghk}}{k}\)
2) \(l-\dfrac{\text{mg}}{\text{k}}\)
3) \(\text H =l -\dfrac{\text{mg}}{\text{k}}+\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\)
4) \(\rm v_{max} = \sqrt{\dfrac{mg^2}{k}+2gh}\)
5) \(\rm \dfrac{d^2}{dt^2}y=-\left(\dfrac{k}{m}\right)y\) และ \(\rm y(t)=\left[\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\right]\sin\left[\sqrt{\dfrac{k}{m}}t+arcsin\left(\dfrac{mg}{\sqrt{\rm m^2g^2 + 2mghk}}\right)\right]\)
6) \(\rm T=2\pi\sqrt{\dfrac{m}{k}}\)
1) \(\rm x =\dfrac{mg}{k}+\dfrac{\sqrt{m^2g^2 + 2mghk}}{k}\)
2) \(l-\dfrac{\text{mg}}{\text{k}}\)
3) \(\text H =l -\dfrac{\text{mg}}{\text{k}}+\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\)
4) \(\rm v_{max} = \sqrt{\dfrac{mg^2}{k}+2gh}\)
5) \(\rm \dfrac{d^2}{dt^2}y=-\left(\dfrac{k}{m}\right)y\) และ \(\rm y(t)=\left[\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\right]\sin\left[\sqrt{\dfrac{k}{m}}t+arcsin\left(\dfrac{mg}{\sqrt{\rm m^2g^2 + 2mghk}}\right)\right]\)
6) \(\rm T=2\pi\sqrt{\dfrac{m}{k}}\)
| 104. | ในการเคลื่อนที่แบบซิมเปิลฮาร์มอนิกของวัตถุใดๆ ความเร่งของวัตถุมีเฟสนำหน้าความเร็วอยู่เท่าใด |
| 105. | การทดลองเรื่องการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย ถ้าใหลู้กตุ้มเคลื่อนที่จาก ไป ไป แล้ว ไป ดังรูปใช้เวลา วินาที คาบของการเคลื่อนที่มีค่าเท่าใด
 |
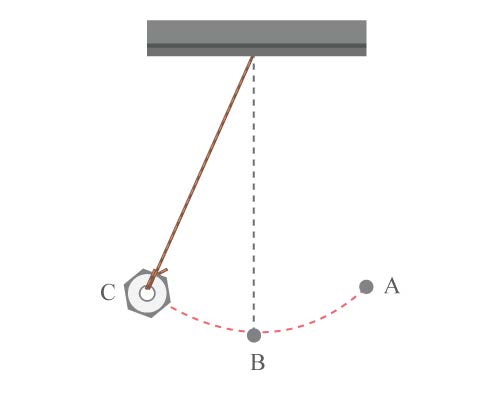| 106. | ถ้าลูกตุ้มในรูป ก แกว่งจากตำแหน่ง (1) ไปตำแหน่ง (2) ใช้เวลา t การแกว่งในรูป ข จากตำแหน่ง a ไป b ไป c ใช้เวลาเท่าใด
 |
| 107. | จงยกตัวอย่างวัตถุที่มีการสั่นที่พบเห็นในชีวิตประจำวัน |
| 108. | มวล 400 กรัม ติดอยู่กับสปริงซึ่ง มีค่านิจสปริง 25.6 นิวตันต่อเมตร โดยเริ่มต้นดึงมวลให้ได้ระยะ 5.00 เซนติเมตร จากตำแหน่งสมดุล แล้วปล่อยให้สั่นอย่างอิสระในแนวระดับ จงหาสมการแสดงการกระจัดในช่วงเวลาต่าง ๆ ของมวลนี้
 |
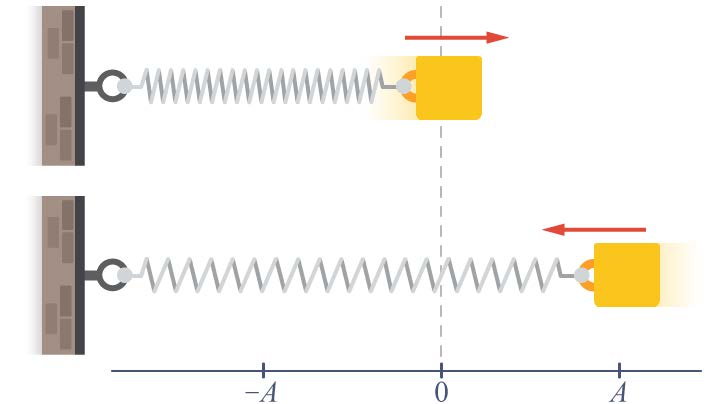| 109. | เมื่อใช้สโตรโบสโคปที่มี 1 ช่อง วัดความถี่ของการสั่นของมวล 0.25 กิโลกรัม ซึ่งผูกกับสปริงที่แขวนในแนวดิ่ง พบว่าเห็นภาพมวลหยุดนิ่งที่หนึ่งได้เมื่ออัตราเร็วของสโตรโบสโคปเป็น 3, 4 และ 12 รอบต่อวินาที ถัดกันไป ถามว่าค่านิจสปริงมีค่ากี่นิวตันต่อเมตร |
| 110. | ปล่อยลูกตุ้มซึ่งมีสายยาว 90 เซนติเมตรจากมุมหนึ่งให้แกว่ง แต่สายลูกตุ้มติดตะปูที่ระยะ 50 เซนติเมตร ใต้จุดที่แขวนในแนวดิ่งลูกตุ้มจะแกว่งกลับมาที่เดิมในเวลาเท่าใด
 |
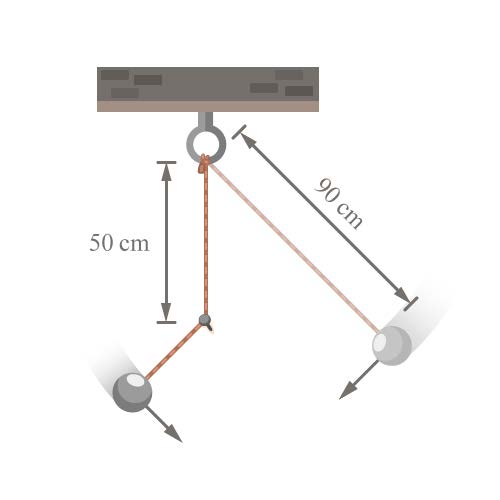| 111. | วัตถุเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย โดยมีความสัมพันธ์ของการกระจัด (y) หน่วยเมตร และเวลา (t) หน่วยวินาที เป็นไปตามสมการ
y = 0.5 sin(10t)
อยากทราบว่าขนาดของความเร่ง ที่ตำแหน่งไกลสุดจากสมดุลมีค่าเท่าไร |
| 112. | นาฬิกาแบบลูกตุ้มเรือนหนึ่งลูกตุ้มแกว่งได้ 60 รอบต่อนาที ความยาวของก้านของลูกตุ้มนาฬิกามีค่ากี่เมตร |
| 113. | ลูกตุ้มมวล m ยาว ℓ เริ่มแกว่งจากหยุดนิ่งในแนวระดับลงไปชนมวล M แล้วติดไปด้วยกัน หลังการชนมวล m จะแกว่งขึ้นไปได้ระยะทางสูงสุดเท่าใดจากพื้น (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |
| 114. | มวล M ตั้งต้นเคลื่อนที่เข้าหากำแพงจากระยะห่าง D ด้วยความเร็วคงที่ v ที่จังหวะเดียวกันกับที่ลูกบอลเล็กๆ มวล m << M กระดอนจาก M แล้วด้วยความเร็ว u > v เทียบกับพื้นไปชนและกระดอนอย่างยืดหยุ่นจากกำแพงแข็งกลับมาชนกับ M อีก ที่จังหวะนี้ m ได้เคลื่อนที่ไปแล้วเป็นระยะทางรวมเท่าใดนับจากเมื่อชน M ครั้งแรก (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |
| 115. | สปริงมีความยาวธรรมชาติ ℓ ปลายหนึ่งยึดติดกำแพง อีกปลายหนึ่งยึดกับมวล m ถูกอัดไว้เป็นระยะทาง \(\dfrac{ℓ}{2}\) แล้วปล่อยให้ดันมวล m ไปชนมวล m เท่ากันอีกก้อนที่แค่เดิมอยู่นิ่งที่ B แล้วติดกันไป จะไปได้ไกลสุดเท่าใดจากจุด B (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 3 ก.ย. 2549)  |
| 116. | จงแปลงค่าของพลังงานจลน์ \(\rm \dfrac{1}{2}mv^2=5\) จูล ไปอยู่ในหน่วยกรัม (มิลลิเมตรต่อวินาที)2 (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 6 ก.ย. 2546) |
| 117. | มวล M อยู่นิ่งบนพื้นระดับลื่นและมีสปริงเบาติดอยู่ด้านซ้าย ค่าคงที่สปริงเท่ากับ k มวล m เคลื่อนที่ด้วยความเร็วต้น u เข้าชน สปริงจะหดเข้าไปมากที่สุดเป็นระยะทางเท่าไร (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 6 ก.ย. 2546)  |
| 118. | โปรเจคไทล์ตั้งต้นจากจุด O เมื่อขึ้นไปถึงจุดสูงสุดก็ระเบิดออกเป็นสองชิ้นมวลเท่ากัน ชิ้นหน้าคือ A ชิ้นหลังคือ B ทันทีหลังระเบิด B มีความเร็วเป็นศูนย์เทียบกับพื้น ชิ้น A จะตกบนพื้นเลยจุดตกของ B ไปเป็นระยะทางกี่เท่าของระยะทาง OC (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |
| 119. | ปล่อยลูกบอลมวล m จากจุดหยุดนิ่งจากที่สูง H จากพื้นทุกครั้งที่ลูกบอลกระทบพื้นจะกระดอนขึ้นด้วยอัตราเร็ว e(< 1) เท่าของอัตราเร็วก่อนกระทบพื้นพอดี ตอนที่ลูกบอลกระดอนขึ้นครั้งที่ n ลูกบอลมีพลังงานจลน์เท่าใด และจะกระดอนขึ้นไปได้สูงเท่าใดก่อนตกกลับลงมาอีก (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 29 ส.ค. 2553) |
| 120. | ลูกปืนตะกั่วลูกหนึ่งเคลื่อนที่ด้วยอัตราเร็ว 200 m/s เข้าใส่เป้าและหยุดนิ่งอยู่ในเป้า สมมุติว่าพลังงานจลน์ทั้งหมดของลูกปืนเปลี่ยนเป็นความร้อนหมด และความร้อนนี้แบ่งไปให้ลูกปืนกับเป้าอย่างละเท่ากัน ลูกปืนมีอุณหภูมิเพิ่มขึ้นเท่าใด ความจุความร้อนจำเพาะของตะกั่วมีค่าเป็น 0.032 เท่าของน้ำ ความจุความร้อนจำเพาะของน้ำมีค่าเท่ากับ 1.00 cal/(g ⋅∘C) และ 1.00 cal มีค่าเท่ากับ 4.186 J (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 30 ส.ค. 2552) |
| 121. | A กับ B เป็นมวลทรงกลมผิวเกลี้ยงรัศมีเท่ากัน A กำลังเคลื่อนที่ในแนว OX เข้าชน B ซึ่งอยู่นิ่งก่อนชนหลังการชนกันอย่างยืดหยุ่น แล้ว B จะกระเด็นทำมุมกี่องศากับแนว OX (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2551)  |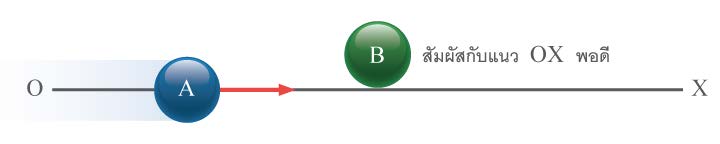
| 122. | ปล่อยมวลเล็ก ๆ ให้ไถลจากจุดหยุดนิ่งที่จุด A เข้าสู่รางวงกลม OB อย่างนุ่มนวล (ไม่มีการสะดุด, กระแทก) จะต้องให้จุด A อยู่สูงจากพื้นระดับเป็นกี่เท่าของรัศมีของราง OB จึงจะทำให้มวลนั้นขึ้นถึงจุด B ได้พอดีโดยไม่แยกตัวจากรางก่อน (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2551)  |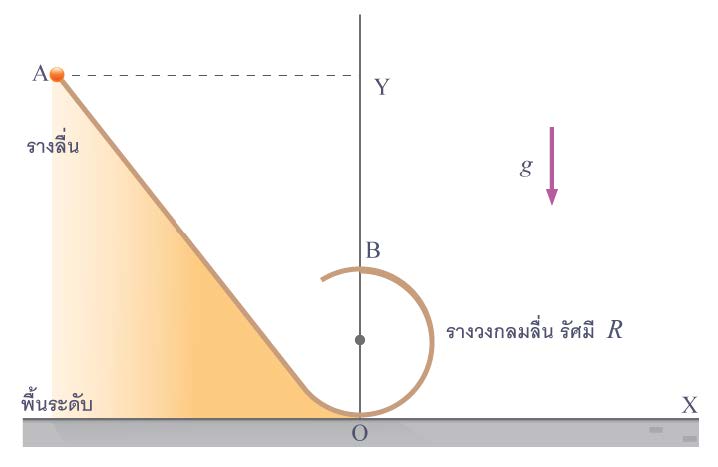
| 123. | ลูกบอลลูกหนึ่งตกลงมาจากที่สูง 10 m กระดอนกับพื้น และลอยกลับขึ้นไปได้สูง 2.5 m ถ้าลูกบอลกระทบพื้นนาน 0.10 s ความเร่งเฉลี่ยของลูกบอลระหว่างที่แตะพื้นมีขนาดเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 31 ส.ค. 2551) |
| 124. | M กับ m ผูกโยงกันด้วยเส้นยางยืดหย่อนๆ อยู่บนผืนระดับรอบเเละลื่นต่อมาดีด M ไปทางขวาด้วยความเร็ว v∘ อึดใจต่อมาขณะที่เส้นยางยืดตึงที่สุดนั้น M มีความเร็วเป็นเท่าไรและพลังงานศักย์ของระบบขณะเดียวกันนั้นมีค่าเท่าไร (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 1 ก.ย. 2556)  |
ตอบ \(\rm v_{_M} = \dfrac{M}{M +m}v_0\) และ \(\rm PE = \dfrac{1}{2}\left(\dfrac{mM}{M +m}\right) v^2_0\)
| 125. | ลูกตุ้ม M ห้อยอยู่นิ่ง ๆ มวล m เคลื่อนที่ด้วยความเร็ว u เข้าชนแล้วติดกันไปจะขึ้นไปได้สูงจากเดิมเป็นระยะทางเท่าไร (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 31 ส.ค. 2557)  |
| 126. | มวล M รูปทรงกลมรัศมี R วางไว้ที่พื้นในห้องที่อุณหภูมิ t∘ จะมีพลังงานศักย์เพิ่มขึ้นหรือลดลงเท่าใด เมื่ออุณหภูมิห้องสูงขึ้นเป็น t1 (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 12 ก.ย. 2547)  |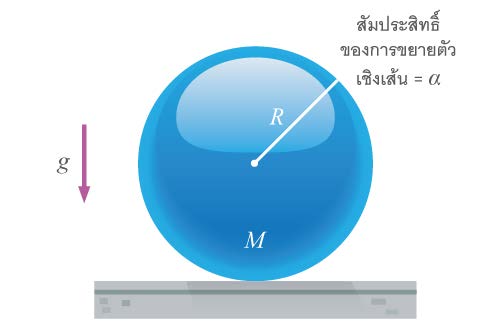
| 127. | มวล m1 กับ m2 ผูกติดกันด้วยเชือกยาว l และถูกเหวี่ยงให้หมุนอย่างอิสระบนโต๊ะระดับด้วยอัตราเร็วเชิงมุม ω ผู้สังเกตในระบบอ้างอิงเฉื่อยจะพบความเร็วสัมพันธ์ระหว่าง m2 กับ m1 มีขนาดเป็นเท่าใด (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 3 ก.ย. 2549)  |
| 128. | จงตอบคำถามต่อไปนี้
1) จงพิสูจน์ว่าในกรอบอ้างอิงจุดศูนย์กลางมวลของระบบ โมเมนตัมของระบบมีค่ารวมกันเป็นศูนย์
2) จงแสดงว่าพลังงานจลน์ทั้งหมดของระบบมีค่าเท่ากับพลังงานจลน์ของจุดศูนย์กลางมวลของระบบบวกกับพลังงานจลน์รอบจุดศูนย์กลางมวลของระบบ
(ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 24 ต.ค. 2552) |
ตอบ
1) จาก นิยามของ \(\rm v_{cm}\)จะได้
2) พลังงานจลน์ของระบบคือ
1) จาก นิยามของ \(\rm v_{cm}\)จะได้
\(\rm v_{cm}=\dfrac{\sum\limits_{i = 1}^{i = n} {m_iv_i} }{\sum\limits_{i = 1}^{i = n} {m_1}}\)
โมเมนตัมรวมของระบบเทียบจุดศูนย์กลางมวล คือ
\(\rm \sum\limits_{i = 1}^{i = n} {m_i{(v-v_{cm})}}i\)
จึงได้ว่า
\(\rm \sum\limits_{i = 1}^{i = n} {m_iv_i} - \sum\limits_{i = 1}^{i = n} {m_iv_{cm}} = 0\)
2) พลังงานจลน์ของระบบคือ
\(\rm \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_i} = \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_i(v_{cm}+v_{i,cm})^2} = \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_{cm}} + \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_{i,cm}}\)
ใช้ผลจากข้อที่แล้วร่วมด้วย เพื่อตัดพจน์ตรงกลางทิ้งไป
\(\rm ∴ KE_{system} = KE_{cm} +KE_{around \,cm}\)
| 129. | 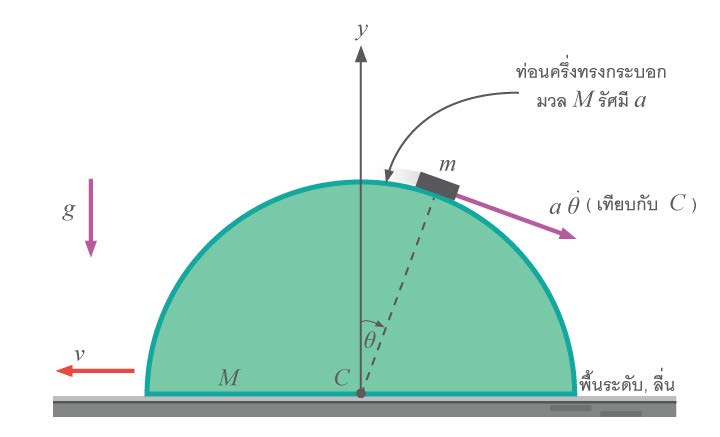 (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 25 ต.ค. 2551) |
ตอบ
1) \(\rm V=\dfrac{m\dotθRcos}{M+m}\)
2) \(\rm 2g(1-\cos\theta) = \left[\dfrac{M+m(1-\cos\theta)^2}{M+m}\right]a\dot\theta^2\)
3) \(\rm \theta=arccos\left[\dfrac{2(M+m)}{2(M+m)+M}\right]\)
1) \(\rm V=\dfrac{m\dotθRcos}{M+m}\)
2) \(\rm 2g(1-\cos\theta) = \left[\dfrac{M+m(1-\cos\theta)^2}{M+m}\right]a\dot\theta^2\)
3) \(\rm \theta=arccos\left[\dfrac{2(M+m)}{2(M+m)+M}\right]\)
| 130. | ออกแรงคงตัวขนาด 10 นิวตัน ลากกล่องใบหนึ่งให้เคลื่นอนที่ด้วยความเร็วคงตัวบนพื้นในแนวระดับที่มีความเสียดทาน จงหางานของแรงที่ลากกล่องและงานของแรงเสียดทานตามลำดับ ถ้าการกระจัดของกล่องเป็น 3 เมตร |
| 131. | หย่อนเชือกที่ผูกกับวัตถุให้เคลื่อนที่ลงเป็นระยะทาง S ด้วยความเร็วคงตัว งานของแรงที่เชือกดึงวัตถุเป็นเท่าใด |
| 132. | แรงที่สปริงทำกับมวลก้อนหนึ่งแสดงดังกราฟความสัมพันธ์ระหว่างแรงสปริงกับการกระจัดของมวลจากตำแหน่งสมดุล ดังรูป
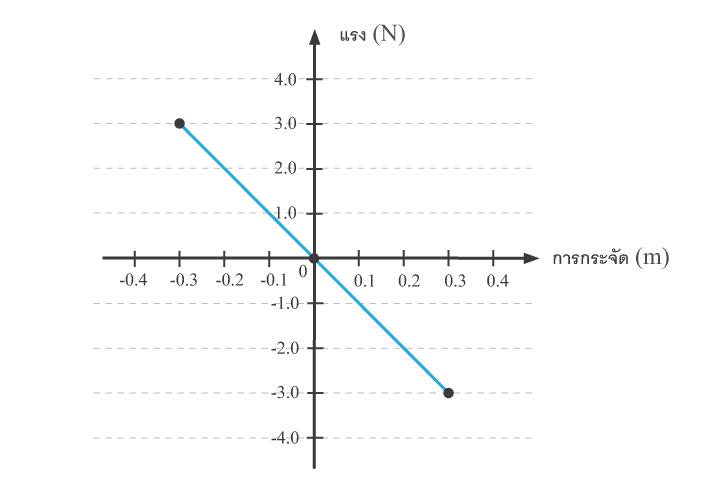 ข. งานของแรงสปริงในช่วงการกระจัดจาก -0.3 ถึง 0.3 เมตร |
| 133. | วัตถุมวล m อยสูู่งจากพื้นเป็นระยะทาง h พลังงานศักย์โน้มถ่วงของวัตถุนี้บนผิวโลกและบนผิวดวงจันทร์เท่ากันหรือไม่ |
| 134. | ถ้ามีแรงกระทำต่อวัตถุในทิศทางเดียวกับการเคลื่อนที่ของวัตถุ พลังงานจลน์ของวัตถุจะเปลี่ยนแปลงหรือไม่ อย่างไร ในทางกลับกันถ้าแรงนั้นมีทิศทางตรงข้าม พลังงานจลน์ของวัตถุจะเปลี่ยนแปลงหรือไม่ อย่างไร |
ตอบ เมื่อมีแรงกระทำต่อวัตถุในทิศทางเดียวกับการเคลื่อนที่ของวัตถุ จะทำให้วัตถุมีความเร็วเพิ่มขึ้น ดังนั้น พลังงานจลน์ของวัตถุจะเพิ่มขึน
ในทางกลับกัน ถ้าแรงที่กระทำต่อวัตถุมีทิศทางตรงข้าม จะทำให้วัตถุมีความเร็วลดลง ดังนั้น พลังงานจลน์ของวัตถุจะลดลง
ในทางกลับกัน ถ้าแรงที่กระทำต่อวัตถุมีทิศทางตรงข้าม จะทำให้วัตถุมีความเร็วลดลง ดังนั้น พลังงานจลน์ของวัตถุจะลดลง
| 135. | ปล่อยลูกกลมอันหนึ่งจากจุด X ตกสู่พื้นตามแนวดิ่งผ่านจุด Y ซึ่งเป็นจุดกึ่งกลางระหว่างตำแหน่ง X กับพื้นถ้าให้ Ep เป็นพลังงานศักย์โน้มถ่วงของวัตถุ และ Ek เป็นพลังงานจลน์ของวัตถุที่ตำแหน่ง Y จงหาความสัมพันธ์ของ Ep กับ Ek
 |
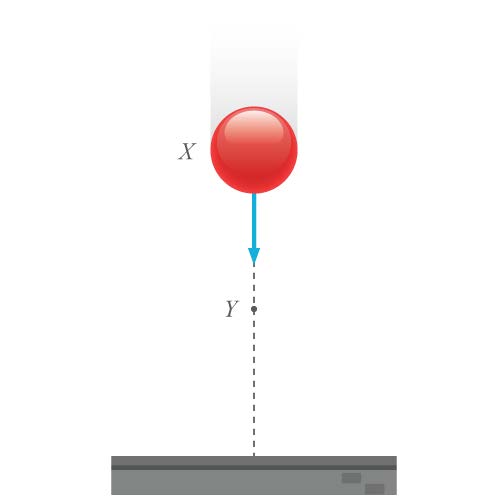| 136. | งานของแรง F ซึ่งกระทำกับวัตถุหนึ่งมีความสัมพันธ์กับระยะทางที่วัตถุเคลื่อนที่ S ดังรูป วัตถุใช้เวลาเคลื่อนที่ทั้งหมด 20 วินาที ในการทำงานของแรง F นี้กำลังเฉลี่ยของแรง F เป็นเท่าใด
 |
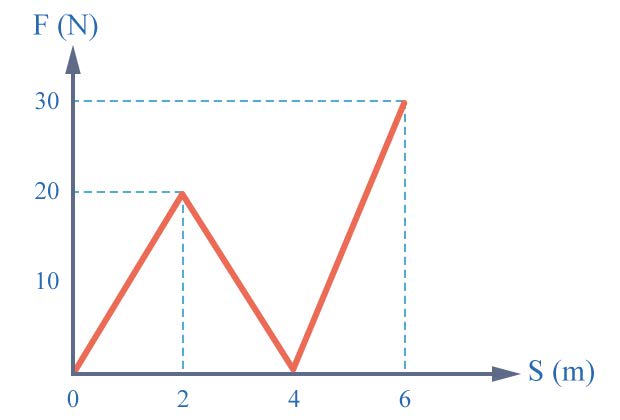| 137. | กรรมกรคนหนึ่งแบกของหนัก 50 กิโลกรัม ขึ้นไปบนภูเขา โดยเริ่มต้นที่จุด O แล้วเดินไปตามทาง OABC ถึงจุดหมายที่จุด C งานที่กรรมกรผู้นี้ทำจะเท่ากับ (ค่า g = 10 m/s2)
 |
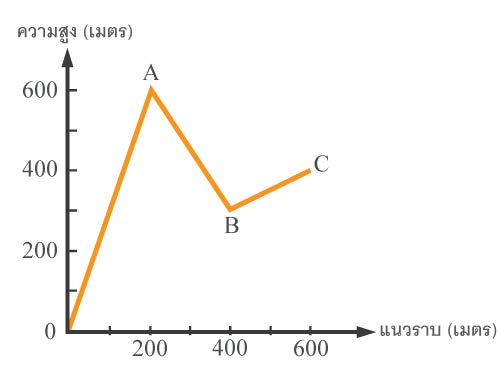| 138. | วัตถุมวล 1 กิโลกรัม เคลื่อนที่เป็นวงกลมอย่างสม่ำเสมอบนพื้นราบด้วยขนาดของความเร็ว 2 เมตรต่อวินาที โดยมีรัศมี 0.5 เมตร งานเนื่องจากแรงสู่ศูนย์กลางเมื่อวัตถุเคลื่อนที่ครึ่งรอบเป็นเท่าใด |
| 139. | กล่องหนัก 15 นิวตัน ถูกลากไปตามพื้นลื่นโดยแรง P = 30 นิวตัน ที่ทำมุม θ = 60∘ ด้วยความเร็ว 3 กิโลเมตรต่อชั่วโมง เป็นเวลา 1 นาที กำลังที่ใช้ในการลากกล่องเป็นเท่าไร
 |
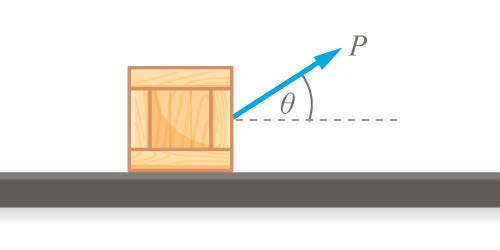| 140. | การเข็นรถไปตามพื้นราบและการเข็นรถไปตามพื้นเอียงด้วยอัตราเร็วคงตัวในระยะทางเท่ากัน กรณีใดต้องทำงานมากกว่ากันเพราะเหตุใด ถ้าถือว่าแรงเสียดทานที่กระทำต่อรถทั้งสองกรณีมีขนาดเท่ากัน |
ตอบ การเข็นรถไปตามพื้นเอียงต้องทำงานมากกว่าการเข็นรถไปตามพื้นราบ
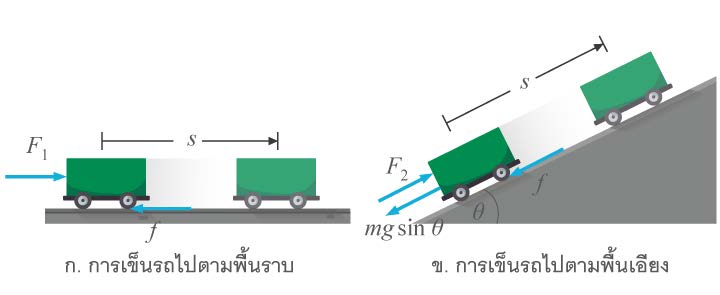
การเข็นรถไปตามพื้นราบ แรงที่กระทำต่อรถ และการกระจัด มีทิศทางเดียวกันงานของแรงที่กระทำต่อรถ คือ W1 = F1s
ดังรูป ก โดย
ดังรูป ก โดย
F1 = f
แต่การเข็น รถ (ขึ้น) ไปตามพื้นเอียง (ที่มีทิศทางทำมุม กับพื้นราบระดับ) แรงที่กระทำต่อรถ และการกระจัด งานของแรงที่กระทำต่อรถคือ W2 = F2s
ดังรูป ข โดย
ดังรูป ข โดย
F2 = mg sin θ + f
จะได ้F2 > F1 ดังนั้น W2 > W1
จึงสรุปได้ว่า การเข็นรถไปตามพื้นเอียงต้องทำงานมากกว่าการเข็นรถไปตามพื้นราบด้วยอัตรา เร็วคงตัวในระยะทางเท่ากันเมือแรงเสียดทานมีค่าเท่ากัน
จึงสรุปได้ว่า การเข็นรถไปตามพื้นเอียงต้องทำงานมากกว่าการเข็นรถไปตามพื้นราบด้วยอัตรา เร็วคงตัวในระยะทางเท่ากันเมือแรงเสียดทานมีค่าเท่ากัน
| 141. | ออกแรงคงที่ F ในแนวระดับดันกล่องใบหนึ่งให้เคลื่อนที่จากหยุดนึ่งไปบนพื้นระดับลื่น จงเขียนกราฟแสดงความสัมพันธ์ระหว่างกำลังขณะใด ๆ ของแรง F กับระยะทางที่วัตถุเคลื่อนที่ |
| 142. | มวล 2 กิโลกรัม เคลื่อนที่ในแนวราบบนพื้นที่มีแรงเสียดทาน 8 นิวตัน เข้าชนสปริงด้วยความเร็ว 2 เมตร/วินาที ทำให้สปริงหดได ้10 เซนติเมตร ค่าคงตัวของสปริงเป็นเท่าใดในหน่วยนิวตัน/เมตร
 |
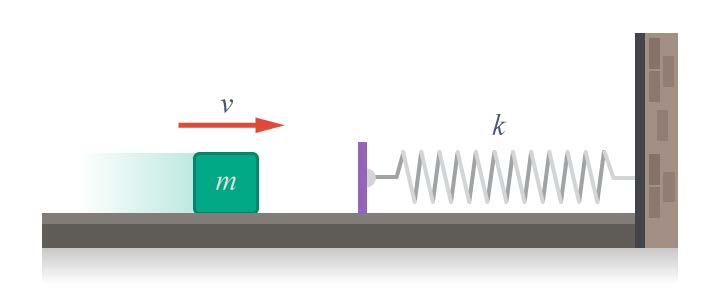| 143. | จากรูป วัตถุเคลื่อนที่ลงจากทางโค้งซึ่งไม่มีแรงเสียดทาน เมื่อเคลื่อนที่ถึงพื้นราบ สัมประสิทธิ์ความเสียดทานระหว่างวัตถุกับพื้นราบเป็น 0.4 อยากทราบค่าวัตถุจะเคลื่นอนที่บนพื้นราบได้ไกลที่สุดเท่าไร
 |
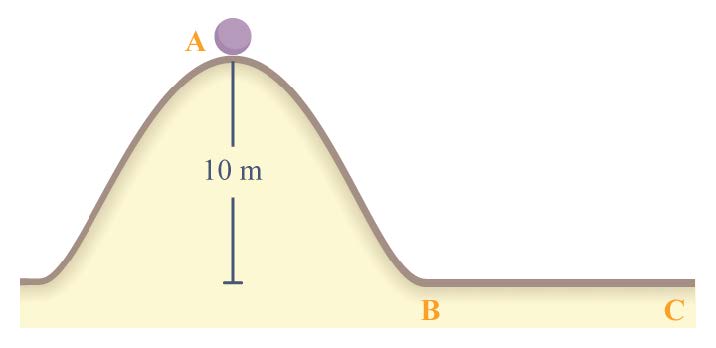| 144. | ผูกมวล m ติดไว้ที่ปลายสปริงเบาซึ่งมีความยาวปกติ 40.0 เซนติเมตร และมีค่าคงตัวสปริงเท่ากับ 100 นิวตันต่อเมตร ถ้าเราแกว่งมวล m เป็นวงกลมบนพื้นโต๊ะลื่นรอบจุด O โดยมีรัศมีการเคลื่อนที่ 50.0 เซนติเมตร ขณะนั้นพลังงานจลน์ของมวลเป็นกี่เท่าของพลังงานศักย์ของสปริง
 |
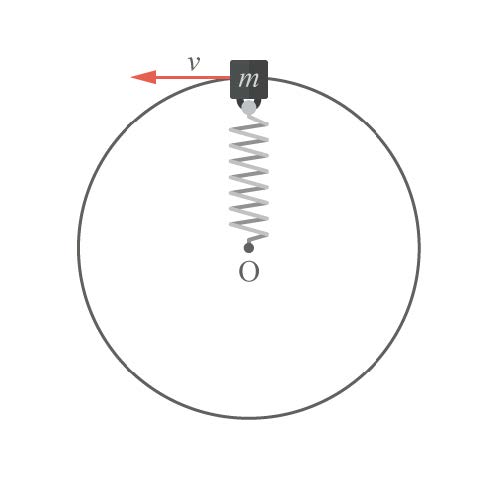| 145. | มวล M กับ m เชื่อมกันด้วยสปริงเบา ๆ กำลังสั่น "อยู่กับที่" เทียบกับระบบอ้างอิงเฉื่อย โดยที่ m สั่นด้วยแอมพลิจูด A จงหาค่าของแอมพลิจูดของการสั่นของ M (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555)  |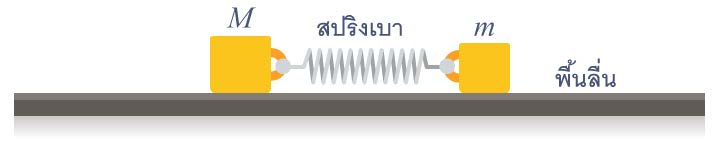
| 146. | ถ้าคุณดันหนังสือกับผนังแนวดิ่งด้วยแรงมากพอหนังสือจะไม่ไถลตกลงมา ถ้าสัมประสิทธิ์ของความเสียดทานสถิตระหว่างหนังสือกับผนังมีค่าเท่ากับ 0.7
1) คุณจะตองออกแรงดันตั้งฉากกับผนังด้วยขนาดอย่างน้อยเท่าใด หนังสือมวล 2.0 kg จึงจะไม่ไถลตกลงมากำหนดว่าความเร่งเนื่องจากแรงโน้มถ่วงโลกมีขนาด 9.8 m/s2
2) ถ้าคุณออกแรงดันขนาด 35N แรงเสียดทานสถิตที่ผนังกระทำต่อหนังสือมีขนาดเท่าใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2548) |
| 147. | ห่วงเล็ก ๆ คล้องอยู่ในห่วงใหญ่ดังรูป โดยที่ห่วงใหญ่มีรัศมี R ถ้าสัมประสิทธิ์ความเสียดทานของทั้งสองห่วงเท่ากับศูนย์ จงหาค่าของมุม θ ที่จุดสมดุลเมื่อห่วงใหญ่หมุนรอบตัวเองด้วยความเร็วเชิงมุม ω สูงมาก ๆ
 |
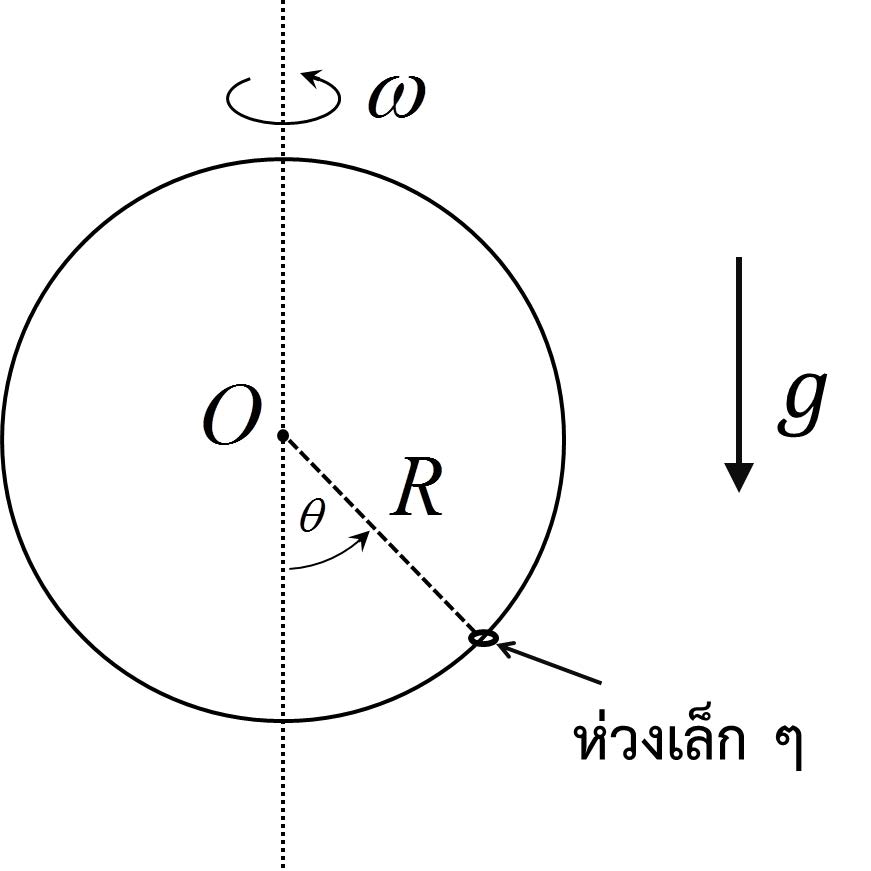| 148. | ดีดวัตถุมวล m ก้อนหนึ่งด้วยอัตราเร็วต้น u ให้ไถลขึ้นไปตามพื้นเอียงซึ่งทำมุม θ กับแนวระดับ เมื่อวัตถุขึ้นไปไดสู้งสุดก็ตกกลับมาตามพื้นเอียง ถ้าสัมประสิทธิ์ของความเสียดทานจลน์ระหว่างวัตถุกับผิวพื้นเอียงมีค่า μk อัตราเร็วของวัตถุขณะที่กลับมาถึงที่ปลายพื้นเอียงมีค่าเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) |
| 149. | ตาชั่งสปริงอันหนึ่งแขวนไว้กับเพดานลิฟต์ที่กำลังเคลื่อนที่ ถ้าปลายล่างของตาชั่งมีวัตถุมวล 10 kg แขวนอยู่และตาชั่งอ่านค่าได ้125 N
1) จงหาความเร่ง (ทิศเเละขนาด) ของลิฟต์
2) ถ้าที่แขวนตาชั่งหลุดจากเพดาน ตาชั่งอ่านค่าเท่าใด
กำหนดว่าขนาดสนามโน้มถ่วงของโลกที่บริเวณนั้นมีค่าเท่ากับ 9.8 N/kg(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) |
| 150. | ในระบบดาวฤกษ์สองดวง m1 กับ m2 ซึ่งโคจรรอบกันและกัน m1 โคจรตามแนววงกลมรัศมี R1 นั้น m2 จะมีอัตราเร็วเชิงเส้นเป็นเท่าใด (ใช้กฎการโน้มถ่วง \(\rm F =\dfrac{Gm_1m_2}{r^2} ,~ r =\) ระยะห่าง) (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555) |
| 151. | ดีดวัตถุมวล m ด้วยอัตราเร็วต้นไปในทางทิศขวามือให้ไถลไปบนผิวแผ่นไม้มวล M แผ่นไม้วางอยู่บนพื้นลื่นอีกทีหนึ่ง ให้ μk และ μs เป็นสัมประสิทธิ์ความเสียดทานจลน์และสัมประสิทธความเสียดทานสถิตระหว่างวัตถุและแผ่นไม้ตามลำดับ
1) แรงเสียดทานที่แผ่นไม้ทำต่อวัตถุมีทิศทางใด และมีขนาดเท่าใด
2) ความเร่งของแผ่นไม้มีทิศทางใด และมีขนาดเท่าใด
3) แผ่นไม้เคลื่อนที่ไปเท่าใด เมื่อวัตถุและแผ่นไม้มีความเร็วเท่ากัน
4) วัตถุไถลไปบนแผ่นไม้เป็นระยะทางเท่าใด (วัดเทียบกับแผ่นไม ้ และวัดตั้งแต่ต้นจนวัตถุเริ่มหยุดไถลบนแผ่นไม้)
5) เมื่อวัตถุหยุดไถล แรงเสียดทานที่แผ่นไม้ทำต่อวัตถุมีขนาดเท่าใด และมีทิศทางใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 29 ส.ค. 2553) |
ตอบ
1) ทิศไปทางซ้าย และ \(\rm f_k = μ_kmg\)
2) ทิศไปทางขวา และ \(\rm a = \dfrac{\mu_kmg}{M}\)
3) แผ่นไม้เคลื่อนที่ไปได้ \(\rm \dfrac{mMu^2}{2\mu_kg(m+M)^2}\)
4) วัตถุไถลไปได้ \(\rm \dfrac{Mu^2}{2\mu_k g(M+m)}\)
5) ไม่เกิดทิศ และแรงเสียดทานจลน์เท่ากับศูนย์
1) ทิศไปทางซ้าย และ \(\rm f_k = μ_kmg\)
2) ทิศไปทางขวา และ \(\rm a = \dfrac{\mu_kmg}{M}\)
3) แผ่นไม้เคลื่อนที่ไปได้ \(\rm \dfrac{mMu^2}{2\mu_kg(m+M)^2}\)
4) วัตถุไถลไปได้ \(\rm \dfrac{Mu^2}{2\mu_k g(M+m)}\)
5) ไม่เกิดทิศ และแรงเสียดทานจลน์เท่ากับศูนย์
| 152. | ท่อนผอม, ตรง, ยาว, มวล M ความยาว L กำลังล้มจากหยุดนิ่งจากแนวดิ่งบนพื้นฝืด จงวิเคราะห์หาแรงเสียดทานที่พื้นกระทำต่อปลายล่างของท่อนทำให้ท่อนไม่ไถลไปทางซ้าย หาแรงปฏิกิริยาที่พื้นกระทำต่อปลายล่าง แล้วหาเงื่อนไขเกี่ยวกับค่าสัมประสิทธิ์ความเสียดทาน (μ) ที่จะทำให้ปลายล่างไม่ไถลไปทางซ้ายเลย [ถึงแม้ว่าในที่สุดจะไปทางขวา] (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 18 ธ.ค. 2554)  |
ตอบ
\(\rm f=\dfrac{3mg}{4}(3\cos\theta-2)\sin\theta\)
\(\rm N = \dfrac{3mg}{4}\left[3\cos^2\theta-2\cos\theta-1+\dfrac{4}{3}\right]\)
\(\rm \mu \approx 0.3706\) โดย \(\rm \mu \ge \dfrac{f}{N}\) ทุกๆ θ
\(\rm f=\dfrac{3mg}{4}(3\cos\theta-2)\sin\theta\)
\(\rm N = \dfrac{3mg}{4}\left[3\cos^2\theta-2\cos\theta-1+\dfrac{4}{3}\right]\)
\(\rm \mu \approx 0.3706\) โดย \(\rm \mu \ge \dfrac{f}{N}\) ทุกๆ θ
| 153. | มวล m1 , m2 โยงกันด้วยเชือกยาว ℓ กำลังตกเข้าหาโลกมวล M ในแนวเข้าสู่ O โดยไม่มีการหมุน จงหาความตึงในเส้นเชือกในเทอมของ r , m1 , m2 , M , ℓ และ G ซึ่งเป็นค่า Gravitational constant และถ้า ℓ ≪ r ความตึงนี้จะมีค่าประมาณเท่าใด (ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 24 มี.ค. 2552)  |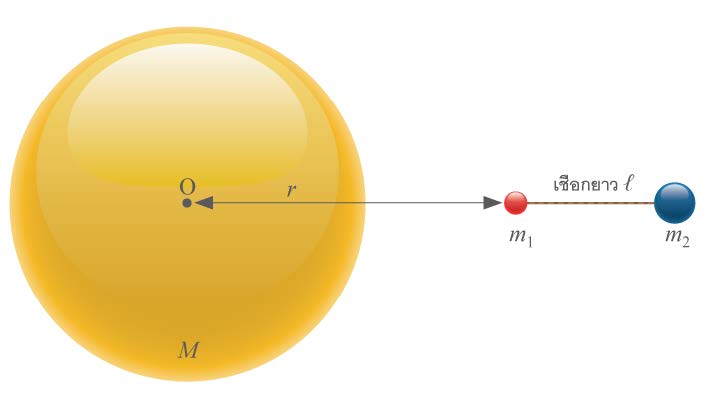
| 154. | ค่อย ๆ วางวัตถุมวล m อย่างช้าๆ ลงบนทางเลื่อน (มวลมากกว่า m มาก ๆ) ในสนามบินสุวรรณภูมิซึ่ง กำลังเลื่อนด้วยอัตราเร็ว u คงตัว ถ้าสัมประสิทธิ์ของความเสียดทานจลน์ระหว่างวัตถุและทางเลื่อนเท่ากับ μk
1) จงหา นานเท่าใดหลังจากวางวัตถุ วัตถุจึงจะหยุดไถล และ
2) วัตถุเคลื่อนที่ไปได้ระยะทางเท่าใด (เทียบกับคนที่ยืนอยู่นอกทางเลื่อน) ในระหว่างช่วงเวลาในข้อ 1)
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 155. | วัตถุเล็ก ๆ ตกจากหยุดนิ่งตามแนวรางลื่นจาก A ไป C แล้วไป B จะใช้เวลาเป็นกี่เท่าของการตกตามแนวรางลื่น A ตรงไป B (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2554)  |
| 156. | M ถูกดีดด้วยความเร็วต้น vo ให้กระตุกโซ่ออกไปจากกองที่ origin O ของระบบอ้างอิงเฉื่อย XOY โซ่มีมวลต่อหน่วยความยาวเป็น λ สัมประสิทธิ์ความเสียดทานระหว่างโซ่และ M กับพื้นเป็น μ จงวิเคราะห์หา:
 ก. สมการเคลื่อนที่ equation of motion ของ M
ข. ความเร็ว v ที่ขณะใดๆ ในรูปของ vo,M, g, μ, λ และ x
ค. ความเร่ง \(\rm\dfrac{d}{dt}v\) ในรูปของ vo,M, g, μ, λ และ x
ง. ความเร่ง \(\rm\dfrac{d}{dt}v\) ที่จังหวะที่ x = 0 เป็นเท่าใด
(ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2548) |
ตอบ
ก. \(\rm (M + λx)\ddot{x}= −μ(M + λx)g − λv^2\)
ข. \(\rm v(x) =\sqrt{\dfrac{3λ M^2v_0^2− 2μg[(M + λx )^3- M^3]}{3λ(M + λx)^2}}\)
ค. \(\rm a = -\mu g-\dfrac{1}{3(M + λx)^3}(3λ M^2v_0^2− 2μg[(M + λx )^3- M^3])\)
ง. \(\rm a = -\mu g-\dfrac{λ}{M}v^2_0\)
ก. \(\rm (M + λx)\ddot{x}= −μ(M + λx)g − λv^2\)
ข. \(\rm v(x) =\sqrt{\dfrac{3λ M^2v_0^2− 2μg[(M + λx )^3- M^3]}{3λ(M + λx)^2}}\)
ค. \(\rm a = -\mu g-\dfrac{1}{3(M + λx)^3}(3λ M^2v_0^2− 2μg[(M + λx )^3- M^3])\)
ง. \(\rm a = -\mu g-\dfrac{λ}{M}v^2_0\)
| 157. | จงอธิบายวิธีการหาแรงลัพธ์ของแรงสามแรงที่อยู่ในแนวเดียวกันโดยวิธีการสร้างรูป ก) โดยวิธีการวาดรูป ข) โดยวิธีการคำนวณ |
ตอบ
ก) ใช้วิธีหางต่อหัว
ข) รวมขนาดของแรงโดยให้กำหนดให้แรงทิศเดียวกันมีค่าเป็นบวก ทิศตรงข้ามมีค่าเป็นลบ
ก) ใช้วิธีหางต่อหัว
ข) รวมขนาดของแรงโดยให้กำหนดให้แรงทิศเดียวกันมีค่าเป็นบวก ทิศตรงข้ามมีค่าเป็นลบ
| 158. | คนสองคนชักเย่อกัน ต่างคนต่างออกแรง F เท่ากันที่ปลายเชือกทั้งสองความตึงในเชือกมีค่าเท่าใด |
ตอบ F
ปลายเชือกทั้งสองด้านถูกดึงด้วยแรง F ทำให้เกิดแรงตึงในเชือกเท่ากับ F ด้วยเพราะปลายเชือกทั้งสองไม่ได้เคลื่อนที่ แรงตึงเชือกจึงต้องเท่ากับแรงดึง F ที่ปลายเชือกทั้งสองด้าน
ปลายเชือกทั้งสองด้านถูกดึงด้วยแรง F ทำให้เกิดแรงตึงในเชือกเท่ากับ F ด้วยเพราะปลายเชือกทั้งสองไม่ได้เคลื่อนที่ แรงตึงเชือกจึงต้องเท่ากับแรงดึง F ที่ปลายเชือกทั้งสองด้าน
| 159. | แรง 5 นิวตัน และ 12 นิวตัน ในระนาบระดับมีทิศตั้งฉากกัน กระทำต่อมวล 10 กิโลกรัม บนพื้นระดับลื่นจงหาขนาดของความเร่งของมวลนี้
 |
| 160. | วัตถุมวล 20 กิโลกรัม มีแรงลัพธ์มากระทำต่อมวล ทำให้มวลเคลื่อนที่โดยมีความเร็วสัมพันธ์กับเวลา ดังกราฟ จงหาแรงลัพธ์ที่กระทำ ต่อวัตถุ  |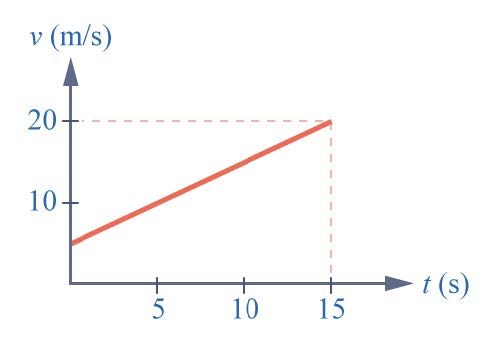
| 161. | กล่องมวล m ไถลลงพื้นเอียงซึ่งทำมุม θ กับแนวระดับด้วยความเร่ง a ต่อมาเพิ่มมวลให้กล่องเป็น 2m ความเร่งจะเป็นเท่าใด ถ้าสัมประสิทธิ์ของความเสียดทานระหว่างกล่องกับพื้นเอียงมีค่าคงที่ |
| 162. | ลิ่มวางอยู่บนพื้นฝืดมาก ผิวบนของลิ่มเป็นผิวราบลื่นนำมวล M มาวางและปล่อยให้ไถลลงบนผิวลื่นนี้แรงที่ลิ่มกดทับพื้นระดับจะเพิ่มขึ้นจากเดิมเท่าใด
 |
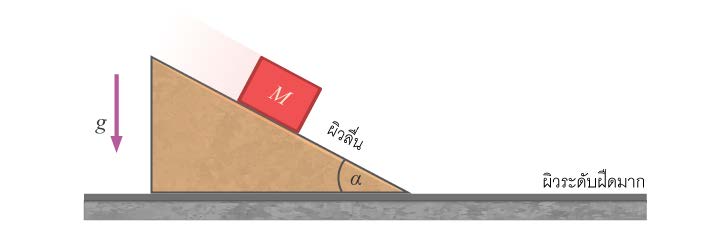| 163. | ในการทดลองเพื่อพิสูจน์กฎการเคลื่อนที่ของนิวตัน มีการชดเชยความฝืดและใช้ขนาดต่างๆ ลากมวล (รถทดลอง) และวัดความเร่ง เมื่อเขียนกราฟระหว่างแรงและความเร่งได้กราฟ
 |
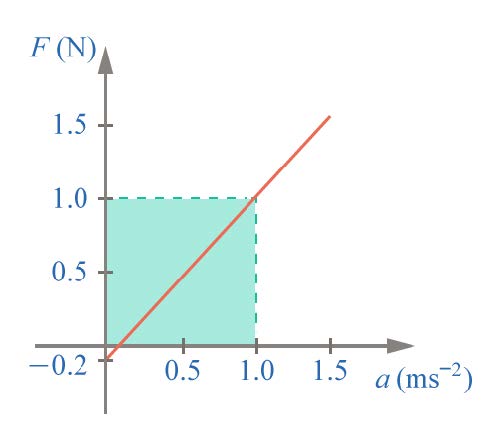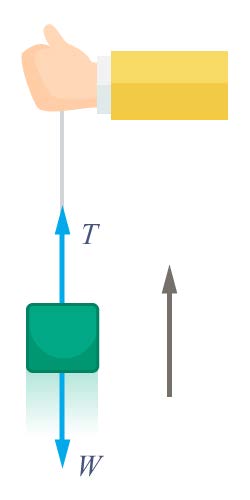
| 164. | ผูกเชือก (ด้ายเย็บผ้าที่เหนียวพอประมาณ) กับถุงทรายดังภาพ ในระหว่างการดึงถุงขึ้นอย่างช้าๆ ทำให้เชือกไม่ขาด กับการดึงถุงขึ้นอย่างรวดเร็วทำให้เชือกขาด เหตุใดจึงเป็นเช่นนั้น จงอธิบาย
 |
ตอบ
แรงที่กระทำต่อถุงทรายจะมี 2 แรงคือแรงดึงเชือก \(\rm \vec{T}\) และน้ำหนักวัตถุ \(\rm m\vec{g}\) พิจารณาเมื่อถุงทรายเคลื่อนที่ขึ้นอย่างช้าๆ ถือว่าถุงทรายมีความเร็วคงตัว แรงลัพธ์ที่กระทำต่อวัตถุเป็นศูนย์ จะได้ขนาดของแรงดึงขึ้นมีค่าเท่ากับขนาดของแรงดึงลง นั้นคือ \(\rm T=mg\)
พิจารณาเมื่อดึงถุงทรายอย่างรวดเร็ว ถุงทรายจะเคลื่อนที่ด้วยความเร่ง
จากกฎการเคลื่อนที่ข้อที่สองของนิวตัน
จะได้
แรงที่กระทำต่อถุงทรายจะมี 2 แรงคือแรงดึงเชือก \(\rm \vec{T}\) และน้ำหนักวัตถุ \(\rm m\vec{g}\) พิจารณาเมื่อถุงทรายเคลื่อนที่ขึ้นอย่างช้าๆ ถือว่าถุงทรายมีความเร็วคงตัว แรงลัพธ์ที่กระทำต่อวัตถุเป็นศูนย์ จะได้ขนาดของแรงดึงขึ้นมีค่าเท่ากับขนาดของแรงดึงลง นั้นคือ \(\rm T=mg\)
พิจารณาเมื่อดึงถุงทรายอย่างรวดเร็ว ถุงทรายจะเคลื่อนที่ด้วยความเร่ง
จากกฎการเคลื่อนที่ข้อที่สองของนิวตัน
\(\rm Σ\vec{F} = m\vec{a}\)
ให้ทิศขึ้นแทนด้วยเครื่องหมาย + และทิศลงแทนด้วยเครื่องหมาย -จะได้
\(\rm T=ma+mg\)
จะเห็นว่า \(\rm T > mg\) เมื่อดึงถุงทรายอย่างรวดเร็วเชือกจะขาด เพราะแรงดึงเชือกมากเกินค่าแรงที่เส้นเชือกรับได้สูงสุด| 165. | สปริงเบาทั้งสามอันเหมือนกันหมด ถ้าสปริงในรูป ก. ยืดออก 4 เซนติเมตร สปริงในรูป ข. ยืดออกรวมเป็นกี่เซนติเมตรเมื่อแขวนมวลขนาดเท่ากันกับรูป ก.
 |
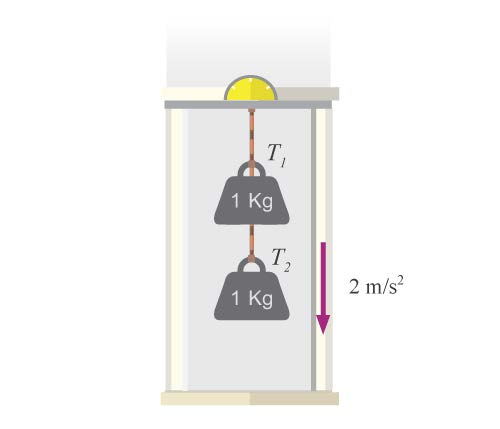
| 166. | มวล 1.0 กิโลกรัมสองก้อน ผูกติดกับเชือกเบาและแขวนติดกับเพดานของลิฟต์ดังรูป ถ้าลิฟต์เคลื่อนที่ลงด้วยความเร่ง 2 m/s2 จงหาแรงตึงในเส้นเชือก T1 และ T2
 |
| 167. | เข็มขัดนิรภัยและที่พิงศีรษะซึ่งติดอยู่กับเบาะในรถยนต์มีไว้เพื่อประโยชน์อะไร จงอธิบายพร้อมเหตุผล |
ตอบ เมื่อรถถูกชนจากด้านหลัง ที่พิงศีรษะสามารถป้องกันไม่ให้ศีรษะเคลื่อนที่ไปด้านหลังมากเกินไปทำให้คอไม่หัก เมื่อถูกชนจากด้านหน้าเข็มขัดนิรภัยจะช่วยไม่ให้ลำตัวกระแทกกับพวงมาลัย
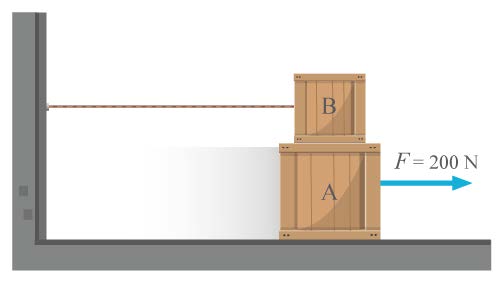
| 168. | จากรูป กล่อง A และ B มีมวล 20 และ 10 กิโลกรัม ดึงวัตถุ A ด้วยแรงขนาน 200 นิวตัน ถ้าสัมประสิทธิ์ของความเสียดทานระหว่าง A กับพื้นและกล่อง A กับกล่อง B เป็น 0.4 และ 0.2 ตามลำดับ จงหาความเร่งของกล่อง A
 |
| 169. | แรงเสียดทานมีผลต่อการเดินเช่นไร จงใหเ้หตุผลประกอบ |
| 170. | จากการทดลองเรื่องสัมประสิทธิ์ความเสียดทาน เมื่อจัดรางไม่ให้พื้นรางอยู่ในแนวระดับ และใช้เครื่องชั่งสปริงเกี่ยวขอของแผ่นไม้ที่มีถุงทรายทับอยู่บนแล้วออกแรง ดึงเครื่องชั่งสปริงให้ทิศของแรงดึงอยู่ในแนวระดับ ทำให้ได้ข้อมูลที่นำไปเขียนกราฟเพื่อแสดงความสัมพันธ์ระหว่างขนาดแรงดึง (F) กับน้ำหนักถุงทรายรวมกับขนาดของน้ำหนักแผ่นไม้ (W) ได้กราฟดังรูป จงหาสัมประสิทธิ์ความเสียดทาน
 |
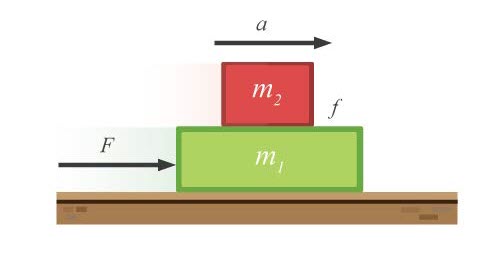
| 171. | กล่องสองใบมวล m1 และ m2 ตามลำดับ วางซ้อนกันบนพื้นราบไร้ความฝืด มีแรง F กระทำต่อกล่อง ทำให้กล่องทั้งสองเคลื่อนที่ไปทางขวาด้วยความเร่ง a ถ้า f เป็นแรงเสียดทานสูงสุดที่มีได้ระหว่างผิวสัมผัสของกล่องทั้งสอง F มีค่าได้มากที่สุดเท่าใด มวล m2 จึงไม่ไถลบน m1
 |
| 172. | ปล่อยวัตถุ A จากหยุดนิ่งลงมาจากที่สูง H ที่เวลา \(\rm\sqrt{\dfrac{H}{2g}}\) หลังจากนั้นก็ปาวัตถุ B ตามลงมา จงหาว่าจะต้องปา B ด้วยอัตราเร็วเท่าใด จึงจะให้ทัน A ที่พื้นพอดี (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
ตอบ \(\rm \dfrac{1}{4}\sqrt{\dfrac{2gH}{3}}\)
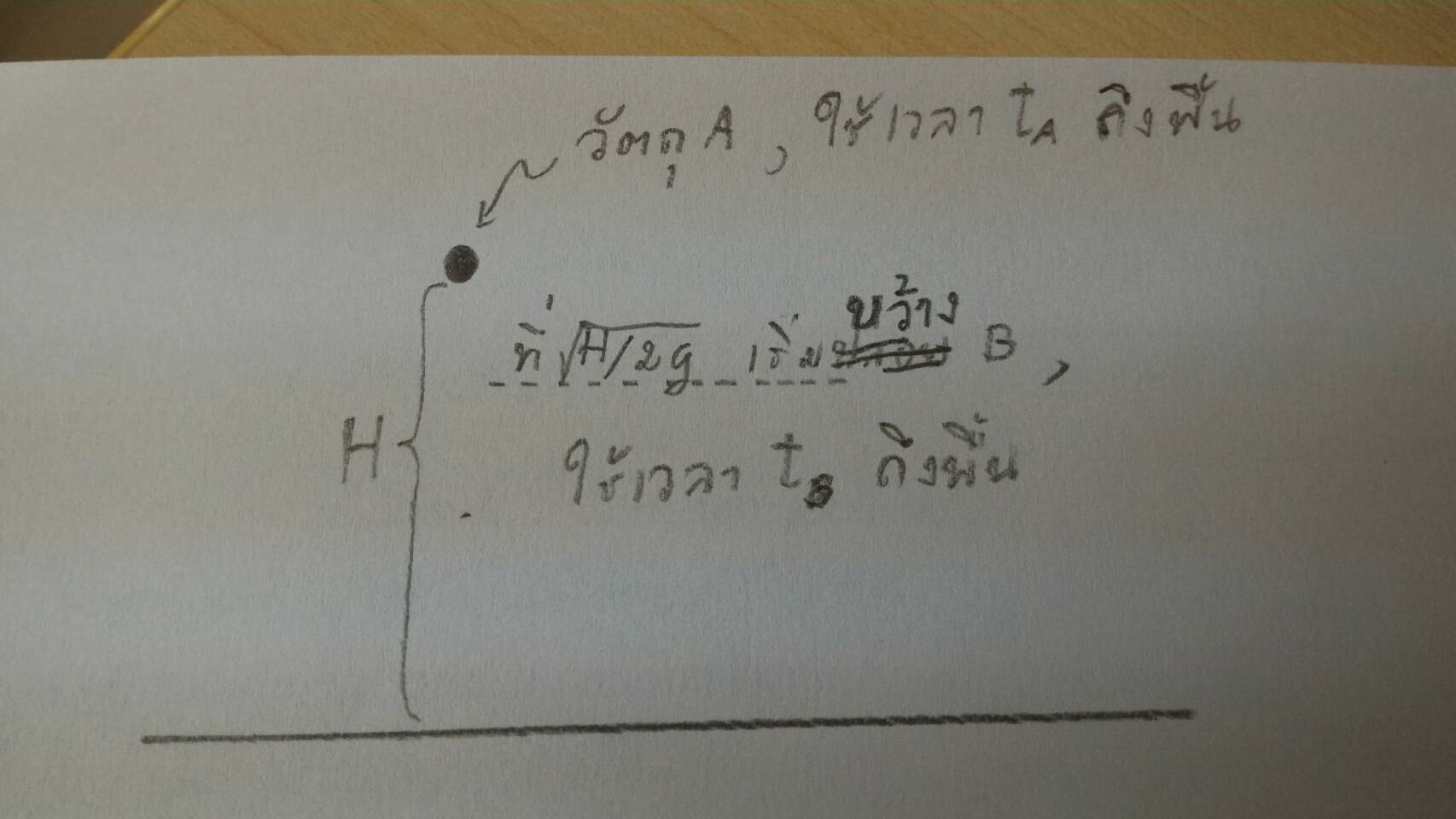(จากรูป) เวลาที่วัตถุ A ใช้ในการเคลื่อนที่ถึงพื้นหาได้จาก
หลังจากเวลา \(\rm\sqrt{\dfrac{H}{2g}}\) ขว้าง B ตามลงไปด้วยอัตราเร็วต้น \(\rm u_B\) และสามารถหาอัตราเร็วของ B ได้จาก
กำหนดให้ \(\rm t_A\)เป็นเวลาที่ A ใช้เคลื่อนที่จนถึงพื้น มีค่าเท่ากับ
ดังนั้น สามารถหาอัตราเร็วของ B ได้จาก
\(\begin{align*} \rm H&=\rm0+\dfrac{1}{2}g(t_A)^2\\ \rm t_A &=\rm\sqrt{\dfrac{2H}{g}} \end{align*}\)
หลังจากที่เวลาผ่านไป \(\rm\sqrt{\dfrac{H}{2g}}\) เริ่มขว้าง B และใช้เวลา \(\rm t_B\) เคลื่อนที่จนถึงพื้นพร้อม A ดังนั้น เขียนสมการได้ว่า
\(\begin{align*} \rm\sqrt{\dfrac{H}{2g}} + t_B&=\rm t_A\\ \rm t_B&=\rm t_A-\sqrt{\dfrac{H}{2g}}\\ \rm t_B&=\rm\sqrt{\dfrac{3H}{2g}} \end{align*}\)
\(\begin{align*} \rm H&= \rm u_B\cdot t_B +\dfrac{1}{2}g(t_B)^2\\ \rm H&=\rm u_B\cdot \sqrt{\dfrac{3H}{2g}}+\dfrac{1}{2}g\dfrac{3H}{2g}\\ \rm u_B&=\rm\dfrac{1}{4}\sqrt{\dfrac {2gH}{3}} \end{align*}\)
\(\rm t_A =\sqrt{\dfrac{H}{2g}}+T\)
สามารถหา T จากการเคลื่อนที่ของ B ด้วยอัตราเร็ว \(\rm v_B\)
\(\begin{align*} \rm H&=\rm u_B \cdot T+\dfrac{1}{2}gT^2\\ 0&=\rm T^2+\sqrt{\dfrac{2H}{g}}T -\dfrac{3H}{2g}\\ \rm T&=\rm+\sqrt{\dfrac{3H}{2g}} \end{align*}\)
หมายเหตุ เลือกค่าเวลาเป็นบวกดังนั้น สามารถหาอัตราเร็วของ B ได้จาก
\(\begin{align*} \rm H&=\rm u_B \cdot \sqrt{\dfrac{3H}{2g}}+\dfrac{1}{2}g\dfrac{3H}{2g}\\ \rm u_B &= \rm \dfrac{1}{4}\sqrt{\dfrac{2gH}{3}} \end{align*}\)
| 173. | รถไฟ A และ B สองขบวนแล่นบนรางตรงเดียวกันมาในทิศทางตรงกันข้ามพนักงานขับรถต่างเห็นรถไฟอีกขบวนหนึ่งอยู่ข้างหน้า จึงดึงห้ามล้อพร้อมกันเมื่อรถไฟทั้งสองอยู่ห่างกัน D และมีอัตราเร็วตอนนั้น uA และ uB สมมุติว่ารถไฟทั้งสองขบวนเคลื่อนที่ช้าลงด้วยความหน่วงคงตัว และรถไฟหยุดพร้อมกันที่ระยะห่างกัน d
1) จงหาอัตราส่วนขนาดความหน่วงของรถไฟ B ต่อขนาดความหน่วงของรถไฟ A
2) จงหาขนาดความหน่วงของรถไฟ A
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
ตอบ
1) \(\rm \dfrac{a_{_B}}{a_{_A}} = \dfrac{u_{_B}}{u_{_A}}\)
2) \(\rm a_{_A}=\dfrac{u_{_A}}{2(D-d)}(u_{_A}+u_{_B})\)
1) \(\rm \dfrac{a_{_B}}{a_{_A}} = \dfrac{u_{_B}}{u_{_A}}\)
2) \(\rm a_{_A}=\dfrac{u_{_A}}{2(D-d)}(u_{_A}+u_{_B})\)
| 174. | รางลื่นรูปวงกลมรัศมี R อยู่ในระนาบดิ่งมวล m ถูกดีดจากจุดล่างสุดให้ไถลขึ้นด้านในของราง พอถึงจุด A มวล m ก็แยกตัวจากรางเเล้วเคลื่อนที่โค้งวกลงมาตัดเเนวระดับเดียวกันกับ A ที่จุด B จงหาค่าของระยะทาง AB ในเทอมของ R กับ θ (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 1 ก.ย. 2556)  |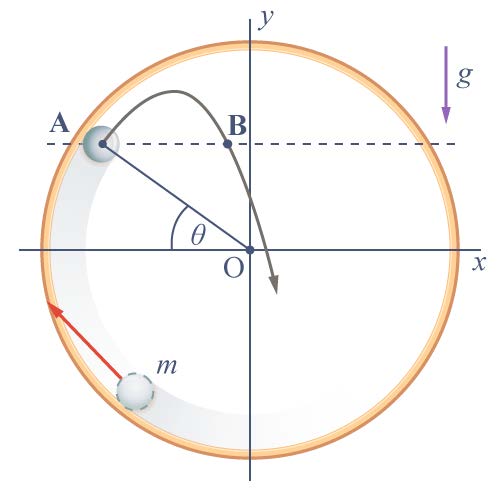
| 175. | นาย A และ นาย B แรกอยู่ห่างกันเป็นระยะทาง d นาย A กับ B ตั้งต้นออกวิ่งเข้าหากันที่จังหวะเดียวกัน A และ B มีอัตราเร็วคงที่เท่ากับ v1 และ v2 ตามลำดับ ทั้งคู่จะชนกันเมื่อ A เคลื่อนที่ได้ระยะทางเท่าไหร่ (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2554)  |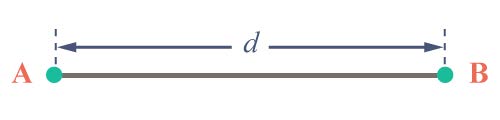
| 176. | นักบิน T และ C ขณะที่กำลังบินด้วยความเร็ว \(\rm \vec v_c\) และ \(\rm \vec v_T\) ตามลำดับเทียบกับพื้นโลกนััน นักบิน T จะพบว่า C กำลังเคลื่อนที่หนีจากเขาด้วยความเร็ว(สัมพันธ์) ขนาดเท่าไร (ตอบในรูป vc vT และ θ)
 |
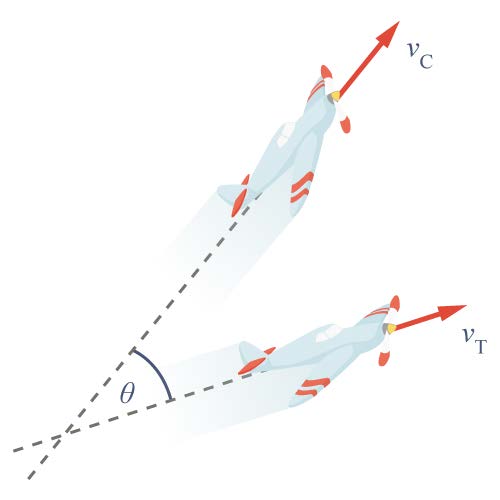| 177. | ระยะทาง AB = D เป็นรางรถไฟตรง เมื่อนกออกบินจาก A พร้อมกันกับที่รถไฟออกจาก B นกบินได้เร็ว รถไฟเคลื่อนที่เร็ว เมื่อนกบินถึงรถไฟก็บินกลับทันทีด้วยความเร็วขนาดเท่าเดิม เมื่อนกบินถึง A รถไฟจะอยู่ห่าง B เท่าไร (กำหนดว่า v > u นกจะได้ไม่ถูกชน)
 |
| 178. | โจ๊กเกอร์วางแผนปล่อยหนูปีศาจออกมาอาละวาดในเมือง เขาเอาหนูปีศาจใส่รถบรรทุกแล่นด้วยอัตราเร็ว 10 m/s ไปตามถนนตรงเเละปล่อยหนูปีศาจออกมาทีละตัว โดยปล่อยหนึ่งตัวต่อวินาที หนูปีศาจเมื่อหลุดจากรถก็วิ่งไปข้างหน้าทันทีด้วยอัตราเร็ว 20 m/s (อัตราเร็วของหนูปีศาจบนถนนไม่ขึ้นกับอัตราเร็วของรถบรรทุก) แบทแมนรู้ข่าวนี้ล่วงหน้าจึงรีบมาจัดการเก็บหนูปีศาจ เขาขับรถค้างคาวแล่นสวนเข้ามาด้วยอัตราเร็ว 20 m/s ในทิศตรงข้ามกับทิศที่หนูวิ่งรถค้างคาวมีเครื่องมือเก็บหนูปีศาจทันทีที่หนูถึงรถ จงหาว่าแบทแมนจะเก็บหนูปีศาจไปทำหนูสะเต๊ะได้กี่ตัวต่อหนึ่งนาที |
| 179. | ปล่อยวัตถุหนึ่งจากหยุดนิ่งจากที่สูงขนาดหนึ่งลงมาในแนวดิ่ง พบว่าในวินาทีสุดท้ายก่อนกระทบพื้น วัตถุเคลื่อนที่ได้ระยะทางหนึ่งในสี่ของความสูงทั้งหมดที่ตกลงมา จงหาว่าวัตถุใช้เวลาทั้งหมดเท่าใดในการตกลงมาก่อนถึงพื้น |
| 180. | รถไฟขบวนหนึ่งกำลังแล่นด้วยอัตราเร็ว vA ไปตามตารางตรง ทันใดนั้น พนักงานขับรถก็สังเกตเห็นรถไฟอีกขบวนหนึ่งที่ระยะห่าง d กำลังแล่นอยู่ข้างหน้าไปในทิศทางเดียวกันด้วยอัตราเร็ว vB เขาจึงดึงห้ามล้อทันที ถ้ารถไฟแล่นต่อด้วยความหน่วงคงตัว เเละรถไฟขบวนหน้าแล่นด้วยความเร็วเท่าเดิมไปเรื่อย ๆ จงหาความหน่วงที่น้อยที่สุดที่จะทำให้หลีกเลี่ยงการชนกับรถไฟขบวนหน้าได้พอดี |
| 181. | โยงวัตถุ A ขึ้นในแนวดิ่งด้วยอัตราเร็ว u และที่เวลา u/g ต่อมาก็โยงวัตถุ B ตามขึ้นไปด้วยอัตราเร็ว u เท่ากัน ถ้าวัตถุทั้งสองชนกันเหนือพื้น จงหาความสูงของตำเเหน่งที่วัตถุทั้งสองชนกัน ในที่นี้ g คือ ขนาดความเร่งสนามโน้มถ่วงโลกที่บริเวณนั้น |
| 182. | ล้อรัศมี R กำลังหมุนอยู่กับที่รอบแกน C ด้วยอัตราเร็ว f รอบต่อวินาที หยดน้ำที่ถูกสลัดออกไปจากจุด A ในแนวระดับจะตกกระทบพื้นระดับห่างจากจุด O เป็นระยะทางเท่าไร
 |
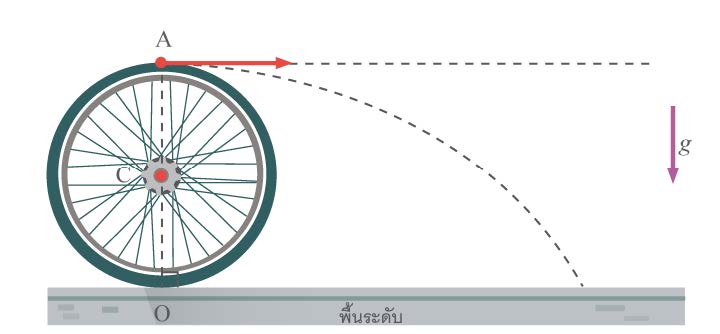| 183. | ยิงกระสุนปืนออกไปในแนวราบ (บนผิวดวงจันทร์) กระสุนกระทบเป้าที่ระยะห่าง 25 เมตร ที่ตำแหน่ง 5 mm ใต้แนวการยิง แต่ถ้าเลื่อนเป้าให้ห่างจากจุดที่ยิงเป็น 50 เมตร ลูกปืนจะกระทบเป้าใต้แนวการยิงกี่มิลลิเมตร |
| 184. | ยิงโปรเจคไทล์อันแรกขึ้นจากพื้นในแนวดิ่งด้วยความเร็วต้น vo ยิงอันที่สองในแนวดิ่งตามขึ้นไปจากจุดเดียวกันด้วยความเร็วต้น \(\rm\dfrac{v_o}{2}\) ในจังหวะที่อันแรกขึ้นถึงจุดสูงสุดพอดี ทั้งคู่จะทันกันที่ตำแหน่งสูงจากพื้นเท่าไร |
| 185. | วัตถุเคลื่อนที่เป็นวงกลมด้วยอัตราเร็วไม่คงตัว นอกจากมีส่วนประกอบความเร่งเข้าสู่ศูนย์กลางแล้วยังมีส่วนประกอบความเร่งในแนว สัมผัสด้วยรถยนต์คันหนึ่งซึ่งเดิมอยู่นิ่งเคลื่อนที่ไปตามเส้นทางวงกลมรัศมี 40.0 m ด้วยส่วนประกอบความเร่งในแนวสัมผัสขนาดคงตัว 2.00 m/s2 ตอนตั้งต้นรถยนต์อยู่ที่ตำแหน่งตะวันตกสุดของวงกลมและกำลังจะแล่นไปในทิศเหนือ 1) หลังจากที่รถยนต์แล่นไปได้ระยะทาง 1/4 ของเส้นรอบวง รถยนต์มีอัตราเร็วเท่าใด และกำลังแล่นไปทางทิศใด
2) ที่จุดนี้ส่วนประกอบความเร่งในแนวเข้าสู่ศูนย์กลางของรถยนต์มีขนาดเท่าใด
3) ที่จุดเดียวกันนี้ความเร่งสุทธิของรถยนต์มีขนาดเท่าใด
|
| 186. |  กำหนดให้ นำไปใช้ได ้\(\left(\dfrac{1.50}{9.8}\right)^{\frac{1}{2}}=0.391\) |
| 187. | รถเคลื่อนที่ไปทางทิศตะวันออกจากจุด A ไปยังจุด B ในเวลา 20 วินาที ได้ระยะทาง 200 เมตร หรือการกระจัด 200 เมตร ไปทางทิศตะวันออก รถคันนี้มีอัตราเร็วเฉลี่ยและความเร็วเฉลี่ยเป็นเท่าใด
 |
ตอบ อัตราเร็วเฉลี่ยและความเร็วเฉลี่ย เท่ากับ 10 m/s มีทิศไปทางทิศตะวันออก
อัตราเร็วเฉลี่ย \(=\) ระยะทาง / เวลา \(\rm= \dfrac{200~m}{20~s} = 10~m/s\)
ความเร็วเฉลี่ย \(=\) การกระจัด / เวลา \(\rm= \dfrac{200~m}{20~s} = 10~m/s\)
ดังนั้น อัตราเร็วเฉลี่ยและความเร็วเฉลี่ย เท่ากับ 10 m/s มีทิศไปทางทิศตะวันออก| 188. | เด็กคนหนึ่งเดินไปทางทิศเหนือได้ระยะทาง 300 เมตร จากนั้นเดินไปทางทิศตะวันออกได้ระยะทาง 400 เมตร ใช้เวลาเดินทางทั้งหมด 500 วินาที เด็กคนนี้เดินด้วยอัตราเร็วเฉลี่ยกี่เมตรต่อวินาที |
ตอบ 1.4 m/s
เรื่อง การเคลื่อนที่แนวตรง
อัตราเร็วเฉลี่ย คือ ระยะทางทั้งหมดในช่วงเวลาที่ใช้ เราสามารถหาอัตราเร็วเฉลี่ยของเด็กคนนี้ได้ ดังนี้
เรื่อง การเคลื่อนที่แนวตรง
อัตราเร็วเฉลี่ย คือ ระยะทางทั้งหมดในช่วงเวลาที่ใช้ เราสามารถหาอัตราเร็วเฉลี่ยของเด็กคนนี้ได้ ดังนี้
\(\rm v =\dfrac{s}{t} = \dfrac{300+400~m}{500~s} = 1.4 ~m/s\)
ดังนั้น เด็กคนนี้เดินด้วยอัตราเร็วเฉลี่ย 1.4 เมตรต่อวินาที| 189. | ถ้าการเคลื่อนที่ของวัตถุที่ลากแถบกระดาษ ซึ่งเครื่องเคาะสัญญาณเวลาที่เคาะทุกๆ \(\dfrac{1}{50}\)วินาที ทำให้เกิดจุดดังรูป จากการสังเกตจุดเหล่านี้จะบอกได้คร่าวๆ ว่าความเร่งเป็นอย่างไร
 |
ตอบ สม่ำเสมอ
จากสมการ
แต่ระยะทางของจุดที่บันทึกได้เพิ่มขึ้นเรื่อยๆ แสดงว่าค่าความเร็วเพิ่มขึ้น นั้นคือจะต้องมีความเร่ง และสังเกตจากรูปพบว่าระยะมีการเพิ่มค่อนข้างสม่ำเสมอ
จึงสรุปว่า เป็นการบันทึกการเคลื่อนที่ที่มีความเร่งสม่ำเสมอ
จากสมการ
v = u + at
เนื่องจาก ความเร็วเริ่มต้นในการเคลื่อนที่คงที่ และโจทย์กำหนดให้บันทึกทุกๆ \(\dfrac{1}{50}\) วินาที นั้นคือ เวลาที่ใช้ในการเคลื่อนที่คงที่แต่ระยะทางของจุดที่บันทึกได้เพิ่มขึ้นเรื่อยๆ แสดงว่าค่าความเร็วเพิ่มขึ้น นั้นคือจะต้องมีความเร่ง และสังเกตจากรูปพบว่าระยะมีการเพิ่มค่อนข้างสม่ำเสมอ
จึงสรุปว่า เป็นการบันทึกการเคลื่อนที่ที่มีความเร่งสม่ำเสมอ
| 190. | กราฟของตำแหน่งวัตถุบนแนวแกน x กับเวลา t เป็นดังรูป ช่วงเวลาใดหรือที่ตำแหน่งใดที่วัตถุไม่มีความเร่ง
 |
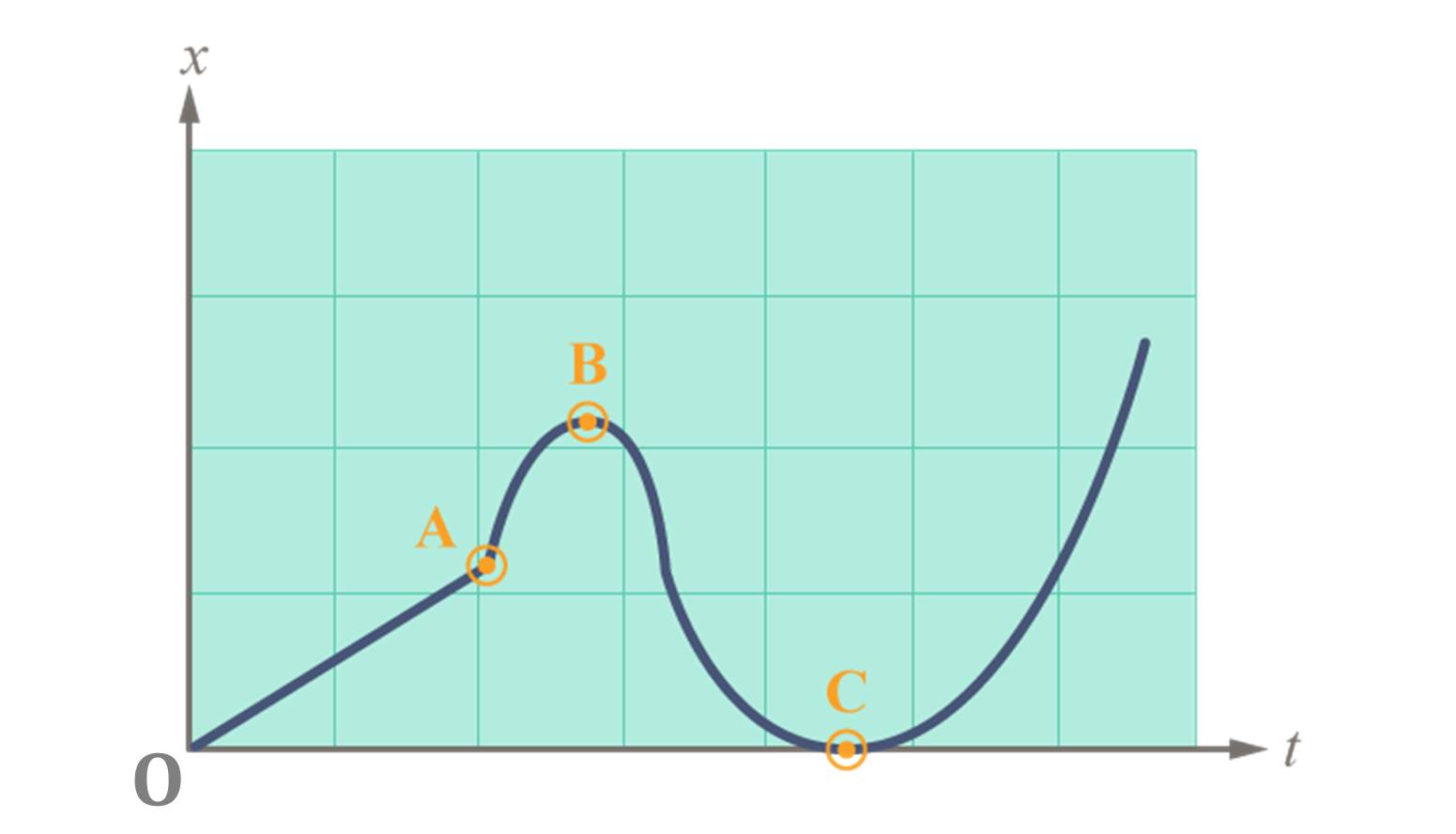ตอบ ช่วง OA
ช่วงที่วัตถุไม่มีความเร่ง คือช่วงที่ความเร็วต้องมีค่าคงที่ จากกราฟแสดงความสัมพันธ์ระหว่างตำแหน่งในแนวแกน x กับ
เวลา t ความชันกราฟซึ่งก็คือ ความเร็วของการเคลื่อนที่ตามสมการ
ช่วงที่วัตถุไม่มีความเร่ง คือช่วงที่ความเร็วต้องมีค่าคงที่ จากกราฟแสดงความสัมพันธ์ระหว่างตำแหน่งในแนวแกน x กับ
เวลา t ความชันกราฟซึ่งก็คือ ความเร็วของการเคลื่อนที่ตามสมการ
\(\rm slope =\dfrac{Δy}{Δx} = \dfrac{Δx}{Δt}= v\)
และช่วงที่กราฟมีความชันคงที่ หรือมีความเร็วคงที่ คือ ช่วง OA| 191. | ลูกบอลลูกหนึ่งถูกปล่อยลงมาจากหน้าต่างถึงพื้น กราฟระหว่างความเร็ว-เวลาของการเคลื่อนที่เป็นดังภาพ อยากทราบว่า ที่จุด A ลูกบอลอยู่ที่ใด และความสูงจากหน้าต่างถึงพื้นเท่ากับเท่าไร
 |
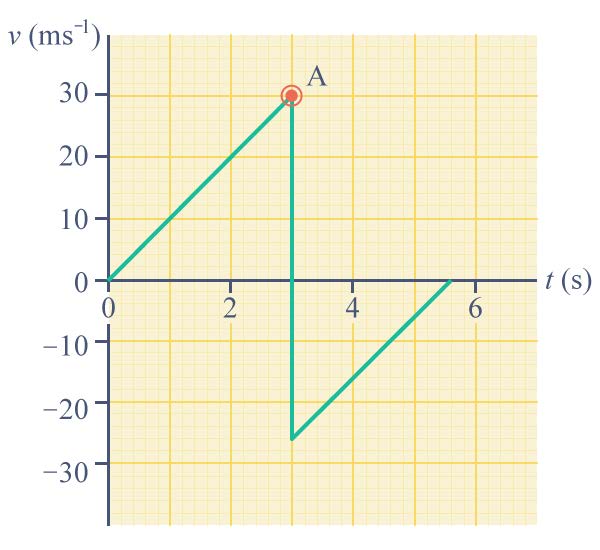ตอบ หน้าต่างอยู่สูงจากพื้น 45 เมตร
ที่จุด A เป็นจุดที่มีความเร็วสูงสุด นั้นคือ จุดที่ลูกบอลกระทบพื้น
ซึ่งตอนนั้นลูกบอลมีความเร็ว 30 m/s
ดังนั้น จากหน้าต่างถึงพื้นลูกบอลใช้เวลา 3 วินาที
ระยะทางจากหน้าต่างถึงพื้น จึงหาได้จาก พื้นที่ใต้กราฟจากเวลา 0 - 3 วินาที
จะได ้
ที่จุด A เป็นจุดที่มีความเร็วสูงสุด นั้นคือ จุดที่ลูกบอลกระทบพื้น
ซึ่งตอนนั้นลูกบอลมีความเร็ว 30 m/s
ดังนั้น จากหน้าต่างถึงพื้นลูกบอลใช้เวลา 3 วินาที
ระยะทางจากหน้าต่างถึงพื้น จึงหาได้จาก พื้นที่ใต้กราฟจากเวลา 0 - 3 วินาที
จะได ้
พื้นที่ใต้กราฟ \(=\dfrac{1}{2}\times30\times3=45\)
ดังนั้น หน้าต่างอยู่สูงจากพื้น 45 เมตร| 192. | รถยนต์คันหนึ่งเคลื่อนที่ในแนวตรงโดยมีความเร็ว 20 เมตรต่อวินาที ต่อมาคนขับได้เร่งเครื่องยนต์ทำให้รถยนต์มีความเร่ง 3 เมตรต่อวินาที2 เป็นเวลา 5 วินาที จงหาความเร็วที่เวลา 5 วินาที |
ตอบ 35 เมตรต่อวินาที มีทิศทางเดียวกับความเร็วเดิม
เดิมรถยนต์มีความเร็ว \(\rm \vec{v_1}\) ต่อมามีความเร่งทำให้ความเร็วเปลี่ยนไป
ดังนั้น ความเร็วที่สิ้นสุดเวลา 5 วินาที คือ \(\rm \vec{v_2} = \vec{v_1}+Δ \vec{v}\)
จาก
เดิมรถยนต์มีความเร็ว \(\rm \vec{v_1}\) ต่อมามีความเร่งทำให้ความเร็วเปลี่ยนไป
ดังนั้น ความเร็วที่สิ้นสุดเวลา 5 วินาที คือ \(\rm \vec{v_2} = \vec{v_1}+Δ \vec{v}\)
\(a = \rm\dfrac{v_2-v_1}{Δt}\)
ดังนั้น
\(\begin{align*} \rm v_2 − v_1 &= a(Δt)\\ \rm v_2 &= v_1 + a(Δt)\\ &=20 \rm ~m/s + (3~m/s^2)(5~s)\\ &=35\rm~m/s \end{align*}\)
ดังนั้น ความเร็วสุดท้ายเท่ากับ 35 เมตรต่อวินาที มีทิศทางเดียวกับความเร็วเดิม| 193. | วัตถุชนิดหนึ่งเคลื่อนที่จากจุด A ไปจุด B ด้วยอัตราเร็ว 6.0 m/s ใช้เวลา 20 วินาที หลังจากนั้นเคลื่อนที่จากจุด B ไปจุด C ด้วยอัตราเร็ว 4.0 m/s ใช้เวลา 10 วินาที จงหาอัตราเร็วเฉลี่ยของวัตถุนี้ในการเคลื่อนที่จากจุด A ไปจุด C
 |
ตอบ 5.3 m/s
จากจุด A ไป B เคลื่อนที่ไปได้ระยะทางเท่ากับ
จากจุด A ไป B เคลื่อนที่ไปได้ระยะทางเท่ากับ
\(\rm S_{AB} = 6.0 × 20 = 120~m\)
จากจุด B ไป C เคลื่อนที่ไปได้ระยะทางเท่ากับ
\(\rm S_{BC} = 4.0 × 10 = 40~m\)
ดังนั้น อัตราเร็วเฉลี่ยจากจุด A ไป C มีค่าเท่ากับ
\(\rm \dfrac{120+40}{20+10}=5.3~m/s\)
| 194. | วัตถุหนึ่งเคลื่อนที่เป็นวงกลมรัศมี 21 เมตร ครบหนึ่งรอบ การกระจัดมีค่าเท่าใด |
ตอบ 0 เมตร
การกระจัดเป็นปริมาณเวกเตอร์ ขนาดของการกระจัดสามารถหาได้จาก ระยะที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดสุดท้ายของการเปลี่ยนตำแหน่งของวัตถุ
จากโจทย์ วัตถุเคลื่อนที่เป็นวงกลมรัศมี เมตร ครบหนึ่งรอบ แสดงว่า วัตถุเคลื่อนที่กลับมายังจุดเริ่มต้น
ดังนั้น การกระจัดของวัตถุจึงมีค่าเป็น 0
การกระจัดเป็นปริมาณเวกเตอร์ ขนาดของการกระจัดสามารถหาได้จาก ระยะที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดสุดท้ายของการเปลี่ยนตำแหน่งของวัตถุ
จากโจทย์ วัตถุเคลื่อนที่เป็นวงกลมรัศมี เมตร ครบหนึ่งรอบ แสดงว่า วัตถุเคลื่อนที่กลับมายังจุดเริ่มต้น
ดังนั้น การกระจัดของวัตถุจึงมีค่าเป็น 0
| 195. | จงเขียนเส้นทางการเคลื่อนที่ของโพรเจกไทล์ที่ยิงด้วยอัตราเร็วต้นและมุมเท่ากันบนดวงจันทร์และบนโลก |
ตอบ
หากคำนึงถึงแรงโน้มถ่วงระหว่างดวงจันทร์และโลกที่มีค่าต่างกันอยู่ประมาณ 6 เท่า ดังนั้น ถ้ายิงโปรเจคไทล์ด้วยมุมและความเร็วต้นเท่ากัน เส้นทางการเคลื่อนที่จะเป็นดังรูป
เมื่อ เส้นสีน้ำเงินแทนการเคลื่อนที่บนโลก
และ เส้นสีส้มแทนการเคลื่อนที่บนดวงจันทร์
หากคำนึงถึงแรงโน้มถ่วงระหว่างดวงจันทร์และโลกที่มีค่าต่างกันอยู่ประมาณ 6 เท่า ดังนั้น ถ้ายิงโปรเจคไทล์ด้วยมุมและความเร็วต้นเท่ากัน เส้นทางการเคลื่อนที่จะเป็นดังรูป
เมื่อ เส้นสีน้ำเงินแทนการเคลื่อนที่บนโลก
และ เส้นสีส้มแทนการเคลื่อนที่บนดวงจันทร์
| 196. | ถ้าต้องการยิงปืนใหญ่ให้ได้ระยะทางในแนวดิ่ง เป็น \(\dfrac{1}{2}\) เท่าของระยะทางในแนวระดับ จะต้องปรับปากกระบอกปืนใหญ่ให้ทำมุมเท่าไรกับแนวระดับ
 |
ตอบ \(\theta = \tan^{-1}2\)
จากสมการหาระยะในแนวระดับ
ดังนั้น \(\rm \theta=\tan^{-1}2\)
จากสมการหาระยะในแนวระดับ
\(\rm S_x=\dfrac{u^2\sin2\theta}{g}=\dfrac{u^2(2\sin\theta\cos\theta)}{g}\)
และจากสมการหาระยะในแนวระดิ่ง
\(\rm S_y = \dfrac{u^2\sin^2\theta}{2g}\)
เราสามารถหามุม θ ที่ทำให้ \(\rm S_y =\dfrac{1}{2}S_x\)ได้ดังนี้ดังนั้น \(\rm \theta=\tan^{-1}2\)
| 197. | ในการทดลองเรื่องการเคลื่อนแนววงกลมในระนาบระดับ ขณะที่กำลังแกว่งให้จุกยางหมุนอยู่นั้นเชือกที่ผูกกับจุกยางขาดออกจากกัน จงอธิบายถึงแรงที่เกี่ยวข้องก่อนและหลังการขาดของเชือก การเคลื่อนที่ของจุกยางเป็นเช่นไรหลังจากที่เชือกขาดไปแล้ว |
ตอบ
ก่อนเชือกขาด มีแรงตึงเชือก(เป็นแรงเข้าสู่ศูนย์กลาง)และแรงโนม้ ถ่วงที่จุกยาง
หลังเชือกขาด มีแค่แรงโน้มถ่วงและจุกยางเคลื่อนที่แบบโพรเจคไทล์
ก่อนเชือกขาด มีแรงตึงเชือก(เป็นแรงเข้าสู่ศูนย์กลาง)และแรงโนม้ ถ่วงที่จุกยาง
หลังเชือกขาด มีแค่แรงโน้มถ่วงและจุกยางเคลื่อนที่แบบโพรเจคไทล์
| 198. | จงอธิบายถึงเงื่อนไขที่ทำให้วัตถุเคลื่อนที่เป็นวงกลม |
| 199. | ผูกวัตถุที่ปลายล่างของเชือกเส้นหนึ่งยาว 1 เมตร ตรึงปลายบนไว้แล้วแกว่งวัตถุให้เป็นวงกลมในระนาบระดับ ถ้าเชือกทำมุม θ กับแนวดิ่งวัตถุจะแกว่งครบรอบในเวลา T วินาที ความเร่งสู่ศูนย์กลางของวัตถุมีค่า |
ตอบ \(\rm \dfrac{4\pi^2\sin\theta}{T^2}\)
เรื่อง การเคลื่อนที่วงกลม
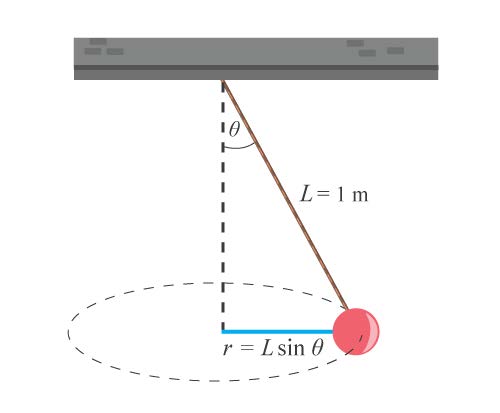
\(\rm \displaystyle ΣF_c = \dfrac{mv^2}{r} = mrω^2=ma_c\)
และจากความสัมพันธ์ระหว่างความเร็วเชิงมุม และคาบ ที่ใช้ในการเคลื่อนที่
\(\rm ω =\dfrac{2\pi}{T} \)
ดังนั้น ความเร่งสู่ศูนย์กลางของวัตถุ สามารถคำนวณได้จาก
\(\begin{align*}
\rm mrω^2 &= \rm ma_c\\
\rm (L~sin θ)\left(\dfrac{2\pi}{T}\right)^2 &= \rm a_c\\
\rm a_c &=\rm\dfrac{4\pi^2\sin\theta}{T^2}~m/s^2
\end{align*}\)
| 200. | ดาวเทียมที่วงโคจรใกล้กับไกลจากโลก จะมีอัตราเร็วในการโคจรต่างกันอย่างไร
 |
ตอบ
โดยปกติดาวเทียมจะโคจรรอบโลกโดยจะอยู่ในบริเวณที่อยู่เหนือบริเวณหนึ่งของโลกเสมอ ทั้งนี้ก็เพื่อรับสัญญาณให้กับพื้นที่ที่กำหนด ดังนั้น ดาวเทียมจึงต้องเคลื่อนที่ด้วยอัตราเร็วเท่ากับการหมุนรอบตัวเองของโลก ดาวเทียมที่อยู่ไกลจากโลกมาก จึงต้องเคลื่อนที่เร็วกว่าดาวเทียมที่อยู่ใกล้ เพราะระยะทางโคจรครบ 1 รอบของดาวเทียมที่อยู่ไกลจากโลก มีค่ามากกว่าระยะทางโคจรครบ 1 รอบของดาวเทียมที่อยู่ใกล้โลกนั้นเอง
โดยปกติดาวเทียมจะโคจรรอบโลกโดยจะอยู่ในบริเวณที่อยู่เหนือบริเวณหนึ่งของโลกเสมอ ทั้งนี้ก็เพื่อรับสัญญาณให้กับพื้นที่ที่กำหนด ดังนั้น ดาวเทียมจึงต้องเคลื่อนที่ด้วยอัตราเร็วเท่ากับการหมุนรอบตัวเองของโลก ดาวเทียมที่อยู่ไกลจากโลกมาก จึงต้องเคลื่อนที่เร็วกว่าดาวเทียมที่อยู่ใกล้ เพราะระยะทางโคจรครบ 1 รอบของดาวเทียมที่อยู่ไกลจากโลก มีค่ามากกว่าระยะทางโคจรครบ 1 รอบของดาวเทียมที่อยู่ใกล้โลกนั้นเอง
| 201. | เด็ก 4 คนนั่งอยู่ริมตลิ่งและขว้างก้อนหินพร้อมกันลงในน้ำคนละก้อน ถ้าแต่ละก้อนตกน้ำที่ตำแหน่งต่างกันคือ A B C และ D โดยมีทางเดินของก้อนหินดังรูป จงพิจารณาว่าก้อนหินที่ตกตรงตำแหน่งใดเป็นก้อนที่ถึงพื้นน้ำก่อน
 |
ตอบ C
ก้อนหินที่ถึงพื้นน้ำก่อน คือก้อนที่ใช้เวลาในการเคลื่อนที่น้อยที่สุด จากรูปเราพบว่าก้อนหินทั้งก้อน ต่างกันที่ความสูงที่ขึ้นไปได้และระยะไกลสุดที่ไปตก โดยความสัมพันธ์
ก้อนหินที่ถึงพื้นน้ำก่อน คือก้อนที่ใช้เวลาในการเคลื่อนที่น้อยที่สุด จากรูปเราพบว่าก้อนหินทั้งก้อน ต่างกันที่ความสูงที่ขึ้นไปได้และระยะไกลสุดที่ไปตก โดยความสัมพันธ์
\(\begin{align*} \rm S_y &=\rm u_yt+\dfrac{1}{2}a_yt^2\\ 0&=\rm u_yt+\dfrac{1}{2}a_yt^2\\ \rm t&=\rm \dfrac{2u_y}{g} \end{align*}\)
ระยะสูงสุด H เราหาอัตราเร็วต้น uy จาก
\(\begin{align*} \rm v^2_y &=\rm u^2_y+2a_yS_y\\ 0&=\rm u^2_y-2gH\\ \rm u_y&=\rm \sqrt{2gH} \end{align*}\)
แทนในสมการข้างต้น เพื่อหาเวลาที่ใช้ในการเคลื่อนที่ จะได ้
\(\rm t=\dfrac{2\sqrt{2gH}}{g}=\dfrac{8H}{g}\)
จากสมการจะเห็นว่า ก้อนหินที่ตกถึงพื้นก่อน จะใช้เวลาในการเคลื่อนที่น้อยสุด นั่นคือก้อนที่ขึ้นไปได้น้อยที่สุดจะตกถึงพื้นก่อน ซึ่งคือ ก้อน C