หัวข้อฟิสิกส์ : มวล แรงและกฎการเคลื่อนที่
| 1. | คาบการแกว่งของนาฬิกาลูกตุ้มอย่างง่ายที่ลวดแขวนยาวขึ้นเพราะอุณหภูมิเพิ่มขึ้น กำหนด ก. คาบ T ของนาฬิกาลูกตุม้ อย่างง่ายเป็นไปตามสูตร \(\text{T} = 2π \sqrt{l/\text{g}}\) เมื่อ l เป็นความยาวของลวดแขวนลูกตุ้มและ g เป็นขนาดความเร่งเนื่องจากแรงโน้มถ่วงของโลก
ข. สัมประสิทธิ์การขยายตัวเชิงเส้นเนื่องจากความร้อน α คือ อัตราส่วนความยาวที่เปลี่ยนไป Δl ต่อความยาวเดิม l เมื่ออุณหภูมิเปลี่ยนไปหนึ่งหน่วย
ค. นักเรียนสามารถใช้การประมาณ \(\rm \sqrt{1+x}≈1 + x/2\) เมื่อ x มีขนาดน้อย 1 กว่ามาก ๆ
นาฬิกาลูกตุ้ม อย่างง่ายเรือนหนึ่งมีลวดแขวนที่มีสัมประสิทธิ์การขยายตัว เชิงเส้นเนื่องจากความร้อนเท่ากับ α และมีคาบแกว่ง T ที่ความยาว l1 เมื่ออุณหภูมิเพิ่มขึ้น Δθ น้อยมาก ๆ เมื่อ เทียบกับอุณหภูมิเดิม และคาบการแกว่งเปลี่ยนไปเป็น T + ΔT จงหาค่าอัตราส่วน ΔT/T ในรูปของตัวแปรที่กำหนดมา(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 2. | มวล M กับ m เชื่อมกันด้วยสปริงเบา ๆ กำลังสั่น "อยู่กับที่" เทียบกับระบบอ้างอิงเฉื่อย โดยที่ m สั่นด้วยแอมพลิจูด A จงหาค่าของแอมพลิจูดของการสั่นของ M (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555) 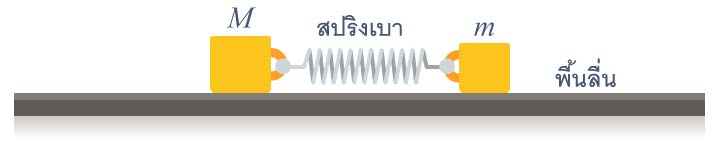 |
| 3. |  (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557) |
| 4. | การเคลื่อนที่ของระบบนี้บรรยายได้ด้วยการเคลื่อนที่ 3 สมการ
\(\rm m\ddot x_1 = +k(x_2 − x_1 − ℓ)\) . . . (1)
จงเขียนอีก 2 สมการให้ครบแล้วแก้สมการเพื่อหาความถี่ของการสั่นพื้นฐานซึ่งมีอยู่ 2 ค่า(ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 26 มี.ค. 2556) 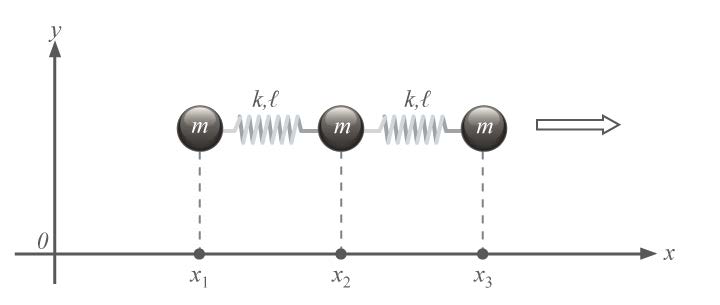 |
ตอบ
\(\rm m\ddot x_2 = +k(x_3-x_2 − ℓ)-k(x_2-x_1 − ℓ)\) . . . (2)
\(\rm m\ddot x_3 = -k(x_3-x_2 − ℓ)\) . . . (3)
\(\rm ω_2=\sqrt{\dfrac{3k}{m}}\)
\(\rm f_2 = \dfrac{1}{2\pi}\sqrt{\dfrac{3k}{m}}\)
\(\rm m\ddot x_2 = +k(x_3-x_2 − ℓ)-k(x_2-x_1 − ℓ)\) . . . (2)
\(\rm m\ddot x_3 = -k(x_3-x_2 − ℓ)\) . . . (3)
\(\rm ω_2=\sqrt{\dfrac{3k}{m}}\)
\(\rm f_2 = \dfrac{1}{2\pi}\sqrt{\dfrac{3k}{m}}\)
| 5. | ล้อทรงกระบอกตันมวล M รัศมี R สามารถหมุนได้คล่องรอบจุด O มีปลายหนึ่งของสปริง k ยึดไว้และอีกปลายของสปริงยึดกับเพดาน มวล m ซึ่งถ่วงขอบของทรงกระบอกทำให้นิ่งและ OA อยู่ในแนวระดับพอดี ต่อมาดึง m ลงนิดหน่อยแล้วปล่อย m จะเคลื่อนขึ้นลงๆ ด้วยคาบของการสั่นเป็นเท่าไร (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2553) 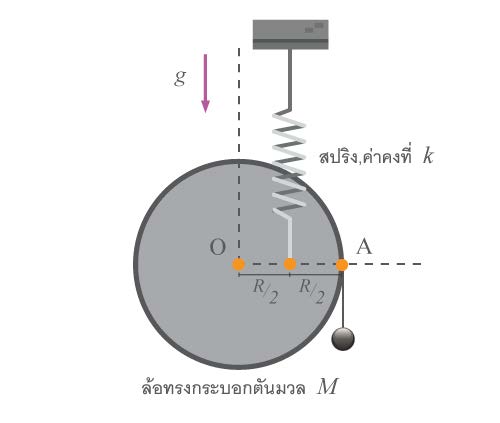 |
| 6. | ลูกกลมโลหะขนาดเล็กมาก 2 ลูกที่เหมือนกันทุกประการ (แต่ละลูกมีมวล m และประจุ q) ถูกแขวนจากเชือกที่ทำจากฉนวนยาว L จงหาค่า x เมื่อระบบอยู่ในสมดุล โดยมุม θ มีขนาดเล็กมากจนประมาณได้ว่า tan θ ≈ sin θ (ตอบในรูปของตัวแปร m, q, L และค่าคงที่มาตรฐานต่างๆ เช่น g) (ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 18 ต.ค. 2554) 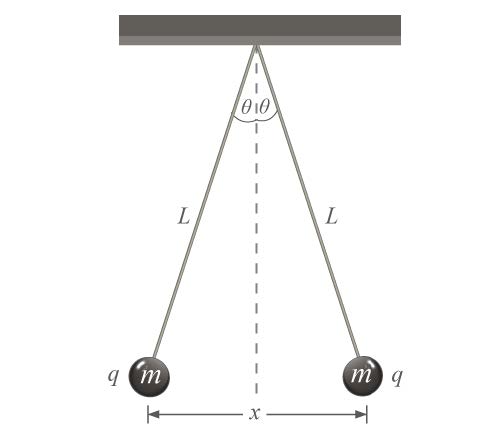 |
| 7. | แผ่นกลมแบนแกว่งได้คล่องในระนาบของแผ่นรอบจุด O ระยะทางจาก O ถึงจุด CM ต้องมีค่าเท่าไร คาบของการแกว่งด้วยแอมพลิจูดเล็ก ๆ จึงจะมีค่าเล็กที่สุด และค่านี้เป็นเท่าไรในรูปของ g , R (ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 24 มี.ค. 2552) 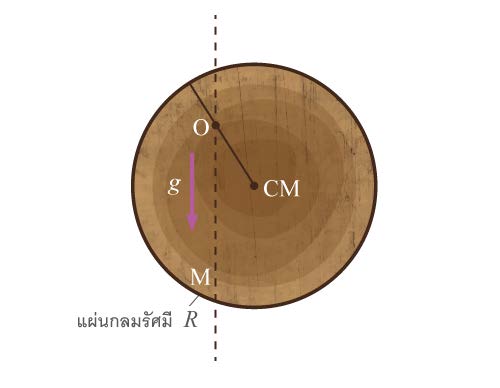 |
| 8. | ภาพนี้แสดงระบบในสภาวะสมดุลเชิงกล l เป็นระยะทางระหว่างรอกทั้งสอง ขณะที่เชือกส่วนนี้ทำมุม θ0 กับแนวดิ่งถ้าดึง M ลงนิดหน่อยแล้วปล่อยระบบจะสั่น ( M และ m เคลื่อนที่ขึ้นลงสลับกัน) จงวิเคราะห์หาคาบของการสั่นด้วยแอมพลิจูดเล็ก ๆ นี้ในเทอมของ m , M , l , g , sin θo (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557) หมายเหตุ \(\dfrac{1}{1+a} ≈ 1-a\) สำหรับ \(|a| ≪ 1\) \(Δ(\cos θ) ≈ −\sin θ ⋅ Δθ\) ถ้ารู้แคลคูลัส... (ไม่รู้ก็ทำได้อยู่แล้ว) |
| 9. | สปริงไร้มวล ความยาวธรรมชาติ l ค่าคงตัวสปริง k ขดหนึ่งวางตั้งตรงอยู่ในแนวดิ่ง ปลายล่างของสปริงถูกยึดไว้กับพื้น ส่วนปลายบนเคลื่อนที่ได้อย่าอิสระ ปล่อยวัตถุมวล m จากที่สูง h จากปลายบนของสปริงให้ตกในแนวดิ่ง ลงมาบนสปริงกำหนดว่าเมื่อวัตถุชนกับสปริง แล้วจะถูกยึดติดกับปลายของสปริงตลอดเวลา สมมุติด้วยว่าความสูงที่ปล่อยวัตถุลงมาไม่สูงมากพอให้สปริงหดสั้นจนถึงพื้นได ้
1) สปริงหดสั้นที่สุดเท่าใด
2) ตำแหน่งสมดุลของวัตถุอยู่สองจากพื้นเท่าใด
3) วัตถุจะกระดอนกลับขึ้นไปสูงสุดจากพื้นเท่าใด
4) วัตถุมีอัตราเร็วสูงสุดเท่าใด
5) ให้ y เป็นตำแหน่งของวัตถุจากตำแหน่งสมดุล โดยให้ y มีค่าเป็นบวกเมื่อวัดขึ้นในแนวดิ่ง ที่ตำแหน่งใด ๆ นี้วัตถุมีความเร่งเท่าใด
จงใหเ้หตุผลแสดงว่าวัตถุจะสั่นขึ้นลงแบบฮาร์มอนิกอย่างง่าย แล้วให้หาว่าตำแหน่ง y ของวัตถุจากตำแหน่งสมดุลที่เวลา t ใด ๆหลังติดกับสปริงเป็นฟังก์ชันอย่างใดของเวลา t
6) การสั่นนี้มีคาบเท่าใด
(ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 24 ต.ค. 2552) |
ตอบ
1) \(\rm x =\dfrac{mg}{k}+\dfrac{\sqrt{m^2g^2 + 2mghk}}{k}\)
2) \(l-\dfrac{\text{mg}}{\text{k}}\)
3) \(\text H =l -\dfrac{\text{mg}}{\text{k}}+\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\)
4) \(\rm v_{max} = \sqrt{\dfrac{mg^2}{k}+2gh}\)
5) \(\rm \dfrac{d^2}{dt^2}y=-\left(\dfrac{k}{m}\right)y\) และ \(\rm y(t)=\left[\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\right]\sin\left[\sqrt{\dfrac{k}{m}}t+arcsin\left(\dfrac{mg}{\sqrt{\rm m^2g^2 + 2mghk}}\right)\right]\)
6) \(\rm T=2\pi\sqrt{\dfrac{m}{k}}\)
1) \(\rm x =\dfrac{mg}{k}+\dfrac{\sqrt{m^2g^2 + 2mghk}}{k}\)
2) \(l-\dfrac{\text{mg}}{\text{k}}\)
3) \(\text H =l -\dfrac{\text{mg}}{\text{k}}+\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\)
4) \(\rm v_{max} = \sqrt{\dfrac{mg^2}{k}+2gh}\)
5) \(\rm \dfrac{d^2}{dt^2}y=-\left(\dfrac{k}{m}\right)y\) และ \(\rm y(t)=\left[\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\right]\sin\left[\sqrt{\dfrac{k}{m}}t+arcsin\left(\dfrac{mg}{\sqrt{\rm m^2g^2 + 2mghk}}\right)\right]\)
6) \(\rm T=2\pi\sqrt{\dfrac{m}{k}}\)
| 10. | ในการเคลื่อนที่แบบซิมเปิลฮาร์มอนิกของวัตถุใดๆ ความเร่งของวัตถุมีเฟสนำหน้าความเร็วอยู่เท่าใด |
| 11. | การทดลองเรื่องการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย ถ้าใหลู้กตุ้มเคลื่อนที่จาก ไป ไป แล้ว ไป ดังรูปใช้เวลา วินาที คาบของการเคลื่อนที่มีค่าเท่าใด
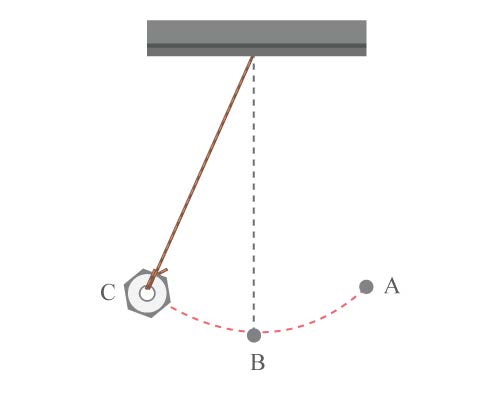 |
| 12. | ถ้าลูกตุ้มในรูป ก แกว่งจากตำแหน่ง (1) ไปตำแหน่ง (2) ใช้เวลา t การแกว่งในรูป ข จากตำแหน่ง a ไป b ไป c ใช้เวลาเท่าใด
 |
| 13. | จงยกตัวอย่างวัตถุที่มีการสั่นที่พบเห็นในชีวิตประจำวัน |
| 14. | มวล 400 กรัม ติดอยู่กับสปริงซึ่ง มีค่านิจสปริง 25.6 นิวตันต่อเมตร โดยเริ่มต้นดึงมวลให้ได้ระยะ 5.00 เซนติเมตร จากตำแหน่งสมดุล แล้วปล่อยให้สั่นอย่างอิสระในแนวระดับ จงหาสมการแสดงการกระจัดในช่วงเวลาต่าง ๆ ของมวลนี้
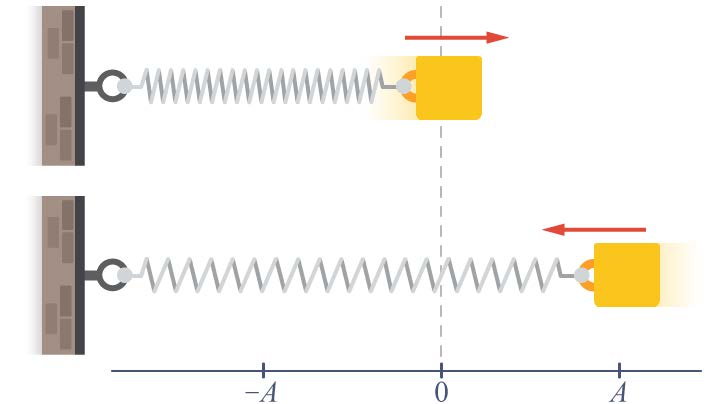 |
| 15. | เมื่อใช้สโตรโบสโคปที่มี 1 ช่อง วัดความถี่ของการสั่นของมวล 0.25 กิโลกรัม ซึ่งผูกกับสปริงที่แขวนในแนวดิ่ง พบว่าเห็นภาพมวลหยุดนิ่งที่หนึ่งได้เมื่ออัตราเร็วของสโตรโบสโคปเป็น 3, 4 และ 12 รอบต่อวินาที ถัดกันไป ถามว่าค่านิจสปริงมีค่ากี่นิวตันต่อเมตร |
| 16. | ปล่อยลูกตุ้มซึ่งมีสายยาว 90 เซนติเมตรจากมุมหนึ่งให้แกว่ง แต่สายลูกตุ้มติดตะปูที่ระยะ 50 เซนติเมตร ใต้จุดที่แขวนในแนวดิ่งลูกตุ้มจะแกว่งกลับมาที่เดิมในเวลาเท่าใด
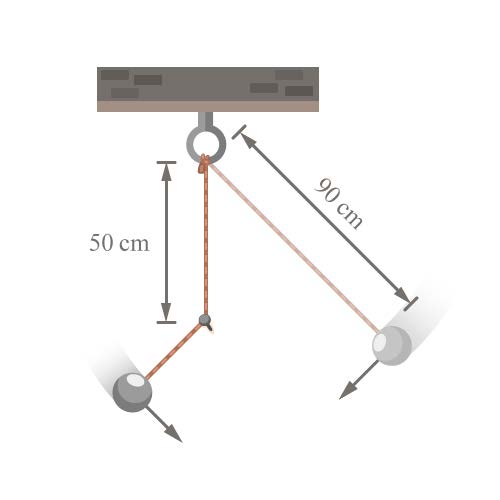 |
| 17. | วัตถุเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย โดยมีความสัมพันธ์ของการกระจัด (y) หน่วยเมตร และเวลา (t) หน่วยวินาที เป็นไปตามสมการ
y = 0.5 sin(10t)
อยากทราบว่าขนาดของความเร่ง ที่ตำแหน่งไกลสุดจากสมดุลมีค่าเท่าไร |
| 18. | นาฬิกาแบบลูกตุ้มเรือนหนึ่งลูกตุ้มแกว่งได้ 60 รอบต่อนาที ความยาวของก้านของลูกตุ้มนาฬิกามีค่ากี่เมตร |
| 19. | มวล M กับ m เชื่อมกันด้วยสปริงเบา ๆ กำลังสั่น "อยู่กับที่" เทียบกับระบบอ้างอิงเฉื่อย โดยที่ m สั่นด้วยแอมพลิจูด A จงหาค่าของแอมพลิจูดของการสั่นของ M (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555) 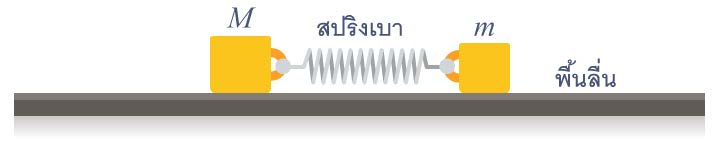 |
| 20. | ถ้าคุณดันหนังสือกับผนังแนวดิ่งด้วยแรงมากพอหนังสือจะไม่ไถลตกลงมา ถ้าสัมประสิทธิ์ของความเสียดทานสถิตระหว่างหนังสือกับผนังมีค่าเท่ากับ 0.7
1) คุณจะตองออกแรงดันตั้งฉากกับผนังด้วยขนาดอย่างน้อยเท่าใด หนังสือมวล 2.0 kg จึงจะไม่ไถลตกลงมากำหนดว่าความเร่งเนื่องจากแรงโน้มถ่วงโลกมีขนาด 9.8 m/s2
2) ถ้าคุณออกแรงดันขนาด 35N แรงเสียดทานสถิตที่ผนังกระทำต่อหนังสือมีขนาดเท่าใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2548) |
| 21. | ห่วงเล็ก ๆ คล้องอยู่ในห่วงใหญ่ดังรูป โดยที่ห่วงใหญ่มีรัศมี R ถ้าสัมประสิทธิ์ความเสียดทานของทั้งสองห่วงเท่ากับศูนย์ จงหาค่าของมุม θ ที่จุดสมดุลเมื่อห่วงใหญ่หมุนรอบตัวเองด้วยความเร็วเชิงมุม ω สูงมาก ๆ
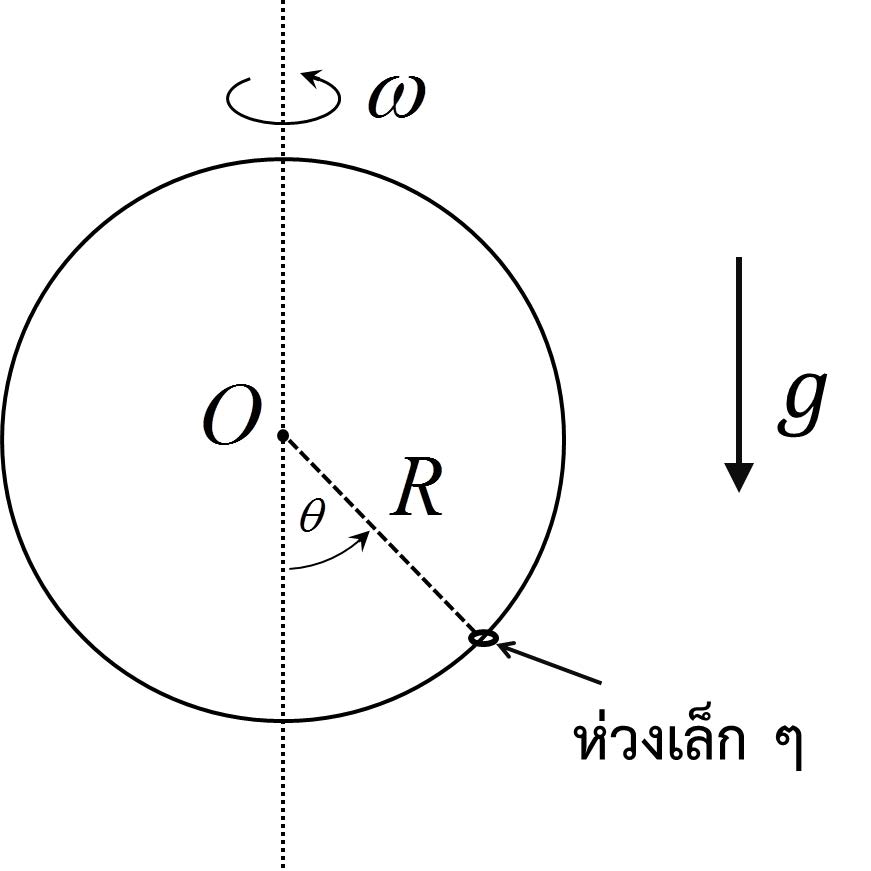 |
| 22. | ดีดวัตถุมวล m ก้อนหนึ่งด้วยอัตราเร็วต้น u ให้ไถลขึ้นไปตามพื้นเอียงซึ่งทำมุม θ กับแนวระดับ เมื่อวัตถุขึ้นไปไดสู้งสุดก็ตกกลับมาตามพื้นเอียง ถ้าสัมประสิทธิ์ของความเสียดทานจลน์ระหว่างวัตถุกับผิวพื้นเอียงมีค่า μk อัตราเร็วของวัตถุขณะที่กลับมาถึงที่ปลายพื้นเอียงมีค่าเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) |
| 23. | ตาชั่งสปริงอันหนึ่งแขวนไว้กับเพดานลิฟต์ที่กำลังเคลื่อนที่ ถ้าปลายล่างของตาชั่งมีวัตถุมวล 10 kg แขวนอยู่และตาชั่งอ่านค่าได ้125 N
1) จงหาความเร่ง (ทิศเเละขนาด) ของลิฟต์
2) ถ้าที่แขวนตาชั่งหลุดจากเพดาน ตาชั่งอ่านค่าเท่าใด
กำหนดว่าขนาดสนามโน้มถ่วงของโลกที่บริเวณนั้นมีค่าเท่ากับ 9.8 N/kg(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) |
| 24. | ในระบบดาวฤกษ์สองดวง m1 กับ m2 ซึ่งโคจรรอบกันและกัน m1 โคจรตามแนววงกลมรัศมี R1 นั้น m2 จะมีอัตราเร็วเชิงเส้นเป็นเท่าใด (ใช้กฎการโน้มถ่วง \(\rm F =\dfrac{Gm_1m_2}{r^2} ,~ r =\) ระยะห่าง) (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555) |
| 25. | ดีดวัตถุมวล m ด้วยอัตราเร็วต้นไปในทางทิศขวามือให้ไถลไปบนผิวแผ่นไม้มวล M แผ่นไม้วางอยู่บนพื้นลื่นอีกทีหนึ่ง ให้ μk และ μs เป็นสัมประสิทธิ์ความเสียดทานจลน์และสัมประสิทธความเสียดทานสถิตระหว่างวัตถุและแผ่นไม้ตามลำดับ
1) แรงเสียดทานที่แผ่นไม้ทำต่อวัตถุมีทิศทางใด และมีขนาดเท่าใด
2) ความเร่งของแผ่นไม้มีทิศทางใด และมีขนาดเท่าใด
3) แผ่นไม้เคลื่อนที่ไปเท่าใด เมื่อวัตถุและแผ่นไม้มีความเร็วเท่ากัน
4) วัตถุไถลไปบนแผ่นไม้เป็นระยะทางเท่าใด (วัดเทียบกับแผ่นไม ้ และวัดตั้งแต่ต้นจนวัตถุเริ่มหยุดไถลบนแผ่นไม้)
5) เมื่อวัตถุหยุดไถล แรงเสียดทานที่แผ่นไม้ทำต่อวัตถุมีขนาดเท่าใด และมีทิศทางใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 29 ส.ค. 2553) |
ตอบ
1) ทิศไปทางซ้าย และ \(\rm f_k = μ_kmg\)
2) ทิศไปทางขวา และ \(\rm a = \dfrac{\mu_kmg}{M}\)
3) แผ่นไม้เคลื่อนที่ไปได้ \(\rm \dfrac{mMu^2}{2\mu_kg(m+M)^2}\)
4) วัตถุไถลไปได้ \(\rm \dfrac{Mu^2}{2\mu_k g(M+m)}\)
5) ไม่เกิดทิศ และแรงเสียดทานจลน์เท่ากับศูนย์
1) ทิศไปทางซ้าย และ \(\rm f_k = μ_kmg\)
2) ทิศไปทางขวา และ \(\rm a = \dfrac{\mu_kmg}{M}\)
3) แผ่นไม้เคลื่อนที่ไปได้ \(\rm \dfrac{mMu^2}{2\mu_kg(m+M)^2}\)
4) วัตถุไถลไปได้ \(\rm \dfrac{Mu^2}{2\mu_k g(M+m)}\)
5) ไม่เกิดทิศ และแรงเสียดทานจลน์เท่ากับศูนย์
| 26. | ท่อนผอม, ตรง, ยาว, มวล M ความยาว L กำลังล้มจากหยุดนิ่งจากแนวดิ่งบนพื้นฝืด จงวิเคราะห์หาแรงเสียดทานที่พื้นกระทำต่อปลายล่างของท่อนทำให้ท่อนไม่ไถลไปทางซ้าย หาแรงปฏิกิริยาที่พื้นกระทำต่อปลายล่าง แล้วหาเงื่อนไขเกี่ยวกับค่าสัมประสิทธิ์ความเสียดทาน (μ) ที่จะทำให้ปลายล่างไม่ไถลไปทางซ้ายเลย [ถึงแม้ว่าในที่สุดจะไปทางขวา] (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 18 ธ.ค. 2554)  |
ตอบ
\(\rm f=\dfrac{3mg}{4}(3\cos\theta-2)\sin\theta\)
\(\rm N = \dfrac{3mg}{4}\left[3\cos^2\theta-2\cos\theta-1+\dfrac{4}{3}\right]\)
\(\rm \mu \approx 0.3706\) โดย \(\rm \mu \ge \dfrac{f}{N}\) ทุกๆ θ
\(\rm f=\dfrac{3mg}{4}(3\cos\theta-2)\sin\theta\)
\(\rm N = \dfrac{3mg}{4}\left[3\cos^2\theta-2\cos\theta-1+\dfrac{4}{3}\right]\)
\(\rm \mu \approx 0.3706\) โดย \(\rm \mu \ge \dfrac{f}{N}\) ทุกๆ θ
| 27. | มวล m1 , m2 โยงกันด้วยเชือกยาว ℓ กำลังตกเข้าหาโลกมวล M ในแนวเข้าสู่ O โดยไม่มีการหมุน จงหาความตึงในเส้นเชือกในเทอมของ r , m1 , m2 , M , ℓ และ G ซึ่งเป็นค่า Gravitational constant และถ้า ℓ ≪ r ความตึงนี้จะมีค่าประมาณเท่าใด (ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 24 มี.ค. 2552) 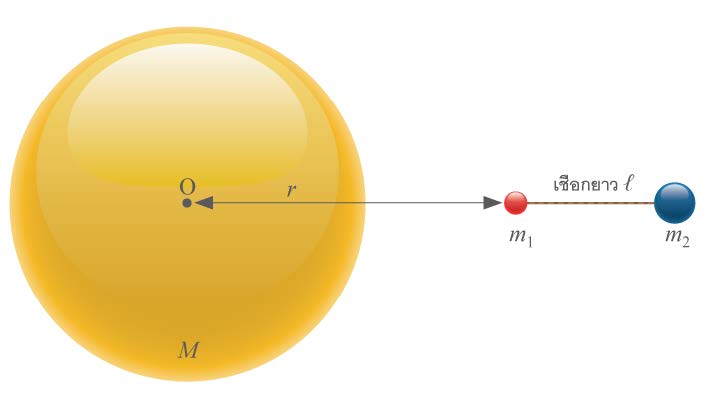 |
| 28. | ค่อย ๆ วางวัตถุมวล m อย่างช้าๆ ลงบนทางเลื่อน (มวลมากกว่า m มาก ๆ) ในสนามบินสุวรรณภูมิซึ่ง กำลังเลื่อนด้วยอัตราเร็ว u คงตัว ถ้าสัมประสิทธิ์ของความเสียดทานจลน์ระหว่างวัตถุและทางเลื่อนเท่ากับ μk
1) จงหา นานเท่าใดหลังจากวางวัตถุ วัตถุจึงจะหยุดไถล และ
2) วัตถุเคลื่อนที่ไปได้ระยะทางเท่าใด (เทียบกับคนที่ยืนอยู่นอกทางเลื่อน) ในระหว่างช่วงเวลาในข้อ 1)
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 29. | วัตถุเล็ก ๆ ตกจากหยุดนิ่งตามแนวรางลื่นจาก A ไป C แล้วไป B จะใช้เวลาเป็นกี่เท่าของการตกตามแนวรางลื่น A ตรงไป B (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2554)  |
| 30. | M ถูกดีดด้วยความเร็วต้น vo ให้กระตุกโซ่ออกไปจากกองที่ origin O ของระบบอ้างอิงเฉื่อย XOY โซ่มีมวลต่อหน่วยความยาวเป็น λ สัมประสิทธิ์ความเสียดทานระหว่างโซ่และ M กับพื้นเป็น μ จงวิเคราะห์หา:
 ก. สมการเคลื่อนที่ equation of motion ของ M
ข. ความเร็ว v ที่ขณะใดๆ ในรูปของ vo,M, g, μ, λ และ x
ค. ความเร่ง \(\rm\dfrac{d}{dt}v\) ในรูปของ vo,M, g, μ, λ และ x
ง. ความเร่ง \(\rm\dfrac{d}{dt}v\) ที่จังหวะที่ x = 0 เป็นเท่าใด
(ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2548) |
ตอบ
ก. \(\rm (M + λx)\ddot{x}= −μ(M + λx)g − λv^2\)
ข. \(\rm v(x) =\sqrt{\dfrac{3λ M^2v_0^2− 2μg[(M + λx )^3- M^3]}{3λ(M + λx)^2}}\)
ค. \(\rm a = -\mu g-\dfrac{1}{3(M + λx)^3}(3λ M^2v_0^2− 2μg[(M + λx )^3- M^3])\)
ง. \(\rm a = -\mu g-\dfrac{λ}{M}v^2_0\)
ก. \(\rm (M + λx)\ddot{x}= −μ(M + λx)g − λv^2\)
ข. \(\rm v(x) =\sqrt{\dfrac{3λ M^2v_0^2− 2μg[(M + λx )^3- M^3]}{3λ(M + λx)^2}}\)
ค. \(\rm a = -\mu g-\dfrac{1}{3(M + λx)^3}(3λ M^2v_0^2− 2μg[(M + λx )^3- M^3])\)
ง. \(\rm a = -\mu g-\dfrac{λ}{M}v^2_0\)
| 31. | จงอธิบายวิธีการหาแรงลัพธ์ของแรงสามแรงที่อยู่ในแนวเดียวกันโดยวิธีการสร้างรูป ก) โดยวิธีการวาดรูป ข) โดยวิธีการคำนวณ |
ตอบ
ก) ใช้วิธีหางต่อหัว
ข) รวมขนาดของแรงโดยให้กำหนดให้แรงทิศเดียวกันมีค่าเป็นบวก ทิศตรงข้ามมีค่าเป็นลบ
ก) ใช้วิธีหางต่อหัว
ข) รวมขนาดของแรงโดยให้กำหนดให้แรงทิศเดียวกันมีค่าเป็นบวก ทิศตรงข้ามมีค่าเป็นลบ
| 32. | คนสองคนชักเย่อกัน ต่างคนต่างออกแรง F เท่ากันที่ปลายเชือกทั้งสองความตึงในเชือกมีค่าเท่าใด |
ตอบ F
ปลายเชือกทั้งสองด้านถูกดึงด้วยแรง F ทำให้เกิดแรงตึงในเชือกเท่ากับ F ด้วยเพราะปลายเชือกทั้งสองไม่ได้เคลื่อนที่ แรงตึงเชือกจึงต้องเท่ากับแรงดึง F ที่ปลายเชือกทั้งสองด้าน
ปลายเชือกทั้งสองด้านถูกดึงด้วยแรง F ทำให้เกิดแรงตึงในเชือกเท่ากับ F ด้วยเพราะปลายเชือกทั้งสองไม่ได้เคลื่อนที่ แรงตึงเชือกจึงต้องเท่ากับแรงดึง F ที่ปลายเชือกทั้งสองด้าน
| 33. | แรง 5 นิวตัน และ 12 นิวตัน ในระนาบระดับมีทิศตั้งฉากกัน กระทำต่อมวล 10 กิโลกรัม บนพื้นระดับลื่นจงหาขนาดของความเร่งของมวลนี้
 |
| 34. | วัตถุมวล 20 กิโลกรัม มีแรงลัพธ์มากระทำต่อมวล ทำให้มวลเคลื่อนที่โดยมีความเร็วสัมพันธ์กับเวลา ดังกราฟ จงหาแรงลัพธ์ที่กระทำ ต่อวัตถุ 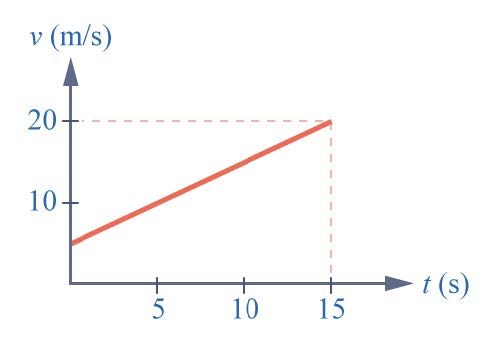 |
| 35. | กล่องมวล m ไถลลงพื้นเอียงซึ่งทำมุม θ กับแนวระดับด้วยความเร่ง a ต่อมาเพิ่มมวลให้กล่องเป็น 2m ความเร่งจะเป็นเท่าใด ถ้าสัมประสิทธิ์ของความเสียดทานระหว่างกล่องกับพื้นเอียงมีค่าคงที่ |
| 36. | ลิ่มวางอยู่บนพื้นฝืดมาก ผิวบนของลิ่มเป็นผิวราบลื่นนำมวล M มาวางและปล่อยให้ไถลลงบนผิวลื่นนี้แรงที่ลิ่มกดทับพื้นระดับจะเพิ่มขึ้นจากเดิมเท่าใด
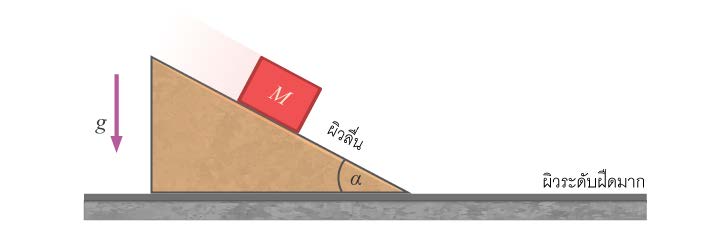 |
| 37. | ในการทดลองเพื่อพิสูจน์กฎการเคลื่อนที่ของนิวตัน มีการชดเชยความฝืดและใช้ขนาดต่างๆ ลากมวล (รถทดลอง) และวัดความเร่ง เมื่อเขียนกราฟระหว่างแรงและความเร่งได้กราฟ
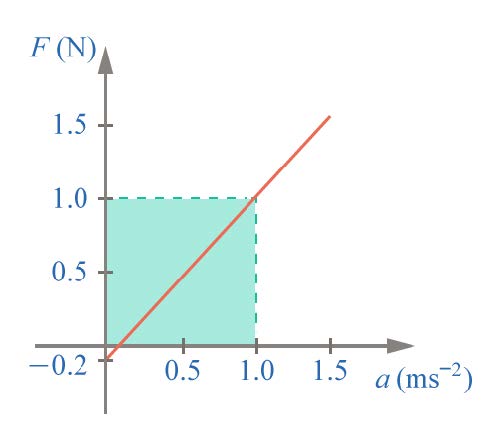 |
| 38. | ผูกเชือก (ด้ายเย็บผ้าที่เหนียวพอประมาณ) กับถุงทรายดังภาพ ในระหว่างการดึงถุงขึ้นอย่างช้าๆ ทำให้เชือกไม่ขาด กับการดึงถุงขึ้นอย่างรวดเร็วทำให้เชือกขาด เหตุใดจึงเป็นเช่นนั้น จงอธิบาย
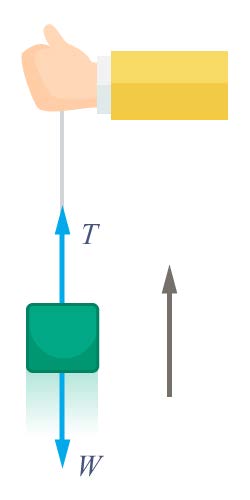 |
ตอบ
แรงที่กระทำต่อถุงทรายจะมี 2 แรงคือแรงดึงเชือก \(\rm \vec{T}\) และน้ำหนักวัตถุ \(\rm m\vec{g}\) พิจารณาเมื่อถุงทรายเคลื่อนที่ขึ้นอย่างช้าๆ ถือว่าถุงทรายมีความเร็วคงตัว แรงลัพธ์ที่กระทำต่อวัตถุเป็นศูนย์ จะได้ขนาดของแรงดึงขึ้นมีค่าเท่ากับขนาดของแรงดึงลง นั้นคือ \(\rm T=mg\)
พิจารณาเมื่อดึงถุงทรายอย่างรวดเร็ว ถุงทรายจะเคลื่อนที่ด้วยความเร่ง
จากกฎการเคลื่อนที่ข้อที่สองของนิวตัน
จะได้
แรงที่กระทำต่อถุงทรายจะมี 2 แรงคือแรงดึงเชือก \(\rm \vec{T}\) และน้ำหนักวัตถุ \(\rm m\vec{g}\) พิจารณาเมื่อถุงทรายเคลื่อนที่ขึ้นอย่างช้าๆ ถือว่าถุงทรายมีความเร็วคงตัว แรงลัพธ์ที่กระทำต่อวัตถุเป็นศูนย์ จะได้ขนาดของแรงดึงขึ้นมีค่าเท่ากับขนาดของแรงดึงลง นั้นคือ \(\rm T=mg\)
พิจารณาเมื่อดึงถุงทรายอย่างรวดเร็ว ถุงทรายจะเคลื่อนที่ด้วยความเร่ง
จากกฎการเคลื่อนที่ข้อที่สองของนิวตัน
\(\rm Σ\vec{F} = m\vec{a}\)
ให้ทิศขึ้นแทนด้วยเครื่องหมาย + และทิศลงแทนด้วยเครื่องหมาย -จะได้
\(\rm T=ma+mg\)
จะเห็นว่า \(\rm T > mg\) เมื่อดึงถุงทรายอย่างรวดเร็วเชือกจะขาด เพราะแรงดึงเชือกมากเกินค่าแรงที่เส้นเชือกรับได้สูงสุด| 39. | สปริงเบาทั้งสามอันเหมือนกันหมด ถ้าสปริงในรูป ก. ยืดออก 4 เซนติเมตร สปริงในรูป ข. ยืดออกรวมเป็นกี่เซนติเมตรเมื่อแขวนมวลขนาดเท่ากันกับรูป ก.
 |
| 40. | มวล 1.0 กิโลกรัมสองก้อน ผูกติดกับเชือกเบาและแขวนติดกับเพดานของลิฟต์ดังรูป ถ้าลิฟต์เคลื่อนที่ลงด้วยความเร่ง 2 m/s2 จงหาแรงตึงในเส้นเชือก T1 และ T2
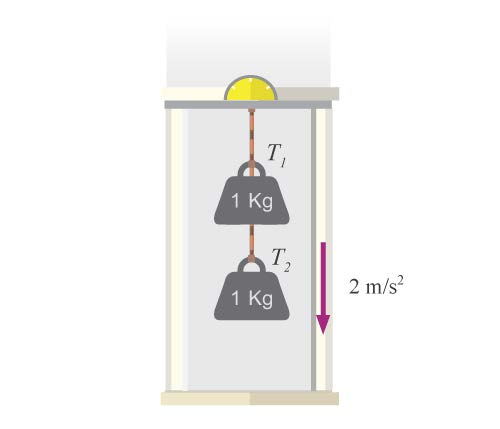 |
| 41. | เข็มขัดนิรภัยและที่พิงศีรษะซึ่งติดอยู่กับเบาะในรถยนต์มีไว้เพื่อประโยชน์อะไร จงอธิบายพร้อมเหตุผล |
ตอบ เมื่อรถถูกชนจากด้านหลัง ที่พิงศีรษะสามารถป้องกันไม่ให้ศีรษะเคลื่อนที่ไปด้านหลังมากเกินไปทำให้คอไม่หัก เมื่อถูกชนจากด้านหน้าเข็มขัดนิรภัยจะช่วยไม่ให้ลำตัวกระแทกกับพวงมาลัย
| 42. | จากรูป กล่อง A และ B มีมวล 20 และ 10 กิโลกรัม ดึงวัตถุ A ด้วยแรงขนาน 200 นิวตัน ถ้าสัมประสิทธิ์ของความเสียดทานระหว่าง A กับพื้นและกล่อง A กับกล่อง B เป็น 0.4 และ 0.2 ตามลำดับ จงหาความเร่งของกล่อง A
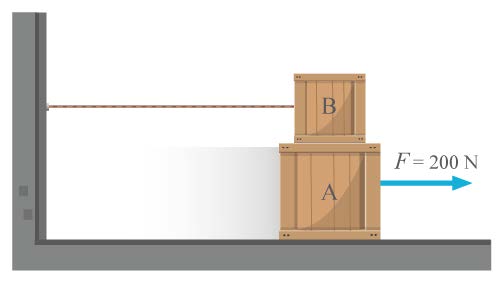 |
| 43. | แรงเสียดทานมีผลต่อการเดินเช่นไร จงใหเ้หตุผลประกอบ |
| 44. | จากการทดลองเรื่องสัมประสิทธิ์ความเสียดทาน เมื่อจัดรางไม่ให้พื้นรางอยู่ในแนวระดับ และใช้เครื่องชั่งสปริงเกี่ยวขอของแผ่นไม้ที่มีถุงทรายทับอยู่บนแล้วออกแรง ดึงเครื่องชั่งสปริงให้ทิศของแรงดึงอยู่ในแนวระดับ ทำให้ได้ข้อมูลที่นำไปเขียนกราฟเพื่อแสดงความสัมพันธ์ระหว่างขนาดแรงดึง (F) กับน้ำหนักถุงทรายรวมกับขนาดของน้ำหนักแผ่นไม้ (W) ได้กราฟดังรูป จงหาสัมประสิทธิ์ความเสียดทาน
 |
| 45. | กล่องสองใบมวล m1 และ m2 ตามลำดับ วางซ้อนกันบนพื้นราบไร้ความฝืด มีแรง F กระทำต่อกล่อง ทำให้กล่องทั้งสองเคลื่อนที่ไปทางขวาด้วยความเร่ง a ถ้า f เป็นแรงเสียดทานสูงสุดที่มีได้ระหว่างผิวสัมผัสของกล่องทั้งสอง F มีค่าได้มากที่สุดเท่าใด มวล m2 จึงไม่ไถลบน m1
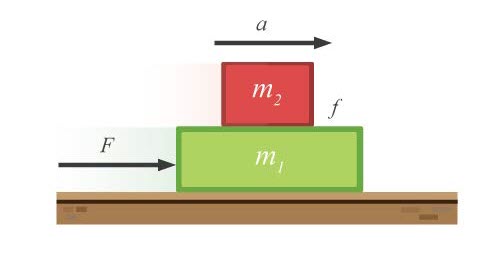 |

