หัวข้อฟิสิกส์ทั้งหมด
| 1. | ให้การเคลื่อนที่ของวัตถุหนึ่งในสองมิติ เป็นไปตามสมการ
\(\rm \vec r(t) = (4.0t^2-9.0)\hat i + (2.0t - 5.0)\hat j \)
โดย r มีหน่วย เมตร และ t มีหน่วย วินาที แล้ววัตถุจะตัดแกน x ที่วินาทีใด |
| A | 0.0 s |
| B | 0.4 s |
| C | 0.6 s |
| D | 1.5 s |
| E | 2.5 s |
ตอบ (E)
จาก
จาก
\(\rm \vec r(t) = x(t)\hat i + y(t)\hat j \)
วัตถุตัดแกน x เมื่อ y(t) = 0
\(\begin{align*}\rm 2.0(t) -5.0 &= 0\\ \therefore \rm t &= 2.5 ~\rm s \end{align*}\)
| 2. | กำหนดกราฟความเร็วเทียบกับเวลาของรถคันหนึ่ง อยากทราบว่า ความเร่งที่วินาทีที่ 90 เท่ากับข้อใด
 |
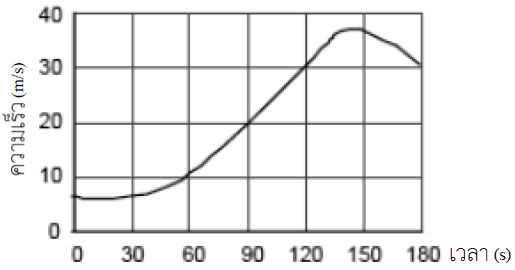| A | 0.22 m/s2 |
| B | 0.33 m/s2 |
| C | 1.0 m/s2 |
| D | 9.8 m/s2 |
| E | 30 m/s2 |
ตอบ (B)
จากโจทย์เป็นกราฟ v-t ความเร่งที่ t ใดๆ จึงหาจากความชันของกราฟที่ t นั้นๆ
ประมาณช่วง t = 60 – 120 s เป็นเส้นตรง เลือกพิกัด (60,10) และ (120,30) จะได้
จากโจทย์เป็นกราฟ v-t ความเร่งที่ t ใดๆ จึงหาจากความชันของกราฟที่ t นั้นๆ
ประมาณช่วง t = 60 – 120 s เป็นเส้นตรง เลือกพิกัด (60,10) และ (120,30) จะได้
\(\begin{align*} {{\rm{a}}_{t\, = \,90}} &= \frac{{\Delta {\rm{v}}}}{{\Delta {\rm{t}}}}\\ &= \frac{{30 - 10}}{{120 - 60}}\\ &= \frac{{20}}{{60}}\\ &= 0.33\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}} \end{align*}\)
| 3. | ให้ตำแหน่งของวัตถุกำหนดจากฟังก์ชันของเวลา x = 8t – 3t2 โดย x มีหน่วยเมตร และ t ในหน่วยวินาที แล้วความเร็วเฉลี่ยในช่วง t = 1 ถึง t = 2 s เท่ากับข้อใด |
| A | - 2 m/s |
| B | - 1 m/s |
| C | - 0.5 m/s |
| D | 0.5 m/s |
| E | 1 m/s |
ตอบ (B)
ข้อนี้ถามความเร็วเฉลี่ย จะได้
ความเร็วเฉลี่ย = \(\dfrac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}} = \dfrac{{{{\rm{x}}_2} - {{\rm{x}}_1}}}{{{{\rm{t}}_2} - {{\rm{t}}_1}}}\)
( ส่วนความเร็ว ณ ขณะใดๆ \(= \rm v(t)=\dfrac{{{\rm{dx}}}}{{{\rm{dt}}}} = \mathop {{\rm{lim}}}\limits_{\Delta {\rm{t}} \to 0} = \dfrac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}}\) )ข้อนี้ถามความเร็วเฉลี่ย จะได้
\(\begin{align*} \frac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}} &= \frac{{{{\rm{x}}_{{\rm{t = 2}}}} - {{\rm{x}}_{{\rm{t = 1}}}}}}{{2 - 1}}\\ &= \frac{{(8(2) - 3{{(2)}^2}) - (8(1) - 3{{(1)}^2})}}{{2 - 1}}\\ &= - 1\,\,{\rm{m/s}} \end{align*}\)
| 4. | วัตถุถูกปล่อยจากหยุดนิ่ง และเคลื่อนที่ได้ระยะทาง h ในวินาทีแรก จงหาระยะที่วัตถุเคลื่อนที่ได้ในวินาทีที่สอง |
| A | h |
| B | 2h |
| C | 3h |
| D | 4h |
| E | h2 |
ตอบ (C)
ถ้าปล่อยวัตถุจากหยุดนิ่ง แล้วเกิดการเคลื่อนที่แสดงว่ามีความเร่ง a เกิดขึ้น
จาก v(t) = at จะได้
ถ้าปล่อยวัตถุจากหยุดนิ่ง แล้วเกิดการเคลื่อนที่แสดงว่ามีความเร่ง a เกิดขึ้น
จาก v(t) = at จะได้
\({\rm{x(t)}} = \int {{\rm{v dt}} = \dfrac{1}{2}} {\rm{a}}{{\rm{t}}^{\rm{2}}}\)
สมมุติให้ x(0) = 0 จากโจทย์จะได้
\(\begin{array}{l} {\rm{x(t = 1)}} = \dfrac{1}{2}{\rm{a(1}}{{\rm{)}}^{\rm{2}}} = {\rm{h}}\\ {\rm{x(t = 2)}} = \dfrac{1}{2}{\rm{a(2}}{{\rm{)}}^{\rm{2}}} = 4{\rm{h}} \end{array}\)
ดังนั้น ในวินาทีที่ 2 วัตถุเคลื่อนที่ไปได้ \(\rm x(t = 2) – x(t = 1) = 4h – h =3h\)| 5. | มีลังใส่ของเล่นถูกวางนิ่งไว้บนรถเลื่อนหิมะคันหนึ่ง ขณะเดียวกันมีแรงดึงรถเลื่อนขึ้นเนินเขาด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ โดยลังไม่ได้ถูกยึดกับรถเลื่อนไว้ แล้วข้อใดคือแรงที่จะต้องรองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา |
| A | แรงเสียดทานสถิตของรถเลื่อนที่กระทำกับลังของเล่น |
| B | แรงตั้งฉากของพื้นหิมะที่กระทำกับรถเลื่อน |
| C | แรงตั้งฉากของรถเลื่อนที่กระทำกับลังของเล่น |
| D | แรงโน้มถ่วงที่กระทำต่อรถเลื่อน |
| E | ไม่มีแรงใดรองรับ |
ตอบ (A)
จากโจทย์ให้ลังใส่ของมีความเร่ง แสดงว่าต้องมีแรงที่กระทำกับลังเกิดขึ้น
เมื่อเขียนแผนภาพจะได้ 
สังเกตว่า มีแรงเสียดทานระหว่างลังกับเลื่อนหิมะ f เพียงแรงเดียวที่มีทิศเดียวกับ a (และทำให้ a เป็นบวก)
ดังนั้น มีแรงเสียดทานที่รองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา
จากโจทย์ให้ลังใส่ของมีความเร่ง แสดงว่าต้องมีแรงที่กระทำกับลังเกิดขึ้น
เมื่อเขียนแผนภาพจะได้
ดังนั้น มีแรงเสียดทานที่รองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา
| 6. | ในเวลา t = 0 รถลาก เริ่มเคลื่อนที่จากหยุดนิ่งในแนวเส้นตรง ด้วยความเร็วตามฟังก์ชัน v = 5t2 , โดย v มีหน่วย m / s และ t มีหน่วย s ข้อใดแสดงการเคลื่อนที่ของรถจาก t = 0 ถึง t ได้ถูกต้องที่สุด |
| A | 5t3 |
| B | 5t3/3 |
| C | 10t |
| D | 15t2 |
| E | 5t/2 |
ตอบ (B)
จาก
จากเงื่อนไขเริ่มต้นให้ x(t = 0) = 0 จะได้
จาก
\(\begin{align*} {\rm{x}} &= \int {{\rm{v dt}}} \\ {\rm{x(t)}} &= \int\limits_{{\rm{t = 0}}}^{\rm{t}} {{\rm{5}}{{\rm{t}}^{\rm{2}}}{\rm{dt}}} \\ &= \dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}{\rm{ + c}} \end{align*}\)
( c เป็นค่าคงที่ )จากเงื่อนไขเริ่มต้นให้ x(t = 0) = 0 จะได้
\(\begin{array}{l} {\rm{0 = }}\dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}{\rm{ + c }}\\ {\rm{c = 0}} \end{array}\)
ดังนั้น \(\rm x(t) = \dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}\)| 7. | พลังงานศักย์ทางเคมีที่ถูกเก็บไว้ในแบตเตอรี่จะถูกแปลงเป็นพลังงานจลน์ที่ช่วยเพิ่มอัตราเร็วของรถของเล่นจาก 0 เป็น 2 ไมล์ต่อชั่วโมง แล้วเพิ่มจาก 2 เป็น 4 ไมล์ต่อชั่วโมง ถ้าไม่คำนึงถึงพลังงานที่กลายเป็นพลังงานความร้อนเนื่องจากแรงเสียดทาน และแรงต้านอากาศ แล้วข้อใดเปรียบเทียบพลังงานที่ต้องใช้ในการขับเคลื่อนจาก 2 เป็น 4 ไมล์ต่อชั่วโมงกับพลังงานที่ต้องใช้จาก 0 เป็น 2 ไมล์ต่อชั่วโมงได้ถูกต้องที่สุด |
| A | ใช้พลังงานเป็นครึ่งหนึ่ง |
| B | ใช้พลังงานเท่ากัน |
| C | ใช้พลังงานเป็นสองเท่า |
| D | ใช้พลังงานเป็นสามเท่า |
| E | ใช้พลังงานเป็นสี่เท่า |
ตอบ (D)
จากสูตรพลังงานจลน์
จะได้ Ek ที่ใช้เปลี่ยน v จาก 0 เป็น 2 ไมล์ต่อชั่วโมง เท่ากับ
จากสูตรพลังงานจลน์
\({{\rm{E}}_{\rm{k}}} = \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2}\)
เมื่อ m = มวลวัตถุ , v = ความเร็ววัตถุจะได้ Ek ที่ใช้เปลี่ยน v จาก 0 เป็น 2 ไมล์ต่อชั่วโมง เท่ากับ
\({{\rm{E}}_{{\rm{k(0}} \to 2)}} = \dfrac{1}{2}{\rm{m(2}}{{\rm{)}}^2} - \dfrac{1}{2}{\rm{m(0}}{{\rm{)}}^2} = 2{\rm{m}}\)
และ Ek ที่ใช้เปลี่ยน v จาก 2 เป็น 4 ไมล์ต่อชั่วโมง เท่ากับ
\({{\rm{E}}_{{\rm{k(2}} \to 4)}} = \dfrac{1}{2}{\rm{m(4}}{{\rm{)}}^2} - \dfrac{1}{2}{\rm{m(2}}{{\rm{)}}^2} = 6{\rm{m}}\)
ดังนั้น \(\dfrac{{{{\rm{E}}_{{\rm{k(2}} \to 4)}}}}{{{{\rm{E}}_{{\rm{k(0}} \to 2)}}}} = \dfrac{{6{\rm{m}}}}{{2{\rm{m}}}} = 3\)| 8. | ถ้าดาวฤกษ์สองดวงอยู่ห่างกันมาก แล้วพลังงานศักย์โน้มถ่วงของทั้งสองเท่ากับศูนย์ ถ้าดาวทั้งสองดวงห่างกัน d พลังงานศักย์โน้มถ่วงของระบบจะเท่ากับ U แล้วดาวที่ห่างกัน 2d พลังงานศักย์โน้มถ่วงของระบบจะเท่ากับข้อใด |
| A | U/4 |
| B | U/2 |
| C | U |
| D | 2U |
| E | 4U |
ตอบ (B)
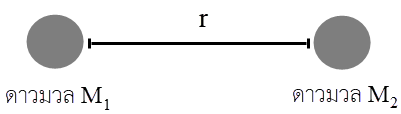จาก
จะได้ว่า
ดังนั้น
\({\rm{U}} = \dfrac{{ - {\rm{G}}{{\rm{M}}_{\rm{1}}}{{\rm{M}}_{\rm{2}}}}}{{\rm{r}}}\)
ดังนั้น \({\rm{U}} \propto \dfrac{1}{{\rm{r}}}\)จะได้ว่า
\(\dfrac{{{{\rm{U}}_{\rm{1}}}}}{{{{\rm{U}}_{\rm{2}}}}}{\rm{ = }}\dfrac{{{{\rm{r}}_{\rm{2}}}}}{{{{\rm{r}}_{\rm{1}}}}}\)
ให้ U1 = U, r1 = d และ r2 = 2dดังนั้น
\(\begin{array}{l} \dfrac{{\rm{U}}}{{{{\rm{U}}_{\rm{2}}}}}{\rm{ = }}\dfrac{{{\rm{2d}}}}{{\rm{d}}}\\ {{\rm{U}}_{\rm{2}}} = \dfrac{{\rm{U}}}{2} \end{array}\)
| 9. | ให้พื้นเอียงถูกวางอยู่บนพื้นลื่น และมีกล่องที่เดิมอยู่นิ่งค่อยๆ เลื่อนลงมาจากพื้นเอียงที่มีความขรุขระ แล้วการเคลื่อนที่ของจุดศูนย์กลางมวลของระบบกล่องและพื้นเอียงจะเป็นไปตามข้อใด |
| A | จะไม่มีการเคลื่อนที่เกิดขึ้น |
| B | มีการเคลื่อนที่ตามแนวนอนด้วยอัตราเร็วคงที่ |
| C | มีการเคลื่อนที่ตามแนวนอนด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ |
| D | มีการเคลื่อนที่ตามแนวตั้งด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ |
| E | มีการเคลื่อนที่ทั้งในแนวตั้ง และแนวนอน |
ตอบ (D)
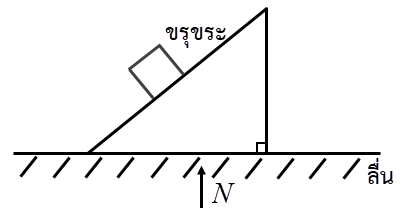หลักการ คือ จุดศูนย์กลางมวลจะเคลื่อนที่ได้เมื่อมีแรงภายนอกมากระทำ
พิจารณาแกน X : พื้นลื่นจึงไม่มีแรงเสียดทาน
ดังนั้น จุดศูนย์กลางมวลในแนวแกน X ไม่เคลื่อนที่
พิจารณาแกน Y : มีแรง N จากพื้นในทิศขึ้น
จาก
(เพิ่มเติม แรงเสียดทานระหว่างพื้นเอียงกับกล่องเป็นแรงภายใน จึงไม่ส่งผลต่อจุดศูนย์กลางมวลของทั้งระบบ)
พิจารณาแกน X : พื้นลื่นจึงไม่มีแรงเสียดทาน
ดังนั้น จุดศูนย์กลางมวลในแนวแกน X ไม่เคลื่อนที่
พิจารณาแกน Y : มีแรง N จากพื้นในทิศขึ้น
จาก
\(\begin{align*} \sum \rm F_y &= \rm ma_y\\ \rm a_y &> 0 \end{align*} \)
ดังนั้น จุดศูนย์กลางมวลจะเคลื่อนที่ในแนวแกน Y ด้วยความเร่ง(เพิ่มเติม แรงเสียดทานระหว่างพื้นเอียงกับกล่องเป็นแรงภายใน จึงไม่ส่งผลต่อจุดศูนย์กลางมวลของทั้งระบบ)
| 10. | ล้อมวล 1 kg สองวง มีแกนล้อคงที่ จากที่เดิมอยู่นิ่งมีแรงมากระทำ ดังรูป สมมุติว่า แกนล้อและซี่ล้อมีมวลเบามาก และความเฉื่อยในการหมุนเท่ากับ I = mR2 ถ้าต้องการให้ความเร่งเชิงมุมของทั้งสองล้อมีค่าเท่ากัน แล้วแรง F2 ที่กระทำบนแกนล้อควรเท่ากับข้อใด
 |
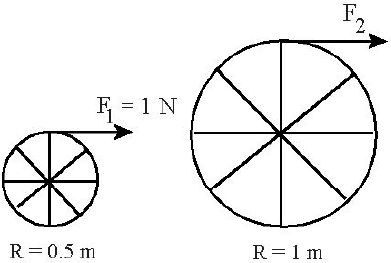| A | 0.25 N |
| B | 0.5 N |
| C | 1 N |
| D | 2 N |
| E | 4 N |
ตอบ (D)
จาก
พิจารณาล้อ 1 (R = 0.5 m)
ดังนั้น
จาก
\(\sum {\tau = {\rm{I}}\alpha } \)
พิจารณาล้อ 1 (R = 0.5 m)
\(\begin{align*} \rm F_1R &= \rm m_1^2\alpha \\ \rm{F}_1&= \rm mR_1\alpha \end{align*}\)
พิจารณาล้อ 2 (R = 1 m)
\({{\rm{F}}_{\rm{2}}}{\rm{ = m}}{{\rm{R}}_2}\alpha \)
ดังนั้น
\(\begin{array}{c} \dfrac{{{{\rm{F}}_{\rm{2}}}}}{{{{\rm{F}}_{\rm{1}}}}}{\rm{ = }}\dfrac{{{{\rm{R}}_{\rm{2}}}}}{{{{\rm{R}}_{\rm{1}}}}}\\ \dfrac{{{{\rm{F}}_{\rm{2}}}}}{1}{\rm{ = }}\dfrac{1}{{0.5}}\\ {{\rm{F}}_{\rm{2}}} = 2{\rm{N}} \end{array}\)
| 11. | ให้แผ่นกลม, ห่วง และทรงกลม มีมวล และรัศมีเท่ากัน และจะหมุนอย่างอิสระรอบแกนที่ผ่านจุดศูนย์กลางของวัตถุ โดยสมมุติว่าห่วงเชื่อมกับแกนหมุนด้วยซี่ล้อรถ ถ้าวัตถุที่เดิมอยู่นิ่ง ถูกกระทำที่วงด้านนอกด้วยแรงเดียวกัน ในเวลาเดียวกัน แล้วข้อใดจัดอันดับพลังงานจลน์ของวัตถุจากน้อยไปมาก หลังเวลาผ่านไป t ได้ถูกต้อง
 |
| A | แผ่นกลม, ห่วง, ทรงกลม |
| B | ทรงกลม, แผ่นกลม, ห่วง |
| C | ห่วง, ทรงกลม, แผ่นกลม |
| D | แผ่นกลม, ทรงกลม, ห่วง |
| E | ห่วง, แผ่นกลม, ทรงกลม |
ตอบ (E)
จากโจทย์ให้ทุกวัตถุถูกหมุนด้วย F เท่ากัน รัศมีเท่ากัน ดังนั้น ทอร์กต้องเท่ากัน
เนื่องจาก วัตถุที่มีโมเมนต์ความเฉื่อย (I) มาก จะหมุนช้า ทำให้พลังงานจลน์มีค่าน้อย
ดังนั้น การเรียงลำดับพลังงานจลน์จากน้อยไปมาก ต้องเรียงลำดับ I จากมากไปน้อย ดังนี้
จากโจทย์ให้ทุกวัตถุถูกหมุนด้วย F เท่ากัน รัศมีเท่ากัน ดังนั้น ทอร์กต้องเท่ากัน
เนื่องจาก วัตถุที่มีโมเมนต์ความเฉื่อย (I) มาก จะหมุนช้า ทำให้พลังงานจลน์มีค่าน้อย
ดังนั้น การเรียงลำดับพลังงานจลน์จากน้อยไปมาก ต้องเรียงลำดับ I จากมากไปน้อย ดังนี้
ห่วง (\({\rm{M}}{{\rm{R}}^{\rm{2}}}\)) , แผ่นกลม (\(\dfrac{1}{2}{\rm{M}}{{\rm{R}}^{\rm{2}}}\)) , ทรงกลม (\(\dfrac{2}{5}{\rm{M}}{{\rm{R}}^{\rm{2}}}\))
| 12. | หินหนัก 2 kg แขวนที่ปลายไม้เมตรสม่ำเสมอยาว 1 เมตร ด้วยเชือกเบา ถ้าไม้เมตรเกิดสมดุลเมื่อหินที่แขวนอยู่ อยู่ห่างจากจุดหมุนไป 0.20 m แล้วไม้เมตรมีมวลเท่าใด  |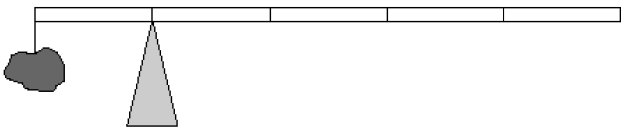
| A | 0.20 kg |
| B | 1.00 kg |
| C | 1.33 kg |
| D | 2.00 kg |
| E | 3.00 kg |
ตอบ (C)
ให้หินมีมวล m และไม้เมตรมีมวล M
จากไม้เมตรเกิดสมดุลแสดงว่า
ให้หินมีมวล m และไม้เมตรมีมวล M
โมเมนต์ตาม \(=\) โมเมนต์ทวน
\(\begin{align*} \dfrac{4}{5}{\rm{Mg}}(0.40) &= \rm mg(0.20) + \dfrac{1}{5}{\rm{Mg}}(0.10)\\ \left( {\dfrac{4}{5}(0.40) - \dfrac{1}{5}(0.10)} \right)\rm M &= (0.20)(2)\\ \rm M &= \dfrac{4}{3} \end{align*}\)
ดังนั้น ไม้เมตรมีมวล \(\dfrac{4}{3} = 1.33 \rm ~~kg\)| 13. | ถ้าวัตถุหนึ่งเคลื่อนที่ไปตามแกน x พุ่งชนแบบยืดหยุ่นกับวัตถุแบบเดียวกันที่เดิมอยู่นิ่ง แล้วกราฟในข้อใดแสดงโมเมนตัม P เทียบกับเวลา t ของแต่ละวัตถุได้ถูกต้อง |
| A |  |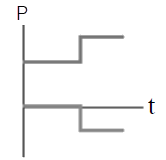
| B |  |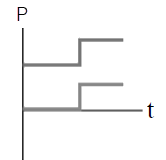
| C |  |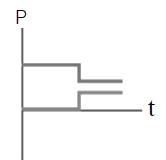
| D |  |
| E |  |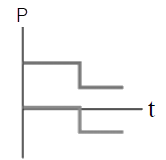
ตอบ (D)
โจทย์ให้เป็นการชนแบบยืดหยุ่นแสดงว่า
1) อนุรักษ์โมเมนตัม \(\sum \rm P\) ก่อนชน = \(\sum \rm P\)หลังชน
2) อนุรักษ์พลังงาน \(\rm E\)ก่อน = \(\rm E\)หลัง
พิจารณาจากเงื่อนไข 1)
จากกราฟจะเห็นว่า กราฟ (B), (E) มีการเปลี่ยนแปลงหลังชนไปในทำนองเดียวกัน (เพิ่มขึ้นเหมือนกัน หรือลดลงเหมือนกัน) ซึ่งขัดกับการอนุรักษ์โมเมนตัม
ดังนั้น กราฟ (B), (E) ไม่ใช่คำตอบ
และเมื่อวาดรูปจากกราฟ (A) จะได้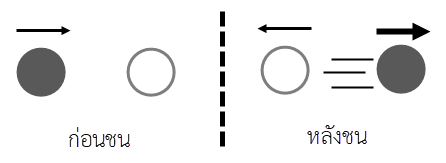
สังเกตว่า วัตถุที่อยู่นิ่งไม่ควรเด้งกลับหลังถูกชน
ดังนั้น กราฟ (A) ไม่ใช่คำตอบ
พิจารณาจากเงื่อนไข 2)
จากกราฟ (C)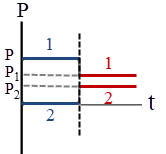
จากกราฟ (D)
ดังนั้น กราฟ (D) ถูกต้อง
โจทย์ให้เป็นการชนแบบยืดหยุ่นแสดงว่า
1) อนุรักษ์โมเมนตัม \(\sum \rm P\) ก่อนชน = \(\sum \rm P\)หลังชน
2) อนุรักษ์พลังงาน \(\rm E\)ก่อน = \(\rm E\)หลัง
พิจารณาจากเงื่อนไข 1)
จากกราฟจะเห็นว่า กราฟ (B), (E) มีการเปลี่ยนแปลงหลังชนไปในทำนองเดียวกัน (เพิ่มขึ้นเหมือนกัน หรือลดลงเหมือนกัน) ซึ่งขัดกับการอนุรักษ์โมเมนตัม
ดังนั้น กราฟ (B), (E) ไม่ใช่คำตอบ
และเมื่อวาดรูปจากกราฟ (A) จะได้
ดังนั้น กราฟ (A) ไม่ใช่คำตอบ
พิจารณาจากเงื่อนไข 2)
จากกราฟ (C)
\(\rm E\)ก่อน \(=\dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} + 0 = \dfrac{1}{2}\dfrac{{{{\rm{m}}^2}{{\rm{v}}^2}}}{{\rm{m}}} = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
\(\rm E\)หลัง \(=\dfrac{1}{2}{\rm{mv}}_1^2 + \dfrac{1}{2}{\rm{mv}}_2^2 = \dfrac{1}{2}\dfrac{{{\rm{P}}_1^{^2}}}{{\rm{m}}} + \dfrac{1}{2}\dfrac{{{\rm{P}}_2^{^2}}}{{\rm{m}}} = \dfrac{1}{{2{\rm{m}}}}\left( {{\rm{P}}_1^{^2} + {\rm{P}}_2^{^2}} \right)\)
จากกราฟสังเกตว่า \(\rm P_1 + P_2 \approx P\) แสดงว่า
\(\rm E\)ก่อน \(\approx \dfrac{1}{{2{\rm{m}}}}{\left( {{{\rm{P}}_1} + {{\rm{P}}_2}} \right)^2} = \dfrac{1}{{2{\rm{m}}}}({\rm{P}}_1^2 + {\rm{P}}_2^2 + 2{{\rm{P}}_1}{{\rm{P}}_2}) > \) \(\rm E\)หลัง
ซึ่งขัดกับการอนุรักษ์พลังงาน ดังนั้น กราฟ (C) ไม่ใช่คำตอบจากกราฟ (D)
\(\rm E\)ก่อน \(= \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} + 0 = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
\(\rm E\)หลัง \(= 0 + \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
ซึ่ง \(\rm E\)ก่อน = \(\rm E\)หลังดังนั้น กราฟ (D) ถูกต้อง
| 14. | ให้อัตราเร็วของรถยนต์ที่มีระบบขับเคลื่อนล้อหลังมีขนาดเพิ่มขึ้น แล้วทิศทางของแรงเสียดทานบนยางรถยนต์จะเป็นไปตามข้อใด |
| A | ที่ล้อหน้ามีทิศถอยหลัง ที่ล้อหลังมีทิศไปข้างหน้า |
| B | ที่ล้อหน้ามีทิศไปข้างหน้า ที่ล้อหลังมีทิศถอยหลัง |
| C | ทุกล้อมีทิศไปข้างหน้า |
| D | ทุกล้อมีทิศถอยหลัง |
| E | แรงเสียดทานเป็นศูนย์ |
ตอบ (A)
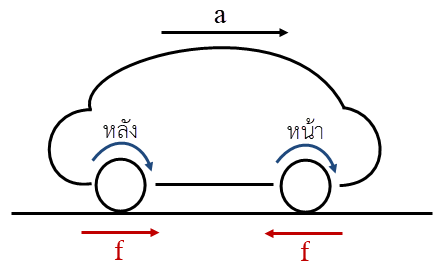ล้อหลัง : จะตะกุยพื้นเพื่อดันรถไปข้างหน้า ทำให้ล้อที่สัมผัสพื้นเคลื่อนที่ไปด้านหลัง \((\leftarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหลังจะมีทิศไปข้างหน้า \((\rightarrow)\)
ล้อหน้า : เพลาของล้อหน้าจะเคลื่อนที่ไปข้างหน้า \((\rightarrow)\) ทำให้ล้อส่วนที่สัมผัสพื้นเคลื่อนที่ตามเพลา คือ ไปข้างหน้า \((\rightarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหน้าจะมีทิศไปข้างหลัง \((\leftarrow)\)
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหลังจะมีทิศไปข้างหน้า \((\rightarrow)\)
ล้อหน้า : เพลาของล้อหน้าจะเคลื่อนที่ไปข้างหน้า \((\rightarrow)\) ทำให้ล้อส่วนที่สัมผัสพื้นเคลื่อนที่ตามเพลา คือ ไปข้างหน้า \((\rightarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหน้าจะมีทิศไปข้างหลัง \((\leftarrow)\)
| 15. | ให้แผ่นกลมสม่ำเสมอ (I = \(\dfrac{1}{2}\)MR2) มีมวล 8.0 kg สามารถหมุนรอบแกนโดยไม่มีแรงเสียดทาน และมีเชือกคล้องผ่านแผ่นกลมนั้น และแขวนมวล 6.0 kg เอาไว้ ดังรูป ถ้าเชือกไม่มีการไถล แล้วแรงตึงเชือกขณะมวลหย่อนลงมาเท่ากับข้อใด
 |
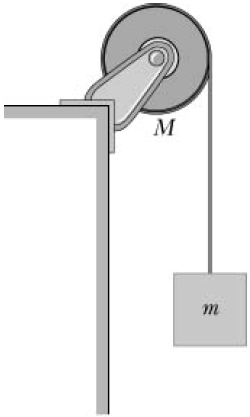| A | 20.0 N |
| B | 24.0 N |
| C | 34.3 N |
| D | 60.0 N |
| E | 80.0 N |
ตอบ (B)
โจทย์ให้ \(\rm M = 8.0 kg ,~ m = 6.0 kg\) ให้เชือกมีแรงตึง \(\rm T\)
พิจารณามวล \(\rm M\)
จาก \(\sum {\tau = {\rm{I}}\alpha }\)
จาก \(\sum {{\rm{F = ma}}}\)
พิจารณามวล \(\rm M\)
จาก \(\sum {\tau = {\rm{I}}\alpha }\)
\(\begin{align*} \rm TR &= \dfrac{{\rm{1}}}{{\rm{2}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}\alpha \\ \alpha &= \dfrac{{{\rm{2T}}}}{{{\rm{MR}}}} \end{align*}\)
จากเงื่อนไขเชือกไม่ไถลทำให้
\(\rm a = \alpha \rm R = \left( {\dfrac{{{\rm{2T}}}}{{{\rm{MR}}}}} \right){\rm{R}} = \dfrac{{{\rm{2T}}}}{{\rm{M}}}\)
พิจารณามวล \(\rm m\)จาก \(\sum {{\rm{F = ma}}}\)
\({\rm{mg}} - {\rm{T = ma}}\)
แทน \({\rm{a = }}\dfrac{{{\rm{2T}}}}{{\rm{M}}}\) จะได้
\(\begin{align*} \rm mg - T &= m \dfrac{{{\rm{2T}}}}{{\rm{M}}}\\ \rm T &=\dfrac{{{\rm{mg}}}}{{1 + \dfrac{{{\rm{2m}}}}{{\rm{M}}}}}\\ &= \dfrac{{{\rm{6}}{\rm{.0(10)}}}}{{1 + \dfrac{{{\rm{2(6}}{\rm{.0)}}}}{{8.0}}}}\\ &= 24\,\,{\rm{N}} \end{align*}\)
ดังนั้น \(\rm T = 24 ~~N\)| 16. | ให้ลูกเบสบอลตกใส่ด้านบนของลูกบาส ขณะที่ลูกบาสกระแทกพื้นแล้วกระเด้งกลับด้วยอัตราเร็ว 4.0 m/s และพุ่งชนกับลูกเบสบอลที่ตกลงมาด้วยอัตราเร็ว 4.0 m/s หลังการชนลูกเบสบอลพุ่งกลับขึ้นไป ดังรูป และลูกบาสกลับมาอยู่นิ่งทันทีหลังการชน ถ้าลูกเบสบอลมวล 0.2 kg และลูกบาสมวล 0.5 kg และไม่สนแรงต้านอากาศ ไม่สนการดลเนื่องจากแรงโน้มถ่วง เพราะช่วงเวลาในการชนนั้นสั้นมาก แล้วอัตราเร็วของลูกเบสบอลหลังการชนกับลูกบาสที่พุ่งขึ้นมาเท่ากับข้อใด
 |
| A | 4.0 m/s |
| B | 6.0 m/s |
| C | 8.0 m/s |
| D | 12.0 m/s |
| E | 16.0 m/s |
ตอบ (B)
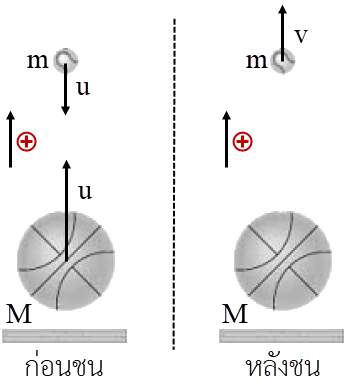โจทย์ให้ M = 0.5 kg, m = 0.2 kg, u = 4.0 m/s
ใช้หลักการอนุรักษ์โมเมนตัม (ในแนวดิ่ง)
ใช้หลักการอนุรักษ์โมเมนตัม (ในแนวดิ่ง)
ก่อนชน = หลังชน
\(\begin{align*} {\rm{Mu}} - {\rm{mu}} &= \rm M(0) + mv\\ {\rm{Mu}} - {\rm{mu}} &= \rm mv\\ v &= \left( {\frac{{{\rm{M}} - {\rm{m}}}}{{\rm{m}}}} \right){\rm{u}}\\ &= \left( {\frac{{0.5 - 0.2}}{{0.2}}} \right)4.0\\ &= 6.0\,\,{\rm{m/s}} \end{align*}\)
\(\begin{align*} {\rm{Mu}} - {\rm{mu}} &= \rm M(0) + mv\\ {\rm{Mu}} - {\rm{mu}} &= \rm mv\\ v &= \left( {\frac{{{\rm{M}} - {\rm{m}}}}{{\rm{m}}}} \right){\rm{u}}\\ &= \left( {\frac{{0.5 - 0.2}}{{0.2}}} \right)4.0\\ &= 6.0\,\,{\rm{m/s}} \end{align*}\)
| 17. | ให้วัตถุเล็กๆ ถูกขว้างไปออกจากตึกสูง 50.0 m ตามแนวนนอนด้วยอัตราเร็วต้น 10.0 m/s ตามแนววิถีที่วัตถุเคลื่อนที่ไปจะมีองค์ประกอบที่เป็นความเร่งที่สัมผัสกับแนววิถีการเคลื่อนที่ และความเร่งที่ตั้งฉากกับแนววิถี แล้วความเร่งของวัตถุในแนวสัมผัสกับแนวตั้งฉากจะมีค่าเท่ากัน หลังวัตถุถูกโยนออกไปกี่วินาที ไม่ต้องคำนึงถึงแรงต้านอากาศ |
| A | 2.00 s |
| B | 1.50 s |
| C | 1.00 s |
| D | 0.50 s |
| E | ที่ความสูงนั้นยังไม่สามารถทำให้เกิดเหตุการณ์นั้นได้ |
ตอบ (A)
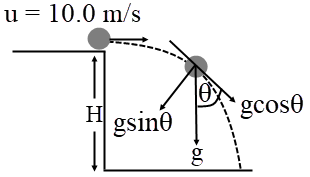จากรูป ความเร่งในแนวตั้งฉาก \(= \rm g\sin\theta\) และ ความเร่งในแนวสัมผัส \(=\rm g\cos\theta\)
โดยความเร่งในแนวตั้งฉาก \(=\) ความเร่งในแนวสัมผัส เมื่อ \(\rm g\sin\theta = g\cos\theta\)
ดังนั้น \(\tan\theta = 1\)
แสดงว่า \(\dfrac{{\rm{u}}}{{\rm{v}}} = \tan {\rm{\theta }} = 1\) ด้วย เมื่อ \(v\) เป็นความเร็วในแนวดิ่งของวัตถุ
จาก \(\rm v = gt\)
จาก
โดยความเร่งในแนวตั้งฉาก \(=\) ความเร่งในแนวสัมผัส เมื่อ \(\rm g\sin\theta = g\cos\theta\)
ดังนั้น \(\tan\theta = 1\)
แสดงว่า \(\dfrac{{\rm{u}}}{{\rm{v}}} = \tan {\rm{\theta }} = 1\) ด้วย เมื่อ \(v\) เป็นความเร็วในแนวดิ่งของวัตถุ
จาก \(\rm v = gt\)
\({\rm{t = }}\dfrac{{\rm{v}}}{{\rm{g}}}{\rm{ = }}\dfrac{{\rm{u}}}{{\rm{g}}} \approx \dfrac{{10.0}}{{10.0}} = 1.00\,\,{\rm{s}}\)
ตรวจสอบระยะทางที่ตก (s) จาก
\({\rm{s = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{{\rm{t}}^{\rm{2}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{ \times 10 \times }}{{\rm{1}}^{\rm{2}}}{\rm{ = 5m < 50}}{\rm{.0m}}\)
ดังนั้น ความสูงเพียงพอที่จะทำให้เกิดเหตุการณ์นั้นได้| 18. | ก้อนน้ำแข็งเล็กๆ ที่เดิมอยู่นิ่ง ไหลลงมาตามแผ่นน้ำแข็งโค้งที่ไม่มีแรงเสียดทาน ดังรูป แล้วที่จุด A จะเป็นจุดเชื่อมแผ่นน้ำแข็งกับพื้นเอียงที่ยกขึ้นมา 30° จากแนวระดับ และมีสัมประสิทธิ์เสียดทาน μk ความยาวทางลาดยาว \(\dfrac{3}{2}\rm h\) ถ้าก้อนน้ำแข็งนิ่งสนิทที่ปลายด้านล่างของพื้นเอียง แล้ว μk เท่ากับข้อใด
 |
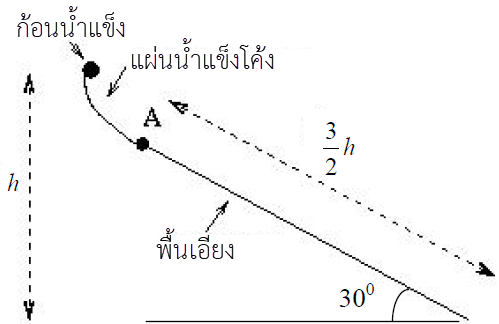| A | 0.866 |
| B | 0.770 |
| C | 0.667 |
| D | 0.385 |
| E | 0.333 |
ตอบ (B)
จากงานและพลังงาน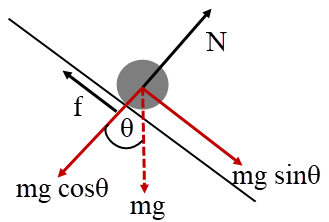
โดย \({\rm{f}} = {{\rm{\mu }}_{\rm{k}}}{\rm{N}} = {{\rm{\mu }}_{\rm{k}}}{\rm{mg}}\cos \theta \) จะได้ว่า
จากงานและพลังงาน
พลังงานศักย์โน้มถ่วง \(+\) งานที่แรงเสียดทานทำ (ติดลบ) \(= 0\) (น้ำแข็งหยุดนิ่งที่ปลายราง)
\(\rm mgh + \left( – f\left( {\dfrac{3}{2}{\rm{h}}} \right) \right)= 0\)
วาดรูปจากโจทย์
\(\rm mgh + \left( – f\left( {\dfrac{3}{2}{\rm{h}}} \right) \right)= 0\)
\(\begin{align*} \rm mgh &=\dfrac{{\rm{3}}}{{\rm{2}}}{\rm{fh}}\\ \rm mg &= \dfrac{{\rm{3}}}{{\rm{2}}}{\rm{(}}{{\rm{\mu }}_{\rm{k}}}{\rm{mg ~cos}}\theta {\rm{)}}\\ {{\rm{\mu }}_{\rm{k}}} &= \dfrac{{\rm{2}}}{{\rm{3}}}\dfrac{1}{{{\rm{cos30}}^\circ }}\\ &= \dfrac{4}{{3\sqrt 3 }}\\ &\approx 0.770 \end{align*}\)
| 19. | ให้สปริงที่ไม่ได้เป็นไปตาม กฎของฮุค มีแรง F = – kx2 โดย k เป็นค่านิจสปริง x เป็นระยะสปริงที่ยังไม่ถูกยืดจากระบบที่แสดง ดังรูป ถ้านำวัตถุมวล m ติดกับสปริงที่เดิมอยู่นิ่ง แล้วระยะยืดของสปริงจนระบบหยุดนิ่งชั่วขณะเท่ากับข้อใด สมมุติว่า ทุกพื้นผิวและรอกไม่มีแรงเสียดทาน
 |
| A | \(\rm \left(\dfrac{3mg}{2k}\right)^{1/2}\) |
| B | \(\rm \left(\dfrac{mg}{k}\right)^{1/2}\) |
| C | \(\rm \left(\dfrac{2mg}{k}\right)^{1/2}\) |
| D | \(\rm \left(\dfrac{\sqrt3mg}{2k}\right)^{1/2}\) |
| E | \(\rm \left(\dfrac{3\sqrt3mg}{2k}\right)^{1/2}\) |
ตอบ (A)
จากโจทย์บอกระบบหยุดนิ่งชั่วขณะ แสดงว่าตอนนั้นระบบต้องไม่มีพลังงานจลน์
สมมุติให้วัตถุเคลื่อนที่ไปได้ระยะทาง x
ตอนสุดท้าย
เพิ่มเติม ข้อนี้ใช้สมดุลแรงไม่ได้ เพราะ ตรงจุดนี้วัตถุยังมีความเร็วอยู่ (Ek ≠ 0)
จากโจทย์บอกระบบหยุดนิ่งชั่วขณะ แสดงว่าตอนนั้นระบบต้องไม่มีพลังงานจลน์
สมมุติให้วัตถุเคลื่อนที่ไปได้ระยะทาง x
ตอนสุดท้าย
Eสปริง \(\displaystyle = - \int {{\rm{Fdx}} = - \left( { - \int {{\rm{k}}{{\rm{x}}^{\rm{2}}}{\rm{dx}}} } \right){\rm{ = }}\dfrac{{\rm{1}}}{{\rm{3}}}{\rm{k}}{{\rm{x}}^{\rm{3}}}} \)
ตอนแรก
Eศักย์ \(= {\rm{mg ~x}}\sin 30^\circ = \dfrac{1}{2}{\rm{mg ~x}}\)
จากกฎอนุรักษ์พลังงาน
\(\begin{align*} \dfrac{1}{3}{\rm{k}}{{\rm{x}}^3} &= \dfrac{1}{2}{\rm{mgx}}\\ \rm x &= \sqrt {\dfrac{3}{2}\dfrac{{{\rm{mg}}}}{{\rm{k}}}} \end{align*}\)
ดังนั้น ระยะยืดเท่ากับ \({\left( {\dfrac{{3{\rm{mg}}}}{{2{\rm{k}}}}} \right)^{\frac{1}{2}}}\) เพิ่มเติม ข้อนี้ใช้สมดุลแรงไม่ได้ เพราะ ตรงจุดนี้วัตถุยังมีความเร็วอยู่ (Ek ≠ 0)
Ek = Eศักย์ – Eสปริง = \(\dfrac{1}{2}{\rm{mg x}} - \dfrac{{\rm{1}}}{{\rm{3}}}{\rm{k}}{{\rm{x}}^{\rm{3}}} = \sqrt {\dfrac{1}{8}\dfrac{{{{\rm{m}}^{\rm{3}}}{{\rm{g}}^{\rm{3}}}}}{{\rm{k}}}} - \sqrt {\dfrac{1}{{24}}\dfrac{{{{\rm{m}}^{\rm{3}}}{{\rm{g}}^{\rm{3}}}}}{{\rm{k}}}} \ne 0\)
เพราะ สมดุลแรงบอกแค่ว่า a = 0 ไม่ได้บอกว่า v = 0 หรือไม่| 20. | จุดมวลเล็กๆ เคลื่อนที่ไปตามแนวนอนระหว่างผนังสองด้านที่ไม่มีแรงเสียดทาน ด้วยพลังงานจลน์เริ่มต้น E ทุกครั้งที่ชนกับผนัง มวลจะสูญเสียพลังงานจลน์ไป \(\dfrac{1}{2}\) ไปเป็นพลังงานความร้อน แล้ววัตถุจะชนกับผนังได้กี่ครั้ง ก่อนที่ความเร็วของมวลจะลดลงจนเหลือ \(\dfrac{1}{8}\) เท่าของของเดิม |
| A | 3 |
| B | 4 |
| C | 6 |
| D | 8 |
| E | 16 |
ตอบ (C)
จาก
v2, E2 เป็นความเร็ว (ที่ลดลงไป 8 เท่า) และพลังงาน ณ ขณะนั้น
จะได้
ดังนั้น ต้องชน 6 ครั้ง
\(\begin{array}{l} {{\rm{E}}_{\rm{k}}} = \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2}\\ {{\rm{E}}_{\rm{k}}} \propto {{\rm{v}}^2} \end{array}\)
ให้ v1, E1 เป็นความเร็วและพลังงานตอนแรกv2, E2 เป็นความเร็ว (ที่ลดลงไป 8 เท่า) และพลังงาน ณ ขณะนั้น
จะได้
\(\rm \displaystyle \frac{{{E_2}}}{{{E_1}}} = \frac{{v_2^2}}{{v_1^2}} = {\left( {\frac{1}{8}} \right)^2} = {\left( {\frac{1}{2}} \right)^6}\)
| 21. | ถ้าความเฉื่อยในการหมุนรอบแกนที่ผ่านจุดศูนย์กลางของทรงกลมตันคือ I แล้วความเฉื่อยในการหมุนรอบทรงกลมที่มีความหนาแน่นเท่ากัน แต่มีรัศมีเป็นสองเท่าจะเท่ากับข้อใด |
| A | 2I |
| B | 4I |
| C | 8I |
| D | 16I |
| E | 32I |
ตอบ (E)
จาก
และ
จาก
\({\rm{I}} \propto {\rm{m}}{{\rm{R}}^{\rm{2}}}\)
เมื่อ m = มวลวัตถุ , R = รัศมีวัตถุและ
\({\rm{m}} \propto \rho {{\rm{R}}^3}\)
ดังนั้น
\({\rm{I}} \propto \rho {{\rm{R}}^{\rm{5}}}\)
จากโจทย์ให้ R เป็น 2 เท่า จะได้ I เป็น 25 = 32 เท่า| 22. | จรวดสองลำอยู่ในอวกาศที่มีสนามโน้มถ่วงน้อยมาก ให้ผู้สังเกตอยู่ในกรอบอ้างอิงที่จรวดทั้งสองเดิมอยู่นิ่ง มวลของจรวดเป็น m และ 9m เมื่อมีแรงคงที่ F มากระทำกับจรวดมวล m เป็นระยะทาง d จะทำให้จรวดได้รับโมเมนตัม p ถ้ามีแรง F เท่าเดิม มากระทำกับจรวดมวล 9m เป็นระยะทางเท่ากัน d แล้วโมเมนตัมที่จรวดมวล 9m จะได้รับเท่ากับข้อใด |
| A | p/9 |
| B | p/3 |
| C | p |
| D | 3p |
| E | 9p |
ตอบ (D)
พิจารณาจรวดมวล m ใดๆ
จาก \(a = \dfrac{F}{m}\) จะได้
จากโจทย์ ถ้าเปลี่ยน \(m\) เป็น \(9m\) แล้ว p จะเป็น \(\sqrt {\rm{9}} {\rm{p = 3p}}\)
พิจารณาจรวดมวล m ใดๆ
\(\begin{align*} \rm v(t) &=\dfrac{{\rm{F}}}{{\rm{m}}}{\rm{t}}\\ \rm x(t) &=\dfrac{{\rm{1}}}{{\rm{2}}}\frac{{\rm{F}}}{{\rm{m}}}{{\rm{t}}^{\rm{2}}}= \frac{{\rm{1}}}{{\rm{2}}}\frac{{\rm{m}}}{{\rm{F}}}{{\rm{v}}^{\rm{2}}} = \frac{{\rm{1}}}{{\rm{2}}}\frac{{{{\rm{p}}^{\rm{2}}}}}{{{\rm{Fm}}}} \end{align*}\)
ที่ \(x = d\) จะได้
\(\begin{align*} \dfrac{{\rm{1}}}{{\rm{2}}}\frac{{{{\rm{p}}^{\rm{2}}}}}{{{\rm{Fm}}}} &= {\rm{d}}\\ {\rm{p}} &= \sqrt {{\rm{2Fmd}}} \end{align*}\)
ดังนั้น \({\rm{p}} \propto \sqrt {\rm{m}}\)จากโจทย์ ถ้าเปลี่ยน \(m\) เป็น \(9m\) แล้ว p จะเป็น \(\sqrt {\rm{9}} {\rm{p = 3p}}\)
| 23. | ถ้าดาวรัศมี R หมุนด้วยอัตราเร็วเชิงมุม ω รอบแกนที่ผ่านขั้วโลกเหนือ แล้วอัตราส่วนของแรงตั้งฉากที่พื้นกระทำกับคนคนหนึ่งที่เส้นศูนย์สูตร กับคนที่ขั้วโลกเหนือเท่ากับข้อใด สมมุติว่ามีสนามโน้มถ่วงคงที่ g และทั้งสองคนอยู่นิ่งเทียบเมื่อกับดาวเคราะห์ และอยู่ที่ระดับน้ำทะเล |
| A | g/Rω2 |
| B | Rω2/g |
| C | 1 – Rω2/g |
| D | 1 + g /Rω2 |
| E | 1 + Rω2/g |
ตอบ (C)
ให้ N1 เป็นแรงตั้งฉากที่พื้นกระทำกับคนที่อยู่ที่ขั้วโลกเหนือ
และ N2 เป็นแรงตั้งฉากที่พื้นกระทำกับคนที่อยู่ที่เส้นศูนย์สูตร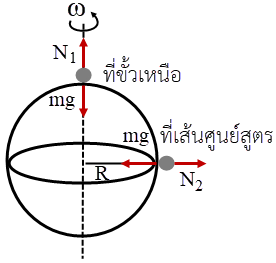
ที่ขั้วเหนือ
ดังนั้น \(\dfrac{{{{\rm{N}}_{\rm{2}}}}}{{{{\rm{N}}_{\rm{1}}}}} = \dfrac{{{\rm{g}} - {\rm{R}}{{\rm{\omega }}^2}}}{{\rm{g}}} = 1 - \dfrac{{{\rm{R}}{{\rm{\omega }}^{\rm{2}}}}}{{\rm{g}}}\)
ให้ N1 เป็นแรงตั้งฉากที่พื้นกระทำกับคนที่อยู่ที่ขั้วโลกเหนือ
และ N2 เป็นแรงตั้งฉากที่พื้นกระทำกับคนที่อยู่ที่เส้นศูนย์สูตร
\(\rm N_1 = mg\)
ที่เส้นศูนย์สูตร มีความเร่งสู่ศูนย์กลาง
\(\begin{align*} \rm mg – N_2 &=\rm mRω^2\\ \rm N_2 &=\rm m(g –Rω^2) \end{align*}\)
ดังนั้น \(\dfrac{{{{\rm{N}}_{\rm{2}}}}}{{{{\rm{N}}_{\rm{1}}}}} = \dfrac{{{\rm{g}} - {\rm{R}}{{\rm{\omega }}^2}}}{{\rm{g}}} = 1 - \dfrac{{{\rm{R}}{{\rm{\omega }}^{\rm{2}}}}}{{\rm{g}}}\)
| 24. | ถ้าเตะบอลมวล m ออกไปกลางอากาศ โดยไม่สนแรงต้านอากาศ แต่สมมุติว่า มีลมที่มีแรงคงที่ F0 กระทำในทิศทาง – x แล้วขนาดมุมเหนือแกน x ในทิศบวก ที่เตะบอลแล้วบอลจะถูกพัดกลับมาที่จุดเดิมเท่ากับข้อใด ให้แสดงในเทอมของ F0 และความเร่งโน้มถ่วง g |
| A | tan-1 (F0/mg) |
| B | tan-1 (mg/F0) |
| C | sin-1 (F0/mg) |
| D | ขนาดของมุมจะขึ้นกับแรงที่เตะ |
| E | ไม่มีมุมใดที่ทำให้เกิดเหตุการณ์ดังกล่าว |
ตอบ (B)
จากโจทย์หา effective gravity (geff) (รวมความเร่ง)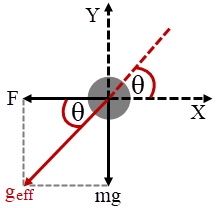
จะพบว่า geff ทำมุม \({\rm{\theta }} = {\tan ^{ - 1}}\left( {\dfrac{{{\rm{mg}}}}{{{{\rm{F}}_{\rm{0}}}}}} \right)\) กับแกน X
หากมองในมุมมองของโลกที่มี geff เป็นสนามโน้มถ่วง และต้องการให้วัตถุกลับมาที่เดิม ก็ต้องโยนวัตถุขึ้นในแนวดิ่ง แต่ถ้ามองในมุมมองปกติก็ต้องโยนลูกบอลทำมุม \({\rm{\theta }} = {\tan ^{ - 1}}\left( {\dfrac{{{\rm{mg}}}}{{{{\rm{F}}_{\rm{0}}}}}} \right)\) เท่ากับมุมของ geff ลูกบอลจึงจะกลับมาที่เดิม
จากโจทย์หา effective gravity (geff) (รวมความเร่ง)
หากมองในมุมมองของโลกที่มี geff เป็นสนามโน้มถ่วง และต้องการให้วัตถุกลับมาที่เดิม ก็ต้องโยนวัตถุขึ้นในแนวดิ่ง แต่ถ้ามองในมุมมองปกติก็ต้องโยนลูกบอลทำมุม \({\rm{\theta }} = {\tan ^{ - 1}}\left( {\dfrac{{{\rm{mg}}}}{{{{\rm{F}}_{\rm{0}}}}}} \right)\) เท่ากับมุมของ geff ลูกบอลจึงจะกลับมาที่เดิม
| 25. | จงหาคาบของการสั่นเล็ก ๆ ของ เครื่องเล่นทางน้ำที่เรียกว่า water pogo ที่มีลักษณะเป็นแท่งมวล m คล้ายกล่อง (รูปสี่เหลี่ยมด้านขนาน) มีความยาว L , กว้าง w และ สูง h และสั่นขึ้นลงในน้ำที่มีความหนาแน่น ρ สมมุติว่า water pogo มีความยาว L และกว้าง w และอยู่ในแนวนอนตลอดเวลา คำแนะนำ : แรงลอยตัวบนวัตถุหาจาก FB = ρVg โดย V คือ ปริมาตรของของเหลวที่ถูกแทนที่ และ ρ คือ ความหนาแน่นของของเหลว สมมุติว่าที่สมดุล water pogo จะลอย (ไม่จม) |
| A | \(\rm 2\pi\sqrt{\dfrac{L}{g}}\) |
| B | \(\rm \pi\sqrt{\dfrac{\rho w^2L^2g}{mh^2}}\) |
| C | \(\rm 2\pi\sqrt{\dfrac{mh^2}{\rho w^2L^2g}}\) |
| D | \(\rm 2\pi\sqrt{\dfrac{m}{\rho wLg}}\) |
| E | \(\rm \pi\sqrt{\dfrac{m}{\rho wLg}}\) |
ตอบ (D)
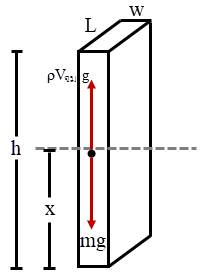เขียนสมการนิวตัน
จาก \({\rm{w = }}\sqrt {\dfrac{{{\rm{\rho Lwg}}}}{{\rm{m}}}} \) จะได้ว่า
\(\begin{align*} \rm mg ~– ρV_{จม}g &= {\rm{m}}\frac{{{{\rm{d}}^{\rm{2}}}{\rm{x}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\\ {\rm{mg }}-\rm\rho (xLw) &= \rm m\dfrac{{{{\rm{d}}^{\rm{2}}}{\rm{x}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\\ \frac{{{\rm{\rho Lwg}}}}{{\rm{m}}}{\rm{ }}\left( {\frac{{\rm{m}}}{{{\rm{\rho Lw}}}}--{\rm{x}}} \right) &= \dfrac{{{{\rm{d}}^{\rm{2}}}{\rm{x}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\\ - \frac{{{\rm{\rho Lwg}}}}{{\rm{m}}}{\rm{ }}\left( {{\rm{x}}-\frac{{\rm{m}}}{{{\rm{\rho Lw}}}}} \right) &= \dfrac{{{{\rm{d}}^{\rm{2}}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\left( {{\rm{x}}-\frac{{\rm{m}}}{{{\rm{\rho Lw}}}}} \right) \end{align*}\)
เป็นสมการ simple harmonic ( อยู่ในรูปของ \(-{{\rm{w}}^2}{\rm{x = }}\dfrac{{{{\rm{d}}^{\rm{2}}}{\rm{x}}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}}\) )จาก \({\rm{w = }}\sqrt {\dfrac{{{\rm{\rho Lwg}}}}{{\rm{m}}}} \) จะได้ว่า
\(\therefore {\rm{T = }}\dfrac{{{\rm{2\pi }}}}{{\rm{w}}}{\rm{ = 2\pi }}\sqrt {\dfrac{{\rm{m}}}{{{\rm{\rho Lwg}}}}} \)
| 26. | มีเด็ก ๆ อยู่บนรถลากเลื่อน และรถลากเลื่อนที่เดิมอยู่นิ่งจะเคลื่อนที่ลงมาจากเนินหิมะที่ทำมุม 25° (เทียบกับแนวนอน) ซึ่งเคลื่อนที่ไป 85 เมตร ใน 17 วินาที ถ้าไม่สนแรงต้านอากาศ แล้วสัมประสิทธิ์แรงเสียดทานจลน์ระหว่างรถเลื่อนกับเนินหิมะเท่ากับข้อใด |
| A | 0.36 |
| B | 0.40 |
| C | 0.43 |
| D | 1.00 |
| E | 2.01 |
ตอบ (B)
เมื่อความเร่งมีค่าคงที่ และรถลากเลื่อนเดิมอยู่นิ่ง จะได้ว่า
พิจารณาแกน y ที่ตั้งฉากกับเนินเอียง จะมี ay = 0 ดังนั้น แรงตั้งฉากจะเท่ากับ
เมื่อความเร่งมีค่าคงที่ และรถลากเลื่อนเดิมอยู่นิ่ง จะได้ว่า
\({\rm{\Delta x = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{a}}{{\rm{t}}^{\rm{2}}}\)
ดังนั้น a = 0.588 m/s2พิจารณาแกน y ที่ตั้งฉากกับเนินเอียง จะมี ay = 0 ดังนั้น แรงตั้งฉากจะเท่ากับ
\(\rm N = mg~ cosθ \) --- (1)
จากกฎข้อที่สองของนิวตัน แรงที่ขนานกับพื้นเอียง คือ f = แรงเสียดทานจลน์ จะได้
\(\rm mg~ sinθ − f = ma\) --- (2)
ใช้ f = μN แทนในสมการ (1) และ (2) จะได้
\(\begin{align*} \mu &= \tan \theta - \dfrac{{\rm{a}}}{{{\rm{g~ cos \theta }}}}\\ &= \tan 25 - \dfrac{{{\rm{0}}{\rm{.588 ~m/}}{{\rm{s}}^2}}}{{{\rm{(10 ~m/}}{{\rm{s}}^{\rm{2}}}{\rm{ ) ~cos 25}}}}\\ &= 0.40 \end{align*}\)
| 27. | ให้สถานีอวกาศประกอบด้วย สองห้องนั่งเล่นที่เชื่อมกับอาคารศูนย์กลาง และอยู่ตรงข้าม กัน โดยทางเชื่อมทั้งสองยาวเท่ากัน แต่ละห้องนั่งเล่นจะมีนักบินอวกาศที่มีมวลเท่ากัน N คน ส่วนมวลของสถานีอวกาศถือว่าน้อยมากเมื่อเทียบกับมวลของนักบินอวกาศ และขนาดของอาคารศูนย์กลางกับห้องนั่งเล่นจะเล็กมากเมื่อเทียบกับความยาวของทางเชื่อม ในช่วงแรกๆ สถานีอวกาศจะหมุนเพื่อให้นักบินอวกาศรู้สึกว่ายังอยู่ในสนามโน้มถ่วง g ถ้านักบินอวกาศสองคน จากแต่ละห้องนั่งเล่นมายังอาคารศูนย์กลาง และนักบินอวกาศเริ่มรู้สึกถึงสนามแรงโน้มถ่วง g' แล้วอัตราส่วน g'/g เท่ากับข้อใดในเทอมของ N
 |
| A | \(\rm 2N/(N – 1)\) |
| B | \(\rm N/(N – 1)\) |
| C | \(\rm \sqrt{(N – 1)/N}\) |
| D | \(\rm \sqrt{N/(N – 1)}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (E)
กรอบอ้างอิงนี้ ความเร่งจะมีค่าเท่ากับสนามโน้มถ่วง และเราจะแทนปริมาณต่างๆ ที่เปลี่ยนแปลงหลังนักบินอวกาศมาที่อาคารศูนย์กลางด้วยการเติม ไพร์ม เข้าไป เนื่องจาก v = r ω และการเคลื่อนที่เป็นวงกลม และรัศมีคงที่
จะได้
กรอบอ้างอิงนี้ ความเร่งจะมีค่าเท่ากับสนามโน้มถ่วง และเราจะแทนปริมาณต่างๆ ที่เปลี่ยนแปลงหลังนักบินอวกาศมาที่อาคารศูนย์กลางด้วยการเติม ไพร์ม เข้าไป เนื่องจาก v = r ω และการเคลื่อนที่เป็นวงกลม และรัศมีคงที่
จะได้
\(\dfrac{{{\rm{g'}}}}{{\rm{g}}}{\rm{ = }}\dfrac{{{{{\rm{v'}}}^{\rm{2}}}}}{{{{\rm{v}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{{{{\rm{\omega '}}}^{\rm{2}}}}}{{{{\rm{\omega }}^{\rm{2}}}}}\) --- (1)
โดยโมเมนตัมเชิงมุมจะถูกอนุรักษ์ไว้ เพราะไม่มีทอร์กภายนอกมากระทำในระบบ จึงได้
\({\rm{I\omega = I'\omega '}}\) --- (2)
เพราะทางเชื่อมยาวมาก เราจึงถือว่านักบินอวกาศเป็นจุดมวลหนึ่ง สมมุติให้ r เป็นระยะห่างจากอาคารศูนย์กลางถึงห้องนั่งเล่น และ m เป็นมวลของนักบินอวกาศหนึ่งคน จากที่แต่ละห้องนั่งเล่นมีนักบินอวกาศ N คน จะได้ว่าความเฉื่อยในการหมุนก่อนนักบินอวกาศจะเคลื่อนที่เท่ากับ
\({\rm{I = 2Nm}}{{\rm{r}}^{\rm{2}}}\) --- (3)
หลังนักบินอวกาศสองคนไปถึงอาคารศูนย์กลาง จะได้
\({\rm{I' = 2(N}}-1){\rm{m}}{{\rm{r}}^{\rm{2}}}\) --- (4)
เมื่อแทน (3) และ (4) ใน (2) เราจะได้
\(\begin{align*} {\rm{2Nm}}{{\rm{r}}^{\rm{2}}}\rm \omega &= \rm 2(N -1){\rm{m}}{{\rm{r}}^{\rm{2}}}{\rm{\omega '}}\\ \frac{{{\rm{\omega '}}}}{{\rm{\omega }}} &= \frac{{\rm{N}}}{{{\rm{N}}-1}} \end{align*}\)
เมื่อนำ \(\dfrac{{{\rm{\omega '}}}}{{\rm{\omega }}} = \dfrac{{\rm{N}}}{{{\rm{N}}-1}}\) ไปแทนใน (1) จะได้
\(\dfrac{{{\rm{g'}}}}{{\rm{g}}} = \dfrac{{{\rm{\omega '}}}}{{\rm{\omega }}} = \dfrac{{\rm{N}}}{{{\rm{N}}-1}}\)
สังเกตว่า ไม่มีตัวเลือกใดถูกเลยจึงตอบข้อ (E)| 28. | แบบจำลองอย่างง่ายของจักรยานมวล M สองล้อ แต่ละล้อสัมผัสพื้นที่จุดหนึ่ง และระยะฐานล้อ (ระยะจากจุดสัมผัสกับพื้นของล้อหนึ่งถึงอีกล้อหนึ่ง) เท่ากับ w มีจุดศูนย์กลางมวลของจักรยานอยู่กึ่งกลางระหว่างล้อและอยู่สูง h เหนือพื้นดิน สมมุติให้จักรยานกำลังเคลื่อนที่ไป ทางขวา แต่มีการชะลอตัวในอัตราคงที่ มีความเร่ง a และในที่นี้จะไม่สนแรงต้านอากาศ
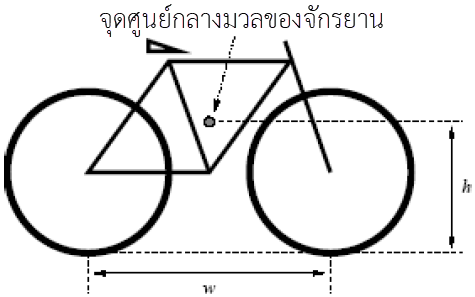 ค่า μ สูงสุดที่ล้อทั้งสองยังคงสัมผัสกับพื้นดิน เท่ากับข้อใด |
| A | \(\rm \dfrac{w}{2h}\) |
| B | \(\rm \dfrac{h}{2w}\) |
| C | \(\rm \dfrac{2h}{w}\) |
| D | \(\rm \dfrac{w}{h}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (A)
จากสมดุลสถิตในกรอบอ้างอิงที่กำหนดให้ เราต้องหาทอร์กที่จุดศูนย์กลางมวลก่อน ให้ N1 เป็นแรงตั้งฉากบนล้อหน้า, N2 เป็นแรงตั้งฉากบนล้อหลัง, f1 เป็นแรงเสียดทานที่ล้อหน้า และ f2 แรงเสียดเสียดทานที่ล้อหลัง ถ้าล้อหน้ายังไม่สัมผัสกับพื้นดิน แล้ว N1 = f1 = 0
จากทอร์กของแรงเสียดทานที่ล้อหลังในทิศทวนเข็มนาฬิกา = ทอร์กจากแรงตั้งฉากที่ล้อหลังในทิศตามเข็มนาฬิกา จะได้
จากสมดุลสถิตในกรอบอ้างอิงที่กำหนดให้ เราต้องหาทอร์กที่จุดศูนย์กลางมวลก่อน ให้ N1 เป็นแรงตั้งฉากบนล้อหน้า, N2 เป็นแรงตั้งฉากบนล้อหลัง, f1 เป็นแรงเสียดทานที่ล้อหน้า และ f2 แรงเสียดเสียดทานที่ล้อหลัง ถ้าล้อหน้ายังไม่สัมผัสกับพื้นดิน แล้ว N1 = f1 = 0
จากทอร์กของแรงเสียดทานที่ล้อหลังในทิศทวนเข็มนาฬิกา = ทอร์กจากแรงตั้งฉากที่ล้อหลังในทิศตามเข็มนาฬิกา จะได้
\({{\rm{f}}_2}{\rm{h = }}{{\rm{N}}_2}\dfrac{{\rm{w}}}{2}\)
แทน f2 = μN2 จะได้
\(\begin{align*} {\rm{\mu }}{{\rm{N}}_2}\rm h &={{\rm{N}}_2}\dfrac{{\rm{w}}}{2}\\ \rm\mu &= \dfrac{{\rm{w}}}{{2{\rm{h}}}} \end{align*}\)
| 29. | แบบจำลองอย่างง่ายของจักรยานมวล M สองล้อ แต่ละล้อสัมผัสพื้นที่จุดหนึ่ง และระยะฐานล้อ (ระยะจากจุดสัมผัสกับพื้นของล้อหนึ่งถึงอีกล้อหนึ่ง) เท่ากับ w มีจุดศูนย์กลางมวลของจักรยานอยู่กึ่งกลางระหว่างล้อและอยู่สูง h เหนือพื้นดิน สมมุติให้จักรยานกำลังเคลื่อนที่ไป ทางขวา แต่มีการชะลอตัวในอัตราคงที่ มีความเร่ง a และในที่นี้จะไม่สนแรงต้านอากาศ
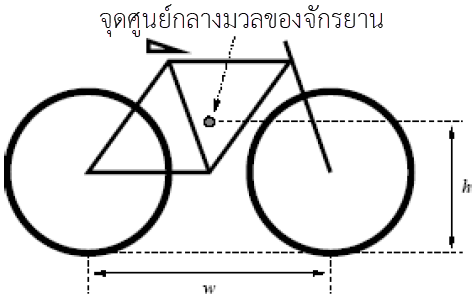 ค่า a สูงสุดที่ล้อทั้งสองยังคงสัมผัสกับพื้นดิน เท่ากับข้อใด |
| A | \(\rm \dfrac{wg}{h}\) |
| B | \(\rm \dfrac{wg}{2h}\) |
| C | \(\rm \dfrac{hg}{2w}\) |
| D | \(\rm \dfrac{h}{2wg}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (B)
จากกฎข้อที่สองของนิวตัน สำหรับการเคลื่อนในแนวนอน จะได้
จากกฎข้อที่สองของนิวตัน สำหรับการเคลื่อนในแนวนอน จะได้
\(\rm f_1 + f_2 = Ma\) --- (1)
จากทอร์กตามเข็มเท่ากับทอร์กทวนเข็ม จะได้
\(\rm \dfrac{{{{\rm{N}}_2}{\rm{w}}}}{2} = \dfrac{{{{\rm{N}}_1}{\rm{w}}}}{2} + ({f_1} + {f_2})h\) --- (2)
แทน (1) ใน (2) จะได้
\(\begin{align*} {\rm{Mah}} &= \dfrac{{\rm{w}}}{2}{\rm{(}}{{\rm{N}}_2}-{{\rm{N}}_1})\\ {\rm{a}} &= \dfrac{{\rm{w}}}{2}\dfrac{{{\rm{(}}{{\rm{N}}_2}-{{\rm{N}}_1})}}{{{\rm{Mh}}}} \end{align*}\)
ชัดเจนว่า จะเกิดค่า \(a\) สูงสุด เมื่อ N1 = 0 และ N2 = Mg จึงได้
\({\rm{a}} = \dfrac{{{\rm{w}}g}}{{2{\rm{h}}}}\)
| 30. | แบบจำลองอย่างง่ายของจักรยานมวล M สองล้อ แต่ละล้อสัมผัสพื้นที่จุดหนึ่ง และระยะฐานล้อ (ระยะจากจุดสัมผัสกับพื้นของล้อหนึ่งถึงอีกล้อหนึ่ง) เท่ากับ w มีจุดศูนย์กลางมวลของจักรยานอยู่กึ่งกลางระหว่างล้อและอยู่สูง h เหนือพื้นดิน สมมุติให้จักรยานกำลังเคลื่อนที่ไป ทางขวา แต่มีการชะลอตัวในอัตราคงที่ มีความเร่ง a และในที่นี้จะไม่สนแรงต้านอากาศ
 ถ้าทั้งสองล้อมีการลื่นไถล (หมายถึง มีการลื่นออกไปโดยไม่หมุน) แล้วค่า a สูงสุดที่ล้อทั้งสองยังคงสัมผัสกับพื้นดิน เท่ากับข้อใด |
| A | \(\rm \dfrac{wg}{h}\) |
| B | \(\rm \dfrac{wg}{3h}\) |
| C | \(\rm \dfrac{2wg}{3h}\) |
| D | \(\rm \dfrac{hg}{2w}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (E)
จากกฎข้อที่สองของนิวตัน สำหรับการเคลื่อนในแนวนอน จะได้
จากกฎข้อที่สองของนิวตัน สำหรับการเคลื่อนในแนวนอน จะได้
\(\rm f_1 + f_2 = Ma\) --- (1)
จากทอร์กตามเข็มเท่ากับทอร์กทวนเข็ม จะได้
\(\rm \dfrac{{{{\rm{N}}_2}{\rm{w}}}}{2} = \dfrac{{{{\rm{N}}_1}{\rm{w}}}}{2} + ({f_1} + {f_2})h\) --- (2)
แทน (1) ใน (2) จะได้
\(\begin{align*} {\rm{Mah}} &= \dfrac{{\rm{w}}}{2}{\rm{(}}{{\rm{N}}_2}-{{\rm{N}}_1})\\ {\rm{a}} &= \dfrac{{\rm{w}}}{2}\dfrac{{{\rm{(}}{{\rm{N}}_2}-{{\rm{N}}_1})}}{{{\rm{Mh}}}} \end{align*}\)
ชัดเจนว่า จะเกิดค่า \(a\) สูงสุด เมื่อ N1 = 0 และ N2 = Mg จึงได้
\({\rm{a}} = \dfrac{{{\rm{w}}g}}{{2{\rm{h}}}}\)
จะเห็นว่าคำตอบไม่ได้ขึ้นสัมประสิทธิ์ของแรงเสียดทานของแต่ละล้อ และไม่สนว่าพื้นเป็นอย่างไร ดังนั้น การลื่นไถลจึงไม่มีผลใด ๆ และคำตอบคือ \({\rm{a}} = \dfrac{{{\rm{w}}g}}{{2{\rm{h}}}}\) เหมือนเดิม
ซึ่งไม่มีในตัวเลือก จึงตอบข้อ (E)
ซึ่งไม่มีในตัวเลือก จึงตอบข้อ (E)
| 31. | ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 แล้วอัตราส่วน L/d เท่ากับข้อใด |
| A | \(3\sqrt2\) |
| B | \(3\) |
| C | \(12\) |
| D | \(2\sqrt3\) |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
พิจารณาความเฉื่อยในการหมุนรอบจุดศูนย์กลางของคานบางสม่ำเสมอ จะได้
พิจารณาความเฉื่อยในการหมุนรอบจุดศูนย์กลางของคานบางสม่ำเสมอ จะได้
\({{\rm{I}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{\rm{1}}}{{{\rm{12}}}}{\rm{m}}{{\rm{L}}^{\rm{2}}}\)
จากโจทย์ให้ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 เมื่อแทนที่ Icm จะได้
\(\begin{align*}{\rm{m}}{{\rm{d}}^{\rm{2}}} &= \dfrac{{\rm{1}}}{{{\rm{12}}}}{\rm{m}}{{\rm{L}}^{\rm{2}}}\\ {{\rm{L}}^{\rm{2}}} &= {\rm{12}}{{\rm{d}}^{\rm{2}}}\\ \dfrac{{\rm{L}}}{{\rm{d}}} &= \sqrt {12} \end{align*}\)
ดังนั้น \(\rm L/d = 2\sqrt3\)| 32. | ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 ถ้าคานถูกแขวน ณ ตำแหน่งที่ห่างจากจุดศูนย์กลางไป kd และถูกสั่นเบาๆ ด้วยความถี่เชิงมุม β\(\sqrt{ \rm \dfrac{g}{d}}\) แล้วค่าของ β ในเทอมของ k เท่ากับข้อใด |
| A | \(\rm 1+k^2\) |
| B | \(\rm \sqrt{1+k^2}\) |
| C | \(\rm \sqrt{\dfrac{k}{1+k}}\) |
| D | \(\rm \sqrt{\dfrac{k^2}{1+k}}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (E)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
เราจะได้
ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
\({\tau _{\rm{p}}}=\rm - mg~k~d ~sin \theta\) --- (1)
ให้ p ที่ห้อยอยู่หมายถึง จุดหมุน จากนั้นเราจะใช้ทฤษฎีบทของแกนขนานหาความเฉื่อยในการหมุนรอบจุดหมุน จะได้ว่า\(\rm I_p = I_{cm} + mh^2 = md^2 + m (kd)^2\)
\(\rm I_p = md^2 (1+k^2) \) --- (2)
จากนั้นใช้กฎข้อที่สองของนิวตันหาการหมุนของแกนที่ผ่านจุดหมุน สังเกตว่าแรงที่จุดหมุนไม่ได้ทำให้เกิดทอร์กกับแกนที่ผ่านจุดหมุนเลย เมื่อใช้สมการที่ (1) และ (2) จะได้ว่า
\(\begin{align*} {\tau _{\rm{p}}} &=\rm I{{\rm{ }}_{\rm{p}}}{\rm{\alpha }}\\ \rm - mg~k~d ~sin \theta &= \rm m{{\rm{d}}^{\rm{2}}}\left( {{\rm{1 + }}{{\rm{k}}^{\rm{2}}}} \right)\frac{{{{\rm{d}}^{\rm{2}}}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}} \end{align*}\)
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - \dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}{\rm{\theta }}\)
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - {{\rm{\omega }}^2}{\rm{\theta }}\)
เราจะได้
\({\rm{\omega = }}\sqrt {\dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}} \)
จากโจทย์ให้ \({\rm{\omega }} = \beta \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}}\)ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)
| 33. | (เกินหลักสูตรการสอบเข้า สอวน. 1) ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 ถ้าคานถูกแขวน ณ ตำแหน่งที่ห่างจากจุดศูนย์กลางไป kd และถูกสั่นเบาๆ ด้วยความถี่เชิงมุม β\(\sqrt{ \rm \dfrac{g}{d}}\) ค่าของ β สูงสุด จะเท่ากับข้อใด |
| A | \(1\) |
| B | \(\sqrt2\) |
| C | \(1/\sqrt2\) |
| D | ไม่สามารถหาค่า β สูงสุดได้ |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
เราจะได้
เราจะต้องหาค่า k ที่ทำให้ β มีค่าสูงสุด โดยการหาอนุพันธ์เทียบ k ทั้งสองข้างจะได้
สังเกตว่า \(\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = 0}}\) เมื่อ k = 1
แทน k = 1 ใน \({\rm{\beta = }}\sqrt {\dfrac{{\rm{k}}}{{{\rm{1 + }}{{\rm{k}}^{\rm{2}}}}}} \) จะได้ \({\rm{\beta = }}\sqrt {\dfrac{{\rm{1}}}{{\rm{2}}}} \)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
\({\tau _{\rm{p}}}=\rm - mg~k~d ~sin \theta\) --- (1)
ให้ p ที่ห้อยอยู่หมายถึง จุดหมุน จากนั้นเราจะใช้ทฤษฎีบทของแกนขนานหาความเฉื่อยในการหมุนรอบจุดหมุน จะได้ว่า\(\rm I_p = I_{cm} + mh^2 = md^2 + m (kd)^2\)
\(\rm I_p = md^2 (1+k^2) \) --- (2)
จากนั้นใช้กฎข้อที่สองของนิวตันหาการหมุนของแกนที่ผ่านจุดหมุน สังเกตว่าแรงที่จุดหมุนไม่ได้ทำให้เกิดทอร์กกับแกนที่ผ่านจุดหมุนเลย เมื่อใช้สมการที่ (1) และ (2) จะได้ว่า
\(\begin{align*} {\tau _{\rm{p}}} &=\rm I{{\rm{ }}_{\rm{p}}}{\rm{\alpha }}\\ \rm - mg~k~d ~sin \theta &= \rm m{{\rm{d}}^{\rm{2}}}\left( {{\rm{1 + }}{{\rm{k}}^{\rm{2}}}} \right)\frac{{{{\rm{d}}^{\rm{2}}}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}} \end{align*}\)
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - \dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}{\rm{\theta }}\)
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - {{\rm{\omega }}^2}{\rm{\theta }}\)
เราจะได้
\({\rm{\omega = }}\sqrt {\dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}} \)
จากโจทย์ให้ \({\rm{\omega }} = \beta \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}}\) ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)เราจะต้องหาค่า k ที่ทำให้ β มีค่าสูงสุด โดยการหาอนุพันธ์เทียบ k ทั้งสองข้างจะได้
\({\rm{2\beta }}\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = }}\dfrac{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}} - {\rm{k(2k)}}}}{{{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{{\rm{1}} - {{\rm{k}}^{\rm{2}}}}}{{{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}^{\rm{2}}}}}\)
สังเกตว่า \(\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = 0}}\) เมื่อ k = 1
แทน k = 1 ใน \({\rm{\beta = }}\sqrt {\dfrac{{\rm{k}}}{{{\rm{1 + }}{{\rm{k}}^{\rm{2}}}}}} \) จะได้ \({\rm{\beta = }}\sqrt {\dfrac{{\rm{1}}}{{\rm{2}}}} \)
| 34. | วัตถุมวล m ผูกติดกับทรงกระบอก รัศมี R ด้วยเชือกเบา ที่เวลา t = 0 วัตถุมีความเร็วต้น v0 ในทิศตั้งฉากกับเชือกที่มีความยาวเชือก L0 และแรงตึงในเส้นเชือกไม่เท่ากับศูนย์ ให้ทุกการเคลื่อนที่เกิดขึ้นบนพื้นที่ไม่มีแรงเสียดทานในแนวนอน ทรงกระบอกยังคงนิ่งอยู่บนพื้นและไม่มีการหมุน โดยวัตถุจะเคลื่อนหมุนวนไปรอบ ๆ ทรงกระบอก ซึ่งเชือกจะขาดเมื่อแรงตึงเชือกเกิน Tmax จงตอบคำถามในรูปของ Tmax , m, L0 , R , และ v0  |
| A | \(\rm mv_0R\) |
| B | \(\rm \dfrac{m^2v_0^3}{T_{max}}\) |
| C | \(\rm mv_0L_0\) |
| D | \(\rm \dfrac{T_{max}R^2}{v_0}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (B)
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ
โดย r คือ รัศมีของวงแกว่งรอบทรงกระบอก (เชือกที่ยังไม่พันรอบทรงกระบอก)
ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ
\({\rm{K = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{2}}}\)
ดังนั้น อัตราเร็วของวัตถุจะเท่ากับ v0 เสมอ และโมเมนตัมเชิงมุมของวัตถุที่กระทำกับแกนของทรงกระบอกจะเท่ากับ\(\rm L = mv_0r\) --- (1)
โดย r คือ รัศมีของวงแกว่งรอบทรงกระบอก (เชือกที่ยังไม่พันรอบทรงกระบอก)
ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
\({{\rm{T}}_{{\rm{max}}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{r}}}\)
หรือ \({\rm{r = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{{{\rm{T}}_{{\rm{max}}}}}}\) เมื่อนำไปแทนใน (1) จะได้
\({\rm{L = }}\dfrac{{{{\rm{m}}^2}{\rm{v}}_{\rm{0}}^{\rm{3}}}}{{{{\rm{T}}_{{\rm{max}}}}}}\)
| 35. | วัตถุมวล m ผูกติดกับทรงกระบอก รัศมี R ด้วยเชือกเบา ที่เวลา t = 0 วัตถุมีความเร็วต้น v0 ในทิศตั้งฉากกับเชือกที่มีความยาวเชือก L0 และแรงตึงในเส้นเชือกไม่เท่ากับศูนย์ ให้ทุกการเคลื่อนที่เกิดขึ้นบนพื้นที่ไม่มีแรงเสียดทานในแนวนอน ทรงกระบอกยังคงนิ่งอยู่บนพื้นและไม่มีการหมุน โดยวัตถุจะเคลื่อนหมุนวนไปรอบ ๆ ทรงกระบอก ซึ่งเชือกจะขาดเมื่อแรงตึงเชือกเกิน Tmax จงตอบคำถามในรูปของ Tmax , m, L0 , R , และ v0  |
| A | \(\rm \dfrac{mv^2_0}{2}\) |
| B | \(\rm \dfrac{mv^2_0R}{2L_0}\) |
| C | \(\rm \dfrac{mv^2_0R^2}{2L^2_0}\) |
| D | \(\rm \dfrac{mv^2_0L_0^2}{2R^2}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (A)
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ จึงได้
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ จึงได้
\({\rm{K = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{2}}}\)
| 36. | วัตถุมวล m ผูกติดกับทรงกระบอก รัศมี R ด้วยเชือกเบา ที่เวลา t = 0 วัตถุมีความเร็วต้น v0 ในทิศตั้งฉากกับเชือกที่มีความยาวเชือก L0 และแรงตึงในเส้นเชือกไม่เท่ากับศูนย์ ให้ทุกการเคลื่อนที่เกิดขึ้นบนพื้นที่ไม่มีแรงเสียดทานในแนวนอน ทรงกระบอกยังคงนิ่งอยู่บนพื้นและไม่มีการหมุน โดยวัตถุจะเคลื่อนหมุนวนไปรอบ ๆ ทรงกระบอก ซึ่งเชือกจะขาดเมื่อแรงตึงเชือกเกิน Tmax จงตอบคำถามในรูปของ Tmax , m, L0 , R , และ v0  |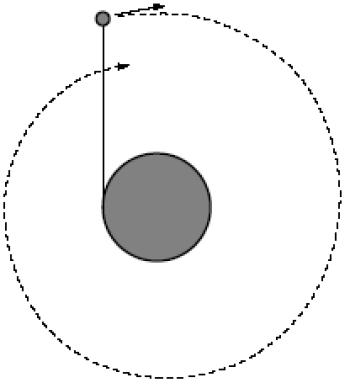
| A | \(\rm L_0 – πR\) |
| B | \(\rm L_0 –2 πR\) |
| C | \(\rm L_0 – \sqrt{18}πR\) |
| D | \(\rm \dfrac{mv^2_0}{T_{max}}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
จากอัตราเร็วของวัตถุจะเท่ากับ v0 เสมอ โมเมนตัมเชิงมุมของวัตถุที่กระทำกับแกนของทรงกระบอกจะเท่ากับ
ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
จากอัตราเร็วของวัตถุจะเท่ากับ v0 เสมอ โมเมนตัมเชิงมุมของวัตถุที่กระทำกับแกนของทรงกระบอกจะเท่ากับ
\(\rm L = mv_0r\)
โดย r คือ รัศมีของวงแกว่งรอบทรงกระบอก (เชือกที่ยังไม่พันรอบทรงกระบอก)ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
\({{\rm{T}}_{{\rm{max}}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{r}}}\)
ดังนั้น \({\rm{ r = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{{{\rm{T}}_{{\rm{max}}}}}}\)| 37. | ให้เชือกเบาที่มีความยืดหยุ่นตามกฎของฮุค จะขาดเมื่อมีแรงตึง Tmax หากนำเชือกมาตรึงปลายด้านหนึ่งไว้ ส่วนปลายอีกด้านผูกกับมวล 3m และมวลที่สองขนาด m ซึ่งเล็กกว่า และมีอัตราเร็วต้น v0 พุ่งเข้าชนกับมวลแรก แล้วติดไปด้วยกัน จึงทำให้เชือกถูกดึงจนขาดออก โดยพลังงานจลน์สุดท้ายของมวลทั้งสองจะเท่ากับศูนย์ ถ้าการชนนั้นเกิดขึ้นในหนึ่งมิติ และยืดหยุ่นสมบูรณ์ แล้วขณะเชือกขาดมวลแรกจะหลุดออกไปด้วยอัตราเร็วสุดท้าย vf สมมุติให้ทุกการเคลื่อนที่เกิดขึ้นในแนวนอนและพื้นไม่มีแรงเสียดทาน แล้วค่า vf / v0 เท่ากับข้อใด |
| A | \(1/\sqrt{12}\) |
| B | \(1/\sqrt{2}\) |
| C | \(1/\sqrt{6}\) |
| D | \(1/\sqrt{3}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
โจทย์ให้เชือกขาดเมื่อถึงแรงตึงค่าหนึ่ง และเมื่อเชือกขาดก็จะเกิดพลังงานศักย์ U0 ขึ้น ในการชนที่ไม่ยืดหยุ่น (ขณะเชือกยังไม่ขาด) เราจะใช้กฎอนุรักษ์โมเมนตัม จึงได้ว่า
เนื่องจากทุกพลังงานศักย์ที่เกิดขึ้นจะถูกเปลี่ยนเป็นพลังงานจลน์ ทำให้ทราบว่าเชือกจะขาดเมื่อ
ต่อไปพิจารณา การชนแบบยืดหยุ่น เริ่มจากหาความเร็วต้นของมวลแต่ละอันหลังเกิดการชน (ขณะเชือกยังไม่ขาด)
วิธีที่ง่ายที่สุดคือหาจากจุดศูนย์กลางมวล จะได้
ในกรอบอ้างอิงนี้ ที่จุดศูนย์กลางมวลก่อนเกิดการชน m จะมีความเร็วเท่ากับ และ 3m มีความเร็วเท่ากับ \(\dfrac{{ - {{\rm{v}}_0}}}{4}\) สำหรับการชนแบบยืดหยุ่นในหนึ่งมิติ และจุดศูนย์กลางมวลแต่ละอันจะมีความเร็วหลังการชนเท่ากับก่อนชน แต่มีทิศทางตรงข้ามกับความเร็วก่อนชน ดังนั้น ความเร็วของ 3m หลังเกิดการชนจะไปทางขวาด้วย \(\dfrac{{ + {{\rm{v}}_0}}}{4}\)
เมื่อแปลง (2) กลับไปเราจะได้อัตราเร็วของ 3m หลังเกิดการชนเท่ากับ \(\dfrac{{ {{\rm{v}}_0}}}{2}\) และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) จะเท่ากับ
โจทย์ให้เชือกขาดเมื่อถึงแรงตึงค่าหนึ่ง และเมื่อเชือกขาดก็จะเกิดพลังงานศักย์ U0 ขึ้น ในการชนที่ไม่ยืดหยุ่น (ขณะเชือกยังไม่ขาด) เราจะใช้กฎอนุรักษ์โมเมนตัม จึงได้ว่า
\(\begin{align*} {\rm{m}}{{\rm{v}}_{\rm{0}}} &=\rm 4mv'\\ \rm v' &=\dfrac{{{{\rm{v}}_{\rm{0}}}}}{{\rm{4}}} \end{align*}\)
และพลังงานศักย์ของมวลทั้งสองหลังเกิดการชนจะเท่ากับ
\({{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
เนื่องจากทุกพลังงานศักย์ที่เกิดขึ้นจะถูกเปลี่ยนเป็นพลังงานจลน์ ทำให้ทราบว่าเชือกจะขาดเมื่อ
\({{\rm{U}}_{\rm{0}}}{\rm{ = }}{{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (1)
ต่อไปพิจารณา การชนแบบยืดหยุ่น เริ่มจากหาความเร็วต้นของมวลแต่ละอันหลังเกิดการชน (ขณะเชือกยังไม่ขาด)
วิธีที่ง่ายที่สุดคือหาจากจุดศูนย์กลางมวล จะได้
\({{\rm{v}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{{{\rm{v}}_0}}}{{\rm{4}}}\) --- (2)
ในกรอบอ้างอิงนี้ ที่จุดศูนย์กลางมวลก่อนเกิดการชน m จะมีความเร็วเท่ากับ และ 3m มีความเร็วเท่ากับ \(\dfrac{{ - {{\rm{v}}_0}}}{4}\) สำหรับการชนแบบยืดหยุ่นในหนึ่งมิติ และจุดศูนย์กลางมวลแต่ละอันจะมีความเร็วหลังการชนเท่ากับก่อนชน แต่มีทิศทางตรงข้ามกับความเร็วก่อนชน ดังนั้น ความเร็วของ 3m หลังเกิดการชนจะไปทางขวาด้วย \(\dfrac{{ + {{\rm{v}}_0}}}{4}\)
เมื่อแปลง (2) กลับไปเราจะได้อัตราเร็วของ 3m หลังเกิดการชนเท่ากับ \(\dfrac{{ {{\rm{v}}_0}}}{2}\) และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) จะเท่ากับ
\({{\rm{K}}_{\rm{2}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (3)
แต่โจทย์กำหนดให้เชือกต้องขาด จากที่เราทราบว่า U0 ของพลังงานจนล์ของ 3m จะถูกส่งไปที่เชือก เราจะใช้กฎอนุรักษ์พลังงานร่วมกับสมการที่ (1) และ (3) จะได้
\({{\rm{K}}_{\rm{3}}}{\rm{ = }}{{\rm{K}}_{\rm{2}}} - {{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}} - \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\)
หาค่า vf / v0 จาก K3 ดังนี้
\(\begin{align*} {{\rm{K}}_{\rm{3}}}&= \dfrac{{{\rm{3mv}}_f^{\rm{2}}}}{{\rm{2}}} =\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\\ \frac{{{{\rm{v}}_{\rm{f}}}}}{{{{\rm{v}}_{\rm{0}}}}} &= \sqrt {\frac{1}{6}} \end{align*}\)
| 38. | ให้เชือกเบาที่มีความยืดหยุ่นตามกฎของฮุค จะขาดเมื่อมีแรงตึง Tmax หากนำเชือกมาตรึงปลายด้านหนึ่งไว้ ส่วนปลายอีกด้านผูกกับมวล 3m และมวลที่สองขนาด m ซึ่งเล็กกว่า และมีอัตราเร็วต้น v0 พุ่งเข้าชนกับมวลแรก แล้วติดไปด้วยกัน จึงทำให้เชือกถูกดึงจนขาดออก โดยพลังงานจลน์สุดท้ายของมวลทั้งสองจะเท่ากับศูนย์ ถ้าการชนนั้นเกิดขึ้นในหนึ่งมิติ และยืดหยุ่นสมบูรณ์ แล้วขณะเชือกขาดมวลแรกจะหลุดออกไปด้วยอัตราเร็วสุดท้าย vf สมมุติให้ทุกการเคลื่อนที่เกิดขึ้นในแนวนอนและพื้นไม่มีแรงเสียดทาน แล้วอัตราส่วนของพลังงานจลน์สุทธิของระบบของมวลทั้งสองหลังการชนแบบยืดยุ่นสมบูรณ์และเชือกได้ขาดออก กับ พลังงานจลน์เริ่มต้นของมวลที่สองก่อนเกิดการชน เท่ากับข้อใด |
| A | 1/4 |
| B | 1/3 |
| C | 1/2 |
| D | 3/4 |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
พลังงานศักย์ของมวลทั้งสองหลังเกิดการชนเท่ากับ
และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) เท่ากับ
จากในกรอบอ้างอิง ที่จุดศูนย์กลางมวลหลังเกิดการชน m จะมีความเร็วเท่ากับ \(\dfrac{{ - 3{{\rm{v}}_0}}}{4}\) เมื่อแปลงกลับไปเราจะหาความเร็วของ m หลังชนกับมวลที่มี \(\dfrac{{{{\rm{v}}_0}}}{2}\) ได้ ดังนั้น พลังงานจลน์ของมวล m หลังเกิดการชนแบบยืดหยุ่นเท่ากับ
ใช้สมการ (1) และค่า K3 หาพลังงานจลน์รวมของระบบหลังเกิดการชนแบบยืดหยุ่นจะได้
ดังนั้น อัตราส่วนของพลังงานจลน์สุทธิของระบบหลังเกิดการชนแบบยืดหยุ่นกับพลังงานจลน์เริ่มต้นของมวล m ก่อนชนและทำให้เชือกขาดจะเท่ากับ
พลังงานศักย์ของมวลทั้งสองหลังเกิดการชนเท่ากับ
\({{\rm{K}}_{\rm{1}}} = \dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) เท่ากับ
\({{\rm{K}}_{\rm{2}}} = \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
จากโจทย์กำหนดให้เชือกต้องขาด และเราทราบว่า U0 ของพลังงานจนล์ของ 3m จะถูกส่งไปที่เชือก เราจะใช้กฎอนุรักษ์พลังงานร่วมกับ K1 และ K2 จะได้
\({{\rm{K}}_{\rm{3}}}{\rm{ = }}{{\rm{K}}_{\rm{2}}} - {{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}} - \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\)
จากในกรอบอ้างอิง ที่จุดศูนย์กลางมวลหลังเกิดการชน m จะมีความเร็วเท่ากับ \(\dfrac{{ - 3{{\rm{v}}_0}}}{4}\) เมื่อแปลงกลับไปเราจะหาความเร็วของ m หลังชนกับมวลที่มี \(\dfrac{{{{\rm{v}}_0}}}{2}\) ได้ ดังนั้น พลังงานจลน์ของมวล m หลังเกิดการชนแบบยืดหยุ่นเท่ากับ
\({{\rm{K}}_{\rm{4}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (1)
ใช้สมการ (1) และค่า K3 หาพลังงานจลน์รวมของระบบหลังเกิดการชนแบบยืดหยุ่นจะได้
\({{\rm{K}}_4}{\rm{ + }}{{\rm{K}}_{\rm{3}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{8} + \dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}} = \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{8}\)
ดังนั้น อัตราส่วนของพลังงานจลน์สุทธิของระบบหลังเกิดการชนแบบยืดหยุ่นกับพลังงานจลน์เริ่มต้นของมวล m ก่อนชนและทำให้เชือกขาดจะเท่ากับ
\(\dfrac{{\frac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{8}}}{{\frac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{2}}} = \dfrac{3}{4}\)
| 39. | นกบินเป็นเส้นตรง โดยเริ่มต้นบินด้วยอัตราเร็ว 10 m/s แล้วเพิ่มอัตราเร็วอย่างสม่ำเสมอจนถึง 18 m/s ได้ระยะทางทั้งหมด 40 m ความเร่งของนกเท่ากับข้อใด |
| A | 0.1 m/s2 |
| B | 0.2 m/s2 |
| C | 2.0 m/s2 |
| D | 2.8 m/s2 |
| E | 5.6 m/s2 |
ตอบ (D)
ให้เวลาผ่านไป t จาก \({\rm{a = }}\dfrac{{{\rm{\Delta v}}}}{{{\rm{\Delta t}}}}\) จะได้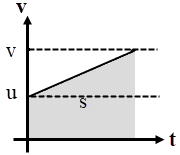
จาก s = พื้นที่สี่เหลี่ยมคางหมู
ให้เวลาผ่านไป t จาก \({\rm{a = }}\dfrac{{{\rm{\Delta v}}}}{{{\rm{\Delta t}}}}\) จะได้
\(\rm v – u = at\)
\(\rm t= \dfrac{{{\rm{v}} - {\rm{u}}}}{{\rm{a}}}\) --- (1)
จาก \({\rm{v = }}\dfrac{{{\rm{\Delta s}}}}{{{\rm{\Delta t}}}}\) ดังนั้น s เป็นพื้นที่ใต้กราฟ v – t
\(\rm s = \dfrac{1}{2}(v + u)t\)
จาก (1)
\(\begin{align*} {\rm{s}} &= \frac{1}{2}(v + u)(\frac{{v - u}}{{\rm{a}}})\\ a &= \frac{1}{2}\left( {\frac{{(v + u)(v - u)}}{{\rm{s}}}} \right) \end{align*}\)
แทนค่า
\(\begin{align*} a &= \frac{1}{2}\left( {\frac{{(18 + 10)(18 - 10)}}{{{\rm{40}}}}} \right)\\ &= \frac{1}{2}\left( {\frac{{8 \times 28}}{{{\rm{40}}}}} \right)\\ &= 2.8\,\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}} \end{align*}\)
| 40. | แมลงสาบไต่อยู่ภายในลูกบาศก์ที่มีความยาวด้าน 3 m ถ้าแมลงสาบเริ่มจากมุมซ้ายล่างที่ด้านหลังของลูกบาศก์ แล้วไต่มาถึงมุมบนขวาที่ด้านหน้าของลูกบาศก์ แล้วการกระจัดของแมลงสาบเท่ากับข้อใด |
| A | \(3\sqrt2 \rm ~m\) |
| B | \(3^3\sqrt2 \rm ~m\) |
| C | \(3\sqrt3 \rm ~m\) |
| D | \(\rm 3m\) |
| E | \(\rm 9m\) |
ตอบ (C)
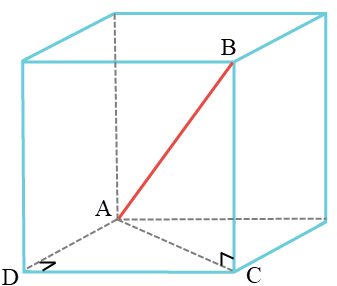สามเหลี่ยม ADC
\(\begin{align*} {\rm{A}}{{\rm{C}}^{\rm{2}}} &= \rm A{{\rm{D}}^{\rm{2}}}{\rm{ + D}}{{\rm{C}}^{\rm{2}}}\\ {\rm{A}}{{\rm{C}}^{\rm{2}}} &= {{\rm{3}}^{\rm{2}}}{\rm{ + }}{{\rm{3}}^{\rm{2}}}{\rm{ = 18 }}{{\rm{m}}^{\rm{2}}} \end{align*}\)
สามเหลี่ยม ABC
\(\begin{align*} {\rm{A}}{{\rm{B}}^{\rm{2}}} &= A{{\rm{C}}^{\rm{2}}}{\rm{ + B}}{{\rm{C}}^{\rm{2}}}\\ {\rm{A}}{{\rm{B}}^{\rm{2}}} &= 18 +{{\rm{3}}^{\rm{2}}}{\rm{ = 27 }}{{\rm{m}}^{\rm{2}}} \end{align*}\)
ดังนั้น \(\rm AB = 3\sqrt3 \rm ~m\)| 41. | จากกราฟตำแหน่งเทียบกับเวลาของวัตถุที่เคลื่อนที่เป็นเส้นตรง ข้อใดคือความเร็ว ณ ขณะ t = 2 วินาที
 |
| A | \(-2 \rm ~m/s\) |
| B | \(-\dfrac{1}{2} \rm ~m/s\) |
| C | \(0\rm ~m/s\) |
| D | \(2\rm ~m/s\) |
| E | \(4\rm ~m/s\) |
ตอบ (A)
จาก \(\overrightarrow {\rm{v}} {\rm{ = }}\dfrac{{{\rm{\Delta }}\overrightarrow {\rm{s}} }}{{{\rm{\Delta t}}}}\)= slope
จาก \(\overrightarrow {\rm{v}} {\rm{ = }}\dfrac{{{\rm{\Delta }}\overrightarrow {\rm{s}} }}{{{\rm{\Delta t}}}}\)= slope
slope = \(\dfrac{{0 - 4}}{{2 - 0}} = - 2\)
ดังนั้น \(\rm v = – 2 m/s\)| 42. | กำหนดกราฟความเร็วเทียบกับเวลาของรถของเล่นที่เคลื่อนที่เป็นเส้นตรง
 |
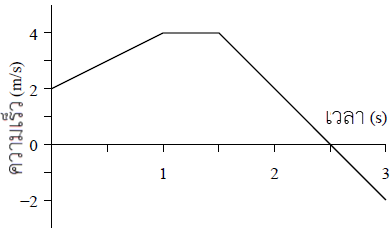| A | 3 m |
| B | 5 m |
| C | 6.5 m |
| D | 7 m |
| E | 7.5 m |
ตอบ (D)
การกระจัด (S) = พื้นที่ใต้กราฟ v – t
Smax = พื้นที่ A + B + C
\(\begin{align*} &=\rm \dfrac{1}{2} (2 + 4)(1) + (0.5)(4) + \dfrac{1}{2} (1)(4) m\\ &= \rm3 + 2 + 2 m\\ &= \rm 7 m\end{align*}\)
เพิ่มเติม : บริเวณพื้นที่ D วัตถุหยุดนิ่งแล้ววิ่งกลับ ทำให้การกระจัดลดลง
| 43. | กำหนดกราฟความเร็วเทียบกับเวลาของรถของเล่นที่เคลื่อนที่เป็นเส้นตรง
 |
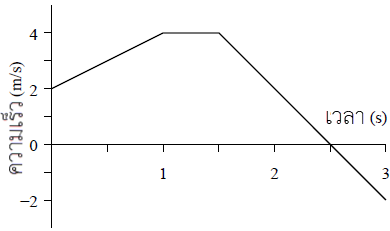| A |  |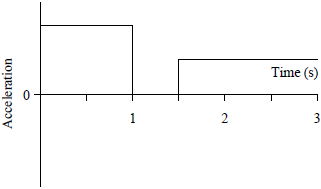
| B |  |
| C |  |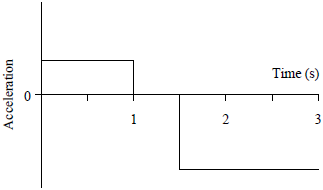
| D |  |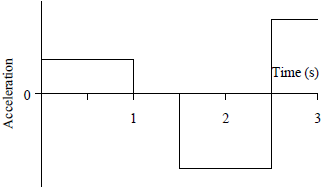
| E |  |
ตอบ (C)
จาก \(\overrightarrow {\rm{a}} {\rm{ = }}\dfrac{{{\rm{\Delta }}\overrightarrow {\rm{v}} }}{{{\rm{\Delta t}}}}=\rm slpoe\) กราฟ v – t
\(\begin{align*} {\rm{slop}}{{\rm{e}}_1} &= \frac{{4 - 2}}{{1 - 0}} = 2\,\,\,{\rm{m/}}{{\rm{s}}^2}\\ {\rm{slop}}{{\rm{e}}_2} &= 0\,\,\,{\rm{m/}}{{\rm{s}}^2}\\ {\rm{slop}}{{\rm{e}}_3} &= \frac{{0 - 4}}{{2.5 - 1.5}} = - 4\,\,\,{\rm{m/}}{{\rm{s}}^2} \end{align*}\)
วาดกราฟ a - t ได้ดังรูป
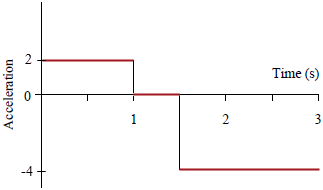
จาก \(\overrightarrow {\rm{a}} {\rm{ = }}\dfrac{{{\rm{\Delta }}\overrightarrow {\rm{v}} }}{{{\rm{\Delta t}}}}=\rm slpoe\) กราฟ v – t
\(\begin{align*} {\rm{slop}}{{\rm{e}}_1} &= \frac{{4 - 2}}{{1 - 0}} = 2\,\,\,{\rm{m/}}{{\rm{s}}^2}\\ {\rm{slop}}{{\rm{e}}_2} &= 0\,\,\,{\rm{m/}}{{\rm{s}}^2}\\ {\rm{slop}}{{\rm{e}}_3} &= \frac{{0 - 4}}{{2.5 - 1.5}} = - 4\,\,\,{\rm{m/}}{{\rm{s}}^2} \end{align*}\)
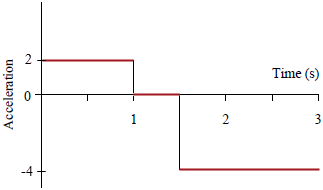
| 44. | ปืนใหญ่ยิงกระสุนแบบโพรเจกไทล์บนพื้นราบ โดยยิงทำมุมขนาดต่างๆ ด้วยอัตราเร็วเดียวกัน ถ้าระยะตกไกลสุดของกระสุนในแนวราบเท่ากับ L แล้วระยะตกของกระสุนที่ยิงทำมุม \(\dfrac{\pi}{6}\) กับแนวราบ เท่ากับข้อใด ไม่ต้องคิดแรงต้านอากาศ |
| A | \(\dfrac{\sqrt 3}{2}\rm L\) |
| B | \(\dfrac{1}{\sqrt 2}\rm L\) |
| C | \(\dfrac{1}{\sqrt 3}\rm L\) |
| D | \(\dfrac{1}{2}\rm L\) |
| E | \(\dfrac{1}{3}\rm L\) |
ตอบ (A)
จะหา D
พิจารณา sy หา t ที่ใช้จากจุดเริ่มต้น \(\to\) จุดสุดท้าย
จาก
ดังนั้น \(\rm L = \dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{g}}}\)
จากโจทย์ แทน θ = \(\pi\)/6 จะได้
พิจารณา sy หา t ที่ใช้จากจุดเริ่มต้น \(\to\) จุดสุดท้าย
จาก
\(\begin{align*} {{\rm{s}}_{\rm{y}}} &= {{\rm{v}}_{\rm{y}}}{\rm{t}} - \frac{1}{2}{\rm{g}}{{\rm{t}}^{\rm{2}}}\\
0 &= {{\rm{v}}_{\rm{y}}}{\rm{t}} - \dfrac{1}{2}{\rm{g}}{{\rm{t}}^{\rm{2}}}\\ \rm t &= \dfrac{{{\rm{2}}{{\rm{v}}_{\rm{y}}}}}{{\rm{g}}} = \dfrac{{{\rm{2vsin\theta }}}}{{\rm{g}}} \end{align*}\)
จะได้
\(\begin{align*} \rm D &= {{\rm{v}}_{\rm{x}}}{\rm{t}}\\
&= \left( {{\rm{v cos\theta }}} \right)\left( {\frac{{{\rm{2v}}}}{{\rm{g}}}{\rm{sin\theta }}} \right)\\
&= \dfrac{{{\rm{2}}{{\rm{v}}^2}}}{{\rm{g}}}{\rm{sin\theta cos\theta }}\\
&= \dfrac{{{{\rm{v}}^2}}}{{\rm{g}}}{\rm{sin2\theta }} \end{align*}\)
จะได้ Dmax เมื่อ sin2θ = 1 (θ = \(\pi\)/4 นั่นเอง) ดังนั้น \(\rm L = \dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{g}}}\)
จากโจทย์ แทน θ = \(\pi\)/6 จะได้
\({\rm{D = }}\,\,\dfrac{{{{\rm{v}}^2}}}{{\rm{g}}}{\rm{sin}}\left( {{\rm{2}} \cdot \dfrac{\pi }{6}} \right)\,\, = \,\,{\rm{L~sin}}\left( {\dfrac{\pi }{3}} \right)\,\, = \,\,\dfrac{{\sqrt 3 }}{2}{\rm{L}}\)
| 45. | เลื่อนหิมะเคลื่อนที่ด้วยอัตราเร็ว 2.0 m/s บนพื้นหิมะ ให้คนและเลื่อนมีมวลรวมกัน 120 kg และเด็กอีกคน (mเด็ก = 40 kg) พุ่งเข้ามาในทิศตรงข้ามกับเลื่อนหิมะ แล้วกระโดดขึ้นเลื่อนจากทางด้านหน้า ถ้าเด็กคนนั้นมีอัตราเร็วก่อนขึ้นไปบนเลื่อน 5.0 m/s แล้วอัตราเร็วใหม่ของเลื่อนจะเท่ากับข้อใด ไม่ต้องคิดผลของแรงเสียดทาน |
| A | 0.25 m/s |
| B | 0.33 m/s |
| C | 2.75 m/s |
| D | 3.04 m/s |
| E | 3.67 m/s |
ตอบ (A)
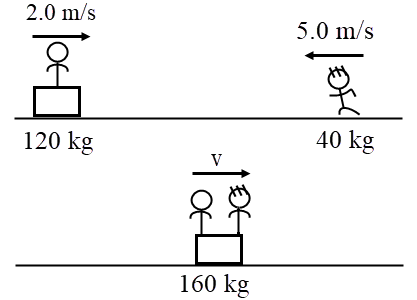จากกฎอนุรักษ์โมเมนตัม
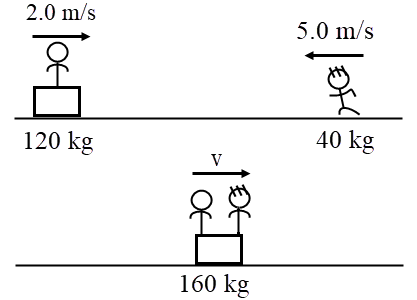
\(\begin{align*} (120)(2.0) + (40)( - 5.0) &= 160v\\ 240 - 200 &= 160v\\ v &= 0.25 \rm ~~m/s \end{align*} \)
| 46. | ชายคนหนึ่งเล่นเครื่องเล่นโดยหันหลังพิงกับกำแพงของถังทรงกระบอกที่มีเส้นผ่าศูนย์กลาง 8.0 m ถ้าถังหมุนรอบแกนที่ผ่านศูนย์กลางในอัตรา 45 รอบ/นาที แล้วนำพื้นใต้เท้าที่ชายคนนั้นยืนอยู่ออกไป จงหาค่าสัมประสิทธิ์แรงเสียดทานสถิตระหว่างกำแพงกับชายคนนั้นที่น้อยที่สุดที่ทำให้เขาไม่หล่นลงไป |
| A | 0.0012 |
| B | 0.056 |
| C | 0.11 |
| D | 0.53 |
| E | 8.9 |
ตอบ (C)
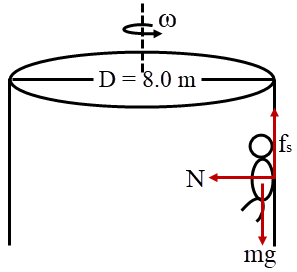จาก 45 รอบ/นาที = \(\dfrac{{45 \times 2\pi }}{{60}}\) rad / s = \(\dfrac{3}{2}\pi \) s-1
คนไม่หล่นลงไป
แต่ fs ≤ μsN จะได้
คนไม่หล่นลงไป
fs = mg --- (1)
การเคลื่อนที่แบบวงกลม
N = mω2R --- (2)
แต่ fs ≤ μsN จะได้
\(\begin{align*} {\rm{mg}} &\le {{\rm{\mu }}_{\rm{s}}}{\rm{m}}{{\rm{\omega }}^{\rm{2}}}{\rm{R}}\\ {{\rm{\mu }}_{\rm{s}}} &\ge \frac{{\rm{g}}}{{{{\rm{\omega }}^{\rm{2}}}{\rm{R}}}} \sim \frac{{10}}{{{{\left( {\frac{3}{2}\pi } \right)}^2}\left( {\frac{8}{2}} \right)}} = \frac{{10}}{{9{\pi ^2}}} = 0.11 \end{align*}\)
| 47. | บอลมวล m1 เคลื่อนที่ในทิศบวกตามแกน x ด้วยอัตราเร็วต้น v0 แล้วชนกับบอลมวล m2 ซึ่งเดิมอยู่นิ่ง หลังจากการชน บอลมวล m1 มีความเร็ว v1x \(\hat x\) + v1y\(\hat y\) และบอลมวล m2 มีความเร็ว v2x \(\hat x\) + v2y\(\hat y\) จงพิจารณาข้อความต่อไปนี้
I) 0 = m1v1x + m1v2x
II) m1v0 = m1v1y +m2v2y
III) 0 = m1v1y + m2v2y
IV) m1v0 = m1v1x + m1v1y
V) m1v0 = m1v1x + m2v2x
ข้อใดสอดคล้องกับระบบ |
| A | I และ II |
| B | III และ V |
| C | II และ V |
| D | III และ IV |
| E | I และ III |
ตอบ (B)
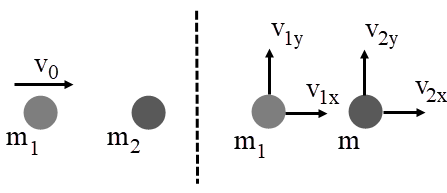จากกฎอนุรักษ์โมเมนตัม
แนวแกน x
แนวแกน y
ดังนั้น III และ V สอดคล้องกับระบบ
แนวแกน x
m1v0 = m1v1x + m2v2x
ตรงกับข้อ (V)แนวแกน y
0 = m1v1x + m2v2y
ตรงกับข้อ (III)ดังนั้น III และ V สอดคล้องกับระบบ
| 48. | จากการทดลองลากกล่องไม้หนักๆ ที่วางอยู่บนพื้นด้วยเครื่องชั่งสปริง ได้บันทึกแรงที่ใช้ในแต่ละครั้งกับความเร่งของบล็อกไม้ ดังนี้ แล้วมวลของกล่องไม้ควรเท่ากับข้อใด |
| A | 3 kg |
| B | 5 kg |
| C | 10 kg |
| D | 20 kg |
| E | 30 kg |
ตอบ (B)
เขียนสมการนิวตัน
จากข้อมูล เมื่อนำมาวาดกราฟ จะได้ f = 2.52 N และ m = 4.98 \(\approx\) 5 kg
เขียนสมการนิวตัน
\(\begin{align*} {\rm{F}} - {\rm{f}} &= {\rm{ma}}\\ {\rm{F}} &= {\rm{ma}} + {\rm{f}} \end{align*}\)
จะได้ m เป็น slope และ f เป็น จุดตัดแกน yจากข้อมูล เมื่อนำมาวาดกราฟ จะได้ f = 2.52 N และ m = 4.98 \(\approx\) 5 kg
| 49. | จากการทดลองลากกล่องไม้หนักๆ ที่วางอยู่บนพื้นด้วยเครื่องชั่งสปริง ได้บันทึกแรงที่ใช้ในแต่ละครั้งกับความเร่งของบล็อกไม้ ดังนี้
 |
| A | 0.05 |
| B | 0.07 |
| C | 0.09 |
| D | 0.5 |
| E | 0.6 |
ตอบ (A)
เขียนสมการนิวตัน
จากข้อมูล เมื่อนำมาวาดกราฟ จะได้ f = 2.52 N และ m = 4.98
จาก f = μN
เขียนสมการนิวตัน
\(\begin{align*} {\rm{F}} - {\rm{f}} &= {\rm{ma}}\\ {\rm{F}} &= {\rm{ma}} + {\rm{f}} \end{align*}\)
จะได้ m เป็น slope และ f เป็น จุดตัดแกน yจากข้อมูล เมื่อนำมาวาดกราฟ จะได้ f = 2.52 N และ m = 4.98
จาก f = μN
\(\begin{align*} f &=\rm \mu N\\ \mu &=\rm \frac{f}{{mg}} = \frac{{2.52}}{{4.98 \times 10}} \approx 0.05 \end{align*}\)
| 50. | แผ่นกลมสม่ำเสมอหมุนด้วยความเร็วเชิงมุมคงที่รอบแกนที่ผ่านศูนย์กลาง และตั้งฉากกับระนาบแผ่นกลม และมีพลังงานจลน์เท่ากับ E ถ้าแผ่นกลมแบบเดียวกันหมุนด้วยความเร็วเชิงมุมเดียวกัน แต่หมุนรอบแกนที่ขอบของแผ่นกลม (แกนยังคงตั้งฉากกับระนาบแผ่นกลม) แล้วพลังงานจลน์จะมีค่าเท่ากับข้อใด |
| A | \(\dfrac{1}{2}\rm E\) |
| B | \(\dfrac{3}{2}\rm E\) |
| C | \(2\rm E\) |
| D | \(3\rm E\) |
| E | \(4\rm E\) |
ตอบ (D)
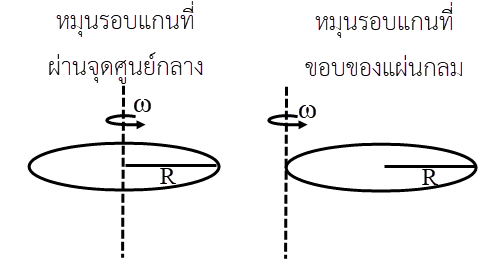กรณี หมุนที่จุดศูนย์กลาง
พลังงานจลน์การหมุน = \(\dfrac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)
แผ่นกลม \({\rm{I}} = \dfrac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)
จากทฤษฎีแกนขนาน
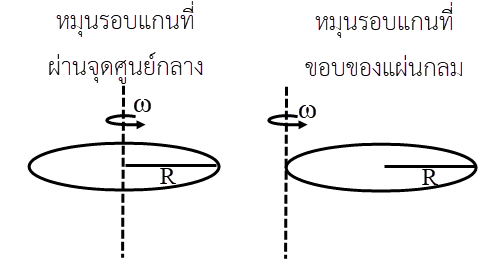
พลังงานจลน์การหมุน = \(\dfrac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)
แผ่นกลม \({\rm{I}} = \dfrac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)
\({\rm{E = }}\dfrac{{\rm{1}}}{{\rm{2}}}\left( {\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}} \right){{\rm{\omega }}^{\rm{2}}}\)
กรณี หมุนที่ขอบของวงกลมจากทฤษฎีแกนขนาน
\(\rm I_{ขอบ} = I + mR^2 = \dfrac{1}{2}mR^2 + mR^2 = \dfrac{3}{2}mR^2\)
จะได้
\(\rm E_{ขอบ} = \dfrac{1}{2}(I_{ขอบ}) ω^2 = \dfrac{1}{2}(\dfrac{3}{2}mR^2) ω^2\)
ดังนั้น \(\rm E_{ขอบ} = 3E\)| 51. | ติดมวลก้อนหนึ่งกับผนังด้วยสปริงที่มีค่านิจสปริง k ขณะสปริงมีความยาวตามปกติ มวลจะได้รับความเร็วต้นค่าหนึ่ง ทำให้สปริงสั่นด้วยแอมพลิจูด A ถ้าเปลี่ยนสปริงให้มีค่านิจสปริง 2k และมวลได้รับความเร็วต้นเท่าเดิม แล้วแอมพลิจูดของการสั่นเท่ากับข้อใด |
| A | \(\dfrac{1}{2}\rm A\) |
| B | \(\dfrac{1}{\sqrt 2}\rm A\) |
| C | \(\sqrt{2}\rm A\) |
| D | \(2\rm A\) |
| E | \(2\rm A\) |
ตอบ (B)
ถ้าสปริงยืดที่ระยะ x = A สปริงจะมีความเร็ว = 0 (ถ้ายังวิ่งต่อ ก็ไม่ใช่ระยะมากที่สุด)
ให้ความเร็วต้น = v
จากกฎอนุรักษ์พลังงาน
ให้ความเร็วต้น = v
จากกฎอนุรักษ์พลังงาน
\(\begin{array}{l} \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} = \dfrac{1}{2}{\rm{k}}{{\rm{A}}^2}\\ \,\,\,\,\,\therefore {\rm{A}} \propto \dfrac{{\rm{v}}}{{\sqrt {\rm{k}} }} \end{array}\)
ถ้าเปลี่ยน k \(\to\) 2k โดย v คงที่ จะได้
\(\begin{align*} \frac{{{\rm{A'}}}}{{\rm{A}}} &= \sqrt {\frac{{\rm{k}}}{{{\rm{2k}}}}} \\ \rm A' &=\frac{{\rm{A}}}{{\sqrt {\rm{2}} }} \end{align*}\)
| 52. | เครื่องกักเก็บพลังงานประกอบด้วย มวลที่เหมือนกันสองชิ้นที่เชื่อมกันด้วยเชือก และจะหมุนรอบจุดศูนย์กลางมวล โดยพลังงานที่ถูกเพิ่มเข้ามาจะถูกเก็บไว้โดยการม้วนพันเชือกให้เชือกระหว่างมวลมีความยาวลดลง โดยไม่มีแรงภายนอกมากระทำ ถ้าเดิมเครื่องมีพลังงานจลน์ E และหมุนด้วยความเร็วเชิงมุม ω จากนั้นเพิ่มพลังงานจนเครื่องหมุนด้วยความเร็วเชิงมุม 2ω แล้วพลังงานจลน์ของเครื่องนี้จะมีค่าเท่ากับข้อใด |
| A | \(\sqrt 2\rm E\) |
| B | \(2\rm E\) |
| C | \(2\sqrt 2\rm E\) |
| D | \(4\rm E\) |
| E | \(8\rm E\) |
ตอบ (B)
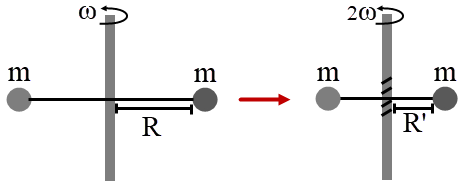การเพิ่มพลังงานช่วยให้เชือกหด แรงทั้งหมดผ่านแกนเชือก
ดังนั้น อนุรักษ์โมเมนตัมเชิงมุมรอบจุดศูนย์กลาง
ดังนั้น อนุรักษ์โมเมนตัมเชิงมุมรอบจุดศูนย์กลาง
\(\rm L = mωR^2 =\) ค่าคงที่
ดังนั้น
\(\begin{align*} {\rm{m\omega }}{{\rm{R}}^2} &= {\rm{m(2w)}}{{{\rm{R'}}}^2}\\ \rm {{R'}^2} &= \frac{{{{\rm{R}}^2}}}{2} \end{align*}\)
จะได้
\(\begin{align*} \rm E' &=\frac{{\rm{1}}}{{\rm{2}}}{\rm{I'}}{{{\rm{\omega '}}}^{\rm{2}}}\\ &= \frac{{\rm{1}}}{{\rm{2}}}\left( {{\rm{m}}{{{\rm{R'}}}^{\rm{2}}}} \right){{{\rm{\omega '}}}^{\rm{2}}}\\ &= \frac{{\rm{1}}}{{\rm{2}}}\left( {{\rm{m}}\frac{{{{\rm{R}}^{\rm{2}}}}}{{\rm{2}}}} \right){{\rm{(2\omega )}}^{\rm{2}}}\\ &= \frac{{\rm{1}}}{{\rm{2}}} \cdot 4\left( {\frac{1}{2}{\rm{m}}{{\rm{R}}^2}{{\rm{\omega }}^{\rm{2}}}} \right)\\ &= 2{\rm{E}} \end{align*}\)
ดังนั้น \({\rm{E'}} = 2{\rm{E}}\)| 53. | โต๊ะกลมสม่ำเสมอมีเส้นผ่านศูนย์กลาง 4.0 m มวล 50.0 kg มีขาโต๊ะที่เบามากสูง 1.0 m และห่างกัน 3.0 m ถ้าช่างไม้คนหนึ่งไปนั่งที่ขอบโต๊ะ แล้วมวลมากสุดของช่างไม้ ที่ทำให้โต๊ะไม่กระดกเท่ากับข้อใด สมมุติว่าแรงที่ช่างไม้กระทำตั้งฉากกับโต๊ะ และกระทำที่ขอบโต๊ะเท่านั้น
 |
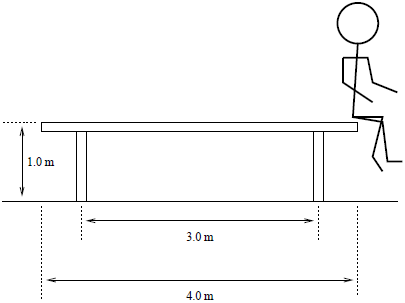| A | 67 kg |
| B | 75 kg |
| C | 81 kg |
| D | 150 kg |
| E | 350 kg |
ตอบ (D)
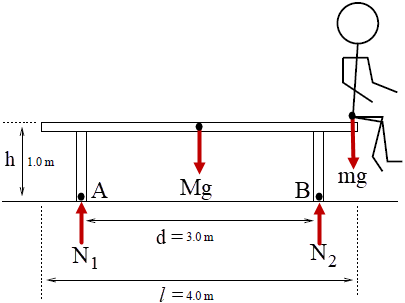สมการนิวตัน
\(\rm mg + Mg = N_1 + N_2\)
สมดุลทอร์ก จุดหมุนที่ A
\({\rm{Mg}}\dfrac{{\rm{d}}}{{\rm{2}}}{\rm{ + mg}}\left( {{\rm{d }} + \dfrac{{l - {\rm{d}}}}{2}} \right) = {{\rm{N}}_{\rm{2}}}{\rm{d}}\)
เงื่อนไขพื้นไม่กระดก (กระดกพอดี ถ้าช่างมวลมากที่สุด)
\(\rm N_1 = 0\)
จะได้ว่า
\(\begin{align*} {\rm{Mg}}\frac{{\rm{d}}}{{\rm{2}}}{\rm{ + mg}}\left( {{\rm{d }} + \frac{{l - {\rm{d}}}}{2}} \right) &= {{\rm{N}}_{\rm{2}}}{\rm{d = (m + M)gd}}\\ {\rm{mg}}\left( {\frac{{l - {\rm{d}}}}{2}} \right) &= \frac{1}{2}{\rm{Mgd}} \end{align*}\)
ดังนั้น \(\rm {\rm{m = }}\left( {\dfrac{{\rm{d}}}{{l - {\rm{d}}}}} \right){\rm{M}} = \dfrac{{3.0}}{{4.0 - 1.0}}(50.0) = 150~kg\)| 54. | สปริงเบาที่มีค่านิจสปริง k ถูกจับตั้งขึ้นให้ปลายด้านหนึ่งติดอยู่กับพื้น ส่วนปลายด้านบนปล่อยอิสระ ถ้าปล่อยลูกบอลมวล m จากแนวตั้งให้ลงไปติดกับสปริง กล่าวคือ ลูกบอลพุ่งชนกับสปริงในแนวตั้ง แล้วเกิดการสั่นในแนวตั้ง ให้ y เป็นความสูงวัดจากปลายสปริงตอนที่ยังไม่ยืดไม่หด จงหาความเร่ง a ของมวลขณะที่สั่นและอยู่ที่ความสูง y เหนือปลายสปริงตอนที่ยังไม่ยืดไม่หด และให้ทิศลงเป็นลบ โดยไม่ต้องคิดแรงต้านอากาศ กำหนดให้ g คือ ความเร่งในการตกอย่างอิสระ และ v คือ อัตราเร็วที่ตำแหน่งนั้น |
| A | a = mv2/y + g |
| B | a = mv2/k – g |
| C | a = (k/m)y – g |
| D | a = – (k/m)y + g |
| E | a = – (k/m)y – g |
ตอบ (E)
จากกฎของนิวตัน
\(\begin{align*} - {\rm{mg}} - {\rm{ky}} &= {\rm{ma}}\\ {\rm{a}} &= - \frac{{\rm{k}}}{{\rm{m}}}{\rm{y}} - {\rm{g}} \end{align*}\)
| 55. | มวล m อยู่นิ่ง ณ จุดสมดุล ขณะถูกแขวนในแนวตั้งบนสปริงที่เดิมยาว L มีค่านิจสปริง k ดังรูป
 |
| A | (a/g)L |
| B | (g/a)L |
| C | m(g + a)/k |
| D | m(g – a)/k |
| E | ma/k |
ตอบ (E)
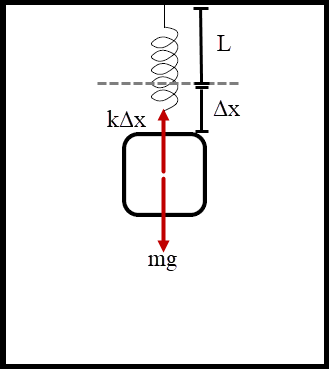
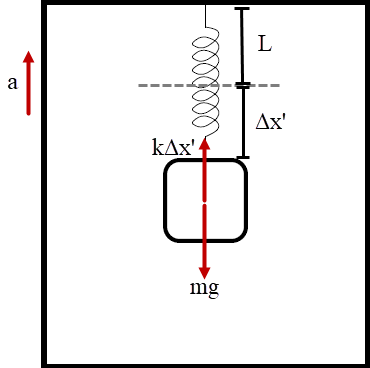เมื่อแขวนมวล m สปริงจะยืดจนถึงจุดสมดุล
ให้จุดสมดุล สปริงยืด \(\Delta {\rm{x}}\) จะได้
จาก (1) และ (2)
ให้จุดสมดุล สปริงยืด \(\Delta {\rm{x}}\) จะได้
\({\rm{mg = k}}\Delta {\rm{x}}\) --- (1)
เมื่อลิฟต์มีความเร่ง a ทิศขึ้น สปริงจะยืดมากขึ้น จาก \(\Delta {\rm{x}}\) เป็น \(\Delta {\rm{x'}}\) จะได้\({\rm{ k}}\Delta {\rm{x'}}-{\rm{mg = ma}}\) --- (2)
จาก (1) และ (2)
\(\begin{align*} {\rm{k}}\Delta {\rm{x'}}-{\rm{k}}\Delta \rm x &= \rm ma\\ \left( {\Delta {\rm{x'}}-\Delta {\rm{x}}} \right) &= \dfrac{{{\rm{ma}}}}{{\rm{k}}} \end{align*}\)
| 56. | วงแหวนสม่ำเสมอ รัศมี R อยู่คงที่ที่จุดหนึ่ง และให้อนุภาคหนึ่งอยู่ในแนวแกนกลางวงแหวนในระยะที่ไกลมาก ( เทียบกับ R ) และสามารถเข้าไปสู่วงแหวนด้วยอิทธิพลจากแรงโน้มถ่วงของวงแหวนได้ โดยอนุภาคนั้นจะมีอัตราเร็วสูงสุด v ถ้าเราเปลี่ยนวงแหวน ให้มีความหนาแน่นเชิงเส้นเท่าเดิม แต่มีรัศมี 2R แล้วทำการทดลองซ้ำ แล้วอัตราเร็วสูงสุดใหม่ของอนุภาคจะเท่ากับข้อใด |
| A | \(\dfrac{1}{2}\rm v\) |
| B | \(\dfrac{1}{\sqrt2}\rm v\) |
| C | \(\rm v\) |
| D | \(\sqrt2\rm v\) |
| E | \(2\rm v\) |
ตอบ (C)
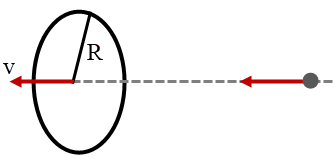ให้วงแหวนมีความหนาแน่นเชิงเส้น = \(\lambda \)
อนุภาค (ณ ใดๆ) มีพลังงาน = 0
อนุภาค (ณ ความเร็วสูงสุด) มีพลังงาน = Ekmax + Ep
เมื่อ Ekmax คือ พลังงานจลน์ของวัตถุ ณ ความเร็วสูงสุด
Ep คือ พลังงานศักย์โน้มถ่วงที่เกิดจากวงแหวน ขณะที่วัตถุมีความเร็วสูงสุด
จากกฎอนุรักษ์พลังงาน
Ep น้อยสุด เมื่อวัตถุอยู่ใกล้วงแหวนมากที่สุด นั่นคือ กำลังผ่านจุดศูนย์กลางของวงแหวน
ดังนั้น ถ้าเปลี่ยนจาก R เป็น 2R ความเร็วสูงสุดของวัตถุก็ยังคงเป็น v
อนุภาค (ณ ใดๆ) มีพลังงาน = 0
อนุภาค (ณ ความเร็วสูงสุด) มีพลังงาน = Ekmax + Ep
เมื่อ Ekmax คือ พลังงานจลน์ของวัตถุ ณ ความเร็วสูงสุด
Ep คือ พลังงานศักย์โน้มถ่วงที่เกิดจากวงแหวน ขณะที่วัตถุมีความเร็วสูงสุด
จากกฎอนุรักษ์พลังงาน
Ekmax + Ep = 0
Ep = – Ekmax = มีค่าน้อยสุด
Ep น้อยสุด เมื่อวัตถุอยู่ใกล้วงแหวนมากที่สุด นั่นคือ กำลังผ่านจุดศูนย์กลางของวงแหวน
\({{\rm{E}}_{{\rm{p min}}}} = - \dfrac{{{\rm{GMm}}}}{{\rm{R}}} = - \dfrac{{{\rm{Gm(2\pi R\lambda }})}}{{\rm{R}}} = - {\rm{2\pi \lambda mG}}\)
จะได้
\(- \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} = - 2{\rm{\pi \lambda mG}}\)
นั่นคือ v ไม่ขึ้นกับ Rดังนั้น ถ้าเปลี่ยนจาก R เป็น 2R ความเร็วสูงสุดของวัตถุก็ยังคงเป็น v
| 57. | รถคันหนึ่งมีเครื่องยนต์ที่ให้กำลังคงที่ เมื่อเร่งเครื่องจากที่เดิมอยู่นิ่ง ที่เวลา t = 0 และมีความเร่งเท่ากับ a0 ที่เวลา t = t0 แล้วความเร่งที่ t = 2t0 เท่ากับข้อใด ไม่ต้องคำนึงพลังงานที่สูญเสียไปกับแรงเสียดทาน |
| A | \(\dfrac{1}{2}\rm a_0\) |
| B | \(\dfrac{1}{\sqrt2}\rm a_0\) |
| C | \(\rm a_0\) |
| D | \(\sqrt2\rm a_0\) |
| E | \(2\rm a_0\) |
ตอบ (B)
ให้กำลังของรถยนต์ = P
จะได้
แทน a1 = a0 , t1 = t0 , t2 = 2t0 เพื่อหา a2
จะได้
ให้กำลังของรถยนต์ = P
จะได้
\({\rm{Pt = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{v}}^{\rm{2}}}\)
เมื่อ t คือ เวลาที่รถยนต์แล่นจากหยุดนิ่ง
\(\begin{align*}
\rm v(t) &= \rm \sqrt {\frac{{2P}}{m}t} \\
\rm a(t) &= \rm \dfrac{{dv}}{{dt}} = \dfrac{1}{2}\sqrt {\frac{{2P}}{{mt}}} \\
\rm a &\propto \rm \dfrac{1}{{\sqrt t }}
\end{align*}\)
ดังนั้น \(\dfrac{{{{\rm{a}}_{\rm{1}}}}}{{{{\rm{a}}_{\rm{2}}}}}{\rm{ = }}\sqrt {\dfrac{{{{\rm{t}}_{\rm{2}}}}}{{{{\rm{t}}_{\rm{1}}}}}} \)แทน a1 = a0 , t1 = t0 , t2 = 2t0 เพื่อหา a2
จะได้
\(\begin{align*}
\frac{{{{\rm{a}}_{\rm{0}}}}}{{{{\rm{a}}_{\rm{2}}}}} &= \sqrt {\rm{2}} \\
{{\rm{a}}_{\rm{2}}} &= \frac{1}{{\sqrt {\rm{2}} }}{{\rm{a}}_{\rm{0}}}
\end{align*}\)
| 58. | ให้มอดุลัสของยังมีค่าเท่ากับ E ซึ่งค่านี้จะใช้วัดความแข็งของวัสดุ ถ้าวัสดุนั้นมีค่า E มากกว่า วัสดุนั้นก็จะมีความแข็งมากกว่า ลองพิจารณาคานเหล็กหน้าตัดสี่เหลี่ยมมุมฉาก ที่ปลายด้านหนึ่งถูกตรึงตามแนวนอนกับกำแพง และสามารถเอียงตามน้ำหนักของตัวคานได้ ถ้าคานยาว L, หนา h, กว้าง w, ความหนาแน่น ρ, และมอดุลัสของยังเท่ากับ E ความเร่งโน้มถ่วงเท่ากับ g แล้วระยะทางที่ปลายอีกข้างหนึ่งเคลื่อนที่ไปจะเท่ากับข้อใด (คำแนะนำ: อาจจะใช้การตัดตัวเลือกที่ไม่น่าจะเป็นได้ออกก่อน ซึ่งตัวเลือกทั้งหมดมีหน่วยถูกต้อง) |
| A | \(\rm h ~exp\left(\dfrac{ρgL}{E}\right)\) |
| B | \(\rm 2\dfrac{ρgL^2}{E}\) |
| C | \(\rm \sqrt{2Lh}\) |
| D | \(\rm \dfrac{3}{2}\dfrac{ρgL^4}{Eh^2}\) |
| E | \(\rm \sqrt{3}\dfrac{EL}{\rho gh}\) |
ตอบ (D)
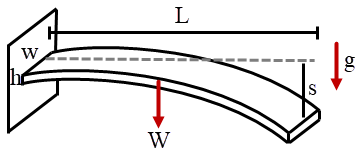กำหนดให้ s เป็นระยะทางที่ปลายเหล็กเคลื่อนที่
(1) ถ้า E มาก วัสดุจะแข็งแรง ทำให้ การงอ \(\downarrow ~\to\) s \(\downarrow\) (ตัดข้อ C,E)
(2) ถ้า L มาก จะทำให้ s \(\uparrow\) เพราะเหล็กยาว น้ำหนักเหล็กยิ่งมาก เหล็กจะเบนได้มากกว่า (ไม่มีการตัดข้อเพิ่ม)
(3) ถ้า h มาก จะทำให้ s \(\downarrow\) เพราะผนังมีแรง N ทำกับคาน ยิ่ง h มาก ทอร์กของแรง N ก็ยิ่งมากทำให้ช่วยพยุงแท่งเหล็กได้ดี s จึงน้อย (ตัดข้อ A,B)
ดังนั้น ข้อ (D) เป็นไปได้มากที่สุด
(1) ถ้า E มาก วัสดุจะแข็งแรง ทำให้ การงอ \(\downarrow ~\to\) s \(\downarrow\) (ตัดข้อ C,E)
(2) ถ้า L มาก จะทำให้ s \(\uparrow\) เพราะเหล็กยาว น้ำหนักเหล็กยิ่งมาก เหล็กจะเบนได้มากกว่า (ไม่มีการตัดข้อเพิ่ม)
(3) ถ้า h มาก จะทำให้ s \(\downarrow\) เพราะผนังมีแรง N ทำกับคาน ยิ่ง h มาก ทอร์กของแรง N ก็ยิ่งมากทำให้ช่วยพยุงแท่งเหล็กได้ดี s จึงน้อย (ตัดข้อ A,B)
ดังนั้น ข้อ (D) เป็นไปได้มากที่สุด
| 59. | พิจารณาอนุภาคที่เดิมอยู่นิ่ง แล้วแตกตัวออกเป็นสองอนุภาค หรือสามอนุภาค แล้วข้อใดต่อไปนี้เป็นจริงสำหรับการแตกตัวเป็นสองอนุภาค แต่เป็นเท็จสำหรับการแตกตัวเป็นสามอนุภาค (ไม่มีแรงภายนอกใดมากระทำ) |
| A | เวกเตอร์ความเร็วของอนุภาคที่แตกออกมาจะอยู่ในระนาบเดียวเท่านั้น |
| B | ถ้ากำหนดพลังงานจลน์สุทธิของระบบ และมวลของแต่ละอนุภาคที่แตกออกมาให้ ก็สามารถหาอัตราเร็วของแต่ละอนุภาคได้ |
| C | ถ้ากำหนดอัตราเร็วของทั้งหมด แต่ไม่บอกของหนึ่งอนุภาคที่แตกออกมาให้ ก็สามารถหาอัตราเร็วของอนุภาคที่เหลือได้ |
| D | โมเมนตัมรวมของอนุภาคที่แตกออกมาจะเท่ากับศูนย์ |
| E | ไม่มีข้อใดถูก |
ตอบ (B)
| ข้อ | แตกเป็น 2 อนุภาค | แตกเป็น 3 อนุภาค |
| (A) | เป็นจริง เพราะ 2 เวกเตอร์ จะอยู่ในระนาบเดียวกันเสมอ | เป็นจริง เพราะ ในกรณีที่มี 2 เวกเตอร์อยู่ในระนาบเดียวกัน แต่เวกเตอร์ที่ 3 ไม่อยู่ในระนาบดังกล่าว ก็จะเกิด component ของเวกเตอร์ในแนวตั้งฉากกับระนาบ ทำให้ผลรวมเวกเตอร์ไม่มีทางเป็น 0 ดังนั้น เวกเตอร์ความเร็ว 3 เวกเตอร์ ต้องอยู่ในระนาบเดียวกัน |
| (B) | เป็นจริง เพราะ จากกฎอนุรักษ์โมเมนตัม
m1v1 = m2v2
และพลังงานรวม
\({\rm{E = }}\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{m}}_{\rm{1}}}{\rm{v}}_{\rm{1}}^{\rm{2}} + \dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{m}}_{\rm{2}}}{\rm{v}}_2^{\rm{2}}\)
สังเกตว่า 2 สมการ 2 ตัวแปร สามารถหาความเร็วของแต่ละอนุภาคได้ |
เป็นเท็จ เพราะ จากกฎอนุรักษ์โมเมนตัม
m1v1 + m2v2 + m3v3 = 0
และพลังงานรวม
\({\rm{E = }}\displaystyle\sum\limits_{i = 1}^3 {\frac{{\rm{1}}}{{\rm{2}}}{{\rm{m}}_{\rm{i}}}{\rm{v}}_i^{\rm{2}}}\)
สังเกตว่า 2 สมการ มากกว่า 2 ตัวแปร ไม่สามารถหาความเร็วของแต่ละอนุภาคได้ |
| (C) | เป็นเท็จ เพราะจากกฎอนุรักษ์โมเมนตัม
\(\begin{align*} {{\rm{m}}_{\rm{1}}}{{\rm{v}}_{\rm{1}}} &= {{\rm{m}}_{\rm{2}}}{{\rm{v}}_{\rm{2}}}\\ {{\rm{v}}_{\rm{2}}} &= \frac{{{{\rm{m}}_{\rm{2}}}}}{{{{\rm{m}}_{\rm{1}}}}}{{\rm{v}}_{\rm{1}}} \end{align*}\)
ถ้าไม่ทราบ m1, m2 ก็ไม่สามารถหา v2 |
เป็นเท็จ เพราะจากกฎอนุรักษ์โมเมนตัม
\({{\rm{m}}_{\rm{1}}}{\overrightarrow {\rm{v}} _{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\overrightarrow {\rm{v}} _{\rm{2}}}{\rm{ + }}{{\rm{m}}_{\rm{3}}}{\overrightarrow {\rm{v}} _{\rm{3}}}{\rm{ = 0}}\)
ทราบเพียงขนาดของ \({\overrightarrow {\rm{v}} _{\rm{1}}}\) และ \({\overrightarrow {\rm{v}} _{\rm{2}}}\)ไม่ทราบ m1, m2, m3 และทิศทางของ \({\overrightarrow {\rm{v}} _{\rm{1}}},{\overrightarrow {\rm{v}} _{\rm{2}}},{\overrightarrow {\rm{v}} _{\rm{3}}}\) จึงไม่สามารถหาขนาดของ \({\overrightarrow {\rm{v}} _{\rm{3}}}\) ได้ |
| (D) | เป็นจริง เพราะไม่มีแรงภายนอกมากระทำ จึงใช้กฎอนุรักษ์โมเมนตัมได้ ดังนั้น โมเมนตัมรวมของอนุภาคที่แตกออกมาจะเท่ากับศูนย์ |
เป็นจริง เพราะไม่มีแรงภายนอกมากระทำ จึงใช้กฎอนุรักษ์โมเมนตัมได้ ดังนั้น โมเมนตัมรวมของอนุภาคที่แตกออกมาจะเท่ากับศูนย์ |
| 60. | กระสุนมวล m1 ชนกับลูกตุ้มมวล m2 ที่ห้อยลงมาจากเชือกยาว L ด้วยความเร็วตามแนวนอน v0 ถ้าการชนนี้ไม่ยืดหยุ่นสมบูรณ์และกระสุนฝังเข้าด้านในลูกตุ้ม แล้วความเร็วต่ำสุดของ v0 ที่ทำให้ลูกตุ้ม (พร้อมกระสุนที่อยู่ภายใน) หมุนวนเป็นวงกลมตามแนวตั้งเท่ากับข้อใด |
| A | \(\rm 2\sqrt{Lg}\) |
| B | \(\rm \sqrt{5Lg}\) |
| C | \(\rm (m_1+m_2)2\sqrt{Lg}/m_1\) |
| D | \(\rm (m_1-m_2)\sqrt{Lg}/m_2\) |
| E | \(\rm (m_1+m_2)\sqrt{5Lg}/m_1\) |
ตอบ (E)
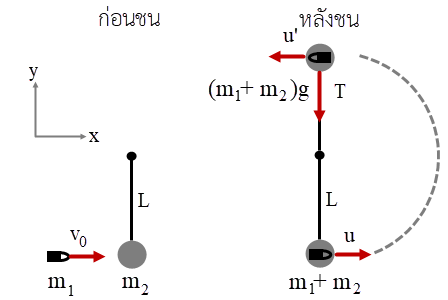จากกฎอนุรักษ์โมเมนตัมแนวแกน x
จะได้
จากกฎอนุรักษ์พลังงาน
จากสมการเคลื่อนที่วงกลม
ถ้าต้องการ v0 ต่ำสุดที่ทำให้มวล m1, m2 วนครบรอบ ต้องให้ T = 0 ณ จุดสูงสุด (เชือกกำลังหย่อนพอดี)
จะได้
จะได้
\(\rm m_1v_0 = (m_1 + m_2)u\)
\({\rm{u = }}\dfrac{{{{\rm{m}}_{\rm{1}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}}}{{\rm{v}}_{\rm{0}}}\) --- (1)
พิจารณา ก้อน m1 กับ m2 ณ จุดสูงสุดของวงกลม ให้ก้อนดังกล่าวมีความเร็ว \(\rm{u'}\)จากกฎอนุรักษ์พลังงาน
\(\begin{align*} \frac{1}{2}{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{{\rm{u'}}}^{\rm{2}}}{\rm{ + (}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}\rm)g(2L) &= \frac{1}{2}{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{\rm{u}}^{\rm{2}}}\\ \frac{1}{2}{{{\rm{u'}}}^{\rm{2}}}\rm + g2L &= \frac{1}{2}{{\rm{u}}^{\rm{2}}} \end{align*}\)
\({{\rm{u'}}^{\rm{2}}} = {{\rm{u}}^{\rm{2}}} - 4{\rm{gL }}\) --- (2)
จากสมการเคลื่อนที่วงกลม
\({\rm{ (}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)g + T = }}\dfrac{{{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{{\rm{u'}}}^{\rm{2}}}}}{{\rm{L}}}\)
เมื่อ T คือความตึงเชือกถ้าต้องการ v0 ต่ำสุดที่ทำให้มวล m1, m2 วนครบรอบ ต้องให้ T = 0 ณ จุดสูงสุด (เชือกกำลังหย่อนพอดี)
จะได้
\(\begin{align*} {\rm{ (}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}\rm)g + T &= \dfrac{{{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{{\rm{u'}}}^{\rm{2}}}}}{{\rm{L}}}\\ {\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}\rm)g + 0 &= \frac{{{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{{\rm{u'}}}^{\rm{2}}}}}{{\rm{L}}}\\ \rm g &= \frac{{{{{\rm{u'}}}^{\rm{2}}}}}{{\rm{L}}} \end{align*}\)
จาก (2)
\(\begin{align*} \rm gL &= {{\rm{u}}^{\rm{2}}} - 4{\rm{gL}}\\ \rm u &= \sqrt {{\rm{5gL}}} \end{align*}\)
จาก (1)
\(\begin{align*} \frac{{{{\rm{m}}_{\rm{1}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}}}{{\rm{v}}_{\rm{0}}} &=\sqrt {{\rm{5gL}}} \\ {{\rm{v}}_{\rm{0}}}&=\left( {\frac{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}}}{{{{\rm{m}}_{\rm{1}}}}}} \right)\sqrt {{\rm{5gL}}} \end{align*}\)
| 61. | ถ้าดาวทรงกลมสม่ำเสมอสองดวง มีความหนาแน่นเท่ากัน แต่รัศมีไม่เท่ากัน แล้วปริมาณในข้อใดที่ดาวทั้งสองจะมีค่าเท่ากัน |
| A | ความเร็วหลุดพ้นที่ผิวของดาว |
| B | ความเร่งโน้มถ่วงที่ผิวของดาว |
| C | คาบในการโคจรของดาวเทียม เหนือผิวดาวพอดีในวงโคจรวงกลม |
| D | คาบในการโคจรของดาวเทียม ที่ระยะห่างใดๆ จากจุดศูนย์กลาง ในวงโคจรวงกลม |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
ดาวสองดวงมี ρ เท่ากัน แต่ R1 ≠ R2 จะได้ว่า M1 ≠ M2 แต่
จาก กฎอนุรักษ์พลังงาน อนุภาคมวล m จะเคลื่อนที่ห่างจากดาว แล้วไปหยุดนิ่งพอดีที่ระยะอนันต์
B) ความเร่งที่ผิวของดาว (g) = \(\dfrac{{{\rm{GM}}}}{{{{\rm{R}}^{\rm{2}}}}}\) จะได้ g1 ≠ g2
C) คาบการโคจรดาวเทียม (T)
เขียนสมการเคลื่อนที่แบบวงกลม
ข้อ D) r ใดๆ โดยที่ r1 = r2 จะได้ว่า ดังนั้น T1 ≠ T2
ดังนั้น ตอบข้อ C)
ดาวสองดวงมี ρ เท่ากัน แต่ R1 ≠ R2 จะได้ว่า M1 ≠ M2 แต่
\(\begin{align*}
\frac{{{{\rm{M}}_{\rm{1}}}}}{{\frac{{\rm{4}}}{{\rm{3}}}{\rm{\pi R}}_{\rm{1}}^{\rm{3}}}} &= \frac{{{{\rm{M}}_{\rm{2}}}}}{{\frac{{\rm{4}}}{{\rm{3}}}{\rm{\pi R}}_{\rm{2}}^{\rm{3}}}} = {\rm{\rho }}\\
\frac{{{{\rm{M}}_{\rm{1}}}}}{{{\rm{R}}_{\rm{1}}^{\rm{3}}}} &= \frac{{{{\rm{M}}_{\rm{2}}}}}{{{\rm{R}}_{\rm{2}}^{\rm{3}}}}
\end{align*}\)
A) ให้ความเร็วหลุดพ้นที่ผิวดาว = vจาก กฎอนุรักษ์พลังงาน อนุภาคมวล m จะเคลื่อนที่ห่างจากดาว แล้วไปหยุดนิ่งพอดีที่ระยะอนันต์
\(\begin{align*}
\frac{1}{2}{\rm{m}}{{\rm{v}}^2} + \left( {\frac{{{\rm{ - G}}}}{{{\rm{MmR}}}}} \right) &= 0\\
\rm v &= \sqrt {\frac{{{\rm{2GM}}}}{{\rm{R}}}}
\end{align*}\)
จะได้ v1 ≠ v2B) ความเร่งที่ผิวของดาว (g) = \(\dfrac{{{\rm{GM}}}}{{{{\rm{R}}^{\rm{2}}}}}\) จะได้ g1 ≠ g2
C) คาบการโคจรดาวเทียม (T)
เขียนสมการเคลื่อนที่แบบวงกลม
\(\begin{align*}
{\rm{m}}{{\rm{\omega }}^{\rm{2}}}\rm r &= \frac{{{\rm{GMm}}}}{{{{\rm{r}}^{\rm{2}}}}}\\
\omega &= \sqrt {\frac{{{\rm{GM}}}}{{{{\rm{r}}^{\rm{3}}}}}}
\end{align*}\)
หรือ
\(\rm T = \dfrac{{{\rm{2\pi }}}}{{\rm{\omega }}}{\rm{ = 2\pi }}\sqrt {\dfrac{{\rm{1}}}{{\rm{G}}}\dfrac{{{{\rm{r}}^{\rm{3}}}}}{{\rm{M}}}}\)
ข้อ C) r = R ใดๆ จะได้ว่า \({\rm{T }} \propto \sqrt {\dfrac{{{{\rm{R}}^{\rm{3}}}}}{{\rm{M}}}} \) ดังนั้น T1 = T2ข้อ D) r ใดๆ โดยที่ r1 = r2 จะได้ว่า ดังนั้น T1 ≠ T2
ดังนั้น ตอบข้อ C)
| 62. | ยิงบอลขึ้นฟ้าจากพื้นด้วยอัตราเร็วต้นในแนวตั้ง v0 และบอลที่ตกกลับลงมาจะกระเด้งกับพื้นในแนวตั้ง เนื่องจากการชนนั้นไม่ยืดหยุ่น บอลจึงสูญเสียความเร็วไปตามสัดส่วนค่าหนึ่งทุกครั้งที่เกิดการกระเด้ง เช่น ถ้าอัตราเร็วก่อนกระทบพื้นคือ v แล้วอัตราเร็วหลังกระทบพื้นจะเท่ากับ rv โดยค่าคงที่ r < 1 แล้วเวลารวมที่บอลเคลื่อนที่ไปได้จะเท่ากับข้อใด สมมุติว่าเวลาที่บอลกระทบพื้นสั้นมาก |
| A | \(\rm \dfrac{2 v_0}{g} \dfrac{1}{1-r}\) |
| B | \(\rm \dfrac{v_0}{g} \dfrac{r}{1-r}\) |
| C | \(\rm \dfrac{2v_0}{g} \dfrac{1-r}{r}\) |
| D | \(\rm \dfrac{2v_0}{g} \dfrac{1}{1-r^2}\) |
| E | \(\rm \dfrac{2v_0}{g} \dfrac{1}{1+(1-r)^2}\) |
ตอบ (A)
พิจารณาการตกกระทบพื้นครั้งที่ ใดๆ
จะได้ vn = rnv0
จะได้ vn = rnv0
tn (เวลาเด้งขึ้น – ลง) = \(2\left( {\dfrac{{{{\rm{v}}_{\rm{n}}}}}{{\rm{g}}}} \right)\)
tn = \(\dfrac{{2{{\rm{v}}_{\rm{0}}}}}{{\rm{g}}}{{\rm{r}}^{\rm{n}}}\)
ดังนั้น tรวม = \(\displaystyle\sum\limits_{{\rm{n = 0}}}^\infty {{{\rm{t}}_{\rm{n}}}} {\rm{ = }}\frac{{{\rm{2}}{{\rm{v}}_{\rm{0}}}}}{{\rm{g}}}\left( {{\rm{1 + r + }}{{\rm{r}}^{\rm{2}}}{\rm{ + }}...} \right){\rm{ = }}\frac{{{\rm{2}}{{\rm{v}}_{\rm{0}}}}}{{\rm{g}}}\left( {\frac{1}{{1 - {\rm{r}}}}} \right)\)| 63. | ดาวเทียมสองดวงถูกยิงออกจากตำแหน่ง R จากศูนย์กลางดาวเคราะห์ที่มีรัศมีเล็กมาก และดาวเทียมทั้งสองถูกยิงออกไปในทิศตั้งฉากกับเส้นรัศมี ถ้าดาวเทียมดวงแรกถูกยิงด้วยอัตราเร็ว v0 และเข้าสู่วงโคจรวงกลม ส่วนดาวเทียมดวงที่สองถูกยิงด้วยอัตราเร็ว \(\dfrac{1}{2}\)v0 แล้วระยะใกล้สุดของดาวเทียมที่สองกับดาวเคราะห์ขณะอยู่ในวงโคจรเท่ากับข้อใด |
| A | \(\rm\dfrac{1}{\sqrt2}R\) |
| B | \(\rm\dfrac{1}{2}R\) |
| C | \(\rm\dfrac{1}{3}R\) |
| D | \(\rm\dfrac{1}{4}R\) |
| E | \(\rm\dfrac{1}{7}R\) |
ตอบ (E)
ให้ดาวเคราะห์มวล = M
พิจารณาดาวเทียมดวงแรก
สมการการเคลื่อนที่วงกลม
ที่ระยะใกล้กับดาวที่สุด ดาวเทียมจะมีความเร็ว u และตั้งฉากกับเส้นรัศมี ระยะจาก O ถึงมวล เท่ากับ r
จากกฎอนุรักษ์พลังงาน
จากกฎอนุรักษ์โมเมนตัมเชิงมุม
ดังนั้น ระยะที่ใกล้ดาวเคราะที่สุด คือ \(\rm \dfrac{R}{7}\)
ให้ดาวเคราะห์มวล = M
พิจารณาดาวเทียมดวงแรก
\(\begin{align*} \frac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{R}}} &= \frac{{{\rm{GMm}}}}{{{{\rm{R}}^{\rm{2}}}}}\\ {\rm{v}}_{\rm{0}}^{\rm{2}} &= \frac{{{\rm{GM}}}}{{\rm{R}}} \end{align*}\)
พิจารณาดาวเทียมดวงที่สอง
จากกฎอนุรักษ์พลังงาน
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{u}}^{\rm{2}}} - \frac{{{\rm{GMm}}}}{{\rm{r}}} &= \frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{\left( {\frac{{\rm{1}}}{{\rm{2}}}{{\rm{v}}_{\rm{0}}}} \right)^{\rm{2}}} - \frac{{{\rm{GMm}}}}{{\rm{R}}}\\ \frac{{\rm{1}}}{{\rm{2}}}{{\rm{u}}^{\rm{2}}} - \frac{{{\rm{GM}}}}{{\rm{r}}} &= \frac{{\rm{1}}}{{\rm{8}}}{\rm{v}}_0^2 - \frac{{{\rm{GM}}}}{{\rm{R}}} \end{align*}\)
จาก \({\rm{v}}_{\rm{0}}^{\rm{2}} = \dfrac{{{\rm{GM}}}}{{\rm{R}}}\)
\(\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{u}}^{\rm{2}}} - \dfrac{{{\rm{GM}}}}{{\rm{r}}} = \dfrac{{\rm{1}}}{{\rm{8}}}\dfrac{{{\rm{GM}}}}{{\rm{R}}} - \dfrac{{{\rm{GM}}}}{{\rm{R}}}\)
\(\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{u}}^{\rm{2}}} - \dfrac{{{\rm{GM}}}}{{\rm{r}}} = - \dfrac{7}{{\rm{8}}}\dfrac{{{\rm{GM}}}}{{\rm{R}}}\) --- (1)
จากกฎอนุรักษ์โมเมนตัมเชิงมุม
\({\rm{mR}}\left( {\dfrac{{\rm{1}}}{{\rm{2}}}} \right){{\rm{v}}_{\rm{0}}}{\rm{ = mru}}\)
\({\rm{u = }}\left( {\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{v}}_{\rm{0}}}} \right)\left( {\dfrac{{\rm{R}}}{{\rm{r}}}} \right)\) --- (2)
แทน (2) และ \({\rm{v}}_{\rm{0}}^{\rm{2}} = \dfrac{{{\rm{GM}}}}{{\rm{R}}}\) ใน (1)
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\left( {\frac{{\rm{1}}}{{\rm{2}}}{{\rm{v}}_{\rm{0}}}} \right)^{\rm{2}}}\left( {\frac{{{{\rm{R}}^{\rm{2}}}}}{{{{\rm{r}}^{\rm{2}}}}}} \right) - \frac{{{\rm{GM}}}}{{\rm{r}}} &= - \frac{7}{{\rm{8}}}\frac{{{\rm{GM}}}}{{\rm{R}}}\\ \frac{{\rm{1}}}{{\rm{8}}}\left( {\frac{{{\rm{GM}}}}{{\rm{R}}}} \right)\left( {\frac{{{{\rm{R}}^{\rm{2}}}}}{{{{\rm{r}}^{\rm{2}}}}}} \right) - \frac{{{\rm{GM}}}}{{\rm{r}}} &= - \frac{7}{{\rm{8}}}\frac{{{\rm{GM}}}}{{\rm{R}}}\\ \frac{{\rm{1}}}{{\rm{8}}}\left( {\frac{{\rm{R}}}{{{{\rm{r}}^{\rm{2}}}}}} \right) - \frac{{\rm{1}}}{{\rm{r}}} &= - \frac{7}{{\rm{8}}}\frac{{\rm{1}}}{{\rm{R}}} \end{align*}\)
คูณ 8Rr2
\(\begin{align*} \rm {R^2} - 8Rr &= \rm - 7{r^2}\\ \rm 7{r^2} - 8Rr\, + {R^2} &= 0\\ \rm (7r - R)(r - R) &= 0\\ \rm r &= \rm R,\frac{R}{7} \end{align*}\)
เนื่องจาก R เป็นระยะขณะเริ่มปล่อย จึงไม่ใช่คำตอบดังนั้น ระยะที่ใกล้ดาวเคราะที่สุด คือ \(\rm \dfrac{R}{7}\)
| 64. | ถ้าก้อนดินขนาดใหญ่หล่นออกจากกำแพงลงสู่พื้นดิน แล้วกราฟข้อใด แสดงความเร่งที่จุดศูนย์กลางมวลของก้อนดินกับเวลา ได้ดีที่สุด |
| A |  |
| B |  |
| C |  |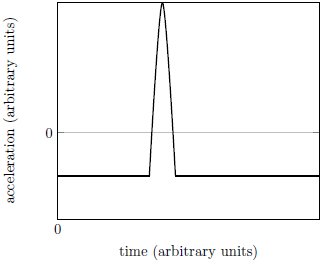
| D |  |
| E |  |
ตอบ (B)
ในการตกอย่างอิสระ ความเร่งจะเป็นค่าคงที่และมีค่าประมาณ
-10 m/s2 ทิศลง หลังจากนั้นจะมีแรงดันจากพื้น ทำให้มีความเร่งในทิศขึ้น แรงดันจะมีค่าสูงสุดค่าหนึ่ง แล้วลดลงจนเป็นศูนย์ เมื่อก้อนดินหยุดนิ่ง
ในการตกอย่างอิสระ ความเร่งจะเป็นค่าคงที่และมีค่าประมาณ
-10 m/s2 ทิศลง หลังจากนั้นจะมีแรงดันจากพื้น ทำให้มีความเร่งในทิศขึ้น แรงดันจะมีค่าสูงสุดค่าหนึ่ง แล้วลดลงจนเป็นศูนย์ เมื่อก้อนดินหยุดนิ่ง
| 65. | บล็อกสม่ำเสมอมวล 10 kg เดิมอยู่นิ่งถูกปล่อยลงมาจากพื้นเอียงที่มีความยาว 10 m เอียง 30◦ และเคลื่อนที่ลงมาจนถึงด้านล่าง ถ้าสัมประสิทธิ์แรงเสียดทานสถิตและแรงเสียดทานจลน์เท่ากับ μs = μk = 0.1 พลังงานที่สูญเสียไปกับแรงเสียดทานเท่ากับข้อใด |
| A | 0 J |
| B | 22 J |
| C | 43 J |
| D | 87 J |
| E | 164 J |
ตอบ (D)
แรงตั้งฉากที่เกิดขึ้นจะเท่ากับ \(100 (\sqrt3/2) \rm ~N\) ดังนั้น แรงเสียดทานจะเท่ากับ \(5\sqrt 3 \rm~ N\) เมื่อกระทำเป็นระยะ \(10\rm~ m\) พลังงานจะสูญเสียไปจะเท่ากับ \(50\sqrt 3 \rm ~J\) มีค่าประมาณ \(87 \rm~J\)
แรงตั้งฉากที่เกิดขึ้นจะเท่ากับ \(100 (\sqrt3/2) \rm ~N\) ดังนั้น แรงเสียดทานจะเท่ากับ \(5\sqrt 3 \rm~ N\) เมื่อกระทำเป็นระยะ \(10\rm~ m\) พลังงานจะสูญเสียไปจะเท่ากับ \(50\sqrt 3 \rm ~J\) มีค่าประมาณ \(87 \rm~J\)
| 66. | มวล 3.0 kg เคลื่อนที่ 40 m/s ไปทางขวาเกิดการพุ่งชนแล้วติดไปกับมวล 2.0 kg ที่กำลังเคลื่อนที่ไปทางขวา 20 m/s หลังเกิดการชน พลังงานจลน์ของระบบเท่ากับข้อใด หลังการชน |
| A | 600 J |
| B | 1200 J |
| C | 2600 J |
| D | 2800 J |
| E | 3400 J |
ตอบ (C)
ใช้กฎการอนุรักษ์โมเมนตัม จะได้ความเร็วต้นที่จุดศูนย์กลางมวลเท่ากับ \((3·40+2·20)/5 = 32 ~\rm m/s\) หลังการชน
ดังนั้น พลังงานจลน์จะเท่ากับ \(\dfrac{{{{\rm{m}}_{{\rm{tot}}}}{{\rm{V}}^2}}}{2} ≈ 2600\rm~ J\)
ใช้กฎการอนุรักษ์โมเมนตัม จะได้ความเร็วต้นที่จุดศูนย์กลางมวลเท่ากับ \((3·40+2·20)/5 = 32 ~\rm m/s\) หลังการชน
ดังนั้น พลังงานจลน์จะเท่ากับ \(\dfrac{{{{\rm{m}}_{{\rm{tot}}}}{{\rm{V}}^2}}}{2} ≈ 2600\rm~ J\)
| 67. | ให้ลูกบาสที่เดิมอยู่นิ่งถูกปล่อยลงมากระแทกพื้น ถ้าพิจารณาเฉพาะลูกบาสในช่วงก่อนและหลังกระแทกพื้น แล้วข้อความใดต่อไปนี้เป็นจริง |
| A | โมเมนตัม และพลังงานสุทธิของลูกบาสจะถูกอนุรักษ์ไว้ |
| B | โมเมนตัมของลูกบาสจะถูกอนุรักษ์ไว้ แต่พลังงานจลน์ไม่ถูกอนุรักษ์ไว้ |
| C | พลังงานสุทธิของลูกบาสจะถูกอนุรักษ์ไว้ แต่โมเมนตัมไม่ถูกอนุรักษ์ไว้ |
| D | พลังงานจลน์ของลูกบาสจะถูกอนุรักษ์ไว้ แต่โมเมนตัมไม่ถูกอนุรักษ์ไว้ |
| E | พลังงานจลน์ และโมเมนตัมของลูกบาสไม่ได้ถูกอนุรักษ์ไว้ |
ตอบ (E)
โมเมนตัมของลูกบาสไม่ถูกอนุรักษ์ไว้ เพราะมีแรงภายนอกจากพื้นดินมากระทำ
พลังงานจลน์ไม่ถูกอนุรักษ์ไว้ เพราะมีการเปลี่ยนพลังงานบางส่วนเป็นคลื่นเสียง เป็นการสั่นสะเทือนกับพื้น ฯลฯ
โมเมนตัมของลูกบาสไม่ถูกอนุรักษ์ไว้ เพราะมีแรงภายนอกจากพื้นดินมากระทำ
พลังงานจลน์ไม่ถูกอนุรักษ์ไว้ เพราะมีการเปลี่ยนพลังงานบางส่วนเป็นคลื่นเสียง เป็นการสั่นสะเทือนกับพื้น ฯลฯ
| 68. | ฮาร์ดดิสก์ในคอมพิวเตอร์จะหมุนถึงอัตราเร็วที่ต้องการภายใน 10 รอบ แต่เมื่อปิดเครื่องมันจะหมุนได้ถึง 50 รอบ ก่อนหยุดลง สมมุติว่า ฮาร์ดดิสก์มีความเร่งเชิงมุม α1 ในช่วงแรก และช่วงการชะลอมีความเร่งเชิงมุม α2 แล้วอัตราส่วน α1 / α2 เท่ากับข้อใด |
| A | \(\dfrac{1}{5}\) |
| B | \(\dfrac{1}{\sqrt5}\) |
| C | \(\sqrt5\) |
| D | \(5\) |
| E | \(25\) |
ตอบ (D)
ให้ ω0 คือ ความเร็วที่ต้องการ
เมื่อ ωf2 – ωi2 = 2αθ โดยในช่วงแรก ωi = 0, ωf = ω0 และในช่วงหลัง ωi = ω0, ωf = 0
แล้วค่าของ αθ จะเท่ากันทั้งสองกรณี ดังนั้น ความเร่งที่ได้จะมีค่าเป็นสัดส่วนห้าเท่า
ให้ ω0 คือ ความเร็วที่ต้องการ
เมื่อ ωf2 – ωi2 = 2αθ โดยในช่วงแรก ωi = 0, ωf = ω0 และในช่วงหลัง ωi = ω0, ωf = 0
แล้วค่าของ αθ จะเท่ากันทั้งสองกรณี ดังนั้น ความเร่งที่ได้จะมีค่าเป็นสัดส่วนห้าเท่า
| 69. | คานเบายาว L ถูกตรึงด้านหนึ่งไว้ และมีแรงกด F กระทำที่ปลายคานด้านที่ไม่ถูกตรึง จนคานยุบลงไปเป็นระยะ x โดยที่ระยะที่ยุบลงไปเป็น x นี้แปรผันตรงกับขนาดของ F และเป็นสัดส่วนผกผันกับโมเมนตัดขวาง I ซึ่งมีหน่วย m4 การยุบนี้ยังขึ้นอยู่กับมอดุลัสของยัง E ซึ่งมีหน่วย N / m2 แล้ว x จะแปรผันตรงกับ L อย่างไร |
| A | \(\rm x ∝ \sqrt L\) |
| B | \(\rm x ∝ L\) |
| C | \(\rm x ∝ L^2\) |
| D | \(\rm x ∝ L^3\) |
| E | \(\rm x ∝ L^4\) |
ตอบ (D)
ใช้การวิเคราะห์หน่วย โดยสมมุติว่า x ∝ FaEbIcLd
จะได้ a = 1, b = – 1, c = – 1 และ d = 3 ซึ่งจะทำให้ x มีหน่วยเป็น m
ดังนั้น x ∝ L3
ใช้การวิเคราะห์หน่วย โดยสมมุติว่า x ∝ FaEbIcLd
จะได้ a = 1, b = – 1, c = – 1 และ d = 3 ซึ่งจะทำให้ x มีหน่วยเป็น m
ดังนั้น x ∝ L3
| 70. | ให้ลูกตุ้มยาว L แกว่งอยู่ภายในกล่องใบหนึ่ง หากมีคนยกกล่องขึ้นมาแล้วค่อยๆ เขย่าในแนวตั้งด้วยความถี่ ω และให้แอมพลิจูดคงที่ตามช่วงเวลาหนึ่งที่กำหนด แล้วแอมพลิจูดสุดท้ายของลูกตุ้มจะมีค่ามากที่สุด เมื่อ ω เท่ากับข้อใด |
| A | \(\rm ω = \sqrt{4g/L}\) |
| B | \(\rm ω = \sqrt{2g/L}\) |
| C | \(\rm ω = \sqrt{g/L}\) |
| D | \(\rm ω = \sqrt{g/4L}\) |
| E | \(ω\) ไม่มีผลต่อแอมพลิจูดของลูกตุ้มอย่างมีนัยสำคัญ |
ตอบ (A)
ภายในกล่อง การสั่นตามแนวตั้งจะเท่ากับ g และมีความถี่ในการสั้น ω ในการเพิ่มแอมพลิจูด แรงโน้มถ่วงจะต้องเพิ่มขึ้นขณะลูกตุ้มเคลื่อนที่ลง และน้อยลงขณะลูกตุ้มเคลื่อนที่ขึ้น จึงทำให้เกิดเรโซแนนซ์ (resonance)
ดังนั้น การสั่นของลูกตุ้มแต่ละรอบจะต้องเกิดการสั่นของกล่อง 2 รอบ จึงได้ว่า \(\rm ω = \sqrt{2g/L}\)
ภายในกล่อง การสั่นตามแนวตั้งจะเท่ากับ g และมีความถี่ในการสั้น ω ในการเพิ่มแอมพลิจูด แรงโน้มถ่วงจะต้องเพิ่มขึ้นขณะลูกตุ้มเคลื่อนที่ลง และน้อยลงขณะลูกตุ้มเคลื่อนที่ขึ้น จึงทำให้เกิดเรโซแนนซ์ (resonance)
ดังนั้น การสั่นของลูกตุ้มแต่ละรอบจะต้องเกิดการสั่นของกล่อง 2 รอบ จึงได้ว่า \(\rm ω = \sqrt{2g/L}\)
| 71. | ให้สัมประสิทธิ์แรงเสียดทานสถิตและแรงเสียดทานจลน์ระหว่างลูกบอลและพื้นเท่ากับ μs = μk = μ ถ้าตอนเริ่มต้นบอลได้รับอัตราเร็วในแนวนอน โดยไม่มีความเร็วเชิงมุมรอบจุดศูนย์กลางมวล แล้วกราฟในข้อใด แสดงความเร็วเชิงมุมของลูกบอลรอบจุดศูนย์กลางมวลเทียบกับเวลา ได้ดีที่สุด |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (C)
แรงเสียดทานจลน์ μN จะกระทำด้วยทอร์กคงที่ ขณะที่ลูกบอลไถลไปกับพื้น
ดังนั้น ความเร็วเชิงมุมต้นจะเพิ่มขึ้นแบบเป็นเส้นตรง และความเร็วเชิงมุมจะคงที่หลังเกิดการหมุนโดยไม่ไถล
แรงเสียดทานจลน์ μN จะกระทำด้วยทอร์กคงที่ ขณะที่ลูกบอลไถลไปกับพื้น
ดังนั้น ความเร็วเชิงมุมต้นจะเพิ่มขึ้นแบบเป็นเส้นตรง และความเร็วเชิงมุมจะคงที่หลังเกิดการหมุนโดยไม่ไถล
| 72. | บอลมวล 3.0 kg เคลื่อนที่ไปทางทิศตะวันออก 10 m/s แล้วชนแบบยืดหยุ่นกับบอลมวล 2.0 kg ที่กำลังเคลื่อนที่ไปทางทิศตะวันตก 15 m/s แล้วข้อความใดต่อไปนี้ถูกต้อง หลังเกิดการชน |
| A | บอลทั้งสองจะพุ่งไปทางทิศตะวันออก |
| B | บอลมวล 3.0 kg เคลื่อนที่ไปทางทิศตะวันตก 15 m/s |
| C | บอลมวล 2.0 kg เคลื่อนที่ไปทางทิศเหนือ 10 m/s |
| D | บอลมวล 3.0 kg หยุดนิ่ง |
| E | บอลมวล 2.0 kg เคลื่อนที่ไปทางทิศใต้ 15 m/s |
ตอบ (E)
เนื่องจากโมเมนตัมสุทธิที่จุดศูนย์กลางมวลต้องมีค่าเป็นศูนย์ ทำให้โมเมนตัมสุดท้ายจะต้องมีค่าเท่ากัน และมีทิศตรงข้าม และเพื่ออนุรักษ์พลังงาน ความเร็วสุดท้ายของแต่ละลูกจะต้องเท่ากับความเร็วต้น ซึ่งข้อที่ครอบคลุมทั้งหมดคือ (E) ( ส่วนบอลมวล 3.0 kg จะเคลื่อนที่ไปทางทิศเหนือ 10 m/s หลังการชน )
เนื่องจากโมเมนตัมสุทธิที่จุดศูนย์กลางมวลต้องมีค่าเป็นศูนย์ ทำให้โมเมนตัมสุดท้ายจะต้องมีค่าเท่ากัน และมีทิศตรงข้าม และเพื่ออนุรักษ์พลังงาน ความเร็วสุดท้ายของแต่ละลูกจะต้องเท่ากับความเร็วต้น ซึ่งข้อที่ครอบคลุมทั้งหมดคือ (E) ( ส่วนบอลมวล 3.0 kg จะเคลื่อนที่ไปทางทิศเหนือ 10 m/s หลังการชน )
| 73. | ให้ลูกโป่งที่มีอากาศบรรจุไว้จมลงในน้ำที่ความลึก h และมีแรงลอยตัว B0 เมื่อลูกโป่งจมลงที่ความลึก 2h จะมี แรงลอยตัว B สมมุติว่า น้ำไม่สามารถบีบอัดได้ แต่ลูกโป่งและอากาศสามารถบีบอัดได้ แล้วแรงลอยตัว B จะเป็นไปตามข้อใด |
| A | B ≥ 2B0 |
| B | B0 < B < 2B0 |
| C | B = B0 |
| D | B < B0 |
| E | คำตอบขึ้นกับแรงบีบอัดของลูกโป่งและอากาศ |
ตอบ (D)
แรงลอยตัวคือ ρV โดย ρ คือความหนาแน่นของน้ำ และ V คือปริมาตรน้ำจะถูกแทนที่ เนื่องจากน้ำไม่สามารถบีบอัดตัวได้ แสดงว่า ρ จะคงที่ ส่วน V จะลดลง ส่วนลูกโป่งและอากาศนั้นสามารถบีบอัดได้
แรงลอยตัวคือ ρV โดย ρ คือความหนาแน่นของน้ำ และ V คือปริมาตรน้ำจะถูกแทนที่ เนื่องจากน้ำไม่สามารถบีบอัดตัวได้ แสดงว่า ρ จะคงที่ ส่วน V จะลดลง ส่วนลูกโป่งและอากาศนั้นสามารถบีบอัดได้
| 74. | วงเชือกถูกหมุนด้วยความเร็วเชิงมุม ω0 ในอวกาศคลื่นตามขวางในเส้นเชือกมีอัตราเร็วเชิงมุม v0 เมื่อวัดในกรอบอ้างอิงที่หมุนไปพร้อมกับเชือก (เห็นเชือกอยู่นิ่งในกรอบอ้างอิงนี้) ถ้าเพิ่มความเร็วเชิงมุมของเชือกเป็นสองเท่า แล้วอัตราเร็วใหม่ของคลื่นตามขวางที่วัดในกรอบอ้างอิงที่หมุนไปพร้อมกับเชือก (เห็นเชือกอยู่นิ่งในกรอบอ้างอิงนี้) จะเท่ากับข้อใด |
| A | \(\rm v_0\) |
| B | \(\sqrt 2 \rm v_0\) |
| C | \(2\rm v_0\) |
| D | \(4\rm v_0\) |
| E | \(8 \rm v_0\) |
ตอบ (C)
พิจารณาที่ส่วนเล็ก ๆ ของเชือก แรงตึงที่ปลายแต่ละด้านของเชือกจะเข้าสู่ศูนย์กลาง ดังนั้น \(\rm T ∝ ω^2\) ทำให้อัตราเร็วคลื่นเท่ากับ \(\rm v = \sqrt{T/μ}∝ ω\) ซึ่งตรงกับข้อ (C)
พิจารณาที่ส่วนเล็ก ๆ ของเชือก แรงตึงที่ปลายแต่ละด้านของเชือกจะเข้าสู่ศูนย์กลาง ดังนั้น \(\rm T ∝ ω^2\) ทำให้อัตราเร็วคลื่นเท่ากับ \(\rm v = \sqrt{T/μ}∝ ω\) ซึ่งตรงกับข้อ (C)
| 75. | ให้เด็กคนหนึ่งยืนอยู่ในสถานีอวกาศวงกลมที่กำลังหมุนอยู่ ถ้าเขาโยนลูกบอลไปในทิศทางหนึ่งขณะสถานีอวกาศกำลังหมุน แล้วลูกบอลย้อนกลับมาหาเขาหลังสถานีอวการหมุนไปได้ครึ่งรอบ แล้ววิถีของลูกบอลจากจุดที่เด็กคนนั้นเห็นจะเป็นไปตามข้อใด ให้เด็กยืนอยู่ที่ด้านล่างของสถานีอวกาศ แต่รูปจะแสดงเฉพาะตำแหน่งเริ่มต้นของลูกบอลเท่านั้น |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (C)
โจทย์บอกว่าเด็กรับลูกบอลได้ ดังนั้นวิถีของลูกบอลจะต้องเริ่มและสิ้นสุดที่เด็กคนนั้น ทำให้ข้อ A และ E ไม่ใช่คำตอบ เหลือ B, C, D พิจารณาที่ความเร็วของเด็กขณะขว้างลูกบอลออกไป ขณะที่ลูกบอลจะเคลื่อนที่ไปข้างหน้า ตัวเด็กก็จะเคลื่อนที่ไปทางขวา ดังนั้น ในมุมมองของเด็ก ความเร็วสัมพัทธ์จะมีการเคลื่อนที่สองทิศทาง คือ ไปข้างหน้าและไปทางซ้าย จึงตอบข้อ C
โจทย์บอกว่าเด็กรับลูกบอลได้ ดังนั้นวิถีของลูกบอลจะต้องเริ่มและสิ้นสุดที่เด็กคนนั้น ทำให้ข้อ A และ E ไม่ใช่คำตอบ เหลือ B, C, D พิจารณาที่ความเร็วของเด็กขณะขว้างลูกบอลออกไป ขณะที่ลูกบอลจะเคลื่อนที่ไปข้างหน้า ตัวเด็กก็จะเคลื่อนที่ไปทางขวา ดังนั้น ในมุมมองของเด็ก ความเร็วสัมพัทธ์จะมีการเคลื่อนที่สองทิศทาง คือ ไปข้างหน้าและไปทางซ้าย จึงตอบข้อ C
| 76. | ให้กล่องสองอัน มีมวล m1 = 2.0 และ m2 = 1.0 วางซ้อนกันบนโต๊ะลื่น ดังรูป ถ้าสัมประสิทธิ์แรงเสียดทานสถิตระหว่างกล่องทั้งสองเท่ากับ μs = 0.20 แล้วแรงในแนวนอนน้อยสุดที่กระทำกับกล่องด้านบน เพื่อให้กล่องด้านบนไถลไปบนกล่องล่างเท่ากับข้อใด
 |
| A | 4.0 N |
| B | 6.0 N |
| C | 8.0 N |
| D | 12.0 N |
| E | กล่องบนจะไม่มีทางไถลไปบนกล่องล่าง |
ตอบ (D)
สมมุติว่า มวล m1 กำลังจะขยับ แล้วแรงเสียดทานมากสุดที่เป็นไปได้จะเท่ากับ 4 N ในขณะที่ m1 และ m2 มีความเร่งเท่ากัน จะได้ F – 4 N = 8 N
ดังนั้น F = 12 N
สมมุติว่า มวล m1 กำลังจะขยับ แล้วแรงเสียดทานมากสุดที่เป็นไปได้จะเท่ากับ 4 N ในขณะที่ m1 และ m2 มีความเร่งเท่ากัน จะได้ F – 4 N = 8 N
ดังนั้น F = 12 N
| 77. | หลอดด้ายทำจากทรงกระบอกและมีแผ่นวงกลมบางๆ ติดหัวท้ายกระบอก ดังรูป ให้ทรงกระบอกมีรัศมี r = 0.75 cm แผ่นวงกลมแต่ละวงมีรัศมี R = 1.00 cm และมีเชือกพันรอบแกนหลอดด้ายสองสามรอบ แล้วขนาดของ θ ที่ดึงเชือกแล้วหลอดด้ายจะเคลื่อนที่โดยไม่หมุนเท่ากับข้อใด
 |
| A | 31.2° |
| B | 41.4° |
| C | 54.0° |
| D | 60.8° |
| E | 81.5° |
ตอบ (B)
หากไม่ต้องการให้หลอดด้ายกลิ้ง ต้องมีทอร์กเป็นศูนย์ ณ จุดที่หลอดด้ายสัมผัสกับพื้น กรณีนั้นจะเกิดขึ้นเมื่อด้ายอยู่ในแนวที่ตัดกับจุดที่สัมผัสพื้น เมื่อวาดสามเหลี่ยมมุมฉากจะได้ sin(90° - θ) = r / R เมื่อแทนค่าจะได้ θ = 41.4
สังเกตว่า การเลือกจุดสัมผัสพื้นเป็นจุดอ้างอิง ทำให้ไม่ต้องคำนึงถึงแรงเสียดทาน
หากไม่ต้องการให้หลอดด้ายกลิ้ง ต้องมีทอร์กเป็นศูนย์ ณ จุดที่หลอดด้ายสัมผัสกับพื้น กรณีนั้นจะเกิดขึ้นเมื่อด้ายอยู่ในแนวที่ตัดกับจุดที่สัมผัสพื้น เมื่อวาดสามเหลี่ยมมุมฉากจะได้ sin(90° - θ) = r / R เมื่อแทนค่าจะได้ θ = 41.4
สังเกตว่า การเลือกจุดสัมผัสพื้นเป็นจุดอ้างอิง ทำให้ไม่ต้องคำนึงถึงแรงเสียดทาน
| 78. | ถ้าคุณยืนถือหนังสือฟิสิกส์เล่มใหญ่อยู่บนเครื่องชั่ง แล้วอ่านน้ำหนักได้ 700 นิวตัน ขณะยืนนิ่งอยู่ และที่เวลา t = 1 s คุณเริ่มยกหนังสือขึ้น จน t = 2 s หนังสืออยู่สูงขึ้นไปครึ่งเมตรแล้วหยุดนิ่งอีกครั้ง แล้วกราฟในข้อใด แสดงน้ำหนักที่อ่านได้เทียบกับเวลาได้ดีที่สุด |
| A |  |
| B |  |
| C |  |
| D |  |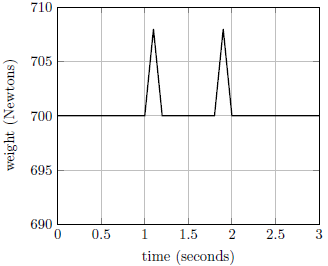
| E |  |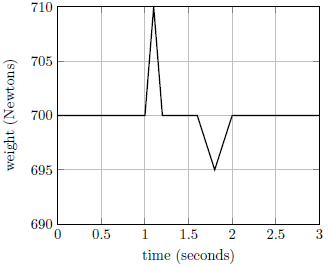
ตอบ (E)
ความเร็วที่จุดศูนย์กลางมวลของคุณและหนังสือไม่ว่าจะก่อนหรือหลังก็จะเท่ากับศูนย์เสมอ
ดังนั้น ค่าเฉลี่ยที่อ่านสเกลได้จะต้องเท่ากับ 700 N (ซึ่งรวมกับน้ำหนักด้วย) โดยช่วงต้นค่าจะเพิ่มขึ้น เพราะมีการใส่แรงอย่างฉบับพลันบนหนังสือ ทำให้มีแรงจากหนังสือกดลงมา และในช่วงท้ายค่าก็จะลดต่ำลง เพราะ ความเร็วของหนังสือลดลง
ความเร็วที่จุดศูนย์กลางมวลของคุณและหนังสือไม่ว่าจะก่อนหรือหลังก็จะเท่ากับศูนย์เสมอ
ดังนั้น ค่าเฉลี่ยที่อ่านสเกลได้จะต้องเท่ากับ 700 N (ซึ่งรวมกับน้ำหนักด้วย) โดยช่วงต้นค่าจะเพิ่มขึ้น เพราะมีการใส่แรงอย่างฉบับพลันบนหนังสือ ทำให้มีแรงจากหนังสือกดลงมา และในช่วงท้ายค่าก็จะลดต่ำลง เพราะ ความเร็วของหนังสือลดลง
| 79. | เครื่องบินจะบินโดยใช้การเอียงบริเวณขอบส่วนปลายปีกของเครื่องลงด้วยมุมเล็ก ๆ θ เรียกว่า มุมที่สร้างแรงยกตัว ขณะออกบิน ถ้าเครื่องบินมีอัตราเร็วบนพื้นดิน v แล้วแรงยกตัวจะแปรผันตาม v2θ และแรงฉุดเพื่อเอาชนะแรงต้านอากาศจะแปรผันตาม v2 พิจารณาเครื่องบินที่อยู่บนระดับความสูงหนึ่ง และมีอัตราเร็วคงที่ตอนอยู่บนพื้นดิน v ถ้ามีลมพัดจากหางไปยังหัวเครื่องบินด้วยความเร็ว w < v (ขนาดของ w วัดเทียบกับพื้นดิน) ( อากาศจะช่วยดันเครื่องบิน ให้บินไปยังทิศที่เราต้องการ ) แล้วกำลังของเครื่องยนต์ และมุมที่สร้างแรงยกตัวจะเปลี่ยนไปอย่างไร เพื่อให้ความเร็วของเครื่องบินยังคงบินในแนวระดับด้วยอัตราเร็วเท่าเดิม |
| A | กำลังของเครื่องยนต์จะลดลง และมุมที่สร้างแรงยกตัวจะลดลง |
| B | กำลังของเครื่องยนต์จะลดลง และมุมที่สร้างแรงยกตัวจะเท่าเดิม |
| C | กำลังของเครื่องยนต์จะลดลง และมุมที่สร้างแรงยกตัวจะเพิ่มขึ้น |
| D | กำลังของเครื่องยนต์จะเพิ่มขึ้น และมุมที่สร้างแรงยกตัวจะลดลง |
| E | กำลังของเครื่องยนต์จะเพิ่มขึ้น และมุมที่สร้างแรงยกตัวจะเพิ่มขึ้น |
ตอบ (C)
ให้ u เป็นความเร็วสัมพัทธ์ระหว่างเครื่องบินกับอากาศ หากต้องคงแรงยกไว้ ในกรณีที่ u ลดลง θ ต้องเพิ่มขึ้น
ส่วนแรงฉุดนั้นแปรผันกับ u2 ทำให้กำลังของเครื่องยนต์ที่แปรผันกับ u3 ต้องลดลง
ให้ u เป็นความเร็วสัมพัทธ์ระหว่างเครื่องบินกับอากาศ หากต้องคงแรงยกไว้ ในกรณีที่ u ลดลง θ ต้องเพิ่มขึ้น
ส่วนแรงฉุดนั้นแปรผันกับ u2 ทำให้กำลังของเครื่องยนต์ที่แปรผันกับ u3 ต้องลดลง
| 80. | ไม้กระโดดจำลองประกอบด้วยสปริงเบามีค่านิจสปริง k ติดที่ด้านล่างของบล็อกมวล m ให้ไม้กระโดดถูกปล่อยลง โดยสปริงจะกระแทกพื้นด้วยอัตราเร็ว v หลังจากการกระแทกแล้ว ส่วนปลายด้านล่างของสปริงจะถูกยึดติดกับพื้น
 |
| A | \(\rm v\) |
| B | \(\rm v + 2mg^2/kv\) |
| C | \(\rm v + mg^2/kv\) |
| D | \(\rm \sqrt{v + 2mg^2/kv}\) |
| E | \(\rm \sqrt{v + mg^2/kv}\) |
ตอบ (E)
จุดสมดุลอยู่ต่ำกว่าตำแหน่งที่สปริงไม่ยืดไม่หดเท่ากับ Δy
ดังนั้น พลังงานเริ่มต้นจะเท่ากับ \(\rm E = mv^2/2 + K (Δy)^2/2\) ความเร็วสูงสุดหาจาก \(\rm mv_{max}^ 2 / 2 = E\)
จะได้ \(\rm v_{max} = \sqrt{(v^2 +mg^2/k)}\) และมวลจะสั่นรอบจุดสมดุล
จุดสมดุลอยู่ต่ำกว่าตำแหน่งที่สปริงไม่ยืดไม่หดเท่ากับ Δy
ดังนั้น พลังงานเริ่มต้นจะเท่ากับ \(\rm E = mv^2/2 + K (Δy)^2/2\) ความเร็วสูงสุดหาจาก \(\rm mv_{max}^ 2 / 2 = E\)
จะได้ \(\rm v_{max} = \sqrt{(v^2 +mg^2/k)}\) และมวลจะสั่นรอบจุดสมดุล
| 81. | ให้สปริงที่มีความยาวตามปกติ l1 มีค่านิจสปริง k1 วางขนานกับสปริงที่มีความยาวตามปกติ l2 และมีค่านิจสปริง k2 และมีแรง F กระทำในแต่ละด้าน
 |
| A | k = k1 + k2 และ l = l1l2/(l1 + l2) |
| B | k = k1 + k2 และ l = ( l1 k1 + l2 k2 )/( k1 + k2 ) |
| C | k = k1 + k2 และ l = ( l1 k2 + l2 k1 )/( k1 + k2 ) |
| D | k = ( l1 k1 + l2 k2 )/ (l1+l2) และ l = ( l1 k1 + l2 k2 )/( k1 + k2 ) |
| E | k = ( l2 k1 + l1 k2 )/ (l1+l2) และ l = ( l1 k2 + l2 k1 )/( k1 + k2 ) |
ตอบ (B)
แรงในการคงสภาพเท่ากับ F = k1 (x - l1) + k2 (x - l2) = k (x - l) จากนั้นหาคำตอบด้วยพีชคณิต
แรงในการคงสภาพเท่ากับ F = k1 (x - l1) + k2 (x - l2) = k (x - l) จากนั้นหาคำตอบด้วยพีชคณิต
| 82. | (เกินหลักสูตรสอบเข้า สอวน.) ในการทดสอบอัตราเร็วเสียง นักเรียนคนหนึ่งวัดระยะทางที่คลื่นเสียงเดินทางไปได้ 75.0 ± 2.0 cm และใช้เวลาในการเดินทาง 2.15 ± 0.10 ms สมมุติว่าความคลาดเคลื่อนมีการกระจายตัวแบบ Gaussian (มีการแจกแจงแบบปกติ) แล้วอัตราเร็วที่คำนวณได้ควรเท่ากับข้อใด |
| A | 348.8 ± 0.5 m/s |
| B | 348.8 ± 0.8 m/s |
| C | 349 ± 8 m/s |
| D | 349 ± 15 m/s |
| E | 349 ± 19 m/s |
ตอบ (E)
คำตอบข้อนี้เราจะใช้เศษส่วนความคลาดเคลื่อน ( ถ้าต้องการคำอธิบายเพิ่มให้ดูการหา F = ma ) จาก v ∝ d / t เศษส่วนความคลาดเคลื่อนของการวัด หาจาก
คำตอบข้อนี้เราจะใช้เศษส่วนความคลาดเคลื่อน ( ถ้าต้องการคำอธิบายเพิ่มให้ดูการหา F = ma ) จาก v ∝ d / t เศษส่วนความคลาดเคลื่อนของการวัด หาจาก
\(\sqrt{ \left(\dfrac{2.0}{75.0}\right)^2 + \left(\dfrac{0.10}{2.15} \right)^2} = 5.4%\)
แปลงเป็นค่าคลาดเคลื่อนได้ (0.054)(349 m/s) =19 m/s| 83. | ให้เชือกที่แข็งแรงและสม่ำเสมอยาว L วางราบบนโต๊ะที่มีความยาว L/3 และมีสัมประสิทธิ์แรงเสียดทาน μs = 1/7 โดยทั้งสองด้านของโต๊ะจะมีเชือกยาว L/3 เลยออกมาจากโต๊ะเท่ากัน ให้เชือกพาดผ่านขอบโต๊ะที่โค้งและมีความลื่น และไร้แรงเสียดทาน สมมุติว่า เราดึงปลายเชือกด้านหนึ่งที่ห้อยอยู่เป็นระยะ x แล้วปล่อยไว้นิ่งๆ โดยปลายเชือกทั้งสองด้านยังไม่แตะพื้น แล้วค่า x มากสุดที่เชือกจะไม่หล่นลงมาเท่ากับข้อใด |
| A | L/42 |
| B | L/21 |
| C | L/14 |
| D | 2L/21 |
| E | 3L/14 |
ตอบ (A)
มีแค่เชือกส่วนที่อยู่บนโต๊ะเท่านั้นที่เกิดแรงเสียดทาน และมวลของเชือกบนโต๊ะเท่ากับเป็น M / 3 ดังนั้น แรงเสียดทานที่ต้องเอาชนะเท่ากับ
ผลต่างระหว่างแรงของเชือกสองด้านที่เลยออกมาจึงเท่ากับ
ดังนั้น เงื่อนไขในการลื่นหล่นลงมา คือ Δf > f หรือ x > L / 42
มีแค่เชือกส่วนที่อยู่บนโต๊ะเท่านั้นที่เกิดแรงเสียดทาน และมวลของเชือกบนโต๊ะเท่ากับเป็น M / 3 ดังนั้น แรงเสียดทานที่ต้องเอาชนะเท่ากับ
f = μmg = 1/7(mg/3)
ผลต่างระหว่างแรงของเชือกสองด้านที่เลยออกมาจึงเท่ากับ
ΔF = 2x (mg/L)
ดังนั้น เงื่อนไขในการลื่นหล่นลงมา คือ Δf > f หรือ x > L / 42
| 84. | คานสม่ำเสมอยาว L มวล M มีจุดหมุนอยู่ที่ระยะ x ห่างจากศูนย์กลางคาน ถ้าคานที่เดิมอยู่นิ่งถูกปล่อยลงมาจากตำแหน่งในแนวนอน แล้วคาบของการแกว่งจะน้อยสุดเมื่อ x เท่ากับข้อใด |
| A | \(\rm x = L/2\) |
| B | \(\rm x = L/2\sqrt3\) |
| C | \(\rm x = L/4\) |
| D | \(\rm x = L/4\sqrt3\) |
| E | \(\rm x = L/12\) |
ตอบ (B)
คานในที่นี้เสมือนเป็นลูกตุ้ม และมีคาบเป็นสัดส่วนกับ \(\rm \sqrt{I/Mgx}\) โดย \(\rm I = ML^2/12 + Mx^2\) โดยทฤษฎีบทแกนขนาน เราควรจะเลือก x ที่ทำให้ \(\rm (L^2/12 + x^2)/x\) ต่ำสุด เราสามารถหาโดยใช้แคลคูลัสหรือใช้กรณีการเท่ากันใน AM-GM inequality ซึ่งทั้งสองวิธีจะได้ \(\rm x = L/2\sqrt3\)
สำหรับ AM-GM inequality
ให้ \(\rm a = L^2/12x ,~ b = x\) จะได้ว่า
ซึ่งเป็นจุดที่ \(\dfrac{{{{\rm{L}}^2}}}{{12{\rm{x}}}}{\rm{ + }}\,\,{\rm{x}}\) มีค่าน้อยสุด
คานในที่นี้เสมือนเป็นลูกตุ้ม และมีคาบเป็นสัดส่วนกับ \(\rm \sqrt{I/Mgx}\) โดย \(\rm I = ML^2/12 + Mx^2\) โดยทฤษฎีบทแกนขนาน เราควรจะเลือก x ที่ทำให้ \(\rm (L^2/12 + x^2)/x\) ต่ำสุด เราสามารถหาโดยใช้แคลคูลัสหรือใช้กรณีการเท่ากันใน AM-GM inequality ซึ่งทั้งสองวิธีจะได้ \(\rm x = L/2\sqrt3\)
สำหรับ AM-GM inequality
ให้ \(\rm a = L^2/12x ,~ b = x\) จะได้ว่า
\(\begin{align*} \frac{{(a + b)}}{2}\,\, &\ge \,\,\sqrt {{\rm{ab}}} \\ \frac{{{{\rm{L}}^2}}}{{12{\rm{x}}}}\,\, + \,\,{\rm{x}}\,\, &\ge \,\,2\sqrt {\frac{{{{\rm{L}}^2}}}{{12}}} \end{align*}\)
และทั้งสองข้างจะเท่ากัน เมื่อ a = b หรือ \({\rm{x}} = \sqrt {\dfrac{{{{\rm{L}}^2}}}{{12}}} \)ซึ่งเป็นจุดที่ \(\dfrac{{{{\rm{L}}^2}}}{{12{\rm{x}}}}{\rm{ + }}\,\,{\rm{x}}\) มีค่าน้อยสุด
| 85. | ให้มวล m สองอัน เชื่อมติดกันบนรอก ดังรูป
 |
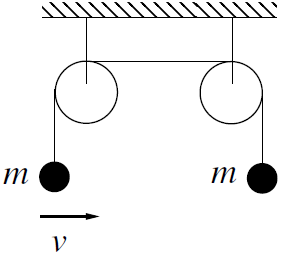| A | ยังคงอยู่นิ่ง |
| B | จะสั่นในแนวตั้ง และมีการเคลื่อนที่สุทธิในทิศขึ้น |
| C | จะสั่นในแนวตั้ง และมีการเคลื่อนที่สุทธิในทิศลง |
| D | จะสั่นในแนวตั้ง โดยไม่มีการเคลื่อนที่สุทธิ |
| E | จะสั่นในแนวนอน โดยไม่มีการเคลื่อนที่สุทธิ |
ตอบ (B)
มวลที่อยู่ด้านขวาจะสั่นเพราะแรงตึงในเส้นเชือกเกิดการสั่น แต่มันจะไม่สั่นในแนวนอน เพราะ ไม่ทอร์กในแนวนั้น สมมุติว่าการสั่นเกิดขึ้นในแนวนอนโดยไม่มีแรงลัพธ์ แล้วค่าเฉลี่ยแรงตึงในแกน y ที่กระทำบนมวลทางด้านซ้ายจะเท่ากับ mg แต่ในทางตรงข้ามแรงตึงบนแกน x จะไม่เท่ากับศูนย์ ทำให้ค่าเฉลี่ยของแรงตึงมีค่ามากกว่า mg ดังนั้น มวลทางขวาจึงสั่นและเคลื่อนที่ขึ้นไปข้างบน
มวลที่อยู่ด้านขวาจะสั่นเพราะแรงตึงในเส้นเชือกเกิดการสั่น แต่มันจะไม่สั่นในแนวนอน เพราะ ไม่ทอร์กในแนวนั้น สมมุติว่าการสั่นเกิดขึ้นในแนวนอนโดยไม่มีแรงลัพธ์ แล้วค่าเฉลี่ยแรงตึงในแกน y ที่กระทำบนมวลทางด้านซ้ายจะเท่ากับ mg แต่ในทางตรงข้ามแรงตึงบนแกน x จะไม่เท่ากับศูนย์ ทำให้ค่าเฉลี่ยของแรงตึงมีค่ามากกว่า mg ดังนั้น มวลทางขวาจึงสั่นและเคลื่อนที่ขึ้นไปข้างบน
| 86. | ให้มวล m1 และ m2 เชื่อมกันด้วยคานแข็งเบายาว L วางราบบนโต๊ะลื่น ที่เวลา t = 0 มวลก้อนแรกได้รับแรงดลในทิศตั้งฉากกับคาน จนมีอัตราเร็ว v ในขณะนั้นมวลก้อนที่สองยังคงอยู่นิ่ง แล้วมวลก้อนที่สองจะหยุดนิ่งอีกครั้งตอน t เท่ากับข้อใด |
| A | \(\rm t = 2πL / v\) |
| B | \(\rm t = π ( m_1 + m_2 )L / m_2v \) |
| C | \(\rm t = 2πm_2L / ( m_1 + m_2 )v\) |
| D | \(\rm t = 2πm_1m_2L / ( m_1 + m_2 )^2v\) |
| E | \(\rm t = 2πm_1L / ( m_1 + m_2 )v \) |
ตอบ (A)
ข้อนี้มีสองการเคลื่อนที่ซ้อนทับกันอยู่ มวลทั้งสองเคลื่อนที่ด้วยอัตราเร็ว \(\rm m_1v / (m_1 + m_2)\) และการเคลื่อนที่เป็นวงกลมรอบจุดศูนย์กลางมวล โดยอัตราเร็วของมวลก้อนแรกเท่ากับ \(\rm m_2v / (m_1 + m_2)\) แล้วมวลก้อนสองหยุดนิ่งอีกครั้งหลังวนเป็นวงกลมครบหนึ่งรอบ รัศมีวงกลมของมวลก้อนแรก (เมื่อมองจากจุดศูนย์กลางมวล) เท่ากับ \(\rm Lm_2 / (m_1 + m_2)\) จะมีคาบ \(\rm t = 2πL / v\) หรือคิดจากรัศมีและมีมวลของก้อนที่สองก็ได้เช่นกัน
ข้อนี้มีสองการเคลื่อนที่ซ้อนทับกันอยู่ มวลทั้งสองเคลื่อนที่ด้วยอัตราเร็ว \(\rm m_1v / (m_1 + m_2)\) และการเคลื่อนที่เป็นวงกลมรอบจุดศูนย์กลางมวล โดยอัตราเร็วของมวลก้อนแรกเท่ากับ \(\rm m_2v / (m_1 + m_2)\) แล้วมวลก้อนสองหยุดนิ่งอีกครั้งหลังวนเป็นวงกลมครบหนึ่งรอบ รัศมีวงกลมของมวลก้อนแรก (เมื่อมองจากจุดศูนย์กลางมวล) เท่ากับ \(\rm Lm_2 / (m_1 + m_2)\) จะมีคาบ \(\rm t = 2πL / v\) หรือคิดจากรัศมีและมีมวลของก้อนที่สองก็ได้เช่นกัน
| 87. | มวล m ถูกวางที่จุดศูนย์กลางของครึ่งทรงกลมบางที่มีรัศมี R และมีมวลหนาแน่น σ โดย σ มีหน่วย kg/m2
 |
| A | \(\rm (1/3) (πGmσ)\) |
| B | \(\rm (2/3) (πGmσ) \) |
| C | \(\rm (1/\sqrt2) (πGmσ) \) |
| D | \(\rm (3/4) (πGmσ)\) |
| E | \(\rm πGmσ\) |
ตอบ (E)
เราจะใช้กฏข้อที่สามของนิวตันในการหาแรง โดยแรงจากทรงกลมต่อ m จะเท่ากับแรงจาก m ที่กระทำต่อทรงกลม พิจารณาส่วนเล็กๆ ของทรงกลม เนื่องจากความดันจากแรงที่กระทำบนพื้นที่เล็กๆ เท่ากับ \(\rm P = Gmσ / R^2\) ซึ่งเท่ากันทุกส่วนของทรงกลม เราจึงสามารถพิจารณาเสมือนทรงกลมบรรจุแก๊สที่มีความดัน P เนื่องจากครึ่งวงกลมไม่สามารถขยับเองได้ แรงลัพธ์บนทรงกลมจึงเท่ากับ \(\rm πR2P\) ( คิดจากprojected area ) ดังนั้นแรงที่กระทำบนมวล m เท่ากับ \(\rm π (Gmσ)\)
เราจะใช้กฏข้อที่สามของนิวตันในการหาแรง โดยแรงจากทรงกลมต่อ m จะเท่ากับแรงจาก m ที่กระทำต่อทรงกลม พิจารณาส่วนเล็กๆ ของทรงกลม เนื่องจากความดันจากแรงที่กระทำบนพื้นที่เล็กๆ เท่ากับ \(\rm P = Gmσ / R^2\) ซึ่งเท่ากันทุกส่วนของทรงกลม เราจึงสามารถพิจารณาเสมือนทรงกลมบรรจุแก๊สที่มีความดัน P เนื่องจากครึ่งวงกลมไม่สามารถขยับเองได้ แรงลัพธ์บนทรงกลมจึงเท่ากับ \(\rm πR2P\) ( คิดจากprojected area ) ดังนั้นแรงที่กระทำบนมวล m เท่ากับ \(\rm π (Gmσ)\)
| 88. | ไม้บรรทัด และวัดความยาวท่อได้ 1.00 ± 0.01 m โดยใช้ไม้เมตร หากต้องการให้ผลลัพธ์แม่นยำขึ้น เราสามารถทำได้หลายวิธี ดังนี้
วิธีที่ 1 : เปลี่ยนจากไม้บรรทัด เป็น คาลิปเปอร์ ที่มีความคลาดเคลื่อน 0.01 cm
วิธีที่ 2 : เปลี่ยนจากไม้เมตร เป็น ตลับเมตร ที่มีความคลาดเคลื่อน 0.001 m
วิธีที่ 3 : วัดใหม่ โดยแยกเป็นสิบครั้งแล้วหาค่าเฉลี่ยของผลลัพธ์
ข้อใดเปรียบเทียบความคลาดเคลื่อนของแต่ละวิธีได้ถูกต้องที่สุด |
| A | วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด ในขณะที่วิธีที่ 1 และ 2 มีความคลาดเคลื่อนเท่ากัน |
| B | วิธีที่ 3 มีความคลาดเคลื่อนสูงที่สุด ในขณะที่วิธีที่ 1 และ 2 มีความคลาดเคลื่อนเท่ากัน |
| C | วิธีที่ 1 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 2 มีความคลาดเคลื่อนต่ำที่สุด |
| D | วิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด |
| E | วิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด |
ตอบ (D)
คำตอบข้อนี้เราจะใช้เศษส่วนความคลาดเคลื่อน ( ถ้าต้องการคำอธิบายเพิ่มให้ดูการหา F = ma ) ตามกฎที่อธิบายไว้ที่ เศษส่วนความคลาดเคลื่อนของค่าเฉลี่ยของการทดลอง N ที่เป็นอิสระ คือ จะถูกลดลงโดย \(\rm 1 / \sqrt N\) พื้นที่ผิวหาจากรัศมีคูณความยาว ดังนั้น เศษส่วนความคลาดเคลื่อนที่จะถูกเพิ่มเข้าไปในแต่ละวิธีจะได้ดังนี้
ดังนั้น วิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด
คำตอบข้อนี้เราจะใช้เศษส่วนความคลาดเคลื่อน ( ถ้าต้องการคำอธิบายเพิ่มให้ดูการหา F = ma ) ตามกฎที่อธิบายไว้ที่ เศษส่วนความคลาดเคลื่อนของค่าเฉลี่ยของการทดลอง N ที่เป็นอิสระ คือ จะถูกลดลงโดย \(\rm 1 / \sqrt N\) พื้นที่ผิวหาจากรัศมีคูณความยาว ดังนั้น เศษส่วนความคลาดเคลื่อนที่จะถูกเพิ่มเข้าไปในแต่ละวิธีจะได้ดังนี้
วิธีที่ 1: \(\sqrt{ (1\%)^2 + (1\%)^2 }≈ 1.4\% \)
วิธีที่ 2: \(\sqrt{(0.1\%)^2 +(10\%)^2} ≈ 10\% \)
วิธีที่ 3: \(\sqrt{(1\%)^2 +(10\%)^2}/10≈ 3.3\% \)
ดังนั้น วิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด และวิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด
| 89. | กราฟข้อใด แสดงอัตราเร็วกับเวลาของวัตถุที่ถูกขว้างขึ้นไปโดยมีแรงต้านอากาศ ได้ดีที่สุด |
| A |  |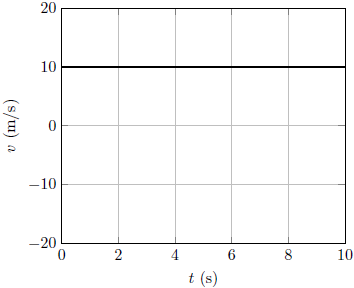
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (D)
ความเร็วสุดท้ายควรเป็นค่าคงที่และมีค่าเป็นลบ ทำให้ตัดตัวเลือกออกไปหมด จนเหลือแค่ข้อ (D) สังเกตว่า ขนาดของความเร่งควรจะลดลงด้วยเช่นกัน
ความเร็วสุดท้ายควรเป็นค่าคงที่และมีค่าเป็นลบ ทำให้ตัดตัวเลือกออกไปหมด จนเหลือแค่ข้อ (D) สังเกตว่า ขนาดของความเร่งควรจะลดลงด้วยเช่นกัน
| 90. | มวล 3.0 kg เคลื่อนที่ไปทางขวาด้วยอัตราเร็ว 30 m/s พุ่งชนกับมวล 2.0 kg ที่เคลื่อนที่ไปทางซ้ายด้วยอัตราเร็ว 20 m/s หลังการชน จุดศูนย์กลางมวลของระบบจะเคลื่อนที่ไปด้วยอัตราเร็วเท่าใด |
| A | 5 m/s |
| B | 10 m/s |
| C | 20 m/s |
| D | 24 m/s |
| E | 26 m/s |
ตอบ (B)
ความเร็วที่จุดศูนย์กลางของมวลจะถูกอนุรักษ์ด้วยกฎการอนุรักษ์โมเมนตัม ดังนั้น เราจึงไม่จำเป็นต้องคำนวณหาการชนที่เกิดขึ้น โดยก่อนชน โมเมนตัมสุทธิจะเท่ากับ 50 kg m/s และมวลสุทธิเท่ากับ 5 kg ดังนั้น อัตราเร็วที่จุดศูนย์กลางของมวลเท่ากับ 10 m/s
ความเร็วที่จุดศูนย์กลางของมวลจะถูกอนุรักษ์ด้วยกฎการอนุรักษ์โมเมนตัม ดังนั้น เราจึงไม่จำเป็นต้องคำนวณหาการชนที่เกิดขึ้น โดยก่อนชน โมเมนตัมสุทธิจะเท่ากับ 50 kg m/s และมวลสุทธิเท่ากับ 5 kg ดังนั้น อัตราเร็วที่จุดศูนย์กลางของมวลเท่ากับ 10 m/s
| 91. | ให้บอลลูกแรกเคลื่อนที่ไปตามแกน x แล้วชนกับบอลลูกที่สองที่เดิมอยู่นิ่ง และมีมวลเท่ากัน แล้วหลังเกิดการชนข้อใดกล่าวผิด |
| A | โมเมนตัมสุดท้ายสุทธิตามแกน x จะเท่ากับโมเมนตัมเริ่มต้นของบอลลูกแรก |
| B | พลังงานจลน์สุทธิหลังเกิดการชน จะเท่ากับพลังงานจลน์เริ่มต้นของบอลลูกแรก |
| C | โมเมนตัมสุดท้ายของลูกบอลทั้งสองตามแกน y ที่ถูกเพิ่มเข้ามาจะเป็นศูนย์ |
| D | อัตราเร็วสุดท้ายของจุดศูนย์กลางมวลของลูกบอลทั้งสอง มีค่าเท่ากับครึ่งหนึ่งของอัตราเร็วต้นของบอลลูกแรก |
| E | ลูกบอลทั้งสองจะไม่สามารถหยุดนิ่ง หลังเกิดการชนกันได้ |
ตอบ (B)
ข้อ (A), (C) และ (E) เป็นจริง ตามกฎการอนุรักษ์โมเมนตัม ข้อ (D) เป็นจริง ตามผลลัพธ์ของ ptot = mtot vCM ส่วนข้อ (B) เป็นเท็จ เพราะการชนนั้นอาจ ไม่ยืดหยุ่นบางส่วน หรือ ไม่ยืดหยุ่นสมบูรณ์
ข้อ (A), (C) และ (E) เป็นจริง ตามกฎการอนุรักษ์โมเมนตัม ข้อ (D) เป็นจริง ตามผลลัพธ์ของ ptot = mtot vCM ส่วนข้อ (B) เป็นเท็จ เพราะการชนนั้นอาจ ไม่ยืดหยุ่นบางส่วน หรือ ไม่ยืดหยุ่นสมบูรณ์
| 92. | ให้ดาวเทียมอยู่ในวงโคจรวงรีรอบโลก และเครื่องยนต์สามารถให้แรงดลค่าหนึ่งได้เพียงครั้งเดียว เพื่อให้ดาวเทียมได้พลังงานมากที่สุด แรงดลควรเป็นไปตามข้อใด
 |
| A | ควรมีทิศตามความเร็วของดาวเทียม และใช้ขณะอยู่จุดใกล้สุด |
| B | ควรมีทิศตามความเร็วของดาวเทียม และใช้ขณะอยู่จุดไกลสุด |
| C | ควรมีทิศพุ่งเข้าหาโลก และใช้ขณะอยู่จุดใกล้สุด |
| D | ควรมีทิศพุ่งเข้าหาโลก และใช้ขณะอยู่จุดไกลสุด |
| E | ควรมีทิศพุ่งออกจากโลก และใช้ขณะอยู่จุดไกลสุด |
ตอบ (A)
ผลต่างความเร็ว Δv มีขนาดคงที่ เพราะพลังงานจลน์แปรผันตาม v2 ซึ่งผลต่างที่มากที่สุดจะเกิดขึ้น เมื่อแรงดลขนานกับความเร็ว และความเร็วมากสุดจะขึ้นเกิดที่ จุดใกล้สุด
ผลต่างความเร็ว Δv มีขนาดคงที่ เพราะพลังงานจลน์แปรผันตาม v2 ซึ่งผลต่างที่มากที่สุดจะเกิดขึ้น เมื่อแรงดลขนานกับความเร็ว และความเร็วมากสุดจะขึ้นเกิดที่ จุดใกล้สุด
| 93. | มวลสองอันถูกแขวนอยู่บนรอกด้วยเชือกเบา และรอกนั้นตั้งอยู่บนพื้นเอียง ดังรูป ถ้าทุกพื้นผิวไม่มีแรงเสียดทาน และมวลทั้งสองที่เดิมอยู่นิ่งถูกปล่อยออก แล้วพื้นเอียงจะเป็นไปตามข้อใด
 |
| A | จะมีความเร่งไปทางซ้าย ถ้า m1 < m2 |
| B | จะมีความเร่งไปทางขวา ถ้า m1 < m2 |
| C | จะมีความเร่งไปทางซ้าย โดยไม่สนมวลที่ถูกแขวนไว้ |
| D | จะมีความเร่งไปทางขวา โดยไม่สนมวลที่ถูกแขวนไว้ |
| E | พื้นเอียงไม่เคลื่อนที่ไปไหน |
ตอบ (E)
พื้นเอียงจะไม่เคลื่อนที่ไปไหน ซึ่งอธิบายได้หลายแบบ แต่เหตุผลง่ายๆ คือ ระบบนี้ไม่มีโมนตัมที่กระทำในแนวนอน
มีเพียงแค่มวลที่เลื่อนขึ้นเลื่อนลง (ในเชือกไม่มีโมเมนตัมในแนวนอน เพราะเป็นเชือกเบา)
พื้นเอียงจะไม่เคลื่อนที่ไปไหน ซึ่งอธิบายได้หลายแบบ แต่เหตุผลง่ายๆ คือ ระบบนี้ไม่มีโมนตัมที่กระทำในแนวนอน
มีเพียงแค่มวลที่เลื่อนขึ้นเลื่อนลง (ในเชือกไม่มีโมเมนตัมในแนวนอน เพราะเป็นเชือกเบา)
| 94. | ลังใส่ของมวล m = 15 kg ถูกดันขึ้นไปบนทางลาดที่ความยาว 5.00 m และทำมุม 20° กับแนวราบ ด้วยแรง F = 1.00 ×103 N ในทิศที่ขนานกับทางลาด และแรงเสียดทานที่ต้านการเคลื่อนที่เท่ากับ f = 4.00 × 102 N ถ้าเดิมลังอยู่นิ่ง แล้วอัตราเร็วของลัง ณ จุดบนสุดของทางลาดเท่ากับข้อใด |
| A | 4.24 m/s |
| B | 5.11 m/s |
| C | 7.22 m/s |
| D | 8.26 m/s |
| E | 9.33 m/s |
ตอบ (A)
แรงโน้มถ่วงที่ขนานไปกับทางลาดและมีค่าเท่ากับ -mg sinθ = -393 N ทำให้ได้แรงสุทธิเท่ากับ 207 N
สำหรับวัตถุที่มีมวล 115 kg ความเร่งจะเท่ากับ 1.8 m/s2 และความเร็วจะเท่ากับ \(\rm\sqrt{2ad}= 4.24 ~m/s\)
แรงโน้มถ่วงที่ขนานไปกับทางลาดและมีค่าเท่ากับ -mg sinθ = -393 N ทำให้ได้แรงสุทธิเท่ากับ 207 N
สำหรับวัตถุที่มีมวล 115 kg ความเร่งจะเท่ากับ 1.8 m/s2 และความเร็วจะเท่ากับ \(\rm\sqrt{2ad}= 4.24 ~m/s\)
| 95. | ให้รถมีความเร่งมากสุดเท่ากับ a0 และความเร่งต่ำสุดเท่ากับ – a0 แล้วเวลาสั้นสุดที่ทำให้รถที่เดิมอยู่นิ่งวิ่งไปหยุดที่ระยะทาง d เท่ากับข้อใด |
| A | \(\rm \sqrt{d/2a_0}\) |
| B | \(\rm \sqrt{d/a_0}\) |
| C | \(\rm \sqrt{2d/a_0}\) |
| D | \(\rm \sqrt{3d/2a_0}\) |
| E | \(2\rm \sqrt{d/a_0}\) |
ตอบ (E)
คำตอบข้อนี้จะใช้วิธีเร่งสูงสุดในครึ่งแรก และเบรกสูงสุดในครึ่งหลัง
เนื่องจากครึ่งแรกและครึ่งหลังใช้เวลา \(\rm \sqrt{d/a_0}\) เท่ากัน ดังนั้น เวลาทั้งหมดเท่ากับ \(2\rm \sqrt{d/a_0}\)
คำตอบข้อนี้จะใช้วิธีเร่งสูงสุดในครึ่งแรก และเบรกสูงสุดในครึ่งหลัง
เนื่องจากครึ่งแรกและครึ่งหลังใช้เวลา \(\rm \sqrt{d/a_0}\) เท่ากัน ดังนั้น เวลาทั้งหมดเท่ากับ \(2\rm \sqrt{d/a_0}\)
| 96. | แผ่นกลมรัศมี r กลิ้งอย่างสม่ำเสมอโดยไม่มีการไถล วนอยู่ภายในห่วงที่ถูกตรึงไว้ และห่วงมีรัศมี R ถ้าคาบการกลิ้ง ของแผ่นกลมเท่ากับ T แล้วอัตราเร็วขณะหนึ่งของจุดที่อยู่ตรงข้ามกับจุดที่แผ่นกลมสัมผัสกับห่วงเท่ากับข้อใด  |
| A | \(\rm 2π(R + r)/T\) |
| B | \(\rm 2π(R + 2r)/T\) |
| C | \(\rm 4π(R – 2r)/T\) |
| D | \(\rm 4π(R– r)/T\) |
| E | \(\rm 4π(R + r)/T\) |
ตอบ (D)
จุดศูนย์กลางของมวลของแผ่นกลมจะอยู่ห่างจากจุดศูนย์กลางห่วง \(\rm R – r\) และอัตราเร็วที่จุดศูนย์กลางของแผ่นกลมจะเท่ากับ \(\rm ω (R – r) = (2π / T) (R – r)\) โดยอัตราเร็วของจุดที่อยู่ตรงข้ามกับจุดที่แผ่นกลมสัมผัสกับห่วงจะเป็นสองเท่าของอัตราเร็วที่จุดศูนย์กลางของแผ่นกลม โดยที่แผ่นกลมหมุนรอบจุดที่สัมผัสนั้นอย่างรวดเร็ว
ดังนั้น \(\rm v = 4π (R – r) / T\)
จุดศูนย์กลางของมวลของแผ่นกลมจะอยู่ห่างจากจุดศูนย์กลางห่วง \(\rm R – r\) และอัตราเร็วที่จุดศูนย์กลางของแผ่นกลมจะเท่ากับ \(\rm ω (R – r) = (2π / T) (R – r)\) โดยอัตราเร็วของจุดที่อยู่ตรงข้ามกับจุดที่แผ่นกลมสัมผัสกับห่วงจะเป็นสองเท่าของอัตราเร็วที่จุดศูนย์กลางของแผ่นกลม โดยที่แผ่นกลมหมุนรอบจุดที่สัมผัสนั้นอย่างรวดเร็ว
ดังนั้น \(\rm v = 4π (R – r) / T\)
| 97. | แท่งไม้สม่ำเสมอมวล m เดิมวางราบอยู่บนพื้น ปลายด้านหนึ่งมีเชือกผูกไว้ เมื่อดึงเชือกขึ้นในแนวตั้งด้วยแรงตึงคงที่ F แล้วจุดศูนย์กลางมวลของแท่งไม้จะเคลื่อนที่ขึ้นด้วยความเร่ง a < g แล้วแรงปกติ N ที่พื้นกระทำกับแท่งไม้ในอีกด้านที่ไม่ถูกยกขึ้น หลังจากที่แท่งไม้ด้านขวาถูกยกขึ้นเหนือพื้นดินเพียงนิดเดียว เท่ากับข้อใด |
| A | N = mg |
| B | mg > N > mg/2 |
| C | N = mg/2 |
| D | mg/2 > N > 0 |
| E | N = 0 |
ตอบ (B)
จากกฎข้อที่สองของนิวตัน จะได้การเคลื่อนที่ในแนวตั้งเท่ากับ
เมื่อเกิดทอร์กที่ปลายซ้ายของแท่งไม้ เราจะได้
แก้สองสมการจะได้ N
ซึ่งผลลัพธ์อยู่ในช่วงคำตอบของข้อ (B)
จากกฎข้อที่สองของนิวตัน จะได้การเคลื่อนที่ในแนวตั้งเท่ากับ
\(\rm F + N – m g = ma\)
เมื่อเกิดทอร์กที่ปลายซ้ายของแท่งไม้ เราจะได้
\(\tau = {\rm{FL}} - \dfrac{{{\rm{mgL}}}}{2}~,\rm I = \dfrac{1}{3}{\rm{m}}{{\rm{L}}^2}~,\alpha = \dfrac{a}{{{\rm{L/2}}}}\)
แก้สองสมการจะได้ N
\(\rm N = \dfrac{1}{3}ma+ \dfrac{1}{2}mg\)
ซึ่งผลลัพธ์อยู่ในช่วงคำตอบของข้อ (B)
| 98. | กราฟข้อใด แสดงความเร่งกับเวลาของวัตถุที่เคลื่อนที่ขึ้นไปโดยมีแรงต้านอากาศได้ดีที่สุด |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (E)
ความเร่งควรสิ้นสุดลงที่ศูนย์ ตามความเร็วปลายของวัตถุ และกราฟควรเริ่มต้นด้วยค่าที่น้อยกว่า -10 m/s2 เนื่องจากมีแรงต้านอากาศที่กระทำในทิศเดียวกับแรงโน้มถ่วง
ความเร่งควรสิ้นสุดลงที่ศูนย์ ตามความเร็วปลายของวัตถุ และกราฟควรเริ่มต้นด้วยค่าที่น้อยกว่า -10 m/s2 เนื่องจากมีแรงต้านอากาศที่กระทำในทิศเดียวกับแรงโน้มถ่วง
| 99. | ให้สปริงเบาในอุดมคติถูกตรึงปลายด้านหนึ่งไว้ ส่วนปลายอีกด้านติดมวลไว้ แล้วสปริงจะสั่นด้วยความถี่เชิงมุม ω ถ้าปลายสปริงถูกตรึงไว้ทั้งสองด้าน แล้วตัดแบ่งครึ่งเพื่อนำมวลไปติดไว้กึ่งกลางระหว่างสปริงทั้งสอง
 |
| A | \(ω/2\) |
| B | \(ω\) |
| C | \(\sqrt2ω\) |
| D | \(2ω\) |
| E | \(4ω\) |
ตอบ (D)
การแบ่งครึ่งสปริง จะทำให้ค่านิจสปริงเพิ่มขึ้นเป็นสองเท่า หมายความ ถ้าแรง F ยึดสปริงเดิมได้ระยะ x แล้วแรงนั้นจะยืดสปริงใหม่ได้ระยะ x´ = x / 2 ซึ่งเป็นไปตาม F = – kx โดย k´ = 2k จากโจทย์ระบบใหม่ประกอบด้วยสปริงสองอันที่มีค่านิจสปริงเป็นสองเท่าของสปริงเดิม แสดงว่าค่านิจสปริงของระบบจะเพิ่มขึ้นสี่เท่า เนื่องจากความถี่เชิงมุมเท่ากับรากที่สองของค่านิจสปริง ดังนั้น ความถี่เชิงมุมใหม่จะเพิ่มขึ้นเป็นสองเท่า
การแบ่งครึ่งสปริง จะทำให้ค่านิจสปริงเพิ่มขึ้นเป็นสองเท่า หมายความ ถ้าแรง F ยึดสปริงเดิมได้ระยะ x แล้วแรงนั้นจะยืดสปริงใหม่ได้ระยะ x´ = x / 2 ซึ่งเป็นไปตาม F = – kx โดย k´ = 2k จากโจทย์ระบบใหม่ประกอบด้วยสปริงสองอันที่มีค่านิจสปริงเป็นสองเท่าของสปริงเดิม แสดงว่าค่านิจสปริงของระบบจะเพิ่มขึ้นสี่เท่า เนื่องจากความถี่เชิงมุมเท่ากับรากที่สองของค่านิจสปริง ดังนั้น ความถี่เชิงมุมใหม่จะเพิ่มขึ้นเป็นสองเท่า
| 100. | (เกินหลักสูตรการสอบเข้า สอวน.) นักเรียนกลุ่มหนึ่งต้องการวัดความเร่งโน้มถ่วงด้วยลูกตุ้มอย่างง่าย พวกเขาใช้ลูกตุ้มที่มีความยาว L = 1.00 ± 0.05 m และวัดคาบของการแกว่งในหนึ่งครั้งได้ T = 2.00 ± 0.10 s ถ้าสมมุติว่า ทุกความคลาดเคลื่อนมีการกระจายตัวแบบ Gaussian (มีการแจกแจงแบบปกติ) แล้วความเร่งโน้มถ่วงที่คำนวณจากผลการทดลองนี้ ควรได้ค่าตามข้อใด |
| A | 9.87 ± 0.05 m/s2 |
| B | 9.87 ± 0.15 m/s2 |
| C | 9.9 ± 0.25 m/s2 |
| D | 9.9 ± 1.1 m/s2 |
| E | 9.9 ± 1.5 m/s2 |
ตอบ (D)
จากสูตรคาบของลูกตุ้มจัดรูปใหม่จะได้ \(\rm g = 4π^2L / T^2\) จากนั้นใช้ standard error propagation rules เพื่อหาค่าความคลาดเคลื่อน โดยใช้สูตรส่วนเบี่ยงเบนมาตรฐาน ดังนี้
(A) ถ้า x มีความคลาดเคลื่อนสัมพัทธ์เท่ากับ Δx / x แล้ว xn จะมีความคลาดเคลื่อนสัมพัทธ์เท่ากับ
ในกรณีนี้ ความคลาดเคลื่อนสัมพัทธ์ของ L เท่ากับ 5% ความคลาดเคลื่อนสัมพัทธ์ของ T เท่ากับ 5% และความคลาดเคลื่อนสัมพัทธ์ของ 1/T2 เท่ากับ 10% ความคลาดเคลื่อนสัมพัทธ์ของ g เท่ากับ \(\sqrt {{{0.1}^2} + {{0.05}^2}} \approx 11\%\) ซึ่งตรงกับข้อ (D)
จากสูตรคาบของลูกตุ้มจัดรูปใหม่จะได้ \(\rm g = 4π^2L / T^2\) จากนั้นใช้ standard error propagation rules เพื่อหาค่าความคลาดเคลื่อน โดยใช้สูตรส่วนเบี่ยงเบนมาตรฐาน ดังนี้
(A) ถ้า x มีความคลาดเคลื่อนสัมพัทธ์เท่ากับ Δx / x แล้ว xn จะมีความคลาดเคลื่อนสัมพัทธ์เท่ากับ
\(\rm Δ(x^n)/x^n = | n | ~Δx / x\)
(B) ถ้ามีสองตัวแปรที่เป็นอิสระต่อกันคูณกันอยู่ ความคลาดเคลื่อนสัมพัทธ์จะเท่ากับ
\(\rm \dfrac{{\Delta (xy)}}{{xy}} = \sqrt {{{\left( {\dfrac{{\Delta x}}{x}} \right)}^2} + {{\left( {\dfrac{{\Delta y}}{y}} \right)}^2}} \)
(C) ความคลาดเคลื่อนสัมพัทธ์จะไม่เปลี่ยนแปลงตามการปรับขนาดของตัวแปร ในกรณีนี้ ความคลาดเคลื่อนสัมพัทธ์ของ L เท่ากับ 5% ความคลาดเคลื่อนสัมพัทธ์ของ T เท่ากับ 5% และความคลาดเคลื่อนสัมพัทธ์ของ 1/T2 เท่ากับ 10% ความคลาดเคลื่อนสัมพัทธ์ของ g เท่ากับ \(\sqrt {{{0.1}^2} + {{0.05}^2}} \approx 11\%\) ซึ่งตรงกับข้อ (D)
| 101. | ให้เชือกเบามีเส้นผ่านศูนย์กลาง 2.54 cm (1 นิ้ว) ถูกแขวนในแนวราบ และอยู่ระหว่างต้นไม้สองต้นที่ห่างกัน 18.0 m แล้วนักไต่เชือกคนหนึ่งเดินไปที่จุดกึ่งกลางของเชือกและทำให้เกิดแรงตึง 7300 N จนเชือกหย่อนลงมาทำมุม 1.50° กับแนวราบ
 |
| A | 1.5 × 106 N/m2 |
| B | 2.0 × 108 N/m2 |
| C | 2.2 × 109 N/m2 |
| D | 2.4 × 1010 N/m2 |
| E | 4.2 × 1010 N/m2 |
ตอบ (E)
ความเครียดของเชือกเท่ากับ
ความเครียดของเชือกเท่ากับ
\(\dfrac{{\Delta L}}{L} = \dfrac{{{L_0}/\cos \theta - {L_0}}}{{{L_0}}} = \dfrac{1}{{\cos \theta }} - 1 \approx \dfrac{{{\theta ^2}}}{2}\)
จาก L0 เป็นความนาวเริ่มต้น จะได้มอดุลัสของยังเท่ากับ
\(Y = \dfrac{{7300{\rm{N}}}}{{\pi {{(0.0127m)}^2}}}{\left( {\dfrac{{{{(1.50\pi /180)}^2}}}{2}} \right)^{ - 1}} = 4.2 \times {10^{10}}~\rm N/m^2\)
| 102. | ให้มวลที่เหมือนกันสามชิ้นเชื่อมกับคานแข็งแบบเดียวกัน และมีจุดหมุนที่จุด A เมื่อมวลก้อนล่างสุดถูกดันในแนวนอนเบาๆ ไปทางซ้าย จะเกิดการแกว่งด้วยคาบ T1 เมื่อเปลี่ยนเป็นดันเบาๆ ที่ด้านหน้าแบบตั้งฉากกับกระดาษ จะได้คาบของการแกว่งเท่ากับ T2 แล้วอัตราส่วน T1/T2 เท่ากับข้อใด
 |
| A | \(1/2\) |
| B | \(1\) |
| C | \(\sqrt3\) |
| D | \(2\sqrt2\) |
| E | \(2\sqrt5\) |
ตอบ (C)
ทั้งสองกรณีนั้นเป็นการเคลื่อนที่แบบลูกตุ้ม ซึ่งมีคาบแปรผันกับ \(\rm \sqrt{I / Mgx }\) โดย x คือ ระยะจากจุดหมุนถึงจุดศูนย์กลางมวล และ I คือ โมเมนต์ความเฉื่อยรอบจุดหมุน เนื่องจาก x เท่ากันทั้งสองกรณี จะได้ว่า \(\rm T_1 / T_2 ∝ \sqrt{I_1/I_2}= \sqrt3\) ในกรณีที่สองนั้นเฉพาะมวลด้านล่างทำให้เกิดโมเมนต์ความเฉื่อย
ทั้งสองกรณีนั้นเป็นการเคลื่อนที่แบบลูกตุ้ม ซึ่งมีคาบแปรผันกับ \(\rm \sqrt{I / Mgx }\) โดย x คือ ระยะจากจุดหมุนถึงจุดศูนย์กลางมวล และ I คือ โมเมนต์ความเฉื่อยรอบจุดหมุน เนื่องจาก x เท่ากันทั้งสองกรณี จะได้ว่า \(\rm T_1 / T_2 ∝ \sqrt{I_1/I_2}= \sqrt3\) ในกรณีที่สองนั้นเฉพาะมวลด้านล่างทำให้เกิดโมเมนต์ความเฉื่อย
| 103. | ถ้ายานอวกาศที่อยู่ในวงโคจรวงกลมรอบโลก มีคาบในการโคจรยาวนาน เพราะได้รับผลกระทบจากแรงต้านอากาศ ซึ่งทำให้พลังงานสุทธิของยานอวกาศลง 1 J แล้วพลังงานจลน์ของดาวเทียมจะเป็นไปตามข้อใด |
| A | จะเพิ่มขึ้น 1 J |
| B | ยังคงเท่าเดิม |
| C | จะลดลง \(\frac{1}{2}\) J |
| D | จะลดลง 1 J |
| E | จะลดลง 2 J |
ตอบ (A)
แม้จะมีแรงต้าน (จากอากาศที่เบาบาง) ที่ทำให้ดาวเทียมเคลื่อนที่ช้าลงแต่ ดาวเทียมจะยังคงอยู่ในวงโคจรวงกลม
ในวงโคจร พลังงานสุทธิจะเท่ากับ E = K + V โดยv = - 2K หรือ E = - K ถ้าพลังงานสุทธิลดลง ΔE
แล้วพลังงานจลน์จะเพิ่มขึ้น ΔE
แม้จะมีแรงต้าน (จากอากาศที่เบาบาง) ที่ทำให้ดาวเทียมเคลื่อนที่ช้าลงแต่ ดาวเทียมจะยังคงอยู่ในวงโคจรวงกลม
ในวงโคจร พลังงานสุทธิจะเท่ากับ E = K + V โดยv = - 2K หรือ E = - K ถ้าพลังงานสุทธิลดลง ΔE
แล้วพลังงานจลน์จะเพิ่มขึ้น ΔE
| 104. | สถานีอวกาศทรงกระบอกสามารถสร้าง “แรงโน้มถ่วงเทียม” จากการหมุนด้วยความถี่เชิงมุม ω ให้พิจารณาในกรอบอ้างอิงที่สถานีอวกาศกำลังหมุน ถ้านักบินอวกาศเดิมยืนนิ่งอยู่บนพื้น และหันหน้าไปในทิศที่สถานีอวกาศกำลังหมุน แล้วเขากระโดดขึ้นในแนวตั้งเทียบกับพื้นด้วยอัตราเร็วต้นที่น้อยกว่าอัตราเร็วของพื้น แล้วหลังหลุดออกจากพื้น การเคลื่อนที่ของเขาเทียบกับพื้นของสถานีอวกาศจะเป็นไปตามข้อใด
 |
| A | จะมีส่วนประกอบของความเร่ง ที่มีทิศชี้ไปยังพื้นเสมอ และจะตกกลับมาที่จุดเดิมที่เคยกระโดดขึ้น |
| B | จะมีส่วนประกอบของความเร่ง ที่มีทิศชี้ไปยังพื้นเสมอ และจะตกกลับมาหน้าจุดเดิมที่เคยกระโดดขึ้น |
| C | จะมีส่วนประกอบของความเร่ง ที่มีทิศชี้ไปยังพื้นเสมอ และจะตกกลับมาหลังจุดเดิมที่เคยกระโดดขึ้น |
| D | จะมีส่วนประกอบของความเร่ง ที่มีทิศชี้ออกจากพื้นเสมอ และจะตกกลับมาหลังจุดเดิมที่เคยกระโดดขึ้น |
| E | จะมีความเร่งเป็นศูนย์เมื่อเทียบกับพื้น และเขาจะไม่กลับมาสู่พื้นอีก |
ตอบ (B)
ในการหาคำตอบ เราอาจจะวาดทิศทางของนักบินในกรอบอ้างอิงเดิมโดยใช้เส้นตรงอย่างง่าย
โดยนักบินจะถึงพื้น ตรง 'ด้านหน้า' ของจุดที่กระโดดเสมอ
ในการหาคำตอบ เราอาจจะวาดทิศทางของนักบินในกรอบอ้างอิงเดิมโดยใช้เส้นตรงอย่างง่าย
โดยนักบินจะถึงพื้น ตรง 'ด้านหน้า' ของจุดที่กระโดดเสมอ
| 105. | มีทรายร่วงลงมาเป็นสายจากเฮลิคอปเตอร์ที่เคลื่อนที่ไปทางขวาด้วยอัตราเร็วคงที่ v แล้วเปลี่ยนทิศกระทันหันไปทางซ้ายแล้วมีอัตราเร็วคงที่ v ถ้าไม่คิดถึงแรงต้านอากาศ แล้วรูปร่างของสายทรายที่มองเห็นจากพื้นดิน จะเป็นไปตามข้อใด ให้จุดสีดำ คือ เฮลิคอปเตอร์ |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (D)
ถ้าทรายร่วงลงมาจากเฮลิคอปเตอร์ที่บินด้วยความเร็วคงที่ แล้วทิศทางของสายทรายจะต้องร่วงลงมาเส้นตรงเหมือนเดิม ดังนั้น สายทรายที่เห็นควรเป็นเส้นตรงสองเส้นในแนวตั้ง (ไม่คิดแรงต้านอากาศ)
ถ้าทรายร่วงลงมาจากเฮลิคอปเตอร์ที่บินด้วยความเร็วคงที่ แล้วทิศทางของสายทรายจะต้องร่วงลงมาเส้นตรงเหมือนเดิม ดังนั้น สายทรายที่เห็นควรเป็นเส้นตรงสองเส้นในแนวตั้ง (ไม่คิดแรงต้านอากาศ)
| 106. | มวล m ติดกับคานบางยาว l ซึ่งสามารถหมุนเป็นวงกลมในแนวตั้งได้อย่างอิสระด้วยคาบ T แล้วผลต่างของแรงตึงบนคานขณะมวลแกว่งอยู่ที่ด้านบนของวงกลม กับที่ด้านล่างของวงกลมจะเท่ากับข้อใด |
| A | \(\text{6mg}^2\text{T}^2/l\) |
| B | \(4π\text{mg}^2\text{T}^2/l\) |
| C | \(6\rm mg\) |
| D | \(π^2\text{m}l / \rm T^2 \) |
| E | \(4π\text{m}l / \rm T^2\) |
ตอบ (C)
จะมีผลต่าง \(\rm 2mg\) จากแรงโน้มถ่วงที่ต้านแรงดึงขณะมวลอยู่ที่ด้านล่างและด้านบน และผลต่างของแรงสู่ศูนย์กลางจะเท่ากับ
จะมีผลต่าง \(\rm 2mg\) จากแรงโน้มถ่วงที่ต้านแรงดึงขณะมวลอยู่ที่ด้านล่างและด้านบน และผลต่างของแรงสู่ศูนย์กลางจะเท่ากับ
\(Δ(\text{mv}2/l) = 2Δ\text{K}/l = 2(2\text{mg}l)/l = 4\text{mg}\)
ดังนั้น ผลต่างทั้งหมด คือ \(\rm 6mg\)| 107. | ให้ปริมาณฝนที่ตกมีความหนาแน่น n หยดต่อลูกบาศก์เมตร หยดฝนมีรัศมี r0 กระทบพื้นด้วยอัตราเร็ว v0 ความดันบนพื้นดินที่เกิดจากฝนเท่ากับ P0 ถ้าปริมาณความหนาแน่นของฝนเพิ่มขึ้นเป็นสองเท่า แต่หยดฝนมีรัศมีลดลงครึ่งหนึ่ง อัตราเร็วลดลงครึ่งหนึ่ง แล้วความดันใหม่จะเท่ากับข้อใด |
| A | P0 |
| B | P0/2 |
| C | P0/4 |
| D | P0/8 |
| E | P0/16 |
ตอบ (E)
ฝนแต่ละหยดจะมีมวล 1/8 และมีอัตราเร็ว 1/2 ดังนั้น จะมีโมเมนตัมเท่ากับ 1/16 และอัตราการตกลงสู่พื้นของทุกหยดจะเท่ากันหมด จากโจทย์ให้ความหนาแน่นเพิ่มขึ้นเป็นสองเท่า แต่ความเร็วลดลงครึ่งหนึ่ง แล้วความดันใหม่จะเท่ากับ P0/16
ฝนแต่ละหยดจะมีมวล 1/8 และมีอัตราเร็ว 1/2 ดังนั้น จะมีโมเมนตัมเท่ากับ 1/16 และอัตราการตกลงสู่พื้นของทุกหยดจะเท่ากันหมด จากโจทย์ให้ความหนาแน่นเพิ่มขึ้นเป็นสองเท่า แต่ความเร็วลดลงครึ่งหนึ่ง แล้วความดันใหม่จะเท่ากับ P0/16
| 108. | เมื่อยืดสปริงให้ยาวเป็นสองเท่าของความยาวตามปกติ จะมีพลังงานศักย์ U0 ถ้าตัดสปริงครึ่งหนึ่ง แล้วนำแต่ละส่วนมายืดให้ยาวเป็นสองเท่าของความยาวตามปกติ แล้วพลังงานศักย์สุทธิของสปริงทั้งสองเท่ากับข้อใด |
| A | 4U0 |
| B | 2U0 |
| C | U0 |
| D | U0/2 |
| E | U0/4 |
ตอบ (C)
เราสามารถคำนวณโดยตรงจากสูตร U = kx2/2 โดยสปริงที่ถูกตัดออกมาจะมีค่านิจสปริงเพิ่มขึ้นเป็นสองเท่า หรืออีกวิธีหนึ่งคือ คิดจากพลังงาน ซึ่งทั้งหมดจะถูกเก็บไว้ใน microscopically และใน microscopically แต่ละอันจะมีโมเลกุลเท่าเดิมไม่ว่าสปริงจะเต็มอันหรือเหลือแค่ครึ่งเดียว ดังนั้น แม้ว่าสปริงจะถูกตัดออกไปค่าที่ได้ก็จะต้องเท่ากัน
เราสามารถคำนวณโดยตรงจากสูตร U = kx2/2 โดยสปริงที่ถูกตัดออกมาจะมีค่านิจสปริงเพิ่มขึ้นเป็นสองเท่า หรืออีกวิธีหนึ่งคือ คิดจากพลังงาน ซึ่งทั้งหมดจะถูกเก็บไว้ใน microscopically และใน microscopically แต่ละอันจะมีโมเลกุลเท่าเดิมไม่ว่าสปริงจะเต็มอันหรือเหลือแค่ครึ่งเดียว ดังนั้น แม้ว่าสปริงจะถูกตัดออกไปค่าที่ได้ก็จะต้องเท่ากัน
| 109. | ลูกปิงปอง (ทรงกลมกลวง) มวล m อยู่บนพื้นและมีความเร็วต้น v0 มีอัตราเร็วเชิงมุมเป็นศูนย์ที่เวลา t = 0 สัมประสิทธิ์แรงเสียดทานระหว่างลูกปิงปองกับพื้นเป็น μs = μk = μ แล้วเวลาที่ลูกปิงปองจะเริ่มกลิ้งโดยไม่ลื่นไถลเท่ากับข้อใด
 |
| A | t = (2/5)v0/μg |
| B | t = (2/3)v0/μg |
| C | t = v0/μg |
| D | t = (5/3)v0/μg |
| E | t = (3/2)v0/μg |
ตอบ (A)
จากแรงเสียดทานเท่ากับ μmg ดังนั้น ความเร็วจะลดลง เป็น \(\rm \dot{v} = – μg\) ส่วนทอร์กที่กระทำที่จุดศูนย์กลางมวลจะเท่ากับ \(\rm μmgR\) โดย \(\rm R\) คือรัศมี ดังนั้น ความเร็วเชิงมุมจะเพิ่มขึ้น เป็น \(\rm\dot{ω} = (3/2)μg/R\) การหมุนโดยไม่ไถลจะเกิดขึ้นเมื่อ \(\rm v = Rω\) ดังนั้น \(\rm t = (2/5)v_0/μg\)
จากแรงเสียดทานเท่ากับ μmg ดังนั้น ความเร็วจะลดลง เป็น \(\rm \dot{v} = – μg\) ส่วนทอร์กที่กระทำที่จุดศูนย์กลางมวลจะเท่ากับ \(\rm μmgR\) โดย \(\rm R\) คือรัศมี ดังนั้น ความเร็วเชิงมุมจะเพิ่มขึ้น เป็น \(\rm\dot{ω} = (3/2)μg/R\) การหมุนโดยไม่ไถลจะเกิดขึ้นเมื่อ \(\rm v = Rω\) ดังนั้น \(\rm t = (2/5)v_0/μg\)
| 110. | เรือทรงสี่เหลี่ยมมุมฉากมีรูรั่วเล็กๆ อยู่ที่ใต้ท้องเรือ ทำให้มีน้ำไหลเข้ามา และเรือก็ค่อยๆจมลงในน้ำ แล้วกราฟข้อใดแสดงอัตราการไหลของน้ำที่ไหลเข้ามาในเรือเทียบกับเวลา (leak rate) ได้ดีที่สุด สมมุติให้ขณะจมลง เรือยังคงอยู่ในแนวราบ
 |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (A)
จากหลักของอาร์คิมีดีส ผลต่างของระดับน้ำด้านในและด้านนอนจะต้องเท่าเดิมเสมอ ดังนั้น แรงดันที่น้ำจะเข้ามาตามรูรั่วจะต้องคงที่ ตามหลักของแบร์นูลลี ดังนั้น อัตราการไหลของน้ำที่ไหลเข้ามาจะต้องคงที่
จากหลักของอาร์คิมีดีส ผลต่างของระดับน้ำด้านในและด้านนอนจะต้องเท่าเดิมเสมอ ดังนั้น แรงดันที่น้ำจะเข้ามาตามรูรั่วจะต้องคงที่ ตามหลักของแบร์นูลลี ดังนั้น อัตราการไหลของน้ำที่ไหลเข้ามาจะต้องคงที่
| 111. | ให้สัมประสิทธิ์แรงเสียดทานจลน์สถิตระหว่างลูกบอลและทางลาดเท่ากับ μs = μk = μ ถ้าลูกบอลที่เดิมอยู่นิ่ง ถูกปล่อยลงมาจากด้านบนของทางลาด แล้วกราฟข้อใดแสดงความเร่งเชิงมุมของลูกบอลที่จุดศูนย์กลางมวล เทียบกับขนาดมุมของทางลาดได้ดีที่สุด |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (C)
ข้อนี้อาจหาคำตอบโดยใช้วิธี limiting cases สังเกตว่า
ถ้าทางลาดนั้นราบไปกับพื้น ความเร่งเชิงมุมของลูกบอลก็จะเท่ากับ ศูนย์ และถ้าทางลาดนั้นตั้งฉากกับพื้น ลูกบอลก็จะไม่หมุนและมีความเร่งเชิงมุมเป็นศูนย์เช่นกัน หรือใช้วิธีหาความเร่งเชิงมุมของลูกบอล สำหรับกรณีที่ลูกบอลกลิ้งโดยไม่ไถล ความเร่งจะเท่ากับ
ดังนั้น กราฟจะมีส่วนที่เพิ่มขึ้นและลดลงเป็นโค้งเว้า
และมียอดแหลม ณ จุดที่เกิดการไถล ซึ่งตรงกับข้อ (C)
ข้อนี้อาจหาคำตอบโดยใช้วิธี limiting cases สังเกตว่า
ถ้าทางลาดนั้นราบไปกับพื้น ความเร่งเชิงมุมของลูกบอลก็จะเท่ากับ ศูนย์ และถ้าทางลาดนั้นตั้งฉากกับพื้น ลูกบอลก็จะไม่หมุนและมีความเร่งเชิงมุมเป็นศูนย์เช่นกัน หรือใช้วิธีหาความเร่งเชิงมุมของลูกบอล สำหรับกรณีที่ลูกบอลกลิ้งโดยไม่ไถล ความเร่งจะเท่ากับ
g sinθ / (1 + I / MR2) ∝ sinθ
เมื่อมุมสูงมากพอก็จะเกิดการไถล โดยความเร่งเชิงมุมจะแปรผัน ตามแรงเสียดทานจลน์ ซึ่งเป็นสัดส่วนกับ cosθ ดังนั้น กราฟจะมีส่วนที่เพิ่มขึ้นและลดลงเป็นโค้งเว้า
และมียอดแหลม ณ จุดที่เกิดการไถล ซึ่งตรงกับข้อ (C)
| 112. | ให้มวลติดที่ปลายด้านหนึ่งของคานแข็ง และอีกด้านของคานติดกับเพลาลื่นในแนวนอนที่สามารถหมุนได้รอบ 360° มวลถูกแขวนที่ปลายคาน และคานอยู่ในแนวตั้ง ให้มวลจะมีพลังงานจลน์เริ่มต้น K ถ้า K มีขนาดเล็กมาก มวลก็จะเปรียบเสมือนลูกตุ้ม เมื่อสั่นด้วยมุมเล็กๆ จะได้คาบของการแกว่ง T0 แล้วกรณีที่ K เพิ่มขึ้น คาบของมวลจะเป็นไปตามข้อใด |
| A | ยังคงเท่าเดิม |
| B | เพิ่มขึ้น และเข้าใกล้ค่าหนึ่งที่หาค่าได้ |
| C | ลดลง และเข้าใกล้ค่าหนึ่งที่ไม่ใช่ศูนย์ และหาค่าได้ |
| D | ลดลง และเข้าใกล้ศูนย์ |
| E | ตอนแรกจะเพิ่มขึ้น แล้วลดลง |
ตอบ (E)
เมื่อแอมพลิจูดเพิ่มเป็น \(π\) คาบก็จะลู่ออก ดังนั้น ช่วงแรกคาบจะเพิ่มขึ้น (หรืออีกวิธีหนึ่ง สังเกตว่า cosθ ในจัตุภาคจะมีเครื่องหมายตรงกันข้าม ทำให้ลดแรงส่งกลับ และทำให้คาบเพิ่มขึ้น) ถ้าพลังงานเพิ่มขึ้นต่อไปอีก มวลก็จะวนในทิศทางเดียวตลอดไป แล้วคาบก็จะลดลง และเป็นค่าที่สามารถหาค่าได้
เมื่อแอมพลิจูดเพิ่มเป็น \(π\) คาบก็จะลู่ออก ดังนั้น ช่วงแรกคาบจะเพิ่มขึ้น (หรืออีกวิธีหนึ่ง สังเกตว่า cosθ ในจัตุภาคจะมีเครื่องหมายตรงกันข้าม ทำให้ลดแรงส่งกลับ และทำให้คาบเพิ่มขึ้น) ถ้าพลังงานเพิ่มขึ้นต่อไปอีก มวลก็จะวนในทิศทางเดียวตลอดไป แล้วคาบก็จะลดลง และเป็นค่าที่สามารถหาค่าได้
| 113. | (เกินหลักสูตรสอบเข้า สอวน.) ก และ ข กำลังเขียนรายงานผลการทดลอง โดย ก วัดคาบของลูกตุ้มได้ 1.013 ± 0.008 s ในขณะที่ ข วัดได้คาบ 0.997 ± 0.016 s ซึ่งทั้งคู่สามารถสรุปข้อมูลที่ได้ตามวิธีต่อไปนี้
วิธีที่ 1 : ใช้ข้อมูลของ ก โดยไม่สนของ ข
วิธีที่ 2 : ใช้ค่าเฉลี่ยของข้อมูล ก และ ข
วิธีที่ 3 : ใช้ค่าเฉลี่ยถ่วงน้ำหนักของข้อมูล ก และ ข โดยถ่วงให้ ก มีน้ำหนักมากกว่า ข อยู่ 4 เท่า
ข้อใดสรุป ความคลาดเคลื่อนของผลลัพธ์ในแต่ละวิธี ได้ดีที่สุด |
| A | วิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด |
| B | วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด |
| C | วิธีที่ 2 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 1 มีความคลาดเคลื่อนสูงที่สุด |
| D | วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 1 มีความคลาดเคลื่อนสูงที่สุด |
| E | วิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 3 มีความคลาดเคลื่อนสูงที่สุด |
ตอบ (B)
ให้ Δx เป็นความคลาดเคลื่อนในการวัดของ ก จะได้ ความคลาดเคลื่อนของ ข เท่ากับ 2Δx
การหาความคลาดเคลื่อน โดยใช้สูตรส่วนเบี่ยงเบนมาตรฐาน จะมีกฏที่จำเป็น ดังต่อไปนี้
ดังนั้น วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด (ในทางปฏิบัติ) ส่วนวิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด
ให้ Δx เป็นความคลาดเคลื่อนในการวัดของ ก จะได้ ความคลาดเคลื่อนของ ข เท่ากับ 2Δx
การหาความคลาดเคลื่อน โดยใช้สูตรส่วนเบี่ยงเบนมาตรฐาน จะมีกฏที่จำเป็น ดังต่อไปนี้
(A) การคูณด้วยค่าคงที่ : ถ้า x มีความคลาดเคลื่อน Δx แล้ว cx จะมีความคลาดเคลื่อน cΔx
(B) การเพิ่มตัวแปร : ถ้า x มีความคลาดเคลื่อน Δx และ y มีความคลาดเคลื่อน Δy โดยทั้งสองเป็นอิสระต่อกัน แล้ว x + y จะมีความคลาดเคลื่อนเท่ากับ
\(\rm \sqrt{(Δx)^2 +(Δy)^2}\)
เราสามารถหาความคลาดเคลื่อนของทั้งสามวิธีได้ ดังนี้
วิธีที่ 1: \(\rm Δx\)
วิธีที่ 2: \(\rm \sqrt{(Δx)^2 +(2Δx)^2} / 2 = (\sqrt5/2) Δx \)
วิธีที่ 3: \(\rm\sqrt{(4Δx)^2 +(2Δx)^2} / 5 = (2/\sqrt5) Δx \)
ดังนั้น วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด (ในทางปฏิบัติ) ส่วนวิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด
| 114. | แอปเปิ้ลขนาด 0.3 kg เดิมอยู่นิ่ง ร่วงลงมาจากความสูง 40 cm ลงบนพื้นราบ และหยุดนิ่งใน 0.1 s พื้นผิวที่ตกกระแทกพื้นเท่ากับ 4 cm2 แล้วความดันเฉลี่ยของแอปเปิ้ลขณะตกกระแทกพื้นเท่ากับข้อใด ไม่ต้องคำนึงถึงแรงต้านอากาศ |
| A | 67,000 Pa |
| B | 21,000 Pa |
| C | 6,700 Pa |
| D | 210 Pa |
| E | 67 Pa |
ตอบ (B)
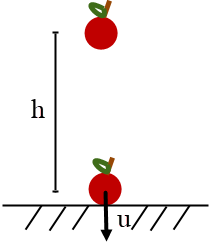จาก v ที่แอปเปิ้ลตกพื้น \({\rm{ = }}\sqrt {{\rm{2gh}}}\) จะได้
โมเมนตัม \(\rm = m\sqrt {2gh}\)
เมื่อกระทบพื้นโมเมนตัมจะถูกเปลี่ยนเป็นแรงดล จะได้
\(\begin{align*}
{\rm{m}}\sqrt {{\rm{2gh}}} &= \rm F\Delta t\\
{\rm{m}}\sqrt {{\rm{2gh}}} &= \rm PA\Delta t\\
\rm P &= \frac{{{\rm{m}}\sqrt {{\rm{2gh}}} {\rm{ }}}}{{{\rm{A\Delta t}}}}\\
\rm P &= \frac{{{\rm{(0}}{\rm{.3)}}\sqrt {{\rm{2}} \times {\rm{10}} \times {\rm{0}}{\rm{.4}}} {\rm{ }}}}{{{\rm{4}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}} \times 0.1}}\\
\rm P &= \frac{{0.8485{\rm{ }}}}{{0.4}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}\\
\rm P &= 2.121 \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}\,\,\,{\rm{N/}}{{\rm{m}}^{\rm{2}}}\\
{\rm{P}} &\approx 21,000\,\,{\rm{Pa}}
\end{align*}\)
| 115. | วัตถุที่เหมือนกัน 3 ชิ้น ถูกวางโต๊ะที่ไม่มีแรงเสียดทาน ดังรูป ให้มวลที่อยู่ตรงกลางอยู่นิ่ง ส่วนอีกสองชิ้นพุ่งเข้าหาวัตถุที่อยู่ตรงกลางด้วยอัตราเร็ว v เหมือนกัน โดยวัตถุที่อยู่ตรงกลางจะอยู่ใกล้กับวัตถุทางซ้ายมากกว่าทางขวา และการเคลื่อนที่ทั้งหมดเกิดขึ้นหนึ่งมิติ ตามแนวนอน
 |
| A | วัตถุตรงกลาง จะเคลื่อนที่ไปทางซ้าย |
| B | วัตถุตรงกลาง จะเคลื่อนที่ไปทางขวา |
| C | วัตถุตรงกลาง หยุดนิ่งอยู่ทางด้านซ้ายของตำแหน่งเริ่มต้น |
| D | วัตถุตรงกลาง หยุดนิ่งอยู่ที่ตำแหน่งเริ่มต้น |
| E | วัตถุตรงกลาง หยุดนิ่งอยู่ทางด้านขวาของตำแหน่งเริ่มต้น |
ตอบ (D)
แบ่งเป็น 3 เหตุการณ์ย่อยๆ
1. วัตถุทางซ้าย ชน วัตถุตรงกลาง
อนุรักษ์ \({\rm{\vec P}}\)
2. วัตถุทางขวา ชน วัตถุตรงกลาง
อนุรักษ์ \({\rm{\vec P}}\)
ดังนั้น วัตถุตรงกลางจะสะท้อนกลับ แล้ววิ่งไปทางซ้ายด้วยความเร็ว v
วัตถุทางขวาจะสะท้อนกลับ แล้ววิ่งไปทางขวาด้วยความเร็ว v
3. วัตถุตรงกลาง ชน วัตถุทางซ้าย ซึ่งหยุดนิ่งอยู่ ณ ตำแหน่งเริ่มต้นของวัตถุกลาง
ในทำนองเดียวกับเหตุการณ์ในข้อ 1 หลังชนวัตถุทางซ้ายจะเคลื่อนที่ไปทางซ้ายด้วยอัตราเร็ว v และวัตถุตรงกลางจะหยุดนิ่ง ณ ตำแหน่งเริ่มต้นของมัน
ดังนั้น ตอบข้อ (D)
แบ่งเป็น 3 เหตุการณ์ย่อยๆ
1. วัตถุทางซ้าย ชน วัตถุตรงกลาง
\({\rm{mv = mv' + mu }} \Rightarrow {\rm{ v' = v }} - {\rm{ u}}\)
อนุรักษ์ E
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{v}}^{\rm{2}}} &= \frac{{\rm{1}}}{{\rm{2}}}{\rm{m(}}{{{\rm{v'}}}^{\rm{2}}} + {u^2})\\ {v^2} &= {(v - u)^2} + {u^2}\\ 2{\rm{uv}} &= {u^2}\\ {\rm{u}} &= 0,\rm\not{2}\not v\\ {\rm{v}} &= \rm v,\rm\not -\not v \end{align*}\)
ดังนั้น วัตถุตรงกลางเคลื่อนที่ไปทางขวา ด้วยความเร็ว v ส่วนวัตถุทางซ้ายหยุดนิ่งอยู่ ณ ตำแหน่งเริ่มต้นของวัตถุกลาง2. วัตถุทางขวา ชน วัตถุตรงกลาง
\({\rm{0 = m}}{{\rm{v}}_1}{\rm{ + m}}{{\rm{v}}_2}{\rm{ }} \Rightarrow {\rm{ }}{{\rm{v}}_1}{\rm{ = }} - {\rm{ }}{{\rm{v}}_{\rm{2}}}\)
อนุรักษ์ E
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\rm{m (}}{{\rm{v}}^{\rm{2}}} + {{\rm{v}}^{\rm{2}}}) &= \frac{{\rm{1}}}{{\rm{2}}}{\rm{m(}}{{\rm{v}}_1}^{\rm{2}} + {{\rm{v}}_2}^{\rm{2}})\\ 2{v^2} &= 2{{\rm{v}}_1}^2\\ {{\rm{v}}_1} &= \rm\not v, - v\\ {{\rm{v}}_2} &= \rm\not- \not v ,v \end{align*}\)
ค่าที่ตัดออก คือ ค่าที่สื่อว่าวัตถุทะลุผ่านกันไป ซึ่งเป็นไปไม่ได้ดังนั้น วัตถุตรงกลางจะสะท้อนกลับ แล้ววิ่งไปทางซ้ายด้วยความเร็ว v
วัตถุทางขวาจะสะท้อนกลับ แล้ววิ่งไปทางขวาด้วยความเร็ว v
3. วัตถุตรงกลาง ชน วัตถุทางซ้าย ซึ่งหยุดนิ่งอยู่ ณ ตำแหน่งเริ่มต้นของวัตถุกลาง
ในทำนองเดียวกับเหตุการณ์ในข้อ 1 หลังชนวัตถุทางซ้ายจะเคลื่อนที่ไปทางซ้ายด้วยอัตราเร็ว v และวัตถุตรงกลางจะหยุดนิ่ง ณ ตำแหน่งเริ่มต้นของมัน
ดังนั้น ตอบข้อ (D)
| 116. | วัตถุที่เหมือนกัน 3 ชิ้น ถูกวางโต๊ะที่ไม่มีแรงเสียดทาน ดังรูป ให้มวลที่อยู่ตรงกลางอยู่นิ่ง ส่วนอีกสองชิ้นพุ่งเข้าหาวัตถุที่อยู่ตรงกลางด้วยอัตราเร็ว v เหมือนกัน โดยวัตถุที่อยู่ตรงกลางจะอยู่ใกล้กับวัตถุทางซ้ายมากกว่าทางขวา และการเคลื่อนที่ทั้งหมดเกิดขึ้นหนึ่งมิติ ตามแนวนอน
 |
| A | วัตถุตรงกลาง จะเคลื่อนที่ไปทางซ้าย |
| B | วัตถุตรงกลาง จะเคลื่อนที่ไปทางขวา |
| C | วัตถุตรงกลาง หยุดนิ่งอยู่ทางด้านซ้ายของตำแหน่งเริ่มต้น |
| D | วัตถุตรงกลาง หยุดนิ่งอยู่ที่ตำแหน่งเริ่มต้น |
| E | วัตถุตรงกลาง หยุดนิ่งอยู่ทางด้านขวาของตำแหน่งเริ่มต้น |
ตอบ (E)
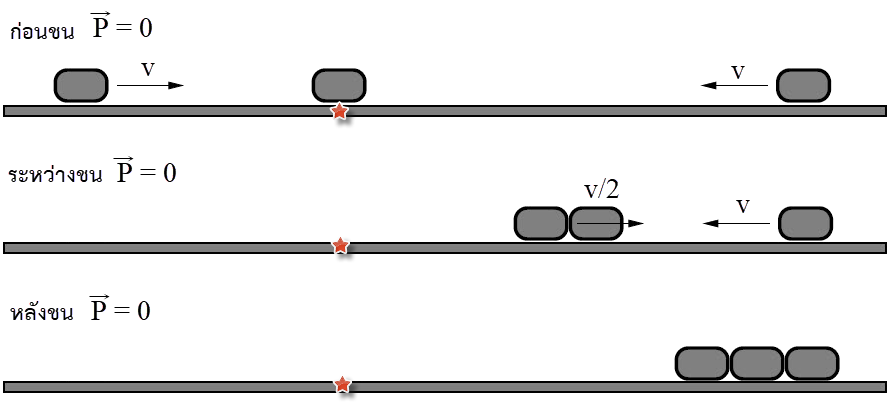สุดท้ายวัตถุทั้งสามจะหยุดนิ่ง เพราะ
1. \(\overrightarrow {\rm{P}} = 0\) จากกฏอนุรักษ์โมเมนตัม
2. มวล 3 ก้อนติดกันเป็นก้อนเดียว
ดังนั้น ความเร็วของมวลทั้งสามเป็น 0 และหยุดนิ่งอยู่ทางด้านขวาของตำแหน่งเริ่มต้น
1. \(\overrightarrow {\rm{P}} = 0\) จากกฏอนุรักษ์โมเมนตัม
2. มวล 3 ก้อนติดกันเป็นก้อนเดียว
ดังนั้น ความเร็วของมวลทั้งสามเป็น 0 และหยุดนิ่งอยู่ทางด้านขวาของตำแหน่งเริ่มต้น
| 117. | นักบินอวกาศมวล 80 kg นั่งอยู่บนยานอวกาศที่กำลังเข้าใกล้พื้นโลก ถ้ายานอวกาศมีความเร่งในทิศขึ้นตั้งฉากกับพื้นโลกเป็นห้าเท่าของความเร่งโน้มถ่วง แล้วแรงที่นักบินกระทำกับยานอวกาศจะเท่ากับข้อใด |
| A | 4800 N |
| B | 4000 N |
| C | 3200 N |
| D | 800 N |
| E | 400 N |
ตอบ (A)
ให้ N เป็นแรงที่ยานทำกับนักบินอวกาศ
กฏของนิวตัน
ดังนั้น แรงที่นักบินกระทำกับยานอวกาศเท่ากับ 4800 N
ให้ N เป็นแรงที่ยานทำกับนักบินอวกาศ
กฏของนิวตัน
\(\begin{align*}
{\rm{N}} - {\rm{mg}} &= {\rm{m(5g)}}\\
{\rm{N}} &= {\rm{mg = 6 \times 80 \times 10 = 4,800 N}}
\end{align*}\)
จากกฏข้อที่ 3 ของนิวตัน (action = reaction) จะได้ว่า แรงที่นักบินอวกาศทำกับยาน เท่ากับ แรงที่ยานทำกับนักบินอวกาศดังนั้น แรงที่นักบินกระทำกับยานอวกาศเท่ากับ 4800 N
| 118. | ดาวเทียมขนาดเท่ากันสามดวง A, B และ C อยู่ในวงโคจรของดาวเคราะห์ ตามรูป ถ้าขนาดของโมเมนตัมเชิงมุมของดาวเทียมที่วัดจากดาวเคราะห์ เท่ากับ LA , LB และ LC แล้วข้อใดต่อไปนี้ถูกต้อง
 |
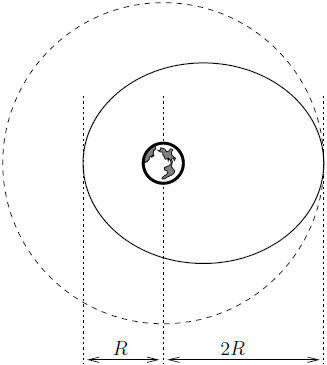| A | LA > LB > LC |
| B | LC > LB > LA |
| C | LB > LC > LA |
| D | LB > LA > LC |
| E | การจัดลำดับขนาดจะแตกต่างกัน ขึ้นอยู่กับช่วงเวลานั้นๆ |
ตอบ (A)
เปรียบเทียบ A, C
จาก vA > vC และ rA > rC ดังนั้น LA > LB
เปรียบเทียบ B, C
พิจารณาจุด B ตรงไหนก็ได้ เพราะ \({\overrightarrow {\rm{L}} _{\rm{B}}}\) รอบโลกคงที่ เนื่องจากไม่มีทอร์กภายนอกมากระทำ
ดังนั้น เมื่อย้าย B มาที่ rB = rC จะได้ vB > vC เพราะ การโคจรเป็นวงรี ต้องใช้พลังงานมากกว่าการโคจรเป็นวงกลม ดังนั้น LB > LC
สรุปว่า LA > LB > LC
เปรียบเทียบ A, C
จาก vA > vC และ rA > rC ดังนั้น LA > LB
เปรียบเทียบ B, C
พิจารณาจุด B ตรงไหนก็ได้ เพราะ \({\overrightarrow {\rm{L}} _{\rm{B}}}\) รอบโลกคงที่ เนื่องจากไม่มีทอร์กภายนอกมากระทำ
ดังนั้น เมื่อย้าย B มาที่ rB = rC จะได้ vB > vC เพราะ การโคจรเป็นวงรี ต้องใช้พลังงานมากกว่าการโคจรเป็นวงกลม ดังนั้น LB > LC
สรุปว่า LA > LB > LC
| 119. | วัตถุถูกโยนด้วยอัตราเร็วต้นคงที่ v0 ด้วยมุมที่แตกต่างกัน α กับแนวราบ ที่ความสูงคงที่ค่าหนึ่ง h เหนือจุดยิง อัตราเร็ว v ของวัตถุจะมีค่าตามฟังก์ชันของมุมเริ่มต้น α ข้อใดอธิบาย v ที่เปลี่ยนไปตามมุม α ได้ดีที่สุด (สมมุติว่า มีความสูง h ตามเงื่อนไข และไม่มีแรงต้านอากาศ) |
| A | v จะเพิ่มขึ้นเป็นลำดับทางเดียวตาม α |
| B | v จะเพิ่มขึ้นถึงค่าวิกฤต vmax ค่าหนึ่ง หลังจากนั้นจะลดลง |
| C | v จะคงที่ โดยไม่ขึ้นกับ α |
| D | v จะลดลงถึงค่าวิกฤต vmin ค่าหนึ่ง หลังจากนั้นจะเพิ่มขึ้น |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
จากกฏการอนุรักษณ์พลังงาน
จากกฏการอนุรักษณ์พลังงาน
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{v}}_{\rm{0}}}^{\rm{2}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{v}}^{\rm{2}}}{\rm{ + mgh}}\\ {\rm{v = }}\sqrt {{{\rm{v}}_{\rm{0}}}^{\rm{2}} - 2{\rm{gh}}} \end{align*}\)
สังเกตว่า v ไม่ได้ขึ้นกับ α| 120. | นกตัวหนึ่งบินเป็นเส้นตรง โดยตอนแรกบิน 10 m/s แล้วเพิ่มอัตราเร็วอย่างสม่ำเสมอจนถึง 15 m/s ได้ระยะทางทั้งหมด 25 m ความเร่งของนกเท่ากับข้อใด |
| A | 5.0 m / s2 |
| B | 2.5 m / s2 |
| C | 2.0 m / s2 |
| D | 0.5 m / s2 |
| E | 0.2 m / s2 |
ตอบ (B)
จาก \({\rm{a = }}\dfrac{{{\rm{dv}}}}{{{\rm{dt}}}}\) จะได้ว่า
จากโจทย์เขียนกราฟได้ ดังนี้
ให้ S เป็นพื้นที่ใต้กราฟ
จาก \({\rm{a = }}\dfrac{{{\rm{dv}}}}{{{\rm{dt}}}}\) จะได้ว่า
\(\begin{align*} \,\,\int\limits_{\rm{u}}^{\rm{v}} \rm dv &= {\int\limits_{\rm{0}}^{\rm{t}} {{\rm{adt}}} } \\ {\rm{v}} - {\rm{u}} &= {\rm{at}} \end{align*}\)
จะได้ว่า \({\rm{t}} = \dfrac{{{\rm{v}} - {\rm{u}}}}{{\rm{a}}}\) และ \({\rm{v}} = {\rm{u + at}}\)จากโจทย์เขียนกราฟได้ ดังนี้
\(\begin{align*} {\rm{S}} &= \frac{1}{2}\left( {{\rm{v + u}}} \right){\rm{t}}\\ \rm{S} &= \frac{1}{2}\left( {{\rm{v + u}}} \right)\left( {\frac{{{\rm{v}} - {\rm{u}}}}{{\rm{a}}}} \right)\\ {\rm{a}} &= \frac{{{{\rm{v}}^2} - {{\rm{u}}^2}}}{{2{\rm{S}}}} = \frac{{{\rm{1}}{{\rm{5}}^2} - {\rm{1}}{{\rm{0}}^2}}}{{2{\rm{(25)}}}} = 2.5\,\,{\rm{m / }}{{\rm{s}}^{\rm{2}}} \end{align*}\)
| 121. | ให้แผ่นกลมหมุนรอบแกนที่ผ่านจุดศูนย์กลาง และตั้งฉากกับระนาบของแผ่นกลม ด้วยความเร็วเชิงมุมตามกราฟด้านล่าง
 |
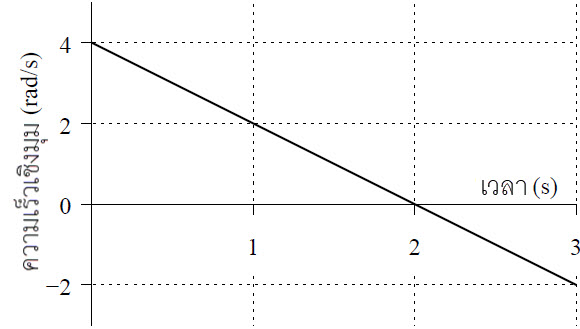| A | – 12 rad / s2 |
| B | – 8 rad / s2 |
| C | – 4 rad / s2 |
| D | – 2 rad / s2 |
| E | 0 rad / s2 |
ตอบ (B)
ให้ α = ความเร่งเชิงมุม (rad/s2) และ ω = ความเร็วเชิงมุม (rad/s)
ให้ α = ความเร่งเชิงมุม (rad/s2) และ ω = ความเร็วเชิงมุม (rad/s)
\({\rm{\alpha = }}\dfrac{{{\rm{\Delta \omega }}}}{{{\rm{\Delta t}}}} = \dfrac{{0 - 4}}{{2 - 0}} = - 2\,\,\,{\rm{rad/}}{{\rm{s}}^2}\)
| 122. | ให้แผ่นกลมหมุนรอบแกนที่ผ่านจุดศูนย์กลาง และตั้งฉากกับระนาบของแผ่นกลม ด้วยความเร็วเชิงมุมตามกราฟด้านล่าง
 |
| A | 9 rad |
| B | 8 rad |
| C | 6 rad |
| D | 4 rad |
| E | 3 rad |
ตอบ (E)
ให้ θ = มุมที่กวาดไป (rad)
จาก θ เป็นพื้นที่ใต้กราฟ ω – t จะได้ว่า
ให้ θ = มุมที่กวาดไป (rad)
จาก θ เป็นพื้นที่ใต้กราฟ ω – t จะได้ว่า
\({\rm{\theta }} = \dfrac{1}{2}(4)(2) - \dfrac{1}{2}(2)(1) = \,\,\,3\,\,\rm rad\)
| 123. | ชายคนหนึ่งยืนอยู่ที่ขอบประตูหนีไฟ เขาขว้างแอปเปิ้ลสองลูกพร้อมกัน โดยอันหนึ่งโยนขึ้นด้วยอัตราเร็ว 7 m/s และอีกอันขว้างลงด้วยอัตราเร็วเท่ากัน ระยะห่างของแอปเปิ้ลทั้งสองที่ วินาทีที่ 2 หลังโยนออกไปเท่ากับข้อใด สมมุติว่าทั้งสองยังไม่ตกถึงพื้น |
| A | 14 m |
| B | 20 m |
| C | 28 m |
| D | 34 m |
| E | 56 m |
ตอบ (C)
เมื่อเวลาผ่านไป 2 วินาที
\(\begin{align*} {{\rm{s}}_1} &= 7(2) - \frac{1}{2}(10)({2^2})\\ \rm s_2 &= 7(2) + \frac{1}{2}(10)({2^2})\\ {{\rm{s}}_1} + {{\rm{s}}_{\rm{2}}} &= 7(2) + 7(2) = \rm 28~m \end{align*}\)
| 124. | มวล 2.25 kg มีการเร่งอัตราเร็วดังกราฟ งานที่กระทำกับมวลได้เท่ากับข้อใด |
| A | 36 J |
| B | 22 J |
| C | 5 J |
| D | – 17 J |
| E | – 36 J |
ตอบ (A)
\(\begin{align*} \rm{W} &= \int {\overrightarrow {\rm{F}} \cdot {\rm{d}}} \overrightarrow {\rm{s}} \\ &= {\rm{m}}\int {\overrightarrow {\rm{a}} \cdot {\rm{d}}\overrightarrow {\rm{s}} } \\ &= \rm m\left( {\frac{1}{2}(4)(8 + 2) - \frac{1}{2}(4)(2)} \right)\\ &=\frac{9}{4}\left( {20 - 4} \right)\\ &= 36\,\,{\rm{J}} \end{align*}\)
| 125. | แบทแมนมวล M = 100 kg ปีนขึ้นดาดฟ้าสูง 30 m จากนั้นโยนเชือกเบาให้โรบินจับไว้ แล้วดึงโรบินที่มีมวลประมาณ 75 kg ขึ้นมาบนดาดฟ้า งานสุทธิที่แบทแมนทำหลังโรบินขึ้นมาบนดาดฟ้าได้เท่ากับข้อใด |
| A | 60 J |
| B | 7 × 103 J |
| C | 5 × 104 J |
| D | 600 J |
| E | 3 × 104 J |
ตอบ (C)
\(\begin{align*}
{\rm{W}} &= {{\rm{M}}_{{\rm{total}}}}{\rm{gh}}\\
&= (100 + 75) \times 10 \times 30\\
&= 525 \times {10^2}\\
&\approx 5 \times {10^4}\,\,{\rm{J}}
\end{align*}\)
| 126. | ก (มวล 33.1 kg) ข (มวล 63.7 kg) และ ค (มวล 24.3 kg) นั่งห่างกันบนกระดานหกสม่ำเสมอที่มีน้ำหนักเบา เว้นระยะห่าง 2.74 m ตามลำดับ (ข อยู่ระหว่าง ก และ ค) ทำให้กระดานหกสมดุล ใครมีทอร์กบนกระดานหกมากที่สุด (ในแง่ของขนาด) ไม่ต้องสนมวลของกระดานหก |
| A | ก |
| B | ข |
| C | ค |
| D | ทั้งสามมีทอร์กเท่ากัน |
| E | ข้อมูลไม่เพียงพอต่อการตอบคำถาม |
ตอบ (B)
กระดานหกสมดุลแสดงว่า ทอร์กรวมรอบจุดหมุนเท่ากับ 0
\(\begin{align*} \rm{{\rm{m}}_{\rm{1}}}{\rm{g}}(d - x) &= \rm{m_2}gx + {m_3}g(d + x)\\ \rm\frac{{{\rm{d}}({m_1} - {m_3})}}{{{m_1} + {m_2} + {m_3}}} &= {\rm{x}} \end{align*}\)
ทอร์กของ ก
\(\begin{align*} \rm{{\rm{m}}_{\rm{1}}}{\rm{g}}(d - x) &= \rm{m_1}g\left( {\frac{{({m_2} + 2{m_3})}}{{{m_1} + {m_2} + {m_3}}}} \right)d\\ &\propto \rm {m_1}({m_2} + 2{m_3}) \approx 30(110) \approx 3300 \end{align*}\)
ทอร์กของ ข
\(\rm{{\rm{m}}_2}{\rm{g}}x \propto {m_2}({m_1} - {m_3}) \approx 60(10) \approx 600\)
ทอร์กของ ค
\(\rm{{\rm{m}}_3}{\rm{g(d + }}x) \propto {m_3}(2{m_1} + {m_2}) \approx 20(60 + 60) \approx 2400\)
ดังนั้น ก มีทอร์กบนกระดานหกมากที่สุด| 127. | บล็อคไม้ (มวล M) ถูกแขวนบนเชือกเบาที่ถูกปักหมุดไว้ กระสุนที่มาด้วยอัตราเร็ว (มีมวล m และอัตราเร็วต้น v0) ชนกับบล็อคที่เวลา t = 0 และฝังอยู่ในนั้น ถ้า S เป็นระบบที่ประกอบด้วย บล็อกและกระสุน แล้วปริมาณใดที่ถูกอนุรักษ์ไว้ในช่วง t = –10 s ถึง t = +10 s
 |
| A | โมเมนตัมเชิงเส้นรวมของ S |
| B | องค์ประกอบในแนวนอนของ โมเมนตัมเชิงเส้นของ S |
| C | พลังงานกลของ S |
| D | โมเมนตัมเชิงมุมของ S ที่วัดเทียบกับแกนตั้งฉากกับหมุด |
| E | ไม่มีปริมาณใดถูกอนุรักษ์ไว้ |
ตอบ (E)
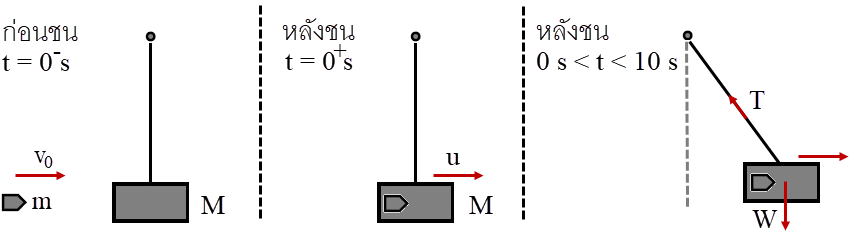พิจารณาแต่ละข้อ
(A) \(\overrightarrow {\rm{P}}\) ไม่อนุรักษ์ เพราะไม่มีแรงกระทำต่อระบบ ดังนั้น โมเมนตัมเชิงเส้นจะไม่ถูกอนุรักษ์ไว้
(B) Py ไม่อนุรักษ์ เพราะมีน้ำหนัก W และ Component แกน y ของ T กระทำต่อระบบ
(C) E ไม่อนุรักษ์ เพราะที่เวลา t = 0- s ถึง t = 0+ s มีการชนแบบไม่ยืดหยุ่น (กระสุนฝังติดไปกับบล็อคไม้)
(D) \(\overrightarrow {\rm{L}}\) ไม่อนุรักษ์ เพราะมี W กระทำต่อระบบซึ่ง W กระทำต่อแนวแรงไม่ผ่านจุดหมุน ทำให้เกิดทอร์กกระทำต่อระบบ
ดังนั้น ตอบ (E) ไม่มีข้อใดอนุรักษ์
(A) \(\overrightarrow {\rm{P}}\) ไม่อนุรักษ์ เพราะไม่มีแรงกระทำต่อระบบ ดังนั้น โมเมนตัมเชิงเส้นจะไม่ถูกอนุรักษ์ไว้
(B) Py ไม่อนุรักษ์ เพราะมีน้ำหนัก W และ Component แกน y ของ T กระทำต่อระบบ
(C) E ไม่อนุรักษ์ เพราะที่เวลา t = 0- s ถึง t = 0+ s มีการชนแบบไม่ยืดหยุ่น (กระสุนฝังติดไปกับบล็อคไม้)
(D) \(\overrightarrow {\rm{L}}\) ไม่อนุรักษ์ เพราะมี W กระทำต่อระบบซึ่ง W กระทำต่อแนวแรงไม่ผ่านจุดหมุน ทำให้เกิดทอร์กกระทำต่อระบบ
ดังนั้น ตอบ (E) ไม่มีข้อใดอนุรักษ์
| 128. | กระเป๋าเดินทาง 22.0 kg ถูกลากด้วยอัตราเร็วคงที่ 1.10 m/s เป็นเส้นตรง โดยนักเรียนคนหนึ่งที่จะไปสอบ IPhO ครั้งที่ 40 ที่ประเทศเม็กซิโก ถ้าเขาลากกระเป๋าที่สนามบินด้วยแรง 1.00×102 N เอียงทำมุมสูง 30.0 องศากับแนวระดับ แล้วสัมประสิทธิ์แรงเสียดทานจลน์ ระหว่างกระเป๋าเดินกับพื้นเท่ากับข้อใด |
| A | μk = 0.013 |
| B | μk = 0.394 |
| C | μk = 0.509 |
| D | μk = 0.866 |
| E | μk = 1.055 |
ตอบ (C)
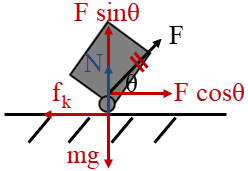กระเป๋าเคลื่อนที่ด้วยความเร็วคงที่ นั่นคือ \(\overrightarrow {\rm{a}} {\rm{ = 0}}\) ดังนั้น \(\sum {\overrightarrow {\rm{F}} } = 0\)
จาก \(\sum {{{\rm{F}}_{\rm{x}}}} = 0\) จะได้ว่า
จาก \(\sum {{{\rm{F}}_{\rm{x}}}} = 0\) จะได้ว่า
\(\begin{align*} {{\rm{f}}_{\rm{k}}}{\rm{ = Fcos\theta }}\\ {{\rm{\mu }}_{\rm{k}}}{\rm{N = Fcos\theta }} \end{align*}\)
จาก \(\sum {{{\rm{F}}_{\rm{y}}}} = 0\) จะได้ว่า
\(\begin{align*} \rm N + Fsin\theta &= \rm mg\\ \rm N &= \rm mg - {\rm{Fsin\theta }}\\ \end{align*}\)
แทน \(\rm N\) ใน \({{\rm{\mu }}_{\rm{k}}}{\rm{N = Fcos\theta }}\) จะได้
\(\begin{align*} {{\rm{\mu }}_{\rm{k}}}\left( {{\rm{mg}} - {\rm{Fsin\theta }}} \right) &= \rm Fcos\theta \\ {{\rm{\mu }}_{\rm{k}}} &= \frac{{{\rm{Fcos\theta }}}}{{{\rm{mg}} - {\rm{Fsin\theta }}}} \end{align*}\)
แทนค่า
\({{\rm{\mu }}_{\rm{k}}}{\rm{ = }}\dfrac{{{\rm{100}}\left( {\frac{{\sqrt 3 }}{2}} \right)}}{{{\rm{220}} - {\rm{100}}\left( {\frac{1}{2}} \right)}} = \dfrac{{5\sqrt 3 }}{{17}} \approx 0.509\)
| 129. | วัตถุมวล m สองอันที่เหมือนกัน นำไปติดที่ปลายทั้งสองของสปริง ที่มีค่านิจสปริง k และวางอยู่บนพื้นที่ไม่แรงเสียดทานในแนวนอน แล้วที่ความถี่เชิงมุม ω ขณะระบบสั่นเท่ากับข้อใด |
| A | \(\rm\sqrt{k/m}\) |
| B | \(\rm\sqrt{2k/m}\) |
| C | \(\rm\sqrt{k/2m}\) |
| D | \(2\rm\sqrt{k/m}\) |
| E | \(\rm\sqrt{k/m}/2\) |
ตอบ (B)
จากโจทย์ระบบจะสั่นรอบจุด cm ของระบบโดยที่ cm อยู่กับที่ เนื่องจากไม่มีแรงภายนอกมากระทำ
ดังนั้น มองว่าจุด cm เป็นกำแพง มีเพียง m 1 มวล และสปริงสั้นลงครึ่งหนึ่ง (k’ = 2k)
จากกฏของนิวตัน
จากโจทย์ระบบจะสั่นรอบจุด cm ของระบบโดยที่ cm อยู่กับที่ เนื่องจากไม่มีแรงภายนอกมากระทำ
ดังนั้น มองว่าจุด cm เป็นกำแพง มีเพียง m 1 มวล และสปริงสั้นลงครึ่งหนึ่ง (k’ = 2k)
\(\begin{align*} - \rm k'x &= \rm m\ddot x\\ \rm \ddot x &= - \frac{{{\rm{k'}}}}{{\rm{m}}}{\rm{x}} \end{align*}\)
ดังนั้น
\(\begin{align*} {{\rm{\omega }}^{\rm{2}}} &=\frac{{{\rm{k'}}}}{{\rm{m}}}{\rm{ = }}\frac{{{\rm{2k}}}}{{\rm{m}}}\\ \rm \omega &=\sqrt {\frac{{{\rm{2k}}}}{{\rm{m}}}} \end{align*}\)
| 130. | ถ้าคุณมีก้อนมวลมาตรฐาน 1 กิโลกรัม และส้อมเสียงในหน่วย Hz นอกจากนี้คุณยังมีเครื่องมือในห้องปฏิบัติการครบเซต แต่เป็นเครื่องมือที่ไม่ได้ให้ค่าในหน่วย SI และไม่ทราบค่าคงที่พื้นฐานใดๆ แล้วปริมาณใดที่สามารถวัดในหน่วย SI ได้ |
| A | ความเร่งเนื่องจากแรงโน้มถ่วง |
| B | อัตราเร็วแสงในสุญญากาศ |
| C | ความหนาแน่นของน้ำอุณหภูมิห้อง |
| D | ค่านิจสปริงของสปริงที่กำหนด |
| E | ความดันอากาศในห้อง |
ตอบ (D)
สิ่งที่รู้ในน่วย SI คือ kg , Hz หรือ s-1
(A) g หน่วย m/s2 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(B) c หน่วย m/s ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(C) ρwater หน่วย kg/m3 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(D) k หน่วย N/m = kg/s2 = kg·Hz2 ได้ เพราะเป็นหน่วยที่รู้ทั้งหมด
(E) P หน่วย N/m2 = kg/m·s2 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
สิ่งที่รู้ในน่วย SI คือ kg , Hz หรือ s-1
(A) g หน่วย m/s2 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(B) c หน่วย m/s ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(C) ρwater หน่วย kg/m3 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(D) k หน่วย N/m = kg/s2 = kg·Hz2 ได้ เพราะเป็นหน่วยที่รู้ทั้งหมด
(E) P หน่วย N/m2 = kg/m·s2 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
| 131. | ลูกตุ้มอย่างง่ายมีเชือกเบาความยาว L แขวนวัตถุมวล m กับจุดหมุนหนึ่ง และปักหมุดเล็กๆ ขวางไว้ใต้จุดหมุนที่ 2L/3 เพื่อให้ลูกตุ้มแกว่งตามรูป ถ้าจับมวลออกไป 5 องศากับแนวตั้ง แล้วปล่อยออก จะต้องใช้เวลานานเท่าใด ลูกตุ้มจึงจะกลับมาที่จุดเริ่มต้น
 |
| A | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(1+\sqrt{\dfrac{2}{3}}\right)\) |
| B | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(2+\dfrac{2}{\sqrt{3}}\right)\) |
| C | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(1+\dfrac{1}{3}\right)\) |
| D | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(1+\sqrt{3}\right)\) |
| E | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(1+\dfrac{1}{\sqrt{3}}\right)\) |
ตอบ (E)
ให้ T1 = คาบการแกว่งรอบจุดหมุนที่อยู่สูง
และ T2 = คาบการแกว่งรอบจุดหมุนที่อยู่เตี้ย
ดังนั้น เวลาที่ใช้ในการแกว่งกลับมาที่เดิม จะเท่ากับ
ให้ T1 = คาบการแกว่งรอบจุดหมุนที่อยู่สูง
และ T2 = คาบการแกว่งรอบจุดหมุนที่อยู่เตี้ย
ดังนั้น เวลาที่ใช้ในการแกว่งกลับมาที่เดิม จะเท่ากับ
\(\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{T}}_{\rm{1}}}{\rm{ + }}\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{T}}_{\rm{2}}}=\dfrac{1}{2}\left({{\rm{2\pi }}\sqrt {\frac{{\rm{L}}}{{\rm{g}}}} {\rm{ + 2\pi \sqrt{\dfrac{L/3}{g}}}}}\right) {\rm{ = \pi }}\sqrt {\frac{{\rm{L}}}{{\rm{g}}}} \left( {{\rm{1 + }}\frac{{\rm{1}}}{{\sqrt {\rm{3}} }}} \right)\)
| 132. | ถ้ากองหลังฟุตบอลสามารถโยนลูกฟุตบอลไปได้ไกลสุด 80 เมตรตามแนวราบ แล้วลูกฟุตบอลที่ถูกโยนไปได้ไกลสุดจะมีจุดสูงสุดเท่ากับข้อใด ไม่ต้องสนแรงต้านอากาศ |
| A | 10 m |
| B | 20 m |
| C | 30 m |
| D | 40 m |
| E | 50 m |
ตอบ (B)
พิจารณาวัตถุความเร็ว v ถูกโยนทำมุม θ กับพื้น
หาเวลาที่ใช้ในการเคลื่อนที่
จาก
ดังนั้น
หาเวลาที่ใช้ในการเคลื่อนที่
จาก
\(\begin{align*} {{\rm{s}}_{\rm{y}}} &= {{\rm{u}}_{\rm{y}}}{\rm{t}} - \frac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{{\rm{t}}^{\rm{2}}}\\ 0 &= {\rm{vsin\theta t}} - \frac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{{\rm{t}}^{\rm{2}}}\\ {\rm{t}} &= \frac{{2{\rm{vsin\theta }}}}{{\rm{g}}} \end{align*}\)
ดังนั้น ระยะเวลาที่วัตถุเคลื่อนที่ในแนวราบ
\({\rm{s = vcos\theta t = }}\dfrac{{{\rm{2}}{{\rm{v}}^{\rm{2}}}{\rm{sin\theta cos\theta }}}}{{\rm{g}}}{\rm{ = }}\dfrac{{{{\rm{v}}^{\rm{2}}}{\rm{sin2\theta }}}}{{\rm{g}}}\)
จะได้ว่า \({{\rm{s}}_{{\rm{max}}}}{\rm{ = }}\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{g}}}\) ที่ \({\rm{2\theta = }}\dfrac{{\rm{\pi }}}{{\rm{2}}}\) หรือ \({\rm{\theta = }}\dfrac{{\rm{\pi }}}{{\rm{4}}}\)ดังนั้น
\(\begin{align*} \rm H &={{\rm{u}}_{\rm{y}}}\left( {\frac{{\rm{t}}}{{\rm{2}}}} \right) - \frac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{\left( {\frac{{\rm{t}}}{{\rm{2}}}} \right)^{\rm{2}}}\\ &\rm =\left(\dfrac{v}{\sqrt2}\right)\left(\dfrac{v/\sqrt2}{g}\right)-\dfrac{1}{2}g\left(\dfrac{v/\sqrt2}{g}\right)^2\\ &= \frac{{{{\rm{v}}^{\rm{2}}}}}{{{\rm{2g}}}} - \frac{{{{\rm{v}}^{\rm{2}}}}}{{{\rm{4g}}}}\\ &= \frac{{{{\rm{v}}^{\rm{2}}}}}{{{\rm{4g}}}}\\ &= \frac{{\rm{1}}}{{\rm{4}}}{\rm{s}}\\ &= 20\,{\rm{m}} \end{align*}\)
| 133. | พิจารณาการชนแบบไม่ยืดหยุ่นสมบูรณ์ของวัตถุสองก้อน ถ้าก้อนที่ 1 มีมวล m และ เคลื่อนที่ไปทางทิศเหนือด้วยอัตราเร็ว v0 ส่วนก้อนที่ 2 มีมวล 3m เคลื่อนที่ไปทางทิศตะวันออกด้วยอัตราเร็ว v0/2 แล้วอัตราเร็วสุดท้ายหลังการชนเท่ากับข้อใด ไม่ต้องคำนึงถึงแรงโน้มถ่วง และถือว่าวัตถุทั้งสองติดไปด้วยกันหลังการชน |
| A | \(\rm7/6v_0\) |
| B | \(\rm\sqrt5/8v_0\) |
| C | \(\rm\sqrt{13}/8v_0\) |
| D | \(\rm5/8v_0\) |
| E | \(\rm\sqrt{13/8}v_0\) |
ตอบ (C)
ใช้กฏอนุรักษ์อนุรักษ์โมเมนตัม
แกน x
แกน x
\({\rm{3m}}\left( {\dfrac{{{{\rm{v}}_{\rm{0}}}}}{{\rm{2}}}} \right){\rm{ = (3m + m)ucos\theta }}\)
\(\dfrac{{{\rm{3}}{{\rm{v}}_{\rm{0}}}}}{{\rm{8}}}{\rm{ = ucos\theta }}\) --- (1)
แกน y
\({\rm{m}}{{\rm{v}}_{\rm{0}}}{\rm{ = (3m + m)usin\theta }}\)
\(\dfrac{{{{\rm{v}}_{\rm{0}}}}}{{\rm{4}}}{\rm{ = usin\theta }}\) --- (2)
นำ (1)2 + (2)2 จะได้
\(\begin{align*} \left( {{{\left( {\frac{3}{8}} \right)}^2}{\rm{ + }}{{\left( {\frac{1}{4}} \right)}^2}} \right){\rm{v}}_{\rm{0}}^{\rm{2}} &= {{\rm{u}}^{\rm{2}}}\\ {{\rm{u}}^{\rm{2}}} &= {\rm{v}}_{\rm{0}}^{\rm{2}}\left( {\frac{{9 + 4}}{{64}}} \right)\\ \rm u &=\frac{{\sqrt {{\rm{13}}} }}{{\rm{8}}}{{\rm{v}}_{\rm{0}}} \end{align*}\)
| 134. | ดาวสองดวงโคจรรอบมวลศูนย์กลางหนึ่ง ดังรูป โดยมวลของดาวเท่ากับ 3M และ M และดาวทั้งสองดวงห่างกัน d
 |
| A | \(\rm-\dfrac{GM^2}{d}\) |
| B | \(\rm\dfrac{3GM^2}{d}\) |
| C | \(\rm-\dfrac{GM^2}{d^2}\) |
| D | \(\rm-\dfrac{3GM^2}{d}\) |
| E | \(\rm-\dfrac{3GM^2}{d^2}\) |
ตอบ (D)
\(\begin{align*} {\rm{V}} &= - {\rm{G}}{{\rm{m}}_{\rm{1}}}{{\rm{m}}_{\rm{2}}}{\rm{r}}\\ &= \frac{{ - {\rm{G(M)(3m)}}}}{{\rm{d}}}\\ &=\rm \frac{{ - 3G{M^2}}}{d} \end{align*}\)
| 135. | ดาวสองดวงโคจรรอบมวลศูนย์กลางหนึ่ง ดังรูป โดยมวลของดาวเท่ากับ 3M และ M และดาวทั้งสองดวงห่างกัน d
 |
| A | \(\rm \pi\sqrt{\dfrac{d^3}{GM}}\) |
| B | \(\rm \dfrac{3\pi}{4}\sqrt{\dfrac{d^3}{GM}}\) |
| C | \(\rm \pi\sqrt{\dfrac{d^3}{3GM}}\) |
| D | \(\rm 2\pi\sqrt{\dfrac{d^3}{GM}}\) |
| E | \(\rm \dfrac{\pi}{4}\sqrt{\dfrac{d^3}{GM}}\) |
ตอบ (A)
ให้ ω = อัตราเร็วเชิงมุมของดาวทั้งสอง , r1 = ระยะจากจุด cm ของ M, 3M ถึงดาวมวล M
และ r2 = ระยะจากจุด cm ของ M, 3M ถึงดาวมวล 3M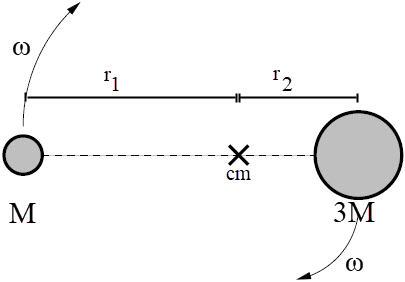
จะได้
ให้ ω = อัตราเร็วเชิงมุมของดาวทั้งสอง , r1 = ระยะจากจุด cm ของ M, 3M ถึงดาวมวล M
และ r2 = ระยะจากจุด cm ของ M, 3M ถึงดาวมวล 3M
\(\begin{array}{c} {\rm{M}}{{\rm{r}}_{\rm{1}}}{\rm{ = 3M}}{{\rm{r}}_{\rm{2}}}\\ {{\rm{r}}_{\rm{1}}}{\rm{ = 3}}{{\rm{r}}_{\rm{2}}} \end{array}\)
จาก r1 + r2 = d จะได้ว่า
\(\begin{align*} {{\rm{r}}_{\rm{1}}} &=\frac{{\rm{3}}}{{\rm{4}}}{\rm{d}}\\ {{\rm{r}}_{\rm{2}}} &=\frac{{\rm{d}}}{{\rm{4}}} \end{align*}\)
จากการเคลื่อนที่แบบวงกลมของดาวมวล 3M
\(\begin{align*} \frac{{{\rm{GM(3M)}}}}{{{{\rm{d}}^{\rm{2}}}}} &= {\rm{(3M)}}{{\rm{\omega }}^{\rm{2}}}{{\rm{r}}_{\rm{2}}}\\ \frac{{{\rm{GM}}}}{{{{\rm{d}}^{\rm{2}}}}} &= {{\rm{\omega }}^{\rm{2}}}\left( {\frac{{\rm{d}}}{4}} \right)\\ \rm \omega &= 2\sqrt {\frac{{{\rm{GM}}}}{{{{\rm{d}}^{\rm{3}}}}}} \end{align*}\)
ดังนั้น \({\rm{T = }}\dfrac{{2\pi }}{{\rm{\omega }}}{\rm{ = }}\pi \sqrt {\dfrac{{{{\rm{d}}^{\rm{3}}}}}{{{\rm{GM}}}}} \)| 136. | นำมวลติดกับสปริงอุดมคติ และสปริงมีความยาวตามปกติ ที่เวลา t = 0 มวลได้รับความเร็วต้น ถ้าคาบการสั่นแบบซิมเปิลฮาร์มอนิกเท่ากับ T แล้ว ณ เวลาใดที่สปริงจะกระทำกับมวลด้วยกำลังที่มากที่สุดเป็นครั้งแรก |
| A | t = 0 |
| B | t = T/8 |
| C | t = T/4 |
| D | t = 3T/8 |
| E | t = T/2 |
ตอบ (D)
จาก
และสมมุติให้ \({\rm{x(t) = }}{{\rm{x}}_0}\cos {\rm{\omega t}}\)
จาก
\(\begin{align*}
{{\rm{\varepsilon }}_{{\rm{spring}}}}&=\frac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{{\rm{x}}^{\rm{2}}}\\
{{\rm{P}}_{{\rm{sping}}}} &=\frac{{{\rm{d}}{{\rm{\varepsilon }}_{{\rm{spring}}}}}}{{{\rm{dt}}}}\\
{{\rm{P}}_{{\rm{sping}}}}&= {\rm{ kxx'}}
\end{align*}\)
ให้ที่ t = 0 สปริงมี x'(0) = 0 และ x(0) = x0และสมมุติให้ \({\rm{x(t) = }}{{\rm{x}}_0}\cos {\rm{\omega t}}\)
\(\begin{align*}
{\rm{x'(t)}} &= - {{\rm{x}}_{\rm{0}}}{\rm{\omega sin\omega t}}\\
{\rm{xx'}} &= - {\rm{x}}_0^2{\rm{\omega sin\omega t cos\omega t}}\\
\rm P &= \rm kxx' = \frac{{ - {\rm{kx}}_0^2{\rm{\omega }}}}{2}{\rm{ sin2\omega t}}
\end{align*}\)
จะได้ Pmax เมื่อ
\(\begin{align*}
{\rm{sin2\omega t }} &= - {\rm{1}}\\
{\rm{2\omega t }} &=\frac{{3\pi }}{2},...\\
\frac{{{\rm{2\pi }}}}{{\rm{T}}}\rm t &=\frac{{3\pi }}{4},...
\end{align*}\)
ดังนั้น \(\rm{t_{min}} = \dfrac{{3\pi }}{8}\)| 137. | บล็อกไม้สี่เหลี่ยมผืนผ้าสม่ำเสมอมวล M ยาว b สูง a อยู่พื้นเอียงดังรูป บล็อกและพื้นเอียงมีสัมประสิทธิ์แรงเสียดทาน μs และพื้นเอียงทำมุม θ กับแนวระดับ ในบางมุมวิกฤติบล็อกอาจพลิกลง หรือไถลไปตามพื้นเอียงก็ได้ จงหาความสัมพันธ์ระหว่าง a, b และ μs ที่ทำให้บล็อกพลิกลง (และไม่ไถล) ที่มุมวิกฤติ อย่าลืมว่า บล็อกเป็นรูปสี่เหลี่ยมผืนผ้า และ a ≠ b
 |
| A | μs > a/b |
| B | μs > 1 – a/b |
| C | μs > b/a |
| D | μs < a/b |
| E | μs < b/a – 1 |
ตอบ (C)
จากบล็อกไม่ไถล แสดงว่า fs = Mgsinθ หรือ fs max > Mgsinθ
ให้ P เป็นจุดหมุน และเกิดทอร์กที่จุด P ที่ Critical angle torque ที่ P = 0 พอดี และ N ผ่านจุด P เนื่องจากกล่องกำลังจะพลิก จะได้ว่า
ให้ P เป็นจุดหมุน และเกิดทอร์กที่จุด P ที่ Critical angle torque ที่ P = 0 พอดี และ N ผ่านจุด P เนื่องจากกล่องกำลังจะพลิก จะได้ว่า
\(\begin{align*} {\rm{Mgsin\theta }}\left( {\frac{{\rm{a}}}{{\rm{2}}}} \right) &= {\rm{ Mgcos\theta }}\left( {\frac{{\rm{b}}}{{\rm{2}}}} \right)\\ {\rm{tan\theta}} &=\frac{{\rm{b}}}{{\rm{a}}} \end{align*}\)
แทนใน fs max > Mgsinθ จะได้
\(\begin{align*} {{\rm{\mu }}_{\rm{s}}}\rm N &> \rm Mgsin\theta\\ {{\rm{\mu }}_{\rm{s}}}{\rm{Mgcos\theta}} &> \rm Mgsin\theta\\ {{\rm{\mu }}_{\rm{s}}} &> \tan\theta\\ {{\rm{\mu }}_{\rm{s}}} &> \frac{{\rm{b}}}{{\rm{a}}} \end{align*}\)
| 138. | แผ่นดิสก์สองแผ่น มีแกนหมุนเบาเสียบที่จุดศูนย์กลางและตั้งฉากกับแผ่นพอดี โดยแกนหมุนจะต้องอยู่ในแนวตั้งตลอดเวลา และดิสก์สามารถหมุนบนแกนได้โดยไม่มีแรงเสียดทาน ถ้าดิสก์หนาเท่ากัน และทำจากวัสดุเดียวกัน แต่รัศมีแตกต่างกันเป็น r1 และ r2 ดิสก์จะมีความเร็วเชิงมุมเป็น ω1 และ ω2 ตามลำดับ เมื่อนำขอบดิสก์มาสัมผัสกัน จะเกิดแรงเสียดทานจนกระทั่งสองแผ่นหยุดชะงัก แล้วข้อใดสรุปความสัมพันธ์ที่เกิดขึ้นได้ถูกต้อง ไม่ต้องคำนึงผลที่เกิดจากแกนหมุนแนวตั้ง
 |
| A | ω12r1 = ω22r2 |
| B | ω1r1 = ω2r2 |
| C | ω1r12 = ω2r22 |
| D | ω1r13 = ω2r23 |
| E | ω1r14 = ω2r24 |
ตอบ (D)
ให้ ρ = ความหนาแน่นของวัสดุ และ ∆t = ความหนา
เมื่อมาสัมผัสกันจะเกิดแรงเสียดทาน (f) ซึ่ง generate torque จนทำให้ทั้ง 2 แผ่นหยุดหมุนพร้อมกัน
พิจารณาแผ่นที่ 1
\(\begin{align*} \rm \tau_1 &=\rm \frac{\Delta L}{\Delta t}\\ \rm\int fr_1dt&=\rm 0 - \left( \frac{1}{2}m_1r_1^2 \right)\omega _1 \\ \rm-\int fr_1dt&=\rm \frac{1}{2}m_1r_1^2 \omega _1\\ \rm-\int fdt&= \frac{1}{2}\frac{{\left( {\pi \Delta {\rm{t}}\rho } \right){\rm{r}}_{\rm{1}}^{\rm{2}}{\omega _{\rm{1}}}}}{{{{\rm{r}}_{\rm{1}}}}}\\ \rm-\int fdt&= \frac{1}{2}\left( {{\rm{\pi \Delta t\rho }}} \right){\rm{r}}_{\rm{1}}^{\rm{3}}{{\rm{\omega }}_{\rm{1}}} \end{align*}\)
พิจารณาแผ่นที่ 2 ในทำนองเดียวกัน จะได้
ให้ ρ = ความหนาแน่นของวัสดุ และ ∆t = ความหนา
เมื่อมาสัมผัสกันจะเกิดแรงเสียดทาน (f) ซึ่ง generate torque จนทำให้ทั้ง 2 แผ่นหยุดหมุนพร้อมกัน
พิจารณาแผ่นที่ 1
\(\begin{align*} \rm \tau_1 &=\rm \frac{\Delta L}{\Delta t}\\ \rm\int fr_1dt&=\rm 0 - \left( \frac{1}{2}m_1r_1^2 \right)\omega _1 \\ \rm-\int fr_1dt&=\rm \frac{1}{2}m_1r_1^2 \omega _1\\ \rm-\int fdt&= \frac{1}{2}\frac{{\left( {\pi \Delta {\rm{t}}\rho } \right){\rm{r}}_{\rm{1}}^{\rm{2}}{\omega _{\rm{1}}}}}{{{{\rm{r}}_{\rm{1}}}}}\\ \rm-\int fdt&= \frac{1}{2}\left( {{\rm{\pi \Delta t\rho }}} \right){\rm{r}}_{\rm{1}}^{\rm{3}}{{\rm{\omega }}_{\rm{1}}} \end{align*}\)
พิจารณาแผ่นที่ 2 ในทำนองเดียวกัน จะได้
\(\displaystyle- \int {{\rm{fdt}} = \frac{1}{2}\left( {{\rm{\pi \Delta t\rho }}} \right){\rm{r}}_{\rm{2}}^{\rm{3}}{{\rm{\omega }}_2}} \)
ดังนั้น \({\rm{r}}_{\rm{1}}^{\rm{3}}{{\rm{\omega }}_1} = {\rm{r}}_{\rm{2}}^{\rm{3}}{{\rm{\omega }}_2}\)| 139. | ขี่มอเตอร์ไซค์ไต่รอบถังทรงกลมขนาดใหญ่ ถ้าสัมประสิทธิ์แรงเสียดทานระหว่างยางมอเตอร์ไซค์กับผนัง คือ μ แล้ว μ น้อยสุดที่ทำให้มอเตอร์ไซค์ไม่หล่นลงไปเท่ากับข้อใด ตอบในรูป μ ที่แปรผันกับอัตราเร็ว s ของมอเตอร์ไซค์ |
| A | \(\rm\mu \propto {s^0}\) |
| B | \(\rm\mu \propto {s^{ - 1/2}}\) |
| C | \(\rm\mu \propto {s^{ - 1}}\) |
| D | \(\rm\mu \propto {s^{ - 2}}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
| 140. | มวล m ถูกแขวนด้วยสปริงเบาที่ติดอยู่เพดานภายในของกล่องมวล M ขณะกล่องอยู่นิ่งระบบสปริงจะสั่นในแนวตั้งด้วยความถี่เชิงมุม ω ถ้าปล่อยกล่องให้ตกลงอย่างอิสระภายใต้แรงโน้มถ่วง แล้วความถี่เชิงมุมจะเปลี่ยนแปลงอย่างไร |
| A | ω จะไม่เปลี่ยนแปลง |
| B | ω จะเพิ่มขึ้น |
| C | ω จะลดลง |
| D | การสั่นจะไม่เกิดขึ้น ภายใต้เงื่อนไขดังกล่าว |
| E | ω จะเปลี่ยนแปลง โดยขึ้นกับมวล M และ m |
ตอบ (B)
| 141. | ลูกบอลเล็กรัศมี R มวล m ถูกใส่เข้าไปในบอลใหญ่เปลือกบางที่มีมวลเท่ากัน แต่มีรัศมี 2R ให้ตอนแรกลูกบอลเล็กอยู่ที่ผิวด้านข้างของลูกบอลใหญ่ และยังไม่เสียดสีกับพื้นในแนวนอน จากนั้นปล่อยลูกบอลเล็กให้กลิ้งภายในบอลใหญ่ จนหยุดที่ด้านล่างของลูกบอลใหญ่ แล้วลูกบอลใหญ่จะกลิ้งไปได้เท่าไร จากจุดเริ่มต้นที่สัมผัสพื้น
 |
| 142. | รถแบบเดียวกันหลายคันกำลังติดไฟแดงบนถนนหนึ่งเลน ซึ่งจอดต่อกันเป็นแถวเดียว และมีระยะหว่างระหว่างคันเท่ากัน เมื่อขึ้นไฟเขียว รถคันแรกไปทิศขวาด้วยความเร่งคงที่ แล้วรถคันที่สองก็วิ่งแบบเดียวกันใน 0.2 วินาที ให้หลัง และรถคันถัดไปก็จะวิ่งอย่างเดียวกัน ถ้ารถทุกคันเร่งความเร็ว จนมีอัตราเร็ว 45 km/hr จากนั้นวิ่งไปทิศขวาด้วยอัตราเร็วคงที่ พิจารณาการเรียงแถวของรถยนต์ ตามรูป
 |
| A | เปลี่ยนจาก I ไป II ไป III |
| B | เปลี่ยนจาก I ไป II ไป IV |
| C | เปลี่ยนจาก I ไป IV ไม่มี II และ III |
| D | เปลี่ยนจาก I ไป II |
| E | เปลี่ยนจาก I ไป III |
ตอบ (B)
| 143. | ยิงปืนด้วยอัตราเร็ว v0 ออกจากขอบหน้าผาสูง h ทำมุม θ กับแนวนอน โดยไม่คำนึงถึงแรงต้านอากาศ จงหา θ ที่ทำให้กระสุนพุ่งออกไปในแนวราบได้ไกลที่สุด |
| A | 45° < θ < 90° |
| B | θ = 45° |
| C | 0° < θ < 45° |
| D | θ = 0° |
| E | θ < 45° หรือ 45° < θ ขึ้นกับค่า h และ v0 |
ตอบ (C)
| 144. | กำหนดคานสองคาน มีเชือกเบา 7 เส้น ผูกอยู่ในตำแหน่งต่างๆ ดังรูป ถ้ามวลของวัตถุ M1 = 400 g, M2 = 200 g และ M4 = 500 กรัม แล้วมวล M3 มีค่าเท่าใด เมื่อคานอยู่ในสภาวะสมดุล
 |
| 145. | รถไฟเดิมมีมวล M เคลื่อนที่ไปตามแนวราบโดยไม่มีแรงเสียดทาน และมีอัตราเร็วคงที่ เมื่อหิมะเริ่มตกลงมาเกาะรถไฟด้วยอัตรา ρ โดย ρ มีหน่วย kg/s ซึ่งรถไฟจะต้องรักษาระดับอัตราเร็ว v ให้คงที่ แม้จะมีหิมะเกาะสะสมอยู่บนรถไฟ แล้วพลังงานจลน์ของรถไฟและหิมะเพิ่มขึ้นในอัตราเท่าใด |
| A | \(0\) |
| B | \(\rm Mgv\) |
| C | \(\rm \dfrac{1}{2}Mv^2\) |
| D | \(\rm \dfrac{1}{2}\rho v^2\) |
| E | \(\rm \rho v^2\) |
ตอบ (D)
| 146. | รถไฟเดิมมีมวล M เคลื่อนที่ไปตามแนวราบโดยไม่มีแรงเสียดทาน และมีอัตราเร็วคงที่ เมื่อหิมะเริ่มตกลงมาเกาะรถไฟด้วยอัตรา ρ โดย ρ มีหน่วย kg/s ซึ่งรถไฟจะต้องรักษาระดับอัตราเร็ว v ให้คงที่ แม้จะมีหิมะเกาะสะสมอยู่บนรถไฟ กำลังต่ำสุดที่รถไฟต้องใช้รักษาระดับอัตราเร็ว v ให้คงที่ เท่ากับข้อใด |
| A | \(0\) |
| B | \(\rm Mgv\) |
| C | \(\rm \dfrac{1}{2}Mv^2\) |
| D | \(\rm \dfrac{1}{2}\rho v^2\) |
| E | \(\rm \rho v^2\) |
ตอบ (E)
| 147. | ขวด A, B และ C มีฐานเป็นวงกลมรัศมี 2 cm เหมือนกัน ถ้าเทน้ำที่มีปริมาณเท่ากัน ลงในขวดแต่ละใบ โดยไม่ให้มีน้ำล้นออกมา จงเรียงลำดับ แรง F ที่น้ำกระทำกับฐานของขวดจากมากไปหาน้อย  |
| 148. | หูจับแกลลอนนม มี Plug อุดอยู่เนื่องจากข้อผิดพลาดในการผลิต หลังจากเปิดฝา แล้วเทนมบางส่วนออกมา นมที่อยู่ในแกลลอนจะอยู่ต่ำกว่านมที่อยู่ในหูจับ ตามรูป ข้อใดเป็นจริงเกี่ยวกับความดันเกจ P ของนมที่ฐานด้านล่างของแกลลอน เมื่อ ρ คือ ความหนาแน่นของนม  |
| 149. | ทรงกลมตันขนาดเล็กมวล m รัศมีเล็กมาก เชื่อมกับคานบางยาว L มีมวล 2m และทรงกลมตันขนาดเล็กอันที่สองมวล M มีรัศมีเล็กมาก ถูกยิงในแนวตั้งฉากกับคานบางเหนือทรงกลมตันแรกเป็นระยะ h ดังรูป
 |
| 150. | ทรงกลมตันขนาดเล็กมวล m รัศมีเล็กมาก เชื่อมกับคานบางยาว L มีมวล 2m และทรงกลมตันขนาดเล็กอันที่สองมวล M มีรัศมีเล็กมาก ถูกยิงในแนวตั้งฉากกับคานบางเหนือทรงกลมตันแรกเป็นระยะ h ดังรูป
 |
| 151. | เชือกเบาคล้องผ่านรอกที่ไม่มีความฝืด วัตถุมวล M และ M + m ถูกแขวนที่ปลายเชือกแต่ละด้าน ถ้า m = 0 แล้วแรงตึงเชือก T เท่ากับ Mg แล้วกรณีที่เพิ่มค่า m ถึงอนันต์ แรงตึงเชือกจะเปลี่ยนไปอย่างไร |
| A | คงที่ |
| B | ลดลง และเข้าใกล้ค่าคงที่ ที่ไม่ใช่ศูนย์ |
| C | ลดลง และเข้าใกล้ 0 |
| D | เพิ่มขึ้น และเข้าใกล้ค่าคงที่ค่าหนึ่ง |
| E | เพิ่มขึ้น และมีค่าเป็นอนันต์ |
ตอบ (D)
| 152. | กำหนดให้ วัตถุจากจุดนิ่งกลิ้งลงบนพื้นลาดเอียงโดยไม่ไถล ถ้าวัตถุในแต่ละข้อมีมวล M รัศมี R เหมือนกัน แล้วข้อใดมีอัตราเร่งมากสุด ขณะกลิ้งลงมา |
| 153. | กำหนดให้ วัตถุจากจุดนิ่งกลิ้งลงบนพื้นลาดเอียงโดยไม่ไถล ถ้าวัตถุในแต่ละข้อเป็นทรงกลมสม่ำเสมอ ที่เดิมอยู่นิ่งและถูกปล่อยออกเหมือนกัน แล้วข้อใดจะมีอัตราเร็วมากที่สุด หลังจุดศูนย์กลางมวลเคลื่อนที่ตามแนวตั้งไปได้ระยะ h แล้ว |
| A | ทรงกลมมวล M รัศมี R |
| B | ทรงกลมมวล 2M รัศมี \(\frac{1}{2}\) R |
| C | ทรงกลมมวล M/2 รัศมี 2R |
| D | ทรงกลมมวล 3M รัศมี 3R |
| E | ทุกข้อมีอัตราเร็วเท่ากัน |
ตอบ (E)
| 154. | ไม้ท่อนหนึ่งถูกวางพาดกับผนังเอียง ดังรูป ถ้าส่วนปลายของไม้ที่สัมผัสพื้นเคลื่อนที่ด้วยความเร็ว v แล้วอัตราเร็วส่วนปลายที่สัมผัสกับผนังจะมีค่าเท่ากับข้อใด
 |
| A | \(\rm v\dfrac{{\sin \theta }}{{\cos (\alpha - \theta )}}\) |
| B | \(\rm v\dfrac{{\sin (\alpha - \theta )}}{{\cos (\alpha + \theta )}}\) |
| C | \(\rm v\dfrac{{\cos (\alpha - \theta )}}{{\sin (\alpha + \theta )}}\) |
| D | \(\rm v\dfrac{{\cos \theta }}{{\cos (\alpha - \theta )}}\) |
| E | \(\rm v\dfrac{{\sin \theta }}{{\cos (\alpha + \theta )}}\) |
ตอบ (D)
| 155. | วัตถุถูกขว้างลงมาในแนวดิ่งจากอาคารสูง 180 เมตร ถ้าผ่านไป 1.0 วินาที วัตถุเคลื่อนที่ได้ 60 เมตร แล้วอัตราเร็วต้นของวัตถุที่ขว้างลงมาเท่ากับข้อใด |
| 156. | แผ่นกลมถูกดึงด้วยแรง F ผ่านเชือกที่ยึดกับจุดศูนย์กลางมวล ดังรูป สมมุติว่า แผ่นกลมกลิ้งโดยไม่มีการไถล ในช่วงเวลาหนึ่ง ๆ พื้นที่ใดที่มีความเร่งเป็นศูนย์ (ถ้ามี)
 |
| 157. | ลูกฮอกกี้ถูกตีขึ้นทางลาดที่ทำมุม 30◦ กับแนวนอน ได้กราฟอัตราเร็วของลูกฮอกกี้กับเวลา ดังรูป แล้วค่าสัมประสิทธิ์แรงเสียดทานระหว่างลูกฮอกกี้กับทางลาดเท่ากับข้อใด
 |
| 158. | วัตถุมวล m เคลื่อนที่ด้วยอัตราเร็ว v0 ชนกับวัตถุมวล M ซึ่งเดิมอยู่นิ่ง จะได้สัดส่วนการถ่ายโอนโมเมนตัม f คือ ค่าสัมบูรณ์ของโมเมนตัมสุดท้ายของ M หารด้วยโมเมนตัมเริ่มต้นของ m ถ้าการชนนั้นไม่ยืดหยุ่นสมบูรณ์ แล้วเงื่อนไขในข้อใด ที่ทำให้สัดส่วนการถ่ายโอนโมเมนตัมของสองวัตถุ มีค่ามากสุด |
| 159. | วัตถุมวล m เคลื่อนที่ด้วยอัตราเร็ว v0 ชนกับวัตถุมวล M ซึ่งเดิมอยู่นิ่ง จะได้สัดส่วนการถ่ายโอนโมเมนตัม f คือ ค่าสัมบูรณ์ของโมเมนตัมสุดท้ายของ M หารด้วยโมเมนตัมเริ่มต้นของ m ถ้าการชนนั้นยืดหยุ่นสมบูรณ์ แล้วสัดส่วนการถ่ายโอนโมเมนตัมที่มีค่ามากสุด ที่เป็นไปได้ fmax มีค่าเท่าใด |
| A | \(\rm 0 < f_{max} < \dfrac{1}{2}\) |
| B | \(\rm f_{max} = \dfrac{1}{2}\) |
| C | \(\rm \dfrac{1}{2} < f_{max} < \dfrac{3}{2}\) |
| D | \(\rm f_{max} = 2\) |
| E | \(\rm f_{max}\ge 3\) |
ตอบ (D)
| 160. | วัตถุมวล m เคลื่อนที่ด้วยอัตราเร็ว v0 ชนกับวัตถุมวล M ซึ่งเดิมอยู่นิ่ง จะได้สัดส่วนการถ่ายโอนโมเมนตัม f คือ ค่าสัมบูรณ์ของโมเมนตัมสุดท้ายของ M หารด้วยโมเมนตัมเริ่มต้นของ m สัดส่วนการถ่ายโอนพลังงาน คือ ค่าสัมบูรณ์ของพลังงานจลน์สุดท้ายของ M หารด้วยพลังงานจลน์เริ่มต้นของ m ถ้าการชนนั้นยืดหยุ่นสมบูรณ์ แล้วเงื่อนไขในข้อใด ที่ทำให้สัดส่วนการถ่ายโอนพลังงานของสองวัตถุ มีค่ามากสุด |
| 161. | สปริงขณะยังไม่ถูกดึงยาว 1.0 เมตร เมื่อยืดสปริงให้ยาว 10 เมตร การสั่นของคลื่นจากปลายหนึ่งไปสู่อีกปลายใช้เวลา 1.0 วินาที ถ้ายืดสปริงให้ยาว 20 เมตร แล้วเวลาที่ใช้ในการสั่นของคลื่นจากปลายหนึ่งไปสู่อีกปลาย จะมีค่าใกล้เคียงกับข้อใด |
| 162. | บอลมวล m เคลื่อนที่ด้วยอัตราเร็ว v ชนกับสปริงเบาที่มีค่านิจสปริง k โดยสปริงติดอยู่กับกล่องนิ่งมวล M ในอวกาศ ถ้าการชนไม่มีการสูญเสียพลังงานเชิงกล และระบบไม่เกิดการหมุน แล้วระยะหดมากสุดของสปริง x มีค่าเท่ากับข้อใด |
| A | \(\rm x = v\sqrt {\dfrac{{mM}}{{(m + M)k}}}\) |
| B | \(x = v\sqrt {\dfrac{m}{k}}\) |
| C | \(\rm x = v\sqrt {\dfrac{M}{k}}\) |
| D | \(x = v\sqrt {\dfrac{{m + M}}{k}}\) |
| E | \(\rm x = v\sqrt {\dfrac{{{{(m + M)}^3}}}{{mMk}}}\) |
ตอบ (A)
| 163. | ดาวเคราะห์ดวงหนึ่งโคจรรอบดาวฤกษ์ S ดังรูป ให้ระยะครึ่งแกนเอกถึงวงโคจร เท่ากับ a และ ระยะที่สั้นที่สุดระหว่างดาวเคราะห์กับดาวฤกษ์ มีค่าเท่า 0.5a ถ้าดาวเคราะห์เคลื่อนผ่านไป จุด P (จุดบนเส้นตรงที่ผ่านดาวฤกษ์ S และตั้งฉากกับแกนเอก) ด้วยอัตราเร็ว v1 แล้วอัตราเร็ว v2 ขณะผ่านจุด perigee มีค่าเท่ากับข้อใด
 |
| A | \(\rm {v_2} = \dfrac{3}{{\sqrt 5 }}{v_1}\) |
| B | \(\rm {v_2} = \dfrac{3}{{\sqrt 7 }}{v_1}\) |
| C | \(\rm{v_2} = \dfrac{2}{{\sqrt 3 }}{v_1}\) |
| D | \(\rm {v_2} = \dfrac{{\sqrt 7 }}{{\sqrt 3 }}{v_1}\) |
| E | \(\rm {v_2} = 4{v_1}\) |
ตอบ (A)
| 164. | รถขับทวนเข็มนาฬิกาบนถนนโค้งเรียบ ด้วยอัตราเร็วคงที่ ถ้าล้อหน้าซ้ายเคลื่อนที่เป็นวงกลมรัศมี R = 9.60 เมตร และรถกว้าง 1.74 m แล้วอัตราส่วนความเร็วเชิงมุมของการหมุนของเพลาล้อหน้าซ้าย ต่อเพลาล้อหน้าขวาของรถ ขณะเข้าโค้งเท่ากับข้อใด สมมติว่าล้อหมุนโดยไม่ไถล |
| A | 0.331 |
| B | 0.630 |
| C | 0.708 |
| D | 0.815 |
| E | 0.847 |
ตอบ (E)
เนื่องจากความเร็วคงที่ เราจึงใช้ความเร็วเชิงมุมเฉลี่ย ω = Δθ / Δt ได้
โดยทั้งสองล้อจะมี Δt เดียวกัน ส่วน Δθ จะหาจาก
ดังนั้น Δθ ของล้อซ้ายเท่ากับ
เนื่องจากความเร็วคงที่ เราจึงใช้ความเร็วเชิงมุมเฉลี่ย ω = Δθ / Δt ได้
โดยทั้งสองล้อจะมี Δt เดียวกัน ส่วน Δθ จะหาจาก
\(\rm Δθ = S / C\)
โดยที่ S คือ ความยาวส่วนโค้งที่ล้อกวาดไป และ C คือ เส้นรอบวงของล้อ ให้พิจารความยาวส่วนโค้งในหน่วย \(\pi\) เรเดียน จะได้ S = \(\pi\) R ดังนั้น Δθ ของล้อซ้ายเท่ากับ
\(\Delta {\theta _l} = \dfrac{{\pi {\rm{R}}}}{{2\pi {\rm{r}}}}\)
และ Δθ ของล้อขวาเท่ากับ
\(\Delta {\theta _r} = \dfrac{{\pi ({\rm{R + dR)}}}}{{2\pi {\rm{r}}}}\)
จากล้อทั้งสองมีรัศมี r เท่ากัน เมื่อเทียบสัดส่วนจะได้
\(\dfrac{{{\omega _l}}}{{{\omega _r}}} = \dfrac{{\dfrac{{\pi {\rm{R}}}}{{2\pi {\rm{r}}\Delta {\rm{t}}}}}}{{\dfrac{{\pi ({\rm{R + dR)}}}}{{2\pi {\rm{r}}\Delta {\rm{t}}}}}} = \dfrac{{\rm{R}}}{{{\rm{R + dR}}}} = \dfrac{1}{{1 + \dfrac{{{\rm{dR}}}}{{\rm{R}}}}}\)
แทนค่าลงไปจะได้
\(\dfrac{{{\omega _l}}}{{{\omega _r}}} = \frac{1}{{1 + \dfrac{{{\rm{1}}{\rm{.74m}}}}{{{\rm{9}}{\rm{.60m}}}}}} = 0.847\)
| 165. | ชั้นน้ำมันหนา 3.0 cm มีความหนาแน่น ρo = 800 kg / m3 ลอยเหนือน้ำที่มีความหนาแน่น ρw = 1000 kg / m3 กำหนดให้เดิม 1/3 ของทรงกระบอกตันลอยอยู่ในน้ำ อีก 1/3 ลอยอยู่ในน้ำมัน และอีก 1/3 อยู่ในอากาศ ถ้าเติมน้ำมันเพิ่มจนกว่าทรงกระบอกจะลอยในชั้นน้ำมันเท่านั้น แล้วสัดส่วนของทรงกระบอกที่ลอยอยู่ในชั้นน้ำมันเท่ากับข้อใด
 |
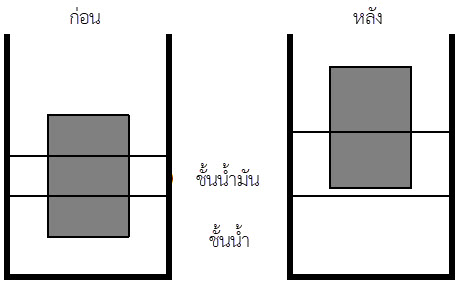| A | 3/5 |
| B | 3/4 |
| C | 2/3 |
| D | 8/9 |
| E | 4/5 |
ตอบ (B)
สมมุติว่า ทรงกระบอกมีปริมาตร 3 ลูกบาศก์เมตร แสดงว่ามวลเข้ามาแทนที่น้ำ 1000 kg และเข้ามาแทนที่น้ำมัน 800 kg โดยไม่ต้องพิจารณาการแทนที่ในอากาศ จะได้มวลที่เข้ามาแทนที่ทั้งหมด 1800 kg ถ้าต้องการให้ทรงกระบอกลอยอยู่ในชั้นน้ำมันเท่านั้น หมายความว่าน้ำมันจะต้องถูกแทนที่ด้วยมวล 1800 kg คิดเป็นปริมาณน้ำมันได้
สมมุติว่า ทรงกระบอกมีปริมาตร 3 ลูกบาศก์เมตร แสดงว่ามวลเข้ามาแทนที่น้ำ 1000 kg และเข้ามาแทนที่น้ำมัน 800 kg โดยไม่ต้องพิจารณาการแทนที่ในอากาศ จะได้มวลที่เข้ามาแทนที่ทั้งหมด 1800 kg ถ้าต้องการให้ทรงกระบอกลอยอยู่ในชั้นน้ำมันเท่านั้น หมายความว่าน้ำมันจะต้องถูกแทนที่ด้วยมวล 1800 kg คิดเป็นปริมาณน้ำมันได้
\({{\rm{V}}_{\rm{o}}}{\rm{ = }}\left( {{\rm{1800 kg}}} \right){\rm{ / }}\left( {{\rm{800 kg/}}{{\rm{m}}^{\rm{3}}}} \right){\rm{ = }}\dfrac{9}{4}{{\rm{m}}^{\rm{3}}}\)
เทียบสัดส่วนที่ลอยอยู่ในชั้นน้ำมันจะเท่ากับ
\(\left( {\dfrac{{\rm{9}}}{{\rm{4}}}{\rm{}}{{\rm{m}}^{\rm{3}}}} \right){\rm{/}}\left( {{\rm{3}}{{\rm{m}}^{\rm{3}}}} \right){\rm{ = }}\dfrac{{\rm{3}}}{{\rm{4}}}{\rm{}}\)
| 166. | นักเรียนวิชาฟิสิกส์เบื้องต้น ฉลองเกรดเทอมแรกของเขาด้วยการทิ้งหนังสือลงมาจากระเบียงลงยังไปกองหิมะด้านล่างสูง 3.00 m ถ้าหนังสือเล่มนี้จมลงไปในหิมะประมาณ 1.00 m และหนังสือมีมวล 5 kg แล้วแรงเฉลี่ยที่หิมะกระทำกับหนังสือเท่ากับข้อใด |
| A | 85 N |
| B | 100 N |
| C | 120 N |
| D | 150 N |
| E | 200 N |
ตอบ (E)
กำหนดตัวแปร H = 3.00 m , h = 1.00 m และ v เป็นอัตราเร็วที่หนังสือตกลงไปถึงพื้น จากหลักจลน์ศาสตร์จะได้
เนื่องจาก a = 3g
ดังนั้น แรงที่หิมะกระทำกลับมาจะเท่ากับ 4mg
หรือคิดจากพลังงานศักย์ที่สูญเสียจากแรงเสียดทาน
กำหนดตัวแปร H = 3.00 m , h = 1.00 m และ v เป็นอัตราเร็วที่หนังสือตกลงไปถึงพื้น จากหลักจลน์ศาสตร์จะได้
\(\rm 2gH = v^2 =2ah\)
โดย a คือ ความเร่งบนหิมะเนื่องจาก a = 3g
ดังนั้น แรงที่หิมะกระทำกลับมาจะเท่ากับ 4mg
หรือคิดจากพลังงานศักย์ที่สูญเสียจากแรงเสียดทาน
\(\rm mg × 4\) เมตร \(\rm = F × 1\) เมตร
ดังนั้น F = 4mg นิวตัน| 167. | ปล่อยลูกปัดให้ไถลไปตามลวดที่ขดเหมือนสปริงในแนวตั้ง ข้อใดคือกราฟขนาดความเร่งลัพธ์ a ต่อเวลา t ของเหตุการณ์ดังกล่าว |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (D)
ความเร่งในแนวสัมผัสกับเกลียวลวดจะเท่ากับ
ความเร่งในแนวสัมผัสกับเกลียวลวดจะเท่ากับ
\(\rm a_t = g~ sin θ\)
โดย θ คือ ขนาดมุมเอียงของเกลียวลวด ถ้าความเร่งมาก ลูกปัดก็จะเคลื่อนที่เร็วขึ้น ตามสมการ
\(\rm v = a_t t\)
เนื่องจากลูกปัดเคลื่อนที่เป็นวงกลม ความเร่งตามเรเดียนจะเท่ากับ
\({\rm{a = }}\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{r}}}{\rm{ = }}\dfrac{{{\rm{a}}_{\rm{t}}^{\rm{2}}}}{{\rm{r}}}{{\rm{t}}^{\rm{2}}}\)
ดังนั้น ความเร่งของลูกปัดจะเท่ากับ
\({\rm{a}} = \sqrt {{{\rm{a}}_{\rm{r}}}^2 + {{\rm{a}}_{\rm{t}}}^2} = {{\rm{a}}_{\rm{t}}}\sqrt {{{\rm{a}}_{\rm{t}}}^2\dfrac{{{{\rm{t}}^4}}}{{{{\rm{r}}^2}}} + 1} \)
| 168. | พิจารณาวัตถุในกล่องที่มีแรงโน้มถ่วงในทิศลง ดังรูป
 แล้วภาพในข้อใด แสดงทิศทางการเคลื่อนที่ของวัตถุภายในกล่องได้ถูกต้อง |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (C)
โดยปกติแล้ว การเคลื่อนที่ที่มีความเร่งจะเคลื่อนที่แบบพาราโบลา ซึ่งตรงกับข้อ (C) และ (E)
แต่ (E) ผิด เพราะ การเคลื่อนที่นั้นจะเกิดในกรณีที่ไม่มีความเร่งในแนวนอน
โดยปกติแล้ว การเคลื่อนที่ที่มีความเร่งจะเคลื่อนที่แบบพาราโบลา ซึ่งตรงกับข้อ (C) และ (E)
แต่ (E) ผิด เพราะ การเคลื่อนที่นั้นจะเกิดในกรณีที่ไม่มีความเร่งในแนวนอน
| 169. | พิจารณาวัตถุในกล่องที่มีแรงโน้มถ่วงในทิศลง ดังรูป
 หากเลือกขนาดความเร่งของกล่องได้ถูกต้อง วัตถุสามารถเคลื่อนที่กลับมายังจุดเริ่มได้อีกครั้ง ภาพในข้อใด แสดงทิศทางการเคลื่อนที่ของวัตถุภายในกล่องได้ถูกต้อง |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (A)
โดยปกติแล้ว การเคลื่อนที่ที่มีความเร่งจะเคลื่อนที่แบบพาราโบลา
ดังนั้น ทิศทางการเคลื่อนที่ของวัตถุภายในกล่องจะเป็นไปตามข้อ (A)
โดยปกติแล้ว การเคลื่อนที่ที่มีความเร่งจะเคลื่อนที่แบบพาราโบลา
ดังนั้น ทิศทางการเคลื่อนที่ของวัตถุภายในกล่องจะเป็นไปตามข้อ (A)
| 170. | (เกินหลักสูตรการสอบเข้า สอวน.) มวลติดกับสปริงที่ยังไม่ถูกยืดออกและตรึงปลายด้านหนึ่งไว้ ถูกวางบนโต๊ะลื่น ถ้าขยับมวลออกมาด้วยระยะ A ขนานกับโต๊ะ แต่ตั้งฉากกับสปริงจนเกิดการสั่น แล้วคาบของการสั่น T จะเปลี่ยนไปอย่างไร |
| A | คาบของการสั่นไม่ได้ขึ้นกับระยะ A |
| B | เพิ่มขึ้น เมื่อ A เพิ่มขึ้น และเข้าใกล้ค่าคงที่ค่าหนึ่ง |
| C | ลดลง เมื่อ A เพิ่มขึ้น และเข้าใกล้ค่าคงที่ค่าหนึ่ง |
| D | หาค่าประมาณเป็นค่าคงที่ได้ เมื่อ A มีค่าเล็กๆ จากนั้นจะเพิ่มขึ้นโดยไม่มีขอบเขต |
| E | หาค่าประมาณเป็นค่าคงที่ได้ เมื่อ A มีค่าเล็กๆ จากนั้นจะลดลงโดยไม่มีขอบเขต |
ตอบ (C)
| 171. | จากกฎของเคปเลอร์ ( Kepler's Laws ) ระบุว่า I. วงโคจรของดาวเคราะห์จะเป็นวงรี โดยมีดวงอาทิตย์เป็นจุดโฟกัส II. เส้นตรงที่เชื่อมระหว่างดาวเคราะห์กับดวงอาทิตย์จะกวาดพื้นที่ได้เท่ากัน ในระยะเวลาที่เท่ากัน III. กำลังสองของคาบการโคจรของดาวเคราะห์ เป็นสัดส่วนโดยตรงกับกำลังสามของกึ่งแกนเอก (semimajor axis) ของวงโคจร กฎข้อใดจะเป็นจริง ถ้าแรงโน้มถ่วงมีสัดส่วนเป็น 1/r3 แทนที่จะเป็น 1/r2 |
| A | เฉพาะข้อ I. |
| B | เฉพาะข้อ II. |
| C | เฉพาะข้อ III. |
| D | ข้อ I. และ II. |
| E | ไม่มีข้อใดเป็นจริง |
ตอบ (B)
เพราะกฎข้อที่สองเป็นไปตามกฎการอนุรักษ์โมเมนตัมเชิงมุม จึงเป็นจริงสำหรับ central potential ใดๆ
ส่วนอีกสองข้อจำเป็นจะต้องแปรผันกับ 1/r2
เพราะกฎข้อที่สองเป็นไปตามกฎการอนุรักษ์โมเมนตัมเชิงมุม จึงเป็นจริงสำหรับ central potential ใดๆ
ส่วนอีกสองข้อจำเป็นจะต้องแปรผันกับ 1/r2
| 172. | ลูกปัดขนาดเล็กวางอยู่บนลูกแก้วกลมลื่นที่มีเส้นผ่านศูนย์กลาง D ดังรูป ถ้าสะกิดให้ลูกปัดลื่นไปตามลูกแก้ว แล้วอัตราเร็ว v ของลูกปัด ขณะไหลตกจากลูกแก้วเท่ากับข้อใด
 |
| A | \(\rm v = \sqrt {gD}\) |
| B | \(\rm v = \sqrt {4gD/5}\) |
| C | \(\rm v = \sqrt {2gD/3}\) |
| D | \(\rm v = \sqrt {gD/2}\) |
| E | \(\rm v = \sqrt {gD/3}\) |
ตอบ (E)
หาคำตอบจากสมการ
หาคำตอบจากสมการ
\(\begin{align*} \rm mgh &=\frac{1}{2}\rm mv^2\\ \rm{mg ~sin}\theta &= \rm m\frac{v^2}{\rm R} \end{align*}\)
| 173. | กล่องสองใบ ถูกผูกติดกันด้วยเชือกเบาสองเส้น และนำไปแขวนไว้บนเพนดาน ดังรูป มวลของกล่องบนและล่างหนัก m1 = 2 kg และ m2 = 4 kg ตามลำดับ ถ้าตัดเชือกที่แขวนกับเพดานแล้วความเร่งของกล่องทั้งสองใบ ขณะกล่องใบบนสุดเริ่มร่วงลงจะเท่ากับข้อใด
 |
| A | กล่องบน: 10 m/s2, กล่องล่าง: 0 |
| B | กล่องบน: 10 m/s2, กล่องล่าง: 10m/s2 |
| C | กล่องบน: 20 m/s2, กล่องล่าง: 10 m/s2 |
| D | กล่องบน: 30 m/s2, กล่องล่าง: 0 |
| E | กล่องบน: 30 m/s2, กล่องล่าง: 10 m/s2 |
ตอบ (D)
แผนภาพของกล่องใบที่ 1 และ 2 ก่อนตัดเชือก สามารถใช้พิจารณาขณะเชือกถูกตัดทันทีได้ เพราะเวลาที่เชือกถูกตัดนั้นสั้นมาก และไม่ก่อให้เกิดแรงที่กระทำต่อกล่องใบที่ 1 ลองใช้ผลที่ได้จากแผนภาพหาความเร่งของกล่องทั้งสองใบดู
แผนภาพของกล่องใบที่ 1 และ 2 ก่อนตัดเชือก สามารถใช้พิจารณาขณะเชือกถูกตัดทันทีได้ เพราะเวลาที่เชือกถูกตัดนั้นสั้นมาก และไม่ก่อให้เกิดแรงที่กระทำต่อกล่องใบที่ 1 ลองใช้ผลที่ได้จากแผนภาพหาความเร่งของกล่องทั้งสองใบดู
| 174. | พลังงานที่ออกมาจากรถทดลองรุ่นทรงลูกบาศก์ จะแปรผันตามมวล m ของรถ และแรงต้านอากาศต่อรถจะแปรผันตาม Av2 โดย v คือ อัตราเร็วของรถ และ A คือ พื้นที่ตัดขวาง เมื่ออยู่บนถนนเรียบรถจะมีอัตราเร็วสูงสุดเป็น vmax สมมุติว่า รถรุ่นนี้มีความหนาแน่นเท่ากันทุกคัน แล้วข้อใดต่อไปนี้เป็นจริง |
| A | \(\rm {v_{\max }} \propto {{\rm{m}}^{1/9}}\) |
| B | \(\rm {v_{\max }} \propto {{\rm{m}}^{1/7}}\) |
| C | \(\rm {v_{\max }} \propto {{\rm{m}}^{1/3}}\) |
| D | \(\rm {v_{\max }} \propto {{\rm{m}}^{2/3}}\) |
| E | \(\rm {v_{\max }} \propto {{\rm{m}}^{3/4}}\) |
ตอบ (A)
จากปริมาตรของลูกบาศก์ L ∝ m1/3 ดังนั้น A ∝ m2/3 และโจทย์ให้ความหนาแน่นเป็นค่าคงที่
จะหาความเร็วได้ ดังนี้
จากปริมาตรของลูกบาศก์ L ∝ m1/3 ดังนั้น A ∝ m2/3 และโจทย์ให้ความหนาแน่นเป็นค่าคงที่
จะหาความเร็วได้ ดังนี้
\(\rm m ∝ P = Fv ∝ Av^3 ∝ m^{2/3} v^3\)
ดังนั้น
\(\rm m ∝ v^9\)
| 175. | ให้ภาชนะที่บรรจุของเหลว มีบล็อกก้อนหนึ่งลอยแบบจมบางส่วนอยู่ ถ้าเราเพิ่มความเร่งให้ทั้งภาชนะ แล้วผลลัพธ์จะเป็นอย่างไร สมมุติว่า ทั้งบล็อกและของเหลวไม่สามารถบีบอัดได้ |
| A | บล็อกจะจมลงไปในของเหลว |
| B | บล็อกในของเหลวจะลอยสูงขึ้น |
| C | บล็อกจะไม่ลอยหรือจมไปจากเดิม |
| D | คำตอบขึ้นอยู่กับทิศทางการเคลื่อนที่ของภาชนะ |
| E | คำตอบขึ้นอยู่กับอัตราการเปลี่ยนแปลงของความเร่ง |
ตอบ (C)
ส่วนที่จมหรือลอยไม่ขึ้นกับค่าความโน้มถ่วง g กล่าวคือ
ส่วนที่จมหรือลอยไม่ขึ้นกับค่าความโน้มถ่วง g กล่าวคือ
ρวัตถุgVวัตถุ = ρเหลวgVแทนที่
Vแทนที่ = (ρวัตถุ Vวัตถุ)/ρเหลว
ดังนั้น บล็อกจะไม่ลอยหรือจมไปจากเดิมVแทนที่ = (ρวัตถุ Vวัตถุ)/ρเหลว
| 176. | วัตถุมวล m1 เริ่มเคลื่อนที่ด้วยอัตราเร็ว v0 แล้วชนกับวัตถุที่เดิมหยุดนิ่ง มวล m2 = αm1 โดยที่ α < 1 การชนกันอาจจะยืดหยุ่นสมบูรณ์ ไม่สมบูรณ์ หรือยืดหยุ่นบางส่วนก็ได้ หลังการชน วัตถุทั้งสองจะเคลื่อนที่ด้วยอัตราเร็ว v1 และ v2 สมมุติว่า เป็นการชนกันหนึ่งมิติ และวัตถุแรกไม่สามารถทะลุผ่านวัตถุสองได้ แล้วอัตราส่วนอัตราเร็วของวัตถุที่สองหลังการชน r2 = v2 / v0 จะอยู่ในช่วงใด |
| A | (1 – α) / (1 + α) ≤ r2 ≤ 1 |
| B | (1 – α) / (1 + α) ≤ r2 ≤ 1 / (1 + α) |
| C | α / (1 + α) ≤ r2 ≤ 1 |
| D | 0 ≤ r2 ≤ 2 α / (1 + α) |
| E | 1 / (1 + α) ≤ r2 ≤ 2 / (1 + α) |
ตอบ (E)
จากกฎการอนุรักษ์โมเมนตัม และพลังงานจลน์ ในกรณีที่การชนนั้นยืดหยุ่นสมบูรณ์ จะได้ว่า
จากกฏการอนุรักษ์โมเมนตัม ในกรณีที่การชนนั้นไม่ยืดหยุ่นสมบูรณ์ จะได้ว่า
ดังนั้น
จากกฎการอนุรักษ์โมเมนตัม และพลังงานจลน์ ในกรณีที่การชนนั้นยืดหยุ่นสมบูรณ์ จะได้ว่า
\(\begin{array}{l}
\rm{r_1} = \dfrac{{{v_1}}}{{{v_0}}} = \dfrac{{1 - \alpha }}{{1 + \alpha }}\\
\rm{r_2} = \dfrac{{{v_2}}}{{{v_0}}} = \dfrac{2}{{1 + \alpha }}
\end{array}\)
เนื่องจาก \(\rm \alpha < 1\) วัตถุ m1 จะมีอิทธิพลมากกว่าวัตถุ m2 ดังนั้น การเคลื่อนที่จะยังคงไปข้างหน้า จากกฏการอนุรักษ์โมเมนตัม ในกรณีที่การชนนั้นไม่ยืดหยุ่นสมบูรณ์ จะได้ว่า
\(\rm {r_1} = {r_2} = \dfrac{1}{{1 + \alpha }}\)
จากที่วัตถุ m2 เคลื่อนที่ไปข้างหน้าเสมอ และวัตถุ m1 ไม่สามารถทะลุผ่านวัตถุ m2 ได้ ดังนั้น วัตถุ m2 จะต้องเคลื่อนที่ด้วยความเร็วที่เป็นบวกมากกว่า (หรือเท่ากับ) วัตถุ m1 ดังนั้น
\(\rm 1/(1 + \alpha ) \le {r_2} \le 2/(1 + \alpha )\)
การหาช่วงคำตอบของ วัตถุ m1 อาจจะยากกว่าเล็กน้อย เพราะสถานการณ์นี้อาจจะมีการกระดอนกลับเกิดขึ้น แต่ในกรณีนี้ \(\rm \alpha < 1\) ทำให้ความเร็วหลังการชนเคลื่อนที่ไปข้างหน้า จึงได้ว่า
\(\rm (1 - \alpha )/(1 + \alpha ) \le {r_1} \le 1/(1 + \alpha )\)
| 177. | (เกินหลักสูตรการสอบเข้า สอวน.) กำหนดคานยาว l วางบนระนาบพื้นลื่น ปลายด้านหนึ่งถูกยึดให้หมุนรอบแกนได้ และปลายอีกด้านติดสปริงยาว L >> l ขณะยังไม่ยืดออก สปริงถูกวางอยู่บนพื้นและตั้งฉากกับคาน และสปริงฝั่งที่ติดกับคานสามารถขยับได้ และปลายอีกข้างเป็นจุดตรึง เมื่อขยับคานหมุนรอบแกนเล็กน้อย สปริงจะสั่นด้วยความถี่ f   |
| A | \(\rm f/2\) |
| B | \(\rm f/\sqrt{2}\) |
| C | \(\rm f\) |
| D | \(\rm \sqrt{2}f\) |
| E | \(\rm 2f\) |
ตอบ (A)
สังเกตว่า สปริงยังคงตั้งฉากกับคานเหมือนเดิม
สมมุติว่า โมเมนต์ความเฉื่อยของคานรอบจุดหมุนคือ I ระยะจากจุดหมุนถึงสปริงคือ r และค่านิจสปริงคือ k เมื่อขยับคานทำมุม θ สปริงจะยืดออก θr และแรงที่กระทำโดยสปริงจะเท่ากับ kθr มีระยะห่างจากจุดหมุน r จะได้สมการการเคลื่อนที่ ดังนี้
สังเกตว่า สปริงยังคงตั้งฉากกับคานเหมือนเดิม
สมมุติว่า โมเมนต์ความเฉื่อยของคานรอบจุดหมุนคือ I ระยะจากจุดหมุนถึงสปริงคือ r และค่านิจสปริงคือ k เมื่อขยับคานทำมุม θ สปริงจะยืดออก θr และแรงที่กระทำโดยสปริงจะเท่ากับ kθr มีระยะห่างจากจุดหมุน r จะได้สมการการเคลื่อนที่ ดังนี้
\(\begin{align*} \rm \tau &= \rm I\alpha \\ \rm - k{r^2}\theta &=\rm I\ddot \theta \end{align*}\)
พิจารณา สูตรความถี่ของการสั่นแบบฮาร์มอนิกอย่างง่าย
\({\rm{f = }}\dfrac{{\rm{1}}}{{{\rm{2}}\pi }}\omega {\rm{ = }}\dfrac{{\rm{1}}}{{{\rm{2}}\pi }}\sqrt {\dfrac{{{\rm{k}}{{\rm{r}}^{\rm{2}}}}}{{\rm{I}}}} \)
จะเห็นว่า ความถี่แปรผันตรงกับระยะห่าง r เมื่อระยะห่างลดลงครึ่งหนึ่ง ความถี่ก็จะลดลงครึ่งหนึ่งเช่นกัน| 178. | (เกินหลักสูตรการสอบเข้า สอวน.) กำหนดคานยาว l วางบนระนาบพื้นลื่น ปลายด้านหนึ่งถูกยึดให้หมุนรอบแกนได้ และปลายอีกด้านติดสปริงยาว L >> l ขณะยังไม่ยืดออก สปริงถูกวางอยู่บนพื้นและตั้งฉากกับคาน และสปริงฝั่งที่ติดกับคานสามารถขยับได้ และปลายอีกข้างเป็นจุดตรึง เมื่อขยับคานหมุนรอบแกนเล็กน้อย สปริงจะสั่นด้วยความถี่ f   |
| A | \(\rm f/3\) |
| B | \(\rm f/\sqrt3\) |
| C | \(\rm f\) |
| D | \(\rm \sqrt3 f\) |
| E | \(\rm 3f\) |
ตอบ (C)
สมมุติว่า โมเมนต์ความเฉื่อยของคานรอบจุดหมุนคือ I ระยะจากจุดหมุนถึงสปริงคือ r และค่านิจสปริงคือ k เมื่อขยับคานทำมุม θ สปริงจะยืดออก θr และแรงที่กระทำโดยสปริงจะเท่ากับ kθr มีระยะห่างจากจุดหมุน r จะได้สมการการเคลื่อนที่ ดังนี้
พิจารณา แรงที่กระทำโดยสปริง คือ kl และระยะห่างจากจุดหมุนคือ lθ จะได้สมการการเคลื่อนที่ ดังนี้
สมมุติว่า โมเมนต์ความเฉื่อยของคานรอบจุดหมุนคือ I ระยะจากจุดหมุนถึงสปริงคือ r และค่านิจสปริงคือ k เมื่อขยับคานทำมุม θ สปริงจะยืดออก θr และแรงที่กระทำโดยสปริงจะเท่ากับ kθr มีระยะห่างจากจุดหมุน r จะได้สมการการเคลื่อนที่ ดังนี้
\(\rm \tau = \rm I\alpha\)
\(\rm - k{r^2}\theta =\rm I\ddot \theta\) --- (1)
สังเกตว่า แรงตึงในสปริงสามารถแทนด้วยค่าคงที่\(\rm - k{r^2}\theta =\rm I\ddot \theta\) --- (1)
พิจารณา แรงที่กระทำโดยสปริง คือ kl และระยะห่างจากจุดหมุนคือ lθ จะได้สมการการเคลื่อนที่ ดังนี้
\(- {\rm{k}}{l^2}\theta = {\rm{I}}\ddot \theta\)
ซึ่งตรงกับสมการการเคลื่อนที่ (1) (โดย r = l) ดังนั้น ความถี่ต้องมีค่า f เท่าเดิม| 179. | ลูกบอลกลิ้งลงมาจากรถบรรทุกที่วิ่งไปทิศขวาด้วยอัตราเร็ว 10.0 m/s ส่วนลูกบอลกลิ้งตามแนวราบด้วยอัตราเร็ว 8.0 m/s ในทิศซ้ายมือของผู้สังเกตบนรถบรรทุก ถ้าลูกบอลตกลงบนพื้นถนนจากความสูง 1.25 m แล้วจุดที่ลูกบอลตกกระทบพื้นขณะนั้น จะห่างจากด้านหลังของรถบรรทุกเท่าใด |
| A | 0.50 m |
| B | 1.0 m |
| C | 4.0 m |
| D | 5.0 m |
| E | 9.0 m |
ตอบ (C)
ใช้สูตร
ดังนั้น ระยะห่างจากรถบรรทุกเท่ากับ (8.0m/s)(0.5s) = 4.0 m
ใช้สูตร
\(\rm d = \dfrac{1}{2}a{t^2}\)
จะได้เวลาในการตกถึงพื้น 0.5s เทียบกับอัตราเร็วรถบรรทุก ดังนั้น ระยะห่างจากรถบรรทุกเท่ากับ (8.0m/s)(0.5s) = 4.0 m
| 180. | (เกินหลักสูตรการสอบเข้า สอวน.) จากรูป ลูกปิงปองมวล m กลิ้งอยู่บนพื้นด้วยความเร็วต้นในแนวนอน v และความเร็วเชิงมุม ω เนื่องจากพื้นมีแรงเสียดทาน ทำให้ความเร็วและความเร็วเชิงมุมของลูกปิงปองเปลี่ยนแปลงไป จงหาความเร็ววิกฤติ vc ที่ทำให้ลูกปิงปองหยุดนิ่ง อย่าลืมว่าลูกปิงปองเป็นทรงกลมกลวง
 |
| A | \(\rm v = \dfrac{2}{3}R\omega \) |
| B | \(\rm v = \dfrac{2}{5}R\omega \) |
| C | \(\rm v = R\omega \) |
| D | \(\rm v = \dfrac{3}{5}R\omega \) |
| E | \(\rm v = \dfrac{5}{3}R\omega \) |
ตอบ (A)
โมเมนตัมเริ่มต้นของลูกปิงปองเท่ากับ mv และโมเมนตัมเชิงมุมรอบจุดศูนย์กลางเร่มต้น เท่ากับ \(\rm I\omega = \dfrac{2}{3}m{R^2}\omega\)
เมื่อลูกปิงปองสัมผัสกับพื้นที่มีแรงเสียดทาน จะเกิดแรงดล \(\rm F\delta t\) และเกิดทอร์ก \(\rm FR\delta t\)
ดังนั้นเราจะได้
โมเมนตัมเริ่มต้นของลูกปิงปองเท่ากับ mv และโมเมนตัมเชิงมุมรอบจุดศูนย์กลางเร่มต้น เท่ากับ \(\rm I\omega = \dfrac{2}{3}m{R^2}\omega\)
เมื่อลูกปิงปองสัมผัสกับพื้นที่มีแรงเสียดทาน จะเกิดแรงดล \(\rm F\delta t\) และเกิดทอร์ก \(\rm FR\delta t\)
ดังนั้นเราจะได้
\(\rm F\delta t = mv\) --- (1)
และ
\(\rm Fr\delta t = \dfrac{2}{3}m{r^2}\omega\) --- (2)
นำ (2) ÷ (1) จะได้
\(\rm R = \dfrac{2}{3}m{R^2}\dfrac{\omega }{v}\)
| 181. | วัตถุที่เดิมหยุดนิ่ง ถูกหมุนและเร่งความเร็วจนมีความเร็วเชิงมุม \(\rm ω = π /15~ rad / s\) และความเร่งเชิงมุม \(\rm α = π / 75~ rad / s^2\) ถ้าวัตถุยังคงหมุนต่อด้วยความเร็วเชิงมุมคงที่ และหยุดด้วยความเร่งเชิงมุมที่มีขนาดเท่ากับความเร่งก่อนหน้านี้ แล้วระยะเวลาที่วัตถุจะหมุนวนครบ 3 รอบเท่ากับข้อใด |
| A | 75 s |
| B | 80 s |
| C | 85 s |
| D | 90 s |
| E | 95 s |
ตอบ (E)
การหมุนทั้งสามแบบ คือ การหมุนด้วยอัตราเร็วเพิ่มขึ้น คงที่ และลดลง ช่วงของการเปลี่ยนความเร็วจะสมมาตรกัน โดยมีระยะห่าง \(\rm \theta = 6\pi\) จึงได้ว่า
แต่ \(\rm \omega = \alpha {t_1}\) ดังนั้น
เมื่อแก้สมการจะได้ t2 = 85 s และ t1 = 5 s เนื่องจาก t1 เกิดขึ้นสองครั้ง
ดังนั้น คำตอบ คือ 95 s
การหมุนทั้งสามแบบ คือ การหมุนด้วยอัตราเร็วเพิ่มขึ้น คงที่ และลดลง ช่วงของการเปลี่ยนความเร็วจะสมมาตรกัน โดยมีระยะห่าง \(\rm \theta = 6\pi\) จึงได้ว่า
\(\rm \theta = \alpha t_1^2 + \omega {t_2}\)
แต่ \(\rm \omega = \alpha {t_1}\) ดังนั้น
\(\rm \theta = \alpha {\left( {\dfrac{\omega }{\alpha }} \right)^2} + \omega {t_2}\)
เมื่อแก้สมการจะได้ t2 = 85 s และ t1 = 5 s เนื่องจาก t1 เกิดขึ้นสองครั้ง
ดังนั้น คำตอบ คือ 95 s
| 182. | ลวดรูปครึ่งวงกลมมีรัศมี R ถูกจับตั้ง ดังรูป ถ้าปล่อยลูกปัดให้ลื่นลงมาจากด้านบนของลวด โดยไม่มีแรงเสียดทานตามแรงโน้มถ่วง แล้วพุ่งออกจากปลายลวดลงไปยังพื้นดินที่ระดับความสูง H อยู่ไกลจากปลายลวดในแนวนอน D
 |
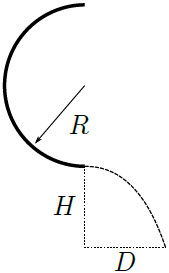| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (D)
ให้ v เป็นอัตราเร็วขณะลูกปัดหล่นออกจากปลายลวด จากกฎการอนุรักษ์พลังงาน จะได้
ให้ v เป็นอัตราเร็วขณะลูกปัดหล่นออกจากปลายลวด จากกฎการอนุรักษ์พลังงาน จะได้
\(\rm\dfrac{1}{2}{v^2} = 2gR\)
ให้ t เป็นเวลาที่ลูกปัดเคลื่อนที่แบบโพรเจกไทล์ จะได้ D = vt และ
\(\rm H = \dfrac{1}{2}g{t^2} = \dfrac{1}{2}g{\left( {\dfrac{D}{v}} \right)^2}\)
รวมสมการจะได้
\(\rm H = \dfrac{1}{8}\dfrac{{{D^2}}}{R}\)
ดังนั้น กราฟ RH เทียบกับ D2 จะเป็นเส้นตรง| 183. | ปริซึมมุมฉาก มีหน้าตัดเป็นรูปสามเหลี่ยมมุมฉาก สูง h ด้านตรงข้ามมุมฉากยาว w = 2h วางอยู่บนพื้นเอียงที่ทำมุมกับแนวนอน θ ข้อใดคือสัมประสิทธิ์ต่ำสุดของแรงเสียดทานสถิตที่ทำให้ปริซึมหมุนกลิ้งลงมา (โดยมีจุดยอดหนึ่งเป็นจุดหมุน) และไม่ไถล
 |
| A | 0.71 |
| B | 1.41 |
| C | 1.50 |
| D | 1.73 |
| E | 3.00 |
ตอบ (E)
ปริซึมจะหมุนกลิ้งลงมา เมื่อจุดศูนย์กลางมวลของปริซึมอยู่สูงกว่ามุมขวาของด้านที่วางบนพื้นเอียง หากอธิบายด้วยตรีโกณมิติ จะกล่าวได้ว่า ปริซึมจะหมุนกลิ้งลงมา เมื่อ
ปริซึมจะหมุนกลิ้งลงมา เมื่อจุดศูนย์กลางมวลของปริซึมอยู่สูงกว่ามุมขวาของด้านที่วางบนพื้นเอียง หากอธิบายด้วยตรีโกณมิติ จะกล่าวได้ว่า ปริซึมจะหมุนกลิ้งลงมา เมื่อ
\(\rm \tan \theta > \mu\)
จะเห็นว่าค่าที่สอดคล้อง คือ ข้อ (E)| 184. | คานเบายาว L ที่วางตัวในแนวดิ่งและปลายบนติดกับมวล m ปลายล่างสัมผัสกับพื้นและติดกับมวล 3m กำหนดให้ไม่มีแรงเสียดทาน และสมมุติว่าทุกอย่างเคลื่อนที่ในระนาบเดียว ถ้า x เป็นระยะกระจัดในแนวนอนของมวล m เมื่อกระทบพื้น แล้วค่า x มีค่าเท่ากับข้อใด |
| A | \(\rm x=\dfrac{3}{4}L\) |
| B | \(\rm x=\dfrac{3}{5}L\) |
| C | \(\rm x=\dfrac{1}{4}L\) |
| D | \(\rm x=\dfrac{1}{3}L\) |
| E | \(\rm x=\dfrac{2}{5}L\) |
ตอบ (A)
เนื่องจากจุดศูนย์กลางมวลของระบบไม่สามารถเคลื่อนที่ในแนวนราบได้ จึงไม่แรงที่กระทำกับในแนวนอน
ดังนั้น \(\rm x=\dfrac{3}{4}L\)
เนื่องจากจุดศูนย์กลางมวลของระบบไม่สามารถเคลื่อนที่ในแนวนราบได้ จึงไม่แรงที่กระทำกับในแนวนอน
ดังนั้น \(\rm x=\dfrac{3}{4}L\)
| 185. | คานเบายาว L ที่วางตัวในแนวดิ่งและปลายบนติดกับมวล m ปลายล่างสัมผัสกับพื้นและติดกับมวล 3m กำหนดให้ไม่มีแรงเสียดทาน และสมมุติว่าทุกอย่างเคลื่อนที่ในระนาบเดียว ถ้า v เป็นอัตราเร็วของมวล m เมื่อกระทบพื้น แล้วค่า v มีค่าเท่ากับข้อใด |
| A | \(\rm v = \sqrt {2gL}\) |
| B | \(\rm v = \sqrt {gL}\) |
| C | \(\rm v = \sqrt {2gL/3}\) |
| D | \(\rm v = \sqrt {3gL/2}\) |
| E | \(\rm v = \sqrt {gL/4}\) |
ตอบ (A)
มวล m จะเคลื่อนที่เฉพาะในแนวตั้งก่อนตกถึงพื้น และในขณะนั้นมวล 3m จะถูกทำให้เคลื่อนที่ แต่ตอนนี้มวล 3m จะยังอยู่นิ่งก่อน และพลังงานจะถูกสงวนไว้ ดังนั้น ทุกพลังงานศักย์ที่จุดศูนย์กลางมวลของระบบจะอยู่ในมวล m จะได้ว่า
ดังนั้น
มวล m จะเคลื่อนที่เฉพาะในแนวตั้งก่อนตกถึงพื้น และในขณะนั้นมวล 3m จะถูกทำให้เคลื่อนที่ แต่ตอนนี้มวล 3m จะยังอยู่นิ่งก่อน และพลังงานจะถูกสงวนไว้ ดังนั้น ทุกพลังงานศักย์ที่จุดศูนย์กลางมวลของระบบจะอยู่ในมวล m จะได้ว่า
\(\rm U = 4mgh\)
เมื่อ h คือ ความสูงของจุดศูนย์กลางมวล โดยที่ \(\rm h = \dfrac{1}{4}L\)ดังนั้น
\(\rm U = mgL\)
และแน่นอนว่า เราต้องแปลงเป็นพลังงานศักย์ของมวล m ก่อนจะได้
\(\rm mgL = \dfrac{1}{2}m{v^2}\)
ดังนั้น \(\rm v = \sqrt {2gL} \)| 186. | หนังยางสม่ำเสมอมวล M และมีค่านิจสปริง k มีรัศมีเดิม R ถ้าขว้างหนังยางออกไปในอากาศ โดยสมมุติว่า หนังยางยังคงเป็นวงกลม และหมุนด้วยอัตราเร็วเชิงมุม ω รอบจุดศูนย์กลางวงแล้วข้อใด คือ รัศมีใหม่ของหนังยาง |
| A | \(\rm ( 2πkR ) / ( 2πk - Mω^2 )\) |
| B | \(\rm( 4πkR ) / ( 4πk - Mω^2 )\) |
| C | \(\rm ( 8π^2 kR ) / ( 8π^2 k - Mω^2 )\) |
| D | \(\rm ( 4π^2 kR ) / ( 4π2 k - Mω^2 )\) |
| E | \(\rm ( 4πkR ) / ( 2πk - Mω^2 )\) |
ตอบ (D)
สำหรับองค์ประกอบของมวล \(\rm\Delta M\)ให้พิจารณา
สำหรับองค์ประกอบของมวล \(\rm\Delta M\)ให้พิจารณา
\(\rm 2T\sin \dfrac{{\Delta \theta }}{2} = \Delta m{\omega ^2}R'\)
จาก \(\sin \dfrac{{\Delta \theta }}{2} \approx \dfrac{{\Delta \theta }}{2}\) จะได้ว่า
\(\rm T = \dfrac{M}{{2\pi }}{\omega ^2}R'\)
ในขณะที่
\(\rm T = k2\pi (R' - R)\)
เทียบ T ทั้งสองสมการ แล้วจัดรูปจะได้
\(\rm R' = \dfrac{{4{\pi ^2}kR}}{{4{\pi ^2}k - M{\omega ^2}}}\)
| 187. | โมเมนต์ความเฉื่อยของรูปสามเหลี่ยมด้านเท่าสม่ำเสมอมวล m แต่ละด้านยาว a แกนที่ผ่านด้านใดด้านหนึ่งและขนานกับด้านนั้นเท่ากับ (1/8)ma2 แล้วโมเมนต์ความเฉื่อยของรูปหกเหลี่ยมด้านเท่ามวล m แต่ละด้านยาว a แกนที่ผ่านสองจุดที่อยู่ฝั่งตรงข้าม เท่ากับข้อใด |
| A | (1/8)ma2 |
| B | (5/24)ma2 |
| C | (17/72)ma2 |
| D | (19/72)ma2 |
| E | (9/32)ma2 |
ตอบ (B)
เราสามารถแบ่งรูปหกเหลี่ยมมวล m เป็นรูปสามเหลี่ยมด้านเท่าได้หกอัน โดยรูปสามเหลี่ยมด้านเท่าสี่อันจะรวมกันได้ (1/8)(m/6)a2 ส่วนอีกสองอันจะรวมกันได้ ((1/24+1/3)a2)(m/6) ตามทฤษฎีบทของแกนขนาน
เมื่อรวมทั้งหมดจะได้ (5/4)(m/6)a2 = (5/24)ma2
เราสามารถแบ่งรูปหกเหลี่ยมมวล m เป็นรูปสามเหลี่ยมด้านเท่าได้หกอัน โดยรูปสามเหลี่ยมด้านเท่าสี่อันจะรวมกันได้ (1/8)(m/6)a2 ส่วนอีกสองอันจะรวมกันได้ ((1/24+1/3)a2)(m/6) ตามทฤษฎีบทของแกนขนาน
เมื่อรวมทั้งหมดจะได้ (5/4)(m/6)a2 = (5/24)ma2
| 188. | นักเรียนสามคน วัดความยาวคานยาว 1.50 เมตร แต่ละคนรายงานความคลาดเคลื่อนในการประมาณค่า เพื่อให้ทราบข้อผิดพลาดที่เกิดขึ้นจากการวัด ดังนี้
ก : วัดครั้งเดียว โดยใช้ตลับเมตรความยาว 2.0 เมตร มีความคลาดเคลื่อน ± 2 มิลลิเมตร
ข : วัดสองครั้ง โดยใช้ไม้เมตร แต่ละครั้งมีความคลาดเคลื่อน ± 2 มิลลิเมตร ซึ่งเขารวมความคลาดเคลื่อนเข้าด้วยกัน
ค : วัดสองครั้ง โดยใช้ไม้บรรทัดสเกลละเอียดสำหรับงานช่าง แต่ละครั้งมีความคลาดเคลื่อน ± 1 มิลลิเมตร ซึ่งเขารวมความคลาดเคลื่อนเข้าด้วยกัน
จากข้อมูล ครูต้องเลือกข้อมูลที่มีความผิดพลาดน้อยที่สุด ข้อใดจัดลำดับความน่าเชื่อถือได้ถูกต้อง |
| 189. | แม่น้ำกว้าง 600 เมตร ไหลไปทางทิศใต้ด้วยอัตราเร็ว 4.0 m/s เรือยนต์เล็กมีอัตราเร็ว 5.0 m/s ในน้ำนิ่งขับข้ามฝั่งไปโดยหันหัวเรือไปในทิศทาง ดังรูป
 |
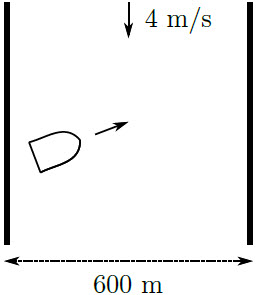| A | 67 s |
| B | 120 s |
| C | 150 s |
| D | 200 s |
| E | 600 s |
ตอบ (D)
อัตราเร็วสัมพัทธ์ของเรือที่กำลังข้ามฝั่งจะเท่ากับ 3.0 m/s และมีเวกเตอร์ตามรูปที่โจทย์กำหนดให้
อัตราเร็วสัมพัทธ์ของเรือที่กำลังข้ามฝั่งจะเท่ากับ 3.0 m/s และมีเวกเตอร์ตามรูปที่โจทย์กำหนดให้
| 190. | ขับรถไปทางทิศเหนืออัตราเร็วคงที่ 80 km/hr เป็นระยะทาง 25 km จากนั้นขับต่อไปด้วยอัตราเร็วคงที่ 75 km/hr อีก 75 km อัตราเร็วเฉลี่ยในการเดินทางครั้งนี้เท่ากับข้อใด |
| A | 55.2 km/hr |
| B | 57.5 km/hr |
| C | 65 km/hr |
| D | 69.6 km/hr |
| E | 72.5 km/hr |
ตอบ (A)
อัตราเร็วเฉลี่ยหาจากระยะทางทั้งหมดหารด้วยเวลาทั้งหมด ในช่วงแรก ระยะทาง 25 km ใช้เวลา 0.31 ชั่วโมง ในช่วงหลัง ระยะทาง 75 km ใช้เวลา 1.5 ชั่วโมง
ดังนั้น อัตราเร็วเฉลี่ย \(=\dfrac{25+75}{1.5+0.31}\approx55.2~\rm km/hr\)
อัตราเร็วเฉลี่ยหาจากระยะทางทั้งหมดหารด้วยเวลาทั้งหมด ในช่วงแรก ระยะทาง 25 km ใช้เวลา 0.31 ชั่วโมง ในช่วงหลัง ระยะทาง 75 km ใช้เวลา 1.5 ชั่วโมง
ดังนั้น อัตราเร็วเฉลี่ย \(=\dfrac{25+75}{1.5+0.31}\approx55.2~\rm km/hr\)
| 191. | แรงต้านการเคลื่อนที่ของเครื่องบินที่ระดับความสูงหนึ่ง หาจาก Ff = kv2 , โดย k คือค่าคงที่ v คือ อัตราเร็วของเครื่องบิน ให้กำลังที่ออกมาจากเครื่องยนต์ คือ P0 เครื่องบินจะบินด้วยอัตราเร็ว v0 ถ้ากำลังที่ออกมาจากเครื่องยนต์เพิ่มขึ้น 100% เป็น 2P0 แล้วเครื่องบินจะบินได้ด้วยอัตราเร็วเท่าใด |
| A | 1.12 v0 |
| B | 1.26 v0 |
| C | 1.41 v0 |
| D | 2.82 v0 |
| E | 8 v0 |
ตอบ (B)
จาก P = Fv ดังนั้น P = kv3 จึงได้
จาก P = Fv ดังนั้น P = kv3 จึงได้
\(\rm v / v_0 = \sqrt[3]{P/P_0}\)
เมื่อแทนค่า จะได้ v = 1.26 v0| 192. | กล่องหนัก 2.0 kg อยู่นิ่งบนพื้นราบ มีค่าสัมประสิทธิ์แรงเสียดทานสถิตระหว่างกล่องและพื้น μ และค่าสัมประสิทธิ์แรงเสียดทานจลน์ระหว่างกล่องและพื้นผิว μk = 0.90 μs ถ้ามีแรงภายนอกมากระทำกับกล่องในแนวนอนขนาด P แล้วข้อใดเป็นกราฟความเร่งของกล่องเทียบกับแรงภายนอก P |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (A)
กล่องจะไม่ขยับจนกว่า P > μsmg เมื่อกล่องเคลื่อนที่จะมีความเร่งเท่ากับ a = P/m – μkg สังเกตว่า กราฟจะไม่ต่อเนื่องที่ P = μsmg และกราฟจะมีความชันเท่ากับ 1/m
หรืออีกวิธีเราอาจพิจารณาว่า จะเกิดอะไรขึ้นถ้าไม่มีแรงมากระทำในแนวราบ
กล่องจะไม่ขยับจนกว่า P > μsmg เมื่อกล่องเคลื่อนที่จะมีความเร่งเท่ากับ a = P/m – μkg สังเกตว่า กราฟจะไม่ต่อเนื่องที่ P = μsmg และกราฟจะมีความชันเท่ากับ 1/m
หรืออีกวิธีเราอาจพิจารณาว่า จะเกิดอะไรขึ้นถ้าไม่มีแรงมากระทำในแนวราบ
| 193. | ยิงกระสุน 470 กรัม ทำมุมเงย 60 องศา ด้วยอัตราเร็วต้น 100 m/s ตรงไปยังเป้าหมายบนกำแพงที่อยู่ห่างออกไป 150 เมตร ดังรูป
 |
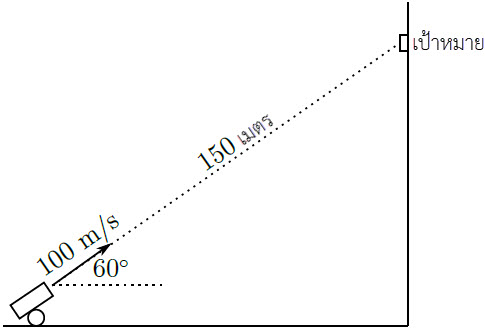| A | 1.3 m |
| B | 2.2 m |
| C | 5.0 m |
| D | 7.1 m |
| E | 11 m |
ตอบ (E)
หากไม่สนแรงโน้มถ่วง เวลาที่กระสุนจะไปถึงเป้าหมายจะเท่ากับ
หากไม่สนแรงโน้มถ่วง เวลาที่กระสุนจะไปถึงเป้าหมายจะเท่ากับ
\(\rm 150~ (m) /100~ (m/s) = 1.5 ~s\)
ในช่วงเวลานั้น ระยะที่กระสุนจะเคลื่อนที่ลงในแนวตั้งจะเท่ากับ\(\rm d = \dfrac{1}{2}gt^2 = 11.25 ~m\)
| 194. | รถของเล่นสามคัน เคลื่อนที่หนึ่งมิติอย่างอิสระตามแนวนอนโดยไม่มีแรงเสียดทาน รถ A มีมวล 1.9 kg ไปทางขวาด้วยอัตราเร็วต้น 1.7 m/s รถ B มีมวล 1.1 kg ไปทางซ้ายด้วยอัตราเร็วต้น 2.5 m/s รถ C มีมวล 1.3 kg จอดอยู่นิ่งๆ ถ้าการชนระหว่างรถ A และ B ยืดหยุ่นสมบูรณ์ ส่วนการชนระหว่างรถ B และ C ไม่ยืดหยุ่นสมบูรณ์
 |
| A | 0.11 m/s |
| B | 0.16 m/s |
| C | 1.4 m/s |
| D | 2.0 m/s |
| E | 3.23 m/s |
ตอบ (A)
จากอัตราเร็วที่จุดศูนย์กลางมวลจะไม่เปลี่ยนไป ไม่ว่าจะเกิดการชนแบบใดก็ตาม จะได้ว่า
จากอัตราเร็วที่จุดศูนย์กลางมวลจะไม่เปลี่ยนไป ไม่ว่าจะเกิดการชนแบบใดก็ตาม จะได้ว่า
\({{\rm{v}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{{\rm{(1}}{\rm{.9 kg)(1}}{\rm{.7 m/s) + (1}}{\rm{.1 kg)( - 2}}{\rm{.5 m/s) + (1}}{\rm{.3 kg)(0 m/s)}}}}{{{\rm{(1}}{\rm{.9 kg) + (1}}{\rm{.1 kg) + (1}}{\rm{.3 kg)}}}}{\rm{ = 0}}{\rm{.11 m/s}}\)
| 195. |  รถ C จอดที่ระยะ 2.0 เมตร ณ จุดที่กำหนดตำแหน่งไว้ ส่วนรถ A อยู่ที่จุดเริ่มต้นที่ระยะศูนย์เมตร ได้เคลื่อนที่ไปทางรถ B ที่อัตราเร็ว v0 สมมุติว่าการชนกันทั้งหมดไม่ยืดหยุ่นสมบูรณ์ แล้วอัตราเร็วสุดท้ายของรถ C เท่ากับข้อใด |
| A | v0/13 |
| B | v0/10 |
| C | v0/9 |
| D | v0/3 |
| E | 2v0/5 |
ตอบ (A)
หลังเกิดการชนครั้งแรก รถทั้งสองคันจะเคลื่อนที่ด้วยอัตราเร็ว v0 / (1+3) หลังเกิดการชนครั้งที่สอง รถทั้งหมดจะเคลื่อนที่ด้วยอัตราเร็ว v0 / (1+3+9)
หลังเกิดการชนครั้งแรก รถทั้งสองคันจะเคลื่อนที่ด้วยอัตราเร็ว v0 / (1+3) หลังเกิดการชนครั้งที่สอง รถทั้งหมดจะเคลื่อนที่ด้วยอัตราเร็ว v0 / (1+3+9)
| 196. |  รถ C จอดที่ระยะ 2.0 เมตร ณ จุดที่กำหนดตำแหน่งไว้ ส่วนรถ A อยู่ที่จุดเริ่มต้นที่ระยะศูนย์เมตร ได้เคลื่อนที่ไปทางรถ B ที่อัตราเร็ว v0 สมมุติว่าการชนกันทั้งหมดยืดหยุ่นสมบูรณ์ แล้วอัตราเร็วสุดท้ายของรถ C เท่ากับข้อใด |
| A | v0/8 |
| B | v0/4 |
| C | v0/2 |
| D | v0 |
| E | 2v0 |
ตอบ (B)
โจทย์ข้อนี้หาคำตอบโดยใช้กฎการอนุรักษ์พลังงานจลน์และโมเมนตัม
สำหรับรถหนึ่งคันในกรณีที่เดิมอยู่นิ่ง และกรณีที่มีอัตราเร็วต้น จะใช้สมการ ดังนี้
เมื่อคำนวณซ้ำอีกครั้ง จะได้อัตราเร็วสุดท้ายของรถคันที่สามเท่ากับ v0/4
โจทย์ข้อนี้หาคำตอบโดยใช้กฎการอนุรักษ์พลังงานจลน์และโมเมนตัม
สำหรับรถหนึ่งคันในกรณีที่เดิมอยู่นิ่ง และกรณีที่มีอัตราเร็วต้น จะใช้สมการ ดังนี้
\({{\rm{v}}_{{\rm{1f}}}}{\rm{ = }}{{\rm{v}}_{\rm{0}}}\dfrac{{{{\rm{m}}_{\rm{1}}}{\rm{ - }}{{\rm{m}}_{\rm{2}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_2}}}\)
และ
\({{\rm{v}}_{{\rm{2f}}}}{\rm{ = }}{{\rm{v}}_{\rm{0}}}\dfrac{{{\rm{2}}{{\rm{m}}_{\rm{1}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_2}}}\)
โดยรถคันแรกจะชนกับรถคันที่สองจากทางด้านหลัง แล้วเคลื่อนที่ไปข้างหน้าด้วยอัตราเร็ว v0/2เมื่อคำนวณซ้ำอีกครั้ง จะได้อัตราเร็วสุดท้ายของรถคันที่สามเท่ากับ v0/4
| 197. | ลูกบอล 0.650 kg เคลื่อนที่ด้วยอัตราเร็ว 5.00 m/s ชนกันลูกบอล 0.750 kg ที่เดิมอยู่นิ่ง หลังการชนลูกบอล 0.750 kg เคลื่อนที่ด้วยอัตราเร็ว 4.00 m/s และลูกบอล 0.650 kg กระเด็นทำมุมฉากกับทิศที่ลูกบอล 0.750 kg เคลื่อนที่ออกไป ถ้าอัตราเร็วสุดท้ายของลูกบอล 0.650 kg เท่ากับข้อใด |
| A | 1.92 m/s |
| B | 2.32 m/s |
| C | 3.0 m/s |
| D | 4.64 m/s |
| E | 5.77 m/s |
ตอบ (A)
คำนวณจากกฎการอนุรักษ์ของโมเมนตัม ซึ่งข้อนี้การชนเป็นรูปสามเหลี่ยมมุมฉาก จะได้
และ \({{\rm{p}}_{{\rm{2f}}}}{\rm{ = (0}}{\rm{.75 kg)(4}}{\rm{.0 m/s) = 3}}{\rm{.0 kg}} \cdot {\rm{m/s}}\)
จึงได้
คำนวณจากกฎการอนุรักษ์ของโมเมนตัม ซึ่งข้อนี้การชนเป็นรูปสามเหลี่ยมมุมฉาก จะได้
\({\rm{p}}_{{\rm{2f}}}^{\rm{2}}{\rm{ + p}}_{{\rm{1f}}}^{\rm{2}}{\rm{ = p}}_{{\rm{1i}}}^{\rm{2}}\)
โดยที่ \({{\rm{p}}_{{\rm{1i}}}}{\rm{ = (0}}{\rm{.65 kg)(5}}{\rm{.0 m/s) = 3}}{\rm{.25 kg}} \cdot {\rm{m/s}}\)และ \({{\rm{p}}_{{\rm{2f}}}}{\rm{ = (0}}{\rm{.75 kg)(4}}{\rm{.0 m/s) = 3}}{\rm{.0 kg}} \cdot {\rm{m/s}}\)
จึงได้
\({{\rm{p}}_{{\rm{1f}}}}{\rm{ = 1}}{\rm{.25 kg}} \cdot {\rm{m/s}}\)
ดังนั้น
\({{\rm{v}}_{{\rm{1f}}}}{\rm{ = 1}}{\rm{.25/0}}{\rm{.65 = 25/13 = 1}}{\rm{.92 ~m/s}}\)
| 198. | ลูกบอล 0.650 kg เคลื่อนที่ด้วยอัตราเร็ว 5.00 m/s ชนกันลูกบอล 0.750 kg ที่เดิมอยู่นิ่ง หลังการชนลูกบอล 0.750 kg เคลื่อนที่ด้วยอัตราเร็ว 4.00 m/s และลูกบอล 0.650 kg กระเด็นทำมุมฉากกับทิศที่ลูกบอล 0.750 kg เคลื่อนที่ออกไป ให้การเปลี่ยนแปลงพลังงานจลน์สุทธิจากการชนครั้งนี้ หาจาก ΔK = Kf - Ki โดย Kf คือ พลังงานจลน์สุดท้ายสุทธิ และ Ki คือ พลังงานจลน์เริ่มต้นสุทธิ แล้วข้อใดต่อไปนี้ถูกต้อง |
| A | \(\rm ΔK = (K_f + K_i)/2\) |
| B | \(\rm K_f < ΔK < K_i\) |
| C | \(\rm 0 < ΔK < K_f\) |
| D | \(\rm ΔK = 0\) |
| E | \(\rm – K_i < ΔK < 0\) |
ตอบ (E)
พิจารณาจากสมการ
พิจารณาจากสมการ
\({\rm{p}}_{{\rm{2f}}}^{\rm{2}}{\rm{ + p}}_{{\rm{1f}}}^{\rm{2}}{\rm{ = p}}_{{\rm{1i}}}^{\rm{2}}\)
จะได้
\(\begin{align*}
\Delta {\rm{K}} &= \frac{1}{2}\left( {\frac{{{\rm{p}}_{{\rm{2f}}}^{\rm{2}}}}{{{{\rm{m}}_2}}} + \frac{{{\rm{p}}_{{\rm{1f}}}^{\rm{2}}}}{{{{\rm{m}}_1}}} - \frac{{{\rm{p}}_{{\rm{1i}}}^{\rm{2}}}}{{{{\rm{m}}_1}}}} \right)\\
&= \frac{1}{2}{\rm{ }}\left( {\frac{{{\rm{p}}_{{\rm{2f}}}^{\rm{2}}}}{{{{\rm{m}}_2}}} - \frac{{{\rm{p}}_{{\rm{2f}}}^{\rm{2}}}}{{{{\rm{m}}_1}}}} \right)
\end{align*}\)
ดังนั้น
\(\Delta \rm K =\dfrac{1}{2}\dfrac{{{\rm{p}}_{{\rm{2f}}}^{\rm{2}}}}{{{{\rm{m}}_1}}}\left( {\dfrac{{{{\rm{m}}_1}}}{{{{\rm{m}}_2}}} - 1} \right)\)
ชัดเจนว่า ค่าที่ได้จะเป็นลบ และมีขนาดเล็กว่า K_i| 199. | ทรงกลมลอยอยู่ในน้ำ โดย 2/3 ของปริมาตรทรงกลมจมอยู่ในน้ำ ถ้าหยิบทรงกลมไปวางในน้ำมันที่มีความหนาแน่น 3/4 ของน้ำ แล้วสัดส่วนของทรงกลมที่จมอยู่ในน้ำมันเท่ากับข้อใด |
| A | 1/12 |
| B | 1/2 |
| C | 8/9 |
| D | 17/12 |
| E | ทรงกลมจะไม่ลอย แต่จะจมในน้ำมัน |
ตอบ (C)
เนื่องจากสัดส่วนที่จมอยู่ในน้ำ เท่ากับ อัตราส่วนของความหนาแน่นของทรงกลม จากโจทย์จะได้
เนื่องจากสัดส่วนที่จมอยู่ในน้ำ เท่ากับ อัตราส่วนของความหนาแน่นของทรงกลม จากโจทย์จะได้
\(\rm {\rho _{{\rm{sphere}}}} = 2/3{\rho _{{\rm{water}}}}\)
เมื่อเปลี่ยนไปวางในน้ำมันส่วนที่จมจะเท่ากับ
\(\displaystyle\rm \frac{{{\rho _{{\rm{sphere}}}}}}{{{\rho _{oil}}}} = \frac{{2/3}}{{3/4}} = \frac{8}{9}\)
| 200. | ให้ลูกตุ้มประกอบไปด้วย ตุ้มขนาดเล็กมวล m ผูกติดกับเชือกยาว L ให้ลูกตุ้มที่เดิมอยู่นิ่งแกว่งลงมาจากจุดที่ทำมุม θmax < 90 องศา แล้วข้อใดกล่าวถูกต้องเกี่ยวกับความเร่งของลูกตุ้ม |
| A | ขนาดของความเร่งจะคงที่ สำหรับการแกว่งนี้ |
| B | ขนาดของความเร่งที่จุดต่ำสุดมีค่าเท่ากับ g ความเร่งเป็นไปตามการตกอย่างอิสระ |
| C | ขนาดของความเร่งเป็นศูนย์ ณ บางจุดของการแกว่งนี้ |
| D | ความเร่งจะชี้ไปที่จุดศูนย์กลางของวงกลมเสมอ |
| E | ความเร่งที่จุดต่ำสุดของการแกว่งจะชี้ขึ้นในแนวตั้ง |
ตอบ (E)
ให้พิจารณาแต่ละสถานการณ์
ให้พิจารณาแต่ละสถานการณ์
| 201. | ให้ลูกตุ้มประกอบไปด้วย ตุ้มขนาดเล็กมวล m ผูกติดกับเชือกยาว L ให้ลูกตุ้มที่เดิมอยู่นิ่งแกว่งลงมาจากจุดที่ทำมุม θmax < 90 องศา พิจารณา ขณะลูกตุ้มทำมุม \(\rm θ = \dfrac{1}{2} θ_{max}\) ขณะแกว่งขึ้น ( ขึ้นไปทาง θmax ) ภาพใดแสดงเวกเตอร์ทิศของความเร่งของลูกตุ้มได้ถูกต้อง |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (D)
การเคลื่อนที่ของลูกตุ้มจะมีความเร่งชี้ไปที่จุดศูนย์กลางการแกว่ง และมีความเร่งในแนวสัมผัสส่วนโค้งที่ชี้ไปที่ด้านล่างของเส้นทางที่ลูกตุ้มผ่าน
การเคลื่อนที่ของลูกตุ้มจะมีความเร่งชี้ไปที่จุดศูนย์กลางการแกว่ง และมีความเร่งในแนวสัมผัสส่วนโค้งที่ชี้ไปที่ด้านล่างของเส้นทางที่ลูกตุ้มผ่าน
| 202. | ให้คานเบายาว 3.0 เมตร สามารถหมุนตามแนวนอนได้อย่างอิสระรอบจุดศูนย์กลาง ที่ปลายคานมีวัตถุสองชิ้นมวล 5.0 กิโลกรัม วางอยู่ วัตถุสามารถเลื่อนได้อย่างอิสระบนคาน โดยไม่มีแรงเสียดทาน และมีเชือกเบาผูกวัตถุทั้งสองชิ้นไว้ไม่ให้หล่นออกจากคาน ให้เดิมระบบหมุน 4.0 เรเดียนต่อวินาที ถือว่าระบบไม่มีแรงเสียดทาน และไม่สนใจความไม่เสถียรของระบบ แล้วแรงตึงเชือกเดิมเท่ากับข้อใด |
| A | 60 N |
| B | 106 N |
| C | 120 N |
| D | 240 N |
| E | 480 N |
ตอบ (C)
ข้อนี้หาคำตอบตรงๆ จาก
\({\rm{F = mr}}{\omega ^{\rm{2}}}{\rm{ = (5}}{\rm{.0 kg)(1}}{\rm{.5 m)(4}}{\rm{.0 rad/s}}{{\rm{)}}^{\rm{2}}}{\rm{ = 120 N}}\)
| 203. | ให้คานเบายาว 3.0 เมตร สามารถหมุนตามแนวนอนได้อย่างอิสระรอบจุดศูนย์กลาง ที่ปลายคานมีวัตถุสองชิ้นมวล 5.0 กิโลกรัม วางอยู่ วัตถุสามารถเลื่อนได้อย่างอิสระบนคาน โดยไม่มีแรงเสียดทาน และมีเชือกเบาผูกวัตถุทั้งสองชิ้นไว้ไม่ให้หล่นออกจากคาน ให้เดิมระบบหมุน 4.0 เรเดียนต่อวินาที ถือว่าระบบไม่มีแรงเสียดทาน และไม่สนใจความไม่เสถียรของระบบ ถ้าเชือกค่อยๆ ตึงขึ้น ด้วยมอเตอร์เบาอันเล็กๆ ติดที่อยู่บนวัตถุชิ้นหนึ่ง โดยมอเตอร์จะช่วยดึงทั้งสองวัตถุให้เข้ามาใกล้จุดศูนย์กลางของแกนหมุน แล้วงานที่มอเตอร์ใช้ดึงทั้งสองวัตถุจากปลายคานมาอยู่ที่ระยะ 0.5 เมตร จากจุดศูนย์กลางของแกนหมุนเท่ากับข้อใด |
| A | 120 J |
| B | 180 J |
| C | 240 J |
| D | 1440 J |
| E | 1620 J |
ตอบ (D)
งานที่เปลี่ยนเป็นพลังงานหาจาก
แทน Ii = 22.5 kg·m2 , If = 2.5 kg·m2 และ L = 90 kg·m2 / s
งานที่เปลี่ยนเป็นพลังงานหาจาก
\(\rm W = \dfrac{1}{{2{I_f}}}{L^2} - \dfrac{1}{{2{I_i}}}{L^2}\)
โดย L มาจากกฎการอนุรักษ์โมเมนตัมเชิงมุม ซึ่ง L = Iiωi และ I คือ ความเฉื่อยในการหมุนหรือ mr2 แทน Ii = 22.5 kg·m2 , If = 2.5 kg·m2 และ L = 90 kg·m2 / s
จะได้
\(\rm W = 1440~ J\)
| 204. | พิจารณากราฟพลังงานศักย์กับตำแหน่งของวัตถุ 0.50 kg
 |
| A | วัตถุสมดุลที่ x = 1 cm หรือ x = 3 cm |
| B | พลังงานต่ำสุดสุทธิที่เป็นไปได้สำหรับวัตถุนี้เท่ากับ -10 J |
| C | แรงที่กระทำบนวัตถุที่ x = 4 cm มีค่าประมาณ 1000 N |
| D | ถ้าพลังงานสุทธิของวัตถุเท่ากับ 0 J แล้ววัตถุจะมีพลังงานจลน์ 10 J |
| E | ความเร่งของวัตถุที่ x = 2 cm มีค่าประมาณ 4 cm/s2 |
ตอบ (E)
ให้พิจารณาแต่ละสถานการณ์
ให้พิจารณาแต่ละสถานการณ์
| 205. | เราสามารถใช้ล้อหมุนเพื่อเก็บพลังงานจลน์ได้ ถ้าล้อมีลักษณะเป็นแผ่นกลม มีความหนาแน่น ρ ความทนต่อแรงดึง σ (ใช้หน่วยปาสคาล) รัศมี r และความหนา h และล้อสามารถหมุนที่ความเร็วเชิงมุมสูงสุดได้โดยไม่แตกหัก แล้วข้อใดคือพลังงานจลน์สูงสุดต่อกิโลกรัมที่ล้อสามารถเก็บพลังงานไว้ได้ สมมุติว่า α เป็นค่าคงที่ (ระดับเตรียมสอบ สอวน. ให้ใช้การวิเคราะห์มิติ) |
| A | \(\rm \alpha \sqrt {\rho \sigma /r}\) |
| B | \(\rm \alpha h\sqrt {\rho \sigma /r}\) |
| C | \(\rm \alpha \sqrt {(h/r)} {(\sigma /\rho )^2}\) |
| D | \(\rm \alpha (h/r)(\sigma /\rho )\) |
| E | \(\rm \alpha \sigma /r\) |
ตอบ (E)
ข้อนี้จะใช้การวิเคราะห์มิติ โดยการหาเลขชี้กำลัง a, b, c, d ใน
จะได้
เมื่อแก้สมการจะได้ b = 1, a = -1 และ c = -d แม้ว่าเราจะหาค่า d จากการวิเคราะห์มิติไม่ได้ แต่เราสามารถใช้เหตุผลอธิบายได้ว่า ถ้าแผ่นกลมหนาขึ้นเป็นสองเท่า แล้วความเร็วในการหมุนสูงสุดที่เป็นไปได้ก่อนที่ล้อจะแตกจะไม่เปลี่ยนแปลง แสดงว่า พลังงานและมวลจะต้องเกิดขึ้นสองครั้ง
ดังนั้น d = 0
ข้อนี้จะใช้การวิเคราะห์มิติ โดยการหาเลขชี้กำลัง a, b, c, d ใน
\(\rm ρ^a~ σ^b~ r^c~ h^d\)
ซึ่งมีมิติของพลังงานคิดเป็นต่อมวล จะได้
\(\rm (M / L^3) ^a (M / LT ^2)^b (L)^c (L)^d = (L^2 / T^2)\)
เมื่อแก้สมการจะได้ b = 1, a = -1 และ c = -d แม้ว่าเราจะหาค่า d จากการวิเคราะห์มิติไม่ได้ แต่เราสามารถใช้เหตุผลอธิบายได้ว่า ถ้าแผ่นกลมหนาขึ้นเป็นสองเท่า แล้วความเร็วในการหมุนสูงสุดที่เป็นไปได้ก่อนที่ล้อจะแตกจะไม่เปลี่ยนแปลง แสดงว่า พลังงานและมวลจะต้องเกิดขึ้นสองครั้ง
ดังนั้น d = 0
| 206. | พิจารณาสามกราฟ ที่มาจากข้อมูลเดียวกัน
   |
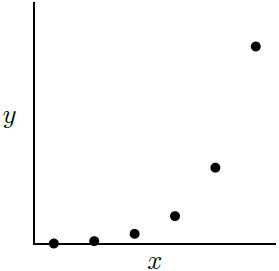| A | y = ax + b |
| B | y = ax2 + b |
| C | y = axb |
| D | y = aebx |
| E | y = a log x + b |
ตอบ (D)
จากกราฟ log เชิงเส้นเป็นเส้นตรง แสดงว่าข้อมูลจะเป็นไปตามสมการ
จากกราฟ log เชิงเส้นเป็นเส้นตรง แสดงว่าข้อมูลจะเป็นไปตามสมการ
\(\rm log\, y = Ax +B\)
หรือ
\(\rm y = ae^{bx}\)
| 207. | มาโนมิเตอร์รูปตัวยู (U-tube manometer) คือ ท่อทรงกระบอกที่โค้งงอเป็นรูปตัว U มีเส้นผ่านศูนย์กลางสม่ำเสมอตลอดเส้น ภายในท่อจะมีน้ำที่มีความหนาแน่น ρw ระดับความสูงของน้ำในท่อทั้งสองฝั่งจะเท่ากับ L ในที่นี้เราจะไม่สนใจความตึงผิวและความหนืดของของเหลว ถ้าน้ำในท่อฝั่งหนึ่งขยับตัวสูงขึ้นมา x แล้วน้ำในท่ออีกฝั่งจะลดลงมา x ด้วยเช่นกัน แล้วความถี่การขึ้นลงของน้ำในท่อเท่ากับข้อใด |
| A | \(\rm \dfrac{1}{{2\pi }}\sqrt {2g/L}\) |
| B | \(\rm 2\pi \sqrt {g/L}\) |
| C | \(\rm \dfrac{1}{{2\pi }}\sqrt {2L/g}\) |
| D | \(\rm \dfrac{1}{{2\pi }}\sqrt {g/{\rho _w}}\) |
| E | \(\rm 2\pi \sqrt {{\rho _w}gL}\) |
ตอบ (A)
ความถี่ในการสั่นหาจาก
ถ้าระยะทางที่ของเหลวเคลื่อนที่ไปได้เท่ากับ x แล้วแรงดึงกลับสุทธิบนของไหลจะเท่ากับ 2xgAρ
จะได้ k = 2gAρ
ดังนั้น
ความถี่ในการสั่นหาจาก
\(\rm f = \dfrac{1}{{2\pi }}\sqrt {k/m} \)
โดย m คือ มวล ซึ่งเท่ากับ LAρ โดย L เป็นความยาวทั้งหมดของของเหลว และมี k เป็นค่านิจสปริงถ้าระยะทางที่ของเหลวเคลื่อนที่ไปได้เท่ากับ x แล้วแรงดึงกลับสุทธิบนของไหลจะเท่ากับ 2xgAρ
จะได้ k = 2gAρ
ดังนั้น
\(f = \dfrac{1}{{2\pi }}\sqrt {2g/L}\)
| 208. | มาโนมิเตอร์รูปตัวยู (U-tube manometer) คือ ท่อทรงกระบอกที่โค้งงอเป็นรูปตัว U มีเส้นผ่านศูนย์กลางสม่ำเสมอตลอดเส้น ภายในท่อจะมีน้ำที่มีความหนาแน่น ρw ระดับความสูงของน้ำในท่อทั้งสองฝั่งจะเท่ากับ L ในที่นี้เราจะไม่สนใจความตึงผิวและความหนืดของของเหลว ถ้าเติมน้ำมันที่มีความหนาแน่นครึ่งหนึ่งของน้ำลงไปในด้านหนึ่งของท่อ จนกระทั่งความยาวของลำน้ำมันเท่ากับความยาวของลำน้ำ จงหาผลต่างความสูงของน้ำและน้ำมันที่จุดสมดุล |
| A | L |
| B | L/2 |
| C | L/3 |
| D | 3L/4 |
| E | L/4 |
ตอบ (B)
ข้อนี้จะต้องหาแรงที่ทำให้เกิดสมดุล สมมุติให้ x คือ ความสูงของน้ำในหลอดฝั่งที่มีเฉพาะแต่น้ำ
จะได้
ข้อนี้จะต้องหาแรงที่ทำให้เกิดสมดุล สมมุติให้ x คือ ความสูงของน้ำในหลอดฝั่งที่มีเฉพาะแต่น้ำ
จะได้
\(\rm xρ_w = (L – x) ρ_w + Lρ_o\)
หรือ
\(\begin{array}{l}
{\rm{x = L - x + L/2}}\\
{\rm{x = 3L/4}}
\end{array}\)
ดังนั้น ผลต่างความสูงของน้ำและน้ำมันที่จุดสมดุลจะเท่ากับ
\(\rm (2 L – x) – x = 2(L – x) = L / 2\)
| 209. | ยิงวัตถุขึ้นฟ้าด้วยอัตราเร็ว 50 m/s แล้วตกกลับลงมาพื้นดินด้วยสัมประสิทธิ์การกระแทก CR = 0.9 หมายความว่า วัตถุจะมีการกระเด้งกลับด้วยอัตราเร็ว 90% ของอัตราเร็วที่ตกลงมา จงหาเวลารวมที่ใช้ ตั้งแต่เริ่มยิ่งวัตถุจนกระทั้งตกกลับลงมาถึงพื้นแล้วหยุดนิ่ง สมมุติว่าเวลาในการกระแทกเป็นศูนย์ (การกระเด้งกลับเกิดขึ้นอย่างรวดเร็ว) เหตุการณ์นี้เป็นแบบอุดมคติ และไม่สนใจผลควอนตัมใด ๆ ที่อาจเกิดขึ้นกับการกระแทก |
| A | 71 s |
| B | 100 s |
| C | 141 s |
| D | 1000 s |
| E | ∞ (วัตถุจะไม่มีวันหยุดนิ่ง) |
ตอบ (B)
ในการกระแทกพื้นจะมี CR = vf / vi และเวลาที่ลูกลอยกลางอากาศระหว่างกระแทกพื้นสองครั้งเท่ากับ t = 2v / g
โดย v คือ อัตราเร็วต้นขณะวัตถุพุ่งขึ้นจากการกระแทก เราจะได้ลำดับอนันต์ คือ
ในการกระแทกพื้นจะมี CR = vf / vi และเวลาที่ลูกลอยกลางอากาศระหว่างกระแทกพื้นสองครั้งเท่ากับ t = 2v / g
โดย v คือ อัตราเร็วต้นขณะวัตถุพุ่งขึ้นจากการกระแทก เราจะได้ลำดับอนันต์ คือ
\({{\rm{t}}_{\rm{n}}}{\rm{ = }}\dfrac{{\rm{2}}}{{\rm{g}}}{{\rm{v}}_{\rm{n}}}{\rm{ = }}\dfrac{{\rm{2}}}{{\rm{g}}}{{\rm{v}}_{\rm{0}}}{\rm{C}}_{\rm{R}}^{\rm{n}}\)
เมื่อหาผลรวม เราจะได้อนุกรมที่เป็นเวลารวมทั้งหมด คือ
\({\rm{T = }}\sum {\dfrac{{\rm{2}}}{{\rm{g}}}} {{\rm{v}}_{\rm{0}}}{\rm{C}}_{\rm{R}}^{\rm{n}}{\rm{ = }}\dfrac{{\rm{2}}}{{\rm{g}}}{{\rm{v}}_{\rm{0}}}\sum {{\rm{C}}_{\rm{R}}^{\rm{n}}} = \dfrac{{\rm{2}}}{{\rm{g}}}{{\rm{v}}_{\rm{0}}}\dfrac{1}{{1 - {{\rm{C}}_{\rm{R}}}}}\)
ดังนั้น
\({\rm{T = }}\dfrac{{\rm{2}}}{{{\rm{10 m/}}{{\rm{s}}^{\rm{2}}}}}{\rm{(50 m/s)}}\dfrac{1}{{1 - 0.9}} = {\rm{100 s}}\)
| 210. | ปล่อยลูกบอลตันกลิ้งจากจุดนิ่งไปตามพื้นเอียงที่มีมุม θ ต่างๆ แต่ความสูง h มีค่าเท่ากัน ค่าสัมประสิทธิ์ของแรงเสียดทานสถิต และแรงเสียดทานจลน์ทั้งสองมีค่าเท่ากับ μ กราฟใดแสดงพลังงานจลน์สุทธิของลูกบอลที่ด้านล่างของพื้นเอียง ที่เปลี่ยนไปตามมุม θ ต่างๆ ได้ถูกต้อง |
| A |  |
| B |  |
| C |  |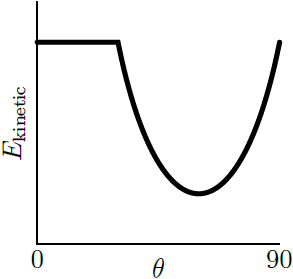
| D |  |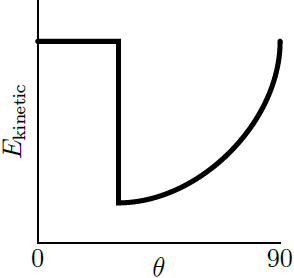
| E |  |
ตอบ (C)
เนื่องจากลูกบอลจะกลิ้งโดยไม่ไถล ถ้า θ มีค่าน้อยกว่ามุมวิกฤติ ดังนั้น สำหรับ θ ที่น้อยกว่ามุมวิกฤติ จึงไม่มีพลังงานที่สูญเสียไปกับแรงเสียดทาน แต่สำหรับ θ ที่มากกว่ามุมวิกฤติ ลูกบอลจะเกิดการไถลและมีพลังงานที่สูญเสียไปกับแรงเสียดทาน และถ้า θ = 90 องศา ลูกจะตกลงมาตรงๆ โดยไม่มีแรงเสียดทาน จึงไม่มีพลังงานที่สูญเสียไป
ดังนั้น กราฟจะต้องมีมุมหนึ่งที่มีการสูญเสียพลังงานไปกับแรงเสียดทานมากที่สุด
เนื่องจากลูกบอลจะกลิ้งโดยไม่ไถล ถ้า θ มีค่าน้อยกว่ามุมวิกฤติ ดังนั้น สำหรับ θ ที่น้อยกว่ามุมวิกฤติ จึงไม่มีพลังงานที่สูญเสียไปกับแรงเสียดทาน แต่สำหรับ θ ที่มากกว่ามุมวิกฤติ ลูกบอลจะเกิดการไถลและมีพลังงานที่สูญเสียไปกับแรงเสียดทาน และถ้า θ = 90 องศา ลูกจะตกลงมาตรงๆ โดยไม่มีแรงเสียดทาน จึงไม่มีพลังงานที่สูญเสียไป
ดังนั้น กราฟจะต้องมีมุมหนึ่งที่มีการสูญเสียพลังงานไปกับแรงเสียดทานมากที่สุด
| 211. | วัตถุ 2.0 kg เดิมหยุดนิ่งตกลงมาจากความสูง 5.0 เมตร ไปโดนวัตถุ 6.0 kg ที่ตั้งอยู่บนสปริงเบาที่มีค่านิจสปริง k = 72 N / m จากการกระแทก ทำให้วัตถุทั้งสองติดไปด้วยกันและทำให้สปริงเกิดการสั่น จงหาว่าวัตถุ 6.0 kg จะเคลื่อนที่ไปได้ไกลเท่าไรจากจุดเริ่มต้น |
| A | 0.27 m |
| B | 1.1 m |
| C | 2.5 m |
| D | 2.8 m |
| E | 3.1 m |
ตอบ (B)
ใช้กฎการอนุรักษ์พลังงานหาอัตราเร็วของวัตถุ 2.0 kg ขณะก่อนเกิดการชน จะได้
พิจารณา
ดังนั้น วัตถุจะเคลื่อนไปได้ไกล 1.1 m ( จริงๆ ควรปัดเป็น 1.2 m )
ใช้กฎการอนุรักษ์พลังงานหาอัตราเร็วของวัตถุ 2.0 kg ขณะก่อนเกิดการชน จะได้
\(\rm {{\rm{m}}_1}{\rm{gy}} = (2.0kg)(10m/s)(5.0m) = 100J\)
ซึ่งมีค่าเท่ากับพลังงานจลน์ จะได้
\({\rm{v = }}\sqrt {{\rm{2}}{{\rm{K}}_{\rm{1}}}{\rm{/}}{{\rm{m}}_{\rm{1}}}} {\rm{ = 10}}{\rm{.0 m/s}}\)
เนื่องจากการชนนั้นไม่ยืดหยุ่น จึงได้
\({{\rm{v}}_{\rm{f}}}{\rm{ = }}{{\rm{v}}_{\rm{1}}}{\rm{ }}\dfrac{{{{\rm{m}}_{\rm{1}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}}}{\rm{ = 2}}{\rm{.5 m/s}}\)
ใช้กฎการอนุรักษ์พลังงานอีกครั้ง
\({{\rm{K}}_{\rm{f}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{m}}_{\rm{t}}}{{\rm{v}}^{\rm{2}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{(8}}{\rm{.0kg)(2}}{\rm{.5m/s}}{{\rm{)}}^{\rm{2}}}{\rm{ = 25~J}}\)
ขณะสปริงถูกบีบจะมีการเปลี่ยนแปลงพลังงานศักย์โน้มถ่วง เราจึงต้องแก้สมการเพื่อหาค่า x พิจารณา
\(\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{{\rm{x}}^2}{\rm{ + }}{{\rm{m}}_{\rm{t}}}{\rm{gx = }}{{\rm{K}}_{\rm{f}}}\)
หรือ
\({\rm{36}}{{\rm{x}}^2}{\rm{ + 20x}}-25{\rm{ = 0}}\)
จะได้ค่า x = – 1.15 และ x = 0.6 mดังนั้น วัตถุจะเคลื่อนไปได้ไกล 1.1 m ( จริงๆ ควรปัดเป็น 1.2 m )
| 212. | อัตราเร็วของคลื่นตามขวางในเส้นลวดเหล็ก หาจาก
\(\rm v = \sqrt {\dfrac{T}{{M/L}}}\)
โดย T คือ แรงตึงในเส้นลวด M คือ มวล และ L คือ ความยาวลวด สมมุติว่าไม่มีการยืดจากแรงตึง ถ้าลวดเหล็กสองอันที่ยาวเท่ากัน แต่เส้นแรกมีรัศมี r1 เส้นที่สองรัศมี r2 = 4r1 แต่ละสายถูกดึงให้ตึงที่สุดเท่าที่จะตึงได้โดยไม่ขาดออก แล้วอัตราส่วนความถี่มูลฐานของการสั่น ของลวดทั้งสองเส้น f1/f2 เท่ากับข้อใด |
| A | \(1\) |
| B | \(\sqrt2\) |
| C | \(2\) |
| D | \(2\sqrt2\) |
| E | \(4\) |
ตอบ (A)
ลวดจะขาดเมื่อ T > σA โดยที่ σ คือความต้านทานแรงดึง และ A เป็นพื้นที่หน้าตัด จะได้
เนื่องจากสมการนี้ไม่ขึ้นอยู่กับความยาวของสตริง ดังนั้น อัตราเร็วของคลื่นในลวดทั้งสองเส้นจะเท่ากัน และจาก v = fλ และลวดมีความยาวเท่ากัน
ดังนั้น ความถี่มูลฐานของการสั่นของทั้งสองจะเท่ากัน
ลวดจะขาดเมื่อ T > σA โดยที่ σ คือความต้านทานแรงดึง และ A เป็นพื้นที่หน้าตัด จะได้
\({\rm{v = }}\sqrt {\dfrac{{\rm{T}}}{{{\rm{M/L}}}}} = \sqrt {\dfrac{{\sigma {\rm{AL}}}}{{\rm{M}}}} = \sqrt {\dfrac{\sigma }{\rho }}\)
โดย ρ คือ ความหนาแน่น เนื่องจากสมการนี้ไม่ขึ้นอยู่กับความยาวของสตริง ดังนั้น อัตราเร็วของคลื่นในลวดทั้งสองเส้นจะเท่ากัน และจาก v = fλ และลวดมีความยาวเท่ากัน
ดังนั้น ความถี่มูลฐานของการสั่นของทั้งสองจะเท่ากัน
| 213. | รถกระป๋อง A และ B เหมือนกันทุกประการ แต่ละคันมีมวล m ทั้งสองคันเชื่อมกันด้วยสปริงที่มีค่านิจสปริง k และมีสปริงอีกสองเส้นเชื่อมรถทั้งสองกับกำแพง ดังรูป รถสามารถขยับตามการสั่นของสปริงได้อย่างอิสระ และมีทิศทางเดียวโดยไม่มีความฝืด
 \(\rm {x_{\rm{A}}}(t) = {x_0}sin{\omega _1}t = {x_{\rm{B}}}(t)\)
โดย \(\rm x_{_A}\) และ \(\rm x_{_B}\) คือ ระยะของรถเทียบกับตำแหน่งสมดุลของรถแต่ละคัน ภายใต้เงื่อนไขเริ่มต้นอีกแบบ รถสองคันจะมีเฟสการแกว่ง คือ \(\rm {x_{\rm{A}}}(t) = {x_0}sin{\omega _2}t = - {x_{\rm{B}}}(t)\)
อัตราส่วน \(\rm {\omega _2}/{\omega _1}\) จะมีค่าเท่ากับข้อใด |
| A | \(\sqrt3\) |
| B | \(2\) |
| C | \(2\sqrt2\) |
| D | \(3\) |
| E | \(5\) |
ตอบ (A)
( ข้อนี้เราอาจใช้เมทริกซ์ช่วยในการหาคำตอบ แต่ก็ต้องระมัดระวังการแยกพิจารณาด้วย )
กรณีที่พิจารณาแต่ละช่วง เราจะต้องแยกพิจารณาสองมวลที่เป็นค่าคงที่ ดังนั้น แรงของ A ที่กระทำบน B จะเป็นค่าคงที่ ในกรณีนี้มีสปริงเดียวเท่านั้นที่ให้แรงต่างออกไป ดังนั้น ความถี่เชิงมุมจะเท่ากับ
อีกกรณีหนึ่ง เราจะใช้จุดกึ่งกลางของสปริงอันกลางเป็นจุดอ้างอิง
ดังนั้น วัตถุเหมือนเคลื่อนที่อยู่ภายใต้สปริงสองอันที่ขนานกัน โดยเส้นหนึ่งยาว L อีกเส้นยาว L / 2 เนื่องจากสปริงมีค่านิจสปริง k เท่ากันและขนานกัน จะได้ค่านิจสปริงเท่ากับ 2k ดังนั้น ค่านิจสปริงสุทธิจะเท่ากับ k + 2k = 3k จึงมีความถี่ตามสมการ
( ข้อนี้เราอาจใช้เมทริกซ์ช่วยในการหาคำตอบ แต่ก็ต้องระมัดระวังการแยกพิจารณาด้วย )
กรณีที่พิจารณาแต่ละช่วง เราจะต้องแยกพิจารณาสองมวลที่เป็นค่าคงที่ ดังนั้น แรงของ A ที่กระทำบน B จะเป็นค่าคงที่ ในกรณีนี้มีสปริงเดียวเท่านั้นที่ให้แรงต่างออกไป ดังนั้น ความถี่เชิงมุมจะเท่ากับ
\(\rm {\omega _1} = \sqrt {k{\rm{ }}/{\rm{ }}m}\)
อีกกรณีหนึ่ง เราจะใช้จุดกึ่งกลางของสปริงอันกลางเป็นจุดอ้างอิง
ดังนั้น วัตถุเหมือนเคลื่อนที่อยู่ภายใต้สปริงสองอันที่ขนานกัน โดยเส้นหนึ่งยาว L อีกเส้นยาว L / 2 เนื่องจากสปริงมีค่านิจสปริง k เท่ากันและขนานกัน จะได้ค่านิจสปริงเท่ากับ 2k ดังนั้น ค่านิจสปริงสุทธิจะเท่ากับ k + 2k = 3k จึงมีความถี่ตามสมการ
\(\rm {\omega _2} = \sqrt {3k{\rm{ }}/{\rm{ }}m} = \sqrt 3 = {\omega _1}\)
ดังนั้น \(\rm {\omega _2}/{\omega _1} = \sqrt 3\)| 214. | รถเลี้ยวขวาด้วยอัตราเร็วคงที่เป็นวงกลม ให้ X เป็นเวกเตอร์โมเมนตัมเชิงมุมรอบศูนย์กลางของวงกลม และ Y เป็นเวกเตอร์ความเร่งของรถ จากมุมมองของคนขับข้อใดต่อไปนี้ถูกต้อง |
| A | X ไปทางซ้าย และ Y ไปทางซ้าย |
| B | X ไปข้างหน้า และ Y ไปทางขวา |
| C | X พุ่งลง และ Y ไปข้างหน้า |
| D | X ไปทางซ้าย และ Y ไปทางขวา |
| E | X พุ่งลง และ Y ไปทางขวา |
ตอบ (E)
ใช้กฎมือขวาในการหาโมเมนตัมเชิงมุม โดยความเร่งมีทิศพุ่งเข้าจุดศูนย์กลางของการเคลื่อนที่แบบวงกลม
ใช้กฎมือขวาในการหาโมเมนตัมเชิงมุม โดยความเร่งมีทิศพุ่งเข้าจุดศูนย์กลางของการเคลื่อนที่แบบวงกลม
| 215. | ลูกบอลกลิ้งลงมาจากพื้นเอียงโดยไม่ไถล ดังรูป
 |
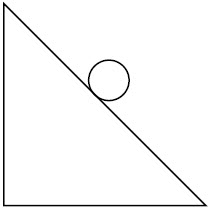| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (E)
ข้อที่ถูกต้อง คือ ข้อที่มีแรงกระทำทั้งในทิศตั้งฉาก และขนานกับพื้นเอียง สังเกตว่า ถ้าลูกบอลกลิ้งลงมาโดยมีความเร่ง แล้วแรงเสียดทานจะต้องน้อยกว่าแรงโน้มถ่วงในทิศขนานกับพื้นเอียง
ข้อที่ถูกต้อง คือ ข้อที่มีแรงกระทำทั้งในทิศตั้งฉาก และขนานกับพื้นเอียง สังเกตว่า ถ้าลูกบอลกลิ้งลงมาโดยมีความเร่ง แล้วแรงเสียดทานจะต้องน้อยกว่าแรงโน้มถ่วงในทิศขนานกับพื้นเอียง
| 216. | วัตถุที่มีความหนาแน่นสม่ำเสมอ มีส่วนที่ลอยพ้นน้ำอยู่ 20% ของวัตถุ ถ้าออกแรงกดที่ด้านบนของวัตถุ 3 N จะทำให้วัตถุจมทั้งชิ้น แล้ววัตถุมีปริมาตรเท่าใด ให้ความหนาแน่นของน้ำเท่ากับ ρน้ำ = 1000 kg/m3 |
| A | Vวัตถุ = 0.3 ลิตร |
| B | Vวัตถุ = 0.67 ลิตร |
| C | Vวัตถุ = 1.2 ลิตร |
| D | Vวัตถุ = 1.5 ลิตร |
| E | Vวัตถุ = 3.0 ลิตร |
ตอบ (D)
วัตถุที่จมลงไปในน้ำจะต้องมีแรงต้านมากระทำกับแรงลอยตัวที่เพิ่มขึ้น 0.2 ρน้ำ Vg
ดังนั้น Vวัตถุ = 1.5 ลิตร
วัตถุที่จมลงไปในน้ำจะต้องมีแรงต้านมากระทำกับแรงลอยตัวที่เพิ่มขึ้น 0.2 ρน้ำ Vg
ดังนั้น Vวัตถุ = 1.5 ลิตร
| 217. | จากข้อความที่กำหนด จงหาจำนวนชิ้นส่วน N1 , N2 และ N3 ให้ถูกต้อง ให้สมมุติว่าไม่มีแรงภายนอกมากระทำ และ ในกรณีที่ไม่สามารถสรุปจำนวนชิ้นส่วนได้ให้ใช้ N = 1 • ถ้าวัตถุระเบิดเป็น N1 ชิ้น (หรือจำนวนชิ้นน้อยกว่านี้) โดยที่ทราบมวลของแต่ละชิ้นและทราบพลังงานจลน์รวม แล้วเราจะสามารถหาพลังงานจลน์ของแต่ละชิ้นได้ • ถ้าวัตถุระเบิดเป็น N2 ชิ้น (หรือจำนวนชิ้นน้อยกว่านี้) ความเร็วของวัตถุแต่ละชิ้นจะต้องอยู่บนเส้นตรงเดียวกัน • ถ้าวัตถุระเบิดเป็น N3 ชิ้น (หรือจำนวนชิ้นน้อยกว่านี้) ความเร็วของวัตถุแต่ละชิ้นจะต้องอยู่บนระนาบ |
| A | N1 = 2, N2 = 1, N3 = 1 |
| B | N1 = 1, N2 = 2, N3 = 3 |
| C | N1 = 2, N2 = 2, N3 = 3 |
| D | N1 = 3, N2 = 2, N3 = 3 |
| E | N1 = 2, N2 = 3, N3 = 4 |
ตอบ (C)
จากโจทย์จะได้ว่า
N1 = 2
เพราะ จากกฎการอนุรักษ์โมเมนตัม เมื่อเรารู้พลังงานจลน์รวม เราก็สามารถหาพลังงานของแต่ละก้อนได้ (2 สมการ 2 ตัวแปร)
N2 = 2
เพราะ ถ้ามากกว่านี้แล้ว ความเร็วของวัตถุแต่ละชิ้นไม่จำเป็นต้องอยู่บนเส้นตรงเดียวกัน
N3 = 3
ลองวาดเวกเตอร์ 2 อันก่อน การเพิ่มอันที่ 3 เข้าไปแล้วทำให้ผลรวมเป็นศูนย์นั้น เวกเตอร์ที่ 3 ต้องอยู่บนระนาบเดียวกัน (หากมี 4 เวกเตอร์แล้ว ไม่จำเป็นต้องอยู่ในระนาบเดียวกันก็รวมเป็นศูนย์ได้)
จากโจทย์จะได้ว่า
N1 = 2
เพราะ จากกฎการอนุรักษ์โมเมนตัม เมื่อเรารู้พลังงานจลน์รวม เราก็สามารถหาพลังงานของแต่ละก้อนได้ (2 สมการ 2 ตัวแปร)
N2 = 2
เพราะ ถ้ามากกว่านี้แล้ว ความเร็วของวัตถุแต่ละชิ้นไม่จำเป็นต้องอยู่บนเส้นตรงเดียวกัน
N3 = 3
ลองวาดเวกเตอร์ 2 อันก่อน การเพิ่มอันที่ 3 เข้าไปแล้วทำให้ผลรวมเป็นศูนย์นั้น เวกเตอร์ที่ 3 ต้องอยู่บนระนาบเดียวกัน (หากมี 4 เวกเตอร์แล้ว ไม่จำเป็นต้องอยู่ในระนาบเดียวกันก็รวมเป็นศูนย์ได้)
| 218. | ขี่จักรยานตามรางที่เป็นวงกลมรัศมี 30 m ด้วยอัตราเร็วคงที่ 10 m / s (เร็วมาก!) แล้วขนาดของมุมในการเข้าโค้งของผู้ขี่จักรยานเทียบกับแนวตั้ง ที่ไม่ทำให้จักรยานล้มเท่ากับข้อใด สมมุติว่า ความสูงของคนขี่จักรยานเตี้ยกว่าความยาวรัศมีของราง |
| A | 9.46° |
| B | 9.59° |
| C | 18.4° |
| D | 19.5° |
| E | 70.5° |
ตอบ (C)
แรงที่พุ่งเข้าหาจุดศูนย์กลาง เท่ากับ mv2/r และแรงที่พุ่งไปที่พื้น เท่ากับ mg โดยแรงที่พุ่งเข้าหาจุดศูนย์กลางมาจากแรงเสียดทานและแรงจากจุดที่กระทำกับพื้น ส่วนแรงตั้งฉากเท่ากับแรงโน้มถ่วงและแรงจากจุดที่กระทำกับพื้น ดังนั้น การหาขนาดของมุมจะหาจาก tan θ โดย
แรงที่พุ่งเข้าหาจุดศูนย์กลาง เท่ากับ mv2/r และแรงที่พุ่งไปที่พื้น เท่ากับ mg โดยแรงที่พุ่งเข้าหาจุดศูนย์กลางมาจากแรงเสียดทานและแรงจากจุดที่กระทำกับพื้น ส่วนแรงตั้งฉากเท่ากับแรงโน้มถ่วงและแรงจากจุดที่กระทำกับพื้น ดังนั้น การหาขนาดของมุมจะหาจาก tan θ โดย
\(\rm \tan \theta = \dfrac{{{v^2}}}{{gr}}\)
| 219. | ลูกบาศก์มวล 10 kg แต่ละด้านยาว 5 m สามารถขยับไปตามพื้นราบได้อย่างอิสระโดยไม่มีแรงเสียดทาน ภายในลูกบาศก์มีกล่องเล็กๆ มวล 2 kg ซึ่งเคลื่อนที่ภายในลูกบาศก์ โดยไม่มีแรงเสียดทาน ที่เวลา t = 0 ถ้ากล่องเล็กๆ เคลื่อนที่ด้วยความเร็ว 5 m / s ไปยังด้านหนึ่งของกล่อง โดยลูกบาศก์ยังคงหยุดนิ่ง และสัมประสิทธิ์การกระแทกสำหรับการชนกันระหว่างลูกบาศก์กับกล่องเท่ากับ 90% หมายความว่าอัตราเร็วสัมพัทธ์ระหว่างลูกบาศก์กับกล่อง หลังการชนจะเท่ากับ 90% ของอัตราเร็วสัมพัทธ์ระหว่างลูกบาศก์กับกล่อง ก่อนการชน
 |
| A | 0 m |
| B | 50 m |
| C | 100 m |
| D | 200 m |
| E | 300 m |
ตอบ (B)
วิธีที่ง่ายที่สุดคือ พิจารณาจากการเคลื่อนที่ที่จุดศูนย์กลางมวลของระบบ โดยใช้กฎการอนุรักษ์โมเมนตัม จะได้อัตราเร็วเท่ากับ
เนื่องจาก จุดศูนย์กลางมวลอยู่ภายในกล่องลูกบาศก์ ดังนั้น ตำแหน่งของกล่องเล็กจะเคลื่อนที่จากตำแหน่งเดิมไปราวๆ 50 m เช่นกัน (คำตอบอื่นอยู่ภายนอกกล่องลูกบาศก์)
วิธีที่ง่ายที่สุดคือ พิจารณาจากการเคลื่อนที่ที่จุดศูนย์กลางมวลของระบบ โดยใช้กฎการอนุรักษ์โมเมนตัม จะได้อัตราเร็วเท่ากับ
\({{\rm{v}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{{\rm{(2kg)(5m/s)}}}}{{{\rm{(2kg) + (10kg)}}}}{\rm{ = }}\dfrac{{\rm{5}}}{{\rm{6}}}{\rm{m/s}}\)
หลังผ่านไปหนึ่งนาที จุดศูนย์กลางมวลจะเคลื่อนที่ไปได้ \(\rm \left( {\dfrac{{\rm{5}}}{{\rm{6}}}{\rm{m/s}}} \right)(60s) = 50m\)เนื่องจาก จุดศูนย์กลางมวลอยู่ภายในกล่องลูกบาศก์ ดังนั้น ตำแหน่งของกล่องเล็กจะเคลื่อนที่จากตำแหน่งเดิมไปราวๆ 50 m เช่นกัน (คำตอบอื่นอยู่ภายนอกกล่องลูกบาศก์)
| 220. | คานยาว 1.00 m มีความหนาแน่นสม่ำเสมอ มีจุดหมุนห่างจากปลายคาน 30 cm ถ้าคานเกิดสมดุลเมื่อวางวัตถุมวล 50.0 g ให้ห่างจากปลายคาน 20 cm (อ้างอิงปลายเดิม) แล้วคานมีมวลเท่าไร |
| 221. | นำวัตถุมวล M ไปแขวนกับสปริงที่มีค่านิจสปริง k และปล่อยให้แขวนลงมาในแนวตั้ง โดยคาบของการสั่นเท่ากับ T0 ถ้าตัดสปริงให้เหลือครึ่งเดียวแต่ยังใช้มวลเท่าเดิม แล้วนำไปวางบนพื้นลื่นที่เอียง θ กับแนวนอน แล้วคาบของการสั่นบนพื้นเอียงในเทอมของ T0 เท่ากับข้อใด |
| A | \(\rm T_0\) |
| B | \(\rm T_0/2\) |
| C | \(\rm 2T_0\sin θ\) |
| D | \(\rm T_0/\sqrt2\) |
| E | \(\rm T_0\sin θ / \sqrt2\) |
ตอบ (D)
ค่านิจสปริงจะแปรผกผันกับความยาวตามธรรมชาติของสปริง จากโจทย์ เมื่อตัดสปริงให้เหลือครึ่งเดียว แล้วค่านิจสปริงก็จะเพิ่มขึ้นเป็นสองเท่า ส่วนการนำสปริงไปวางบนพื้นเอียงแม้ว่าจะทำให้ตำแหน่งสมดุลของมวลเปลี่ยนไป แต่จะไม่ส่งผลใดๆ ต่อคาบของการสั่นของสปริง ดังนั้น คาบของการสั่นใหม่จะเท่ากับ
ค่านิจสปริงจะแปรผกผันกับความยาวตามธรรมชาติของสปริง จากโจทย์ เมื่อตัดสปริงให้เหลือครึ่งเดียว แล้วค่านิจสปริงก็จะเพิ่มขึ้นเป็นสองเท่า ส่วนการนำสปริงไปวางบนพื้นเอียงแม้ว่าจะทำให้ตำแหน่งสมดุลของมวลเปลี่ยนไป แต่จะไม่ส่งผลใดๆ ต่อคาบของการสั่นของสปริง ดังนั้น คาบของการสั่นใหม่จะเท่ากับ
\({\rm{T = 2}}\pi \sqrt {\dfrac{{\rm{m}}}{{{\rm{2k}}}}} {\rm{ = }}\dfrac{{\rm{1}}}{{\sqrt {\rm{2}} }}{\rm{2}}\pi \sqrt {\dfrac{{\rm{m}}}{{\rm{k}}}} {\rm{ = }}\dfrac{{{{\rm{T}}_{\rm{0}}}}}{{\sqrt {\rm{2}} }}\)
| 222. | กำหนด กราฟแรงที่กระทำกับวัตถุหนัก 5.00 ตามเวลาที่เปลี่ยนแปลงไป ดังรูป ถ้าความเร็วที่ t = 0.0 s คือ +1.0 m / s แล้วความเร็วของวัตถุที่ t = 7 s คือข้อใด  |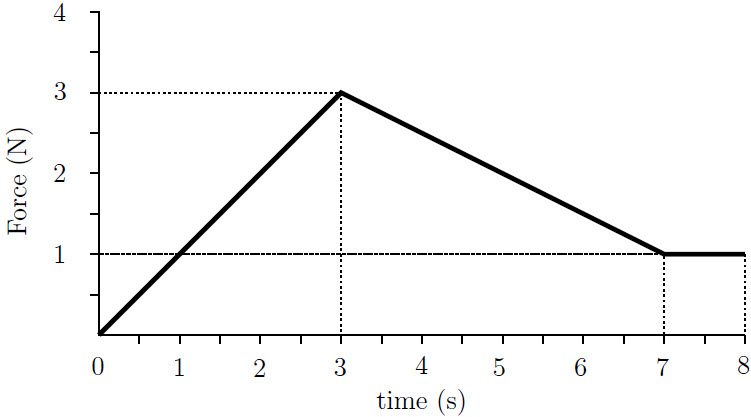
| A | 2.45 m/s |
| B | 2.50 m/s |
| C | 3.50 m/s |
| D | 12.5 m/s |
| E | 15.0 m/s |
ตอบ (C)
จากพื้นที่ใต้กราฟเท่ากับโมเมนตัมที่เปลี่ยนไป จะได้ว่า
ดังนั้น ความเร็วของวัตถุที่ t = 7 s คือ 1.0 + 2.5 = 3.5 m/s
จากพื้นที่ใต้กราฟเท่ากับโมเมนตัมที่เปลี่ยนไป จะได้ว่า
\(\Delta {\rm{p = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{(3~s)(3~N) + }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{(4 ~s)(3~N + 1~N) = 12/5 ~N}} \cdot {\rm{s}}\)
แสดงว่าจะมีอัตราเร็วเพิ่มขึ้นมาอีก \(\rm \Delta v{\rm{ = 2}}{\rm{.5~ m/s}}\)ดังนั้น ความเร็วของวัตถุที่ t = 7 s คือ 1.0 + 2.5 = 3.5 m/s
| 223. | รถบังคับวิทยุถูกผูกติดกับเสาด้วยเชือกยาว 3.00 m และถูกบังคับให้วิ่งเป็นวงกลม ด้วยความเร็วเชิงมุมเริ่มต้น 1.00 rad / s และเร่งความเร็วต่อเนื่องด้วยอัตรา 4.00 rad / s2 ถ้าเชือกขาดเมื่อความเร่งสู่ศูนย์กลางเกิน 2.43×102 m / s2 แล้วเราสามารถเร่งความเร็วรถได้นานแค่ไหนก่อนเชือกขาด |
| A | 0.25 s |
| B | 0.50 s |
| C | 1.00 s |
| D | 1.50 s |
| E | 2.00 s |
ตอบ (E)
เชือกจะขาดเมื่อ ac มีค่าสูงกว่าแรงตึงสูงสุด นั่นคือ
เชือกจะขาดเมื่อ ac มีค่าสูงกว่าแรงตึงสูงสุด นั่นคือ
\({{\rm{a}}_{\rm{c}}}{\rm{ = r}}{{\rm{\omega }}^{\rm{2}}}{\rm{ = r}}{\left( {\frac{1}{2}\alpha {{\rm{t}}^{\rm{2}}}{\rm{ + \omega }}_0^2} \right)^2}\)
จัดให้อยู่ในรูปของ t
\({\rm{t = }}\sqrt {\dfrac{2}{\alpha }\left( {\sqrt {\dfrac{{{{\rm{a}}_{\rm{c}}}}}{{\rm{r}}} - {{\rm{\omega }}_0}} } \right)} {\rm{ }}\)
ดังนั้น t = 2s| 224. | มวล m ติดสปริงในอุดมคติ ถูกนำไปวางในแนวนอนบนพื้นลื่น จากนั้นดึงมวลเล็กน้อย แล้วปล่อยออก ข้อใดแสดงกราฟพลังงานจลน์กับฟังก์ชันของพลังงานศักย์ได้ถูกต้องที่สุด |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (E)
เนื่องจากพลังงานจะถูกอนุรักษ์ไว้ ดังนั้น ผลรวมจะต้องเป็นค่าคงที่ค่าหนึ่ง
ดังนั้น กราฟจะต้องเป็นเส้นตรงที่ลาดลงมา และมีความชันคงที่
เนื่องจากพลังงานจะถูกอนุรักษ์ไว้ ดังนั้น ผลรวมจะต้องเป็นค่าคงที่ค่าหนึ่ง
ดังนั้น กราฟจะต้องเป็นเส้นตรงที่ลาดลงมา และมีความชันคงที่
| 225. | เฮลิคอปเตอร์กระดาษ มีรัศมีใบพัด r มีน้ำหนัก W ถูกปล่อยที่ความสูง h กลางอากาศที่มีความหนาแน่น ρ
 \(\rm T = kh^α r^βρ^δ W^ω\)
โดยที่ k เป็นค่าคงที่ที่ไม่มีมิติ (ค่าแท้จริงคือ 1.164) α, β, δ, และ ω เป็นค่าคงตัวของเลขชี้กำลังที่ต้องหาแล้วค่า α เท่ากับข้อใด |
| A | α = -1 |
| B | α = -1/2 |
| C | α = 0 |
| D | α = 1/2 |
| E | α = 1 |
ตอบ (E)
เมื่อเฮลิคอปเตอร์ไปถึงความเร็วสุดท้าย มันก็จะตกลงมาด้วยอัตราเร็วคงที่ ตาม h = vT โดย v เป็นความเร็วปลาย ในกรณีนี้ α = 1
เมื่อเฮลิคอปเตอร์ไปถึงความเร็วสุดท้าย มันก็จะตกลงมาด้วยอัตราเร็วคงที่ ตาม h = vT โดย v เป็นความเร็วปลาย ในกรณีนี้ α = 1
| 226. | เฮลิคอปเตอร์กระดาษ มีรัศมีใบพัด r มีน้ำหนัก W ถูกปล่อยที่ความสูง h กลางอากาศที่มีความหนาแน่น ρ สมมุติว่า เฮลิคอปเตอร์ไปถึง
 \(\rm T = kh^α r^βρ^δ W^ω\)
โดยที่ k เป็นค่าคงที่ที่ไม่มีมิติ (ค่าแท้จริงคือ 1.164) α, β, δ, และ ω เป็นค่าคงตัวของเลขชี้กำลังที่ต้องหาแล้วค่า β เท่ากับข้อใด |
| A | β = 1/3 |
| B | β = 1/2 |
| C | β = 2/3 |
| D | β = 1 |
| E | ข้อมูลไม่เพียงพอสำหรับการหาค่า β |
ตอบ (D)
เมื่อเฮลิคอปเตอร์ไปถึงความเร็วสุดท้าย มันก็จะตกลงมาด้วยอัตราเร็วคงที่ ตาม h = vT โดย v เป็นความเร็วปลาย ในกรณีนี้ α = 1
จากนั้นใช้การวิเคราะห์มิติกับมวลที่เราสนใจ
สังเกตว่า δ = – ω มีเฉพาะ W ที่เป็นหน่วยของเวลา (ส่วนกลับของกำลังสอง) โดย ω = –1/2 แต่ \(\rm \sqrt {\rho /W}\) มีหน่วยเป็นความยาว–2เวลา–1 และเรารู้ว่า α = 1 ดังนั้น β = 1
เมื่อเฮลิคอปเตอร์ไปถึงความเร็วสุดท้าย มันก็จะตกลงมาด้วยอัตราเร็วคงที่ ตาม h = vT โดย v เป็นความเร็วปลาย ในกรณีนี้ α = 1
จากนั้นใช้การวิเคราะห์มิติกับมวลที่เราสนใจ
สังเกตว่า δ = – ω มีเฉพาะ W ที่เป็นหน่วยของเวลา (ส่วนกลับของกำลังสอง) โดย ω = –1/2 แต่ \(\rm \sqrt {\rho /W}\) มีหน่วยเป็นความยาว–2เวลา–1 และเรารู้ว่า α = 1 ดังนั้น β = 1
| 227. | (เกินหลักสูตรการสอบเข้า สอวน.) แผ่นกลมมวล M มีโมเมนต์ความเฉื่อย I รัศมี R มีเชือกพันรอบแผ่นกลมไว้ ดังรูป แผ่นกลมกลิ้งอย่างอิสระไปตามทิศทางที่แสดงดังรูป มีแรงคงที่ T กระทำที่ปลายเชือก และทำให้แผ่นกลมมีความเร่งบนพื้นลื่น  |
| A | \(\rm \dfrac{I}{{M{R^2}}}\) |
| B | \(\rm \dfrac{{M{R^2}}}{I}\) |
| C | \(\rm \dfrac{I}{{3M{R^2}}}\) |
| D | \(\rm \dfrac{I}{{M{R^2} + I}}\) |
| E | \(\rm \dfrac{{M{R^2}}}{{M{R^2} + I}}\) |
ตอบ (D)
แรง T จะทำให้เกิดความเร่งที่จุดศูนย์กลางมวลของแผ่นกลมในอัตรา a = T / M และทำให้เกิดทอร์กบนแผ่นกลมที่จุดศูนย์กลางมวลตาม τ = RT ดังนั้น ความเร่งเชิงมุม α จะเท่ากับ RT / I
หลังผ่านไป t ความเร็วของแผ่นกลมจะเท่ากับ v = at และความเร็วเชิงมุมจะเท่ากับ ω = αt จะได้
แรง T จะทำให้เกิดความเร่งที่จุดศูนย์กลางมวลของแผ่นกลมในอัตรา a = T / M และทำให้เกิดทอร์กบนแผ่นกลมที่จุดศูนย์กลางมวลตาม τ = RT ดังนั้น ความเร่งเชิงมุม α จะเท่ากับ RT / I
หลังผ่านไป t ความเร็วของแผ่นกลมจะเท่ากับ v = at และความเร็วเชิงมุมจะเท่ากับ ω = αt จะได้
KEการเลื่อนที่ = \(\dfrac{1}{2}{\rm{M}}{\left( {\dfrac{{\rm{T}}}{{\rm{M}}}} \right)^2}{{\rm{t}}^2}\)
และ
KEการหมุน = \(\dfrac{1}{2}{\rm{I}}{\left( {\dfrac{{{\rm{RT}}}}{{\rm{I}}}} \right)^2}{{\rm{t}}^2}\)
เมื่อหาอัตราส่วนของทั้งสองจะได้
KEการเลื่อนที่ / KEสุทธิ
\(\begin{align*} &= \frac{{\frac{1}{2}{\rm{M}}{{\left( {\frac{{\rm{T}}}{{\rm{M}}}} \right)}^2}{{\rm{t}}^2}}}{{\frac{1}{2}{\rm{M}}{{\left( {\frac{{\rm{T}}}{{\rm{M}}}} \right)}^2}{{\rm{t}}^2} + \frac{1}{2}{\rm{I}}{{\left( {\frac{{{\rm{RT}}}}{{\rm{I}}}} \right)}^2}{{\rm{t}}^2}}}\\ &= \frac{{\frac{1}{{\rm{M}}}}}{{\frac{1}{{\rm{M}}} + \frac{{{{\rm{R}}^{\rm{2}}}}}{{\rm{I}}}}}\\ &= \frac{{\rm{I}}}{{{\rm{M}}{{\rm{R}}^{\rm{2}}}{\rm{ + I}}}} \end{align*}\)
\(\begin{align*} &= \frac{{\frac{1}{2}{\rm{M}}{{\left( {\frac{{\rm{T}}}{{\rm{M}}}} \right)}^2}{{\rm{t}}^2}}}{{\frac{1}{2}{\rm{M}}{{\left( {\frac{{\rm{T}}}{{\rm{M}}}} \right)}^2}{{\rm{t}}^2} + \frac{1}{2}{\rm{I}}{{\left( {\frac{{{\rm{RT}}}}{{\rm{I}}}} \right)}^2}{{\rm{t}}^2}}}\\ &= \frac{{\frac{1}{{\rm{M}}}}}{{\frac{1}{{\rm{M}}} + \frac{{{{\rm{R}}^{\rm{2}}}}}{{\rm{I}}}}}\\ &= \frac{{\rm{I}}}{{{\rm{M}}{{\rm{R}}^{\rm{2}}}{\rm{ + I}}}} \end{align*}\)
| 228. | ให้ทอร์กสูงสุดที่ออกมาจากเครื่องยนต์ของรถทดลองมวล m คือ τ อัตราเร็วเชิงมุมสูงสุดของเครื่องยนต์คือ ω เครื่องยนต์มีกำลังที่ออกมาคงที่ P และเครื่องยนต์เชื่อมต่อกับล้ออย่างไม่มีการสูญเสียพลังงาน ถ้าล้อมีรัศมี R และสัมประสิทธิ์ของแรงเสียดทานสถิตระหว่างล้อกับถนนคือ μ แล้วอัตราเร็วสูงสุดที่รถสามารถวิ่งบนพื้นเอียง 30 องศา ได้เท่ากับข้อใด สมมุติว่า ไม่มีการสูญเสียจากแรงเสียดทาน และ μ มีขนาดใหญ่พอที่จะทำให้ยางไม่ไถลขณะวิ่ง |
| A | \(\rm v = 2P/(mg)\) |
| B | \(\rm v = 2P/(\sqrt3mg)\) |
| C | \(\rm v = 2P/( μmg)\) |
| D | \(\rm v = τω /(mg)\) |
| E | \(\rm v = τω /( μmg)\) |
ตอบ (A)
จากหลักพื้นฐาน P = Fv เมื่อ F แรงของน้ำหนักที่ขนานกับพื้นเอียง จะได้
ดังนั้น v = 2P/(mg)
จากหลักพื้นฐาน P = Fv เมื่อ F แรงของน้ำหนักที่ขนานกับพื้นเอียง จะได้
\(\rm v = P/mg sin θ\)
โจทย์ให้ θ = 30°ดังนั้น v = 2P/(mg)
| 229. | วัตถุมวล m1 เคลื่อนที่ด้วยอัตราเร็ว v0 ชนกับวัตถุมวล m2 = αm1 โดย α < 1 จากเดิมหยุดนิ่ง การชนนี้อาจยืดหยุ่นสมบูรณ์ ไม่ยืดหยุ่นสมบูรณ์ หรือ ไม่ยืดหยุ่นบางส่วนก็ได้ หลังการชนวัตถุทั้งสองเคลื่อนที่ด้วยอัตราเร็ว v1 และ v2 สมมุติว่า การชนเกิดขึ้นในหนึ่งมิติและวัตถุแรกไม่สามารถพุ่งผ่านวัตถุสองได้ หลังการชน อัตราส่วนอัตราเร็ว r1 = v1 / v0 ของวัตถุแรกจะอยู่ในช่วงใด |
| A | (1 – α) / (1 + α) ≤ r1 ≤ 1 |
| B | (1 – α) / (1 + α) ≤ r1 ≤ 1 / (1 + α) |
| C | α / (1 + α) ≤ r1 ≤ 1 |
| D | 0 ≤ r1 ≤ 2α / (1 + α) |
| E | 1 / (1 + α) ≤ r1 ≤ 2 / (1 + α) |
ตอบ (B)
จากกฎการอนุรักษ์โมเมนตัมและพลังงานจลน์ในการชนแบบยืดหนุ่ยสมบูรณ์ จะได้
จากกฏการอนุรักษ์โมเมนตัม ในกรณีที่การชนนั้นไม่ยืดหยุ่นสมบูรณ์ จะได้ว่า
ดังนั้น
จากกฎการอนุรักษ์โมเมนตัมและพลังงานจลน์ในการชนแบบยืดหนุ่ยสมบูรณ์ จะได้
\(\begin{array}{c}
{{\rm{r}}_1} = \dfrac{{{{\rm{v}}_{\rm{1}}}}}{{{{\rm{v}}_{\rm{0}}}}} = \dfrac{{1 - {\rm{\alpha }}}}{{1 + {\rm{\alpha }}}}\\
{{\rm{r}}_2} = \dfrac{{{{\rm{v}}_2}}}{{{{\rm{v}}_{\rm{0}}}}} = \dfrac{2}{{1 + {\rm{\alpha }}}}
\end{array}\)
เนื่องจาก α < 1 วัตถุ m1 จะมีอิทธิพลมากกว่าวัตถุ m2 ดังนั้น การเคลื่อนที่จะยังคงไปข้างหน้า จากกฏการอนุรักษ์โมเมนตัม ในกรณีที่การชนนั้นไม่ยืดหยุ่นสมบูรณ์ จะได้ว่า
\({{\rm{r}}_{\rm{1}}}{\rm{ = }}{{\rm{r}}_{\rm{2}}} = \dfrac{1}{{1 + {\rm{\alpha }}}}\)
จากที่วัตถุ m2 เคลื่อนที่ไปข้างหน้าเสมอ และวัตถุ m1 ไม่สามารถทะลุผ่านวัตถุ m2 ได้ ดังนั้น วัตถุ m2 จะต้องเคลื่อนที่ด้วยความเร็วที่เป็นบวกมากกว่า (หรือเท่ากับ) วัตถุ m1 ดังนั้น
\(1/(1 + {\rm{\alpha }}) \le {{\rm{r}}_2} \le 2/(1 + {\rm{\alpha }})\)
การหาช่วงคำตอบของ วัตถุ m1 อาจจะยากกว่าเล็กน้อย เพราะสถานการณ์นี้อาจจะมีการกระดอนกลับเกิดขึ้น แต่ในกรณีนี้ α < 1 ทำให้ความเร็วหลังการชนเคลื่อนที่ไปข้างหน้า จึงได้ว่า
\((1 - {\rm{\alpha }})/(1 + {\rm{\alpha }}) \le {{\rm{r}}_1} \le 1/(1 + {\rm{\alpha }})\)
| 230. | เมฆละอองฝุ่นทรงกลมในอวกาศ มีความหนาแน่นสม่ำเสมอ ρ0 มีรัศมี R0 และมีความเร่งโน้มถ่วงที่ผิวเมฆเป็น g0 ถ้าการเกิดก้อนเมฆ (การขยายตัวเนื่องจากความร้อน) ทำให้รัศมีของเมฆเป็น 2R0 และละอองฝุ่นยังคงกระจายตัวอย่างสม่ำเสมอ แล้วความเร่งโน้มถ่วงปัจจุบันที่ระยะ R0 จากศูนย์กลางของก้อนเมฆ เท่ากับข้อใด |
| A | g0 / 32 |
| B | g0 / 16 |
| C | g0 / 8 |
| D | g0 / 4 |
| E | g0 / 2 |
ตอบ (C)
จากกฎของนิวตัน แรงโน้มถ่วงสำหรับวัตถุที่เป็นทรงกลมจะขึ้นกับมวลที่อยู่ภายในระยะจากศูนย์กลางมวลถึงตำแหน่งที่วัดเท่านั้น
ในทางกลับกันความหนาแน่นจะลดขนาดลง 1/8
จากกฎของนิวตัน แรงโน้มถ่วงสำหรับวัตถุที่เป็นทรงกลมจะขึ้นกับมวลที่อยู่ภายในระยะจากศูนย์กลางมวลถึงตำแหน่งที่วัดเท่านั้น
\({\rm{g = }}\dfrac{{{\rm{GM}}}}{{{{\rm{r}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{{\rm{4\pi }}}}{{\rm{3}}}{\rm{G\rho r}}\)
ซึ่งค่าสุดท้ายนั้นจะเป็นจริง เมื่อความหนาแน่นนั้นสม่ำเสมอในทางกลับกันความหนาแน่นจะลดขนาดลง 1/8
| 231. | พิจารณกล่องและเครื่องชั่งสองอัน ดังรูป ให้เครื่องชั่ง A รับน้ำหนักกล่องผ่านเชือกเบา ภายในกล่องมีรอกแขวนลงมาจากด้านบน และมีเชือกเบาอีกเส้นคล้องผ่านรอก ให้ปลายด้านหนึ่งยึดกับพื้นกล่อง และปลายอีกด้านหนึ่งผูกกับเครื่องชั่ง B ความตึงในเส้นเชือกที่อ่านจากเครื่องชั่งทั้งสองคือ TA และ TB ให้เดิมเครื่องชั่ง A อ่านได้ 30 นิวตัน และเครื่องชั่ง B อ่านได้ 20 นิวตัน
 ( ดัดแปลงมาจากการสาธิตของ Richard Berg ) |
| A | 35 นิวตัน |
| B | 40 นิวตัน |
| C | 45 นิวตัน |
| D | 50 นิวตัน |
| E | 60 นิวตัน |
ตอบ (B)
จากกล่องใบดังกล่าว สิ่งที่เราควรทราบคือ เมื่อเครื่องชั่ง B ถูกดึงด้วยแรง 10 นิวตัน แล้วเครื่องชั่ง A ก็จะถูกแรงดึงด้วยแรง 10 นิวตัน เพื่อให้ระบบเกิดสมดุล
ดังนั้น เครื่องชั่ง A จะอ่านค่าได้ 40 นิวตัน
จากกล่องใบดังกล่าว สิ่งที่เราควรทราบคือ เมื่อเครื่องชั่ง B ถูกดึงด้วยแรง 10 นิวตัน แล้วเครื่องชั่ง A ก็จะถูกแรงดึงด้วยแรง 10 นิวตัน เพื่อให้ระบบเกิดสมดุล
ดังนั้น เครื่องชั่ง A จะอ่านค่าได้ 40 นิวตัน
| 232. | เฮลิคอปเตอร์บินตามแนวนอนด้วยอัตราเร็วคงที่ มีสายเคเบิลที่ยืดหยุ่นสมบูรณ์ตลอดเส้นผูกติดไว้ที่ใต้เฮลิคอปเตอร์ และมีแรงต้านอากาศกระทำกับสายเคเบิลอยู่พอสมควร แล้วข้อใดแสดงลักษณะของสายเคเบิลขณะที่เฮลิคอปเตอร์บินไปทางขวาได้ถูกต้องที่สุด |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (B)
เมื่อมีแรงต้านอากาศกระทำกับสายเคเบิล ก็จะเกิดแรงที่กระทำในแนวนอนกับสายเคเบิลที่ผูกติดอยู่ใต้เฮลิคอปเตอร์ เนื่องจากแรงต้านอากาศแปรผันตามความยาวของสายเคเบิลที่ห้อยลงมาที่จุดใดก็ได้ ดังนั้น สายเคเบิลจะเอียงเป็นเส้นทแยงมุมตามข้อ (B)
(หากมีมวลแขวนอยู่ที่ปลายสายเคเบิลจะตอบข้อ (D))
เมื่อมีแรงต้านอากาศกระทำกับสายเคเบิล ก็จะเกิดแรงที่กระทำในแนวนอนกับสายเคเบิลที่ผูกติดอยู่ใต้เฮลิคอปเตอร์ เนื่องจากแรงต้านอากาศแปรผันตามความยาวของสายเคเบิลที่ห้อยลงมาที่จุดใดก็ได้ ดังนั้น สายเคเบิลจะเอียงเป็นเส้นทแยงมุมตามข้อ (B)
(หากมีมวลแขวนอยู่ที่ปลายสายเคเบิลจะตอบข้อ (D))
| 233. | (เกินหลักสูตรการสอบเข้า สอวน.) นักวิทยาศาสตร์ได้สร้างสถานีอวกาศแห่งใหม่ที่มีรูปร่างคล้ายล้อรถ มีรัศมี R โครงสร้างทั้งหมดมีมวล M อยู่ที่ส่วนขอบ เมื่อนักบินอวกาศมาถึงสถานี สถานีจะหมุนในอัตราที่ทำให้วัตถุที่ขอบของสถานีมีความเร่งสู่ศูนย์กลางเป็น g ให้ใกล้เคียงกับแรงโน้มถ่วงของโลก โดยสภาวะนั้นต้องพึ่งจรวดเล็กสองลำ แต่ละลำมีแรงดัน T นิวตัน ให้ติดตั้งบนขอบของสถานี แล้วจรวดต้องใช้เวลาเดินเครื่อง t เท่าใด จึงจะทำให้เกิดสภาวะที่ต้องการ (ดัดแปลงมาจาก Physics for Scientists and Engineers โดย Richard Wolfson) |
| A | \(\rm t = \sqrt{gR^3} M / (2T)\) |
| B | \(\rm t = \sqrt{gR} M / (2T)\) |
| C | \(\rm t = \sqrt{gR} M / T\) |
| D | \(\rm t = \sqrt{gR/\pi} M / T\) |
| E | \(\rm t = \sqrt{gR} M / (\pi T)\) |
ตอบ (B)
ความเร่งที่เราต้องการ คือ
ความเร่งที่เราต้องการ คือ
\({\rm{g = }}{{\rm{\omega }}^{\rm{2}}}{\rm{R}} \to {\rm{\omega = }}\sqrt {{\rm{g/R}}}\)
แรงที่จรวดสองลำ เท่ากับ
\({\rm{2TR = M}}{{\rm{R}}^{\rm{2}}}{\rm{\alpha }} \to {\rm{\alpha = 2T/MR}}\)
ดังนั้น เวลาที่ใช้เท่ากับ
\({\rm{t = \omega /\alpha = }}\frac{{\sqrt {{\rm{gR}}} {\rm{M}}}}{{{\rm{2T}}}}\)
| 234. | (เกินหลักสูตรการสอบเข้า สอวน.) ให้รอกสองอัน ทำจากโลหะชนิดเดียวกันมีความหนาแน่น ρ (แสดงดังรูป) รอก A เป็นแบบแผ่นกลมสม่ำเสมอมีรัศมี R รอก B เป็นแบบวงแหวน ส่วนที่กลวงมีรัศมี R/2 นำกล่องสองใบมวล M = αm (α > 1) แขวนกับรอกผ่านเชือกเบา และหมุนโดยไม่ไถล แล้วอัตราส่วนความเร่งในระบบ A กับ B เท่ากับข้อใด ถ้ามวลของรอก A เท่ากับ M + m
 |
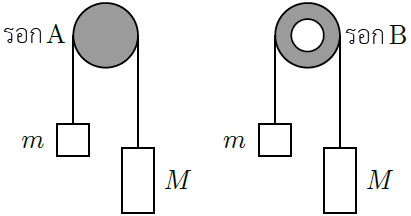| A | aA / aB = 47 / 48 |
| B | aA / aB = 31 / 32 |
| C | aA / aB = 15 / 16 |
| D | aA / aB = 9 / 6 |
| E | aA / aB = 3 / 4 |
ตอบ (A)
โจทย์ข้อนี้ เป็นโจทย์ปัญหาความสมดุลของแรงในเครื่องกลทั่วไป
สำหรับมวล M จะมีค่าตามสมการ
สำหรับมวล m จะมีค่าตามสมการ
เมื่อรวมสมการจะได้
และ βB = 1/2(1 – (1/4)(1/4)) = 15/32 เพราะรอกเป็นวงแหวนจึงต้องลบส่วนที่กลวงออกไป
ดังนั้น อัตราส่วนความเร่งจะเท่ากับ \(\dfrac{{{{\rm{a}}_{\rm{A}}}}}{{{{\rm{a}}_{\rm{B}}}}}{\rm{ = }}\dfrac{{47}}{{48}}\)
โจทย์ข้อนี้ เป็นโจทย์ปัญหาความสมดุลของแรงในเครื่องกลทั่วไป
สำหรับมวล M จะมีค่าตามสมการ
\({\rm{Ma = Mg}} - {{\rm{T}}_{\rm{M}}}\)
โดย TM คือ แรงตึงเชือกที่แขวนมวล Mสำหรับมวล m จะมีค่าตามสมการ
\({\rm{ma = }}{{\rm{T}}_{\rm{M}}} - {\rm{mg}}\)
สำหรับรอก จะมีค่าตามสมการ
\({\rm{I\alpha = R (}}{{\rm{T}}_{\rm{M}}} - {{\rm{t}}_{\rm{m}}}{\rm{)}}\)
โดย α = a / R และ I คือ โมเมนต์ความเฉื่อยเมื่อรวมสมการจะได้
\({\rm{Ia/}}{{\rm{R}}^{\rm{2}}}{\rm{ = (Mg }} - {\rm{Ma)}} - {\rm{(ma + mg)}}\)
หรือ
\({\rm{a = g}}\dfrac{{{\rm{M}} - {\rm{m}}}}{{{\rm{I/}}{{\rm{R}}^{\rm{2}}}{\rm{ + M + m}}}}\)
ให้โมเมนต์ความเฉื่อยของรอกทั้งสองอัน คือ I = β (M + m) R2 แล้วอัตราส่วนความเร่งจะเท่ากับ
\(\dfrac{{{{\rm{a}}_{\rm{A}}}}}{{{{\rm{a}}_{\rm{B}}}}}{\rm{ = }}\dfrac{{{{\rm{\beta }}_{\rm{B}}}{\rm{ + 1}}}}{{{{\rm{\beta }}_{\rm{A}}}{\rm{ + 1}}}}\)
โดย βA = 1/2 เพราะเป็นแผ่นกลมสม่ำเสมอและ βB = 1/2(1 – (1/4)(1/4)) = 15/32 เพราะรอกเป็นวงแหวนจึงต้องลบส่วนที่กลวงออกไป
ดังนั้น อัตราส่วนความเร่งจะเท่ากับ \(\dfrac{{{{\rm{a}}_{\rm{A}}}}}{{{{\rm{a}}_{\rm{B}}}}}{\rm{ = }}\dfrac{{47}}{{48}}\)
| 235. | ดาวเคราะห์มวล M และ m << M อยู่ในวงโคจรรอบจุดศูนย์กลางมวล ภายใต้แรงดึงดูดซึ่งกันและกัน และดาวทั้งสองอยู่ห่างกัน R ซึ่งมีขนาดใหญ่กว่าดาวทั้งสองดวง ถ้าชิ้นส่วนเล็ก ๆ ขนาด δm << m จากดาวมวล m ถูกดูดไปยังดาวมวล M โดยการถ่ายโอนนี้เกิดขึ้นในขณะที่วงโคจรของดาวทั้งสองยังเป็นวงกลม และยังคงห่างกัน R แล้วข้อความใดต่อไปนี้ถูกต้อง |
| A | แรงดึงดูดระหว่างดาวทั้งสองจะเพิ่มขึ้น |
| B | แรงดึงดูดระหว่างดาวทั้งสองจะยังคงที่ |
| C | โมเมนตัมเชิงมุมสุทธิของระบบจะเพิ่มขึ้น |
| D | โมเมนตัมเชิงมุมสุทธิของระบบจะยังคงที่ |
| E | คาบของวงโคจรของดาวเคราะห์ทั้งสองจะยังคงเป็นค่าคงที่ |
ตอบ (E)
แรงระหว่างดาวเคราะห์ทั้งสองดวง คือ
ขั้นตอนสุดท้าย หาคาบของการเคลื่อนที่จากสมการ v = 2πr / T จะได้
ดังนั้น ข้อ (E) คือ คำตอบที่ถูกต้อง (นักเรียนสามารถใช้กฎของเคปเลอร์ตอบได้เลยเช่นกัน)
แรงระหว่างดาวเคราะห์ทั้งสองดวง คือ
\({\rm{F = G}}\dfrac{{{\rm{Mm}}}}{{{{\rm{R}}^{\rm{2}}}}}\)
แรงใหม่ F´ จะเท่ากับ
\(\begin{align*}
\rm{F'} &= \rm G\frac{{{\rm{(M + }}\delta {\rm{m)(m}}--\delta {\rm{m)}}}}{{{{\rm{r}}^{\rm{2}}}}}\\
&= \rm G\frac{{{\rm{Mm}}--{\rm{(M}}--{\rm{m)}}\delta {\rm{m}}--{{(\delta {\rm{m}})}^2}}}{{{{\rm{R}}^{\rm{2}}}}}
\end{align*}\)
เราสามารถประมาณกับสมการแรกได้
\({\rm{F' = }}\left( {{\rm{1}}-\dfrac{{\delta {\rm{m}}}}{{\rm{m}}}} \right){\rm{F}}\)
การเคลื่อนที่สู่ศูนย์กลางจะเท่ากับ
\(\rm mv^2/r = F\)
โดย r คือระยะทางจาก m ถึงจุดศูนย์กลางมวล โดย
\({\rm{r = }}\dfrac{{\rm{M}}}{{{\rm{M + m}}}}{\rm{R}}\)
เมื่อแสดงในเทอมของโมเมนตัมเชิงมุม จะได้
\({{\rm{L}}_{\rm{m}}}{\rm{ = mvr = }}\sqrt {{\rm{m(m}}{{\rm{v}}^{\rm{2}}}{\rm{/r)}}{{\rm{r}}^{\rm{3}}}} {\rm{ = }}\sqrt {{\rm{m}}{{\rm{r}}^{\rm{3}}}{\rm{F}}} \)
หรือ
\({{\rm{L}}_{\rm{m}}}{\rm{ = }}\sqrt {\dfrac{{{\rm{m}}{{\rm{M}}^{\rm{3}}}{\rm{RGmM}}}}{{{{{\rm{(m + M)}}}^{\rm{3}}}}}} = {\rm{m}}{{\rm{M}}^{\rm{2}}}\sqrt {\dfrac{{{\rm{GR}}}}{{{{{\rm{(m + M)}}}^{\rm{3}}}}}} \)
จากความสมมาตร จะได้
\({{\rm{L}}_{\rm{M}}}{\rm{ = }}{{\rm{m}}^{\rm{2}}}{\rm{M}}\sqrt {\dfrac{{{\rm{GR}}}}{{{{{\rm{(m + M)}}}^{\rm{3}}}}}}\)
ดังนั้น ผลรวมเท่ากับ
\({\rm{L = }}{{\rm{L}}_{\rm{m}}}{\rm{ + }}{{\rm{L}}_{\rm{M}}}{\rm{ = mM}}\sqrt {\dfrac{{{\rm{GR}}}}{{{\rm{m + M}}}}}\)
จะเห็นว่า Mm จะลดลง เมื่อ δm ถูกถ่ายจาก m ไปสู่ M แสดงว่ามีทอร์กจากภายนอกมากระทำขั้นตอนสุดท้าย หาคาบของการเคลื่อนที่จากสมการ v = 2πr / T จะได้
\({\rm{T = }}\dfrac{{{\rm{2\pi r}}}}{{\rm{v}}}{\rm{ = 2\pi }}\sqrt {\dfrac{{{\rm{mr}}}}{{\rm{F}}}}\)
เมื่อรวมกับสมการด้านบน จะได้
\({\rm{T = 2\pi }}\sqrt {\dfrac{{{\rm{mMR}}}}{{{\rm{m + M}}}}\dfrac{{{{\rm{R}}^{\rm{2}}}}}{{{\rm{GmM}}}}} = {\rm{2\pi }}\sqrt {\dfrac{{{{\rm{R}}^{\rm{3}}}}}{{{\rm{G(m + M)}}}}}\)
จะเห็นว่าค่าที่ได้เป็นค่าคงที่ดังนั้น ข้อ (E) คือ คำตอบที่ถูกต้อง (นักเรียนสามารถใช้กฎของเคปเลอร์ตอบได้เลยเช่นกัน)
| 236. | นักบินอวกาศมวล 100 kg พกปืนที่บรรจุกระสุนขนาดใหญ่ไว้ 10 kg ตัวปืนและชุดนักบินมีมวลน้อยมาก เมื่อเหนี่ยวไกกระสุนจะพุ่งออกด้วยอัตราเร็วสัมพัทธ์ 50 m/s เทียบกับนักบิน แล้วขณะเหนี่ยวไก นักบินอวกาศจะได้รับแรงดลจากปืนเท่าใด |
| A | 455 Ns |
| B | 500 Ns |
| C | 550 Ns |
| D | 5000 Ns |
| E | 5500 Ns |
ตอบ (A)
พิจารณาที่จุดศูนย์กลางมวล เนื่องจากกระสุนมีมวลมากเมื่อเทียบกับนักบิน จึงต้องคิดด้วยความระมัดระวัง
เนื่องจากแรงดลที่ส่งออกมาคือ โมเมนตัมสุดท้ายของนักบิน
ให้นักบินมีมวล m1 มีความเร็วสุดท้ายเป็น v1 และตัวปืนมีมวล m2 มีความเร็วสุดท้ายเป็น v2
จากกฎการอนุรักษ์โมเมนตั้มจะได้
พิจารณาที่จุดศูนย์กลางมวล เนื่องจากกระสุนมีมวลมากเมื่อเทียบกับนักบิน จึงต้องคิดด้วยความระมัดระวัง
เนื่องจากแรงดลที่ส่งออกมาคือ โมเมนตัมสุดท้ายของนักบิน
ให้นักบินมีมวล m1 มีความเร็วสุดท้ายเป็น v1 และตัวปืนมีมวล m2 มีความเร็วสุดท้ายเป็น v2
จากกฎการอนุรักษ์โมเมนตั้มจะได้
\(\rm m_1v_1 + m_2v_2 = 0\)
และความเร็วสัมพัทธ์เท่ากับ ( สมมุติให้ v1 > 0 )
\(\rm v_r = v_1 – v_2\)
นำไปแทนค่าจะได้
\(\begin{align*}
{{\rm{m}}_{\rm{1}}}{{\rm{v}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{(}}{{\rm{v}}_{\rm{1}}}-{{\rm{v}}_{\rm{r}}}) &= 0\\
{{\rm{m}}_{\rm{1}}}{{\rm{v}}_{\rm{1}}} &= \frac{{{{\rm{m}}_{\rm{1}}}{{\rm{m}}_{\rm{2}}}}}{{{{\rm{m}}_{\rm{1}}} + {{\rm{m}}_{\rm{2}}}}}{{\rm{v}}_{\rm{r}}}
\end{align*}\)
ดังนั้น J = m1v1 = 455 Ns| 237. | นักบินอวกาศมวล 100 kg พกปืนที่บรรจุกระสุนขนาดใหญ่ไว้ 10 kg ตัวปืนและชุดนักบินมีมวลน้อยมาก เมื่อเหนี่ยวไกกระสุนจะพุ่งออกด้วยอัตราเร็วสัมพัทธ์ 50 m/s เทียบกับนักบิน หากก่อนหน้านี้นักบินอวกาศมาด้วยความเร็ว 10 m/s (วัดในกรอบอ้างอิงหนึ่ง) แล้วเขาต้องการยิงปืน เพื่อให้ความเร็วของเขาเปลี่ยนไปจากเดิมเป็นมุมที่มากที่สุดเมื่อเทียบกับทิศเดิม (วัดในกรอบอ้างอิงเดียวกัน) แล้วขนาดของมุมที่มากที่สุดเท่ากับข้อใด (คำแนะนำ: ลองวาดภาพประกอบดู) |
| A | 24.4° |
| B | 26.6° |
| C | 27.0° |
| D | 30.0° |
| E | 180.0° |
ตอบ (C)
โมเมนตัมสุดท้ายของนักบินจะเท่ากับผลรวมของโมเมนตัมเริ่มต้นกับแรงดลที่กระทำกับนักบิน
โดยโมเมนตัมเริ่มต้นของนักบินเท่ากับ
θ จะมากที่สุด เมื่อเวกเตอร์ \(\overrightarrow {{{\rm{p}}_{\rm{f}}}}\) สัมผัสกับวงกลม
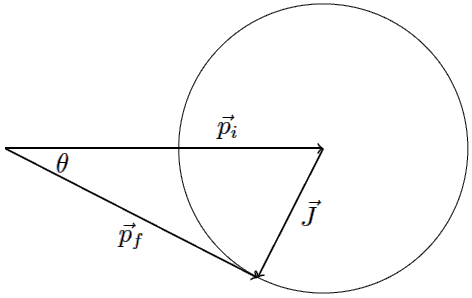ดังนั้น ค่า θ มากสุดเท่ากับ
โมเมนตัมสุดท้ายของนักบินจะเท่ากับผลรวมของโมเมนตัมเริ่มต้นกับแรงดลที่กระทำกับนักบิน
โดยโมเมนตัมเริ่มต้นของนักบินเท่ากับ
\(\rm P_i = (100 ~kg)(10 ~m/s) = 1000 ~kg\cdot m/s\)
และแรงดลที่เกิดขึ้นจะเป็นค่าค่าหนึ่งที่มีขนาดเล็กกว่าแรงดลที่นักบินอวกาศได้รับจากปืน (455 Ns) (สังเกตว่า แรงดลจะเท่ากับทุกแรงเฉื่อยในกรอบอ้างอิงต่างๆ) และโมเมนตัมสุดท้ายของนักบินจะถูกจำกัดอยู่ภายในวงกลมด้านล่าง
\({\rm{\theta = arcsin}}\dfrac{{\rm{J}}}{{{{\rm{p}}_{\rm{i}}}}}{\rm{ = 27}}{\rm{.}}{{\rm{0}}^ \circ }\)
| 238. | ปล่อยกล่องมวล m จากหยุดนิ่ง ให้ลงมาตามทางลาดโดยไม่มีแรงเสียดทาน ที่ความสูง h1 จากฐานของทางลาด เมื่อเลื่อนมาถึงฐานทางลาดแรกมันจะเลื่อนขึ้นทางลาดที่สอง โดยสัมประสิทธิ์แรงเสียดทานของกล่องกับทางลาดที่สองเท่ากับ μk ถ้าทั้งสองทางลาดทำมุม θ กับแนวนอน แล้วความสูง h2 ที่วัดจากฐานของทางลาดที่สองที่ทำให้กล่องขึ้นไปได้ เท่ากับข้อใด |
| A | h2 = (h1 sinθ) / (μk cosθ + sinθ) |
| B | h2 = (h1 sinθ) / (μk + sinθ) |
| C | h2 = (h1 sinθ) / (μk cos2 θ + sinθ) |
| D | h2 = (h1 sinθ) / (μk cos2 θ + sin2 θ) |
| E | h2 = (h1 cosθ) / (μk sinθ + cosθ) |
ตอบ (A)
ใช้หลักการของงานและพลังงาน
ใช้หลักการของงานและพลังงาน
| 239. | ผู้สังเกตยืนอยู่ด้านข้างของด้านหน้าขบวนรถไฟที่จอดอยู่ เมื่อรถไฟเริ่มวิ่งด้วยความเร่งคงที่ โบกี้แรกจะผ่านผู้สังเกตไปโดยใช้เวลา 5 วินาที ต้องใช้เวลาเท่าไร โบกี้ที่ 10 (คิดเฉพาะโบกี้นี้) ถึงจะผ่านผู้สังเกตไป |
| A | 1.07 s |
| B | 0.98 s |
| C | 0.91 s |
| D | 0.86 s |
| E | 0.81 s |
ตอบ (E)
จากสูตร
และ t1 เริ่มขณะโบกี้แรกวิ่งผ่านผู้สังเกตไป จะได้ \({\rm{L = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{at}}_{\rm{1}}^{\rm{2}}\)
สมมุติให้ หนึ่งโบกี้ยาว L และ t2 เริ่มขณะโบกี้ที่ 10 วิ่งมาถึงผู้สังเกต จะได้
ดังนั้น \({{\rm{t}}_{\rm{2}}}{\rm{ = }}\sqrt {{\rm{9}} \cdot {\rm{25}}{{\rm{s}}^{\rm{2}}}} {\rm{ = 15 ~s}}\) และ \({{\rm{t}}_{\rm{3}}}{\rm{ = }}\sqrt {{\rm{10}} \cdot {\rm{25}}{{\rm{s}}^{\rm{2}}}} {\rm{ = 15}}{\rm{.81 ~s}}\)
ดังนั้น โบกี้ที่ 10 ใช้เวลา 15 – 15.81 = 0.81 s ในการผ่านผู้สังเกตไป
จากสูตร
\(\Delta {\rm{x = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{a}}{{\rm{t}}^{\rm{2}}}{\rm{ + }}{{\rm{v}}_{\rm{i}}}{\rm{t}}\)
โดย t0 = 0 คือ เวลาที่รถไฟเริ่มเคลื่อนที่ และรถไฟโบกี้แรกยังอยู่แนวเดียวกับผู้สังเกตและ t1 เริ่มขณะโบกี้แรกวิ่งผ่านผู้สังเกตไป จะได้ \({\rm{L = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{at}}_{\rm{1}}^{\rm{2}}\)
สมมุติให้ หนึ่งโบกี้ยาว L และ t2 เริ่มขณะโบกี้ที่ 10 วิ่งมาถึงผู้สังเกต จะได้
\({\rm{9L = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{at}}_{\rm{2}}^{\rm{2}}\)
สุดท้าย t3 คือ เวลาที่โบกี้ที่ 10 วิ่งผ่านไป
\({\rm{10L = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{at}}_{\rm{3}}^{\rm{2}}\)
จากสมการ t1 จะได้ \({\rm{2L/a = 25}}{{\rm{s}}^{\rm{2}}}\)
| 240. | ก ยืนห่างจากกำแพง 20 m และ ข ยืนห่างจากกำแพงเดียวกัน 10 m ถ้า ก โยนลูกบอลทำมุมเงย 30◦ และชนแบบยืดหยุ่นกับกำแพง แล้ว ก ต้องโยนลูกบอลด้วยความเร็วเท่าไร ลูกบอลจึงจะตกที่ ข พอดี ให้ ก และ ข ให้มีความสูงเท่ากัน และทั้งคู่อยู่ในแนวตั้งฉากเดียวกันกับกำแพง |
| A | 11 m/s |
| B | 15 m/s |
| C | 19 m/s |
| D | 30 m/s |
| E | 35 m/s |
ตอบ (C)
กำแพงในข้อนี้เปรียบเสหมือนกระจกเงาที่สะท้อนการชนของลูกบอลแบบยืดหยุ่นสมบูรณ์ และระยะทางที่ต้องเคลื่อนที่จาก ก ถึง ข เท่ากับ 30 เมตร จากสูตรระยะทางจะได้
กำแพงในข้อนี้เปรียบเสหมือนกระจกเงาที่สะท้อนการชนของลูกบอลแบบยืดหยุ่นสมบูรณ์ และระยะทางที่ต้องเคลื่อนที่จาก ก ถึง ข เท่ากับ 30 เมตร จากสูตรระยะทางจะได้
\({\rm{R = }}\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{g}}}{\rm{sin2\theta }}\)
เราจะได้
\({{\rm{v}}^{\rm{2}}}{\rm{ = }}\dfrac{{{\rm{gR}}}}{{{\rm{sin 2\theta }}}} \approx \dfrac{{{\rm{300 }}{{\rm{m}}^{\rm{2}}}{\rm{/}}{{\rm{s}}^{\rm{2}}}}}{{\sqrt {\rm{3}} {\rm{/2}}}}\)
ดังนั้น v มีค่าประมาณ 19 m/s| 241. | ก โยนบอลให้ ข ที่อยู่ห่างออกไป l และ ก สามารถกำหนดเวลา t ที่บอลจะลอยไป จากอัตราเร็วที่ใช้ ซึ่งเขาจะใช้อัตราเร็วเท่าไรก็ได้จนถึง vmax และเลือกมุมที่ใช้ในการโยนเท่าไรก็ได้ ในช่วง 0◦ ถึง 90◦ ถ้าไม่คำนึงถึงแรงต้านอากาศ และถือว่า ก และ ข ความสูงเท่ากัน แล้วข้อความใดต่อไปนี้ผิด |
| A | ถ้า vmax < \(\sqrt{\text{g}l} \) แล้วบอลจะไม่สามารถไปถึง ข ได้ |
| B | กรณีที่บอลไปถึง ข ถ้า vmax เพิ่มขึ้น (ขณะที่ l คงตัว) แล้วค่าต่ำสุดของ t ต้องลดลง |
| C | กรณีที่บอลไปถึง ข ถ้า vmax เพิ่มขึ้น (ขณะที่ l คงตัว) แล้วค่าสูงสุดของ t ต้องเพิ่มขึ้น |
| D | กรณีที่บอลไปถึง ข ถ้า l เพิ่มขึ้น (ขณะที่ vmax คงตัว) แล้วค่าต่ำสุดของ t ต้องเพิ่มขึ้น |
| E | กรณีที่บอลไปถึง ข ถ้า l เพิ่มขึ้น (ขณะที่ vmax คงตัว) แล้วค่าสูงสุดของ t ต้องเพิ่มขึ้น |
ตอบ (A)
ข้อ (A) เป็นไปตามค่ามากสุดของการเคลื่อนที่แบบโพรเจกไทล์
สำหรับใครที่ต้องการคิดเลข จะลองคำนวณหาผลลัพธ์ดูก็ได้ กำหนดให้ θ เป็นมุมที่โยนออกไป และ v0 เป็นอัตราเร็วต้น จะได้
ข้อ (A) เป็นไปตามค่ามากสุดของการเคลื่อนที่แบบโพรเจกไทล์
สำหรับใครที่ต้องการคิดเลข จะลองคำนวณหาผลลัพธ์ดูก็ได้ กำหนดให้ θ เป็นมุมที่โยนออกไป และ v0 เป็นอัตราเร็วต้น จะได้
\(\begin{array}{l} 2{{\rm{v}}_0}\sin {\rm{\theta }} = {\rm{gt}}\\ {\rm{(}}{{\rm{v}}_0}\cos{\rm{\theta )t}} = l \end{array}\)
จาก sin2 θ + cos2 θ = 1
\(\begin{align*} {{\rm{v}}_{\rm{0}}}^{\rm{2}} &={\left( {\frac{{{\rm{gt}}}}{{\rm{2}}}} \right)^2}{\rm{ + }}{\left( {\frac{l}{{\rm{t}}}} \right)^2}\\ \frac{{{{\rm{g}}^2}}}{{\rm{4}}}{{\rm{t}}^4} - {{\rm{v}}_{\rm{0}}}^{\rm{2}}{{\rm{t}}^2} + {l^2} &= 0\\ {{\rm{t}}^2} &= 2\frac{{{{\rm{v}}_{\rm{0}}}^{\rm{2}} \pm \sqrt {{{\rm{v}}_{\rm{0}}}^{\rm{4}} - {{\rm{g}}^2}{l^2}} }}{{{{\rm{g}}^2}}} \end{align*}\)
จากผลลัพธ์สังเกตว่า การเพิ่ม l จะส่งผลต่อเวลาในการเคลื่อนที่ทั้งสองทิศทาง และการเพิ่ม vmax ก็จะทำให้เวลามากสุดที่ลอยอยู่ในอากาศมากขึ้นเช่นกัน สำหรับเวลาน้อยสุดที่บอลจะลอยไป จะหาจาก
\(\begin{align*} {\rm{t}}{{\rm{\_}}^2} &= 2\frac{{{{\rm{v}}_{\rm{0}}}^{\rm{2}} - \sqrt {{{\rm{v}}_{\rm{0}}}^{\rm{4}} - {{\rm{g}}^2}{l^2}} }}{{{{\rm{g}}^2}}}\\ \frac{{\partial ({\rm{t}}{{\rm{\_}}^2})}}{{\partial ({{\rm{v}}_{\rm{0}}}^2)}} &= \frac{2}{{{{\rm{g}}^2}}}\left( {1 - \frac{{2{{\rm{v}}_{\rm{0}}}^{\rm{2}}}}{{2\sqrt {{{\rm{v}}_{\rm{0}}}^{\rm{4}} - {{\rm{g}}^2}{l^2}} }}} \right)\\ \frac{{\partial ({\rm{t}}{{\rm{\_}}^2})}}{{\partial ({{\rm{v}}_{\rm{0}}}^2)}} &= \frac{2}{{{{\rm{g}}^2}}}\left( {1 - \frac{1}{{\sqrt {{\rm{1}} - \frac{{{{\rm{g}}^2}{l^2}}}{{{{\rm{v}}_{\rm{0}}}^{\rm{4}}}}} }}} \right) \end{align*}\)
สังเกตว่า ขวามือเป็นลบเสมอ ดังนั้น t_ จะมีค่าน้อยสุด เมื่อเราเลือก v0 มากสุด| 242. | ให้ขาตั้งสองขายึดกันด้วยบานพับที่ไม่มีแรงเสียดทาน และสัมประสิทธิ์แรงเสียดทาน ระหว่างพื้นกับขาตั้งเท่ากับ μ แล้วค่า θ สูงสุดในข้อใด ที่ทำให้ขาตั้งไม่ยุบลง
 |
| A | sinθ = 2μ |
| B | sinθ/2 = μ/2 |
| C | tanθ/2 = μ |
| D | tanθ = 2μ |
| E | tanθ/2 = 2μ |
ตอบ (E)
เนื่องจากแต่ละขาต้องสร้างสมดุลของแรงเสียดทานจากแรงในแนวนอนของขาอีกข้าง ผ่านจุดยอดของขาตั้งพิจารณาที่ทอร์กสมดุล
ส่วนแรงตั้งฉากที่กระทำกับขาตั้งจะมีค่าเท่ากับน้ำหนักของขาตั้ง ดังนั้น
เนื่องจากแต่ละขาต้องสร้างสมดุลของแรงเสียดทานจากแรงในแนวนอนของขาอีกข้าง ผ่านจุดยอดของขาตั้งพิจารณาที่ทอร์กสมดุล
\(\dfrac{{\rm{L}}}{{\rm{2}}}\left( {{\rm{M / 2}}} \right){\rm{ g sin \alpha = LF}}{{\rm{}}_{\rm{f}}}{\rm{cos \alpha }}\)
โดย Ff คือ แรงเสียดทานบนขาแต่ละข้าง และ \({\rm{ \alpha = }}\dfrac{1}{2}\theta\)ส่วนแรงตั้งฉากที่กระทำกับขาตั้งจะมีค่าเท่ากับน้ำหนักของขาตั้ง ดังนั้น
\({{\rm{F}}_{\rm{N}}}{\rm{ = (M/2)g}}\)
จับเทียบจะได้
\({{\rm{F}}_{\rm{N}}}{\rm{ = (M/2)g}}\)
หรือ
\(\dfrac{{\rm{L}}}{{\rm{2}}}\left( {{\rm{M / 2}}} \right){\rm{ g sin \alpha = L}}\mu \left( {{\rm{M / 2}}} \right){\rm{g cos \alpha }}\)
ดังนั้น tan θ / 2 = 2μ | 243. | นักเรียนก้าวเข้าไปในลิฟต์และขึ้นไปอยู่บนเครื่องชั่ง เมื่อลิฟต์เคลื่อนที่จากชั้นบนสุด ไปชั้นล่างสุดของอาคาร นักเรียนได้บันทึกน้ำหนักตามเวลาที่เปลี่ยนไป ดังนี้
 |
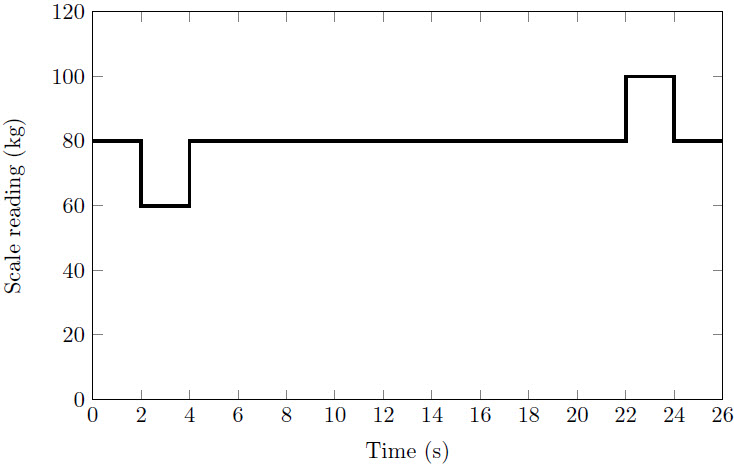| A | ช่วงวินาทีที่ 2 ถึง 4 |
| B | ที่วินาทีที่ 4 |
| C | ช่วงวินาทีที่ 4 ถึง 22 |
| D | ที่วินาทีที่ 22 |
| E | ช่วงวินาทีที่ 22 ถึง 24 |
ตอบ (C)
ค่าที่อ่านจากเครื่องชั่งจะไม่ใช่น่ำหนักแท้จริงของนักเรียน แต่เป็นแรงตั้งฉาก FN ที่กระทำกับขาที่เหยียบเครื่องชั่ง ซึ่งเป็นไปตามค่า g ดังนี้
โดยแรงตั้งฉากจะมีทิศชี้ขึ้นไปยังนักเรียน ส่วนแรงดึงดูด mg จะมีทิศลงเสมอ ดังนั้น ความเร่งของนักเรียนขณะเคลื่อนที่ลงจะเท่ากับ
เมื่อรวมสมการและจัดรูปใหม่จะได้
เนื่องจากลิฟท์เริ่มจากหยุดนิ่ง ดังนั้น ความเร็วต้นของนักเรียนจะต้องเป็นศูนย์ แสดงว่า มวลของนักเรียนต้องเป็น 80 kg จากกราฟจะเห็นว่ามีสองคาบที่มีความเร่งสม่ำเสมอ โดยจุดแรกที่เกิดการลดลงจะมีความเร่งเท่ากับ
ดังนั้น ความเร็วในการเคลื่อนที่ลงสูงสุดจะเกิดขึ้นในช่วงที่มีความเร่งสม่ำเสมอ ในข้อนี้จะเกิดขึ้นในช่วงวินาทีที่ 4 ถึง 22
ค่าที่อ่านจากเครื่องชั่งจะไม่ใช่น่ำหนักแท้จริงของนักเรียน แต่เป็นแรงตั้งฉาก FN ที่กระทำกับขาที่เหยียบเครื่องชั่ง ซึ่งเป็นไปตามค่า g ดังนี้
\(\rm m_{scale} g = F_N\)
โดยแรงตั้งฉากจะมีทิศชี้ขึ้นไปยังนักเรียน ส่วนแรงดึงดูด mg จะมีทิศลงเสมอ ดังนั้น ความเร่งของนักเรียนขณะเคลื่อนที่ลงจะเท่ากับ
\(\rm ma = mg – F_N\)
เมื่อรวมสมการและจัดรูปใหม่จะได้
\({\rm{a = g}}\left( {1 - \dfrac{{{{\rm{m}}_{{\rm{scale}}}}}}{{\rm{m}}}} \right)\)
เนื่องจากลิฟท์เริ่มจากหยุดนิ่ง ดังนั้น ความเร็วต้นของนักเรียนจะต้องเป็นศูนย์ แสดงว่า มวลของนักเรียนต้องเป็น 80 kg จากกราฟจะเห็นว่ามีสองคาบที่มีความเร่งสม่ำเสมอ โดยจุดแรกที่เกิดการลดลงจะมีความเร่งเท่ากับ
\({\rm{a = }}\left( {10~{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {1 - \dfrac{{{\rm{60 ~kg }}}}{{{\rm{80 ~kg}}}}} \right) = 2.5~{\rm{ m/}}{{\rm{s}}^2}\)
และในจุดที่สองที่มีการเพิ่มขึ้นก็จะมีขนาดเท่ากันดังนั้น ความเร็วในการเคลื่อนที่ลงสูงสุดจะเกิดขึ้นในช่วงที่มีความเร่งสม่ำเสมอ ในข้อนี้จะเกิดขึ้นในช่วงวินาทีที่ 4 ถึง 22
| 244. | นักเรียนก้าวเข้าไปในลิฟต์และขึ้นไปอยู่บนเครื่องชั่ง เมื่อลิฟต์เคลื่อนที่จากชั้นบนสุด ไปชั้นล่างสุดของอาคาร นักเรียนได้บันทึกน้ำหนักตามเวลาที่เปลี่ยนไป ดังนี้
 |
| A | 50 m |
| B | 80 m |
| C | 100 m |
| D | 150 m |
| E | 400 m |
ตอบ (C)
จากกราฟจะเห็นว่ามีสองคาบที่มีความเร่งสม่ำเสมอ โดยจุดแรกที่เกิดการลดลงจะมีความเร่งเท่ากับ
ความเร็วในการเคลื่อนที่ลงสูงสุดจะเกิดขึ้นในช่วงที่มีความเร่งสม่ำเสมอ ในข้อนี้จะเกิดขึ้นในช่วงวินาทีที่ 4 ถึง 22
ส่วนเวลาที่ใช้เร่งความเร็วจะเกิดขึ้นใน 2 วินาทีแรก ดังนั้น ความเร็วของลิฟท์หลังเร่งความเร็วจะเท่ากับ 5 m/s และคาบในช่วงที่มีความเร่งจะมีค่าประมาณ 20 s และเคลื่อนที่ไปได้ประมาณ 100 m
จากการคำนวณก็ทำให้ได้คำตอบที่ชัดเจนอยู่แล้ว หรือเราจะพิจารณากราฟของความเร็วกับเวลาก็ได้
โดยระยะทางที่เคลื่อนที่ไปได้เท่ากับพื้นที่ใต้กราฟ ซึ่งมีค่าเท่ากับ 100 m
จากกราฟจะเห็นว่ามีสองคาบที่มีความเร่งสม่ำเสมอ โดยจุดแรกที่เกิดการลดลงจะมีความเร่งเท่ากับ
\({\rm{a = }}\left( {10~{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {1 - \dfrac{{{\rm{60~ kg }}}}{{{\rm{80~ kg}}}}} \right) = 2.5~{\rm{ m/}}{{\rm{s}}^2}\)
และในจุดที่สองที่มีการเพิ่มขึ้นก็จะมีขนาดเท่ากันความเร็วในการเคลื่อนที่ลงสูงสุดจะเกิดขึ้นในช่วงที่มีความเร่งสม่ำเสมอ ในข้อนี้จะเกิดขึ้นในช่วงวินาทีที่ 4 ถึง 22
ส่วนเวลาที่ใช้เร่งความเร็วจะเกิดขึ้นใน 2 วินาทีแรก ดังนั้น ความเร็วของลิฟท์หลังเร่งความเร็วจะเท่ากับ 5 m/s และคาบในช่วงที่มีความเร่งจะมีค่าประมาณ 20 s และเคลื่อนที่ไปได้ประมาณ 100 m
จากการคำนวณก็ทำให้ได้คำตอบที่ชัดเจนอยู่แล้ว หรือเราจะพิจารณากราฟของความเร็วกับเวลาก็ได้
| 245. | ให้รถยนต์และรถบรรทุกมีโมเมนตัมเดียวกัน รถบรรทุกมีน้ำหนักเป็นสิบเท่าของรถยนต์ ข้อใดเปรียบเทียบพลังงานจลน์ของรถทั้งสองคันได้ถูกต้อง |
| A | พลังงานจลน์ของรถบรรทุก มีค่ามากกว่า 100 เท่า |
| B | พลังงานจลน์ของรถบรรทุก มีค่ามากกว่า 10 เท่า |
| C | พลังงานจลน์ของรถทั้งคัน มีค่าเท่ากัน |
| D | พลังงานจลน์ของรถยนต์ มีค่ามากกว่า 10 เท่า |
| E | พลังงานจลน์ของรถยนต์ มีค่ามากกว่า 100 เท่า |
ตอบ (D)
เขียนพลังจลน์ในเทอมของโมเมนตัมจะได้
เขียนพลังจลน์ในเทอมของโมเมนตัมจะได้
\({\rm{K = }}\dfrac{{{{\rm{p}}^{\rm{2}}}}}{{{\rm{2m}}}}\)
ดังนั้น อัตราส่วนจะอยู่ในรูป
\(\dfrac{{{{\rm{K}}_1}}}{{{{\rm{K}}_2}}}{\rm{ = }}\dfrac{{{{\rm{m}}_2}}}{{{{\rm{m}}_1}}}\)
จากโจทย์จึงสรุปว่า พลังงานจลน์ของรถยนต์ มีค่ามากกว่า 10 เท่า| 246. | รถบรรทุกมีความเร็วเริ่มต้น v คนขับได้เบรกจนกระทั่งรถหยุด โดยเบรกกระทำกับรถด้วยแรงคงที่ F ระยะทางที่รถบรรทุกเคลื่อนที่ไปจนกระทั่งหยุดคือ x และเวลาที่ใช้ในการหยุดรถคือ t แล้วข้อใดแสดงพลังงานจลน์เริ่มต้นของรถบรรทุกได้ถูกต้อง (พลังงานจลน์ก่อนคนขับเบรก) |
| A | Fx |
| B | Fvt |
| C | Fxt |
| D | Ft |
| E | ถูกทั้งข้อ (A) และ (B) |
ตอบ (A)
ข้อนี้พิจารณาเฉพาะขนาด สังเกตว่า
ข้อนี้พิจารณาเฉพาะขนาด สังเกตว่า
\({{\rm{K}}_{\rm{i}}}{\rm{ = }}\delta {\rm{K = W = Fx}}\)
| 247. | รถบรรทุกมีความเร็วเริ่มต้น v คนขับได้เบรกจนกระทั่งรถหยุด โดยเบรกกระทำกับรถด้วยแรงคงที่ F ระยะทางที่รถบรรทุกเคลื่อนที่ไปจนกระทั่งหยุดคือ x และเวลาที่ใช้ในการหยุดรถคือ t แล้วข้อใดต่อไปนี้แสดงโมเมนตัมเริ่มต้นของรถบรรทุกได้ถูกต้อง (โมเมนตัมก่อนคนขับรถเบรก) |
| A | Fx |
| B | Ft/2 |
| C | Fxt |
| D | 2Ft |
| E | 2Fx/v |
ตอบ (E)
พิจารณาเฉพาะขนาด จะได้
พิจารณาเฉพาะขนาด จะได้
\({{\rm{p}}_{\rm{i}}}{\rm{ = }}\Delta {\rm{p = Ft}}\)
แต่
\(\displaystyle {\rm{x = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{a}}{{\rm{t}}^{\rm{2}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{(at)t = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{vt}}\)
ดังนั้น pi = 2Fx/v| 248. | ข้อใดคือวิธีแยกบอลกลมตัน กับบอลกลมกลวง ที่มีรัศมีและมวลเท่ากัน ได้ดีที่สุด |
| A | ดูจากการโคจรของมวลทดสอบบอลนั้น |
| B | ดูจากเวลาที่วัตถุกลิ้งลงมาจากพื้นเอียง |
| C | ดูจากแรงไทดัลที่กระทำกับวัตถุในของเหลว |
| D | ดูจากลักษณะการลอยตัวของวัตถุในน้ำ |
| E | ดูจากแรงที่กระทำกับวัตถุในสนามโน้มถ่วงที่สม่ำเสมอ |
ตอบ (B)
ข้อ (B) เป็นวิธีที่เหมาะสมที่สุด เพราะบอลตันจะมีโมเมนต์ความเฉื่อยน้อยกว่าบอลกลมกลวง ทำให้มีความเร่งตอนลงมาจากพื้นเอียงเร็วกว่า
สำหรับข้อ (A) และ (C) เป็นการตรวจสนามโน้มถ่วงนอกวัตถุ สำหรับวัตถุที่เป็นทรงกลม ผลลัพธ์ที่ได้จะขึ้นกับมวลเท่านั้น ส่วนข้อ (E) ค่าที่ได้ขึ้นกับมวลรวมของวัตถุเท่านั้น และข้อ (D) ค่าที่ได้จะขึ้นอยู่กับรูปทรงภายนอกของวัตถุ
ข้อ (B) เป็นวิธีที่เหมาะสมที่สุด เพราะบอลตันจะมีโมเมนต์ความเฉื่อยน้อยกว่าบอลกลมกลวง ทำให้มีความเร่งตอนลงมาจากพื้นเอียงเร็วกว่า
สำหรับข้อ (A) และ (C) เป็นการตรวจสนามโน้มถ่วงนอกวัตถุ สำหรับวัตถุที่เป็นทรงกลม ผลลัพธ์ที่ได้จะขึ้นกับมวลเท่านั้น ส่วนข้อ (E) ค่าที่ได้ขึ้นกับมวลรวมของวัตถุเท่านั้น และข้อ (D) ค่าที่ได้จะขึ้นอยู่กับรูปทรงภายนอกของวัตถุ
| 249. | บล็อกไม้รูปสามเหลี่ยมมุมฉากมวล M วางอยู่บนโต๊ะ ดังรูป มีลูกบาศก์ไม้ขนาดเล็ก มวล m สองอัน วางในแต่ละด้านของด้านประกอบมุมฉาก ให้พื้นผิวสัมผัสระหว่างลูกบาศก์และบล็อกไม้ไม่มีแรงเสียดทาน และในขณะที่ลูกบาศก์เล็กเลื่อนลงมา บล็อกไม้สามเหลี่ยมจะยังคงอยู่ที่เดิม แล้วแรงในแนวตั้งฉากกับผิวสัมผัส (Normal Force) ของระบบกับโต๊ะเท่ากับข้อใด
 |
| A | 2mg |
| B | 2mg + Mg |
| C | mg + Mg |
| D | Mg + mg(sinα + sinβ) |
| E | Mg + mg(cosα + cosβ) |
ตอบ (C)
จากโจทย์ มีสองแรงที่กระทำลูกบาศก์แต่ละอัน คือ แรงตั้งฉากจากบล็อกไม้รูปสามเหลี่ยม และแรงโน้มถ่วง โดยแรงตั้งฉากจะต้องสมดุลกับแรงโน้มถ่วง พิจารณาที่ลูกบาศก์ซ้าย จะได้
จึงได้แรงทั้งหมดเท่ากับ
ดังนั้น Ftot = mg + Mg
สังเกตว่า แรงในแนวนอนของแรงตั้งฉากมาจากลูกบาศก์ซ้าย จะได้
ดังนั้น แรงแนวนอนสุทธิจึงเท่ากับ ศูนย์ ซึ่งสอดคล้องกับที่โจทย์ระบุว่าบล็อกไม้รูปสามเหลี่ยมจะไม่เคลื่อนที่บนโต๊ะ
จากโจทย์ มีสองแรงที่กระทำลูกบาศก์แต่ละอัน คือ แรงตั้งฉากจากบล็อกไม้รูปสามเหลี่ยม และแรงโน้มถ่วง โดยแรงตั้งฉากจะต้องสมดุลกับแรงโน้มถ่วง พิจารณาที่ลูกบาศก์ซ้าย จะได้
\(\rm F_N = mg~ cos α\)
แรงในแนวตั้งของแรงตั้งฉากจะถูกส่งผ่านบล็อกไม้รูปสามเหลี่ยมไปยังพื้นดิน จะได้
\(\rm F_{N_y} = mg ~cos2α\)
สำหรับลูกบาศก์ขวาก็เป็นไปในทำนองเดียวกัน นอกจากนี้ยังมีแรงที่พื้นต้องรับน้ำหนักของบล็อกไม้รูปสามเหลี่ยมอีกจึงได้แรงทั้งหมดเท่ากับ
\(\rm F_{tot} = mg~ cos^2 α + mg~ cos^2 β + Mg\)
เนื่องจากบล็อกไม้เป็นรูปสามเหลี่ยมมุมฉาก แสดงว่า cos2 α + cos2 β = 1 ดังนั้น Ftot = mg + Mg
สังเกตว่า แรงในแนวนอนของแรงตั้งฉากมาจากลูกบาศก์ซ้าย จะได้
\(\rm F_{N_x} = mg ~cos α~ sin α\)
ส่วนลูกบาศก์ขวาจะมีแรงตั้งฉากในแนวนอนเท่ากับ mg cos β sin β ในทิศตรงข้าม แต่เพราะบล็อกไม้เป็นรูปสามเหลี่ยมมุมฉาก แสดงว่า cos α sin α = cos β sin βดังนั้น แรงแนวนอนสุทธิจึงเท่ากับ ศูนย์ ซึ่งสอดคล้องกับที่โจทย์ระบุว่าบล็อกไม้รูปสามเหลี่ยมจะไม่เคลื่อนที่บนโต๊ะ
| 250. | (เกินหลักสูตรการสอบเข้า สอวน.) ทรงกลมกลวงมวล M รัศมี R มีของเหลวมวล M บรรจุไว้เต็ม โดยไม่มีแรงเสียดทาน (ไม่มีความหนืด) ทรงกลมที่เดิมอยู่นิ่ง ถูกปล่อยลงมาจากทางลาดที่ทำมุม θ กับแนวนอน โดยไม่มีการไถล แล้วความเร่งของทรงกลมหลังปล่อยลงมาเท่ากับข้อใด สมมุติว่า ความเร่งของการตกอย่างอิสระคือ g โมเมนต์ความเฉื่อยของทรงกลมกลวงรัศมี r มวล m ที่จุดศูนย์กลางมวล คือ \(\rm I = \dfrac{2}{3} mr^2\) โมเมนต์ความเฉื่อยของทรงกลมตันรัศมี r มวล m ที่จุดศูนย์กลางมวล คือ \(\rm I = \dfrac{2}{5} mr^2\) |
| A | \(\rm a = g ~sinθ\) |
| B | \(\rm a = \dfrac{3}{4} g ~sinθ\) |
| C | \(\rm a = \dfrac{1}{2} g ~sinθ\) |
| D | \(\rm a = \dfrac{3}{8} g ~sinθ\) |
| E | \(\rm a = \dfrac{3}{5} g ~sinθ\) |
ตอบ (B)
ข้อนี้เราอาจคำนวณจากทอร์กหรือพลังงานที่เกิดขึ้น โดยทอร์กที่กระทำกับแกนที่ผ่านจุดสัมผัสจะเท่ากับ
จากโจทย์จะได้โมเมนต์ความเฉื่อยคือ
จากกฎการอนุรักษ์พลังงานจะได้ว่า
ข้อนี้เราอาจคำนวณจากทอร์กหรือพลังงานที่เกิดขึ้น โดยทอร์กที่กระทำกับแกนที่ผ่านจุดสัมผัสจะเท่ากับ
\(\rm τ = RF~ sinθ = 2MgR ~sin θ\)
ความเร่งเชิงมุมเท่ากับ \(\rm τ = Iα\)
\({\rm{I = }}\dfrac{{\rm{2}}}{{\rm{3}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}{\rm{ + M}}{{\rm{R}}^{\rm{2}}}{\rm{ + M}}{{\rm{R}}^{\rm{2}}}{\rm{ = }}\dfrac{{\rm{8}}}{{\rm{3}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}\)
ดังนั้น ความเร่งเท่ากับ
\({\rm{a = \alpha R = }}\dfrac{{{\rm{2MgRsin\theta }}}}{{\dfrac{{\rm{8}}}{{\rm{3}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}}}{\rm{R = }}\dfrac{{\rm{3}}}{{\rm{4}}}{\rm{g sin\theta }}\)
หรืออีกวิธีคือ พิจารณาที่พลังงานจลน์ของวัตถุ จะได้
\(\begin{align*} \rm T &= \frac{{\rm{1}}}{{\rm{2}}}{\rm{(2M)}}{{\rm{v}}^{\rm{2}}}{\rm{ + }}\frac{{\rm{1}}}{{\rm{2}}} \cdot \frac{{\rm{2}}}{{\rm{3}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}{{\rm{\omega }}^{\rm{2}}}\\ \rm T &=\frac{{\rm{4}}}{{\rm{3}}}{\rm{M}}{{\rm{v}}^{\rm{2}}} \end{align*}\)
และพลังงานศักย์ที่เกิดกับแกน y ในแนวตั้ง \(\rm U = – (2M) gy\)จากกฎการอนุรักษ์พลังงานจะได้ว่า
\(\begin{align*} \rm \frac{d}{dt}(T + U) &= 0\\ \frac{{\rm{8}}}{{\rm{3}}}{\rm{Mv}}\frac{{{\rm{dv}}}}{{{\rm{dt}}}} &= -{\rm{(2M)g}}\frac{{{\rm{dy}}}}{{{\rm{dt}}}} \end{align*}\)
แต่ \(\dfrac{{{\rm{dy}}}}{{{\rm{dt}}}}\rm= -v\,{\rm{sin\theta }}\)ดังนั้น ความเร่งจะเท่ากับ
\({\rm{a}} = \dfrac{{{\rm{dv}}}}{{{\rm{dt}}}}{\rm{ = }}\dfrac{{\rm{3}}}{{\rm{4}}}{\rm{gsin\theta }}\)
| 251. | ที่วงแหวนด้านนอกของดาวเสาร์ การระบุชั้นที่เป็นส่วนหนึ่งของดาวเสาร์ หรือชั้นที่เป็นดาวบริวารของดาวเสาร์ เราจะต้องทราบความสัมพันธ์ระหว่าง ความเร็ว v ของแต่ละชั้นในวงแหวน และระยะทางที่วัดจากศูนย์กลางของดาวเสาร์ R ของแต่ละชั้นเสียก่อน จงพิจารณาว่าข้อความใดต่อไปนี้ถูกต้อง |
| A | ถ้า v ∝ R แสดงว่า ชั้นนั้นเป็นส่วนหนึ่งของดาวเสาร์ |
| B | ถ้า v2 ∝ R แสดงว่า ชั้นนั้นเป็นดาวบริวารของดาวเสาร์ |
| C | ถ้า v ∝ 1/R แสดงว่า ชั้นนั้นเป็นส่วนหนึ่งของดาวเสาร์ |
| D | ถ้า v2 ∝ 1/R แสดงว่า ชั้นนั้นเป็นส่วนหนึ่งของดาวเสาร์ |
| E | ถ้า v ∝ R2 แสดงว่า ชั้นนั้นเป็นดาวบริวารของดาวเสาร์ |
ตอบ (A)
หากเป็นชั้นที่เป็นส่วนหนึ่งของดาวเสาร์ แล้ว ω = v / R จะเป็นค่าคงที่
แสดงว่า v ∝ R
หากเป็นชั้นที่เป็นดาวบริวารของดาวเสาร์ จะได้
หากเป็นชั้นที่เป็นส่วนหนึ่งของดาวเสาร์ แล้ว ω = v / R จะเป็นค่าคงที่
แสดงว่า v ∝ R
หากเป็นชั้นที่เป็นดาวบริวารของดาวเสาร์ จะได้
\(\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{R}}} = \dfrac{{{\rm{GM}}}}{{{{\rm{r}}^{\rm{2}}}}}\)
แสดงว่า v2 ∝ 1/R| 252. | รถเข็นมวล m เคลื่อนที่ไปทางขวาด้วยความเร็ว 12 m/s ชนแบบยืดหยุ่นกับรถเข็นมวล 4.0 kg ที่เดิมอยู่นิ่ง หลังการชน รถเข็นมวล m เคลื่อนที่ไปทางซ้ายด้วยความเร็ว 6.0 m/s ถ้าการชนแบบยืดหยุ่นเกิดในมิติเดียว แล้วความเร็วที่จุดศูนย์กลางมวล (vcm) ของรถเข็นทั้งสองคัน ก่อนชนเท่ากับข้อใด |
| A | vcm = 2.0 m/s |
| B | vcm = 3.0 m/s |
| C | vcm = 6.0 m/s |
| D | vcm = 9.0 m/s |
| E | vcm = 18 m/s |
ตอบ (B)
พิจารณาที่จุดศูนย์กลางมวลของรถเข็น โดยพื้นฐานแล้วรถเข็นจะต้องมีโมเมนตัมเท่ากันแต่ตรงข้ามกัน เพื่อให้โมเมนตัมรวมเป็นศูนย์ หลังการชนแบบยืดหยุ่น โมเมนตัมจะมีทิศย้อนกลับ ซึ่งชัดเจนจากกฎการอนุรักษ์พลังงานรวม และโมเมนตัม
ดังนั้น ความเร็วของจุดศูนย์กลางมวลจึงเท่ากับ 3 m/s เพื่อให้ความเร็วต้นของ m ไปทางขวา 9 m/s และความเร็วสุดท้ายของ m ไปทางซ้าย 9 m/s
สังเกตว่า เราไม่จำเป็นต้องรู้มวล และความเร็วปลายของรถเข็นคันอื่น ๆ เลย
หรืออาจใช้สมการ
พิจารณาที่จุดศูนย์กลางมวลของรถเข็น โดยพื้นฐานแล้วรถเข็นจะต้องมีโมเมนตัมเท่ากันแต่ตรงข้ามกัน เพื่อให้โมเมนตัมรวมเป็นศูนย์ หลังการชนแบบยืดหยุ่น โมเมนตัมจะมีทิศย้อนกลับ ซึ่งชัดเจนจากกฎการอนุรักษ์พลังงานรวม และโมเมนตัม
ดังนั้น ความเร็วของจุดศูนย์กลางมวลจึงเท่ากับ 3 m/s เพื่อให้ความเร็วต้นของ m ไปทางขวา 9 m/s และความเร็วสุดท้ายของ m ไปทางซ้าย 9 m/s
สังเกตว่า เราไม่จำเป็นต้องรู้มวล และความเร็วปลายของรถเข็นคันอื่น ๆ เลย
หรืออาจใช้สมการ
\(\rm 12m = 6 m + 4 v^2\)
และ
\(\dfrac{1}{2}{\rm{m}} \times {12^2} = \dfrac{1}{2}{\rm{m}} \times {6^2} + \dfrac{1}{2} \times 4 \times {\rm{v}}_2^2\)
แก้สมการแล้วหาคำตอบ จะได้
\({{\rm{v}}_{{\rm{cm}}}} = \dfrac{{12~{\rm{m}}}}{{{\rm{m}} + 4}} = 3\,\,{\rm{m/s}}\)
| 253. | คานสม่ำเสมอ มีส่วนหนึ่งจมอยู่ในน้ำและปลายด้านหนึ่งถูกแขวนไว้ ดังรูป ถ้าคานมีความหนาแน่นเป็น 5/9 ของน้ำ แล้วที่ภาวะสมดุล สัดส่วนของคานที่อยู่เหนือน้ำจะเท่ากับข้อใด
 |
| A | 0.25 |
| B | 0.33 |
| C | 0.5 |
| D | 0.67 |
| E | 0.75 |
ตอบ (D)
สมมุติให้ α เป็นสัดส่วนของคานที่อยู่เหนือน้ำ, l เป็นความยาวของคาน, V เป็นปริมาตรของคาน, ρw เป็นความหนาแน่นของน้ำ และ ρr เป็นความหนาแน่นของคาน จากนั้นพิจารณาทอร์กที่จุดหมุน โดยแรงโน้มถ่วงที่กระทำกับทอร์กเท่ากับ
ดังนั้น
สมมุติให้ α เป็นสัดส่วนของคานที่อยู่เหนือน้ำ, l เป็นความยาวของคาน, V เป็นปริมาตรของคาน, ρw เป็นความหนาแน่นของน้ำ และ ρr เป็นความหนาแน่นของคาน จากนั้นพิจารณาทอร์กที่จุดหมุน โดยแรงโน้มถ่วงที่กระทำกับทอร์กเท่ากับ
\({{\rm{\tau }}_{\rm{g}}}{\rm{ = }}{{\rm{\rho }}_{\rm{r}}}{\rm{V g }} \cdot \dfrac{{\rm{1}}}{{\rm{2}}}l\)
เนื่องจาก 1 – α คือส่วนที่คานจมอยู่ใต้น้ำ และจุดศูนย์กลางของส่วนที่จมอยู่ใต้น้ำจะอยู่ห่างจากจุดหมุนป็นระยะ (α + \(\frac{1}{2}\)(1 – α))l ดังนั้น แรงลอยที่กระทำกับทอร์กจะเท่ากับ
\(\begin{align*} {{\rm{\tau }}_{\rm{b}}} &={{\rm{\rho }}_{\rm{w}}}{\rm{(1}}-{\rm{\alpha )V g }} \cdot {\rm{(\alpha + }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{(1}}-{\rm{\alpha ))}}l\\ {{\rm{\tau }}_{\rm{b}}}&= \frac{{\rm{1}}}{{\rm{2}}}{{\rm{\rho }}_{\rm{w}}}{\rm{(1}}-{{\rm{\alpha }}^{\rm{2}}}{\rm{)V g}}l \end{align*}\)
เนื่องจากทอร์กต้องเท่ากัน จะได้
\(\begin{align*} {{\rm{\tau }}_{\rm{g}}}&={{\rm{\tau }}_{\rm{b}}}\\ {\rm{ }}\frac{{\rm{1}}}{{\rm{2}}}{{\rm{\rho }}_{\rm{r}}} &= \frac{{\rm{1}}}{{\rm{2}}}{{\rm{\rho }}_{\rm{w}}}{\rm{(1}}-{{\rm{\alpha }}^{\rm{2}}}{\rm{)}}\\ \frac{{{{\rm{\rho }}_{\rm{r}}}}}{{{{\rm{\rho }}_{\rm{w}}}}} &= {\rm{1}}-{{\rm{\alpha }}^{\rm{2}}} \end{align*}\)
จากโจทย์ให้ \(\dfrac{{{{\rm{\rho }}_{\rm{r}}}}}{{{{\rm{\rho }}_{\rm{w}}}}} = \dfrac{5}{9}\)ดังนั้น
\(\begin{align*} \frac{{\rm{5}}}{9} &= {\rm{1}}-{{\rm{\alpha }}^{\rm{2}}}\\ {\rm{\alpha }} &= \frac{2}{3} \end{align*}\)
| 254. | แนวคิดจาก โจทย์โอลิมปิกฟิสิกส์นานาชาติ 2012 ที่ เอสโตเนีย อนุภาคขนาดเล็กจำนวนมากรวมตัวเป็นเมฆทรงกลมในอวกาศ ที่สภาวะหยุดนิ่ง อนุภาคจะมีความหนาแน่นของมวลต่อปริมาตรเป็น ρ0 และมีรัศมี r0 ถ้าแรงโน้มถ่วงทำให้ยุบตัว โดยมีเฉพาะแรงโน้มถ่วงที่กระทำระหว่างกัน (ไม่มีแรงอื่น) แล้วต้องใช้เวลานานแค่ไหนเมฆจึงจะยุบตัวสมบูรณ์ (ค่าจริงของ 0.5427 คือ\(\sqrt{\frac{3\pi}{32}}\)) |
| A | \(\rm \dfrac{0.5427}{r_0^2\sqrt{G\rho_0}}\) |
| B | \(\rm \dfrac{0.5427}{r_0\sqrt{G\rho_0}}\) |
| C | \(\rm \dfrac{0.5427}{\sqrt{r_0}\sqrt{G\rho_0}}\) |
| D | \(\rm \dfrac{0.5427}{\sqrt{G\rho_0}}\) |
| E | \(\rm \dfrac{0.5427}{\sqrt{G\rho_0}}r_0\) |
ตอบ (D)
ข้อนี้ต้องหาคำตอบด้วยวิธีวิเคราะห์เชิงมิติ ซึ่งจะพิจารณาจาก
โดยขนาดของ t เป็น [T], ขนาดของ G เป็น [L]3 [M]-1 [T]-2 , ขนาดของ ρ0 เป็น [L]-3 [M] และขนาดของ r0 เป็น [L] จะได้
ข้อนี้ต้องหาคำตอบด้วยวิธีวิเคราะห์เชิงมิติ ซึ่งจะพิจารณาจาก
\({\rm{t = 0}}{\rm{.527~}}{{\rm{G}}^{{\rm{ - 1/2}}}}{\rho _{\rm{0}}}^{{\rm{ - 1/2}}}{\rm{r}}_0^{\rm{n}}\)
(เนื่องจากในทุกตัวเลือก ตัวแปร G และ ρ0 มีเลขชี้กำลังเดียวกัน) โดยขนาดของ t เป็น [T], ขนาดของ G เป็น [L]3 [M]-1 [T]-2 , ขนาดของ ρ0 เป็น [L]-3 [M] และขนาดของ r0 เป็น [L] จะได้
\(\begin{align*} \rm [T] &= ([L{{\rm{]}}^{\rm{3}}}{{\rm{[M]}}^{{\rm{ - 1}}}}{{\rm{[T]}}^{{\rm{ - 2}}}}{{\rm{)}}^{{\rm{ - 1/2}}}}{{\rm{([L}}{{\rm{]}}^{{\rm{ - 3}}}}{\rm{[M])}}^{{\rm{ - 1/2}}}}{{\rm{[L]}}^{\rm{n}}}\\ \rm[T] &= {\rm{[T][L}}{{\rm{]}}^{\rm{n}}}\\ \rm n &= 0 \end{align*}\)
สังเกตว่า เวลาในการยุบตัวไม่ได้ขึ้นกับขนาดของเมฆเลย| 255. | วัตถุมวลเท่ากันสองอันเชื่อมกันด้วยคานเบา และโคจรรอบดาวเคราะห์ดวงหนึ่ง โดยคานมีความยาวระดับหนึ่ง แต่สั้นกว่ารัศมีวงโคจร ขณะโคจร คานจะอยู่ในลักษณะตั้งฉากกับดาวเคราะห์เสมอ • มีแรงเกิดขึ้นที่คานหรือไม่ ? ถ้ามีจะเป็นแรงดึงหรือแรงอัด ? • จะเกิดสภาวะสมดุลเสถียร ไม่เสถียร หรือตามธรรมชาติ เมื่อมีการรบกวนการทำมุมของคานเพียงเล็กน้อย ? ( การรบกวนในที่นี้ คือ การรบกวนการรักษาอัตราการหมุนที่ทำให้คานยังคงตั้งฉากกับดาวเคราะห์ )  |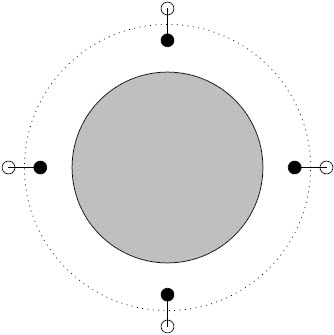
| A | ไม่มีแรงใดเกิดขึ้น และมีสภาวะสมดุลตามธรรมชาติ |
| B | มีแรงดึงเกิดขึ้น และมีสภาวะสมดุลเสถียร |
| C | มีแรงอัดเกิดขึ้น และมีสภาวะสมดุลเสถียร |
| D | มีแรงดึงเกิดขึ้น และมีสภาวะสมดุลไม่เสถียร |
| E | มีแรงอัดเกิดขึ้น และมีสภาวะสมดุลไม่เสถียร |
ตอบ (D)
เนื่องจากแรงโน้มถ่วงคิดจาก 1/r2 ดังนั้น แรงดึงดูดของมวลด้านในจะมากกว่ามวลด้านนอก ในขณะที่มวลทั้งสองมีความเร็วเชิงมุมเดียวกัน ดังนั้น ความเร่งสู่ศูนย์กลางจะเท่ากับ r แสดงว่ามวลด้านนอกต้องมีแรงสู่ศูนย์กลางมากกว่ามวลด้านใน
ให้ Fa เป็นแรงสู่ศูนย์กลาง
สำหรับมวลด้านนอก Fa > Fg ดังนั้น มวลด้านนอกจึงดึงให้คานยึดออก (หรือคานออกแรงดึงเข้า)
และในทำนองเดียวกันสำหรับมวลด้านใน Fa < Fg จึงตอบข้อ (D)
เพื่อให้เข้าใจง่ายลองพิจารณาที่จุด C.M. ว่า มวลด้านนอกมีแรงพุ่งออกในแนวรัศมี และมีแรงดึงจากคาน ส่วนมวลด้านในมีแรงพุ่งเข้าในแนวรัศมี และมีแรงตึงจากคาน เมื่อคานถูกรบกวนให้เปลี่ยนมุมเล็กน้อยแรงเหล่านี้จะสร้างทอร์กที่ทำให้คานคงสภาพไว้ คานจึงเกิดความสมดุลเสถียร
เนื่องจากแรงโน้มถ่วงคิดจาก 1/r2 ดังนั้น แรงดึงดูดของมวลด้านในจะมากกว่ามวลด้านนอก ในขณะที่มวลทั้งสองมีความเร็วเชิงมุมเดียวกัน ดังนั้น ความเร่งสู่ศูนย์กลางจะเท่ากับ r แสดงว่ามวลด้านนอกต้องมีแรงสู่ศูนย์กลางมากกว่ามวลด้านใน
ให้ Fa เป็นแรงสู่ศูนย์กลาง
สำหรับมวลด้านนอก Fa > Fg ดังนั้น มวลด้านนอกจึงดึงให้คานยึดออก (หรือคานออกแรงดึงเข้า)
และในทำนองเดียวกันสำหรับมวลด้านใน Fa < Fg จึงตอบข้อ (D)
เพื่อให้เข้าใจง่ายลองพิจารณาที่จุด C.M. ว่า มวลด้านนอกมีแรงพุ่งออกในแนวรัศมี และมีแรงดึงจากคาน ส่วนมวลด้านในมีแรงพุ่งเข้าในแนวรัศมี และมีแรงตึงจากคาน เมื่อคานถูกรบกวนให้เปลี่ยนมุมเล็กน้อยแรงเหล่านี้จะสร้างทอร์กที่ทำให้คานคงสภาพไว้ คานจึงเกิดความสมดุลเสถียร
| 256. | อนุภาคมวล 1 kg สองอัน มีสถานะเริ่มต้น ดังรูป
 |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |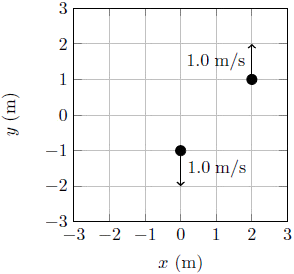
ตอบ (E)
ประการแรก โมเมนตัมเชิงเส้นจะต้องถูกอนุรักษ์ไว้ จากสถานะเริ่มต้นที่โมเมนตัมเชิงเส้นเป็นศูนย์ แสดงว่าข้อ (B) ไม่ใช่คำตอบ และโมเมนตัมเชิงมุมที่จุดใด ๆ จะต้องถูกอนุรักษ์ไว้ด้วย จากสถานะเริ่มต้นที่โมเมนตัมเชิงเส้นเป็นศูนย์ ดังนั้น โมเมนตัมเชิงมุมจะมีค่าเท่ากันทุกจุดไม่ว่าจะเป็นจุดอ้างอิงใด จึงพิจารณาเพียงจุดใดหนึ่งจุดก็พอ จากโมเมนตัมเชิงมุมรวมต้องเท่ากับ 2 kg m2/s ในทิศทวนเข็มนาฬิกา จึงตัดข้อ (C) และ (D) ออกไป สุดท้าย เนื่องจากโมเมนตัมเชิงเส้นของระบบจะต้องเป็นศูนย์ แสดงว่าจุดศูนย์กลางมวลจะต้องไม่เคลื่อนที่ ข้อ (A) จึงไม่ใช่คำตอบ
ประการแรก โมเมนตัมเชิงเส้นจะต้องถูกอนุรักษ์ไว้ จากสถานะเริ่มต้นที่โมเมนตัมเชิงเส้นเป็นศูนย์ แสดงว่าข้อ (B) ไม่ใช่คำตอบ และโมเมนตัมเชิงมุมที่จุดใด ๆ จะต้องถูกอนุรักษ์ไว้ด้วย จากสถานะเริ่มต้นที่โมเมนตัมเชิงเส้นเป็นศูนย์ ดังนั้น โมเมนตัมเชิงมุมจะมีค่าเท่ากันทุกจุดไม่ว่าจะเป็นจุดอ้างอิงใด จึงพิจารณาเพียงจุดใดหนึ่งจุดก็พอ จากโมเมนตัมเชิงมุมรวมต้องเท่ากับ 2 kg m2/s ในทิศทวนเข็มนาฬิกา จึงตัดข้อ (C) และ (D) ออกไป สุดท้าย เนื่องจากโมเมนตัมเชิงเส้นของระบบจะต้องเป็นศูนย์ แสดงว่าจุดศูนย์กลางมวลจะต้องไม่เคลื่อนที่ ข้อ (A) จึงไม่ใช่คำตอบ
| 257. | การทดสอบลูกตุ้มอย่างง่าย ประกอบด้วย ลูกตุ้มมวล m ที่ยึดกับแกนหมุนด้วยแท่งเบายาว L ภายใต้สนามโน้มถ่วงคงที่ ลูกตุ้มที่เดิมอยู่นิ่งจะถูกปล่อยลงมาจากมุม θ0 < π / 2 กับแนวเดิม และคาบของการแกว่งคือ T0 โดยไม่คำนึงถึงแรงต้านอากาศและแรงเสียดทาน ขณะที่ลูกตุ้มแกว่ง มุม θg ใด ที่ทำให้เกิดแรงตึงที่แท่งยึดลูกตุ้มมากที่สุด |
| A | แรงตึงมากสุดที่ θg = θ0 |
| B | แรงตึงมากสุดที่ θg = 0 |
| C | แรงตึงมากสุดในช่วง 0 < θg < θ0 |
| D | แรงตึงคงที่ |
| E | ไม่ข้อใดถูกต้อง เพราะ 0 < θ0 < \(\pi\) / 2 |
ตอบ (B)
มวลจะมีความเร่งพุ่งไปทางแกนหมุน เพราะมีความเร่งสู่ศูนย์กลาง ถ้ามวลมีความเร็ว v ความเร่งจะเท่ากับ
สรุปว่า ที่ θg = 0 จะทำให้เกิดแรงตึงที่แท่งยึดลูกตุ้มมากที่สุด
มวลจะมีความเร่งพุ่งไปทางแกนหมุน เพราะมีความเร่งสู่ศูนย์กลาง ถ้ามวลมีความเร็ว v ความเร่งจะเท่ากับ
\({{\rm{a}}_{\rm{c}}}{\rm{ = }}\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{L}}}\)
และมีสองแรงที่กระทำในแนวรัศมี คือ แรงตึงในแท่งยึดลูกตุ้มที่มีทิศพุ่งเข้า และแรงที่แตกมาจากแรงโน้มถ่วงที่มีทิศพุ่งออก ให้ θ เป็นมุมที่กางออกมาจากเส้นในแนวตั้งของแรงโน้มถ่วง จะได้
\(\rm F_{g,rad} = mg \,cos θ\)
จากกฎข้อที่สองของนิวตัน จะได้แรงตึง F เท่ากับ
\(\rm F – F_{g, rad} = ma_c\)
และทั้งสองสมการจะมีค่าเพิ่มขึ้น เมื่อมวลเข้าใกล้จุดต่ำสุดของการแกว่ง ดังนั้น แรงตึงสูงสุดเกิดขึ้นที่นั้น สรุปว่า ที่ θg = 0 จะทำให้เกิดแรงตึงที่แท่งยึดลูกตุ้มมากที่สุด
| 258. | การทดสอบลูกตุ้มอย่างง่าย ประกอบด้วย ลูกตุ้มมวล m ที่ยึดกับแกนหมุนด้วยแท่งเบายาว L ภายใต้สนามโน้มถ่วงคงที่ ลูกตุ้มที่เดิมอยู่นิ่งจะถูกปล่อยลงมาจากมุม θ0 < π / 2 กับแนวเดิม และคาบของการแกว่งคือ T0 โดยไม่คำนึงถึงแรงต้านอากาศและแรงเสียดทาน แรงตึงมากสุดที่แท่งยึดลูกตุ้ม จะมีค่าเท่าใด |
| A | mg |
| B | 2mg |
| C | mL θ0/T02 |
| D | mg sinθ0 |
| E | mg(3 – 2 cosθ0) |
ตอบ (E)
เนื่องจากแท่งยึดลูกตุ้มจะเกิดแรงตึงสูงสุดเมื่อมวลอยู่ที่จุดต่ำสุดของการแกว่ง
ที่จุดต่ำสุด ระยะทางตามแนวตั้งที่มวลเคลื่อนที่ไปได้จะเท่ากับ L (1 – cos θ0) ดังนั้น จากกฎการอนุรักษ์พลังงาน จะได้ว่า
เนื่องจากแท่งยึดลูกตุ้มจะเกิดแรงตึงสูงสุดเมื่อมวลอยู่ที่จุดต่ำสุดของการแกว่ง
ที่จุดต่ำสุด ระยะทางตามแนวตั้งที่มวลเคลื่อนที่ไปได้จะเท่ากับ L (1 – cos θ0) ดังนั้น จากกฎการอนุรักษ์พลังงาน จะได้ว่า
\(\dfrac{1}{2}{\rm{m}}{{\rm{v}}^{\rm{2}}}{\rm{ = mgL(1}}-{\rm{cos }}{{\rm{\,\theta }}_{\rm{0}}}{\rm{)}}\)
และที่จุดต่ำสุดจะมีแรงตึงเท่ากับ
\(\begin{align*}
\rm F &=\rm mg + 2mg(1 - cos\,{{\rm{\theta }}_{\rm{0}}}{\rm{)}}\\
\rm F &= \rm mg(3 -2cos\, {{\rm{\theta }}_{\rm{0}}}{\rm{)}}
\end{align*}\)
ดังนั้น แรงตึงมากสุดจะเท่ากับ mg(3 – 2 cosθ0)| 259. | การทดสอบลูกตุ้มอย่างง่าย ประกอบด้วย ลูกตุ้มมวล m ที่ยึดกับแกนหมุนด้วยแท่งเบายาว L ภายใต้สนามโน้มถ่วงคงที่ ลูกตุ้มที่เดิมอยู่นิ่งจะถูกปล่อยลงมาจากมุม θ0 < π / 2 กับแนวเดิม และคาบของการแกว่งคือ T0 โดยไม่คำนึงถึงแรงต้านอากาศและแรงเสียดทาน ถ้าทำการทดลองใหม่ด้วยแท่งยึดลูกตุ้มยาว 4L โดยใช้มุมเดิมคือ θ0 จะได้คาบของการแกว่งคือ T แล้วข้อความใดต่อไปนี้ถูกต้อง |
| A | T = 2T0 โดยไม่คำนึงถึง θ0 |
| B | T > 2T0 โดย T ≈ 2T0 ถ้า θ0 << 1 |
| C | T < 2T0 โดย T ≈ 2T0 ถ้า θ0 << 1 |
| D | T > 2T0 ในบาง θ0 และ T < 2T0 ในบาง θ0 |
| E | ไม่สามารถหาค่า T และ 2T0 ได้ เพราะไม่ใช่การแกว่งแบบมีคาบ ( ยกเว้นกรณี θ0 << 1 ) |
ตอบ (A)
การแกว่งนี้จะมีคาบที่แน่นอน (ลองพิจารณาที่ θ ใดๆ จะพบว่าพลังงานจะถูกอนุรักษ์ไว้ และอนุภาคจะกลับสู่สภาวะหยุดนิ่งที่จังหวะหนึ่ง) จากการวิเคราะห์เชิงมิติ จะได้คาบของการแกว่งเท่ากับ
การแกว่งนี้จะมีคาบที่แน่นอน (ลองพิจารณาที่ θ ใดๆ จะพบว่าพลังงานจะถูกอนุรักษ์ไว้ และอนุภาคจะกลับสู่สภาวะหยุดนิ่งที่จังหวะหนึ่ง) จากการวิเคราะห์เชิงมิติ จะได้คาบของการแกว่งเท่ากับ
\({\rm{T = f(}}{{\rm{\theta }}_{\rm{0}}}{\rm{)}}\sqrt {\dfrac{{{l_0}}}{g}}\)
ดังนั้น ที่ θ0 ใดๆ จะมีคาบการแกว่งแปรผันกับ \(\sqrt {{l_0}}\)
| 260. | กำหนดภาพจำลองเท้ามนุษย์ ดังรูป ถ้านักเรียนมวล m = 60 kg ยืนด้วยนิ้วเท้าเดียว แล้วแรงตึง T ในเอ็นร้อยหวายควรเท่ากับข้อใด
 |
| A | T = 600 N |
| B | T = 1200 N |
| C | T = 1800 N |
| D | T = 2400 N |
| E | T = 3000 N |
ตอบ (D)
จากโจทย์น้ำหนักของนักเรียนคนนั้นเท่ากับ W = mg = 600 N ซึ่งเป็นน้ำหนักที่นิ้วเท้าต้องรองรับไว้ ส่วนข้อเท้าจะเป็นจุดแบ่งสมดุลของทอร์ก จะได้
จากโจทย์น้ำหนักของนักเรียนคนนั้นเท่ากับ W = mg = 600 N ซึ่งเป็นน้ำหนักที่นิ้วเท้าต้องรองรับไว้ ส่วนข้อเท้าจะเป็นจุดแบ่งสมดุลของทอร์ก จะได้
\(\begin{align*} \rm T \cdot 5 cm &= 600 \rm N \cdot {\rm{ 20 cm}}\\ \rm{T} &= 2400\rm~ N \end{align*}\)
| 261. | คนมวล m กระโดดบันจี้จัมลงมาจากสะพานสูง ได้ระยะตกสูงสุด H จากนั้นเชือกจะหน่วงให้เขาอยู่นิ่งชั่วขณะก่อนที่จะตีกลับขึ้นไป ให้เชือกมีความยืดหยุ่นสมบูรณ์ ตามกฎแรงของฮุค (Hooke's force law) มีค่านิจสปริง k และสามารถยืดจากความยาวเดิม L0 ถึง L = L0 + h ได้ และแรงตึงสูงสุดในเส้นเชือกจะเท่ากับสี่เท่าของน้ำหนักคน แล้วค่านิจสปริงควรมีค่าเท่าใด |
| A | \(\rm k=\dfrac{mg}{h}\) |
| B | \(\rm k=\dfrac{2mg}{h}\) |
| C | \(\rm k=\dfrac{mg}{H}\) |
| D | \(\rm k=\dfrac{4mg}{H}\) |
| E | \(\rm k=\dfrac{8mg}{H}\) |
ตอบ (E)
ในขณะที่เชือกยืดตัวสูงสุด ทุกพลังงานศักย์โน้มถ่วงจะถูกเปลี่ยนเป็นพลังงานงานศักย์ของสปริง
ในขณะที่เชือกยืดตัวสูงสุด ทุกพลังงานศักย์โน้มถ่วงจะถูกเปลี่ยนเป็นพลังงานงานศักย์ของสปริง
\({\rm{mgH = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{{\rm{h}}^{\rm{2}}}\)
เมื่อแทนแรงตึงสูงสุดที่มีค่าเท่ากับสี่เท่าของน้ำหนักคน ผลลัพธ์ขณะเชือกยืดตัวสูงสุดจะเท่ากับ
\(\rm kh = 4mg\)
ตัดตัวแปร h ได้
\({\rm{k = }}\dfrac{{{\rm{8mg}}}}{{\rm{H}}}\)
| 262. | คนมวล m กระโดดบันจี้จัมลงมาจากสะพานสูง ได้ระยะตกสูงสุด H จากนั้นเชือกจะหน่วงให้เขาอยู่นิ่งชั่วขณะก่อนที่จะตีกลับขึ้นไป ให้เชือกมีความยืดหยุ่นสมบูรณ์ ตามกฎแรงของฮุค (Hooke's force law) มีค่านิจสปริง k และสามารถยืดจากความยาวเดิม L0 ถึง L = L0 + h ได้ และแรงตึงสูงสุดในเส้นเชือกจะเท่ากับสี่เท่าของน้ำหนักคน จงหาระยะยืดสูงสุดของเชือก h |
| A | \(\rm h=\dfrac{1}{2}H\) |
| B | \(\rm h=\dfrac{1}{4}H\) |
| C | \(\rm h=\dfrac{1}{5}H\) |
| D | \(\rm h=\dfrac{2}{5}H\) |
| E | \(\rm h=\dfrac{1}{8}H\) |
ตอบ (A)
ในขณะที่เชือกยืดตัวสูงสุด ทุกพลังงานศักย์โน้มถ่วงจะถูกเปลี่ยนเป็นพลังงานงานศักย์ของสปริง
ในขณะที่เชือกยืดตัวสูงสุด ทุกพลังงานศักย์โน้มถ่วงจะถูกเปลี่ยนเป็นพลังงานงานศักย์ของสปริง
\({\rm{mgH = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{{\rm{h}}^{\rm{2}}}\)
เมื่อแทนแรงตึงสูงสุดที่มีค่าเท่ากับสี่เท่าของน้ำหนักคน ผลลัพธ์ขณะเชือกยืดตัวสูงสุดจะเท่ากับ
\(\rm kh = 4mg\)
ตัดตัวแปร k และ mg ได้
\({\rm{h = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{H}}\)
| 263. | กล่องหนัก W เลื่อนลงมาจากพื้นเอียง 30◦ ด้วยอัตราเร็วคงที่ ภายใต้แรงโน้มถ่วงและแรงเสียดทาน ถ้าเพิ่มแรง P กระทำกับกล่องในแนวนอนจะทำให้กล่องเคลื่อนที่ขึ้นด้วยอัตราเร็วคงที่ แล้วขนาดของ P ควรเท่ากับข้อใด |
| A | \(\rm P = W/2\) |
| B | \(\rm P = 2W/\sqrt3\) |
| C | \(\rm P = W\) |
| D | \(\rm P = \sqrt3W\) |
| E | \(\rm P = 2W\) |
ตอบ (D)
ถ้ากล่องเคลื่อนที่ลงมาด้วยอัตราเร็วคงที่ จะได้ tan θ = μ
ถ้ากล่องถูกแรง P ผลักขึ้นพื้นเอียงในแนวนอนด้วยความเร็วคงที่ จะได้
ถ้ากล่องเคลื่อนที่ลงมาด้วยอัตราเร็วคงที่ จะได้ tan θ = μ
ถ้ากล่องถูกแรง P ผลักขึ้นพื้นเอียงในแนวนอนด้วยความเร็วคงที่ จะได้
\(\rm F_N = mg \,cos θ + P \,sin θ\)
ดังนั้น แรงเสียดทานจะเท่ากับ
\(\rm F_f = μ (mg \,cos θ + P \,sin θ)\)
ซึ่งแรงจะสมดุลด้วยแรงโน้มถ่วง และการผลักขึ้นพื้นเอียง จึงได้
\(\rm P cos θ = μ (mg \,cos θ + P \,sin θ) + mg \,sin θ\)
เมื่อหารตลอดสมการด้วย cosθ และแทน tan θ = μ จะได้
\(\begin{align*}
\rm P &= \rm \mu (W + P\mu ) + W\mu \\
&= \frac{{{\rm{2\mu }}}}{{1 - {{\rm{\mu }}^2}}}{\rm{W}}\\
&= \frac{{{\rm{2}}\frac{1}{{\sqrt 3 }}}}{{1 - \frac{1}{3}}}{\rm{W}}
\end{align*}\)
ดังนั้น \({\rm{P = }}\sqrt 3 {\rm{W}}\)| 264. | พิจารณาหยดน้ำจากก๊อกที่อยู่เหนืออ่างล้างจานประมาณ 10 cm ขณะที่หยดหนึ่งแตะอ่าง มีหนึ่งหยดอยู่ในอากาศ และมีอีกหยดรออยู่ปากก๊อก แล้วระยะห่างของหยดน้ำที่อยู่ในอากาศกับหยดที่แตะอ่างเท่ากับข้อใด |
| A | ระหว่าง 0 ถึง 2 cm |
| B | ระหว่าง 2 ถึง 4 cm |
| C | ระหว่าง 4 ถึง 6 cm |
| D | ระหว่าง 6 ถึง 8 cm |
| E | ระหว่าง 8 ถึง 10 cm |
ตอบ (D)
| 265. | กระสุนปืนใหญ่ถูกยิงด้วยความเร็วต้น v0 เหนือระดับพื้นดิน อยากทราบว่า มุมเงยเล็กสุด θmin ที่ทำให้กระสุนมีความสูง H มากกว่าระยะในแนวนอน R ที่วัดจากจุดยิงถึงจุดตกพื้นเท่ากับข้อใด |
| 266. | รูปสามเหลี่ยมด้านเท่า ถูกวางบนพื้นเอียงที่มีแรงเสียดทานสูงเกินกว่าจะลื่นไถลลงมาได้ แต่ถ้าพื้นเอียงมีความชันมากๆ วัตถุจะ "กลิ้ง" (โดยมีจุดยอดเป็นจุดหมุน) ลงมาได้ แล้วมุมเอียงที่วัตถุจะเริ่มกลิ้งลงมาเท่ากับข้อใด |
| A | 30° |
| B | 45° |
| C | 60° |
| D | การกลิ้งเกิดขึ้นได้กับทุกมุมที่มากกว่าศูนย์ |
| E | ถ้าไถลลงมาไม่ได้ ก็ไม่มีทางกลิ้งลงมาได้ |
ตอบ (C)
| 267. | วัตถุที่เดิมหยุดนิ่งระเบิดออกเป็นสามส่วนเท่าๆ กัน โดยไม่คิดแรงภายนอก ถ้าชิ้นส่วนสองชิ้นแตกออกเป็นมุมฉากกับชิ้นอื่น ๆ ด้วยอัตราเร็ว v เท่ากัน แล้วอัตราเร็วของชิ้นที่สามเท่ากับข้อใด |
| 268. | วัตถุ 12 kg เคลื่อนที่ 4 m / s ไปทางทิศตะวันออก พุ่งชนกับวัตถุ 6 kg ที่เคลื่อนที่ 2 m / s ไปทางทิศตะวันตก ถ้าหลังการชนวัตถุเคลื่อนที่ไปด้วยกัน แล้วพลังงานจลน์ที่สูญเสียไปกับการชนกันนี้เท่ากับข้อใด |
| 269. | นำปืนใหญ่สองลำมาเรียงในแนวดิ่ง ให้มีระยะห่าง 200 m และหันปากกระบอกเข้าหากัน เมื่อจุดฉนวนยิง ความเร็วจากปากกระบอกปืนด้านล่างจะเท่ากับ 25 m/s และความเร็วจากปากกระบอกปืนด้านบนจะเท่ากับ 55 m/s
 |
| 270. | นำปืนใหญ่สองลำมาเรียงในแนวดิ่ง ให้มีระยะห่าง 200 m และหันปากกระบอกเข้าหากัน เมื่อจุดฉนวนยิง ความเร็วจากปากกระบอกปืนด้านล่างจะเท่ากับ 25 m/s และความเร็วจากปากกระบอกปืนด้านบนจะเท่ากับ 55 m/s
 |
| 271. | วัตถุมวล m = 3.0 kg เคลื่อนที่ตามแนวนอนไปชนกับสปริงเบา ที่มีค่านิจสปริง k = 80.0 N/m สัมประสิทธิ์ แรงเสียดทานระหว่างวัตถุกับพื้น คือ μk = 0.50 ถ้าวัตถุมีอัตราเร็ว 2.0 m/s เมื่อวัตถุชนกับสปริง แล้วระยะหดของสปริงจะเท่ากับข้อใด |
| 272. | ดาวเคราะห์ทรงกลมสม่ำเสมอรัศมี R มีความเร่งโน้มถ่วงที่ผิวของดาวเท่ากับ g แล้วความเร็วหลุดพ้นของวัตถุจากพื้นผิวดาวเคราะห์จะเท่ากับข้อใด |
| A | \(\rm \dfrac{1}{2}\sqrt{gR}\) |
| B | \(\rm \sqrt{gR}\) |
| C | \(\rm \sqrt{2gR}\) |
| D | \(\rm 2\sqrt{gR}\) |
| E | ไม่สามารถแสดงความเร็วหลุดพ้นของวัตถุ ด้วยเทอมของ g และได้ R |
ตอบ (C)
| 273. | วัตถุสี่ชิ้นถูกวางไว้บนพื้นเอียง จากนั้นปล่อยให้กลิ้งลงมาโดยมีไม่การไถล และไม่คำนึงถึงแรงต้านการหมุน และแรงต้านทานอากาศ • วัตถุ A เป็นลูกบอลทองเหลืองตัน เส้นผ่านศูนย์กลาง d • วัตถุ B เป็นลูกบอลทองเหลืองตัน เส้นผ่าศูนย์กลาง 2d • วัตถุ C เป็นลูกบอลทองเหลืองกลวง เส้นผ่านศูนย์กลาง d • วัตถุ D เป็นลูกบอลอลูมิเนียมตัน เส้นผ่าศูนย์กลาง d (อะลูมิเนียมมีความหนาแน่นน้อยกว่าทองเหลือง) ให้วัตถุถูกวางในลักษณะที่ศูนย์กลางมวลของวัตถุทั้งหมดกลิ้งไปในระยะเดียวกัน และเวลาที่ใช้ในการกลิ้งเป็น T ข้อความใดต่อไปนี้ถูกต้อง |
| A | TB > TC > TA = TD |
| B | TB > TC > TA = TD |
| C | TB > TC > TA = TD |
| D | TC > TA = TB = TD |
| E | TA = TB = TC = TD |
ตอบ (D)
| 274. | จากรูป นาย ก ดึงเชือกที่คล้องผ่านรอกที่ถูกยึดไว้ เพื่อขยับกล่องด้วยอัตราเร็วคงที่ v สัมประสิทธิ์แรงเสียดทานระหว่างกล่องกับพื้นเป็น μ < 1 สมมุติว่า รอกเบามากและไม่มีแรงเสียดทานระหว่างเชือกและรอก ข้อความใดถูกต้องขณะกล่องเคลื่อนที่
 |
| A | แรงบนเส้นเชือกเป็นค่าคงที่ |
| B | แรงเสียดทานระหว่างพื้นกับกล่องจะลดลง |
| C | แรงตั้งฉากของพื้นที่กระทำกับกล่องจะเพิ่มขึ้น |
| D | ความดันกล่องที่พื้นจะเพิ่มขึ้น |
| E | ความดันกล่องที่พื้นเป็นค่าคงที่ |
ตอบ (B)
| 275. | ห่วงโลหะสามารถกลิ้งรอบจุดศูนย์กลางได้ มีเชือกเบาสองเส้นผูกติดไว้ที่จุด A และ B ( ยึดติดไว้โดยที่ A และ B ไม่สามารถเลื่อนได้ ) และปลายเชือกอีกด้านผูกติดกับจุดศูนย์กลาง O นอกจากนี้ยังมีวัตถุหนัก G ถูกผูกไว้ที่จุด O ให้เชือกมีความยาวคงที่ น้ำหนัก G มีเฉพาะเชือกที่รับน้ำหนักไว้ และเดิมเส้นตรง OA อยู่ในแนวนอน
 |
| A | T1 จะลดลง |
| B | T1 จะเพิ่มขึ้น |
| C | T2 จะเพิ่มขึ้น |
| D | T2 จะเป็นศูนย์หลังจากหยุดหมุน |
| E | T2 ตอนแรกจะเพิ่มขึ้น จากนั้นจะลดลง |
ตอบ (D)
| 276. | กำหนด กราฟของแรงที่กระทำกับรถเข็นขนาด 40 kg เทียบกับตำแหน่ง x ของรถเข็น ซึ่งเคลื่อนที่ในหนึ่งมิติบนแกน x ถ้าที่ x = 0 รถเข็นมีความเร็ว -3.0 m / s (ในทิศลบ) แล้วข้อใดคืออัตราเร็วสูงสุดของรถเข็น
 |
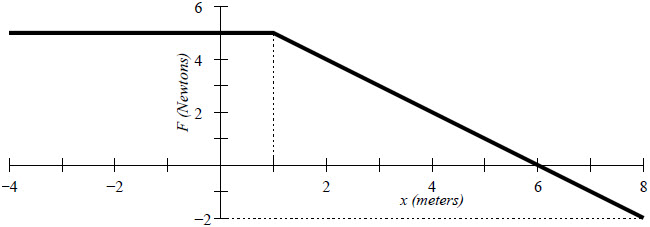| 277. | ทรงกระบอกรัศมี a เดิมหนัก 80 N หลังเจาะรูให้ห่างจากเส้นผ่านศูนย์กลางไป 2a/5 จะมีน้ำหนัก 65 N จุดศูนย์กลางของทรงกระบอกและรูจะสูงเท่ากัน และเส้นผ่านศูนย์กลางจะขนานกัน ดังรูป
 |
| 278. | รถมวล m มีเครื่องยนต์ที่มีกำลังออกมาคงที่ P สมมุติมีแรงเสียดทานเฉพาะล้อกับพื้นเอียง (ไม่มีแรงเสียดทานที่ส่วนอื่นๆ) แล้วอัตราเร็วสูงสุดคงที่ vmax ที่รถคันนี้สามารถขับขึ้นพื้นเอียงทำมุม θ กับแนวนอนได้ เท่ากับข้อใด
 |
| A | \(\rm v_{max} = P/(mg\, sinθ)\) |
| B | \(\rm v_{max} = P^2 sinθ /mg\) |
| C | \(\rm v_{max} = \sqrt{2P/mg}/ sinθ\) |
| D | ไม่มีอัตราเร็วสูงสุดคงที่ |
| E | อัตราเร็วสูงสุดคงที่ขึ้นกับความยาวของพื้นเอียง |
ตอบ (A)
| 279. | รถกระป๋องมีความเร่งในแนวนอนด้วยความเร่ง \(\vec{a}\) ภายในมีกล่องมวล M ต่อกับสปริงสองเส้นที่มีค่านิจสปริง k1 และ k2 ถ้ากล่องสามารถขยับได้โดยไม่มีแรงเสียดทานในแนวนอน แล้วความถี่ในการสั่นของกล่องเท่ากับข้อใด |
| A | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{k_1+k_2}{M}+a}\) |
| B | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{k_1k_2}{(k_1+k_2)M}}\) |
| C | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{k_1k_2}{(k_1+k_2)M}+a}\) |
| D | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{|k_1-k_2|}{M}}\) |
| E | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{|k_1+k_2|}{M}}\) |
ตอบ (E)
| 280. | กำหนกกราฟ log / log จากแอมพลิจูดและคาบของการสั่นที่ไม่เป็นเชิงเส้น ดังรูป
 |
| A | \(\rm T = 1000A^2\) |
| B | \(\rm T = 100A^3\) |
| C | \(\rm T = 2A+3\) |
| D | \(\rm T = 3\sqrt A\) |
| E | คาบเป็นอิสระกับแอมพลิจูดในระบบการสั่น |
ตอบ (A)
| 281. | มวลแขวนอยู่บนเพดานภายในกล่องด้วยสปริงในอุดมคติ เดิมให้กล่องอยู่นิ่ง ส่วนมวลจะมีความเร็วเริ่มต้น และมีการสั่นเฉพาะในแนวตั้ง เมื่อมวลทิ้งตัวถึงจุดต่ำสุด กล่องจะถูกปล่อยให้ร่วงลงมา หากพิจารณาเฉพาะภายในกล่อง ปริมาณใดต่อไปนี้จะไม่เปลี่ยนแปลง ขณะกล่องร่วงลง โดยไม่สนแรงต้านอากาศ |
| A | แอมพลิจูดของการสั่น |
| B | คาบของการสั่น |
| C | อัตราเร็วสูงสุดของมวล |
| D | ความสูงขณะที่มวลมีอัตราเร็วสูงสุด |
| E | ตำแหน่งที่สูงที่สุดของมวล |
ตอบ ไม่มีข้อใดถูก
เพราะ ทุกตัวเลือกจะมีการเปลี่ยนแปลงเมื่อปล่อยกล่องลงมา
เพราะ ทุกตัวเลือกจะมีการเปลี่ยนแปลงเมื่อปล่อยกล่องลงมา
| 282. | ใช้มอเตอร์ 1,500 วัตต์ สูบน้ำจากความสูงแนวตั้ง 2.0 เมตร จากชั้นใต้ดินที่มีน้ำท่วมอยู่ ผ่านท่อทรงกระบอก ถ้าน้ำไหลออกจากปากท่อด้วยอัตราเร็ว 2.5 m / s โดยไม่มีแรงเสียดทาน และสมมุติว่าพลังงานทั้งหมดของมอเตอร์ใช้ไปกับการสูบน้ำ แล้วรัศมีของท่อน้ำควรเท่ากับข้อใด ให้ความหนาแน่นของน้ำเป็น ρ = 1000 /m3 |
| 283. | ภาชนะบรรจุน้ำถูกวางบนเครื่องชั่ง อ่านน้ำหนักได้ M1 = 45 kg และบล็อกไม้ถูกแขวนบนเครื่องชั่งที่สอง อ่านน้ำหนักได้ M2 = 12 kg ถ้าไม้มีความหนาแน่น 0.60 g/cm3 และน้ำมีความหนาแน่น 1.00 g/cm3 เมื่อหย่อนบล็อกไม้ครึ่งหนึ่งลงไปในน้ำ แล้วน้ำหนักที่อ่านได้จากเครื่องชั่งจะเท่ากับข้อใด
 |
| A | M1 = 45 kg และ M2 = 2 kg |
| B | M1 = 45 kg และ M2 = 6 kg |
| C | M1 = 45 kg และ M2 = 10 kg |
| D | M1 = 55 kg และ M2 = 6 kg |
| E | M1 = 55 kg และ M2 = 2 kg |
ตอบ (E)
| 284. | กำหนดระบบสปริงหนึ่งประกอบด้วย แท่นหนัก 10 N อยู่ด้านบนของสปริงสองอัน ซึ่งมีค่านิจสปริง 75 N/m ทั้งสองอัน และด้านบนแท่นมีสปริงที่สามที่มีค่านิจสปริง 75 N/m ถ้าวางลูกบอลหนัก 5.0 N บนสปริงที่สามจนน้ำหนักค่อย ๆ กดสปริงทั้งระบบลง แล้วระยะที่ลูกบอลกดลงมาจะเท่ากับข้อใด
 |
| 285. | เสียงที่เบาที่สุดที่เราได้ยินจะมีความเข้มเสียง I0 = 10–12 W/m2 ถ้าเปลี่ยนเป็นหน่วยพื้นฐานกิโลกรัม, เมตร และวินาที จะมีค่าเท่ากับข้อใด |
| A | I0= 10–12 kg/s3 |
| B | I0= 10–12 kg/s |
| C | I0= 10–12 kg2m/s |
| D | I0= 10–12 kg2m/s2 |
| E | I0= 10–12 kg/m·s3 |
ตอบ (A)
| 286. | เครื่องมือวัดในข้อใด ไม่สามารถ วัดความเร่งโน้มถ่วง (g) ได้ |
| A | เครื่องชั่งสปริง (อ่านค่าในหน่วยแรง) และวัตถุที่ทราบมวล |
| B | คานที่ทราบความยาว, แต่ไม่ทราบมวล และนาฬิกาจับเวลา |
| C | พื้นเอียงที่ทราบความชัน, รถจำลองหลายขนาดๆ ที่ทราบมวล และนาฬิกาจับเวลา |
| D | ปืนที่ยิงแบบโพรเจกไทล์ที่ทราบอัตราเร็ว, กระสุนที่ทราบมวล และไม้บรรทัด |
| E | มอเตอร์ที่ทราบกำลังที่ออกมา, วัตถุที่ทราบมวล, เส้นเชือกที่ทราบความยาว และนาฬิกาจับเวลา |
ตอบ (C)
| 287. | วัตถุมวล m สามชิ้น นำมาติดกันด้วยสปริงแบบเดียวกัน เมื่อวางบนพื้นราบจะเห็นเป็นรูปสามเหลี่ยมที่มีความยาวด้าน l เมื่อหมุนวัตถุรูปสามเหลี่ยมรอบ ๆ จุดศูนย์กลางด้วยความเร็วเชิงมุม ω วัตถุรูปสามเหลี่ยมจะมีความยาวด้านใหม่เป็น 2l แล้วค่านิจสปริง k เท่ากับข้อใด |
| A | \(\rm 2m\omega^2\) |
| B | \(\rm \dfrac{2}{\sqrt3}m\omega^2\) |
| C | \(\rm \dfrac{2}{3}m\omega^2\) |
| D | \(\rm \dfrac{1}{\sqrt3}m\omega^2\) |
| E | \(\rm \dfrac{1}{3}m\omega^2\) |
ตอบ (C)
| 288. | พิจารณาสองวงโคจรรอบดวงอาทิตย์ที่แสดงดังรูป วงโคจร P เป็นวงกลมมีรัศมี R วงโคจร Q เป็นวงรี มีจุดยอดไกลสุด b อยู่ระหว่าง 2R และ 3R และจุดยอดใกล้สุด a อยู่ระหว่าง R/3 และ R/2 ถ้าความเร็วในวงโคจร P เป็น vc ความเร็วในวงโคจร Q ที่จุด a เป็น va และที่จุด b เป็น vb แล้วข้อใดต่อไปนี้ถูกต้อง
 |
| A | vb > vc > 2va |
| B | 2vc > vb > va |
| C | 10vb > va > vc |
| D | vc > va > 4vb |
| E | 2va > \(\sqrt2\)vb > vc |
ตอบ (C)
| 289. | ปั่นจักรยานด้วยอัตราเร็วคงที่ 22.0 km/hr และมีการหยุดพัก 20 นาที ถ้าอัตราเร็วเฉลี่ยของการปั่นจักรยานคือ 17.5 km/hr แล้วระยะทางที่ปั่นจักรยานไปได้เท่ากับข้อใด |
| 290. | กำหนดกราฟแสดงความเร็วต่อเวลาของวัตถุสามชิ้นที่เคลื่อนที่ในหนึ่งมิติ ดังนี้
 |
| 291. | กำหนดกราฟแสดงความเร็วต่อเวลาของวัตถุสามชิ้นที่เคลื่อนที่ในหนึ่งมิติ ดังนี้
 |
| 292. | กำหนดกราฟแสดงความเร็วต่อเวลาของวัตถุสามชิ้นที่เคลื่อนที่ในหนึ่งมิติ ดังนี้
 |
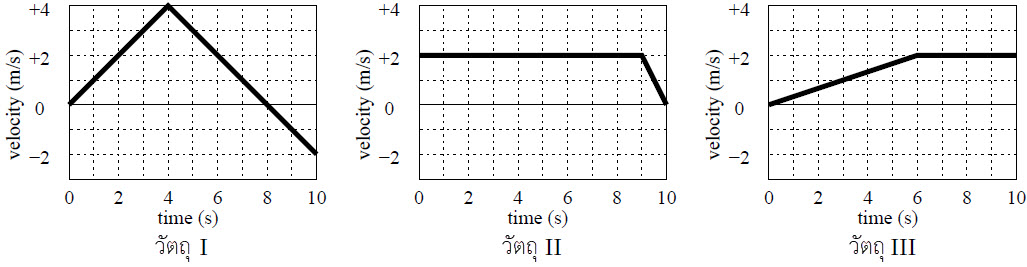| 293. | โลกที่โคจรรอบดวงอาทิตย์ด้วยอัตราเร็วคงที่ จะมีระยะทางห่างจากดวงอาทิตย์ประมาณ 150,000,000 กิโลเมตร ความเร่งของโลกในวงโคจรนี้ควรมีค่าเท่ากับข้อใด |
| 294. | เด็กสะดุดลื่นด้วยความเร็ว vc บนทะเลสาบน้ำแข็ง ไปชนกับเด็กอีกคนที่เดิมอยู่นิ่ง ซึ่งเขามีมวลเป็น 3 เท่าของเด็กคนแรก หลังการชนทั้งคู่ไถลไปด้วยกัน ความเร็วของคู่หลังการชนเท่ากับข้อใด |
| 295. | นักเล่นสเก็ตน้ำแข็งสามารถหมุนรอบตัวเองด้วยความเร็วเชิงมุม ω0 ขณะยืดแขนออก และเมื่อดึงแขนกลับเข้ามาใกล้ตัวความเร็วเชิงมุมจะเปลี่ยนเป็น 2ω0 โดยไม่มีทอร์กภายนอกใด ๆ มากระทำ แล้วอัตราส่วนของพลังงานจลน์ของการหมุนสุดท้ายกับพลังงานจลน์ของการหมุนเริ่มต้น เท่ากับข้อใด |
| 296. | บล็อกไม้หนัก 30 N หากกดให้จมอยู่ในน้ำเต็มชิ้น จะมีแรงลอยตัวจากน้ำกระทำกับบล็อกไม้ 50 N เมื่อปล่อยให้ลอยอย่างอิสระ บล็อกไม้จะลอยขึ้นไปที่ผิวน้ำ แล้วส่วนที่ลอยพ้นน้ำเป็นเศษส่วนเท่าใดของบล็อกไม้ทั้งชิ้นขณะลอยตัวขึ้นไป |
| 297. | สปริงสมดุลยาว 2.0 เมตร มีค่านิจสปริง 10 นิวตัน/เมตร ให้ ก ดึงปลายด้านหนึ่งของสปริงด้วยแรง 3.0 นิวตัน ส่วน ข ดึงปลายอีกด้านด้วยแรง 3.0 นิวตัน ในทิศทางตรงกันข้าม ความยาวของสปริง ณ ปัจจุบันเท่ากับข้อใด |
| 298. | การกระทำในข้อใด ที่ทำให้คาบของลูกตุ้มอย่างง่าย มีค่าเพิ่มขึ้น |
| A | ลดความยาวลูกตุ้ม |
| B | เพิ่มมวลลูกตุ้ม |
| C | เพิ่มแอมพลิจูดการแกว่งของลูกตุ้ม |
| D | แกว่งลูกตุ้มในลิฟท์ที่กำลังเคลื่อนที่ขึ้น ด้วยความเร่ง |
| E | แกว่งลูกตุ้มในลิฟท์ที่กำลังเคลื่อนที่ลง ด้วยอัตราเร็วคงที่ |
ตอบ (C)
| 299. | แก้วโลหะทรงกระบอกขนาดใหญ่ ลอยอยู่ในอ่างสี่เหลี่ยมที่มีน้ำอยู่ครึ่งอ่าง หลังจากนั้นปล่อยน้ำจากก๊อกให้ไหลเข้ามาในแก้วด้วยอัตราคงที่ จนแก้วจมลงไปอยู่ใต้น้ำทั้งใบ กราฟในข้อใดแสดงระดับน้ำในอ่างกับเวลาได้ถูกต้องที่สุด |
| 300. | พิจารณาลูกบอลที่หนักมากๆ และคานเบา แบบเดียวกัน เมื่อนำลูกบอลสองลูกไปติดไว้ที่ปลายแต่ละด้าน จะเกิดปฏิสัมพันธ์แรงโน้มถ่วงซึ่งกันและกัน (ตามรูปด้านซ้าย) แรงบีบบนคานจะเท่ากับ F จากนั้นเพิ่มลูกบอลลูกที่สามให้เป็นจุดยอดของรูปสามเหลี่ยม และมีคานเป็นด้านของรูปสามเหลี่ยมด้านเท่า (ตามรูปด้านขวา) แรงบีบบนคานแต่ละอัน ในกรณีหลังนี้จะเท่ากับข้อใด  |
| A | \(\rm \dfrac{1}{\sqrt3}F\) |
| B | \(\rm \dfrac{\sqrt3}{2}F\) |
| C | \(\rm F\) |
| D | \(\rm\sqrt3F\) |
| E | \(\rm 2 F\) |
ตอบ (C)
| 301. | หลอดด้าย มีแกนทรงกระบอกหน้าตัดวงกลมรัศมี 1 cm มีวงกลมรัศมี 2 cm แปะหัวท้ายแกน ดังรูป เมื่อนำไปวางบนพื้นที่กลิ้งได้โดยไม่ไถล แล้วดึงด้ายที่พันรอบแกนขึ้นทำมุม θ = 90◦ กับแนวระดับ (ดึงขึ้นเท่านั้น) หลอดด้ายจะหมุนไปทางขวา แล้ว θ มากสุดที่ทำให้หลอดด้ายไม่หมุนไปทางขวา เมื่อดึงด้าย เท่ากับข้อใด
 |
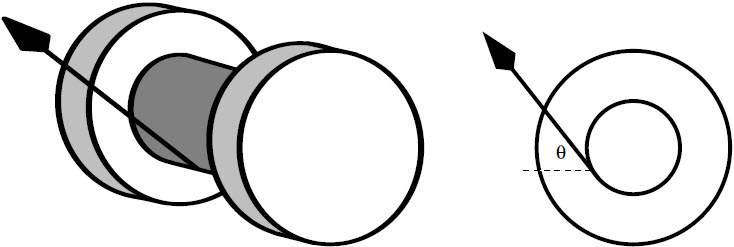| A | θ = 15◦ |
| B | θ = 30◦ |
| C | θ = 45◦ |
| D | θ = 60◦ |
| E | ไม่ข้อใดถูก เพราะ หลอดด้ายจะกลิ้งไปทางขวาเสมอ |
ตอบ (D)
| 302. | กำหนดเชือกที่ผูกลูกตุ้มไว้ที่ตำแหน่งต่างๆ ซึ่งแตกต่างกัน 5 เส้น เชือกทั้งหมดจะถูกห้อยลงมาจากเพดานไปจรดปลายพื้น หากปลดเชือกให้ตกลงสู่พื้น เชือกเส้นใดที่กระทบพื้นแล้วจะเกิดเสียงกระทบเป็นจังหวะแบบสม่ำเสมอ |
| 303. | มวลติดสปริงในแนวตั้งถูกดึงออกมา 20 cm จากสมดุล ถ้ามวล 100 g ผ่านจุดสมดุลด้วยอัตราเร็ว 0.75 m / s แล้วค่านิจสปริงเท่ากับข้อใด |
| 304. | โจ พยามใช้เชือกยกเพื่อนที่อยู่ในกล่องใบหนึ่ง ซึ่งแขวนอยู่ที่ด้านข้างของสะพาน ส่วนโจอยู่บนสะพาน ตัวเชือกมีตะขอเกี่ยวกับกล่อง และถูกพาดกับราวจับที่ถูกยึดไว้แน่น โจพยามยึดกล่องไว้โดยการกดเชือกกับราวด้วยหนังสือฟิสิกส์ที่เบาและไร้แรงเสียดทาน มีสัมประสิทธิ์ความเสียดทานสถิตระหว่างเชือกกับราวเป็น μs และสัมประสิทธิ์ความเสียดทานจลน์ระหว่างเชือกกับราวเป็น μk < μs มวลของกล่องและเพื่อนรวมกันเป็น M และความสูงเริ่มต้น จากกล่องถึงพื้นคือ h และสมมุติว่าเชือกเบามาก
 |
| 305. | โจ พยามใช้เชือกยกเพื่อนที่อยู่ในกล่องใบหนึ่ง ซึ่งแขวนอยู่ที่ด้านข้างของสะพาน ส่วนโจอยู่บนสะพาน ตัวเชือกมีตะขอเกี่ยวกับกล่อง และถูกพาดกับราวจับที่ถูกยึดไว้แน่น โจพยามยึดกล่องไว้โดยการกดเชือกกับราวด้วยหนังสือฟิสิกส์ที่เบาและไร้แรงเสียดทาน มีสัมประสิทธิ์ความเสียดทานสถิตระหว่างเชือกกับราวเป็น μs และสัมประสิทธิ์ความเสียดทานจลน์ระหว่างเชือกกับราวเป็น μk < μs มวลของกล่องและเพื่อนรวมกันเป็น M และความสูงเริ่มต้น จากกล่องถึงพื้นคือ h และสมมุติว่าเชือกเบามาก
 |
| A | \(\rm \sqrt{2gh}(\mu_k/\mu_s)\) |
| B | \(\rm \sqrt{2gh}(1-\mu_k/\mu_s)\) |
| C | \(\rm \sqrt{2gh}\sqrt{\mu_k/\mu_s}\) |
| D | \(\rm \sqrt{2gh}\sqrt{1-\mu_k/\mu_s}\) |
| E | \(\rm \sqrt{2gh}(\mu_s-\mu_k)\) |
ตอบ (D)
| 306. | บล็อกมวล m = 3.0 kg เลื่อนจากพื้นเอียงแรกไปถึงพื้นเอียงที่สอง มีค่าสัมประสิทธิ์แรงเสียดทานจลน์ของบล็อกกับแต่ละพื้นเอียงเท่ากับ μk = 0.40 ถ้าบล็อกเริ่มเลื่อนลงมาจากความสูง h1 = 1.0 m จากพื้นดิน และพื้นเอียงทั้งสองเอียง 30◦ กับแนวระดับ ความสูงที่จากพื้นดิน ที่บล็อกหยุดอยู่ที่พื้นเอียงที่สองเท่ากับข้อใด |
| 307. | วัตถุมวล 2.00 kg เคลื่อนที่ด้วยแรงที่กำหนดจาก
\(\rm \vec F= – (8.00 N / m) (x\hat i + y\hat j )\)
โดย \(\rm \hat i\) และ \(\rm \hat j\) เป็นเวกเตอร์หนึ่งหน่วยในแกน x และ y และเริ่มปล่อยวัตถุด้วยความเร็วต้น \(\rm \vec v= (3.00 m / s)\hat i + (4.00 m / s) \hat j\)แล้วต้องใช้เวลาเท่าไรวัตถุจึงจะกลับมาที่จุดเริ่มต้น |
| 308. | วัตถุมวล 2.00 kg เคลื่อนที่ด้วยแรงที่กำหนดจาก
\(\rm \vec F= – (8.00 N / m) (x\hat i + y\hat j )\)
โดย \(\rm \hat i\) และ \(\rm \hat j\) เป็นเวกเตอร์หนึ่งหน่วยในแกน x และ y และเริ่มปล่อยวัตถุด้วยความเร็วต้น \(\rm \vec v= (3.00 m / s)\hat i + (4.00 m / s) \hat j\)แล้วระยะไกลสุด จากจุดเริ่มต้นถึงวัตถุเท่ากับข้อใด |
| 309. | วิศวกรกำหนดปริมาตร Vm ของโลหะที่ใช้สร้างถังความดันทรงกลมให้คงที่ค่าหนึ่ง โดยสมมุติว่า ผนังของถังบางมาก และมีแรงดันสูงจนเข้าใกล้จุดระเบิด ถ้าปริมาณแก็สที่บรรจุได้เท่ากับ n (หน่วยโมล) ซึ่งไม่ขึ้นกับรัศมี r ของถัง แต่ขึ้นอยู่กับ Vm (หน่วย m3), อุณหภูมิ T (หน่วย K), ค่าคงที่แก๊สในอุดมคติ R (หน่วย J / (K · mol)) และความทนแรงดึงของโลหะ σ (หน่วย N / m2) ค่า n ในเทอมของตัวแปรดังกล่าวเท่ากับข้อใด |
| A | \(\rm n=\dfrac{2}{3}\dfrac{V_mσ}{RT}\) |
| B | \(\rm n=\dfrac{2}{3}\dfrac{\sqrt[3]{V_mσ}}{RT}\) |
| C | \(\rm n=\dfrac{2}{3}\dfrac{\sqrt[3]{V_mσ^2}}{RT}\) |
| D | \(\rm n=\dfrac{2}{3}\dfrac{\sqrt[3]{V_m^2σ}}{RT}\) |
| E | \(\rm n=\dfrac{2}{3}\sqrt[3]{\dfrac{V_mσ^2}{RT}}\) |
ตอบ (A)
| 310. | กำหนด กราฟของทอร์กที่ออกมาจากเครื่องยนต์เบนซินกับฟังก์ชันความถี่ของการหมุน เครื่องยนต์ไม่สามารถทำงานนอกช่วงของกราฟได้
 |
| 311. | วัตถุถูกยิงจากพื้นของดาวทรงกลมสม่ำเสมอที่อยู่นิ่ง ด้วยมุมหนึ่งเทียบกับแนวตั้ง ถ้าวัตถุเคลื่อนที่โดยไม่สนแรงต้านอากาศ และตกกลับในที่สุด โดยนักบินอวกาศชายอธิบายว่าวัตถุจะเคลื่อนที่แบบพาราโบลา ตามกฎการเคลื่อนแบบโพรเจกไทล์ ส่วนนักบินอวกาศหญิงจำกฎของเคปเลอร์ได้ว่า ทุกวงโคจรที่อยู่รอบดาวจะเป็นวงรี (หรือวงกลม) และแรงโน้มถ่วงของทรงกลมสม่ำเสมอจะมีค่าเสมือนกับว่ามวลทั้งหมดรวมกันเป็นจุดมวลที่ศูนย์กลางจุดเดียว แล้วข้อใดอธิบายความแตกต่างของคำอธิบายทั้งสองได้ดีที่สุด |
| A | เนื่องจากการทดลองเกิดใกล้กับผิวของทรงกลม จึงไม่ควรแทนทรงกลมด้วยจุดมวล |
| B | เนื่องจากวัตถุตกกลับมา แสดงว่าวัตถุไม่ได้อยู่ในวงโคจรของดาวนั้น ดังนั้นเส้นทางการเคลื่อนที่อาจจะไม่ใช่วงรี |
| C | นักบินอวกาศหญิง มองข้ามเรื่องการเคลื่อนที่รอบจุดมวล ที่อาจจะเป็นพาราโบลาหรือไฮเพอร์โบลาก็ได้ |
| D | กฎของเคปเลอร์ ใช้กับวงโคจรที่มีขนาดใหญ่เท่านั้น |
| E | วัตถุเคลื่อนที่เป็นวงรี แต่เกือบจะเป็นพาราโบลา เพราะระยะที่ยิงขึ้นไปสั้นมาก เมื่อเทียบกับระยะห่างจากจุดศูนย์กลางของดาวเคราะห์ |
ตอบ (E)
| 312. | เครื่องเล่นแผ่นเสียง มีวงแหวนเทฟลอน ที่มีรัศมีวงใน R และรัศมีวงนอก R + δ ( δ << R) ดังรูป และการหมุนแผ่นเสียงด้วยอัตราคง จะต้องใส่พลังงานให้มากกว่างานจากแรงเสียดทาน ถ้าผู้ผลิตเครื่องเล่นต้องการลดการใช้พลังงาน โดยไม่เปลี่ยนอัตราการหมุน น้ำหนักของเครื่องเล่นหรือ สัมประสิทธิ์แรงเสียดทานของผิวเทฟลอน วิศวกรจึงเสนอสองทางเลือก คือ การเพิ่มความกว้างของแบริ่ง ( เพิ่ม δ ) หรือเพิ่มรัศมี (เพิ่ม R) ข้อใดสรุปผลที่จะตามมาได้ถูกต้อง
 |
| A | การเพิ่ม δ ไม่มีผลต่อกำลังการทำงาน แต่การเพิ่ม R ทำให้กำลังการทำงานเพิ่มขึ้น |
| B | การเพิ่ม δ ไม่มีผลต่อกำลังการทำงาน แต่การเพิ่ม R ทำให้กำลังการทำงานลดลง |
| C | การเพิ่ม δ ทำให้กำลังการทำงานเพิ่มขึ้น แต่การเพิ่ม R ไม่มีผลต่อกำลังการทำงาน |
| D | การเพิ่ม δ ทำให้กำลังการทำงานลดลง แต่การเพิ่ม R ไม่มีผลต่อกำลังการทำงาน |
| E | การเปลี่ยนแปลงทั้งสองไม่มีผลใดๆ ต่อกำลังการทำงาน |
ตอบ (A)
| 313. | ให้ทรงกระบอกกลวงที่มีผนังบางมาก (เช่น แกนกระดาษชำระ) กับบล็อกอันหนึ่ง วางนิ่งอยู่บนระนาบที่มีความชัน θ กับแนวระดับ ถ้าทรงกระบอกกลิ้งลงมาโดยไม่ไถล และบล็อกก็เลื่อนลงมาจากระนาบ มาถึงด้านล่างระนาบพร้อมกัน แล้วค่าสัมประสิทธิ์แรงเสียดทานจลน์ ระหว่างบล็อกกับระนาบเท่ากับข้อใด |
| A | \(0\) |
| B | \(\dfrac{1}{3}\tan\theta\) |
| C | \(\dfrac{1}{2}\tan\theta\) |
| D | \(\dfrac{2}{3}\tan\theta\) |
| E | \(\tan\theta\) |
ตอบ (C)
| 314. | กำหนดกราฟแสดงการเคลื่อนที่ของกระรอกที่วิ่งไปตามสายโทรศัพท์เส้นหนึ่ง และตัวอักษร A ถึง E ใช้อ้างอิงเวลาต่างๆ ดังรูป
 |
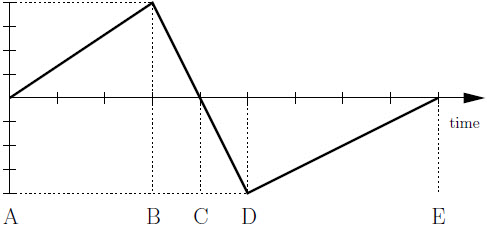| A | จาก A ถึง B |
| B | จาก B ถึง C เท่านั้น |
| C | จาก B ถึง D |
| D | จาก C ถึง D เท่านั้น |
| E | จาก D ถึง E |
ตอบ (C)
| 315. | กำหนดกราฟแสดงการเคลื่อนที่ของกระรอกที่วิ่งไปตามสายโทรศัพท์เส้นหนึ่ง และตัวอักษร A ถึง E ใช้อ้างอิงเวลาต่างๆ ดังรูป
 |
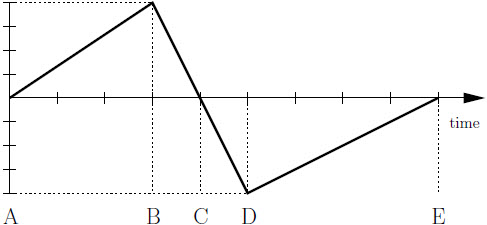| 316. | กำหนดกราฟแสดงการเคลื่อนที่ของกระรอกที่วิ่งไปตามสายโทรศัพท์เส้นหนึ่ง และตัวอักษร A ถึง E ใช้อ้างอิงเวลาต่างๆ ดังรูป
 |
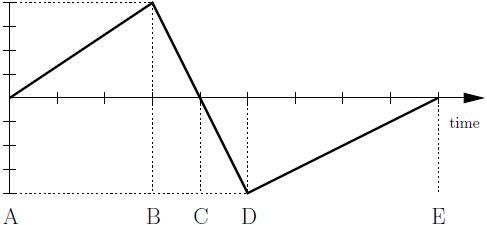| 317. | คนขนของสองทีม ช่วยกันย้ายเปียโนลงมาจากหน้าต่างชั้น 10 ของอพาร์ตเมนต์แห่งหนึ่ง ถ้าเชือกขาดขณะเปียโนอยู่สูงจากพื้นดิน 30 เมตร และทีมขนของบนพื้นดินได้เสียงตะโกนจากทีมด้านบนครั้งแรก ขณะเปียโนอยู่สูงจากพื้นดิน 14 เมตร แล้วพวกเขามีเวลาหนีก่อนเปียโนจะตกใส่เท่าใด |
| 318. | ให้การเคลื่อนที่แบบโพลเจกไทล์ทั้งสองแบบ ถูกยิงจากความสูง 35 เมตร ดังรูป ถ้าแบบแรกถูกยิงด้วยมุมเงย 37° แบบที่สองถูกยิงด้วยมุมก้ม 37° และทั้งสองมีอัตราเร็วต้น v0 = 50 m/s
 |
| 319. | กระสุนปืนถูกยิงทำมุม θ กับแนวนอน และเคลื่อนที่โดยไม่มีแรงต้านอากาศ จะขึ้นไปได้สูงสุด H และระยะตกกลับอยู่ไกลออกไป R แล้วอัตราส่วน H / R เท่ากับข้อใด |
| A | \(\tan \theta\) |
| B | \(2\tan \theta\) |
| C | \(\dfrac{2}{\tan \theta}\) |
| D | \(\dfrac{1}{2}\tan \theta\) |
| E | \(\dfrac{1}{4}\tan \theta\) |
ตอบ (E)
| 320. | แฮร์รี่ นั่งอยู่บนม้าหมุนที่ห่างจากจุดศูนย์กลางไป 2 เมตร มัลฟอย เสกให้แฮร์รี่นั่งอยู่กับที่แล้วเดินเครื่องม้าหมุน ให้เริ่มหมุนรอบแกน ถ้าแฮร์รี่มีมวล 50.0 kg และทนต่อความเร่งได้ 5.0 g’s ก่อนสลบไป แล้วโมเมนตัมเชิงมุมของแฮร์รี่ขณะสลบไปเท่ากับข้อใด |
| 321. | รถพยายามใช้ความเร่งปีนขึ้นเนินที่ทำมุม θ กับแนวนอน สัมประสิทธิ์แรงเสียดทานสถิตระหว่างยางล้อกับเนินเท่ากับ μ > tan θ แล้วความเร่งสูงสุด (ในทิศขึ้นไปตามเนิน) เท่ากับข้อใด ไม่คิดความเฉื่อยในการหมุนของล้อ |
| 322. | ลูกตุ้มมวล M แขวนบนเพดานของรถด้วยเชือกเบายาว L จากรถที่เดิมอยู่นิ่ง เมื่อเร่งรถออกไป ลูกตุ้มจะแกว่งทำมุม θ กับแนวตั้ง ข้อใดคือความเร่งของรถในเทอมของ θ, M, L และ g
 |
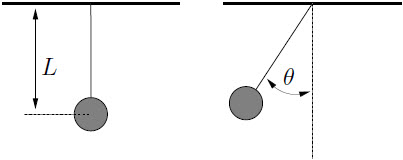| 323. | ให้มวล m1 อยู่บนมวล m2 โดยมวลก้อนล่างวางอยู่บนพื้นราบ และมีเชือกที่ใช้ลากไปตามแนวนอนได้ และมีสัมประสิทธิ์แรงเสียดทานของการเคลื่อนที่ในทุกพื้นผิวเท่ากับ μ ถ้ามีแรง F มากระทำกับเชือก แล้วความเร่งของมวลก้อนล่างเท่ากับข้อใด ให้สมมุติว่า F มีขนาดใหญ่พอที่ทำให้มวลก้อนบนไถลบนก้อนล่าง
 |
| A | a2 = (F – μg (2 m1 + m2)) / m2 |
| B | a2 = (F – μg (m1 + m2)) / m2 |
| C | a2 = (F – μg (m1 + 2 m2)) / m2 |
| D | a2 = (F + μg (m1 + m2)) / m2 |
| E | a2 = (F – μg (m2 – m1)) / m2 |
ตอบ (A)
| 324. | วัตถุสามชิ้นที่มีมวลเท่ากันถูกแขวนไว้บนรอกเล็กๆ ด้วยเชือกเบา ดังรูป ถ้าไม่คำนึงถึงแรงเสียดทาน และสมมุติว่าระบบอยู่ในภาวะสมดุล แล้วอัตราส่วนของ a / b เท่ากับข้อใด ( สเกลของรูปประกอบไม่ใช่ขนาดจริง )
 |
| 325. | ลูกบอลมวล m กลิ้งจนหล่นจากขอบโต๊ะด้วยพลังงานจลน์เริ่มต้น K ที่เวลา t หลังจากลูกบอลหล่นจากขอบโต๊ะจะมีพลังงานจลน์ 3K แล้ว t มีค่าเท่ากับข้อใด ไม่ต้องคำนึงถึงแรงต้านอากาศ |
| A | \(\rm (3/g)\sqrt{K/m}\) |
| B | \(\rm (2/g)\sqrt{K/m}\) |
| C | \(\rm (1/g)\sqrt{8K/m}\) |
| D | \(\rm (K/g)\sqrt{6/m}\) |
| E | \(\rm (2K/g)\sqrt{1/m}\) |
ตอบ (B)
| 326. | ลูกบอลมวล M รัศมี R มีโมเมนต์ความเฉื่อย I = \(\frac{2}{5}\)MR2 ให้เดิมอยู่นิ่งแล้วกลิ้งลงมาจากพื้นเอียง โดยไม่สูญเสียพลังงานจากการเสียดสี จากนั้นกลิ้งไปตามแนวราบจนกระทั่งหลุดออกจากพื้นเอียงไปและพุ่งขึ้นไปในแนวตั้ง ดังรูป แล้วความสูงสูงสุด ymax ของลูกบอลเท่ากับข้อใด ให้ความสูงสูงสุดที่หลุดออกจากปลายพื้นเอียง ymax แสดงในเทอมของ h
 |
| A | \(\rm h\) |
| B | \(\rm \dfrac{25}{49}h\) |
| C | \(\rm \dfrac{2}{5}h\) |
| D | \(\rm \dfrac{5}{7}h\) |
| E | \(\rm \dfrac{7}{5}h\) |
ตอบ (D)
| 327. | วัตถุ 5.0 kg มีอัตราเร็ว 8.0 m / s ไปตามพื้นราบ 2.0 m จนกระทั่งพุ่งชนแบบยืดหยุ่นสมบูรณ์กับวัตถุ 15.0 kg ที่เดิมอยู่นิ่ง ถ้าสัมประสิทธิ์แรงเสียดทานจลน์ระหว่างวัตถุทั้งสองกับพื้นเท่ากับ 0.35 แล้ววัตถุ 15.0 kg จะเคลื่อนที่ไปได้ไกลเท่าใด |
| 328. |  ถ้าบล็อกมวล m มีอัตราเร็วต้น v0 พุ่งขึ้นพื้นเอียงมวล M ไปโดยไม่มีแรงเสียดทาน แล้วขึ้นไปสูง h ตามพื้นเอียง จากนั้นไหลกลับลงมา จงหาความสูง h |
| A | \(\rm h=\dfrac{v^2_0}{2g}\) |
| B | \(\rm h=\dfrac{1}{g}\dfrac{Mv^2_0}{m+M}\) |
| C | \(\rm h=\dfrac{1}{2g}\dfrac{Mv^2_0}{m+M}\) |
| D | \(\rm h=\dfrac{1}{2g}\dfrac{mv^2_0}{m+M}\) |
| E | \(\rm h=\dfrac{v^2_0}{g}\) |
ตอบ (C)
| 329. |  ถ้าบล็อกมวล m มีอัตราเร็วต้น v0 พุ่งขึ้นพื้นเอียงมวล M ไปโดยไม่มีแรงเสียดทาน แล้วขึ้นไปสูง h ตามพื้นเอียง จากนั้นไหลกลับลงมา จงหาอัตราเร็ว v ของมวล m หลังลื่นกลับออกมาจากทางลาด |
| A | \(\rm v=v_0\) |
| B | \(\rm v= \dfrac{m}{m+M}v_0\) |
| C | \(\rm v= \dfrac{M}{m+M}v_0\) |
| D | \(\rm v= \dfrac{M-m}{m}v_0\) |
| E | \(\rm v= \dfrac{M-m}{m+M}v_0\) |
ตอบ (E)
| 330. | ถ้ามวล m สี่อัน ถูกวางไว้ที่จุดยอดของทรงสี่หน้าที่มีความยาวด้าน a แล้วพลังงานศักย์โน้มถ่วงของการจัดวางนี้เท่ากับข้อใด |
| A | \(\rm -2\dfrac{Gm^2}{a}\) |
| B | \(\rm -3\dfrac{Gm^2}{a}\) |
| C | \(\rm -4\dfrac{Gm^2}{a}\) |
| D | \(\rm -6\dfrac{Gm^2}{a}\) |
| E | \(\rm -12\dfrac{Gm^2}{a}\) |
ตอบ (D)
| 331. | ใช้กราฟของพลังงานศักย์ต่อไปนี้ ในการตอบคำถาม
 |
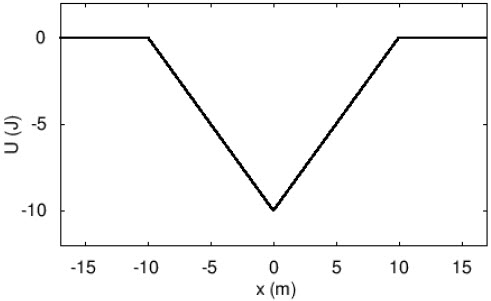| 332. | ใช้กราฟของพลังงานศักย์ต่อไปนี้ ในการตอบคำถาม
  |
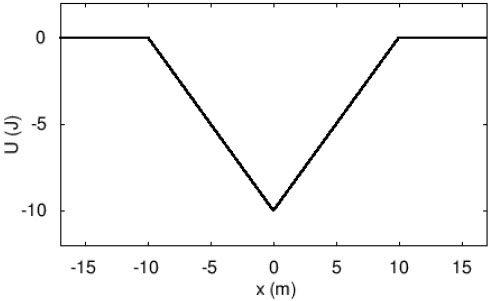| 333. | ใช้กราฟของพลังงานศักย์ต่อไปนี้ ในการตอบคำถาม
  |
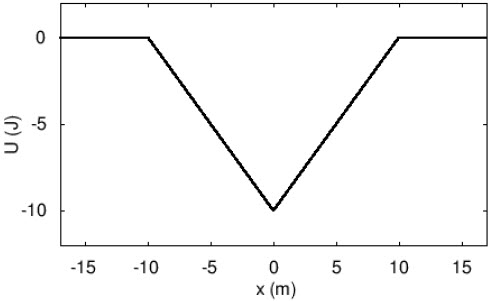| 334. | พลังงานศักย์โน้มถ่วงของลูกบอลตันที่มีความหนาแน่น ρ รัศมี R เท่ากับ E แล้วพลังงานศักย์โน้มถ่วงของลูกบอลตันที่มีความหนาแน่น ρ รัศมี 2R เท่ากับข้อใด |
| 335. | ลูกโป่งบรรจุแก๊สฮีเลียมถูกผูกติดกับพื้นรถด้วยเชือกเส้นหนึ่ง เนื่องจากรถถูกปิดแน่นหนาจึงไม่มีอากาศจากภายนอกมากระทำกับลูกโป่ง ถ้ารถวิ่งเป็นวงกลมด้วยอัตราเร็วคงที่ แล้วข้อใด คือทิศทางของลูกโป่งที่ถูกผูกเอาไว้
 |
| 336. | กำหนดท่อรูปตัว U สองอัน ให้ท่อด้านซ้าย มีพื้นที่หน้าตัด A มีอัตราเร็วของน้ำที่ไหลผ่าน v ส่วนท่อด้านขวามีพื้นที่หน้าตัด A´ = A/2 ถ้าแรงลัพธ์ที่ท่อสัมผัสกันเป็นศูนย์ แล้วอัตราเร็ว v´ ของน้ำที่ไหลผ่านท่อทางด้านขวาเท่ากับข้อใด โดยไม่ต้องสนใจแรงโน้มถ่วง และสมมุติว่า อัตราเร็วของน้ำ ขาเข้า-ขาออก ในแต่ละท่อมีค่าเท่ากัน
 |
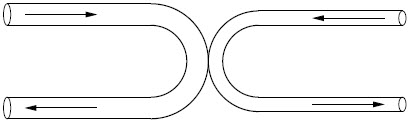| 337. | (เกินหลักสูตรการสอบเข้า สอวน.) แผ่นวงกลมสม่ำเสมอ รัศมี R เดิมมีมวล M แกนหมุนที่จุดศูนย์กลาง ซึ่งตั้งฉากกับแผ่นวงกลมมีโมเมนต์ความเฉื่อย I0 = \(\frac{1}{2}\) MR2 ถ้าเจาะรูบนแผ่นวงกลม ดังรูป แล้วโมเมนต์ความเฉื่อยใหม่ที่แกนหมุนจะเท่ากับข้อใด ให้แสดงในเทอมของรัศมี R มวล M ของแผ่นวงกลมเดิม
 |
| 338. | ยานอวกาศ (ซึ่งมีมวลน้อยมาก) อยู่ในวงโคจรวงรีของดาวเคราะห์ดวงหนึ่ง ระยะใกล้สุดระหว่างยานอวกาศกับดาวเคราะห์เท่ากับ R และระยะไกลสุดเท่ากับ 2R ถ้าที่ระยะไกลสุดยานอวกาศเคลื่อนที่ด้วยอัตราเร็ว v0 จากนั้นเดินเครื่องเข้าสู่วงโคจรวงกลมที่มีรัศมี 2R อัตราเร็วใหม่ที่ได้จะเท่ากับข้อใด
 |
| A | \(\rm \sqrt{3/2}v_0\) |
| B | \(\rm \sqrt{5}v_0\) |
| C | \(\rm \sqrt{3/5}v_0\) |
| D | \(\rm \sqrt2 v_0\) |
| E | \(\rm 2v_0\) |
ตอบ (A)
