ข้อสอบคัดเลือกของทีม USA 2018 (ชุด A) (25 ข้อ)
| 1. | กราฟข้อใด แสดงอัตราเร็วกับเวลาของวัตถุที่ถูกขว้างขึ้นไปโดยมีแรงต้านอากาศ ได้ดีที่สุด |
| A | 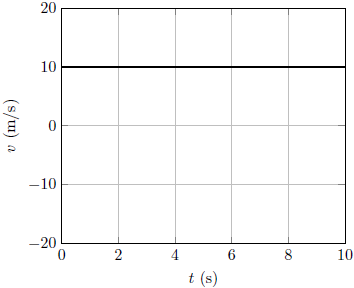 |
| B |  |
| C |  |
| D |  |
| E |  |
ตอบ (D)
ความเร็วสุดท้ายควรเป็นค่าคงที่และมีค่าเป็นลบ ทำให้ตัดตัวเลือกออกไปหมด จนเหลือแค่ข้อ (D) สังเกตว่า ขนาดของความเร่งควรจะลดลงด้วยเช่นกัน
ความเร็วสุดท้ายควรเป็นค่าคงที่และมีค่าเป็นลบ ทำให้ตัดตัวเลือกออกไปหมด จนเหลือแค่ข้อ (D) สังเกตว่า ขนาดของความเร่งควรจะลดลงด้วยเช่นกัน
| 2. | มวล 3.0 kg เคลื่อนที่ไปทางขวาด้วยอัตราเร็ว 30 m/s พุ่งชนกับมวล 2.0 kg ที่เคลื่อนที่ไปทางซ้ายด้วยอัตราเร็ว 20 m/s หลังการชน จุดศูนย์กลางมวลของระบบจะเคลื่อนที่ไปด้วยอัตราเร็วเท่าใด |
| A | 5 m/s |
| B | 10 m/s |
| C | 20 m/s |
| D | 24 m/s |
| E | 26 m/s |
ตอบ (B)
ความเร็วที่จุดศูนย์กลางของมวลจะถูกอนุรักษ์ด้วยกฎการอนุรักษ์โมเมนตัม ดังนั้น เราจึงไม่จำเป็นต้องคำนวณหาการชนที่เกิดขึ้น โดยก่อนชน โมเมนตัมสุทธิจะเท่ากับ 50 kg m/s และมวลสุทธิเท่ากับ 5 kg ดังนั้น อัตราเร็วที่จุดศูนย์กลางของมวลเท่ากับ 10 m/s
ความเร็วที่จุดศูนย์กลางของมวลจะถูกอนุรักษ์ด้วยกฎการอนุรักษ์โมเมนตัม ดังนั้น เราจึงไม่จำเป็นต้องคำนวณหาการชนที่เกิดขึ้น โดยก่อนชน โมเมนตัมสุทธิจะเท่ากับ 50 kg m/s และมวลสุทธิเท่ากับ 5 kg ดังนั้น อัตราเร็วที่จุดศูนย์กลางของมวลเท่ากับ 10 m/s
| 3. | ให้บอลลูกแรกเคลื่อนที่ไปตามแกน x แล้วชนกับบอลลูกที่สองที่เดิมอยู่นิ่ง และมีมวลเท่ากัน แล้วหลังเกิดการชนข้อใดกล่าวผิด |
| A | โมเมนตัมสุดท้ายสุทธิตามแกน x จะเท่ากับโมเมนตัมเริ่มต้นของบอลลูกแรก |
| B | พลังงานจลน์สุทธิหลังเกิดการชน จะเท่ากับพลังงานจลน์เริ่มต้นของบอลลูกแรก |
| C | โมเมนตัมสุดท้ายของลูกบอลทั้งสองตามแกน y ที่ถูกเพิ่มเข้ามาจะเป็นศูนย์ |
| D | อัตราเร็วสุดท้ายของจุดศูนย์กลางมวลของลูกบอลทั้งสอง มีค่าเท่ากับครึ่งหนึ่งของอัตราเร็วต้นของบอลลูกแรก |
| E | ลูกบอลทั้งสองจะไม่สามารถหยุดนิ่ง หลังเกิดการชนกันได้ |
ตอบ (B)
ข้อ (A), (C) และ (E) เป็นจริง ตามกฎการอนุรักษ์โมเมนตัม ข้อ (D) เป็นจริง ตามผลลัพธ์ของ ptot = mtot vCM ส่วนข้อ (B) เป็นเท็จ เพราะการชนนั้นอาจ ไม่ยืดหยุ่นบางส่วน หรือ ไม่ยืดหยุ่นสมบูรณ์
ข้อ (A), (C) และ (E) เป็นจริง ตามกฎการอนุรักษ์โมเมนตัม ข้อ (D) เป็นจริง ตามผลลัพธ์ของ ptot = mtot vCM ส่วนข้อ (B) เป็นเท็จ เพราะการชนนั้นอาจ ไม่ยืดหยุ่นบางส่วน หรือ ไม่ยืดหยุ่นสมบูรณ์
| 4. | ให้ดาวเทียมอยู่ในวงโคจรวงรีรอบโลก และเครื่องยนต์สามารถให้แรงดลค่าหนึ่งได้เพียงครั้งเดียว เพื่อให้ดาวเทียมได้พลังงานมากที่สุด แรงดลควรเป็นไปตามข้อใด
 |
| A | ควรมีทิศตามความเร็วของดาวเทียม และใช้ขณะอยู่จุดใกล้สุด |
| B | ควรมีทิศตามความเร็วของดาวเทียม และใช้ขณะอยู่จุดไกลสุด |
| C | ควรมีทิศพุ่งเข้าหาโลก และใช้ขณะอยู่จุดใกล้สุด |
| D | ควรมีทิศพุ่งเข้าหาโลก และใช้ขณะอยู่จุดไกลสุด |
| E | ควรมีทิศพุ่งออกจากโลก และใช้ขณะอยู่จุดไกลสุด |
ตอบ (A)
ผลต่างความเร็ว Δv มีขนาดคงที่ เพราะพลังงานจลน์แปรผันตาม v2 ซึ่งผลต่างที่มากที่สุดจะเกิดขึ้น เมื่อแรงดลขนานกับความเร็ว และความเร็วมากสุดจะขึ้นเกิดที่ จุดใกล้สุด
ผลต่างความเร็ว Δv มีขนาดคงที่ เพราะพลังงานจลน์แปรผันตาม v2 ซึ่งผลต่างที่มากที่สุดจะเกิดขึ้น เมื่อแรงดลขนานกับความเร็ว และความเร็วมากสุดจะขึ้นเกิดที่ จุดใกล้สุด
| 5. | มวลสองอันถูกแขวนอยู่บนรอกด้วยเชือกเบา และรอกนั้นตั้งอยู่บนพื้นเอียง ดังรูป ถ้าทุกพื้นผิวไม่มีแรงเสียดทาน และมวลทั้งสองที่เดิมอยู่นิ่งถูกปล่อยออก แล้วพื้นเอียงจะเป็นไปตามข้อใด
 |
| A | จะมีความเร่งไปทางซ้าย ถ้า m1 < m2 |
| B | จะมีความเร่งไปทางขวา ถ้า m1 < m2 |
| C | จะมีความเร่งไปทางซ้าย โดยไม่สนมวลที่ถูกแขวนไว้ |
| D | จะมีความเร่งไปทางขวา โดยไม่สนมวลที่ถูกแขวนไว้ |
| E | พื้นเอียงไม่เคลื่อนที่ไปไหน |
ตอบ (E)
พื้นเอียงจะไม่เคลื่อนที่ไปไหน ซึ่งอธิบายได้หลายแบบ แต่เหตุผลง่ายๆ คือ ระบบนี้ไม่มีโมนตัมที่กระทำในแนวนอน
มีเพียงแค่มวลที่เลื่อนขึ้นเลื่อนลง (ในเชือกไม่มีโมเมนตัมในแนวนอน เพราะเป็นเชือกเบา)
พื้นเอียงจะไม่เคลื่อนที่ไปไหน ซึ่งอธิบายได้หลายแบบ แต่เหตุผลง่ายๆ คือ ระบบนี้ไม่มีโมนตัมที่กระทำในแนวนอน
มีเพียงแค่มวลที่เลื่อนขึ้นเลื่อนลง (ในเชือกไม่มีโมเมนตัมในแนวนอน เพราะเป็นเชือกเบา)
| 6. | ลังใส่ของมวล m = 15 kg ถูกดันขึ้นไปบนทางลาดที่ความยาว 5.00 m และทำมุม 20° กับแนวราบ ด้วยแรง F = 1.00 ×103 N ในทิศที่ขนานกับทางลาด และแรงเสียดทานที่ต้านการเคลื่อนที่เท่ากับ f = 4.00 × 102 N ถ้าเดิมลังอยู่นิ่ง แล้วอัตราเร็วของลัง ณ จุดบนสุดของทางลาดเท่ากับข้อใด |
| A | 4.24 m/s |
| B | 5.11 m/s |
| C | 7.22 m/s |
| D | 8.26 m/s |
| E | 9.33 m/s |
ตอบ (A)
แรงโน้มถ่วงที่ขนานไปกับทางลาดและมีค่าเท่ากับ -mg sinθ = -393 N ทำให้ได้แรงสุทธิเท่ากับ 207 N
สำหรับวัตถุที่มีมวล 115 kg ความเร่งจะเท่ากับ 1.8 m/s2 และความเร็วจะเท่ากับ \(\rm\sqrt{2ad}= 4.24 ~m/s\)
แรงโน้มถ่วงที่ขนานไปกับทางลาดและมีค่าเท่ากับ -mg sinθ = -393 N ทำให้ได้แรงสุทธิเท่ากับ 207 N
สำหรับวัตถุที่มีมวล 115 kg ความเร่งจะเท่ากับ 1.8 m/s2 และความเร็วจะเท่ากับ \(\rm\sqrt{2ad}= 4.24 ~m/s\)
| 7. | ให้รถมีความเร่งมากสุดเท่ากับ a0 และความเร่งต่ำสุดเท่ากับ – a0 แล้วเวลาสั้นสุดที่ทำให้รถที่เดิมอยู่นิ่งวิ่งไปหยุดที่ระยะทาง d เท่ากับข้อใด |
| A | \(\rm \sqrt{d/2a_0}\) |
| B | \(\rm \sqrt{d/a_0}\) |
| C | \(\rm \sqrt{2d/a_0}\) |
| D | \(\rm \sqrt{3d/2a_0}\) |
| E | \(2\rm \sqrt{d/a_0}\) |
ตอบ (E)
คำตอบข้อนี้จะใช้วิธีเร่งสูงสุดในครึ่งแรก และเบรกสูงสุดในครึ่งหลัง
เนื่องจากครึ่งแรกและครึ่งหลังใช้เวลา \(\rm \sqrt{d/a_0}\) เท่ากัน ดังนั้น เวลาทั้งหมดเท่ากับ \(2\rm \sqrt{d/a_0}\)
คำตอบข้อนี้จะใช้วิธีเร่งสูงสุดในครึ่งแรก และเบรกสูงสุดในครึ่งหลัง
เนื่องจากครึ่งแรกและครึ่งหลังใช้เวลา \(\rm \sqrt{d/a_0}\) เท่ากัน ดังนั้น เวลาทั้งหมดเท่ากับ \(2\rm \sqrt{d/a_0}\)
| 8. | แผ่นกลมรัศมี r กลิ้งอย่างสม่ำเสมอโดยไม่มีการไถล วนอยู่ภายในห่วงที่ถูกตรึงไว้ และห่วงมีรัศมี R ถ้าคาบการกลิ้ง ของแผ่นกลมเท่ากับ T แล้วอัตราเร็วขณะหนึ่งของจุดที่อยู่ตรงข้ามกับจุดที่แผ่นกลมสัมผัสกับห่วงเท่ากับข้อใด  |
| A | \(\rm 2π(R + r)/T\) |
| B | \(\rm 2π(R + 2r)/T\) |
| C | \(\rm 4π(R – 2r)/T\) |
| D | \(\rm 4π(R– r)/T\) |
| E | \(\rm 4π(R + r)/T\) |
ตอบ (D)
จุดศูนย์กลางของมวลของแผ่นกลมจะอยู่ห่างจากจุดศูนย์กลางห่วง \(\rm R – r\) และอัตราเร็วที่จุดศูนย์กลางของแผ่นกลมจะเท่ากับ \(\rm ω (R – r) = (2π / T) (R – r)\) โดยอัตราเร็วของจุดที่อยู่ตรงข้ามกับจุดที่แผ่นกลมสัมผัสกับห่วงจะเป็นสองเท่าของอัตราเร็วที่จุดศูนย์กลางของแผ่นกลม โดยที่แผ่นกลมหมุนรอบจุดที่สัมผัสนั้นอย่างรวดเร็ว
ดังนั้น \(\rm v = 4π (R – r) / T\)
จุดศูนย์กลางของมวลของแผ่นกลมจะอยู่ห่างจากจุดศูนย์กลางห่วง \(\rm R – r\) และอัตราเร็วที่จุดศูนย์กลางของแผ่นกลมจะเท่ากับ \(\rm ω (R – r) = (2π / T) (R – r)\) โดยอัตราเร็วของจุดที่อยู่ตรงข้ามกับจุดที่แผ่นกลมสัมผัสกับห่วงจะเป็นสองเท่าของอัตราเร็วที่จุดศูนย์กลางของแผ่นกลม โดยที่แผ่นกลมหมุนรอบจุดที่สัมผัสนั้นอย่างรวดเร็ว
ดังนั้น \(\rm v = 4π (R – r) / T\)
| 9. | แท่งไม้สม่ำเสมอมวล m เดิมวางราบอยู่บนพื้น ปลายด้านหนึ่งมีเชือกผูกไว้ เมื่อดึงเชือกขึ้นในแนวตั้งด้วยแรงตึงคงที่ F แล้วจุดศูนย์กลางมวลของแท่งไม้จะเคลื่อนที่ขึ้นด้วยความเร่ง a < g แล้วแรงปกติ N ที่พื้นกระทำกับแท่งไม้ในอีกด้านที่ไม่ถูกยกขึ้น หลังจากที่แท่งไม้ด้านขวาถูกยกขึ้นเหนือพื้นดินเพียงนิดเดียว เท่ากับข้อใด |
| A | N = mg |
| B | mg > N > mg/2 |
| C | N = mg/2 |
| D | mg/2 > N > 0 |
| E | N = 0 |
ตอบ (B)
จากกฎข้อที่สองของนิวตัน จะได้การเคลื่อนที่ในแนวตั้งเท่ากับ
เมื่อเกิดทอร์กที่ปลายซ้ายของแท่งไม้ เราจะได้
แก้สองสมการจะได้ N
ซึ่งผลลัพธ์อยู่ในช่วงคำตอบของข้อ (B)
จากกฎข้อที่สองของนิวตัน จะได้การเคลื่อนที่ในแนวตั้งเท่ากับ
\(\rm F + N – m g = ma\)
เมื่อเกิดทอร์กที่ปลายซ้ายของแท่งไม้ เราจะได้
\(\tau = {\rm{FL}} - \dfrac{{{\rm{mgL}}}}{2}~,\rm I = \dfrac{1}{3}{\rm{m}}{{\rm{L}}^2}~,\alpha = \dfrac{a}{{{\rm{L/2}}}}\)
แก้สองสมการจะได้ N
\(\rm N = \dfrac{1}{3}ma+ \dfrac{1}{2}mg\)
ซึ่งผลลัพธ์อยู่ในช่วงคำตอบของข้อ (B)
| 10. | กราฟข้อใด แสดงความเร่งกับเวลาของวัตถุที่เคลื่อนที่ขึ้นไปโดยมีแรงต้านอากาศได้ดีที่สุด |
| A |  |
| B |  |
| C |  |
| D | 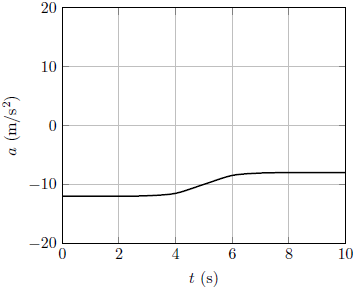 |
| E | 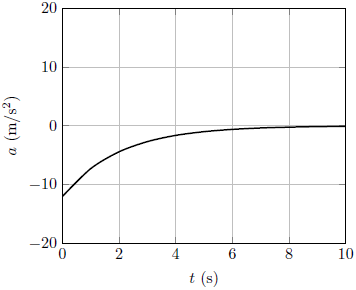 |
ตอบ (E)
ความเร่งควรสิ้นสุดลงที่ศูนย์ ตามความเร็วปลายของวัตถุ และกราฟควรเริ่มต้นด้วยค่าที่น้อยกว่า -10 m/s2 เนื่องจากมีแรงต้านอากาศที่กระทำในทิศเดียวกับแรงโน้มถ่วง
ความเร่งควรสิ้นสุดลงที่ศูนย์ ตามความเร็วปลายของวัตถุ และกราฟควรเริ่มต้นด้วยค่าที่น้อยกว่า -10 m/s2 เนื่องจากมีแรงต้านอากาศที่กระทำในทิศเดียวกับแรงโน้มถ่วง
| 11. | ให้สปริงเบาในอุดมคติถูกตรึงปลายด้านหนึ่งไว้ ส่วนปลายอีกด้านติดมวลไว้ แล้วสปริงจะสั่นด้วยความถี่เชิงมุม ω ถ้าปลายสปริงถูกตรึงไว้ทั้งสองด้าน แล้วตัดแบ่งครึ่งเพื่อนำมวลไปติดไว้กึ่งกลางระหว่างสปริงทั้งสอง
 |
| A | \(ω/2\) |
| B | \(ω\) |
| C | \(\sqrt2ω\) |
| D | \(2ω\) |
| E | \(4ω\) |
ตอบ (D)
การแบ่งครึ่งสปริง จะทำให้ค่านิจสปริงเพิ่มขึ้นเป็นสองเท่า หมายความ ถ้าแรง F ยึดสปริงเดิมได้ระยะ x แล้วแรงนั้นจะยืดสปริงใหม่ได้ระยะ x´ = x / 2 ซึ่งเป็นไปตาม F = – kx โดย k´ = 2k จากโจทย์ระบบใหม่ประกอบด้วยสปริงสองอันที่มีค่านิจสปริงเป็นสองเท่าของสปริงเดิม แสดงว่าค่านิจสปริงของระบบจะเพิ่มขึ้นสี่เท่า เนื่องจากความถี่เชิงมุมเท่ากับรากที่สองของค่านิจสปริง ดังนั้น ความถี่เชิงมุมใหม่จะเพิ่มขึ้นเป็นสองเท่า
การแบ่งครึ่งสปริง จะทำให้ค่านิจสปริงเพิ่มขึ้นเป็นสองเท่า หมายความ ถ้าแรง F ยึดสปริงเดิมได้ระยะ x แล้วแรงนั้นจะยืดสปริงใหม่ได้ระยะ x´ = x / 2 ซึ่งเป็นไปตาม F = – kx โดย k´ = 2k จากโจทย์ระบบใหม่ประกอบด้วยสปริงสองอันที่มีค่านิจสปริงเป็นสองเท่าของสปริงเดิม แสดงว่าค่านิจสปริงของระบบจะเพิ่มขึ้นสี่เท่า เนื่องจากความถี่เชิงมุมเท่ากับรากที่สองของค่านิจสปริง ดังนั้น ความถี่เชิงมุมใหม่จะเพิ่มขึ้นเป็นสองเท่า
| 12. | (เกินหลักสูตรการสอบเข้า สอวน.) นักเรียนกลุ่มหนึ่งต้องการวัดความเร่งโน้มถ่วงด้วยลูกตุ้มอย่างง่าย พวกเขาใช้ลูกตุ้มที่มีความยาว L = 1.00 ± 0.05 m และวัดคาบของการแกว่งในหนึ่งครั้งได้ T = 2.00 ± 0.10 s ถ้าสมมุติว่า ทุกความคลาดเคลื่อนมีการกระจายตัวแบบ Gaussian (มีการแจกแจงแบบปกติ) แล้วความเร่งโน้มถ่วงที่คำนวณจากผลการทดลองนี้ ควรได้ค่าตามข้อใด |
| A | 9.87 ± 0.05 m/s2 |
| B | 9.87 ± 0.15 m/s2 |
| C | 9.9 ± 0.25 m/s2 |
| D | 9.9 ± 1.1 m/s2 |
| E | 9.9 ± 1.5 m/s2 |
ตอบ (D)
จากสูตรคาบของลูกตุ้มจัดรูปใหม่จะได้ \(\rm g = 4π^2L / T^2\) จากนั้นใช้ standard error propagation rules เพื่อหาค่าความคลาดเคลื่อน โดยใช้สูตรส่วนเบี่ยงเบนมาตรฐาน ดังนี้
(A) ถ้า x มีความคลาดเคลื่อนสัมพัทธ์เท่ากับ Δx / x แล้ว xn จะมีความคลาดเคลื่อนสัมพัทธ์เท่ากับ
ในกรณีนี้ ความคลาดเคลื่อนสัมพัทธ์ของ L เท่ากับ 5% ความคลาดเคลื่อนสัมพัทธ์ของ T เท่ากับ 5% และความคลาดเคลื่อนสัมพัทธ์ของ 1/T2 เท่ากับ 10% ความคลาดเคลื่อนสัมพัทธ์ของ g เท่ากับ \(\sqrt {{{0.1}^2} + {{0.05}^2}} \approx 11\%\) ซึ่งตรงกับข้อ (D)
จากสูตรคาบของลูกตุ้มจัดรูปใหม่จะได้ \(\rm g = 4π^2L / T^2\) จากนั้นใช้ standard error propagation rules เพื่อหาค่าความคลาดเคลื่อน โดยใช้สูตรส่วนเบี่ยงเบนมาตรฐาน ดังนี้
(A) ถ้า x มีความคลาดเคลื่อนสัมพัทธ์เท่ากับ Δx / x แล้ว xn จะมีความคลาดเคลื่อนสัมพัทธ์เท่ากับ
\(\rm Δ(x^n)/x^n = | n | ~Δx / x\)
(B) ถ้ามีสองตัวแปรที่เป็นอิสระต่อกันคูณกันอยู่ ความคลาดเคลื่อนสัมพัทธ์จะเท่ากับ
\(\rm \dfrac{{\Delta (xy)}}{{xy}} = \sqrt {{{\left( {\dfrac{{\Delta x}}{x}} \right)}^2} + {{\left( {\dfrac{{\Delta y}}{y}} \right)}^2}} \)
(C) ความคลาดเคลื่อนสัมพัทธ์จะไม่เปลี่ยนแปลงตามการปรับขนาดของตัวแปร ในกรณีนี้ ความคลาดเคลื่อนสัมพัทธ์ของ L เท่ากับ 5% ความคลาดเคลื่อนสัมพัทธ์ของ T เท่ากับ 5% และความคลาดเคลื่อนสัมพัทธ์ของ 1/T2 เท่ากับ 10% ความคลาดเคลื่อนสัมพัทธ์ของ g เท่ากับ \(\sqrt {{{0.1}^2} + {{0.05}^2}} \approx 11\%\) ซึ่งตรงกับข้อ (D)
| 13. | ให้เชือกเบามีเส้นผ่านศูนย์กลาง 2.54 cm (1 นิ้ว) ถูกแขวนในแนวราบ และอยู่ระหว่างต้นไม้สองต้นที่ห่างกัน 18.0 m แล้วนักไต่เชือกคนหนึ่งเดินไปที่จุดกึ่งกลางของเชือกและทำให้เกิดแรงตึง 7300 N จนเชือกหย่อนลงมาทำมุม 1.50° กับแนวราบ
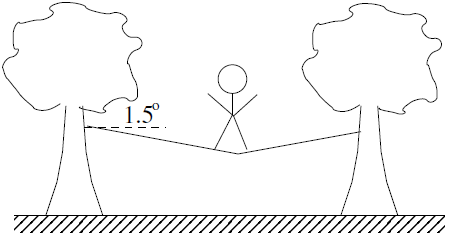 |
| A | 1.5 × 106 N/m2 |
| B | 2.0 × 108 N/m2 |
| C | 2.2 × 109 N/m2 |
| D | 2.4 × 1010 N/m2 |
| E | 4.2 × 1010 N/m2 |
ตอบ (E)
ความเครียดของเชือกเท่ากับ
ความเครียดของเชือกเท่ากับ
\(\dfrac{{\Delta L}}{L} = \dfrac{{{L_0}/\cos \theta - {L_0}}}{{{L_0}}} = \dfrac{1}{{\cos \theta }} - 1 \approx \dfrac{{{\theta ^2}}}{2}\)
จาก L0 เป็นความนาวเริ่มต้น จะได้มอดุลัสของยังเท่ากับ
\(Y = \dfrac{{7300{\rm{N}}}}{{\pi {{(0.0127m)}^2}}}{\left( {\dfrac{{{{(1.50\pi /180)}^2}}}{2}} \right)^{ - 1}} = 4.2 \times {10^{10}}~\rm N/m^2\)
| 14. | ให้มวลที่เหมือนกันสามชิ้นเชื่อมกับคานแข็งแบบเดียวกัน และมีจุดหมุนที่จุด A เมื่อมวลก้อนล่างสุดถูกดันในแนวนอนเบาๆ ไปทางซ้าย จะเกิดการแกว่งด้วยคาบ T1 เมื่อเปลี่ยนเป็นดันเบาๆ ที่ด้านหน้าแบบตั้งฉากกับกระดาษ จะได้คาบของการแกว่งเท่ากับ T2 แล้วอัตราส่วน T1/T2 เท่ากับข้อใด
 |
| A | \(1/2\) |
| B | \(1\) |
| C | \(\sqrt3\) |
| D | \(2\sqrt2\) |
| E | \(2\sqrt5\) |
ตอบ (C)
ทั้งสองกรณีนั้นเป็นการเคลื่อนที่แบบลูกตุ้ม ซึ่งมีคาบแปรผันกับ \(\rm \sqrt{I / Mgx }\) โดย x คือ ระยะจากจุดหมุนถึงจุดศูนย์กลางมวล และ I คือ โมเมนต์ความเฉื่อยรอบจุดหมุน เนื่องจาก x เท่ากันทั้งสองกรณี จะได้ว่า \(\rm T_1 / T_2 ∝ \sqrt{I_1/I_2}= \sqrt3\) ในกรณีที่สองนั้นเฉพาะมวลด้านล่างทำให้เกิดโมเมนต์ความเฉื่อย
ทั้งสองกรณีนั้นเป็นการเคลื่อนที่แบบลูกตุ้ม ซึ่งมีคาบแปรผันกับ \(\rm \sqrt{I / Mgx }\) โดย x คือ ระยะจากจุดหมุนถึงจุดศูนย์กลางมวล และ I คือ โมเมนต์ความเฉื่อยรอบจุดหมุน เนื่องจาก x เท่ากันทั้งสองกรณี จะได้ว่า \(\rm T_1 / T_2 ∝ \sqrt{I_1/I_2}= \sqrt3\) ในกรณีที่สองนั้นเฉพาะมวลด้านล่างทำให้เกิดโมเมนต์ความเฉื่อย
| 15. | ถ้ายานอวกาศที่อยู่ในวงโคจรวงกลมรอบโลก มีคาบในการโคจรยาวนาน เพราะได้รับผลกระทบจากแรงต้านอากาศ ซึ่งทำให้พลังงานสุทธิของยานอวกาศลง 1 J แล้วพลังงานจลน์ของดาวเทียมจะเป็นไปตามข้อใด |
| A | จะเพิ่มขึ้น 1 J |
| B | ยังคงเท่าเดิม |
| C | จะลดลง \(\frac{1}{2}\) J |
| D | จะลดลง 1 J |
| E | จะลดลง 2 J |
ตอบ (A)
แม้จะมีแรงต้าน (จากอากาศที่เบาบาง) ที่ทำให้ดาวเทียมเคลื่อนที่ช้าลงแต่ ดาวเทียมจะยังคงอยู่ในวงโคจรวงกลม
ในวงโคจร พลังงานสุทธิจะเท่ากับ E = K + V โดยv = - 2K หรือ E = - K ถ้าพลังงานสุทธิลดลง ΔE
แล้วพลังงานจลน์จะเพิ่มขึ้น ΔE
แม้จะมีแรงต้าน (จากอากาศที่เบาบาง) ที่ทำให้ดาวเทียมเคลื่อนที่ช้าลงแต่ ดาวเทียมจะยังคงอยู่ในวงโคจรวงกลม
ในวงโคจร พลังงานสุทธิจะเท่ากับ E = K + V โดยv = - 2K หรือ E = - K ถ้าพลังงานสุทธิลดลง ΔE
แล้วพลังงานจลน์จะเพิ่มขึ้น ΔE
| 16. | สถานีอวกาศทรงกระบอกสามารถสร้าง “แรงโน้มถ่วงเทียม” จากการหมุนด้วยความถี่เชิงมุม ω ให้พิจารณาในกรอบอ้างอิงที่สถานีอวกาศกำลังหมุน ถ้านักบินอวกาศเดิมยืนนิ่งอยู่บนพื้น และหันหน้าไปในทิศที่สถานีอวกาศกำลังหมุน แล้วเขากระโดดขึ้นในแนวตั้งเทียบกับพื้นด้วยอัตราเร็วต้นที่น้อยกว่าอัตราเร็วของพื้น แล้วหลังหลุดออกจากพื้น การเคลื่อนที่ของเขาเทียบกับพื้นของสถานีอวกาศจะเป็นไปตามข้อใด
 |
| A | จะมีส่วนประกอบของความเร่ง ที่มีทิศชี้ไปยังพื้นเสมอ และจะตกกลับมาที่จุดเดิมที่เคยกระโดดขึ้น |
| B | จะมีส่วนประกอบของความเร่ง ที่มีทิศชี้ไปยังพื้นเสมอ และจะตกกลับมาหน้าจุดเดิมที่เคยกระโดดขึ้น |
| C | จะมีส่วนประกอบของความเร่ง ที่มีทิศชี้ไปยังพื้นเสมอ และจะตกกลับมาหลังจุดเดิมที่เคยกระโดดขึ้น |
| D | จะมีส่วนประกอบของความเร่ง ที่มีทิศชี้ออกจากพื้นเสมอ และจะตกกลับมาหลังจุดเดิมที่เคยกระโดดขึ้น |
| E | จะมีความเร่งเป็นศูนย์เมื่อเทียบกับพื้น และเขาจะไม่กลับมาสู่พื้นอีก |
ตอบ (B)
ในการหาคำตอบ เราอาจจะวาดทิศทางของนักบินในกรอบอ้างอิงเดิมโดยใช้เส้นตรงอย่างง่าย
โดยนักบินจะถึงพื้น ตรง 'ด้านหน้า' ของจุดที่กระโดดเสมอ
ในการหาคำตอบ เราอาจจะวาดทิศทางของนักบินในกรอบอ้างอิงเดิมโดยใช้เส้นตรงอย่างง่าย
โดยนักบินจะถึงพื้น ตรง 'ด้านหน้า' ของจุดที่กระโดดเสมอ

| 17. | มีทรายร่วงลงมาเป็นสายจากเฮลิคอปเตอร์ที่เคลื่อนที่ไปทางขวาด้วยอัตราเร็วคงที่ v แล้วเปลี่ยนทิศกระทันหันไปทางซ้ายแล้วมีอัตราเร็วคงที่ v ถ้าไม่คิดถึงแรงต้านอากาศ แล้วรูปร่างของสายทรายที่มองเห็นจากพื้นดิน จะเป็นไปตามข้อใด ให้จุดสีดำ คือ เฮลิคอปเตอร์ |
| A | 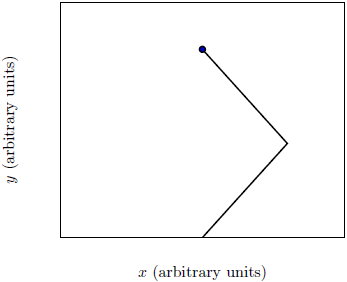 |
| B |  |
| C | 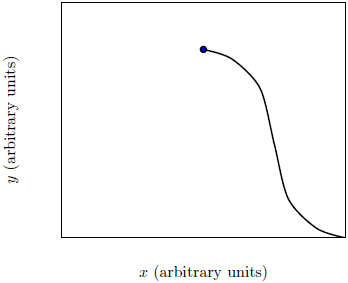 |
| D |  |
| E |  |
ตอบ (D)
ถ้าทรายร่วงลงมาจากเฮลิคอปเตอร์ที่บินด้วยความเร็วคงที่ แล้วทิศทางของสายทรายจะต้องร่วงลงมาเส้นตรงเหมือนเดิม ดังนั้น สายทรายที่เห็นควรเป็นเส้นตรงสองเส้นในแนวตั้ง (ไม่คิดแรงต้านอากาศ)
ถ้าทรายร่วงลงมาจากเฮลิคอปเตอร์ที่บินด้วยความเร็วคงที่ แล้วทิศทางของสายทรายจะต้องร่วงลงมาเส้นตรงเหมือนเดิม ดังนั้น สายทรายที่เห็นควรเป็นเส้นตรงสองเส้นในแนวตั้ง (ไม่คิดแรงต้านอากาศ)
| 18. | มวล m ติดกับคานบางยาว l ซึ่งสามารถหมุนเป็นวงกลมในแนวตั้งได้อย่างอิสระด้วยคาบ T แล้วผลต่างของแรงตึงบนคานขณะมวลแกว่งอยู่ที่ด้านบนของวงกลม กับที่ด้านล่างของวงกลมจะเท่ากับข้อใด |
| A | \(\text{6mg}^2\text{T}^2/l\) |
| B | \(4π\text{mg}^2\text{T}^2/l\) |
| C | \(6\rm mg\) |
| D | \(π^2\text{m}l / \rm T^2 \) |
| E | \(4π\text{m}l / \rm T^2\) |
ตอบ (C)
จะมีผลต่าง \(\rm 2mg\) จากแรงโน้มถ่วงที่ต้านแรงดึงขณะมวลอยู่ที่ด้านล่างและด้านบน และผลต่างของแรงสู่ศูนย์กลางจะเท่ากับ
จะมีผลต่าง \(\rm 2mg\) จากแรงโน้มถ่วงที่ต้านแรงดึงขณะมวลอยู่ที่ด้านล่างและด้านบน และผลต่างของแรงสู่ศูนย์กลางจะเท่ากับ
\(Δ(\text{mv}2/l) = 2Δ\text{K}/l = 2(2\text{mg}l)/l = 4\text{mg}\)
ดังนั้น ผลต่างทั้งหมด คือ \(\rm 6mg\)| 19. | ให้ปริมาณฝนที่ตกมีความหนาแน่น n หยดต่อลูกบาศก์เมตร หยดฝนมีรัศมี r0 กระทบพื้นด้วยอัตราเร็ว v0 ความดันบนพื้นดินที่เกิดจากฝนเท่ากับ P0 ถ้าปริมาณความหนาแน่นของฝนเพิ่มขึ้นเป็นสองเท่า แต่หยดฝนมีรัศมีลดลงครึ่งหนึ่ง อัตราเร็วลดลงครึ่งหนึ่ง แล้วความดันใหม่จะเท่ากับข้อใด |
| A | P0 |
| B | P0/2 |
| C | P0/4 |
| D | P0/8 |
| E | P0/16 |
ตอบ (E)
ฝนแต่ละหยดจะมีมวล 1/8 และมีอัตราเร็ว 1/2 ดังนั้น จะมีโมเมนตัมเท่ากับ 1/16 และอัตราการตกลงสู่พื้นของทุกหยดจะเท่ากันหมด จากโจทย์ให้ความหนาแน่นเพิ่มขึ้นเป็นสองเท่า แต่ความเร็วลดลงครึ่งหนึ่ง แล้วความดันใหม่จะเท่ากับ P0/16
ฝนแต่ละหยดจะมีมวล 1/8 และมีอัตราเร็ว 1/2 ดังนั้น จะมีโมเมนตัมเท่ากับ 1/16 และอัตราการตกลงสู่พื้นของทุกหยดจะเท่ากันหมด จากโจทย์ให้ความหนาแน่นเพิ่มขึ้นเป็นสองเท่า แต่ความเร็วลดลงครึ่งหนึ่ง แล้วความดันใหม่จะเท่ากับ P0/16
| 20. | เมื่อยืดสปริงให้ยาวเป็นสองเท่าของความยาวตามปกติ จะมีพลังงานศักย์ U0 ถ้าตัดสปริงครึ่งหนึ่ง แล้วนำแต่ละส่วนมายืดให้ยาวเป็นสองเท่าของความยาวตามปกติ แล้วพลังงานศักย์สุทธิของสปริงทั้งสองเท่ากับข้อใด |
| A | 4U0 |
| B | 2U0 |
| C | U0 |
| D | U0/2 |
| E | U0/4 |
ตอบ (C)
เราสามารถคำนวณโดยตรงจากสูตร U = kx2/2 โดยสปริงที่ถูกตัดออกมาจะมีค่านิจสปริงเพิ่มขึ้นเป็นสองเท่า หรืออีกวิธีหนึ่งคือ คิดจากพลังงาน ซึ่งทั้งหมดจะถูกเก็บไว้ใน microscopically และใน microscopically แต่ละอันจะมีโมเลกุลเท่าเดิมไม่ว่าสปริงจะเต็มอันหรือเหลือแค่ครึ่งเดียว ดังนั้น แม้ว่าสปริงจะถูกตัดออกไปค่าที่ได้ก็จะต้องเท่ากัน
เราสามารถคำนวณโดยตรงจากสูตร U = kx2/2 โดยสปริงที่ถูกตัดออกมาจะมีค่านิจสปริงเพิ่มขึ้นเป็นสองเท่า หรืออีกวิธีหนึ่งคือ คิดจากพลังงาน ซึ่งทั้งหมดจะถูกเก็บไว้ใน microscopically และใน microscopically แต่ละอันจะมีโมเลกุลเท่าเดิมไม่ว่าสปริงจะเต็มอันหรือเหลือแค่ครึ่งเดียว ดังนั้น แม้ว่าสปริงจะถูกตัดออกไปค่าที่ได้ก็จะต้องเท่ากัน
| 21. | ลูกปิงปอง (ทรงกลมกลวง) มวล m อยู่บนพื้นและมีความเร็วต้น v0 มีอัตราเร็วเชิงมุมเป็นศูนย์ที่เวลา t = 0 สัมประสิทธิ์แรงเสียดทานระหว่างลูกปิงปองกับพื้นเป็น μs = μk = μ แล้วเวลาที่ลูกปิงปองจะเริ่มกลิ้งโดยไม่ลื่นไถลเท่ากับข้อใด
 |
| A | t = (2/5)v0/μg |
| B | t = (2/3)v0/μg |
| C | t = v0/μg |
| D | t = (5/3)v0/μg |
| E | t = (3/2)v0/μg |
ตอบ (A)
จากแรงเสียดทานเท่ากับ μmg ดังนั้น ความเร็วจะลดลง เป็น \(\rm \dot{v} = – μg\) ส่วนทอร์กที่กระทำที่จุดศูนย์กลางมวลจะเท่ากับ \(\rm μmgR\) โดย \(\rm R\) คือรัศมี ดังนั้น ความเร็วเชิงมุมจะเพิ่มขึ้น เป็น \(\rm\dot{ω} = (3/2)μg/R\) การหมุนโดยไม่ไถลจะเกิดขึ้นเมื่อ \(\rm v = Rω\) ดังนั้น \(\rm t = (2/5)v_0/μg\)
จากแรงเสียดทานเท่ากับ μmg ดังนั้น ความเร็วจะลดลง เป็น \(\rm \dot{v} = – μg\) ส่วนทอร์กที่กระทำที่จุดศูนย์กลางมวลจะเท่ากับ \(\rm μmgR\) โดย \(\rm R\) คือรัศมี ดังนั้น ความเร็วเชิงมุมจะเพิ่มขึ้น เป็น \(\rm\dot{ω} = (3/2)μg/R\) การหมุนโดยไม่ไถลจะเกิดขึ้นเมื่อ \(\rm v = Rω\) ดังนั้น \(\rm t = (2/5)v_0/μg\)
| 22. | เรือทรงสี่เหลี่ยมมุมฉากมีรูรั่วเล็กๆ อยู่ที่ใต้ท้องเรือ ทำให้มีน้ำไหลเข้ามา และเรือก็ค่อยๆจมลงในน้ำ แล้วกราฟข้อใดแสดงอัตราการไหลของน้ำที่ไหลเข้ามาในเรือเทียบกับเวลา (leak rate) ได้ดีที่สุด สมมุติให้ขณะจมลง เรือยังคงอยู่ในแนวราบ
 |
| A | 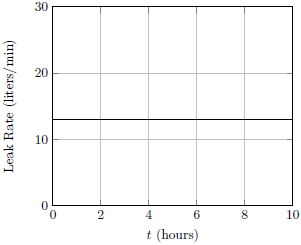 |
| B | 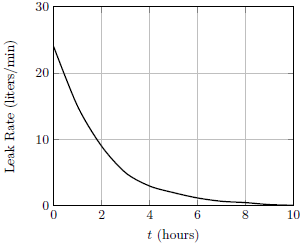 |
| C | 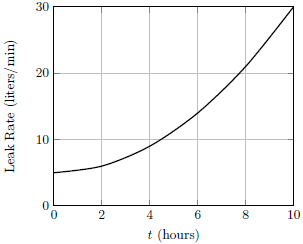 |
| D | 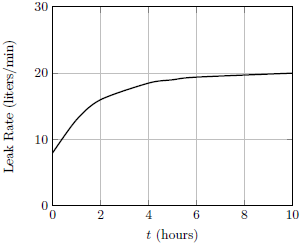 |
| E |  |
ตอบ (A)
จากหลักของอาร์คิมีดีส ผลต่างของระดับน้ำด้านในและด้านนอนจะต้องเท่าเดิมเสมอ ดังนั้น แรงดันที่น้ำจะเข้ามาตามรูรั่วจะต้องคงที่ ตามหลักของแบร์นูลลี ดังนั้น อัตราการไหลของน้ำที่ไหลเข้ามาจะต้องคงที่
จากหลักของอาร์คิมีดีส ผลต่างของระดับน้ำด้านในและด้านนอนจะต้องเท่าเดิมเสมอ ดังนั้น แรงดันที่น้ำจะเข้ามาตามรูรั่วจะต้องคงที่ ตามหลักของแบร์นูลลี ดังนั้น อัตราการไหลของน้ำที่ไหลเข้ามาจะต้องคงที่
| 23. | ให้สัมประสิทธิ์แรงเสียดทานจลน์สถิตระหว่างลูกบอลและทางลาดเท่ากับ μs = μk = μ ถ้าลูกบอลที่เดิมอยู่นิ่ง ถูกปล่อยลงมาจากด้านบนของทางลาด แล้วกราฟข้อใดแสดงความเร่งเชิงมุมของลูกบอลที่จุดศูนย์กลางมวล เทียบกับขนาดมุมของทางลาดได้ดีที่สุด |
| A | 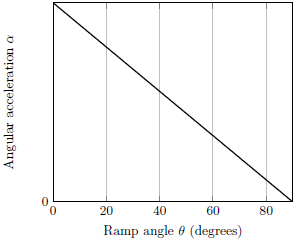 |
| B | 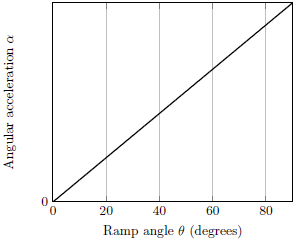 |
| C |  |
| D |  |
| E |  |
ตอบ (C)
ข้อนี้อาจหาคำตอบโดยใช้วิธี limiting cases สังเกตว่า
ถ้าทางลาดนั้นราบไปกับพื้น ความเร่งเชิงมุมของลูกบอลก็จะเท่ากับ ศูนย์ และถ้าทางลาดนั้นตั้งฉากกับพื้น ลูกบอลก็จะไม่หมุนและมีความเร่งเชิงมุมเป็นศูนย์เช่นกัน หรือใช้วิธีหาความเร่งเชิงมุมของลูกบอล สำหรับกรณีที่ลูกบอลกลิ้งโดยไม่ไถล ความเร่งจะเท่ากับ
ดังนั้น กราฟจะมีส่วนที่เพิ่มขึ้นและลดลงเป็นโค้งเว้า
และมียอดแหลม ณ จุดที่เกิดการไถล ซึ่งตรงกับข้อ (C)
ข้อนี้อาจหาคำตอบโดยใช้วิธี limiting cases สังเกตว่า
ถ้าทางลาดนั้นราบไปกับพื้น ความเร่งเชิงมุมของลูกบอลก็จะเท่ากับ ศูนย์ และถ้าทางลาดนั้นตั้งฉากกับพื้น ลูกบอลก็จะไม่หมุนและมีความเร่งเชิงมุมเป็นศูนย์เช่นกัน หรือใช้วิธีหาความเร่งเชิงมุมของลูกบอล สำหรับกรณีที่ลูกบอลกลิ้งโดยไม่ไถล ความเร่งจะเท่ากับ
g sinθ / (1 + I / MR2) ∝ sinθ
เมื่อมุมสูงมากพอก็จะเกิดการไถล โดยความเร่งเชิงมุมจะแปรผัน ตามแรงเสียดทานจลน์ ซึ่งเป็นสัดส่วนกับ cosθ ดังนั้น กราฟจะมีส่วนที่เพิ่มขึ้นและลดลงเป็นโค้งเว้า
และมียอดแหลม ณ จุดที่เกิดการไถล ซึ่งตรงกับข้อ (C)
| 24. | ให้มวลติดที่ปลายด้านหนึ่งของคานแข็ง และอีกด้านของคานติดกับเพลาลื่นในแนวนอนที่สามารถหมุนได้รอบ 360° มวลถูกแขวนที่ปลายคาน และคานอยู่ในแนวตั้ง ให้มวลจะมีพลังงานจลน์เริ่มต้น K ถ้า K มีขนาดเล็กมาก มวลก็จะเปรียบเสมือนลูกตุ้ม เมื่อสั่นด้วยมุมเล็กๆ จะได้คาบของการแกว่ง T0 แล้วกรณีที่ K เพิ่มขึ้น คาบของมวลจะเป็นไปตามข้อใด |
| A | ยังคงเท่าเดิม |
| B | เพิ่มขึ้น และเข้าใกล้ค่าหนึ่งที่หาค่าได้ |
| C | ลดลง และเข้าใกล้ค่าหนึ่งที่ไม่ใช่ศูนย์ และหาค่าได้ |
| D | ลดลง และเข้าใกล้ศูนย์ |
| E | ตอนแรกจะเพิ่มขึ้น แล้วลดลง |
ตอบ (E)
เมื่อแอมพลิจูดเพิ่มเป็น \(π\) คาบก็จะลู่ออก ดังนั้น ช่วงแรกคาบจะเพิ่มขึ้น (หรืออีกวิธีหนึ่ง สังเกตว่า cosθ ในจัตุภาคจะมีเครื่องหมายตรงกันข้าม ทำให้ลดแรงส่งกลับ และทำให้คาบเพิ่มขึ้น) ถ้าพลังงานเพิ่มขึ้นต่อไปอีก มวลก็จะวนในทิศทางเดียวตลอดไป แล้วคาบก็จะลดลง และเป็นค่าที่สามารถหาค่าได้
เมื่อแอมพลิจูดเพิ่มเป็น \(π\) คาบก็จะลู่ออก ดังนั้น ช่วงแรกคาบจะเพิ่มขึ้น (หรืออีกวิธีหนึ่ง สังเกตว่า cosθ ในจัตุภาคจะมีเครื่องหมายตรงกันข้าม ทำให้ลดแรงส่งกลับ และทำให้คาบเพิ่มขึ้น) ถ้าพลังงานเพิ่มขึ้นต่อไปอีก มวลก็จะวนในทิศทางเดียวตลอดไป แล้วคาบก็จะลดลง และเป็นค่าที่สามารถหาค่าได้
| 25. | (เกินหลักสูตรสอบเข้า สอวน.) ก และ ข กำลังเขียนรายงานผลการทดลอง โดย ก วัดคาบของลูกตุ้มได้ 1.013 ± 0.008 s ในขณะที่ ข วัดได้คาบ 0.997 ± 0.016 s ซึ่งทั้งคู่สามารถสรุปข้อมูลที่ได้ตามวิธีต่อไปนี้
วิธีที่ 1 : ใช้ข้อมูลของ ก โดยไม่สนของ ข
วิธีที่ 2 : ใช้ค่าเฉลี่ยของข้อมูล ก และ ข
วิธีที่ 3 : ใช้ค่าเฉลี่ยถ่วงน้ำหนักของข้อมูล ก และ ข โดยถ่วงให้ ก มีน้ำหนักมากกว่า ข อยู่ 4 เท่า
ข้อใดสรุป ความคลาดเคลื่อนของผลลัพธ์ในแต่ละวิธี ได้ดีที่สุด |
| A | วิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด |
| B | วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด |
| C | วิธีที่ 2 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 1 มีความคลาดเคลื่อนสูงที่สุด |
| D | วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 1 มีความคลาดเคลื่อนสูงที่สุด |
| E | วิธีที่ 1 มีความคลาดเคลื่อนต่ำที่สุด ส่วนวิธีที่ 3 มีความคลาดเคลื่อนสูงที่สุด |
ตอบ (B)
ให้ Δx เป็นความคลาดเคลื่อนในการวัดของ ก จะได้ ความคลาดเคลื่อนของ ข เท่ากับ 2Δx
การหาความคลาดเคลื่อน โดยใช้สูตรส่วนเบี่ยงเบนมาตรฐาน จะมีกฏที่จำเป็น ดังต่อไปนี้
ดังนั้น วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด (ในทางปฏิบัติ) ส่วนวิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด
ให้ Δx เป็นความคลาดเคลื่อนในการวัดของ ก จะได้ ความคลาดเคลื่อนของ ข เท่ากับ 2Δx
การหาความคลาดเคลื่อน โดยใช้สูตรส่วนเบี่ยงเบนมาตรฐาน จะมีกฏที่จำเป็น ดังต่อไปนี้
(A) การคูณด้วยค่าคงที่ : ถ้า x มีความคลาดเคลื่อน Δx แล้ว cx จะมีความคลาดเคลื่อน cΔx
(B) การเพิ่มตัวแปร : ถ้า x มีความคลาดเคลื่อน Δx และ y มีความคลาดเคลื่อน Δy โดยทั้งสองเป็นอิสระต่อกัน แล้ว x + y จะมีความคลาดเคลื่อนเท่ากับ
\(\rm \sqrt{(Δx)^2 +(Δy)^2}\)
เราสามารถหาความคลาดเคลื่อนของทั้งสามวิธีได้ ดังนี้
วิธีที่ 1: \(\rm Δx\)
วิธีที่ 2: \(\rm \sqrt{(Δx)^2 +(2Δx)^2} / 2 = (\sqrt5/2) Δx \)
วิธีที่ 3: \(\rm\sqrt{(4Δx)^2 +(2Δx)^2} / 5 = (2/\sqrt5) Δx \)
ดังนั้น วิธีที่ 3 มีความคลาดเคลื่อนต่ำที่สุด (ในทางปฏิบัติ) ส่วนวิธีที่ 2 มีความคลาดเคลื่อนสูงที่สุด

