ข้อสอบคัดเลือกของทีม USA 2011 (25 ข้อ)
| 1. | ปั่นจักรยานด้วยอัตราเร็วคงที่ 22.0 km/hr และมีการหยุดพัก 20 นาที ถ้าอัตราเร็วเฉลี่ยของการปั่นจักรยานคือ 17.5 km/hr แล้วระยะทางที่ปั่นจักรยานไปได้เท่ากับข้อใด |
| 2. | กำหนดกราฟแสดงความเร็วต่อเวลาของวัตถุสามชิ้นที่เคลื่อนที่ในหนึ่งมิติ ดังนี้
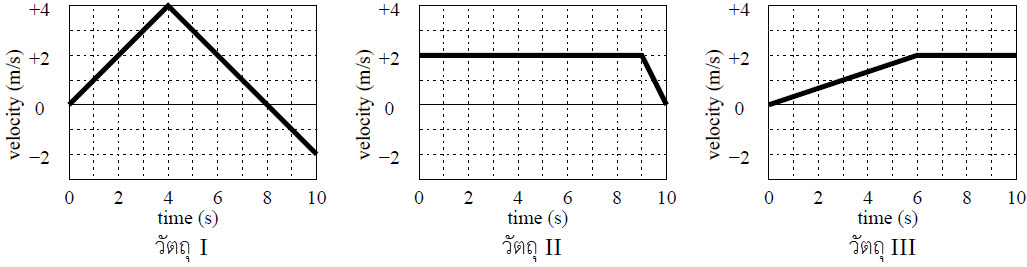 |
| 3. | กำหนดกราฟแสดงความเร็วต่อเวลาของวัตถุสามชิ้นที่เคลื่อนที่ในหนึ่งมิติ ดังนี้
 |
| 4. | กำหนดกราฟแสดงความเร็วต่อเวลาของวัตถุสามชิ้นที่เคลื่อนที่ในหนึ่งมิติ ดังนี้
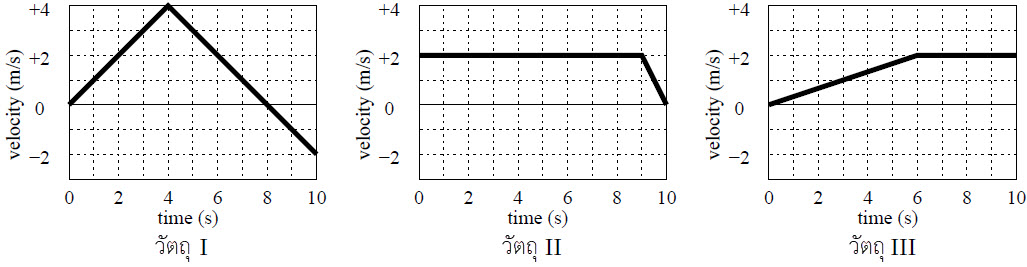 |
| 5. | โลกที่โคจรรอบดวงอาทิตย์ด้วยอัตราเร็วคงที่ จะมีระยะทางห่างจากดวงอาทิตย์ประมาณ 150,000,000 กิโลเมตร ความเร่งของโลกในวงโคจรนี้ควรมีค่าเท่ากับข้อใด |
| 6. | เด็กสะดุดลื่นด้วยความเร็ว vc บนทะเลสาบน้ำแข็ง ไปชนกับเด็กอีกคนที่เดิมอยู่นิ่ง ซึ่งเขามีมวลเป็น 3 เท่าของเด็กคนแรก หลังการชนทั้งคู่ไถลไปด้วยกัน ความเร็วของคู่หลังการชนเท่ากับข้อใด |
| 7. | นักเล่นสเก็ตน้ำแข็งสามารถหมุนรอบตัวเองด้วยความเร็วเชิงมุม ω0 ขณะยืดแขนออก และเมื่อดึงแขนกลับเข้ามาใกล้ตัวความเร็วเชิงมุมจะเปลี่ยนเป็น 2ω0 โดยไม่มีทอร์กภายนอกใด ๆ มากระทำ แล้วอัตราส่วนของพลังงานจลน์ของการหมุนสุดท้ายกับพลังงานจลน์ของการหมุนเริ่มต้น เท่ากับข้อใด |
| 8. | บล็อกไม้หนัก 30 N หากกดให้จมอยู่ในน้ำเต็มชิ้น จะมีแรงลอยตัวจากน้ำกระทำกับบล็อกไม้ 50 N เมื่อปล่อยให้ลอยอย่างอิสระ บล็อกไม้จะลอยขึ้นไปที่ผิวน้ำ แล้วส่วนที่ลอยพ้นน้ำเป็นเศษส่วนเท่าใดของบล็อกไม้ทั้งชิ้นขณะลอยตัวขึ้นไป |
| 9. | สปริงสมดุลยาว 2.0 เมตร มีค่านิจสปริง 10 นิวตัน/เมตร ให้ ก ดึงปลายด้านหนึ่งของสปริงด้วยแรง 3.0 นิวตัน ส่วน ข ดึงปลายอีกด้านด้วยแรง 3.0 นิวตัน ในทิศทางตรงกันข้าม ความยาวของสปริง ณ ปัจจุบันเท่ากับข้อใด |
| 10. | การกระทำในข้อใด ที่ทำให้คาบของลูกตุ้มอย่างง่าย มีค่าเพิ่มขึ้น |
| A | ลดความยาวลูกตุ้ม |
| B | เพิ่มมวลลูกตุ้ม |
| C | เพิ่มแอมพลิจูดการแกว่งของลูกตุ้ม |
| D | แกว่งลูกตุ้มในลิฟท์ที่กำลังเคลื่อนที่ขึ้น ด้วยความเร่ง |
| E | แกว่งลูกตุ้มในลิฟท์ที่กำลังเคลื่อนที่ลง ด้วยอัตราเร็วคงที่ |
ตอบ (C)
| 11. | แก้วโลหะทรงกระบอกขนาดใหญ่ ลอยอยู่ในอ่างสี่เหลี่ยมที่มีน้ำอยู่ครึ่งอ่าง หลังจากนั้นปล่อยน้ำจากก๊อกให้ไหลเข้ามาในแก้วด้วยอัตราคงที่ จนแก้วจมลงไปอยู่ใต้น้ำทั้งใบ กราฟในข้อใดแสดงระดับน้ำในอ่างกับเวลาได้ถูกต้องที่สุด |
| 12. | พิจารณาลูกบอลที่หนักมากๆ และคานเบา แบบเดียวกัน เมื่อนำลูกบอลสองลูกไปติดไว้ที่ปลายแต่ละด้าน จะเกิดปฏิสัมพันธ์แรงโน้มถ่วงซึ่งกันและกัน (ตามรูปด้านซ้าย) แรงบีบบนคานจะเท่ากับ F จากนั้นเพิ่มลูกบอลลูกที่สามให้เป็นจุดยอดของรูปสามเหลี่ยม และมีคานเป็นด้านของรูปสามเหลี่ยมด้านเท่า (ตามรูปด้านขวา) แรงบีบบนคานแต่ละอัน ในกรณีหลังนี้จะเท่ากับข้อใด  |
| A | \(\rm \dfrac{1}{\sqrt3}F\) |
| B | \(\rm \dfrac{\sqrt3}{2}F\) |
| C | \(\rm F\) |
| D | \(\rm\sqrt3F\) |
| E | \(\rm 2 F\) |
ตอบ (C)
| 13. | หลอดด้าย มีแกนทรงกระบอกหน้าตัดวงกลมรัศมี 1 cm มีวงกลมรัศมี 2 cm แปะหัวท้ายแกน ดังรูป เมื่อนำไปวางบนพื้นที่กลิ้งได้โดยไม่ไถล แล้วดึงด้ายที่พันรอบแกนขึ้นทำมุม θ = 90◦ กับแนวระดับ (ดึงขึ้นเท่านั้น) หลอดด้ายจะหมุนไปทางขวา แล้ว θ มากสุดที่ทำให้หลอดด้ายไม่หมุนไปทางขวา เมื่อดึงด้าย เท่ากับข้อใด
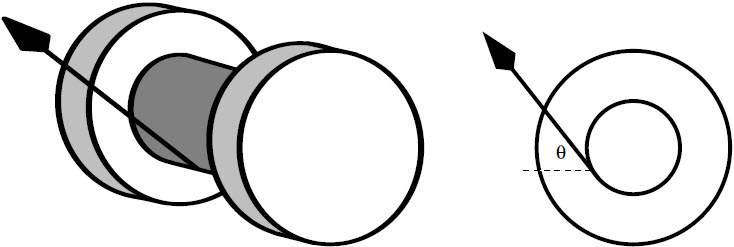 |
| A | θ = 15◦ |
| B | θ = 30◦ |
| C | θ = 45◦ |
| D | θ = 60◦ |
| E | ไม่ข้อใดถูก เพราะ หลอดด้ายจะกลิ้งไปทางขวาเสมอ |
ตอบ (D)
| 14. | กำหนดเชือกที่ผูกลูกตุ้มไว้ที่ตำแหน่งต่างๆ ซึ่งแตกต่างกัน 5 เส้น เชือกทั้งหมดจะถูกห้อยลงมาจากเพดานไปจรดปลายพื้น หากปลดเชือกให้ตกลงสู่พื้น เชือกเส้นใดที่กระทบพื้นแล้วจะเกิดเสียงกระทบเป็นจังหวะแบบสม่ำเสมอ |
| 15. | มวลติดสปริงในแนวตั้งถูกดึงออกมา 20 cm จากสมดุล ถ้ามวล 100 g ผ่านจุดสมดุลด้วยอัตราเร็ว 0.75 m / s แล้วค่านิจสปริงเท่ากับข้อใด |
| 16. | โจ พยามใช้เชือกยกเพื่อนที่อยู่ในกล่องใบหนึ่ง ซึ่งแขวนอยู่ที่ด้านข้างของสะพาน ส่วนโจอยู่บนสะพาน ตัวเชือกมีตะขอเกี่ยวกับกล่อง และถูกพาดกับราวจับที่ถูกยึดไว้แน่น โจพยามยึดกล่องไว้โดยการกดเชือกกับราวด้วยหนังสือฟิสิกส์ที่เบาและไร้แรงเสียดทาน มีสัมประสิทธิ์ความเสียดทานสถิตระหว่างเชือกกับราวเป็น μs และสัมประสิทธิ์ความเสียดทานจลน์ระหว่างเชือกกับราวเป็น μk < μs มวลของกล่องและเพื่อนรวมกันเป็น M และความสูงเริ่มต้น จากกล่องถึงพื้นคือ h และสมมุติว่าเชือกเบามาก
 |
| 17. | โจ พยามใช้เชือกยกเพื่อนที่อยู่ในกล่องใบหนึ่ง ซึ่งแขวนอยู่ที่ด้านข้างของสะพาน ส่วนโจอยู่บนสะพาน ตัวเชือกมีตะขอเกี่ยวกับกล่อง และถูกพาดกับราวจับที่ถูกยึดไว้แน่น โจพยามยึดกล่องไว้โดยการกดเชือกกับราวด้วยหนังสือฟิสิกส์ที่เบาและไร้แรงเสียดทาน มีสัมประสิทธิ์ความเสียดทานสถิตระหว่างเชือกกับราวเป็น μs และสัมประสิทธิ์ความเสียดทานจลน์ระหว่างเชือกกับราวเป็น μk < μs มวลของกล่องและเพื่อนรวมกันเป็น M และความสูงเริ่มต้น จากกล่องถึงพื้นคือ h และสมมุติว่าเชือกเบามาก
 |
| A | \(\rm \sqrt{2gh}(\mu_k/\mu_s)\) |
| B | \(\rm \sqrt{2gh}(1-\mu_k/\mu_s)\) |
| C | \(\rm \sqrt{2gh}\sqrt{\mu_k/\mu_s}\) |
| D | \(\rm \sqrt{2gh}\sqrt{1-\mu_k/\mu_s}\) |
| E | \(\rm \sqrt{2gh}(\mu_s-\mu_k)\) |
ตอบ (D)
| 18. | บล็อกมวล m = 3.0 kg เลื่อนจากพื้นเอียงแรกไปถึงพื้นเอียงที่สอง มีค่าสัมประสิทธิ์แรงเสียดทานจลน์ของบล็อกกับแต่ละพื้นเอียงเท่ากับ μk = 0.40 ถ้าบล็อกเริ่มเลื่อนลงมาจากความสูง h1 = 1.0 m จากพื้นดิน และพื้นเอียงทั้งสองเอียง 30◦ กับแนวระดับ ความสูงที่จากพื้นดิน ที่บล็อกหยุดอยู่ที่พื้นเอียงที่สองเท่ากับข้อใด |
| 19. | วัตถุมวล 2.00 kg เคลื่อนที่ด้วยแรงที่กำหนดจาก
\(\rm \vec F= – (8.00 N / m) (x\hat i + y\hat j )\)
โดย \(\rm \hat i\) และ \(\rm \hat j\) เป็นเวกเตอร์หนึ่งหน่วยในแกน x และ y และเริ่มปล่อยวัตถุด้วยความเร็วต้น \(\rm \vec v= (3.00 m / s)\hat i + (4.00 m / s) \hat j\)แล้วต้องใช้เวลาเท่าไรวัตถุจึงจะกลับมาที่จุดเริ่มต้น |
| 20. | วัตถุมวล 2.00 kg เคลื่อนที่ด้วยแรงที่กำหนดจาก
\(\rm \vec F= – (8.00 N / m) (x\hat i + y\hat j )\)
โดย \(\rm \hat i\) และ \(\rm \hat j\) เป็นเวกเตอร์หนึ่งหน่วยในแกน x และ y และเริ่มปล่อยวัตถุด้วยความเร็วต้น \(\rm \vec v= (3.00 m / s)\hat i + (4.00 m / s) \hat j\)แล้วระยะไกลสุด จากจุดเริ่มต้นถึงวัตถุเท่ากับข้อใด |
| 21. | วิศวกรกำหนดปริมาตร Vm ของโลหะที่ใช้สร้างถังความดันทรงกลมให้คงที่ค่าหนึ่ง โดยสมมุติว่า ผนังของถังบางมาก และมีแรงดันสูงจนเข้าใกล้จุดระเบิด ถ้าปริมาณแก็สที่บรรจุได้เท่ากับ n (หน่วยโมล) ซึ่งไม่ขึ้นกับรัศมี r ของถัง แต่ขึ้นอยู่กับ Vm (หน่วย m3), อุณหภูมิ T (หน่วย K), ค่าคงที่แก๊สในอุดมคติ R (หน่วย J / (K · mol)) และความทนแรงดึงของโลหะ σ (หน่วย N / m2) ค่า n ในเทอมของตัวแปรดังกล่าวเท่ากับข้อใด |
| A | \(\rm n=\dfrac{2}{3}\dfrac{V_mσ}{RT}\) |
| B | \(\rm n=\dfrac{2}{3}\dfrac{\sqrt[3]{V_mσ}}{RT}\) |
| C | \(\rm n=\dfrac{2}{3}\dfrac{\sqrt[3]{V_mσ^2}}{RT}\) |
| D | \(\rm n=\dfrac{2}{3}\dfrac{\sqrt[3]{V_m^2σ}}{RT}\) |
| E | \(\rm n=\dfrac{2}{3}\sqrt[3]{\dfrac{V_mσ^2}{RT}}\) |
ตอบ (A)
| 22. | กำหนด กราฟของทอร์กที่ออกมาจากเครื่องยนต์เบนซินกับฟังก์ชันความถี่ของการหมุน เครื่องยนต์ไม่สามารถทำงานนอกช่วงของกราฟได้
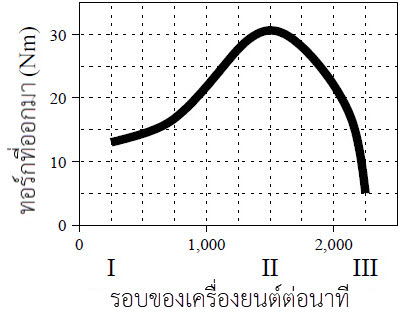 |
| 23. | วัตถุถูกยิงจากพื้นของดาวทรงกลมสม่ำเสมอที่อยู่นิ่ง ด้วยมุมหนึ่งเทียบกับแนวตั้ง ถ้าวัตถุเคลื่อนที่โดยไม่สนแรงต้านอากาศ และตกกลับในที่สุด โดยนักบินอวกาศชายอธิบายว่าวัตถุจะเคลื่อนที่แบบพาราโบลา ตามกฎการเคลื่อนแบบโพรเจกไทล์ ส่วนนักบินอวกาศหญิงจำกฎของเคปเลอร์ได้ว่า ทุกวงโคจรที่อยู่รอบดาวจะเป็นวงรี (หรือวงกลม) และแรงโน้มถ่วงของทรงกลมสม่ำเสมอจะมีค่าเสมือนกับว่ามวลทั้งหมดรวมกันเป็นจุดมวลที่ศูนย์กลางจุดเดียว แล้วข้อใดอธิบายความแตกต่างของคำอธิบายทั้งสองได้ดีที่สุด |
| A | เนื่องจากการทดลองเกิดใกล้กับผิวของทรงกลม จึงไม่ควรแทนทรงกลมด้วยจุดมวล |
| B | เนื่องจากวัตถุตกกลับมา แสดงว่าวัตถุไม่ได้อยู่ในวงโคจรของดาวนั้น ดังนั้นเส้นทางการเคลื่อนที่อาจจะไม่ใช่วงรี |
| C | นักบินอวกาศหญิง มองข้ามเรื่องการเคลื่อนที่รอบจุดมวล ที่อาจจะเป็นพาราโบลาหรือไฮเพอร์โบลาก็ได้ |
| D | กฎของเคปเลอร์ ใช้กับวงโคจรที่มีขนาดใหญ่เท่านั้น |
| E | วัตถุเคลื่อนที่เป็นวงรี แต่เกือบจะเป็นพาราโบลา เพราะระยะที่ยิงขึ้นไปสั้นมาก เมื่อเทียบกับระยะห่างจากจุดศูนย์กลางของดาวเคราะห์ |
ตอบ (E)
| 24. | เครื่องเล่นแผ่นเสียง มีวงแหวนเทฟลอน ที่มีรัศมีวงใน R และรัศมีวงนอก R + δ ( δ << R) ดังรูป และการหมุนแผ่นเสียงด้วยอัตราคง จะต้องใส่พลังงานให้มากกว่างานจากแรงเสียดทาน ถ้าผู้ผลิตเครื่องเล่นต้องการลดการใช้พลังงาน โดยไม่เปลี่ยนอัตราการหมุน น้ำหนักของเครื่องเล่นหรือ สัมประสิทธิ์แรงเสียดทานของผิวเทฟลอน วิศวกรจึงเสนอสองทางเลือก คือ การเพิ่มความกว้างของแบริ่ง ( เพิ่ม δ ) หรือเพิ่มรัศมี (เพิ่ม R) ข้อใดสรุปผลที่จะตามมาได้ถูกต้อง
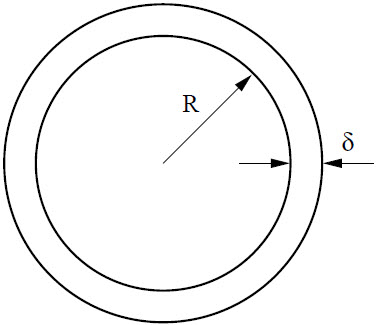 |
| A | การเพิ่ม δ ไม่มีผลต่อกำลังการทำงาน แต่การเพิ่ม R ทำให้กำลังการทำงานเพิ่มขึ้น |
| B | การเพิ่ม δ ไม่มีผลต่อกำลังการทำงาน แต่การเพิ่ม R ทำให้กำลังการทำงานลดลง |
| C | การเพิ่ม δ ทำให้กำลังการทำงานเพิ่มขึ้น แต่การเพิ่ม R ไม่มีผลต่อกำลังการทำงาน |
| D | การเพิ่ม δ ทำให้กำลังการทำงานลดลง แต่การเพิ่ม R ไม่มีผลต่อกำลังการทำงาน |
| E | การเปลี่ยนแปลงทั้งสองไม่มีผลใดๆ ต่อกำลังการทำงาน |
ตอบ (A)
| 25. | ให้ทรงกระบอกกลวงที่มีผนังบางมาก (เช่น แกนกระดาษชำระ) กับบล็อกอันหนึ่ง วางนิ่งอยู่บนระนาบที่มีความชัน θ กับแนวระดับ ถ้าทรงกระบอกกลิ้งลงมาโดยไม่ไถล และบล็อกก็เลื่อนลงมาจากระนาบ มาถึงด้านล่างระนาบพร้อมกัน แล้วค่าสัมประสิทธิ์แรงเสียดทานจลน์ ระหว่างบล็อกกับระนาบเท่ากับข้อใด |
| A | \(0\) |
| B | \(\dfrac{1}{3}\tan\theta\) |
| C | \(\dfrac{1}{2}\tan\theta\) |
| D | \(\dfrac{2}{3}\tan\theta\) |
| E | \(\tan\theta\) |
ตอบ (C)