ข้อสอบคัดเลือกของทีม USA 2012 (25 ข้อ)
| 1. | พิจารณาหยดน้ำจากก๊อกที่อยู่เหนืออ่างล้างจานประมาณ 10 cm ขณะที่หยดหนึ่งแตะอ่าง มีหนึ่งหยดอยู่ในอากาศ และมีอีกหยดรออยู่ปากก๊อก แล้วระยะห่างของหยดน้ำที่อยู่ในอากาศกับหยดที่แตะอ่างเท่ากับข้อใด |
| A | ระหว่าง 0 ถึง 2 cm |
| B | ระหว่าง 2 ถึง 4 cm |
| C | ระหว่าง 4 ถึง 6 cm |
| D | ระหว่าง 6 ถึง 8 cm |
| E | ระหว่าง 8 ถึง 10 cm |
ตอบ (D)
| 2. | กระสุนปืนใหญ่ถูกยิงด้วยความเร็วต้น v0 เหนือระดับพื้นดิน อยากทราบว่า มุมเงยเล็กสุด θmin ที่ทำให้กระสุนมีความสูง H มากกว่าระยะในแนวนอน R ที่วัดจากจุดยิงถึงจุดตกพื้นเท่ากับข้อใด |
| 3. | รูปสามเหลี่ยมด้านเท่า ถูกวางบนพื้นเอียงที่มีแรงเสียดทานสูงเกินกว่าจะลื่นไถลลงมาได้ แต่ถ้าพื้นเอียงมีความชันมากๆ วัตถุจะ "กลิ้ง" (โดยมีจุดยอดเป็นจุดหมุน) ลงมาได้ แล้วมุมเอียงที่วัตถุจะเริ่มกลิ้งลงมาเท่ากับข้อใด |
| A | 30° |
| B | 45° |
| C | 60° |
| D | การกลิ้งเกิดขึ้นได้กับทุกมุมที่มากกว่าศูนย์ |
| E | ถ้าไถลลงมาไม่ได้ ก็ไม่มีทางกลิ้งลงมาได้ |
ตอบ (C)
| 4. | วัตถุที่เดิมหยุดนิ่งระเบิดออกเป็นสามส่วนเท่าๆ กัน โดยไม่คิดแรงภายนอก ถ้าชิ้นส่วนสองชิ้นแตกออกเป็นมุมฉากกับชิ้นอื่น ๆ ด้วยอัตราเร็ว v เท่ากัน แล้วอัตราเร็วของชิ้นที่สามเท่ากับข้อใด |
| 5. | วัตถุ 12 kg เคลื่อนที่ 4 m / s ไปทางทิศตะวันออก พุ่งชนกับวัตถุ 6 kg ที่เคลื่อนที่ 2 m / s ไปทางทิศตะวันตก ถ้าหลังการชนวัตถุเคลื่อนที่ไปด้วยกัน แล้วพลังงานจลน์ที่สูญเสียไปกับการชนกันนี้เท่ากับข้อใด |
| 6. | นำปืนใหญ่สองลำมาเรียงในแนวดิ่ง ให้มีระยะห่าง 200 m และหันปากกระบอกเข้าหากัน เมื่อจุดฉนวนยิง ความเร็วจากปากกระบอกปืนด้านล่างจะเท่ากับ 25 m/s และความเร็วจากปากกระบอกปืนด้านบนจะเท่ากับ 55 m/s
 |
| 7. | นำปืนใหญ่สองลำมาเรียงในแนวดิ่ง ให้มีระยะห่าง 200 m และหันปากกระบอกเข้าหากัน เมื่อจุดฉนวนยิง ความเร็วจากปากกระบอกปืนด้านล่างจะเท่ากับ 25 m/s และความเร็วจากปากกระบอกปืนด้านบนจะเท่ากับ 55 m/s
 |
| 8. | วัตถุมวล m = 3.0 kg เคลื่อนที่ตามแนวนอนไปชนกับสปริงเบา ที่มีค่านิจสปริง k = 80.0 N/m สัมประสิทธิ์ แรงเสียดทานระหว่างวัตถุกับพื้น คือ μk = 0.50 ถ้าวัตถุมีอัตราเร็ว 2.0 m/s เมื่อวัตถุชนกับสปริง แล้วระยะหดของสปริงจะเท่ากับข้อใด |
| 9. | ดาวเคราะห์ทรงกลมสม่ำเสมอรัศมี R มีความเร่งโน้มถ่วงที่ผิวของดาวเท่ากับ g แล้วความเร็วหลุดพ้นของวัตถุจากพื้นผิวดาวเคราะห์จะเท่ากับข้อใด |
| A | \(\rm \dfrac{1}{2}\sqrt{gR}\) |
| B | \(\rm \sqrt{gR}\) |
| C | \(\rm \sqrt{2gR}\) |
| D | \(\rm 2\sqrt{gR}\) |
| E | ไม่สามารถแสดงความเร็วหลุดพ้นของวัตถุ ด้วยเทอมของ g และได้ R |
ตอบ (C)
| 10. | วัตถุสี่ชิ้นถูกวางไว้บนพื้นเอียง จากนั้นปล่อยให้กลิ้งลงมาโดยมีไม่การไถล และไม่คำนึงถึงแรงต้านการหมุน และแรงต้านทานอากาศ • วัตถุ A เป็นลูกบอลทองเหลืองตัน เส้นผ่านศูนย์กลาง d • วัตถุ B เป็นลูกบอลทองเหลืองตัน เส้นผ่าศูนย์กลาง 2d • วัตถุ C เป็นลูกบอลทองเหลืองกลวง เส้นผ่านศูนย์กลาง d • วัตถุ D เป็นลูกบอลอลูมิเนียมตัน เส้นผ่าศูนย์กลาง d (อะลูมิเนียมมีความหนาแน่นน้อยกว่าทองเหลือง) ให้วัตถุถูกวางในลักษณะที่ศูนย์กลางมวลของวัตถุทั้งหมดกลิ้งไปในระยะเดียวกัน และเวลาที่ใช้ในการกลิ้งเป็น T ข้อความใดต่อไปนี้ถูกต้อง |
| A | TB > TC > TA = TD |
| B | TB > TC > TA = TD |
| C | TB > TC > TA = TD |
| D | TC > TA = TB = TD |
| E | TA = TB = TC = TD |
ตอบ (D)
| 11. | จากรูป นาย ก ดึงเชือกที่คล้องผ่านรอกที่ถูกยึดไว้ เพื่อขยับกล่องด้วยอัตราเร็วคงที่ v สัมประสิทธิ์แรงเสียดทานระหว่างกล่องกับพื้นเป็น μ < 1 สมมุติว่า รอกเบามากและไม่มีแรงเสียดทานระหว่างเชือกและรอก ข้อความใดถูกต้องขณะกล่องเคลื่อนที่
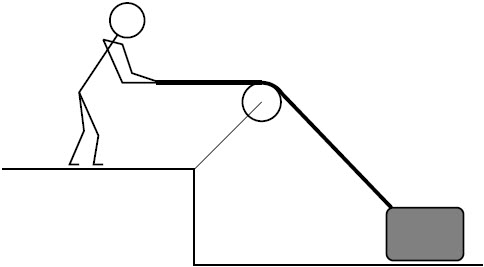 |
| A | แรงบนเส้นเชือกเป็นค่าคงที่ |
| B | แรงเสียดทานระหว่างพื้นกับกล่องจะลดลง |
| C | แรงตั้งฉากของพื้นที่กระทำกับกล่องจะเพิ่มขึ้น |
| D | ความดันกล่องที่พื้นจะเพิ่มขึ้น |
| E | ความดันกล่องที่พื้นเป็นค่าคงที่ |
ตอบ (B)
| 12. | ห่วงโลหะสามารถกลิ้งรอบจุดศูนย์กลางได้ มีเชือกเบาสองเส้นผูกติดไว้ที่จุด A และ B ( ยึดติดไว้โดยที่ A และ B ไม่สามารถเลื่อนได้ ) และปลายเชือกอีกด้านผูกติดกับจุดศูนย์กลาง O นอกจากนี้ยังมีวัตถุหนัก G ถูกผูกไว้ที่จุด O ให้เชือกมีความยาวคงที่ น้ำหนัก G มีเฉพาะเชือกที่รับน้ำหนักไว้ และเดิมเส้นตรง OA อยู่ในแนวนอน
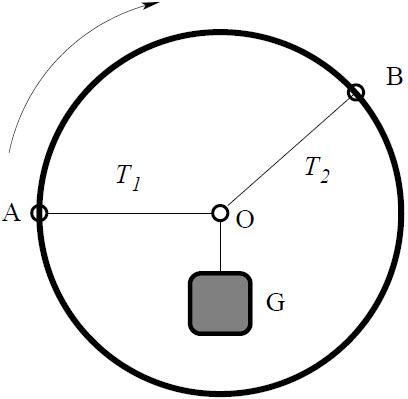 |
| A | T1 จะลดลง |
| B | T1 จะเพิ่มขึ้น |
| C | T2 จะเพิ่มขึ้น |
| D | T2 จะเป็นศูนย์หลังจากหยุดหมุน |
| E | T2 ตอนแรกจะเพิ่มขึ้น จากนั้นจะลดลง |
ตอบ (D)
| 13. | กำหนด กราฟของแรงที่กระทำกับรถเข็นขนาด 40 kg เทียบกับตำแหน่ง x ของรถเข็น ซึ่งเคลื่อนที่ในหนึ่งมิติบนแกน x ถ้าที่ x = 0 รถเข็นมีความเร็ว -3.0 m / s (ในทิศลบ) แล้วข้อใดคืออัตราเร็วสูงสุดของรถเข็น
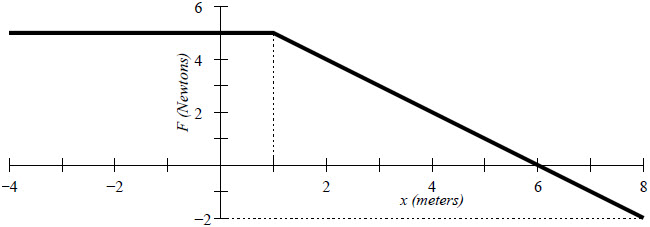 |
| 14. | ทรงกระบอกรัศมี a เดิมหนัก 80 N หลังเจาะรูให้ห่างจากเส้นผ่านศูนย์กลางไป 2a/5 จะมีน้ำหนัก 65 N จุดศูนย์กลางของทรงกระบอกและรูจะสูงเท่ากัน และเส้นผ่านศูนย์กลางจะขนานกัน ดังรูป
 |
| 15. | รถมวล m มีเครื่องยนต์ที่มีกำลังออกมาคงที่ P สมมุติมีแรงเสียดทานเฉพาะล้อกับพื้นเอียง (ไม่มีแรงเสียดทานที่ส่วนอื่นๆ) แล้วอัตราเร็วสูงสุดคงที่ vmax ที่รถคันนี้สามารถขับขึ้นพื้นเอียงทำมุม θ กับแนวนอนได้ เท่ากับข้อใด
 |
| A | \(\rm v_{max} = P/(mg\, sinθ)\) |
| B | \(\rm v_{max} = P^2 sinθ /mg\) |
| C | \(\rm v_{max} = \sqrt{2P/mg}/ sinθ\) |
| D | ไม่มีอัตราเร็วสูงสุดคงที่ |
| E | อัตราเร็วสูงสุดคงที่ขึ้นกับความยาวของพื้นเอียง |
ตอบ (A)
| 16. | รถกระป๋องมีความเร่งในแนวนอนด้วยความเร่ง \(\vec{a}\) ภายในมีกล่องมวล M ต่อกับสปริงสองเส้นที่มีค่านิจสปริง k1 และ k2 ถ้ากล่องสามารถขยับได้โดยไม่มีแรงเสียดทานในแนวนอน แล้วความถี่ในการสั่นของกล่องเท่ากับข้อใด |
| A | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{k_1+k_2}{M}+a}\) |
| B | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{k_1k_2}{(k_1+k_2)M}}\) |
| C | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{k_1k_2}{(k_1+k_2)M}+a}\) |
| D | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{|k_1-k_2|}{M}}\) |
| E | \(\rm \dfrac{1}{2\pi}\sqrt{\dfrac{|k_1+k_2|}{M}}\) |
ตอบ (E)
| 17. | กำหนกกราฟ log / log จากแอมพลิจูดและคาบของการสั่นที่ไม่เป็นเชิงเส้น ดังรูป
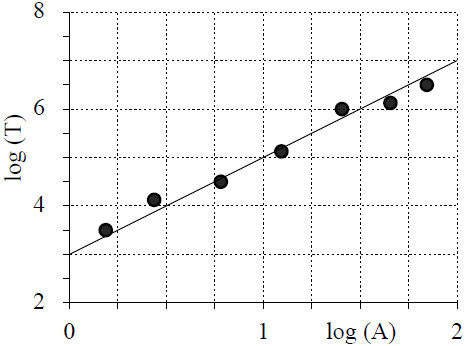 |
| A | \(\rm T = 1000A^2\) |
| B | \(\rm T = 100A^3\) |
| C | \(\rm T = 2A+3\) |
| D | \(\rm T = 3\sqrt A\) |
| E | คาบเป็นอิสระกับแอมพลิจูดในระบบการสั่น |
ตอบ (A)
| 18. | มวลแขวนอยู่บนเพดานภายในกล่องด้วยสปริงในอุดมคติ เดิมให้กล่องอยู่นิ่ง ส่วนมวลจะมีความเร็วเริ่มต้น และมีการสั่นเฉพาะในแนวตั้ง เมื่อมวลทิ้งตัวถึงจุดต่ำสุด กล่องจะถูกปล่อยให้ร่วงลงมา หากพิจารณาเฉพาะภายในกล่อง ปริมาณใดต่อไปนี้จะไม่เปลี่ยนแปลง ขณะกล่องร่วงลง โดยไม่สนแรงต้านอากาศ |
| A | แอมพลิจูดของการสั่น |
| B | คาบของการสั่น |
| C | อัตราเร็วสูงสุดของมวล |
| D | ความสูงขณะที่มวลมีอัตราเร็วสูงสุด |
| E | ตำแหน่งที่สูงที่สุดของมวล |
ตอบ ไม่มีข้อใดถูก
เพราะ ทุกตัวเลือกจะมีการเปลี่ยนแปลงเมื่อปล่อยกล่องลงมา
เพราะ ทุกตัวเลือกจะมีการเปลี่ยนแปลงเมื่อปล่อยกล่องลงมา
| 19. | ใช้มอเตอร์ 1,500 วัตต์ สูบน้ำจากความสูงแนวตั้ง 2.0 เมตร จากชั้นใต้ดินที่มีน้ำท่วมอยู่ ผ่านท่อทรงกระบอก ถ้าน้ำไหลออกจากปากท่อด้วยอัตราเร็ว 2.5 m / s โดยไม่มีแรงเสียดทาน และสมมุติว่าพลังงานทั้งหมดของมอเตอร์ใช้ไปกับการสูบน้ำ แล้วรัศมีของท่อน้ำควรเท่ากับข้อใด ให้ความหนาแน่นของน้ำเป็น ρ = 1000 /m3 |
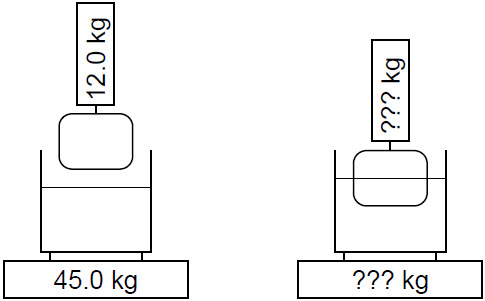
| 20. | ภาชนะบรรจุน้ำถูกวางบนเครื่องชั่ง อ่านน้ำหนักได้ M1 = 45 kg และบล็อกไม้ถูกแขวนบนเครื่องชั่งที่สอง อ่านน้ำหนักได้ M2 = 12 kg ถ้าไม้มีความหนาแน่น 0.60 g/cm3 และน้ำมีความหนาแน่น 1.00 g/cm3 เมื่อหย่อนบล็อกไม้ครึ่งหนึ่งลงไปในน้ำ แล้วน้ำหนักที่อ่านได้จากเครื่องชั่งจะเท่ากับข้อใด
 |
| A | M1 = 45 kg และ M2 = 2 kg |
| B | M1 = 45 kg และ M2 = 6 kg |
| C | M1 = 45 kg และ M2 = 10 kg |
| D | M1 = 55 kg และ M2 = 6 kg |
| E | M1 = 55 kg และ M2 = 2 kg |
ตอบ (E)
| 21. | กำหนดระบบสปริงหนึ่งประกอบด้วย แท่นหนัก 10 N อยู่ด้านบนของสปริงสองอัน ซึ่งมีค่านิจสปริง 75 N/m ทั้งสองอัน และด้านบนแท่นมีสปริงที่สามที่มีค่านิจสปริง 75 N/m ถ้าวางลูกบอลหนัก 5.0 N บนสปริงที่สามจนน้ำหนักค่อย ๆ กดสปริงทั้งระบบลง แล้วระยะที่ลูกบอลกดลงมาจะเท่ากับข้อใด
 |
| 22. | เสียงที่เบาที่สุดที่เราได้ยินจะมีความเข้มเสียง I0 = 10–12 W/m2 ถ้าเปลี่ยนเป็นหน่วยพื้นฐานกิโลกรัม, เมตร และวินาที จะมีค่าเท่ากับข้อใด |
| A | I0= 10–12 kg/s3 |
| B | I0= 10–12 kg/s |
| C | I0= 10–12 kg2m/s |
| D | I0= 10–12 kg2m/s2 |
| E | I0= 10–12 kg/m·s3 |
ตอบ (A)
| 23. | เครื่องมือวัดในข้อใด ไม่สามารถ วัดความเร่งโน้มถ่วง (g) ได้ |
| A | เครื่องชั่งสปริง (อ่านค่าในหน่วยแรง) และวัตถุที่ทราบมวล |
| B | คานที่ทราบความยาว, แต่ไม่ทราบมวล และนาฬิกาจับเวลา |
| C | พื้นเอียงที่ทราบความชัน, รถจำลองหลายขนาดๆ ที่ทราบมวล และนาฬิกาจับเวลา |
| D | ปืนที่ยิงแบบโพรเจกไทล์ที่ทราบอัตราเร็ว, กระสุนที่ทราบมวล และไม้บรรทัด |
| E | มอเตอร์ที่ทราบกำลังที่ออกมา, วัตถุที่ทราบมวล, เส้นเชือกที่ทราบความยาว และนาฬิกาจับเวลา |
ตอบ (C)
| 24. | วัตถุมวล m สามชิ้น นำมาติดกันด้วยสปริงแบบเดียวกัน เมื่อวางบนพื้นราบจะเห็นเป็นรูปสามเหลี่ยมที่มีความยาวด้าน l เมื่อหมุนวัตถุรูปสามเหลี่ยมรอบ ๆ จุดศูนย์กลางด้วยความเร็วเชิงมุม ω วัตถุรูปสามเหลี่ยมจะมีความยาวด้านใหม่เป็น 2l แล้วค่านิจสปริง k เท่ากับข้อใด |
| A | \(\rm 2m\omega^2\) |
| B | \(\rm \dfrac{2}{\sqrt3}m\omega^2\) |
| C | \(\rm \dfrac{2}{3}m\omega^2\) |
| D | \(\rm \dfrac{1}{\sqrt3}m\omega^2\) |
| E | \(\rm \dfrac{1}{3}m\omega^2\) |
ตอบ (C)
| 25. | พิจารณาสองวงโคจรรอบดวงอาทิตย์ที่แสดงดังรูป วงโคจร P เป็นวงกลมมีรัศมี R วงโคจร Q เป็นวงรี มีจุดยอดไกลสุด b อยู่ระหว่าง 2R และ 3R และจุดยอดใกล้สุด a อยู่ระหว่าง R/3 และ R/2 ถ้าความเร็วในวงโคจร P เป็น vc ความเร็วในวงโคจร Q ที่จุด a เป็น va และที่จุด b เป็น vb แล้วข้อใดต่อไปนี้ถูกต้อง
 |
| A | vb > vc > 2va |
| B | 2vc > vb > va |
| C | 10vb > va > vc |
| D | vc > va > 4vb |
| E | 2va > \(\sqrt2\)vb > vc |
ตอบ (C)

