ข้อสอบคัดเลือกของทีม USA 2013 (25 ข้อ)
| 1. | ผู้สังเกตยืนอยู่ด้านข้างของด้านหน้าขบวนรถไฟที่จอดอยู่ เมื่อรถไฟเริ่มวิ่งด้วยความเร่งคงที่ โบกี้แรกจะผ่านผู้สังเกตไปโดยใช้เวลา 5 วินาที ต้องใช้เวลาเท่าไร โบกี้ที่ 10 (คิดเฉพาะโบกี้นี้) ถึงจะผ่านผู้สังเกตไป |
| A | 1.07 s |
| B | 0.98 s |
| C | 0.91 s |
| D | 0.86 s |
| E | 0.81 s |
ตอบ (E)
จากสูตร
และ t1 เริ่มขณะโบกี้แรกวิ่งผ่านผู้สังเกตไป จะได้ \({\rm{L = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{at}}_{\rm{1}}^{\rm{2}}\)
สมมุติให้ หนึ่งโบกี้ยาว L และ t2 เริ่มขณะโบกี้ที่ 10 วิ่งมาถึงผู้สังเกต จะได้
ดังนั้น \({{\rm{t}}_{\rm{2}}}{\rm{ = }}\sqrt {{\rm{9}} \cdot {\rm{25}}{{\rm{s}}^{\rm{2}}}} {\rm{ = 15 ~s}}\) และ \({{\rm{t}}_{\rm{3}}}{\rm{ = }}\sqrt {{\rm{10}} \cdot {\rm{25}}{{\rm{s}}^{\rm{2}}}} {\rm{ = 15}}{\rm{.81 ~s}}\)
ดังนั้น โบกี้ที่ 10 ใช้เวลา 15 – 15.81 = 0.81 s ในการผ่านผู้สังเกตไป
จากสูตร
\(\Delta {\rm{x = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{a}}{{\rm{t}}^{\rm{2}}}{\rm{ + }}{{\rm{v}}_{\rm{i}}}{\rm{t}}\)
โดย t0 = 0 คือ เวลาที่รถไฟเริ่มเคลื่อนที่ และรถไฟโบกี้แรกยังอยู่แนวเดียวกับผู้สังเกตและ t1 เริ่มขณะโบกี้แรกวิ่งผ่านผู้สังเกตไป จะได้ \({\rm{L = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{at}}_{\rm{1}}^{\rm{2}}\)
สมมุติให้ หนึ่งโบกี้ยาว L และ t2 เริ่มขณะโบกี้ที่ 10 วิ่งมาถึงผู้สังเกต จะได้
\({\rm{9L = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{at}}_{\rm{2}}^{\rm{2}}\)
สุดท้าย t3 คือ เวลาที่โบกี้ที่ 10 วิ่งผ่านไป
\({\rm{10L = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{at}}_{\rm{3}}^{\rm{2}}\)
จากสมการ t1 จะได้ \({\rm{2L/a = 25}}{{\rm{s}}^{\rm{2}}}\)
| 2. | ก ยืนห่างจากกำแพง 20 m และ ข ยืนห่างจากกำแพงเดียวกัน 10 m ถ้า ก โยนลูกบอลทำมุมเงย 30◦ และชนแบบยืดหยุ่นกับกำแพง แล้ว ก ต้องโยนลูกบอลด้วยความเร็วเท่าไร ลูกบอลจึงจะตกที่ ข พอดี ให้ ก และ ข ให้มีความสูงเท่ากัน และทั้งคู่อยู่ในแนวตั้งฉากเดียวกันกับกำแพง |
| A | 11 m/s |
| B | 15 m/s |
| C | 19 m/s |
| D | 30 m/s |
| E | 35 m/s |
ตอบ (C)
กำแพงในข้อนี้เปรียบเสหมือนกระจกเงาที่สะท้อนการชนของลูกบอลแบบยืดหยุ่นสมบูรณ์ และระยะทางที่ต้องเคลื่อนที่จาก ก ถึง ข เท่ากับ 30 เมตร จากสูตรระยะทางจะได้
กำแพงในข้อนี้เปรียบเสหมือนกระจกเงาที่สะท้อนการชนของลูกบอลแบบยืดหยุ่นสมบูรณ์ และระยะทางที่ต้องเคลื่อนที่จาก ก ถึง ข เท่ากับ 30 เมตร จากสูตรระยะทางจะได้
\({\rm{R = }}\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{g}}}{\rm{sin2\theta }}\)
เราจะได้
\({{\rm{v}}^{\rm{2}}}{\rm{ = }}\dfrac{{{\rm{gR}}}}{{{\rm{sin 2\theta }}}} \approx \dfrac{{{\rm{300 }}{{\rm{m}}^{\rm{2}}}{\rm{/}}{{\rm{s}}^{\rm{2}}}}}{{\sqrt {\rm{3}} {\rm{/2}}}}\)
ดังนั้น v มีค่าประมาณ 19 m/s| 3. | ก โยนบอลให้ ข ที่อยู่ห่างออกไป l และ ก สามารถกำหนดเวลา t ที่บอลจะลอยไป จากอัตราเร็วที่ใช้ ซึ่งเขาจะใช้อัตราเร็วเท่าไรก็ได้จนถึง vmax และเลือกมุมที่ใช้ในการโยนเท่าไรก็ได้ ในช่วง 0◦ ถึง 90◦ ถ้าไม่คำนึงถึงแรงต้านอากาศ และถือว่า ก และ ข ความสูงเท่ากัน แล้วข้อความใดต่อไปนี้ผิด |
| A | ถ้า vmax < \(\sqrt{\text{g}l} \) แล้วบอลจะไม่สามารถไปถึง ข ได้ |
| B | กรณีที่บอลไปถึง ข ถ้า vmax เพิ่มขึ้น (ขณะที่ l คงตัว) แล้วค่าต่ำสุดของ t ต้องลดลง |
| C | กรณีที่บอลไปถึง ข ถ้า vmax เพิ่มขึ้น (ขณะที่ l คงตัว) แล้วค่าสูงสุดของ t ต้องเพิ่มขึ้น |
| D | กรณีที่บอลไปถึง ข ถ้า l เพิ่มขึ้น (ขณะที่ vmax คงตัว) แล้วค่าต่ำสุดของ t ต้องเพิ่มขึ้น |
| E | กรณีที่บอลไปถึง ข ถ้า l เพิ่มขึ้น (ขณะที่ vmax คงตัว) แล้วค่าสูงสุดของ t ต้องเพิ่มขึ้น |
ตอบ (A)
ข้อ (A) เป็นไปตามค่ามากสุดของการเคลื่อนที่แบบโพรเจกไทล์
สำหรับใครที่ต้องการคิดเลข จะลองคำนวณหาผลลัพธ์ดูก็ได้ กำหนดให้ θ เป็นมุมที่โยนออกไป และ v0 เป็นอัตราเร็วต้น จะได้
ข้อ (A) เป็นไปตามค่ามากสุดของการเคลื่อนที่แบบโพรเจกไทล์
สำหรับใครที่ต้องการคิดเลข จะลองคำนวณหาผลลัพธ์ดูก็ได้ กำหนดให้ θ เป็นมุมที่โยนออกไป และ v0 เป็นอัตราเร็วต้น จะได้
\(\begin{array}{l} 2{{\rm{v}}_0}\sin {\rm{\theta }} = {\rm{gt}}\\ {\rm{(}}{{\rm{v}}_0}\cos{\rm{\theta )t}} = l \end{array}\)
จาก sin2 θ + cos2 θ = 1
\(\begin{align*} {{\rm{v}}_{\rm{0}}}^{\rm{2}} &={\left( {\frac{{{\rm{gt}}}}{{\rm{2}}}} \right)^2}{\rm{ + }}{\left( {\frac{l}{{\rm{t}}}} \right)^2}\\ \frac{{{{\rm{g}}^2}}}{{\rm{4}}}{{\rm{t}}^4} - {{\rm{v}}_{\rm{0}}}^{\rm{2}}{{\rm{t}}^2} + {l^2} &= 0\\ {{\rm{t}}^2} &= 2\frac{{{{\rm{v}}_{\rm{0}}}^{\rm{2}} \pm \sqrt {{{\rm{v}}_{\rm{0}}}^{\rm{4}} - {{\rm{g}}^2}{l^2}} }}{{{{\rm{g}}^2}}} \end{align*}\)
จากผลลัพธ์สังเกตว่า การเพิ่ม l จะส่งผลต่อเวลาในการเคลื่อนที่ทั้งสองทิศทาง และการเพิ่ม vmax ก็จะทำให้เวลามากสุดที่ลอยอยู่ในอากาศมากขึ้นเช่นกัน สำหรับเวลาน้อยสุดที่บอลจะลอยไป จะหาจาก
\(\begin{align*} {\rm{t}}{{\rm{\_}}^2} &= 2\frac{{{{\rm{v}}_{\rm{0}}}^{\rm{2}} - \sqrt {{{\rm{v}}_{\rm{0}}}^{\rm{4}} - {{\rm{g}}^2}{l^2}} }}{{{{\rm{g}}^2}}}\\ \frac{{\partial ({\rm{t}}{{\rm{\_}}^2})}}{{\partial ({{\rm{v}}_{\rm{0}}}^2)}} &= \frac{2}{{{{\rm{g}}^2}}}\left( {1 - \frac{{2{{\rm{v}}_{\rm{0}}}^{\rm{2}}}}{{2\sqrt {{{\rm{v}}_{\rm{0}}}^{\rm{4}} - {{\rm{g}}^2}{l^2}} }}} \right)\\ \frac{{\partial ({\rm{t}}{{\rm{\_}}^2})}}{{\partial ({{\rm{v}}_{\rm{0}}}^2)}} &= \frac{2}{{{{\rm{g}}^2}}}\left( {1 - \frac{1}{{\sqrt {{\rm{1}} - \frac{{{{\rm{g}}^2}{l^2}}}{{{{\rm{v}}_{\rm{0}}}^{\rm{4}}}}} }}} \right) \end{align*}\)
สังเกตว่า ขวามือเป็นลบเสมอ ดังนั้น t_ จะมีค่าน้อยสุด เมื่อเราเลือก v0 มากสุด| 4. | ให้ขาตั้งสองขายึดกันด้วยบานพับที่ไม่มีแรงเสียดทาน และสัมประสิทธิ์แรงเสียดทาน ระหว่างพื้นกับขาตั้งเท่ากับ μ แล้วค่า θ สูงสุดในข้อใด ที่ทำให้ขาตั้งไม่ยุบลง
 |
| A | sinθ = 2μ |
| B | sinθ/2 = μ/2 |
| C | tanθ/2 = μ |
| D | tanθ = 2μ |
| E | tanθ/2 = 2μ |
ตอบ (E)
เนื่องจากแต่ละขาต้องสร้างสมดุลของแรงเสียดทานจากแรงในแนวนอนของขาอีกข้าง ผ่านจุดยอดของขาตั้งพิจารณาที่ทอร์กสมดุล
ส่วนแรงตั้งฉากที่กระทำกับขาตั้งจะมีค่าเท่ากับน้ำหนักของขาตั้ง ดังนั้น
เนื่องจากแต่ละขาต้องสร้างสมดุลของแรงเสียดทานจากแรงในแนวนอนของขาอีกข้าง ผ่านจุดยอดของขาตั้งพิจารณาที่ทอร์กสมดุล
\(\dfrac{{\rm{L}}}{{\rm{2}}}\left( {{\rm{M / 2}}} \right){\rm{ g sin \alpha = LF}}{{\rm{}}_{\rm{f}}}{\rm{cos \alpha }}\)
โดย Ff คือ แรงเสียดทานบนขาแต่ละข้าง และ \({\rm{ \alpha = }}\dfrac{1}{2}\theta\)ส่วนแรงตั้งฉากที่กระทำกับขาตั้งจะมีค่าเท่ากับน้ำหนักของขาตั้ง ดังนั้น
\({{\rm{F}}_{\rm{N}}}{\rm{ = (M/2)g}}\)
จับเทียบจะได้
\({{\rm{F}}_{\rm{N}}}{\rm{ = (M/2)g}}\)
หรือ
\(\dfrac{{\rm{L}}}{{\rm{2}}}\left( {{\rm{M / 2}}} \right){\rm{ g sin \alpha = L}}\mu \left( {{\rm{M / 2}}} \right){\rm{g cos \alpha }}\)
ดังนั้น tan θ / 2 = 2μ | 5. | นักเรียนก้าวเข้าไปในลิฟต์และขึ้นไปอยู่บนเครื่องชั่ง เมื่อลิฟต์เคลื่อนที่จากชั้นบนสุด ไปชั้นล่างสุดของอาคาร นักเรียนได้บันทึกน้ำหนักตามเวลาที่เปลี่ยนไป ดังนี้
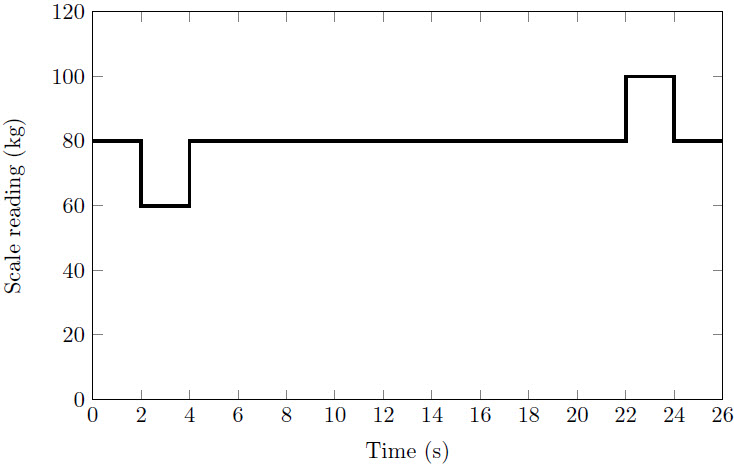 |
| A | ช่วงวินาทีที่ 2 ถึง 4 |
| B | ที่วินาทีที่ 4 |
| C | ช่วงวินาทีที่ 4 ถึง 22 |
| D | ที่วินาทีที่ 22 |
| E | ช่วงวินาทีที่ 22 ถึง 24 |
ตอบ (C)
ค่าที่อ่านจากเครื่องชั่งจะไม่ใช่น่ำหนักแท้จริงของนักเรียน แต่เป็นแรงตั้งฉาก FN ที่กระทำกับขาที่เหยียบเครื่องชั่ง ซึ่งเป็นไปตามค่า g ดังนี้
โดยแรงตั้งฉากจะมีทิศชี้ขึ้นไปยังนักเรียน ส่วนแรงดึงดูด mg จะมีทิศลงเสมอ ดังนั้น ความเร่งของนักเรียนขณะเคลื่อนที่ลงจะเท่ากับ
เมื่อรวมสมการและจัดรูปใหม่จะได้
เนื่องจากลิฟท์เริ่มจากหยุดนิ่ง ดังนั้น ความเร็วต้นของนักเรียนจะต้องเป็นศูนย์ แสดงว่า มวลของนักเรียนต้องเป็น 80 kg จากกราฟจะเห็นว่ามีสองคาบที่มีความเร่งสม่ำเสมอ โดยจุดแรกที่เกิดการลดลงจะมีความเร่งเท่ากับ
ดังนั้น ความเร็วในการเคลื่อนที่ลงสูงสุดจะเกิดขึ้นในช่วงที่มีความเร่งสม่ำเสมอ ในข้อนี้จะเกิดขึ้นในช่วงวินาทีที่ 4 ถึง 22
ค่าที่อ่านจากเครื่องชั่งจะไม่ใช่น่ำหนักแท้จริงของนักเรียน แต่เป็นแรงตั้งฉาก FN ที่กระทำกับขาที่เหยียบเครื่องชั่ง ซึ่งเป็นไปตามค่า g ดังนี้
\(\rm m_{scale} g = F_N\)
โดยแรงตั้งฉากจะมีทิศชี้ขึ้นไปยังนักเรียน ส่วนแรงดึงดูด mg จะมีทิศลงเสมอ ดังนั้น ความเร่งของนักเรียนขณะเคลื่อนที่ลงจะเท่ากับ
\(\rm ma = mg – F_N\)
เมื่อรวมสมการและจัดรูปใหม่จะได้
\({\rm{a = g}}\left( {1 - \dfrac{{{{\rm{m}}_{{\rm{scale}}}}}}{{\rm{m}}}} \right)\)
เนื่องจากลิฟท์เริ่มจากหยุดนิ่ง ดังนั้น ความเร็วต้นของนักเรียนจะต้องเป็นศูนย์ แสดงว่า มวลของนักเรียนต้องเป็น 80 kg จากกราฟจะเห็นว่ามีสองคาบที่มีความเร่งสม่ำเสมอ โดยจุดแรกที่เกิดการลดลงจะมีความเร่งเท่ากับ
\({\rm{a = }}\left( {10~{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {1 - \dfrac{{{\rm{60 ~kg }}}}{{{\rm{80 ~kg}}}}} \right) = 2.5~{\rm{ m/}}{{\rm{s}}^2}\)
และในจุดที่สองที่มีการเพิ่มขึ้นก็จะมีขนาดเท่ากันดังนั้น ความเร็วในการเคลื่อนที่ลงสูงสุดจะเกิดขึ้นในช่วงที่มีความเร่งสม่ำเสมอ ในข้อนี้จะเกิดขึ้นในช่วงวินาทีที่ 4 ถึง 22
| 6. | นักเรียนก้าวเข้าไปในลิฟต์และขึ้นไปอยู่บนเครื่องชั่ง เมื่อลิฟต์เคลื่อนที่จากชั้นบนสุด ไปชั้นล่างสุดของอาคาร นักเรียนได้บันทึกน้ำหนักตามเวลาที่เปลี่ยนไป ดังนี้
 |
| A | 50 m |
| B | 80 m |
| C | 100 m |
| D | 150 m |
| E | 400 m |
ตอบ (C)
จากกราฟจะเห็นว่ามีสองคาบที่มีความเร่งสม่ำเสมอ โดยจุดแรกที่เกิดการลดลงจะมีความเร่งเท่ากับ
ความเร็วในการเคลื่อนที่ลงสูงสุดจะเกิดขึ้นในช่วงที่มีความเร่งสม่ำเสมอ ในข้อนี้จะเกิดขึ้นในช่วงวินาทีที่ 4 ถึง 22
ส่วนเวลาที่ใช้เร่งความเร็วจะเกิดขึ้นใน 2 วินาทีแรก ดังนั้น ความเร็วของลิฟท์หลังเร่งความเร็วจะเท่ากับ 5 m/s และคาบในช่วงที่มีความเร่งจะมีค่าประมาณ 20 s และเคลื่อนที่ไปได้ประมาณ 100 m
จากการคำนวณก็ทำให้ได้คำตอบที่ชัดเจนอยู่แล้ว หรือเราจะพิจารณากราฟของความเร็วกับเวลาก็ได้ โดยระยะทางที่เคลื่อนที่ไปได้เท่ากับพื้นที่ใต้กราฟ ซึ่งมีค่าเท่ากับ 100 m
โดยระยะทางที่เคลื่อนที่ไปได้เท่ากับพื้นที่ใต้กราฟ ซึ่งมีค่าเท่ากับ 100 m
จากกราฟจะเห็นว่ามีสองคาบที่มีความเร่งสม่ำเสมอ โดยจุดแรกที่เกิดการลดลงจะมีความเร่งเท่ากับ
\({\rm{a = }}\left( {10~{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {1 - \dfrac{{{\rm{60~ kg }}}}{{{\rm{80~ kg}}}}} \right) = 2.5~{\rm{ m/}}{{\rm{s}}^2}\)
และในจุดที่สองที่มีการเพิ่มขึ้นก็จะมีขนาดเท่ากันความเร็วในการเคลื่อนที่ลงสูงสุดจะเกิดขึ้นในช่วงที่มีความเร่งสม่ำเสมอ ในข้อนี้จะเกิดขึ้นในช่วงวินาทีที่ 4 ถึง 22
ส่วนเวลาที่ใช้เร่งความเร็วจะเกิดขึ้นใน 2 วินาทีแรก ดังนั้น ความเร็วของลิฟท์หลังเร่งความเร็วจะเท่ากับ 5 m/s และคาบในช่วงที่มีความเร่งจะมีค่าประมาณ 20 s และเคลื่อนที่ไปได้ประมาณ 100 m
จากการคำนวณก็ทำให้ได้คำตอบที่ชัดเจนอยู่แล้ว หรือเราจะพิจารณากราฟของความเร็วกับเวลาก็ได้

| 7. | ให้รถยนต์และรถบรรทุกมีโมเมนตัมเดียวกัน รถบรรทุกมีน้ำหนักเป็นสิบเท่าของรถยนต์ ข้อใดเปรียบเทียบพลังงานจลน์ของรถทั้งสองคันได้ถูกต้อง |
| A | พลังงานจลน์ของรถบรรทุก มีค่ามากกว่า 100 เท่า |
| B | พลังงานจลน์ของรถบรรทุก มีค่ามากกว่า 10 เท่า |
| C | พลังงานจลน์ของรถทั้งคัน มีค่าเท่ากัน |
| D | พลังงานจลน์ของรถยนต์ มีค่ามากกว่า 10 เท่า |
| E | พลังงานจลน์ของรถยนต์ มีค่ามากกว่า 100 เท่า |
ตอบ (D)
เขียนพลังจลน์ในเทอมของโมเมนตัมจะได้
เขียนพลังจลน์ในเทอมของโมเมนตัมจะได้
\({\rm{K = }}\dfrac{{{{\rm{p}}^{\rm{2}}}}}{{{\rm{2m}}}}\)
ดังนั้น อัตราส่วนจะอยู่ในรูป
\(\dfrac{{{{\rm{K}}_1}}}{{{{\rm{K}}_2}}}{\rm{ = }}\dfrac{{{{\rm{m}}_2}}}{{{{\rm{m}}_1}}}\)
จากโจทย์จึงสรุปว่า พลังงานจลน์ของรถยนต์ มีค่ามากกว่า 10 เท่า| 8. | รถบรรทุกมีความเร็วเริ่มต้น v คนขับได้เบรกจนกระทั่งรถหยุด โดยเบรกกระทำกับรถด้วยแรงคงที่ F ระยะทางที่รถบรรทุกเคลื่อนที่ไปจนกระทั่งหยุดคือ x และเวลาที่ใช้ในการหยุดรถคือ t แล้วข้อใดแสดงพลังงานจลน์เริ่มต้นของรถบรรทุกได้ถูกต้อง (พลังงานจลน์ก่อนคนขับเบรก) |
| A | Fx |
| B | Fvt |
| C | Fxt |
| D | Ft |
| E | ถูกทั้งข้อ (A) และ (B) |
ตอบ (A)
ข้อนี้พิจารณาเฉพาะขนาด สังเกตว่า
ข้อนี้พิจารณาเฉพาะขนาด สังเกตว่า
\({{\rm{K}}_{\rm{i}}}{\rm{ = }}\delta {\rm{K = W = Fx}}\)
| 9. | รถบรรทุกมีความเร็วเริ่มต้น v คนขับได้เบรกจนกระทั่งรถหยุด โดยเบรกกระทำกับรถด้วยแรงคงที่ F ระยะทางที่รถบรรทุกเคลื่อนที่ไปจนกระทั่งหยุดคือ x และเวลาที่ใช้ในการหยุดรถคือ t แล้วข้อใดต่อไปนี้แสดงโมเมนตัมเริ่มต้นของรถบรรทุกได้ถูกต้อง (โมเมนตัมก่อนคนขับรถเบรก) |
| A | Fx |
| B | Ft/2 |
| C | Fxt |
| D | 2Ft |
| E | 2Fx/v |
ตอบ (E)
พิจารณาเฉพาะขนาด จะได้
พิจารณาเฉพาะขนาด จะได้
\({{\rm{p}}_{\rm{i}}}{\rm{ = }}\Delta {\rm{p = Ft}}\)
แต่
\(\displaystyle {\rm{x = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{a}}{{\rm{t}}^{\rm{2}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{(at)t = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{vt}}\)
ดังนั้น pi = 2Fx/v| 10. | ข้อใดคือวิธีแยกบอลกลมตัน กับบอลกลมกลวง ที่มีรัศมีและมวลเท่ากัน ได้ดีที่สุด |
| A | ดูจากการโคจรของมวลทดสอบบอลนั้น |
| B | ดูจากเวลาที่วัตถุกลิ้งลงมาจากพื้นเอียง |
| C | ดูจากแรงไทดัลที่กระทำกับวัตถุในของเหลว |
| D | ดูจากลักษณะการลอยตัวของวัตถุในน้ำ |
| E | ดูจากแรงที่กระทำกับวัตถุในสนามโน้มถ่วงที่สม่ำเสมอ |
ตอบ (B)
ข้อ (B) เป็นวิธีที่เหมาะสมที่สุด เพราะบอลตันจะมีโมเมนต์ความเฉื่อยน้อยกว่าบอลกลมกลวง ทำให้มีความเร่งตอนลงมาจากพื้นเอียงเร็วกว่า
สำหรับข้อ (A) และ (C) เป็นการตรวจสนามโน้มถ่วงนอกวัตถุ สำหรับวัตถุที่เป็นทรงกลม ผลลัพธ์ที่ได้จะขึ้นกับมวลเท่านั้น ส่วนข้อ (E) ค่าที่ได้ขึ้นกับมวลรวมของวัตถุเท่านั้น และข้อ (D) ค่าที่ได้จะขึ้นอยู่กับรูปทรงภายนอกของวัตถุ
ข้อ (B) เป็นวิธีที่เหมาะสมที่สุด เพราะบอลตันจะมีโมเมนต์ความเฉื่อยน้อยกว่าบอลกลมกลวง ทำให้มีความเร่งตอนลงมาจากพื้นเอียงเร็วกว่า
สำหรับข้อ (A) และ (C) เป็นการตรวจสนามโน้มถ่วงนอกวัตถุ สำหรับวัตถุที่เป็นทรงกลม ผลลัพธ์ที่ได้จะขึ้นกับมวลเท่านั้น ส่วนข้อ (E) ค่าที่ได้ขึ้นกับมวลรวมของวัตถุเท่านั้น และข้อ (D) ค่าที่ได้จะขึ้นอยู่กับรูปทรงภายนอกของวัตถุ
| 11. | บล็อกไม้รูปสามเหลี่ยมมุมฉากมวล M วางอยู่บนโต๊ะ ดังรูป มีลูกบาศก์ไม้ขนาดเล็ก มวล m สองอัน วางในแต่ละด้านของด้านประกอบมุมฉาก ให้พื้นผิวสัมผัสระหว่างลูกบาศก์และบล็อกไม้ไม่มีแรงเสียดทาน และในขณะที่ลูกบาศก์เล็กเลื่อนลงมา บล็อกไม้สามเหลี่ยมจะยังคงอยู่ที่เดิม แล้วแรงในแนวตั้งฉากกับผิวสัมผัส (Normal Force) ของระบบกับโต๊ะเท่ากับข้อใด
 |
| A | 2mg |
| B | 2mg + Mg |
| C | mg + Mg |
| D | Mg + mg(sinα + sinβ) |
| E | Mg + mg(cosα + cosβ) |
ตอบ (C)
จากโจทย์ มีสองแรงที่กระทำลูกบาศก์แต่ละอัน คือ แรงตั้งฉากจากบล็อกไม้รูปสามเหลี่ยม และแรงโน้มถ่วง โดยแรงตั้งฉากจะต้องสมดุลกับแรงโน้มถ่วง พิจารณาที่ลูกบาศก์ซ้าย จะได้
จึงได้แรงทั้งหมดเท่ากับ
ดังนั้น Ftot = mg + Mg
สังเกตว่า แรงในแนวนอนของแรงตั้งฉากมาจากลูกบาศก์ซ้าย จะได้
ดังนั้น แรงแนวนอนสุทธิจึงเท่ากับ ศูนย์ ซึ่งสอดคล้องกับที่โจทย์ระบุว่าบล็อกไม้รูปสามเหลี่ยมจะไม่เคลื่อนที่บนโต๊ะ
จากโจทย์ มีสองแรงที่กระทำลูกบาศก์แต่ละอัน คือ แรงตั้งฉากจากบล็อกไม้รูปสามเหลี่ยม และแรงโน้มถ่วง โดยแรงตั้งฉากจะต้องสมดุลกับแรงโน้มถ่วง พิจารณาที่ลูกบาศก์ซ้าย จะได้
\(\rm F_N = mg~ cos α\)
แรงในแนวตั้งของแรงตั้งฉากจะถูกส่งผ่านบล็อกไม้รูปสามเหลี่ยมไปยังพื้นดิน จะได้
\(\rm F_{N_y} = mg ~cos2α\)
สำหรับลูกบาศก์ขวาก็เป็นไปในทำนองเดียวกัน นอกจากนี้ยังมีแรงที่พื้นต้องรับน้ำหนักของบล็อกไม้รูปสามเหลี่ยมอีกจึงได้แรงทั้งหมดเท่ากับ
\(\rm F_{tot} = mg~ cos^2 α + mg~ cos^2 β + Mg\)
เนื่องจากบล็อกไม้เป็นรูปสามเหลี่ยมมุมฉาก แสดงว่า cos2 α + cos2 β = 1 ดังนั้น Ftot = mg + Mg
สังเกตว่า แรงในแนวนอนของแรงตั้งฉากมาจากลูกบาศก์ซ้าย จะได้
\(\rm F_{N_x} = mg ~cos α~ sin α\)
ส่วนลูกบาศก์ขวาจะมีแรงตั้งฉากในแนวนอนเท่ากับ mg cos β sin β ในทิศตรงข้าม แต่เพราะบล็อกไม้เป็นรูปสามเหลี่ยมมุมฉาก แสดงว่า cos α sin α = cos β sin βดังนั้น แรงแนวนอนสุทธิจึงเท่ากับ ศูนย์ ซึ่งสอดคล้องกับที่โจทย์ระบุว่าบล็อกไม้รูปสามเหลี่ยมจะไม่เคลื่อนที่บนโต๊ะ
| 12. | (เกินหลักสูตรการสอบเข้า สอวน.) ทรงกลมกลวงมวล M รัศมี R มีของเหลวมวล M บรรจุไว้เต็ม โดยไม่มีแรงเสียดทาน (ไม่มีความหนืด) ทรงกลมที่เดิมอยู่นิ่ง ถูกปล่อยลงมาจากทางลาดที่ทำมุม θ กับแนวนอน โดยไม่มีการไถล แล้วความเร่งของทรงกลมหลังปล่อยลงมาเท่ากับข้อใด สมมุติว่า ความเร่งของการตกอย่างอิสระคือ g โมเมนต์ความเฉื่อยของทรงกลมกลวงรัศมี r มวล m ที่จุดศูนย์กลางมวล คือ \(\rm I = \dfrac{2}{3} mr^2\) โมเมนต์ความเฉื่อยของทรงกลมตันรัศมี r มวล m ที่จุดศูนย์กลางมวล คือ \(\rm I = \dfrac{2}{5} mr^2\) |
| A | \(\rm a = g ~sinθ\) |
| B | \(\rm a = \dfrac{3}{4} g ~sinθ\) |
| C | \(\rm a = \dfrac{1}{2} g ~sinθ\) |
| D | \(\rm a = \dfrac{3}{8} g ~sinθ\) |
| E | \(\rm a = \dfrac{3}{5} g ~sinθ\) |
ตอบ (B)
ข้อนี้เราอาจคำนวณจากทอร์กหรือพลังงานที่เกิดขึ้น โดยทอร์กที่กระทำกับแกนที่ผ่านจุดสัมผัสจะเท่ากับ
จากโจทย์จะได้โมเมนต์ความเฉื่อยคือ
จากกฎการอนุรักษ์พลังงานจะได้ว่า
ข้อนี้เราอาจคำนวณจากทอร์กหรือพลังงานที่เกิดขึ้น โดยทอร์กที่กระทำกับแกนที่ผ่านจุดสัมผัสจะเท่ากับ
\(\rm τ = RF~ sinθ = 2MgR ~sin θ\)
ความเร่งเชิงมุมเท่ากับ \(\rm τ = Iα\)
\({\rm{I = }}\dfrac{{\rm{2}}}{{\rm{3}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}{\rm{ + M}}{{\rm{R}}^{\rm{2}}}{\rm{ + M}}{{\rm{R}}^{\rm{2}}}{\rm{ = }}\dfrac{{\rm{8}}}{{\rm{3}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}\)
ดังนั้น ความเร่งเท่ากับ
\({\rm{a = \alpha R = }}\dfrac{{{\rm{2MgRsin\theta }}}}{{\dfrac{{\rm{8}}}{{\rm{3}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}}}{\rm{R = }}\dfrac{{\rm{3}}}{{\rm{4}}}{\rm{g sin\theta }}\)
หรืออีกวิธีคือ พิจารณาที่พลังงานจลน์ของวัตถุ จะได้
\(\begin{align*} \rm T &= \frac{{\rm{1}}}{{\rm{2}}}{\rm{(2M)}}{{\rm{v}}^{\rm{2}}}{\rm{ + }}\frac{{\rm{1}}}{{\rm{2}}} \cdot \frac{{\rm{2}}}{{\rm{3}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}{{\rm{\omega }}^{\rm{2}}}\\ \rm T &=\frac{{\rm{4}}}{{\rm{3}}}{\rm{M}}{{\rm{v}}^{\rm{2}}} \end{align*}\)
และพลังงานศักย์ที่เกิดกับแกน y ในแนวตั้ง \(\rm U = – (2M) gy\)จากกฎการอนุรักษ์พลังงานจะได้ว่า
\(\begin{align*} \rm \frac{d}{dt}(T + U) &= 0\\ \frac{{\rm{8}}}{{\rm{3}}}{\rm{Mv}}\frac{{{\rm{dv}}}}{{{\rm{dt}}}} &= -{\rm{(2M)g}}\frac{{{\rm{dy}}}}{{{\rm{dt}}}} \end{align*}\)
แต่ \(\dfrac{{{\rm{dy}}}}{{{\rm{dt}}}}\rm= -v\,{\rm{sin\theta }}\)ดังนั้น ความเร่งจะเท่ากับ
\({\rm{a}} = \dfrac{{{\rm{dv}}}}{{{\rm{dt}}}}{\rm{ = }}\dfrac{{\rm{3}}}{{\rm{4}}}{\rm{gsin\theta }}\)
| 13. | ที่วงแหวนด้านนอกของดาวเสาร์ การระบุชั้นที่เป็นส่วนหนึ่งของดาวเสาร์ หรือชั้นที่เป็นดาวบริวารของดาวเสาร์ เราจะต้องทราบความสัมพันธ์ระหว่าง ความเร็ว v ของแต่ละชั้นในวงแหวน และระยะทางที่วัดจากศูนย์กลางของดาวเสาร์ R ของแต่ละชั้นเสียก่อน จงพิจารณาว่าข้อความใดต่อไปนี้ถูกต้อง |
| A | ถ้า v ∝ R แสดงว่า ชั้นนั้นเป็นส่วนหนึ่งของดาวเสาร์ |
| B | ถ้า v2 ∝ R แสดงว่า ชั้นนั้นเป็นดาวบริวารของดาวเสาร์ |
| C | ถ้า v ∝ 1/R แสดงว่า ชั้นนั้นเป็นส่วนหนึ่งของดาวเสาร์ |
| D | ถ้า v2 ∝ 1/R แสดงว่า ชั้นนั้นเป็นส่วนหนึ่งของดาวเสาร์ |
| E | ถ้า v ∝ R2 แสดงว่า ชั้นนั้นเป็นดาวบริวารของดาวเสาร์ |
ตอบ (A)
หากเป็นชั้นที่เป็นส่วนหนึ่งของดาวเสาร์ แล้ว ω = v / R จะเป็นค่าคงที่
แสดงว่า v ∝ R
หากเป็นชั้นที่เป็นดาวบริวารของดาวเสาร์ จะได้
หากเป็นชั้นที่เป็นส่วนหนึ่งของดาวเสาร์ แล้ว ω = v / R จะเป็นค่าคงที่
แสดงว่า v ∝ R
หากเป็นชั้นที่เป็นดาวบริวารของดาวเสาร์ จะได้
\(\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{R}}} = \dfrac{{{\rm{GM}}}}{{{{\rm{r}}^{\rm{2}}}}}\)
แสดงว่า v2 ∝ 1/R| 14. | รถเข็นมวล m เคลื่อนที่ไปทางขวาด้วยความเร็ว 12 m/s ชนแบบยืดหยุ่นกับรถเข็นมวล 4.0 kg ที่เดิมอยู่นิ่ง หลังการชน รถเข็นมวล m เคลื่อนที่ไปทางซ้ายด้วยความเร็ว 6.0 m/s ถ้าการชนแบบยืดหยุ่นเกิดในมิติเดียว แล้วความเร็วที่จุดศูนย์กลางมวล (vcm) ของรถเข็นทั้งสองคัน ก่อนชนเท่ากับข้อใด |
| A | vcm = 2.0 m/s |
| B | vcm = 3.0 m/s |
| C | vcm = 6.0 m/s |
| D | vcm = 9.0 m/s |
| E | vcm = 18 m/s |
ตอบ (B)
พิจารณาที่จุดศูนย์กลางมวลของรถเข็น โดยพื้นฐานแล้วรถเข็นจะต้องมีโมเมนตัมเท่ากันแต่ตรงข้ามกัน เพื่อให้โมเมนตัมรวมเป็นศูนย์ หลังการชนแบบยืดหยุ่น โมเมนตัมจะมีทิศย้อนกลับ ซึ่งชัดเจนจากกฎการอนุรักษ์พลังงานรวม และโมเมนตัม
ดังนั้น ความเร็วของจุดศูนย์กลางมวลจึงเท่ากับ 3 m/s เพื่อให้ความเร็วต้นของ m ไปทางขวา 9 m/s และความเร็วสุดท้ายของ m ไปทางซ้าย 9 m/s
สังเกตว่า เราไม่จำเป็นต้องรู้มวล และความเร็วปลายของรถเข็นคันอื่น ๆ เลย
หรืออาจใช้สมการ
พิจารณาที่จุดศูนย์กลางมวลของรถเข็น โดยพื้นฐานแล้วรถเข็นจะต้องมีโมเมนตัมเท่ากันแต่ตรงข้ามกัน เพื่อให้โมเมนตัมรวมเป็นศูนย์ หลังการชนแบบยืดหยุ่น โมเมนตัมจะมีทิศย้อนกลับ ซึ่งชัดเจนจากกฎการอนุรักษ์พลังงานรวม และโมเมนตัม
ดังนั้น ความเร็วของจุดศูนย์กลางมวลจึงเท่ากับ 3 m/s เพื่อให้ความเร็วต้นของ m ไปทางขวา 9 m/s และความเร็วสุดท้ายของ m ไปทางซ้าย 9 m/s
สังเกตว่า เราไม่จำเป็นต้องรู้มวล และความเร็วปลายของรถเข็นคันอื่น ๆ เลย
หรืออาจใช้สมการ
\(\rm 12m = 6 m + 4 v^2\)
และ
\(\dfrac{1}{2}{\rm{m}} \times {12^2} = \dfrac{1}{2}{\rm{m}} \times {6^2} + \dfrac{1}{2} \times 4 \times {\rm{v}}_2^2\)
แก้สมการแล้วหาคำตอบ จะได้
\({{\rm{v}}_{{\rm{cm}}}} = \dfrac{{12~{\rm{m}}}}{{{\rm{m}} + 4}} = 3\,\,{\rm{m/s}}\)
| 15. | คานสม่ำเสมอ มีส่วนหนึ่งจมอยู่ในน้ำและปลายด้านหนึ่งถูกแขวนไว้ ดังรูป ถ้าคานมีความหนาแน่นเป็น 5/9 ของน้ำ แล้วที่ภาวะสมดุล สัดส่วนของคานที่อยู่เหนือน้ำจะเท่ากับข้อใด
 |
| A | 0.25 |
| B | 0.33 |
| C | 0.5 |
| D | 0.67 |
| E | 0.75 |
ตอบ (D)
สมมุติให้ α เป็นสัดส่วนของคานที่อยู่เหนือน้ำ, l เป็นความยาวของคาน, V เป็นปริมาตรของคาน, ρw เป็นความหนาแน่นของน้ำ และ ρr เป็นความหนาแน่นของคาน จากนั้นพิจารณาทอร์กที่จุดหมุน โดยแรงโน้มถ่วงที่กระทำกับทอร์กเท่ากับ
ดังนั้น
สมมุติให้ α เป็นสัดส่วนของคานที่อยู่เหนือน้ำ, l เป็นความยาวของคาน, V เป็นปริมาตรของคาน, ρw เป็นความหนาแน่นของน้ำ และ ρr เป็นความหนาแน่นของคาน จากนั้นพิจารณาทอร์กที่จุดหมุน โดยแรงโน้มถ่วงที่กระทำกับทอร์กเท่ากับ
\({{\rm{\tau }}_{\rm{g}}}{\rm{ = }}{{\rm{\rho }}_{\rm{r}}}{\rm{V g }} \cdot \dfrac{{\rm{1}}}{{\rm{2}}}l\)
เนื่องจาก 1 – α คือส่วนที่คานจมอยู่ใต้น้ำ และจุดศูนย์กลางของส่วนที่จมอยู่ใต้น้ำจะอยู่ห่างจากจุดหมุนป็นระยะ (α + \(\frac{1}{2}\)(1 – α))l ดังนั้น แรงลอยที่กระทำกับทอร์กจะเท่ากับ
\(\begin{align*} {{\rm{\tau }}_{\rm{b}}} &={{\rm{\rho }}_{\rm{w}}}{\rm{(1}}-{\rm{\alpha )V g }} \cdot {\rm{(\alpha + }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{(1}}-{\rm{\alpha ))}}l\\ {{\rm{\tau }}_{\rm{b}}}&= \frac{{\rm{1}}}{{\rm{2}}}{{\rm{\rho }}_{\rm{w}}}{\rm{(1}}-{{\rm{\alpha }}^{\rm{2}}}{\rm{)V g}}l \end{align*}\)
เนื่องจากทอร์กต้องเท่ากัน จะได้
\(\begin{align*} {{\rm{\tau }}_{\rm{g}}}&={{\rm{\tau }}_{\rm{b}}}\\ {\rm{ }}\frac{{\rm{1}}}{{\rm{2}}}{{\rm{\rho }}_{\rm{r}}} &= \frac{{\rm{1}}}{{\rm{2}}}{{\rm{\rho }}_{\rm{w}}}{\rm{(1}}-{{\rm{\alpha }}^{\rm{2}}}{\rm{)}}\\ \frac{{{{\rm{\rho }}_{\rm{r}}}}}{{{{\rm{\rho }}_{\rm{w}}}}} &= {\rm{1}}-{{\rm{\alpha }}^{\rm{2}}} \end{align*}\)
จากโจทย์ให้ \(\dfrac{{{{\rm{\rho }}_{\rm{r}}}}}{{{{\rm{\rho }}_{\rm{w}}}}} = \dfrac{5}{9}\)ดังนั้น
\(\begin{align*} \frac{{\rm{5}}}{9} &= {\rm{1}}-{{\rm{\alpha }}^{\rm{2}}}\\ {\rm{\alpha }} &= \frac{2}{3} \end{align*}\)
| 16. | แนวคิดจาก โจทย์โอลิมปิกฟิสิกส์นานาชาติ 2012 ที่ เอสโตเนีย อนุภาคขนาดเล็กจำนวนมากรวมตัวเป็นเมฆทรงกลมในอวกาศ ที่สภาวะหยุดนิ่ง อนุภาคจะมีความหนาแน่นของมวลต่อปริมาตรเป็น ρ0 และมีรัศมี r0 ถ้าแรงโน้มถ่วงทำให้ยุบตัว โดยมีเฉพาะแรงโน้มถ่วงที่กระทำระหว่างกัน (ไม่มีแรงอื่น) แล้วต้องใช้เวลานานแค่ไหนเมฆจึงจะยุบตัวสมบูรณ์ (ค่าจริงของ 0.5427 คือ\(\sqrt{\frac{3\pi}{32}}\)) |
| A | \(\rm \dfrac{0.5427}{r_0^2\sqrt{G\rho_0}}\) |
| B | \(\rm \dfrac{0.5427}{r_0\sqrt{G\rho_0}}\) |
| C | \(\rm \dfrac{0.5427}{\sqrt{r_0}\sqrt{G\rho_0}}\) |
| D | \(\rm \dfrac{0.5427}{\sqrt{G\rho_0}}\) |
| E | \(\rm \dfrac{0.5427}{\sqrt{G\rho_0}}r_0\) |
ตอบ (D)
ข้อนี้ต้องหาคำตอบด้วยวิธีวิเคราะห์เชิงมิติ ซึ่งจะพิจารณาจาก
โดยขนาดของ t เป็น [T], ขนาดของ G เป็น [L]3 [M]-1 [T]-2 , ขนาดของ ρ0 เป็น [L]-3 [M] และขนาดของ r0 เป็น [L] จะได้
ข้อนี้ต้องหาคำตอบด้วยวิธีวิเคราะห์เชิงมิติ ซึ่งจะพิจารณาจาก
\({\rm{t = 0}}{\rm{.527~}}{{\rm{G}}^{{\rm{ - 1/2}}}}{\rho _{\rm{0}}}^{{\rm{ - 1/2}}}{\rm{r}}_0^{\rm{n}}\)
(เนื่องจากในทุกตัวเลือก ตัวแปร G และ ρ0 มีเลขชี้กำลังเดียวกัน) โดยขนาดของ t เป็น [T], ขนาดของ G เป็น [L]3 [M]-1 [T]-2 , ขนาดของ ρ0 เป็น [L]-3 [M] และขนาดของ r0 เป็น [L] จะได้
\(\begin{align*} \rm [T] &= ([L{{\rm{]}}^{\rm{3}}}{{\rm{[M]}}^{{\rm{ - 1}}}}{{\rm{[T]}}^{{\rm{ - 2}}}}{{\rm{)}}^{{\rm{ - 1/2}}}}{{\rm{([L}}{{\rm{]}}^{{\rm{ - 3}}}}{\rm{[M])}}^{{\rm{ - 1/2}}}}{{\rm{[L]}}^{\rm{n}}}\\ \rm[T] &= {\rm{[T][L}}{{\rm{]}}^{\rm{n}}}\\ \rm n &= 0 \end{align*}\)
สังเกตว่า เวลาในการยุบตัวไม่ได้ขึ้นกับขนาดของเมฆเลย| 17. | วัตถุมวลเท่ากันสองอันเชื่อมกันด้วยคานเบา และโคจรรอบดาวเคราะห์ดวงหนึ่ง โดยคานมีความยาวระดับหนึ่ง แต่สั้นกว่ารัศมีวงโคจร ขณะโคจร คานจะอยู่ในลักษณะตั้งฉากกับดาวเคราะห์เสมอ • มีแรงเกิดขึ้นที่คานหรือไม่ ? ถ้ามีจะเป็นแรงดึงหรือแรงอัด ? • จะเกิดสภาวะสมดุลเสถียร ไม่เสถียร หรือตามธรรมชาติ เมื่อมีการรบกวนการทำมุมของคานเพียงเล็กน้อย ? ( การรบกวนในที่นี้ คือ การรบกวนการรักษาอัตราการหมุนที่ทำให้คานยังคงตั้งฉากกับดาวเคราะห์ ) 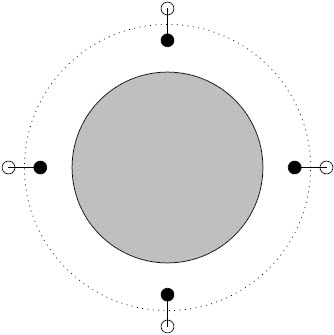 |
| A | ไม่มีแรงใดเกิดขึ้น และมีสภาวะสมดุลตามธรรมชาติ |
| B | มีแรงดึงเกิดขึ้น และมีสภาวะสมดุลเสถียร |
| C | มีแรงอัดเกิดขึ้น และมีสภาวะสมดุลเสถียร |
| D | มีแรงดึงเกิดขึ้น และมีสภาวะสมดุลไม่เสถียร |
| E | มีแรงอัดเกิดขึ้น และมีสภาวะสมดุลไม่เสถียร |
ตอบ (D)
เนื่องจากแรงโน้มถ่วงคิดจาก 1/r2 ดังนั้น แรงดึงดูดของมวลด้านในจะมากกว่ามวลด้านนอก ในขณะที่มวลทั้งสองมีความเร็วเชิงมุมเดียวกัน ดังนั้น ความเร่งสู่ศูนย์กลางจะเท่ากับ r แสดงว่ามวลด้านนอกต้องมีแรงสู่ศูนย์กลางมากกว่ามวลด้านใน
ให้ Fa เป็นแรงสู่ศูนย์กลาง
สำหรับมวลด้านนอก Fa > Fg ดังนั้น มวลด้านนอกจึงดึงให้คานยึดออก (หรือคานออกแรงดึงเข้า)
และในทำนองเดียวกันสำหรับมวลด้านใน Fa < Fg จึงตอบข้อ (D)
เพื่อให้เข้าใจง่ายลองพิจารณาที่จุด C.M. ว่า มวลด้านนอกมีแรงพุ่งออกในแนวรัศมี และมีแรงดึงจากคาน ส่วนมวลด้านในมีแรงพุ่งเข้าในแนวรัศมี และมีแรงตึงจากคาน เมื่อคานถูกรบกวนให้เปลี่ยนมุมเล็กน้อยแรงเหล่านี้จะสร้างทอร์กที่ทำให้คานคงสภาพไว้ คานจึงเกิดความสมดุลเสถียร
เนื่องจากแรงโน้มถ่วงคิดจาก 1/r2 ดังนั้น แรงดึงดูดของมวลด้านในจะมากกว่ามวลด้านนอก ในขณะที่มวลทั้งสองมีความเร็วเชิงมุมเดียวกัน ดังนั้น ความเร่งสู่ศูนย์กลางจะเท่ากับ r แสดงว่ามวลด้านนอกต้องมีแรงสู่ศูนย์กลางมากกว่ามวลด้านใน
ให้ Fa เป็นแรงสู่ศูนย์กลาง
สำหรับมวลด้านนอก Fa > Fg ดังนั้น มวลด้านนอกจึงดึงให้คานยึดออก (หรือคานออกแรงดึงเข้า)
และในทำนองเดียวกันสำหรับมวลด้านใน Fa < Fg จึงตอบข้อ (D)
เพื่อให้เข้าใจง่ายลองพิจารณาที่จุด C.M. ว่า มวลด้านนอกมีแรงพุ่งออกในแนวรัศมี และมีแรงดึงจากคาน ส่วนมวลด้านในมีแรงพุ่งเข้าในแนวรัศมี และมีแรงตึงจากคาน เมื่อคานถูกรบกวนให้เปลี่ยนมุมเล็กน้อยแรงเหล่านี้จะสร้างทอร์กที่ทำให้คานคงสภาพไว้ คานจึงเกิดความสมดุลเสถียร
| 18. | อนุภาคมวล 1 kg สองอัน มีสถานะเริ่มต้น ดังรูป
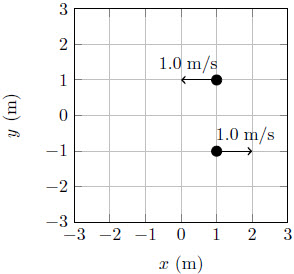 |
| A |  |
| B | 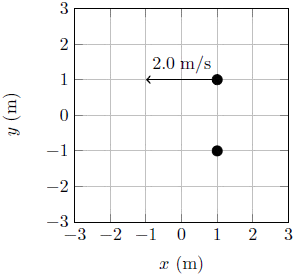 |
| C |  |
| D |  |
| E | 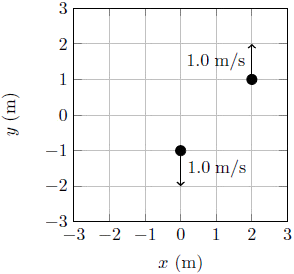 |
ตอบ (E)
ประการแรก โมเมนตัมเชิงเส้นจะต้องถูกอนุรักษ์ไว้ จากสถานะเริ่มต้นที่โมเมนตัมเชิงเส้นเป็นศูนย์ แสดงว่าข้อ (B) ไม่ใช่คำตอบ และโมเมนตัมเชิงมุมที่จุดใด ๆ จะต้องถูกอนุรักษ์ไว้ด้วย จากสถานะเริ่มต้นที่โมเมนตัมเชิงเส้นเป็นศูนย์ ดังนั้น โมเมนตัมเชิงมุมจะมีค่าเท่ากันทุกจุดไม่ว่าจะเป็นจุดอ้างอิงใด จึงพิจารณาเพียงจุดใดหนึ่งจุดก็พอ จากโมเมนตัมเชิงมุมรวมต้องเท่ากับ 2 kg m2/s ในทิศทวนเข็มนาฬิกา จึงตัดข้อ (C) และ (D) ออกไป สุดท้าย เนื่องจากโมเมนตัมเชิงเส้นของระบบจะต้องเป็นศูนย์ แสดงว่าจุดศูนย์กลางมวลจะต้องไม่เคลื่อนที่ ข้อ (A) จึงไม่ใช่คำตอบ
ประการแรก โมเมนตัมเชิงเส้นจะต้องถูกอนุรักษ์ไว้ จากสถานะเริ่มต้นที่โมเมนตัมเชิงเส้นเป็นศูนย์ แสดงว่าข้อ (B) ไม่ใช่คำตอบ และโมเมนตัมเชิงมุมที่จุดใด ๆ จะต้องถูกอนุรักษ์ไว้ด้วย จากสถานะเริ่มต้นที่โมเมนตัมเชิงเส้นเป็นศูนย์ ดังนั้น โมเมนตัมเชิงมุมจะมีค่าเท่ากันทุกจุดไม่ว่าจะเป็นจุดอ้างอิงใด จึงพิจารณาเพียงจุดใดหนึ่งจุดก็พอ จากโมเมนตัมเชิงมุมรวมต้องเท่ากับ 2 kg m2/s ในทิศทวนเข็มนาฬิกา จึงตัดข้อ (C) และ (D) ออกไป สุดท้าย เนื่องจากโมเมนตัมเชิงเส้นของระบบจะต้องเป็นศูนย์ แสดงว่าจุดศูนย์กลางมวลจะต้องไม่เคลื่อนที่ ข้อ (A) จึงไม่ใช่คำตอบ
| 19. | การทดสอบลูกตุ้มอย่างง่าย ประกอบด้วย ลูกตุ้มมวล m ที่ยึดกับแกนหมุนด้วยแท่งเบายาว L ภายใต้สนามโน้มถ่วงคงที่ ลูกตุ้มที่เดิมอยู่นิ่งจะถูกปล่อยลงมาจากมุม θ0 < π / 2 กับแนวเดิม และคาบของการแกว่งคือ T0 โดยไม่คำนึงถึงแรงต้านอากาศและแรงเสียดทาน ขณะที่ลูกตุ้มแกว่ง มุม θg ใด ที่ทำให้เกิดแรงตึงที่แท่งยึดลูกตุ้มมากที่สุด |
| A | แรงตึงมากสุดที่ θg = θ0 |
| B | แรงตึงมากสุดที่ θg = 0 |
| C | แรงตึงมากสุดในช่วง 0 < θg < θ0 |
| D | แรงตึงคงที่ |
| E | ไม่ข้อใดถูกต้อง เพราะ 0 < θ0 < \(\pi\) / 2 |
ตอบ (B)
มวลจะมีความเร่งพุ่งไปทางแกนหมุน เพราะมีความเร่งสู่ศูนย์กลาง ถ้ามวลมีความเร็ว v ความเร่งจะเท่ากับ
สรุปว่า ที่ θg = 0 จะทำให้เกิดแรงตึงที่แท่งยึดลูกตุ้มมากที่สุด
มวลจะมีความเร่งพุ่งไปทางแกนหมุน เพราะมีความเร่งสู่ศูนย์กลาง ถ้ามวลมีความเร็ว v ความเร่งจะเท่ากับ
\({{\rm{a}}_{\rm{c}}}{\rm{ = }}\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{L}}}\)
และมีสองแรงที่กระทำในแนวรัศมี คือ แรงตึงในแท่งยึดลูกตุ้มที่มีทิศพุ่งเข้า และแรงที่แตกมาจากแรงโน้มถ่วงที่มีทิศพุ่งออก ให้ θ เป็นมุมที่กางออกมาจากเส้นในแนวตั้งของแรงโน้มถ่วง จะได้
\(\rm F_{g,rad} = mg \,cos θ\)
จากกฎข้อที่สองของนิวตัน จะได้แรงตึง F เท่ากับ
\(\rm F – F_{g, rad} = ma_c\)
และทั้งสองสมการจะมีค่าเพิ่มขึ้น เมื่อมวลเข้าใกล้จุดต่ำสุดของการแกว่ง ดังนั้น แรงตึงสูงสุดเกิดขึ้นที่นั้น สรุปว่า ที่ θg = 0 จะทำให้เกิดแรงตึงที่แท่งยึดลูกตุ้มมากที่สุด
| 20. | การทดสอบลูกตุ้มอย่างง่าย ประกอบด้วย ลูกตุ้มมวล m ที่ยึดกับแกนหมุนด้วยแท่งเบายาว L ภายใต้สนามโน้มถ่วงคงที่ ลูกตุ้มที่เดิมอยู่นิ่งจะถูกปล่อยลงมาจากมุม θ0 < π / 2 กับแนวเดิม และคาบของการแกว่งคือ T0 โดยไม่คำนึงถึงแรงต้านอากาศและแรงเสียดทาน แรงตึงมากสุดที่แท่งยึดลูกตุ้ม จะมีค่าเท่าใด |
| A | mg |
| B | 2mg |
| C | mL θ0/T02 |
| D | mg sinθ0 |
| E | mg(3 – 2 cosθ0) |
ตอบ (E)
เนื่องจากแท่งยึดลูกตุ้มจะเกิดแรงตึงสูงสุดเมื่อมวลอยู่ที่จุดต่ำสุดของการแกว่ง
ที่จุดต่ำสุด ระยะทางตามแนวตั้งที่มวลเคลื่อนที่ไปได้จะเท่ากับ L (1 – cos θ0) ดังนั้น จากกฎการอนุรักษ์พลังงาน จะได้ว่า
เนื่องจากแท่งยึดลูกตุ้มจะเกิดแรงตึงสูงสุดเมื่อมวลอยู่ที่จุดต่ำสุดของการแกว่ง
ที่จุดต่ำสุด ระยะทางตามแนวตั้งที่มวลเคลื่อนที่ไปได้จะเท่ากับ L (1 – cos θ0) ดังนั้น จากกฎการอนุรักษ์พลังงาน จะได้ว่า
\(\dfrac{1}{2}{\rm{m}}{{\rm{v}}^{\rm{2}}}{\rm{ = mgL(1}}-{\rm{cos }}{{\rm{\,\theta }}_{\rm{0}}}{\rm{)}}\)
และที่จุดต่ำสุดจะมีแรงตึงเท่ากับ
\(\begin{align*}
\rm F &=\rm mg + 2mg(1 - cos\,{{\rm{\theta }}_{\rm{0}}}{\rm{)}}\\
\rm F &= \rm mg(3 -2cos\, {{\rm{\theta }}_{\rm{0}}}{\rm{)}}
\end{align*}\)
ดังนั้น แรงตึงมากสุดจะเท่ากับ mg(3 – 2 cosθ0)| 21. | การทดสอบลูกตุ้มอย่างง่าย ประกอบด้วย ลูกตุ้มมวล m ที่ยึดกับแกนหมุนด้วยแท่งเบายาว L ภายใต้สนามโน้มถ่วงคงที่ ลูกตุ้มที่เดิมอยู่นิ่งจะถูกปล่อยลงมาจากมุม θ0 < π / 2 กับแนวเดิม และคาบของการแกว่งคือ T0 โดยไม่คำนึงถึงแรงต้านอากาศและแรงเสียดทาน ถ้าทำการทดลองใหม่ด้วยแท่งยึดลูกตุ้มยาว 4L โดยใช้มุมเดิมคือ θ0 จะได้คาบของการแกว่งคือ T แล้วข้อความใดต่อไปนี้ถูกต้อง |
| A | T = 2T0 โดยไม่คำนึงถึง θ0 |
| B | T > 2T0 โดย T ≈ 2T0 ถ้า θ0 << 1 |
| C | T < 2T0 โดย T ≈ 2T0 ถ้า θ0 << 1 |
| D | T > 2T0 ในบาง θ0 และ T < 2T0 ในบาง θ0 |
| E | ไม่สามารถหาค่า T และ 2T0 ได้ เพราะไม่ใช่การแกว่งแบบมีคาบ ( ยกเว้นกรณี θ0 << 1 ) |
ตอบ (A)
การแกว่งนี้จะมีคาบที่แน่นอน (ลองพิจารณาที่ θ ใดๆ จะพบว่าพลังงานจะถูกอนุรักษ์ไว้ และอนุภาคจะกลับสู่สภาวะหยุดนิ่งที่จังหวะหนึ่ง) จากการวิเคราะห์เชิงมิติ จะได้คาบของการแกว่งเท่ากับ
การแกว่งนี้จะมีคาบที่แน่นอน (ลองพิจารณาที่ θ ใดๆ จะพบว่าพลังงานจะถูกอนุรักษ์ไว้ และอนุภาคจะกลับสู่สภาวะหยุดนิ่งที่จังหวะหนึ่ง) จากการวิเคราะห์เชิงมิติ จะได้คาบของการแกว่งเท่ากับ
\({\rm{T = f(}}{{\rm{\theta }}_{\rm{0}}}{\rm{)}}\sqrt {\dfrac{{{l_0}}}{g}}\)
ดังนั้น ที่ θ0 ใดๆ จะมีคาบการแกว่งแปรผันกับ \(\sqrt {{l_0}}\)
| 22. | กำหนดภาพจำลองเท้ามนุษย์ ดังรูป ถ้านักเรียนมวล m = 60 kg ยืนด้วยนิ้วเท้าเดียว แล้วแรงตึง T ในเอ็นร้อยหวายควรเท่ากับข้อใด
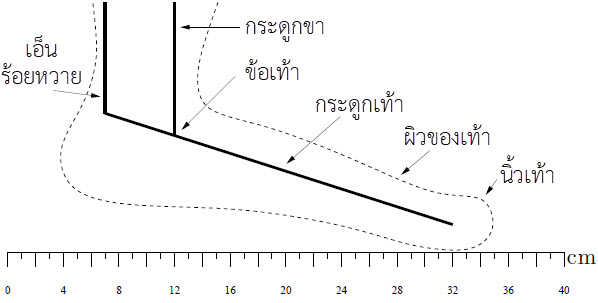 |
| A | T = 600 N |
| B | T = 1200 N |
| C | T = 1800 N |
| D | T = 2400 N |
| E | T = 3000 N |
ตอบ (D)
จากโจทย์น้ำหนักของนักเรียนคนนั้นเท่ากับ W = mg = 600 N ซึ่งเป็นน้ำหนักที่นิ้วเท้าต้องรองรับไว้ ส่วนข้อเท้าจะเป็นจุดแบ่งสมดุลของทอร์ก จะได้
จากโจทย์น้ำหนักของนักเรียนคนนั้นเท่ากับ W = mg = 600 N ซึ่งเป็นน้ำหนักที่นิ้วเท้าต้องรองรับไว้ ส่วนข้อเท้าจะเป็นจุดแบ่งสมดุลของทอร์ก จะได้
\(\begin{align*} \rm T \cdot 5 cm &= 600 \rm N \cdot {\rm{ 20 cm}}\\ \rm{T} &= 2400\rm~ N \end{align*}\)
| 23. | คนมวล m กระโดดบันจี้จัมลงมาจากสะพานสูง ได้ระยะตกสูงสุด H จากนั้นเชือกจะหน่วงให้เขาอยู่นิ่งชั่วขณะก่อนที่จะตีกลับขึ้นไป ให้เชือกมีความยืดหยุ่นสมบูรณ์ ตามกฎแรงของฮุค (Hooke's force law) มีค่านิจสปริง k และสามารถยืดจากความยาวเดิม L0 ถึง L = L0 + h ได้ และแรงตึงสูงสุดในเส้นเชือกจะเท่ากับสี่เท่าของน้ำหนักคน แล้วค่านิจสปริงควรมีค่าเท่าใด |
| A | \(\rm k=\dfrac{mg}{h}\) |
| B | \(\rm k=\dfrac{2mg}{h}\) |
| C | \(\rm k=\dfrac{mg}{H}\) |
| D | \(\rm k=\dfrac{4mg}{H}\) |
| E | \(\rm k=\dfrac{8mg}{H}\) |
ตอบ (E)
ในขณะที่เชือกยืดตัวสูงสุด ทุกพลังงานศักย์โน้มถ่วงจะถูกเปลี่ยนเป็นพลังงานงานศักย์ของสปริง
ในขณะที่เชือกยืดตัวสูงสุด ทุกพลังงานศักย์โน้มถ่วงจะถูกเปลี่ยนเป็นพลังงานงานศักย์ของสปริง
\({\rm{mgH = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{{\rm{h}}^{\rm{2}}}\)
เมื่อแทนแรงตึงสูงสุดที่มีค่าเท่ากับสี่เท่าของน้ำหนักคน ผลลัพธ์ขณะเชือกยืดตัวสูงสุดจะเท่ากับ
\(\rm kh = 4mg\)
ตัดตัวแปร h ได้
\({\rm{k = }}\dfrac{{{\rm{8mg}}}}{{\rm{H}}}\)
| 24. | คนมวล m กระโดดบันจี้จัมลงมาจากสะพานสูง ได้ระยะตกสูงสุด H จากนั้นเชือกจะหน่วงให้เขาอยู่นิ่งชั่วขณะก่อนที่จะตีกลับขึ้นไป ให้เชือกมีความยืดหยุ่นสมบูรณ์ ตามกฎแรงของฮุค (Hooke's force law) มีค่านิจสปริง k และสามารถยืดจากความยาวเดิม L0 ถึง L = L0 + h ได้ และแรงตึงสูงสุดในเส้นเชือกจะเท่ากับสี่เท่าของน้ำหนักคน จงหาระยะยืดสูงสุดของเชือก h |
| A | \(\rm h=\dfrac{1}{2}H\) |
| B | \(\rm h=\dfrac{1}{4}H\) |
| C | \(\rm h=\dfrac{1}{5}H\) |
| D | \(\rm h=\dfrac{2}{5}H\) |
| E | \(\rm h=\dfrac{1}{8}H\) |
ตอบ (A)
ในขณะที่เชือกยืดตัวสูงสุด ทุกพลังงานศักย์โน้มถ่วงจะถูกเปลี่ยนเป็นพลังงานงานศักย์ของสปริง
ในขณะที่เชือกยืดตัวสูงสุด ทุกพลังงานศักย์โน้มถ่วงจะถูกเปลี่ยนเป็นพลังงานงานศักย์ของสปริง
\({\rm{mgH = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{{\rm{h}}^{\rm{2}}}\)
เมื่อแทนแรงตึงสูงสุดที่มีค่าเท่ากับสี่เท่าของน้ำหนักคน ผลลัพธ์ขณะเชือกยืดตัวสูงสุดจะเท่ากับ
\(\rm kh = 4mg\)
ตัดตัวแปร k และ mg ได้
\({\rm{h = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{H}}\)
| 25. | กล่องหนัก W เลื่อนลงมาจากพื้นเอียง 30◦ ด้วยอัตราเร็วคงที่ ภายใต้แรงโน้มถ่วงและแรงเสียดทาน ถ้าเพิ่มแรง P กระทำกับกล่องในแนวนอนจะทำให้กล่องเคลื่อนที่ขึ้นด้วยอัตราเร็วคงที่ แล้วขนาดของ P ควรเท่ากับข้อใด |
| A | \(\rm P = W/2\) |
| B | \(\rm P = 2W/\sqrt3\) |
| C | \(\rm P = W\) |
| D | \(\rm P = \sqrt3W\) |
| E | \(\rm P = 2W\) |
ตอบ (D)
ถ้ากล่องเคลื่อนที่ลงมาด้วยอัตราเร็วคงที่ จะได้ tan θ = μ
ถ้ากล่องถูกแรง P ผลักขึ้นพื้นเอียงในแนวนอนด้วยความเร็วคงที่ จะได้
ถ้ากล่องเคลื่อนที่ลงมาด้วยอัตราเร็วคงที่ จะได้ tan θ = μ
ถ้ากล่องถูกแรง P ผลักขึ้นพื้นเอียงในแนวนอนด้วยความเร็วคงที่ จะได้
\(\rm F_N = mg \,cos θ + P \,sin θ\)
ดังนั้น แรงเสียดทานจะเท่ากับ
\(\rm F_f = μ (mg \,cos θ + P \,sin θ)\)
ซึ่งแรงจะสมดุลด้วยแรงโน้มถ่วง และการผลักขึ้นพื้นเอียง จึงได้
\(\rm P cos θ = μ (mg \,cos θ + P \,sin θ) + mg \,sin θ\)
เมื่อหารตลอดสมการด้วย cosθ และแทน tan θ = μ จะได้
\(\begin{align*}
\rm P &= \rm \mu (W + P\mu ) + W\mu \\
&= \frac{{{\rm{2\mu }}}}{{1 - {{\rm{\mu }}^2}}}{\rm{W}}\\
&= \frac{{{\rm{2}}\frac{1}{{\sqrt 3 }}}}{{1 - \frac{1}{3}}}{\rm{W}}
\end{align*}\)
ดังนั้น \({\rm{P = }}\sqrt 3 {\rm{W}}\)
