การวัดค่าสัมประสิทธิ์การดูดซับเสียง
22-05-2019 อ่าน 15,640
คลื่นเสียงเกิดจาก การสั่นสะเทือนของวัตถุ เมื่อวัตถุเกิดการสั่นสะเทือน จะเกิดการถ่ายโอนพลังงานให้กับอนุภาคของตัวกลาง ทำให้อนุภาคของตัวกลางสั่น แล้วถ่ายโอนไปยังอนุภาคอื่นๆที่อยู่ข้างเคียงให้สั่นตาม เป็นอย่างนี้ต่อเนื่องไปเรื่อยจนกระทั่งถึงอนุภาคตัวกลางที่เป็นตัวรับสัญญาณ ในมนุษย์ คือ หู อนุภาคเหล่านี้สั่นไปกระทบเยื่อแก้วหู ทำให้เยื่อแก้วหูสั่นตาม จึงทำให้เราได้ยินเสียง
เมื่อคลื่นเสียงกระทบพื้นผิววัสดุจะแสดงสมบัติของคลื่น คือ สะท้อน (refection, (\(ρ\))) ส่งผ่าน(transmittion, (\(τ\))) หรือดูดซับ (absorption, (\(α\))) ปริมาณของพลังงานเสียงที่สะท้อน ส่งผ่าน หรือดูดซับขึ้นอยู่กับสมบัติทางกายภาพและพื้นผิวของวัสดุ
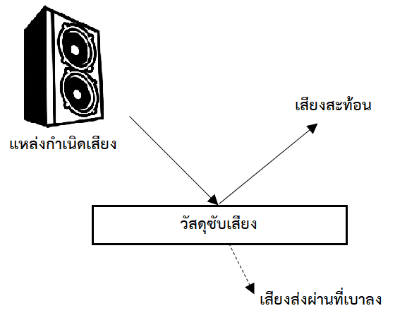
รูป 1 พฤติกรรมของคลื่นเสียงเมื่อกระทบผิววัสดุ
ค่าสัมประสิทธิ์การดูดซับเสียง คือ อัตราส่วนของความเข้มของเสียงที่ถูกดูดซับในวัสดุต่อความเข้มของเสียงที่ตกกระทบ มีค่าระหว่าง 0 ถึง 1 นิยมนำมาใช้ในการอธิบายการดูดซับของวัสดุ ซึ่งมีสมการในการคำนวณดังนี้
วิธีการวัดค่าสัมประสิทธิ์การดูดซับเสียงที่นิยมใช้ คือ
ทดสอบแบบห้องก้องกังวาน เป็นการวัดสัมประสิทธิ์การดูดซับเสียงจากคลื่นเสียงที่มีการกระจายเสียงแบบสุ่มทั่วทั้งห้อง ขนาดห้องมาตรฐานตามข้อกำหนด คือ 200 ลูกบากศ์เมตร ชิ้นงานทดสอบควรมีขนาดประมาณ 10-12 ตารางเมตร สามารถวัดค่าสัมประสิทธิ์การดูดซับเสียงได้ตั้งแต่ช่วง 100-5,000 เฮิรตซ์ โดยคำนวณจากสูตรของซาบีน (Sabine’s Fomular) สามารถอ่านเพิ่มเติมในภาคผนวก 1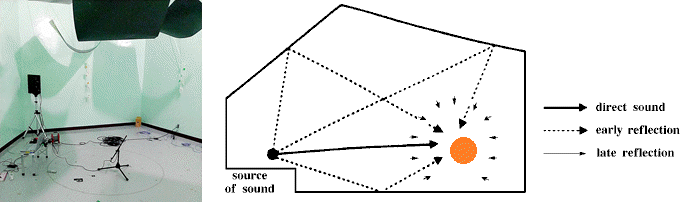
รูป 2 ห้องก้องกังวาน และการกระเสียงแบบสุ่มในห้องก้องกังวาน
การทดสอบแบบหลอดอิมพีแดนซ์ เป็นการวัดสัมประสิทธิ์การดูดซับเสียงจากคลื่นเสียงที่มีการกระจายเสียงในแนวราบ ติดตั้งแหล่งกำเนิดเสียง ที่ปลายด้านหนึ่งของหลอด และตัวอย่างชิ้นงานถูกวางไว้ที่ปลายอีกด้านหนึ่ง โดยใช้กระบวนการของฟังก์ชั่นการส่งผ่าน (Transfer function method) ของการเดินทางของเสียงภายในท่อ สามารถวัดค่าสัมประสิทธิ์การดูดซับเสียงได้ตั้งแต่ช่วง 100-1,600 เฮิรตซ์ โดยสามารถคำนวณได้จาก
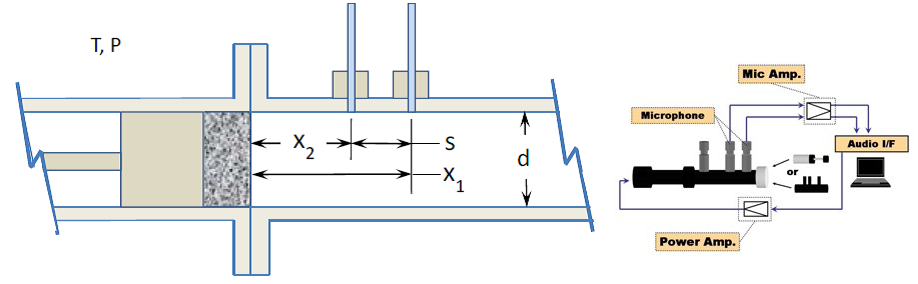
รูป 3 การกระเสียงในหลอดอิมพีแดนซ์ และรูปแบบการเชื่อมต่อการแปลงสัญญาณ
จาก 2 วิธีที่นิยมใช้ในการวัด จะเห็นได้ว่ามีสิ่งหนึ่งที่เหมือนกันคือการเตรียมตัวอย่างชิ้นงานที่ยากลำบาก การทดลองโดยห้องก้องกังวานต้องการชิ้นงานชนาดใหญ่ ส่วนการทดสอบในหลอดอิมพีแดนซ์ก็ต้องการการเตรียมชิ้นงานที่แม่นยำ
หลายปีที่ผ่านมามีการนำเซนเซอร์วัดความดันและความเร็วของเสียง (Sound pressure and particle velocity sensor หรือ Microflown) มาประยุกต์ใช้ในการหาค่าสัมประสิทธิ์การดูดซับเสียง โดยเริ่มแรกเซนเซอร์ตัวนี้ถูกสร้างขึ้นครั้งแรกที่ The university of Twente ประเทศเนเธอร์แลนด์ เพื่อไว้ใช้ในงานสอบเทียบ

รูป 4 เซนเซอร์วัดความดันและความเร็วของเสียง
เซ็นเซอร์ Microflown เป็นตัวแปลงสัญญาณจากระบบเครื่องกลไฟฟ้าจุลภาค (Micro Electro Mechanical Systems : MEMS) ซึ่งสามารถวัดความเร็วของอนุภาคเสียงได้โดยตรง ภายในประกอบด้วยสายไฟสองเส้นทำจากแพลทินัม มีหน้าที่เป็นตัววัดอุณหภูมิ เมื่อจ่ายกระแสไฟฟ้าเข้าไป ขดลวดทั้งสองเส้นจะร้อนขึ้นเกิดเป็นความต้านทานภายในสาย โดยหลักการเมื่ออุณหถูมิเปลี่ยนความต้านทานก็เปลี่ยน ดังนั้นเมื่อความเร็วของอนุภาคเสียงแพร่ผ่านสายจะเกิดการเปลี่ยนแปลงอุณหภูมิบริเวณโดยรอบของสาย ความแตกต่างของอุณภูมินี้ สามารถนำมาคำนวณหาค่าความต้านทานที่เกิดขึ้นและแปลงเป็นสัญญาณความถี่ ตั้งแต่ 20-10000 เฮิรตซ์ แต่อย่างไรก็ตามงานวิจัยส่วนใหญ่ค้นพบว่า ความสามารถของ Microflown ที่ใช้วัดชิ้นงานที่มีขนาดเล็กนั้นมีแม่นยำตั้งแต่ช่วง 100-3150 เฮิรตซ์ โดยคำนวณได้จากสมการ
โดย
\(Z_{EA}\) คือ ค่าฟังก์ชันถ่ายโอนระหว่างความเร็ว และความดัน
\(ρ\) คือ ความหนาแน่นของอากาศ
รูป 5 ขดลวดแพลทินัมภายในเซนเซอร์วัดความดันและความเร็วของเสียง
อ้างอิง
ภาคผนวก 1. สมการของซาบีน (Sabine’s Fomular)
แนวคิดของห้องก้องกังวานตามมาตรฐาน ISO354:2006 งานวิจัยส่วนใหญ่ที่พบมักอ้างถึงสมการของซาบีน เริ่มจากการหาเวลาที่เสียงก้อง (Reverbration time) ภายในห้องก้องกังวานตั้งแต่เริ่มเปิดแหล่งกำเนิดเสียงโดยเริ่มวัดเมื่อระดับความเข้มเสียงต่ำว่า 60 เดซิเบล ไปจนกระทั้งเสียงเงียบ นิยมใช้เสียงขาว (White noise) เนื่องจากมีพลังงานเสียงที่คงที่ โดยเวลาที่เสียงก้องนั้นขึ้นกับปริมาตร (Volume) และความสามารถในการดูดซับเสียงของห้อง ซึ่งการคิดความสามารถในการดูดซับเสียงของห้องทำได้โดยหาผลรวมการดูดซับของพื้นผิววัสดุทั้งหมดภายในห้อง เช่น ผนัง เพดาน พื้น รวมถึงเฟอร์นิเจอร์ทั้งหมดในห้อง
จาก
\(RT_{60}\) คือ เวลาที่เสียงก้อง วัดเมื่อความเข้มเสียงต่ำกว่า 60 เดซิเบล
0.16 คือ ค่าคงที่เชิงประจักษ์
\(V\) คือ ปริมาตรของห้องก้องกังวาน
\(A\) คือ ความสามารถในการดูดซับเสียงของห้อง
\(A\) หาได้จาก
\(\bar{a}\) คือ ค่าเฉลี่ยสัมประสิทธิ์การดูดซับของวัสดุแต่ละชนิด
\(\bar{a}\) หาได้จาก
\(A_T\) คือ พื้นที่การดูดซับเสียงของตัวอย่างทดสอบ
\(c_1T_1\) คือ ความเร็วในการแพร่ของเสียงในอากาศที่อุณหภูมิ \(T_1\)
\(c_2T_2\) คือ ความเร็วในการแพร่ของเสียงในอากาศที่อุณหภูมิ \(T_2\)
\(m\) คือ ค่าสัมประสิทธิ์การลดทอนพลังงาน ตามมาตรฐาน ISO 9613-1
ดังนั้น ค่าสัมประสิทธิ์การดูดซับเสียง หาได้พื้นที่การดูดซับเสียงของตัวอย่างทดสอบต่อพื้นผิววัสดุทั้งหมดรวมชิ้นงานทดสอบภายในห้องก้องกังวาน
ภาคผนวก 2. สมการการทดสอบแบบหลอดอิมพีแดนซ์
จากรูป 2 ที่แสดงการติดตั้งไมโครโฟน ลำโพง และตัวอย่างภายในหลอดอิมพีแดนซ์ เมื่อเปิดแหล่งกำเนิดเสียง เกิดฟังก์ชั่นการถ่ายโอนระหว่างไมโครโฟนสองตัว โดยไมโครโฟนใกล้กับแหล่งกำเนิดเสียงเป็นไมโครโฟนอ้างอิง มีไว้สำหรับแก้ไขความผิดพลาดของเฟสที่ไม่ตรงกับฟังก์ชันการถ่ายโอนในรูปแบบการสะท้อนของแรงดัน
เมื่อ \(k\) คือ จำนวนคลื่น
\(c\) คือ ความเร็วของเสียง s คือระยะทาง
\(x_1\) คือ ระยะทางจากตัวอย่างไปยังไมโครโฟน
นำค่า R มาหาความต้านทานเสียง
ดังนั้น
ภาคผนวก 3. สมการการทดสอบโดยใช้ เซ็นเซอร์ Microflown
จากสมการที่ 13
เมื่อคลื่นเสียงกระทบพื้นผิววัสดุจะแสดงสมบัติของคลื่น คือ สะท้อน (refection, (\(ρ\))) ส่งผ่าน(transmittion, (\(τ\))) หรือดูดซับ (absorption, (\(α\))) ปริมาณของพลังงานเสียงที่สะท้อน ส่งผ่าน หรือดูดซับขึ้นอยู่กับสมบัติทางกายภาพและพื้นผิวของวัสดุ

รูป 1 พฤติกรรมของคลื่นเสียงเมื่อกระทบผิววัสดุ
ค่าสัมประสิทธิ์การดูดซับเสียง คือ อัตราส่วนของความเข้มของเสียงที่ถูกดูดซับในวัสดุต่อความเข้มของเสียงที่ตกกระทบ มีค่าระหว่าง 0 ถึง 1 นิยมนำมาใช้ในการอธิบายการดูดซับของวัสดุ ซึ่งมีสมการในการคำนวณดังนี้
\(α = 1 – (ρ+ τ)\) (1)
วิธีการวัดค่าสัมประสิทธิ์การดูดซับเสียงที่นิยมใช้ คือ
1) วิธีการทดสอบแบบห้องก้องกังวาน (Reverberant room method; ISO 354:2006)
2) การทดสอบแบบหลอดอิมพีแดนซ์ (Impedance tube transfer function method; ISO 10534-2:1998)
ทดสอบแบบห้องก้องกังวาน เป็นการวัดสัมประสิทธิ์การดูดซับเสียงจากคลื่นเสียงที่มีการกระจายเสียงแบบสุ่มทั่วทั้งห้อง ขนาดห้องมาตรฐานตามข้อกำหนด คือ 200 ลูกบากศ์เมตร ชิ้นงานทดสอบควรมีขนาดประมาณ 10-12 ตารางเมตร สามารถวัดค่าสัมประสิทธิ์การดูดซับเสียงได้ตั้งแต่ช่วง 100-5,000 เฮิรตซ์ โดยคำนวณจากสูตรของซาบีน (Sabine’s Fomular) สามารถอ่านเพิ่มเติมในภาคผนวก 1
\(α=\dfrac{A_T}{S} \) (2)

รูป 2 ห้องก้องกังวาน และการกระเสียงแบบสุ่มในห้องก้องกังวาน
การทดสอบแบบหลอดอิมพีแดนซ์ เป็นการวัดสัมประสิทธิ์การดูดซับเสียงจากคลื่นเสียงที่มีการกระจายเสียงในแนวราบ ติดตั้งแหล่งกำเนิดเสียง ที่ปลายด้านหนึ่งของหลอด และตัวอย่างชิ้นงานถูกวางไว้ที่ปลายอีกด้านหนึ่ง โดยใช้กระบวนการของฟังก์ชั่นการส่งผ่าน (Transfer function method) ของการเดินทางของเสียงภายในท่อ สามารถวัดค่าสัมประสิทธิ์การดูดซับเสียงได้ตั้งแต่ช่วง 100-1,600 เฮิรตซ์ โดยสามารถคำนวณได้จาก
\(α=1-|R|^2\) (3)
สามารถอ่านเพิ่มเติมใน ภาคผนวก 2

รูป 3 การกระเสียงในหลอดอิมพีแดนซ์ และรูปแบบการเชื่อมต่อการแปลงสัญญาณ
จาก 2 วิธีที่นิยมใช้ในการวัด จะเห็นได้ว่ามีสิ่งหนึ่งที่เหมือนกันคือการเตรียมตัวอย่างชิ้นงานที่ยากลำบาก การทดลองโดยห้องก้องกังวานต้องการชิ้นงานชนาดใหญ่ ส่วนการทดสอบในหลอดอิมพีแดนซ์ก็ต้องการการเตรียมชิ้นงานที่แม่นยำ
หลายปีที่ผ่านมามีการนำเซนเซอร์วัดความดันและความเร็วของเสียง (Sound pressure and particle velocity sensor หรือ Microflown) มาประยุกต์ใช้ในการหาค่าสัมประสิทธิ์การดูดซับเสียง โดยเริ่มแรกเซนเซอร์ตัวนี้ถูกสร้างขึ้นครั้งแรกที่ The university of Twente ประเทศเนเธอร์แลนด์ เพื่อไว้ใช้ในงานสอบเทียบ

รูป 4 เซนเซอร์วัดความดันและความเร็วของเสียง
เซ็นเซอร์ Microflown เป็นตัวแปลงสัญญาณจากระบบเครื่องกลไฟฟ้าจุลภาค (Micro Electro Mechanical Systems : MEMS) ซึ่งสามารถวัดความเร็วของอนุภาคเสียงได้โดยตรง ภายในประกอบด้วยสายไฟสองเส้นทำจากแพลทินัม มีหน้าที่เป็นตัววัดอุณหภูมิ เมื่อจ่ายกระแสไฟฟ้าเข้าไป ขดลวดทั้งสองเส้นจะร้อนขึ้นเกิดเป็นความต้านทานภายในสาย โดยหลักการเมื่ออุณหถูมิเปลี่ยนความต้านทานก็เปลี่ยน ดังนั้นเมื่อความเร็วของอนุภาคเสียงแพร่ผ่านสายจะเกิดการเปลี่ยนแปลงอุณหภูมิบริเวณโดยรอบของสาย ความแตกต่างของอุณภูมินี้ สามารถนำมาคำนวณหาค่าความต้านทานที่เกิดขึ้นและแปลงเป็นสัญญาณความถี่ ตั้งแต่ 20-10000 เฮิรตซ์ แต่อย่างไรก็ตามงานวิจัยส่วนใหญ่ค้นพบว่า ความสามารถของ Microflown ที่ใช้วัดชิ้นงานที่มีขนาดเล็กนั้นมีแม่นยำตั้งแต่ช่วง 100-3150 เฮิรตซ์ โดยคำนวณได้จากสมการ
\(∝_{_{EA}}=1-\left|\dfrac{(Z_{EA}-ρc)}{(Z_{EA}+ρc)}\right|^2\) (4)
โดย
\(Z_{EA}\) คือ ค่าฟังก์ชันถ่ายโอนระหว่างความเร็ว และความดัน
\(ρ\) คือ ความหนาแน่นของอากาศ
\(c\) คือ ความเร็วของเสียง
สามารถอ่านเพิ่มเติมใน ภาคผนวก 2 และ 3
สามารถอ่านเพิ่มเติมใน ภาคผนวก 2 และ 3

รูป 5 ขดลวดแพลทินัมภายในเซนเซอร์วัดความดันและความเร็วของเสียง
เรียบเรียงโดย
ศิวัช ลาวัลย์วดีกุล
อาจารย์สาขาวิ
อ้างอิง
- [1] International Organization for Standardization, Acoustics- Measurement of sound absorption in a reverberation room, ISO354, 2006.
- [2] International Organization for Standardization, Acoustics– Determination of sound absorption coefficient and impedance in impedance tubes – Part 2: Transferfunction method, ISO10534-2, 1998.
- [3] Otsuru, T., Tomiku, R., Din, N. B. C., Okamoto, N., & Murakami, M. Ensemble averaged surface normal impedance of material using an in-situ technique: Preliminary study using boundary element method. The Journal of the Acoustical Society of America, 125(6). 2009. pp 3784-3791.
ภาคผนวก 1. สมการของซาบีน (Sabine’s Fomular)
แนวคิดของห้องก้องกังวานตามมาตรฐาน ISO354:2006 งานวิจัยส่วนใหญ่ที่พบมักอ้างถึงสมการของซาบีน เริ่มจากการหาเวลาที่เสียงก้อง (Reverbration time) ภายในห้องก้องกังวานตั้งแต่เริ่มเปิดแหล่งกำเนิดเสียงโดยเริ่มวัดเมื่อระดับความเข้มเสียงต่ำว่า 60 เดซิเบล ไปจนกระทั้งเสียงเงียบ นิยมใช้เสียงขาว (White noise) เนื่องจากมีพลังงานเสียงที่คงที่ โดยเวลาที่เสียงก้องนั้นขึ้นกับปริมาตร (Volume) และความสามารถในการดูดซับเสียงของห้อง ซึ่งการคิดความสามารถในการดูดซับเสียงของห้องทำได้โดยหาผลรวมการดูดซับของพื้นผิววัสดุทั้งหมดภายในห้อง เช่น ผนัง เพดาน พื้น รวมถึงเฟอร์นิเจอร์ทั้งหมดในห้อง
จาก
\(RT_{60}= \dfrac{0.16V}{A}\) (5)
\(RT_{60}\) คือ เวลาที่เสียงก้อง วัดเมื่อความเข้มเสียงต่ำกว่า 60 เดซิเบล
0.16 คือ ค่าคงที่เชิงประจักษ์
\(V\) คือ ปริมาตรของห้องก้องกังวาน
\(A\) คือ ความสามารถในการดูดซับเสียงของห้อง
\(A\) หาได้จาก
\(A=S\bar{a}\) (6)
\(S\) คือ พื้นผิววัสดุทั้งหมดภายในห้องก้องกังวาน\(\bar{a}\) คือ ค่าเฉลี่ยสัมประสิทธิ์การดูดซับของวัสดุแต่ละชนิด
\(\bar{a}\) หาได้จาก
\(\bar{a}= \dfrac{s_1 a_1+s_2 a_2+⋯s_n a_n}{n} \) (7)
\(A_T=55.3V\left(\dfrac{1}{c_2 T_2}-\dfrac{1}{c_1 T_1 }\right)-4V(m_2-m_1)\) (8)
\(A_T\) คือ พื้นที่การดูดซับเสียงของตัวอย่างทดสอบ
\(c_1T_1\) คือ ความเร็วในการแพร่ของเสียงในอากาศที่อุณหภูมิ \(T_1\)
\(c_2T_2\) คือ ความเร็วในการแพร่ของเสียงในอากาศที่อุณหภูมิ \(T_2\)
\(m\) คือ ค่าสัมประสิทธิ์การลดทอนพลังงาน ตามมาตรฐาน ISO 9613-1
ดังนั้น ค่าสัมประสิทธิ์การดูดซับเสียง หาได้พื้นที่การดูดซับเสียงของตัวอย่างทดสอบต่อพื้นผิววัสดุทั้งหมดรวมชิ้นงานทดสอบภายในห้องก้องกังวาน
\(α=\dfrac{A_T}{S} \) (9)
ภาคผนวก 2. สมการการทดสอบแบบหลอดอิมพีแดนซ์
จากรูป 2 ที่แสดงการติดตั้งไมโครโฟน ลำโพง และตัวอย่างภายในหลอดอิมพีแดนซ์ เมื่อเปิดแหล่งกำเนิดเสียง เกิดฟังก์ชั่นการถ่ายโอนระหว่างไมโครโฟนสองตัว โดยไมโครโฟนใกล้กับแหล่งกำเนิดเสียงเป็นไมโครโฟนอ้างอิง มีไว้สำหรับแก้ไขความผิดพลาดของเฟสที่ไม่ตรงกับฟังก์ชันการถ่ายโอนในรูปแบบการสะท้อนของแรงดัน
\(R= \dfrac{H_{12}-e^{-jks}}{e^{jks}-H_{12} }×e^{2jkx_1}\) (10)
เมื่อ \(k\) คือ จำนวนคลื่น
\(k=\dfrac{2πf}{c}\) (11)
\(f\) คือ ความถี่ \(c\) คือ ความเร็วของเสียง s คือระยะทาง
\(x_1\) คือ ระยะทางจากตัวอย่างไปยังไมโครโฟน
นำค่า R มาหาความต้านทานเสียง
\(z=\dfrac{z}{ρc}=\dfrac{1+R}{1-R}\) (12)
\(ρ\) คือ ความหนาแน่นของอากาศดังนั้น
\(α=1-|R|^2\) (13)
ภาคผนวก 3. สมการการทดสอบโดยใช้ เซ็นเซอร์ Microflown
จากสมการที่ 13
\(α=1-|R|^2=1-\left|\dfrac{(Z_{EA}-ρc)}{(Z_{EA}+ρc)}\right|^2\) (14)
บทความฟิสิกส์ล่าสุด
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
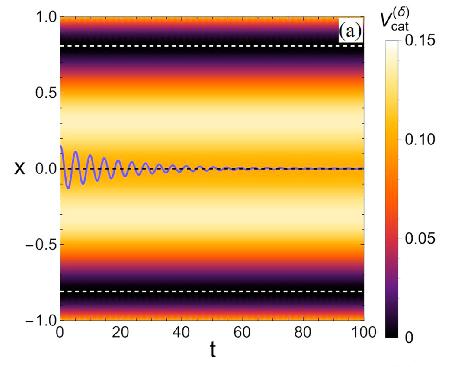 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

