ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )

17-03-2025 อ่าน 395

รูปที่ 1 รูปตัวอย่างแมวน่ารักจากอินเตอร์เน็ต (ที่มา: https://www.pawlicy.com/blog/cat-photos-for-monday/ )

เมื่อไม่นานมานี้ วารสารฟิสิกส์อเมริกัน (American Journal of Physics) ฉบับล่าสุด ได้เผยแพร่บทความชื่อว่าปฏิสัมพันธ์ระหว่างแมว กับมนุษย์จากมุมมองทางฟิสิกส์ ผ่านสมการการเคลื่อนที่ (On cat-human interaction from the viewpoint of physics: An equation of motion) ซึ่งเขียนโดยคุณ Anxo Biasi จากมหาวิทยาลัย Sorbonne ประเทศฝรั่งเศส [1] ซึ่งบทความนี้ได้ถูกเผยแพร่ต่อ และมีการพูดคุยกันบ้างแล้วในหมู่นักฟิสิกส์ไทย แต่ยังไม่ได้เป็นวงกว้างมาก ผู้เขียนจึงอยากนำเรื่องนี้มาเล่าให้ทุกคนฟังโดยทั่วกัน ณ ที่นี้ครับ

แมวนั้นเป็นสัตว์ที่มีเสน่ห์ในตัว คือมีรูปลักษณ์ที่น่ารัก และมีพฤติกรรมที่บางครั้งก็แปลก ตลก บ้างก็ดึงดูดจนทำให้เราตกหลุมรักเจ้าสิ่งมีชีวิตที่น่าฟัดน่ากอดตัวนี้ ในช่วงหลายปีมานี้ความโด่งดังของเจ้าเหมียวได้ขยายไปทั่วจนได้ครอบครองพื้นที่บนโซเชียลมีเดียอย่างมีนัยสำคัญ คือมีบัญชีต่าง ๆ ที่เกี่ยวกับแมวอยู่หลายบัญชี และบัญชีเหล่านั้นก็มียอดเข้าชม และยอดผู้ติดตามนับล้านเลยทีเดียว ส่วนหนึ่งนอกเหนือจากหน้าตาที่น่ารักตะมุตะมิของน้องแล้ว ก็คงมาจากพฤติกรรมที่มีลักษณะที่จำเพาะของน้องที่มีส่วนดึงดูดความสนใจของเราตามที่ได้กล่าวไว้ข้างต้นนั่นเอง แต่อะไรกันล่ะ ที่ทำให้เจ้าเหมียวแสดงลักษณะจำเพาะเหล่านี้ออกมา?

คุณ Anxo เล่าว่าแรงบันดาลใจที่ทำให้เขาสนใจ และเริ่มหาคำตอบให้กับคำถามเหล่านี้ก็มาจากแมวของเขาเองนี่แหละครับ เขาบอกว่าตั้งแต่เขาได้เจ้าเหมียวตัวนี้มา เขาก็เริ่มสังเกตเห็นพฤติกรรมประหลาดเมื่อเจ้าเหมียวเข้ามามีปฏิสัมพันธ์กับเขา และพฤติกรรมเหล่านี้ก็ได้เกิดซ้ำแล้วซ้ำเล่า จนเขาเริ่มพยายามมองการเคลื่อนที่ของเจ้าเหมียวเทียบกับการเคลื่อนที่ของจุดอนุภาค (point particle) ที่เรามักทำกันเป็นปกติในวิชาฟิสิกส์ … นักฟิสิกส์ก็อย่างนี้แหละครับ บางครั้งเราก็สมมติให้วัว หรือไก่เป็นทรงกลมเหมือนกับลูกบอล เพื่อให้ง่ายต่อการพิจารณา [2] … หลังจากพิจารณาเช่นนั้นแล้วเขาก็พบว่าพลวัต ( การเปลี่ยนแปลงในเวลาอันเนื่องมาจากอันตรกิริยา เช่น แรง ในกรณีนี้คือการมีปฏิสัมพันธ์ ) ของเจ้าเหมียวนั้นง่ายเกินคาด ทำได้โดยการมองผ่านจุดสมดุลแบบเสถียร และไม่เสถียรภายใต้สิ่งเร้าจากภายนอกเพียงเท่านั้นเองครับ ( บางคนอาจจะเอ่อ… คืออะไรนะ บางท่านอาจถามว่า ง่ายกี่โมง เดี๋ยวเรามาดูไปพร้อมกันต่อจากนี้ครับ ) เมื่อจับทางได้แล้วคุณ Anxo ก็เริ่มพยายามนึกถึงพฤติกรรมอันเป็นเอกลักษณ์ต่าง ๆ ของเจ้าเหมียวของเขาที่เขาสังเกตเห็นในแต่ละวัน ทั้งจากที่เคยพูดคุยกับเพื่อนหลายคน จากที่เคยได้ยินได้ฟังผ่านทางอินเตอร์เน็ต รวมถึงจากบทความทางวิชาการต่าง ๆ เพื่อนำมาพัฒนาแบบจำลองทางคณิตศาสตร์โดยที่สำคัญ ๆ มีดังนี้

พฤติกรรมที่ 1: น้องแมวโดยปกติมักจะ ( นอน ) พัก โดยทิ้งระยะห่างจากคนไว้ประมาณหนึ่ง
พฤติกรรมที่ 2: เมื่อน้องแมวมา ( นอน ) พักบนตัวคน ไม่ว่าจะที่ตัก บนท้อง หรือที่หลังเรานั้น สิ่งเร้าเพียงน้อยนิดก็สามารถกระตุ้นให้น้องลุกออกจากตัวเราไปได้ อาทิ เห็นแมลงบิน ได้ยินเสียงที่เบาเพียงนิดเดียว ( จนมนุษย์ไม่อาจได้ยิน ) หรือแม้แต่การสลายตัวเป็นอนุภาคเบต้าของอะตอมในกาแล็กซีข้างเคียงก็ด้วย ( อันหลังสุดนี่ออกแนวประชดนะครับ ) สิ่งเร้า หรือสิ่งรบกวนนี้ต้องรุนแรงแค่ไหนจึงจะทำให้น้องลุกออกไปนั้นขึ้นกับว่าน้องติดคนที่เขาทับอยู่มากแค่ไหน
พฤติกรรมที่ 3: เมื่อน้องแมวถูกลูบตามตัว น้องจะเคลื่อนที่ไปมาเป็นการเคลื่อนที่แบบสั่น
พฤติกรรมที่ 4: เมื่อน้องแมวถูกเรียกโดยคน เขาจะไม่ค่อยตอบรับ
พฤติกรรมที่ 5: เมื่อน้องแมวตัดสินใจเดินเข้าหาคนที่เรียกเขา น้องมักถูกดึงดูดความสนใจไปได้ง่ายระหว่างทาง ทำให้มาไม่ถึง
พฤติกรรมที่ 6: ยามค่ำคืน น้องแมวมักจะวิ่งแบบสุ่มข้ามฟากของบ้านไปมา เราเรียกพฤติกรรมแบบนี้ว่า ซูมมี่ส์ (zoomies)
พฤติกรรมที่ 7: น้องแมวครางด้วยเสียงสั่นอย่างเบา ๆ (purr) ออกมาเมื่อเขาถูกใจในฝีมือการลูบของคน

น้องแมวที่บ้านคุณผู้อ่าน หรือที่คุณผู้อ่านเคยเจอเป็นแบบนี้เหมือนกันไหมครับ?

คุณ Anxo ได้กำชับไว้ในบทความว่าแบบจำลองของเขานั้นสนใจแค่ ปฏิสัมพันธ์ของแมวกับมนุษย์ในระบบที่มีแมวหนึ่งตัว และมีมนุษย์ที่อยู่นิ่ง ๆ เพียงหนึ่งคนเท่านั้น และกล่าวอีกว่าพฤติกรรมทั้ง 7 นี้อาจไม่ได้พบเจอเหมือนกันในแมวทุกตัวก็ได้ โดยแมวแต่ละตัวจะแสดงพฤติกรรมทั้ง 7 นี้ออกมามากน้อยแตกต่างกันไปแต่ละตัว อีกทั้งยังออกตัวว่างานนี้เป็นงานเชิงทฤษฎีที่มุ่งหวังผลในเชิงการศึกษาฟิสิกส์ โดยไม่ได้มีการทดลองอะไรในสัตว์ ( การทำการทดลองในสัตว์มีขั้นตอนที่ยุ่งยาก และจำเป็นต้องมีเอกสารรับรองครับ จึงต้องออกตัวครับ )

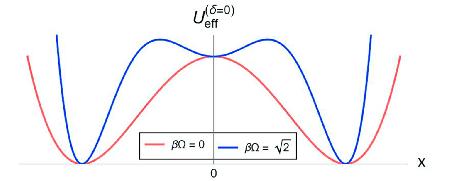
ทีนี้เราจะมาดูที่สมการแมวเหมียว (cat’s equation) กันนะครับ เนื่องจากคุณ Anxo มีวัตถุประสงค์แต่แรกแล้วว่าอยากให้บทความนี้ถูกใช้เป็นเครื่องมือสอนวิชากลศาสตร์แบบฉบับเบื้องต้น (introductory classical mechanics) ด้วย เราจึงพิจารณาว่าการพลวัตของเจ้าเหมียวนั้นเป็นไปตามหลักกลศาสตร์ของนิวตัน (Newton’s mechanics) โดยมีสมมติฐานว่าเจ้าเหมียวรับรู้ถึงอิทธิพลที่กระทำต่อเขาผ่านการเหนี่ยวนำโดยคน แทนด้วยความศักย์ Vcat^{_⁽^δ⁾}และพจน์ความหน่วง ( ในที่นี้ใช้แทนคำว่า ความเสียดทาน บ่งบอกถึงสภาพต้านการเคลื่อนที่เช่นเดียวกัน ) เขียนเป็นสมการได้ว่า

\(m\dfrac{d^2x}{dt^2} = - \dfrac{d}{dx}v^{(δ)}_{cat} - ϵ\dfrac{dx}{dt'}\) .......สมการที่ 1

เมื่อ x(t) เป็นฟังก์ชันจำนวนจริงที่อธิบายถึงระยะห่างของแมวจากมนุษย์ที่เวลา t

ใด ๆ โดยกำหนดให้มนุษย์อยู่ที่ตำแหน่ง x = 0 ให้ m

เป็นมวลของแมวซึ่งมีค่ามากกว่าศูนย์ และกำหนดให้ ϵ

คือสัมประสิทธิ์ความหน่วงโดยมีขนาดมากกว่า 0

และแปรเปลี่ยนไปตามแมวแต่ละตัว ระบบนี้เป็นระบบ 3 มิติ แต่เพื่อให้ง่าย เราจะพิจารณาใน 1 มิติ

สมการนี้สามารถอธิบายคร่าว ๆ ได้ว่าฝั่งขวามือคืออิทธิพลต่าง ๆ ที่กระทำต่อระบบ ( แมว ) ก้อนแรกคืออิทธิพลอันเกิดจากปฏิสัมพันธ์กับคน อีกก้อนเกิดจากความหน่วง ซึ่งความหมายของมันจะถูกพูดถึงในลำดับต่อไป ทางซ้ายมือนั้นแสดงการตอบสนองของระบบต่ออิทธิพลต่าง ๆ ซึ่งจะออกมาในลักษณะของการเปลี่ยนตำแหน่ง x

ไปตามเวลา t

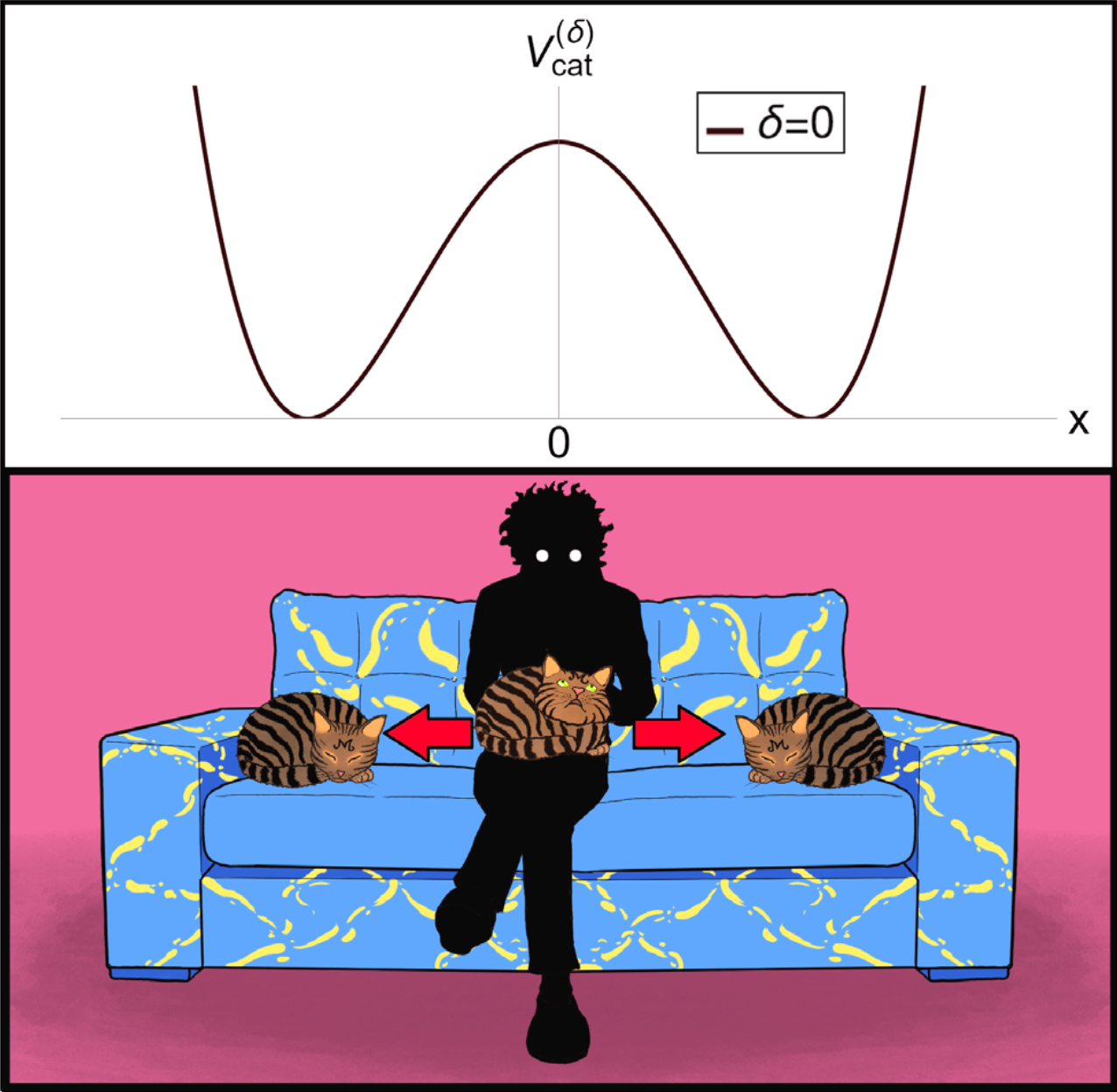
รูปที่ 2: รูปแสดงตำแหน่งจุดพักของน้องแมว ซึ่งตรงกับบริเวณที่กราฟด้านบนมีความชันเป็นศูนย์ โดยตำแหน่งที่คน ( เงาดำ ) นั่งอยู่ (x = 0) เป็นหนึ่งในจุดพักที่กราฟความศักย์มีลักษณะเป็นยอดเนิน แสดงถึงสมดุลที่ไม่เสถียร ( ภาพจากบทความต้นฉบับ [1] )
คำถามต่อมาคือเจ้าความศักย์นี้มีหน้าตาเป็นอย่างไร คุณ Anxo ได้เสนอว่าหากเราเขียนความศักย์นี้เป็น

\(V_{cat}^{(δ)}(X) = g(x^2-1)X^2\dfrac{x^2-δ}{x^2+δ}\) .......สมการที่ 2

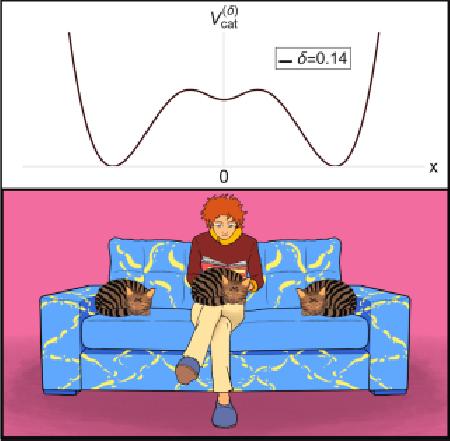
ฟังก์ชันนี้มีความพิเศษเชิงคณิตศาสตร์คือ มันอนุญาตให้เรามีความควบคุมเหนือจุดสมดุล คือเราสามารถเลือกตำแหน่งให้จุดสมดุลได้ และยังเลือกเสถียรภาพให้กับสมดุลนั้นได้อีกด้วย โดยตัวแปร g

คือตัวแปรคู่ควบใส่มาเพื่อความเป็นรูปทั่วไปของฟังก์ชัน มีค่ามากกว่าศูนย์ แต่ในงานนี้จะให้ g = 1 เพื่อให้ง่าย แต่ก็ไม่กระทบต่อคำอธิบายที่จะได้จากแบบจำลอง ตัวแปร δ

นั้นมีความสำคัญ มีค่าตั้งแต่ 0

ถึง 1

เป็นตัวบอกว่าเจ้าเหมียวติดคนที่เขาอยู่ด้วยขนาดไหน δ = 0 หมายความว่าเจ้าเหมียวไม่ค่อยมีเยื่อใยต่อคนคนนั้นเมื่อมีอะไรมาดึงดูดความสนใจเพียงเล็กน้อย ก็พร้อมลุกออกไปอย่างไม่ใยดี เรียกว่าเป็นจุดสมดุล ( น้องมาหยุดพักอยู่ได้ ) แต่ไม่เสถียร ลองมองไปที่กราฟในรูปที่ 2 จะเห็นว่าที่จุด x = 0 ที่คนนั่งอยู่นั้นมีเนินปูดขึ้นมา ลองนึกภาพว่ามีลูกบอลตั้งอยู่บนเนินนั้นนะครับ เพียงสะกิดนิดเดียวลูกบอลก็พร้อมจะวิ่งตกลงไปที่หลุมข้างใดข้างหนึ่ง ( ในงานแปลนี้ ผู้แปลจะเรียกบ่อศักย์ ว่าหลุม หรือหลุมศักย์ ) ซึ่งจุดเหล่านี้แหละครับเสถียรกว่ามาก ลองนึกดูว่าหากคุณสะกิดลูกบอลที่ตกมาอยู่ในหลุมนี้แล้ว เบา ๆ สุดท้ายลูกบอลก็จะตกลงมาที่เดิม ต้องออกแรงสะกิดมากพอลูกบอลจึงจะไม่ไถลลงมาที่หลุมเดิม หลุมสองหลุมนี้เรียกว่าสมดุลเสถียร ( น้องมาหยุดพักได้ และยากที่น้องจะเปลี่ยนที่ ) นี่แหละครับคือภาพที่คุณ Anxo เห็นก่อนหน้านี้ ที่เรียกว่า “การมองผ่านจุดสมดุลแบบเสถียร และไม่เสถียร” ทีนี้ถ้า δ > 0 จะเห็นว่าลักษณะของกราฟบริเวณที่คนนั่งอยู่นั้นเริ่มมีหลุมตื้น ๆ เกิดขึ้น ตามรูปที่ 3 นั่นคือน้องติดคนที่นั่งทับอยู่ในระดับหนึ่งนั่นเอง ยิ่ง δ

เข้าใกล้ 1

มากหลุมยิ่งลึก น้องยิ่งติดคนมาก สลัดออกยาก คุณผู้อ่านเป็นคนที่โชคดีคนนั้นที่มีค่าผูกพันกับน้องสูงสุด (δ = 1) หรือเปล่าครับ

รูปที่ 3: รูปแสดงตำแหน่งจุดพักของน้องแมว ซึ่งตรงกับบริเวณที่กราฟด้านบนมีความชันเป็นศูนย์ โดยตำแหน่งที่คนนั่งอยู่ (x = 0) เป็นหนึ่งในจุดพักที่กราฟความศักย์มีลักษณะเป็นหลุมตื้น แสดงถึงสมดุลที่เสถียร ( ภาพจากบทความต้นฉบับ [1] )

นอกจากนั้นแล้วฟังก์ชันคณิตศาสตร์นี้ยังมีพฤติกรรมลู่เข้าค่าอนันต์ทางบวก เมื่อระยะห่างจากจุดที่คนนั่งอยู่ (x =0) สูงขึ้นด้วย ไม่ว่าจะสูงขึ้นในทางใดก็ตาม สิ่งนี้ช่วยกักบริเวณระบบที่เรากำลังพิจารณาโดยขอบอนันต์อาจมองว่าเป็นขอบของโซฟา หรือขอบของห้องก็ได้ พฤติกรรมของฟังก์ชันลักษณะนี้มักเจอได้เป็นปกติในการทดลองทางฟิสิกส์ในห้องปฏิบัติการที่ระบบมีขอบเขตชัดเจน เช่นในการทดลองอะตอมเย็น (cold atom) หรือในระบบใยแก้วนำแสง (optical fiber)

ณ จุดนี้ พจน์ความหน่วงถูกใส่เข้าไป เพื่อลดพลังงานการเคลื่อนที่ของแมว และทำให้แมวสามารถหยุดพักได้เมื่อเวลาผ่านไปขณะหนึ่ง โดยอัตราการเสียพลังงานในหนึ่งหน่วยเวลาสามารถเขียนได้ว่า

\(\dfrac{dE}{dt} = -ϵ (\dfrac{dx}{dt})^2\) .......สมการที่ 3

เครื่องหมายลบแสดงการสูญเสียพลังงานของระบบ เพราะ ϵ

มีค่าเป็นบวก และปริมาณที่ยกกำลังสองในระบบจำนวนจริงย่อมมีค่าไม่ติดลบ หากไม่มีพจน์นี้น้องแมวของเราคงได้วิ่งไปแบบไม่มีวันหยุด คงเหนื่อยแย่เลยครับ … สำหรับตอนแรกก็ขอปูพื้นฐานให้คุณผู้อ่านไว้เท่านี้ก่อนนะครับ แล้วเราค่อยมาเจาะลึกที่แต่ละพฤติกรรมกันอย่างละเอียดในตอนต่อไป

เอกสารอ้างอิง:
[1] Biasi, A. (2024). On cat–human interaction from the viewpoint of physics: An equation of motion. American Journal of Physics, 92(11), 827-833.
[2] Blundell, S. J., & Blundell, K. M. (2010). Concepts in thermal physics. Oup Oxford.

บทความโดย:
ภัทรพล ธนลิขิต
นักวิจัยด้านฟิสิกส์พลังงานสูงเชิงทฤษฎี และฟิสิกส์ของอะตอมเย็นสุดขีดเชิงปฏิบัติการ
ภาควิชาฟิสิกส์ สถาบันชั้นสูงวิทยาศาสตร์ และเทคโนโลยี เกาหลี

บทความฟิสิกส์ล่าสุด

ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป ) 18-03-2025

ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก ) 18-03-2025

ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ ) 17-03-2025

หรือว่าเราอาศัยอยู่ในโฮโลแกรม ? 24-10-2024