ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025 อ่าน 258
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
รูปที่ 4: รูปตัวอย่างแมวน่ารักจากอินเตอร์เน็ต ( ที่มา: https://cheezburger.com/35473669/30-cute-cat-pictures-for-your-caturday-mood-booster )
ในตอนที่แล้ว เราได้เกริ่นกันไปคร่าว ๆ แล้วนะครับว่าพฤติกรรมทั้ง 7 ของน้องแมว ที่เราจะคุยกันนั้นมีอะไรบ้าง โดยเราได้เริ่มตั้งสมการ และพูดคุยเกี่ยวกับฟังก์ชันความศักย์ รวมถึงการทำความเข้าใจพฤติกรรมของน้องแมวด้วยวิธีการมองผ่านจุดสมดุลแบบเสถียร และไม่เสถียรของกราฟความศักย์กันไปแล้ว ในตอนที่ 2 นี้ เราจะมาคุยกันถึงผลลัพธ์โดยตรงของสมการ และฟังก์ชันความศักย์ในตอนที่ 1 ว่าสามารถนำมาอธิบายพฤติกรรมของน้องแมวได้อย่างไรกันนะครับ …
… จากที่เล่าในตอนที่ 1 จนมาถึงจุดนี้ คุณผู้อ่านคงพอจะเห็นกันแล้วนะครับว่า เพียงเท่านี้เราก็สามารถอธิบาย พฤติกรรมที่ 1: น้องแมวโดยปกติมักจะ ( นอน ) พัก โดยทิ้งระยะห่างจากคนไว้ประมาณหนึ่ง ได้แล้ว คือไม่ว่าจะเริ่มต้นที่จุดใดในห้อง หรือบนโซฟา ไม่ว่าน้องจะมีความเร็วเริ่มต้นเท่าไร สุดท้ายเมื่อเวลาผ่านไประยะนึง ความหน่วงจะค่อย ๆ ทำให้น้องหยุดนิ่ง และหยุดอยู่ที่สมดุลใดสมดุลหนึ่ง โดยเฉพาะสมดุลที่เสถียร ก็คือหลุมสองหลุมที่ห่างจากจุดที่เรานั่งอยู่ตามรูปที่ 2 ( กลับไปดูในตอนที่ 1 นะครับ ) กล่าวคือยิ่งเราไม่ค่อยสนิทกับน้อง สมดุลของเราก็จะยิ่งไม่เสถียร น้องก็อาจจะไม่มาหยุดที่เรา แต่ถ้าเราสนิทกับน้องมาก ก็ยิ่งมีโอกาสที่ท้ายที่สุดแล้วน้องจะมาหยุดที่เรา ( เอามาจำลองความสัมพันธ์ของคน และความรักได้ไหมครับเนี่ย )
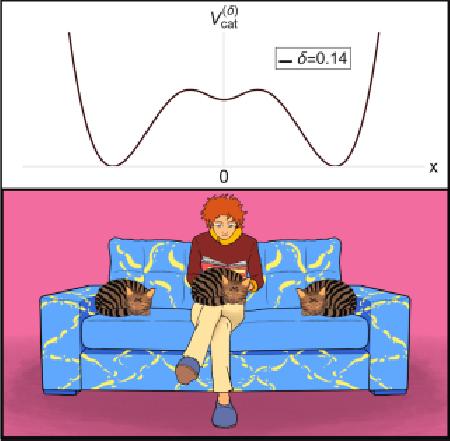
สำหรับ พฤติกรรมที่ 2: เมื่อน้องแมวมา ( นอน ) พักบนตัวคน … สิ่งเร้าเพียงน้อยนิดก็สามารถกระตุ้นให้น้องลุกออกจากตัวเราไปได้ … สิ่งเร้า หรือสิ่งรบกวนนี้ต้องรุนแรงแค่ไหนจึงจะทำให้น้องลุกออกไปนั้นขึ้นกับว่าน้องติดคนที่เขาทับอยู่มากแค่ไหน พฤติกรรมนี้ก็คือการสะกิดลูกบอลที่ผมชวนนึกภาพไปก่อนหน้านี้แหละครับ ที่จุด x = 0
\(\left.\frac{d^2}{dx^2}V^{(δ)}_{cat}\right |_ {x=0} = \begin{cases} -2 &\text{if } {δ=0 }\\ 2 & \text{if } {δ>0 } \end{cases} \) .......สมการที่ 1
นั้นสอดคล้องกับสิ่งที่สังเกตได้ คือ สิ่งเร้าต้องรุนแรงแค่ไหนจึงจะทำให้น้องลุกออกไปนั้นขึ้นกับว่าน้องติด หรือสนิทกับคนที่เขาทับอยู่มากแค่ไหน ถ้าสนิทน้อย δ = 0 δ 
เข้าใกล้ 1 
น้องก็ยิ่งลุกออกไปยากขึ้น ( คลั่งรัก ) นั่นเองครับ
เข้าใกล้ น้องก็ยิ่งลุกออกไปยากขึ้น ( คลั่งรัก ) นั่นเองครับ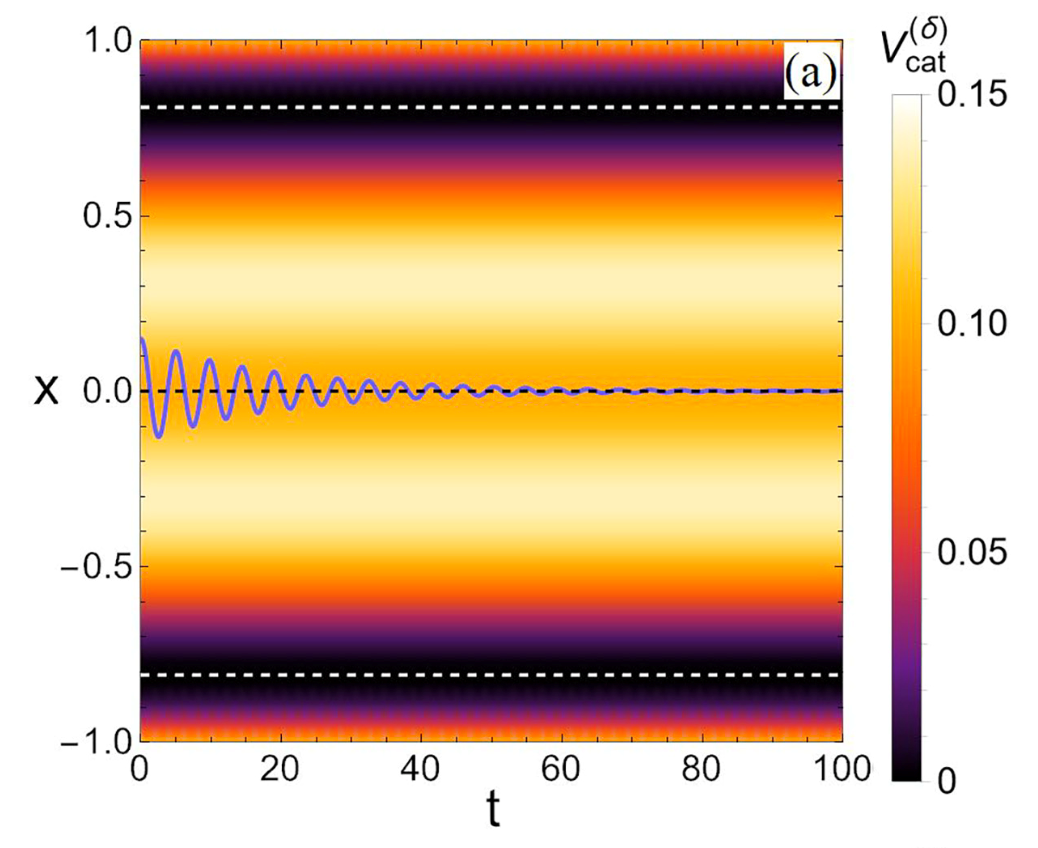
รูปที่ 5: แผนภาพตำแหน่ง และเวลา โดยมีพื้นหลังเป็นแถบสีแสดงความลึกของหลุมศักย์ที่ตำแหน่งต่าง ใช้สำหรับประกอบการอธิบายพฤติกรรมที่ 3 ( ภาพจากบทความต้นฉบับ [1] )
สำหรับพฤติกรรมที่ 3–5 เราจะศึกษาพลวัตของน้องแมวผ่านการเปลี่ยนตำแหน่งไปในเวลา เราจึงจะเสนอข้อมูลในลักษณะต่างจากก่อนหน้าโดยจะใช้แผนภาพที่มีแกนนอนเป็นเวลา และแกนตั้งเป็นตำแหน่ง ลำดับเหตุการณ์จึงเป็นจากซ้ายไปขวา สีพื้นหลังสามารถดูเทียบได้กับแถบสีด้านข้างไล่จากขาว ไปส้ม และไปม่วงเข้ม ยิ่งสีเข้มมากแสดงว่ากราฟเป็นหลุมลึก สีส้มแสดงถึงหลุมที่ตื้น สิ่งนี้คล้ายกราฟของความศักย์ที่เราคุยกันไปก่อนหน้า เพียงแต่ความลึกของกราฟคราวนี้ลึกลงไปในหน้ากระดาษ หรือในหน้าจอนั่นเอง ดังจะเห็นได้จากรูปที่ 5
รูปที่ 5 นี้อธิบาย พฤติกรรมที่ 3: เมื่อน้องแมวถูกลูบตามตัว น้องจะเคลื่อนที่ไปมาคล้ายการเคลื่อนที่แบบสั่น ซึ่งในกรณีนี้ เราพิจารณาเสถียรภาพรอบ ๆ จุดที่คนอยู่ หรือ
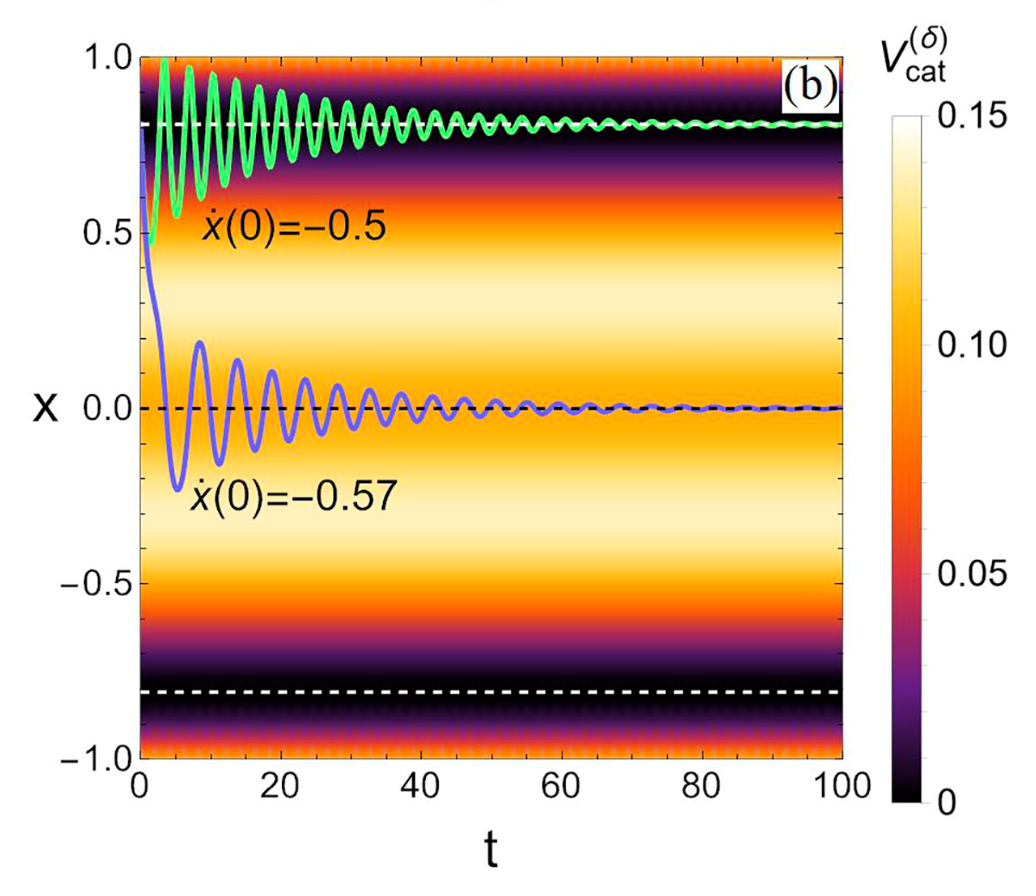
รูปที่ 6: แผนภาพตำแหน่ง และเวลา โดยมีพื้นหลังเป็นแถบสีแสดงความลึกของหลุมศักย์ที่ตำแหน่งต่าง ใช้สำหรับประกอบการอธิบายพฤติกรรมที่ 4 และ 5 ( ภาพจากบทความต้นฉบับ [1] )
พฤติกรรมที่ 4 กับ พฤติกรรมที่ 5 นั้นจะถูกอธิบายด้วยสิ่งที่เรียกว่ากำแพงศักย์ นั่นคือเนินที่กั้นระหว่างหลุมนั่นเอง ในรูปที่ 6 กำแพงศักย์คือแถบสีขาว-เหลืองที่กั้นระหว่างหลุมสีส้ม และหลุมสีม่วงเข้มอยู่ … และแล้วเราก็มาถึง พฤติกรรมที่ 4: เมื่อน้องแมวถูกเรียกโดยคน เขาจะไม่ค่อยตอบรับ ที่หลายคนสงสัย และอดทนรอคอย ว่าทำไมกันนะ เรียกน้องเท่าไรน้องก็ไม่มา มองง่าย ๆ ครับว่าเดิมน้องอยู่ในหลุมสักหลุม ( แถบสีม่วงเข้ม ) ที่อยู่ห่างจากเราออกไป ในเชิงสมการ การเรียกน้องเปรียบเสมือนการให้การดลแก่น้องให้พุ่งเข้าหาคน ซึ่งไปเพิ่มพลังงานจลน์ พูดให้เห็นภาพคือเหมือนเราสะกิดลูกบอลซึ่งอยู่ในหลุมที่เคยพูดถึงก่อนหน้านี้ หากสะกิดไม่แรงพอ ลูกบอลก็จะตกไปที่หลุมเดิม ค่อย ๆ สั่นคล้ายพฤติกรรมที่ 3 และหยุดลง ( ที่หลุมเดิม ) ในที่สุด มาไม่ถึงเรา หรือก็คือการกระตุ้นของเรานั้นไม่น่าสนใจ ไม่เร้าใจพอที่จะดึงดูดความสนใจจากน้องแมวได้ มิหนำซ้ำเรายังมีความหน่วงมาคอยลดทอนการกระตุ้นจากเราไปอย่างรวดเร็วอีก มาถึงจุดนี้เราพอจะเข้าใจพจน์ของความหน่วงนี้แล้วว่าคือ นิสัยเมินเฉย และเบื่อง่ายต่อการกระตุ้นจากเราของน้องแมวนั่นเอง นั่นคือยิ่งน้องเบื่อง่าย อิทธิพลของการกระตุ้นจากการเรียกของคน ที่สำหรับน้องนั้นก็ไม่ค่อยน่าตื่นเต้นอะไรอยู่แล้วยิ่งถูกกลบไปอย่างรวดเร็ว หากมองแบบนี้แล้วจะทำให้เราเข้าใจได้ว่าข้อครหาว่าน้องนั้นหยิ่ง อาจเป็นการว่าร้ายน้องจนเกินไป เพราะจากความเข้าใจของเราในตอนนี้ น้องแค่เบื่อง่ายมาก ๆ อาจเป็นที่เราเองที่กระตุ้นเขาได้ไม่มากพอจนถูกกระบวนการหน่วงจากภายในของน้องกลบไปจนสิ้น ลองหาขนมแมวเลีย หรือของเล่นที่น้องชอบไปช่วยดล กระตุ้นน้องเขาด้วยวิธีนี้ดูครับอาจได้ผล พฤติกรรมนี้สามารถดูได้จากรูปที่ 6 แทนด้วยเส้นการเคลื่อนที่สีเขียวที่ถูกดึงแล้วทำท่าจะเข้าหาตรงกลางเล็กน้อยในตอนแรก แต่สุดท้ายก็กลับไปอยู่ที่หลุมเดิม คือแถบสีม่วงเข้มด้านบนนั่นเอง
พฤติกรรมที่ 5: เมื่อน้องแมวตัดสินใจเดินเข้าหาคนที่เรียกเขา น้องมักถูกดึงดูดความสนใจไปได้ง่ายระหว่างทาง ทำให้มาไม่ถึง นั้นคล้ายกับพฤติกรรมที่ 4 ต่างกันตรงที่คราวนี้เรากระตุ้นน้องได้มากพอจนน้องเริ่มเดินมาหาเราแล้วครับ แต่ถึงกระนั้นความหน่วง หรือความเบื่อง่ายต่อการกระตุ้นของน้องก็ยังแสดงอิทธิพลอยู่ ทำให้น้องอาจถูกดึงความสนใจไปได้ด้วยสิ่งอื่นจนมาไม่ถึงเรา และกลับไปนอนพักอยู่ที่เดิมก็เป็นได้ แต่หากเราเรียกน้องได้สำเร็จนั้น การเคลื่อนที่ของน้องก็จะเป็นไปตามเส้นสีดำในรูปที่ 6 คือน้องถูกดึงมาเคลื่อนที่รอบ ๆ และหยุดในบริเวณที่คนอยู่ ( แถบสีส้ม ) ได้จากการกระตุ้นที่เหมาะสมนั่นเอง
ก่อนที่เราจะไปดูสองพฤติกรรมสุดท้าย เรามาลองพิจารณาพจน์ความหน่วง หรือความเบื่อง่ายของน้องดูอีกทีนะครับ เพราะคุณ Anxo เขาพบว่าพจน์นี้นั้นมีความเกี่ยวข้องกับน้ำหนักตัว หรืออีกนัยนึงก็คืออายุของน้องด้วยนั่นเอง จุดสังเกตอย่างหนึ่งคือการกระตุ้นจากภายนอกนั้นมาในลักษณะของการเพิ่มพลังงานศักย์ให้กับเจ้าเหมียว หากเขียนความเร็วx 
จากสูตรของพลังงานศักย์ Ek x = \(\sqrt{2E_k/m}\)
พฤติกรรมที่ 5: เมื่อน้องแมวตัดสินใจเดินเข้าหาคนที่เรียกเขา น้องมักถูกดึงดูดความสนใจไปได้ง่ายระหว่างทาง ทำให้มาไม่ถึง นั้นคล้ายกับพฤติกรรมที่ 4 ต่างกันตรงที่คราวนี้เรากระตุ้นน้องได้มากพอจนน้องเริ่มเดินมาหาเราแล้วครับ แต่ถึงกระนั้นความหน่วง หรือความเบื่อง่ายต่อการกระตุ้นของน้องก็ยังแสดงอิทธิพลอยู่ ทำให้น้องอาจถูกดึงความสนใจไปได้ด้วยสิ่งอื่นจนมาไม่ถึงเรา และกลับไปนอนพักอยู่ที่เดิมก็เป็นได้ แต่หากเราเรียกน้องได้สำเร็จนั้น การเคลื่อนที่ของน้องก็จะเป็นไปตามเส้นสีดำในรูปที่ 6 คือน้องถูกดึงมาเคลื่อนที่รอบ ๆ และหยุดในบริเวณที่คนอยู่ ( แถบสีส้ม ) ได้จากการกระตุ้นที่เหมาะสมนั่นเอง
ก่อนที่เราจะไปดูสองพฤติกรรมสุดท้าย เรามาลองพิจารณาพจน์ความหน่วง หรือความเบื่อง่ายของน้องดูอีกทีนะครับ เพราะคุณ Anxo เขาพบว่าพจน์นี้นั้นมีความเกี่ยวข้องกับน้ำหนักตัว หรืออีกนัยนึงก็คืออายุของน้องด้วยนั่นเอง จุดสังเกตอย่างหนึ่งคือการกระตุ้นจากภายนอกนั้นมาในลักษณะของการเพิ่มพลังงานศักย์ให้กับเจ้าเหมียว หากเขียนความเร็ว
จากสูตรของพลังงานศักย์ \(\frac{d^2}{{d\tau}^2}\tilde{x} = - \frac{d}{d\tilde{x}}V^{(\epsilon)}_{cat}(\tilde{x})-\tilde{\epsilon}\frac{d}{d\tau}\tilde{x}\) .......สมการที่ 2
โดยที่ \(\tau\)= t / \((\tau)\)= x ( t / m ) \(\tilde{\epsilon}\) = ϵ /\(\sqrt{m}\)
\(\frac{d}{d\tau}E = - \tilde{\epsilon}\left(\frac{d}{d\tau}\tilde{x}\right)^2\).......สมการที่ 3
ทั้งหมดนี้ชี้ให้เห็นว่าค่า
หรือความหน่วง ควรจะขึ้นกับค่า 
เพื่อที่จะสร้างแบบจำลองสำหรับแมวที่มีมวลแตกต่างกัน เพื่อให้เห็นได้ชัดเจน เราลองสมมติให้ ไม่ขึ้นอยู่กับมวล เราจะพบว่าแมวที่มีมวลมากนั้นจะเหนื่อยยากมาก ในขณะที่แมวมวลน้อยนั้นเหนื่อยอย่างรวดเร็ว โลกจะกลับตาลปัตรทันที เพราะค่า 
มีค่าลดลงเมื่อมวลสูงขึ้น เพื่อให้โลกกลับมาเป็นปกติดังเดิม ค่าความหน่วง หรือ จึงควรโตเร็วกว่า \( \sqrt{m}\) เพราะหาก เอกสารอ้างอิง:
[1] Biasi, A. (2024). On cat–human interaction from the viewpoint of physics: An equation of motion. American Journal of Physics, 92(11), 827-833.
บทความโดย:
ภัทรพล ธนลิขิต
นักวิจัยด้านฟิสิกส์พลังงานสูงเชิงทฤษฎี และฟิสิกส์ของอะตอมเย็นสุดขีดเชิงปฏิบัติการ
ภาควิชาฟิสิกส์ สถาบันชั้นสูงวิทยาศาสตร์ และเทคโนโลยี เกาหลี
บทความฟิสิกส์ล่าสุด
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
