ท่าเต้นบัลเล่ต์สุดยากและกฎการอนุรักษ์โมเมนตัมเชิงมุม
24-06-2019 อ่าน 14,569

ถ้าใครชื่นชอบดนตรีคลาสสิกอาจจะรู้จักกับไชคอฟสกี (Tchaikovsky) เขาเป็นคีตกวี (ผู้แต่งทำนองเพลง) ที่มีชื่อเสียงมากชาวรัสเซีย ผลงานที่โด่งดังของเขาเช่น Piano Concerto No. 1 อีกหนึ่งผลงานที่สร้างชื่อให้เขาคือ สวอนเลก (Swan Lake) เป็นบัลเลต์ โอปุสที่ 20 โดยมีเค้าโครงมาจากนิทานของรัสเซีย ในตอนหนึ่งของการแสดงบัลเล่ต์นี้ นักเต้นบัลเล่ต์ต้องเต้นไปเรื่อยๆและหมุนตัวกว่า 32 รอบ ซึ่งนับเป็นท่าเต้นสุดยาก แต่นักแสดงที่ฝึกฝนมาอย่างดีสามารถเต้นท่านี้ได้อย่างไร คำตอบคือมันมีเรื่องของฟิสิกส์เข้ามาเกี่ยวข้องถึงแม้ตัวนักเต้นบัลเล่ต์จะอาจไม่รู้ก็ตาม และเรื่องนี้ก็คือกฎการอนุรักษ์โมเมนตัมเชิงมุม (Conservation of angular momentum)
ทอร์ก (torque) คือปริมาณที่ทำให้เกิดการหมุนของวัตถุอันเนื่องมาจากแรงลัพธ์ที่กระทำต่อวัตถุไม่ผ่านศูนย์กลางมวล ทอร์กเป็นปริมาณเวกเตอร์ มีทิศทางตั้งฉากกับระนาบการหมุนของวัตถุ โดยทิศทางของทอร์กจะพุ่งออกตั้งฉากกับระนาบการหมุนเมื่อวัตถุหมุนในทิศทางทวนเข็มนาฬิกา และทิศทางของทอร์ก จากกฎข้อที่ 2 ของนิวตันในเชิงมุม ถ้าไม่มีทอร์กภายนอกมากระทำต่อระบบแล้ว
\( \dfrac{d\vec{L}}{dt}=0\)
โดยที่ \(\vec{L}\) คือ โมเมนตัมเชิงมุม จะพบว่า
\(\vec{L}\)=ค่าคงที่ (ในระบบโดดเดี่ยว)
จากสมการจะพบว่าผลรวมของโมเมนตัมเชิงมุมในตอนแรก (initial ใช้ตัวย่อ i) จะเท่ากับผลรวมของโมเมนตัมเชิงมุมในเวลาต่อมา (final ใช้ตัวย่อ f) ซึ่งเราเรียกสิ่งนี้ว่ากฎการอนุรักษ์โมเมนตัมเชิงมุม กฎนี้มีความสำคัญมากถือว่าเป็นความรู้พื้นฐานสำคัญทางฟิสิกส์และไม่ใช่เป็นจริงแค่ในกลศาสตร์ของนิวตัน แต่กฎนี้ยังเป็นจริงเมื่ออนุภาคความเร็วใกล้แสง ซึ่งต้องใช้ฟิสิกส์สมัยใหม่เรื่องทฤษฎีสัมพัทธภาพของไอน์สไตน์ และยังใช้ได้แม้แต่ในอนุภาคของระบบขนาดเล็กกว่าอะตอม ซึ่งต้องใช้กลศาสตร์ควอนตัม โดยที่เราสามารถเขียนเป็นสมการได้เป็น
\(\vec{L}\)i = \(\vec{L}\)f
สำหรับโมเมนตัมเชิงมุมในแนวแกนหมุนสามารถเขียนได้เป็น
\(I_{i}\) \(ω_{i}\)=\(I_{f}\) \(ω_{f}\)
โดย \(\vec{L}\),\(I_{}\),\(ω_{}\) คือ โมเมนตัมเชิงมุม โมเมนต์ความเฉื่อยของการหมุน และความเร็วเชิงมุม ตามลำดับ
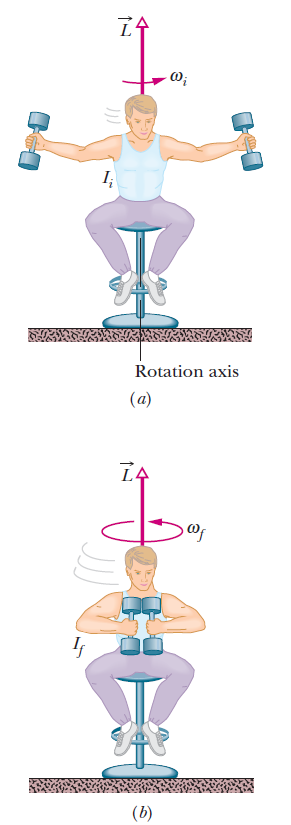
(ภาพจาก Resnick, R., Walker, J. and Halliday, D. (2014). Fundamentals of physics. Hoboken, N.J.: Wiley.)
เพื่อให้เข้าใจง่ายขึ้น ยกตัวอย่างเรานั่งในเก้าอี้หมุนได้ แขนทั้งสองของเราชูออกและถืออุปกรณ์ถ่วงน้ำหนักไว้ เมื่อในเริ่มต้นเรานั่งหมุนตัวโดยที่ชูแขนออก เราจะมีโมเมนต์ความเฉื่อยของการหมุนมาก เมื่อหมุนไปเรื่อยๆเราหุบแขนแนบกับตัวก็จะเป็นการลดโมเมนต์ความเฉื่อยของการหมุนให้น้อยลง ทีนี้ความเร็วเชิงมุมของเราก็จะมากขึ้นทำให้เราหมุนได้เร็วขึ้นในตอนท้ายที่หุบแขน เป็นความสัมพันธ์ดังสมการที่ได้กล่าวมา
นักเต้นบัลเล่ต์ก็ใช้หลักการเดียวกันนี้ตอนที่ต้องหมุนตัว โดยขณะเต้นหมุนตัวใช้การหุบแขนและขาแนบชิดกับตัว ตามกฎการอนุรักษ์โมเมนตัมเชิงมุม โมเมนตัมเชิงมุมจะคงที่ เมื่อมีการลดโมเมนต์ความเฉื่อยของการหมุน ความเร็วเชิงมุมก็จะเพิ่มขึ้น ทำให้สามารถหมุนตัวได้นาน ที่นักเต้นบัลเล่ต์เต้นไปจนหยุดหมุนนั้นก็เพราะแรงเสียดทานที่เกิดขึ้นกับพื้นบริเวณที่เท้าสัมผัสและแรงเสียดทานจากอากาศ เราจะเห็นเหตุการณ์นี้เกิดขึ้
เรายังสามารถใช้กฎการอนุรักษ์โมเมนตัมเชิงมุมกับนักกระโดดน้ำ ที่โมเมนตัมเชิงมุมนั้นคงที่ตลอดการกระโดด แต่นักกระโดดน้ำสามารถควบคุมร่างกายได้ เพราะหลังจากที่กระโดดหมุนตัวโดยมีการหดแนบตัวให้เล็กนี้ ในตอนสุดท้ายนักกระโดดน้ำได้ยืดแขนและขาให้ยาวตรงเพิ่มโมเมนต์ความเฉื่อยของการหมุนและลดความเร็วเชิงมุม ทำให้นักกระโดดน้ำสามารถควบคุมร่างกายให้ตรงได้เมื่อเวลาถึงสัมผัสน้ำ น้ำจะกระจายออกน้อยที่สุด
ฟิสิกส์นั้นวิชาที่สนุกและถ้าเราเอาความรู้วิชาที่เรียนมาไปพยายามอธิบายปรากฎการณ์ต่างๆที่เกิดขึ้นรอบตัวเรา เราจะพบว่าฟิสิกส์สามารถอธิบายสิ่งต่างๆได้ดีตั้งแต่ละดับเล็กขนาดอะตอมไปจนถึงขนาดใหญ่ระดับดาวฤกษ์ต่างๆ เช่นการนำกฎการอนุรักษ์โมเมนตัมเชิงมุมไปอธิบายท่าเต้นบัลเล่ต์สุดยากนี้ เป็นต้น
เรียบเรียงโดย
ณัฐพล โชติศรีศุภรัตน์
ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
อ้างอิง
- Resnick, R., Walker, J. and Halliday, D. (2014). Fundamentals of physics. Hoboken, N.J.: Wiley.
- https://www.ted.com/talks/arleen_sugano_the_physics_of_the_hardest_move_in_ballet/transcript?language=en#t-221605
- https://courses.lumenlearning.com/boundless-physics/chapter/conservation-of-angular-momentum/
บทความฟิสิกส์ล่าสุด
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

