ใช้ความรู้เรื่องสมดุลกลอธิบายว่าทำไมหอเอนเมืองปิซายังคงตั้งตระหง่านได้

https://www.theaustralian.com.au/world/the-times/leaning-tower-of-pisa-is-straightening-up/news-story/56e85cd7cadbdec8c07b10ab5cb722d9

          อิตาลีเป็นพื้นที่ของอาณาจักรโรมันเก่า มีสถานที่ท่องเที่ยวมากมาย เป็นประเทศที่มีสถาปัตยกรรมต่างๆสวยงาม อีกหนึ่งในสถานที่ที่ผู้คนชอบไปถ่ายรูปในอิตาลีคือหอเอนเมืองปิซา (Leaning Tower of Pisa) เป็นหอทรงกระบอกขนาด 8 ชั้นมีความสูง 55.86 เมตร สร้างมาจากหินอ่อนสีขาวสวยงามมาก ตั้งอยู่ที่เมืองปิซา เริ่มสร้างขึ้นในปี ค.ศ. 1173 ใช้เวลาสร้างเกือบสองร้อยปี จึงสร้างเสร็จในปี ค.ศ. 1372 เนื่องมาจากพื้นดินที่นุ่มเกิดการยุบตัวทำให้ต้องมีการหยุดพักการสร้าง ด้วยเหตุนี้เองทำให้หอนี้เอียงอย่างไม่ได้ตั้งใจ ผู้คนชอบไปถ่ายรูปกันมากเพราะหอนี้เอียงอย่างชัดเจนแตกต่างจากสิ่งก่อสร้างอื่นๆ แต่มันก็ไม่ถล่มลงมา ยังคงตั้งตระหง่านอยู่กว่าประมาณ 700 ปี นับตั้งแต่เสร็จสมบูรณ์ แต่ทำไมหอเอนเมืองปิซานี้อย่างตั้งตระหง่านอยู่ได้ เราจะใช้ความรู้เรื่องสมดุลกลมาอธิบายเรื่องนี้กัน


          สิ่งก่อสร้างของมนุษย์ควรจะมั่นคงอันเนื่องมาจากแรงที่มากระทำต่อมัน ยกตัวอย่างเช่นตึกต่างๆเช่นตึกมหานครควรจะมั่นคงอันเนื่องมาจากแรงโน้มถ่วงและแรงลมมากระทำต่อมัน หรือยกตัวอย่างเช่นหนังสือ Feynman Lectures On Physics วางนิ่งอยู่บนโต๊ะ เราเรียกสิ่งนี้ว่ามันมีสภาพสมดุล (equilibrium) หมายถึงภาวะที่วัตถุอยู่ในสภาพนิ่งหรือเคลื่อนที่ด้วยความเร็วคงตัว โดยถ้าวัตถุนั้นไม่ได้มีการเคลื่อนที่ทั้งการหมุนและการเลื่อนที่เราเรียกว่ามันมีสภาพสมดุลสถิตย์ (static equilibrium) 


          โดยถ้าวัตถุแข็งเกร็งอยู่ในสภาพสมดุลสถิตย์แล้ว ผลรวมเว็กเตอร์ของแรงภายนอกทั้งหมดที่กระทำต่อวัตถุนั้นจะเป็นศูนย์

\(\vec{F}\)_net = 0

 

          ถ้าแรงทั้งหมดอยู่ในระนาบแกน  xy จะสามารถเขียนได้เป็น

\(F\)_net,x = 0 ,  \(F\)_net,y = 0 

          และเรายังต้องคำนึงถึงเรื่องทอร์กด้วย โดยในสภาพสมดุลสถิตย์ผลรวมเว็กเตอร์ของทอร์กภายนอกที่กระทำต่อวัตถุ ณ ที่จุดใดๆจะเป็นศูนย์ โดยถ้าแรงอยู่ในระนาบแกน xy เวกเตอร์ทอร์กทั้งหมดจะขนานกับแกน z สมการสมดุลของทอร์กจะเหลือสมการองค์ประกอบเดียว คือ
 

\(T\)_net,z = 0
 

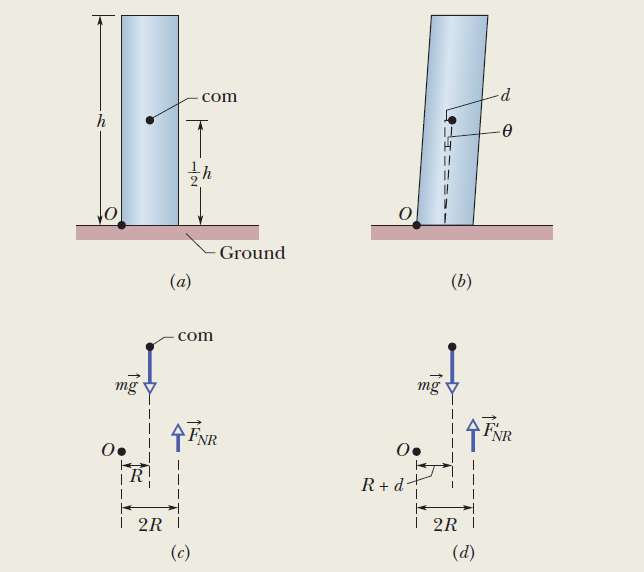
          เมื่อเราเข้าใจเนื้อหานี้แล้ว เราก็สามารถนำมาใช้อธิบายเรื่องหอเอนเมืองปิซาได้ โดยเพื่อความสะดวกเราจะปรับเปลี่ยนข้อมูลเพื่อให้เราแก้สมการได้ง่ายขึ้น โดยสาระสำคัญหลักที่เราต้องการทราบยังคงเดิม เราสมมติให้หอเอนเมืองปิซานี้เป็นทรงกระบวกกลวงมีรัศมี R= 9.8 เมตร สูง 60 เมตร จุดศูนย์กลางมวลตั้งอยู่ตรงกลางของทรงกระบอก โดยทรงกระบอกหนึ่งตั้งอยู่ตรงพอดี ขณะที่อีกอันหนึ่งเอียง 5.5 องศาไปทางขวา ทำให้จุดศูนย์กลางมวลย้ายจากจุดศูนย์กลางมาเป็นระยะทาง d มีแรงตั้งฉาก \(\vec{F}\) _NL ของผนังด้านซ้ายและมีแรงตั้งฉาก \(\vec{F}\) _NR ของผนังด้านขวา เทียบกันแล้ว \(\vec{F}\) _NR ที่เพิ่มขึ้นจากการเอียงจากปรกติเป็นร้อยละเท่าไหร่
 

          Resnick, R., Walker, J. and Halliday, D. (2014). Fundamentals of physics. Hoboken, N.J.: Wiley.

         เพราะว่าหอเอนเมืองปิซายังตั้งอยู่ได้ ดังนั้นมันอยู่ในภาวะสมดุล ดังนั้นผลรวมของทอร์กรอบจุดใดๆจะต้องเป็นศูนย์ เราต้องการรู้  \(\vec{F}\) _NR ที่ฝั่งขวาฉะนั้นเราจึงเลือกจุดหมุน ณ ที่ฝั่งซ้าย โดยจะมีแรงโน้มถ่วง \(m\vec{g}\)  กระทำ ณ ที่จุดศูนย์กลางมวล ในกรณีทรงกระบอกที่ตั้งตรง ไม่ได้ล้มลงฉะนั้นผลรวมของทอร์กรอบจุดใดๆจะต้องเป็นศูนย์ เราจึงสามารถเขียนสมการได้เป็น

 

 

         จะได้

\(F\)_NR = \(\dfrac{1}{2} mg\)

         อีกกรณีทรงกระบอกที่เอียง เราจะได้ระยะทาง d คือ

 

\(d =\)\(\dfrac{1}{2}h \)  \(tan ⁡θ\)

         แรงตั้งฉากของกระบอกที่เอียงคือ \(F\)_'NR แม้จะเอียงแต่ก็ยังตั้งอยู่ได้ฉะนั้นผลรวมของทอร์กรอบจุดใดๆจะต้องเป็นศูนย์ เราจึงสามารถเขียนสมการได้เป็น

 

\(-(R+d)(mg)+(2R)\)\((F\)'_NR \()\)\(=0\)

         
         ย้ายข้างสมการเพื่อหา \(F\)'_NR จะได้

\(F\)'_{NR  \(= \)} \(\dfrac{R+d}{2R}mg\)

         

         เพื่อที่จะหาว่า \(\vec{F}\)_NR ที่เพิ่มขึ้นจากการเอียงจากปรกติเป็นร้อยละเท่าไหร่เราก็จับมาเทียบกันจะได้
 

 

         เมื่อแทนค่าต่างๆแล้วก็จะได้ 
 

\(\dfrac{F'_{NR}}{F_{NR}} = 1.29\)
 

          นั่นหมายความว่าแม้หอเอนเมืองปิซาจะเอียงแค่เพียง 5.5 องศา แต่กำแพงฝั่งที่เอียงต้องรับน้ำหนักเพิ่มมากขึ้นถึงร้อยละ 29 ซึ่งถือว่าเพิ่มขึ้นมาก แรงที่กดลงในดินอ่อนนุ่มนี้จะทำให้เกิดการทรุดตัว และการเอียงก็จะเพิ่มขึ้นอีก แรงที่กดลงก็จะมากขึ้นไปอีกจนในที่สุดหอเอนเมืองปิซาก็จะถล่มลงมา การคำนวณนี้เน้นย้ำให้เห็นว่าแม้มีการเอียงเพิ่มขึ้นไม่กี่องศาแต่แรงที่กดลงมาจะเพิ่มขึ้นอย่างมาก นี่เป็นอันตรายของตึกที่เอียง 

         

ก้อนตะกั่วถ่วงน้ำหนัก
https://en.wikipedia.org/wiki/File:Pisa_schiefer_turm_gewichte_1998_01.jpg

 

          ฉะนั้นคำถามก็คือทำไมหอเอนเมืองปิซายังไม่ถล่มลงมา คำตอบคือเพราะในปี ค.ศ. 1990 หอนี้เอียง 5.5 องศา แต่เพราะวิศวกรได้ทำการซ่อมแซม ระหว่างปี ค.ศ. 1993- ค.ศ. 2001 ทำให้การเอียงลดลงมาเหลือ 3.97 องศา และได้เพิ่มความแข็งแรงของรากฐาน และนำก้อนตะกั่วหนักจำนวนมากมาเป็นน้ำหนักถ่วงที่กำแพงอีกด้านหนึ่ง และเมื่อเปลี่ยนองศาจาก 5.5 องศามาเหลือ 3.97 องศา เมื่อนำไปแทนค่าในสมการ น้ำหนักที่เพิ่มขึ้นจากร้อยละ 29 ก็จะลดลงเหลือร้อยละ 21 นับว่าลดลงอย่างมีนัยสำคัญ สรุปแล้วหอเอนเมืองปิซายังตั้งตระหง่านอยู่ได้เพราะมันอยู่ในสภาพสมดุลสถิตย์และการช่วยเหลือจากวิศวกรในการเพิ่มความเข้มแข็งของรากฐาน ลดองศาการเอียง และนำก้อนตะกั่วหนักจำนวนมากมาเป็นน้ำหนักถ่วงที่กำแพงอีกด้านหนึ่งนั่นเอง


          ในปี ค.ศ. 2008 วิศวกรประกาศว่าหอเอนเมืองปิซาถูกทำให้มั่นคงแข็งแรงและหยุดการเอียงได้เป็นครั้งแรกในประวัติศาสตร์และมันจะมั่นคงแข็งแรงไปอีกอย่างน้อย 200 ปี ก็นับว่ายังมีเวลาเหลืออีกมากสำหรับนักท่องเที่ยวที่ต้องการไปถ่ายรูปหอเอนเมืองปิซานี้
 

เรียบเรียงโดย

ณัฐพล โชติศรีศุภรัตน์
ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ

อ้างอิง