การเพิ่มประสิทธิภาพในวงจรควอนตั้ม
29-04-2020 อ่าน 3,071
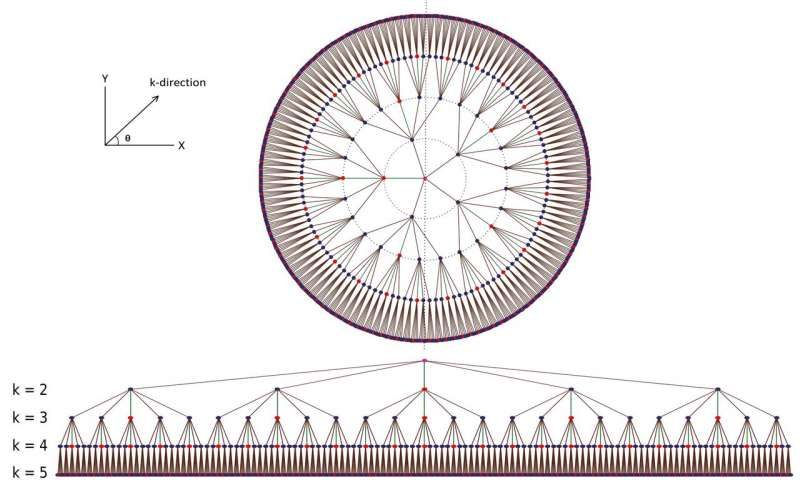
รูปที่1 แสดงชั้นเลเยอร์ของวงจรควอนตั้ม ซึ่งแสดงให้เห็นถึงเลเยอร์ของ error Torrance ที่มีจำนวนเล็กมากๆ
ที่มา Authors/Physical Review Letters
วงจรควอนตั้ม หรือ ที่เรียกว่า Quantum Circuits เป็นตัวต้นแบบหรือเรียกได้ว่าเป็นหัวใจหลักสำคัญ ในการคำนวณสำหรับทางควอนตั้มนั้น ซึ่งภายในจะประกอบไปด้วย ควอนตั้มเกต ที่มีจำพวกที่เรียกว่า วงจรไฟฟ้าสำหรับป้อนกระแส ขึ้น(1) และ ลง(0) ซึ่งอยากจะอธิบาย ณ ตรงนี้ไว้ก่อนว่า บางคนอาจจะสงสัยไม่ได้แตกต่างไรจาก classical computer แบบดั้งเดิม แต่ คอมพิวเตอร์แบบดั้งเดิมนั้น เวลาประมวลผลออกมาเป็นตัวเลขฐานสองนั้น จะมีได้เพียงแค่อย่างเดียวเท่านั้น หมายถึง ไม่ 1(High) ก็ 0(Low)ไปเลย แต่ในทางตรงกันข้าม วงจรควอนตั้มนั้น จะเป็นการเคลื่อนที่ของอิเล็กตรอนในระดับควอนตั้ม ไปมา โดยที่การประมวลผลออกมาเป็นตัวเลขนั้น สามารถออกมาได้แบบคู่กันได้เลย เช่น <00|01> ทำให้ลดระยะเวลาในการประมวลผลนั้นลดลง และมีความแม่นยำมากขึ้น ซึ่งจะเป็นการอธิบายการเกิดวงจรควอนตั้มนั้นเป็นมาอย่างไรกัน ซึ่งมีงานวิจัยชิ้นนึงที่ทำการพัฒนาประสิทธิภาพของวงจรควอนตั้มนั้น ซึ่งจะทำการเปรียบเทียบวงจรแบบควอนตั้มนี้ เหมือนกับบล็อกที่ต่อๆกันจนรวมเป็นส่วนหนึ่งของควอนตั้มคอมพิวเตอร์ ซึ่งจะเป็นการช่วยให้มีการประมวลผลที่รวดเร็วและแม่นยำขึ้น แต่อย่างไรก็ตามอาจจะมีความผิดพลาดในการคำนวณและการประมวลผลอยู่บ้าง ซึ่งเป็นสิ่งที่น่าสนใจในการพัฒนาประสิทธิภาพของวงจรแบบควอนตั้ม นั้นให้มีความผิดพลาดที่มาจากคำนวณให้ได้น้อยที่สุด นักวิจัยจากthe Indian Institute of Science (IISc) ได้ทำการวิจัยและคิดค้น จำนวนอัลกอริทึมของระบบ และ ทำการพัฒนาให้มีประสิทธิภาพสูงสุดในระบบ ซึ่งในงานวิจัยนี้จะได้ถูกตีพิมพ์ในวรสาร Physical Review Letters ซึ่งนักวิจัยได้ให้คำแนะนำเกี่ยวกับการปรับปรุงให้มีประสิทธิภาพสูงสุดสำหรับวงจรควอนตั้ม
การปรับปรุงประสิทธิภาพวงจรควอนตั้มนั้นจะเป็นประโยชน์ต่อการใช้ในสนามไฟฟ้าที่แตกต่างกัน โดยเฉพาะการคำนวณทางควอนตั้ม ซึ่งจะไม่เพียงแค่ประมวลผลเร็ว และ แม่นยำเท่านั้น อีกทั้งยังจะต้องไม่ถูกโจรกรรมข้อมูลได้อีกด้วย ตัวอย่างเช่น การทำธุรกรรมทางการเงินของธนาคารที่เราใช้ในการ ถอนเงิน โอนเงิน จะสามารถปกป้องข้อมูลจากโจรได้ ซึ่งต่อไปการคำนวณทางควอนตั้มในวงจรนั้น จะสามารถนำไปใช้ได้กับการพัฒนาขนส่งมวลชน และ การจำลองสถานะทางการตลาด ในปัจจุบัน จนถึงอนาคตได้อีกด้วย ซึ่งก่อนหน้านี้การคำนวณวงจรแบบดั้งเดิมนั้น จะคำนวณวงจรแบบลอจิก ดั่งเช่น แนนเกต และ นอร์ เกต ซึ่งจะสามารถป้อนกระแสไฟเข้าและออกได้ ในบางคนอาจจะสงสัยอะไรคือ แนนเกต และ นอร์เกต ซึ่งสามารถอธิบายได้ดังต่อไปนี้ ลอจิกเกต เป็นการป้อนวงจรไฟฟ้าเข้าและจะมีกระแสไฟฟ้าออกจากตัววงจร ตัวอย่างเช่น น็อตเกต จะมีตรรกะความเป็นจริงก็คือ เมื่อป้อนกระแสไฟฟ้าเข้าไปเป็น 1(High) สิ่งที่ได้ออกมาจากเอ้าท์พุตจะได้ค่าที่เป็น0(Low) ต่อมา แนนเกตนั้นจะเป็นการผสมผสานระหว่าง วงจรแอนเกต ที่มีตรรกะความจริงคือ เมื่อป้อนวงจรไฟเข้าเป็น 1(High) และ 1(High) จะได้วงจรไฟออกอยู่ที่ 1(High) กับ วงจรน็อตเกตที่ได้กล่าวไปข้างต้น ซึ่งวงจรแอนเกตที่ได้จะมีตรรกะความเป็นจริงดังรูปแสดง รูปที่ 2 และ รูปที่ 3
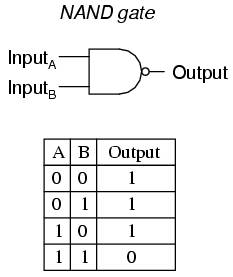
รูปที่2 แสดงตรรกะความจริงของ แนนเกต
ที่มา https://www.toppr.com/ask/question/write-the-logic-symbol-and-truth-table-of-nand-gate/
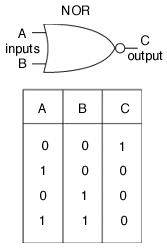
รูปที่3 แสดงตรรกะความจริงของ นอร์เกต
ที่มา http://www.freeinfosociety.com/article.php?id=3
ซึ่งแนนเกตนั้น จะมีตรรกะความเป็นจริงคือ 0(Low)ต่อเมื่อ ไฟเข้าที่วงจรนั้นจะต้องเป็น 1(High) และ 1(High)ด้วยกันทั้งคู่ แต่ในทางตรงกันข้าม นอร์เกต จะมีตรรกะความเป็นจริงคือ 1(High)ก็ต่อเมื่อ วงจรไฟเข้านั้นเป็น 0(Low) และ 0(Low) ด้วยกันทั้งคู่ ซึ่งที่ได้กล่าวไปนั้นจะเป็นในส่วนของการคำนวณวงแบบดั้งเดิม ซึ่งจะมีความคาดเคลื่อนอยู่มากทางทีมวิจัยเลยตระหนักถึงการพัฒนาการคำนวนโดยนำควอนตั้มมาใช้เพื่อลดค่าความคาดเคลื่อนนี้ลง ซึ่งในปี2006 Michael Nielsen จาก University of Queensland ได้พัฒนาในการเพิ่มประสิทธิภาพให้กับวงจรนับของควอนตั้มเกตด้วยการลดระยะทางจุดสองจุดของเกตด้วยการใช้หลักการที่มา https://www.toppr.com/ask/question/write-the-logic-symbol-and-truth-table-of-nand-gate/

รูปที่3 แสดงตรรกะความจริงของ นอร์เกต
ที่มา http://www.freeinfosociety.com/article.php?id=3

รูปที่4 แสดงถึงขอบเขตสเปสของวงจรควอนตั้มในD-dimensionalปริมาตรV
ที่มา Quantum Computation as Geometry
ที่มา Quantum Computation as Geometry
ทางคณิตศาสตร์ ซึ่งมาจากการคำนวณรูปทรงทางเรขาคณิต ซึ่งจะมาจากสูตรการคำนวน

บทความโดย
นวะวัฒน์ เจริญสุข
วิศวกรรมยานยนต์
สถาบันเทคโนโลยีพระจอมเกล้าเจ้าคุณทหารลาดกระบัง
นวะวัฒน์ เจริญสุข
วิศวกรรมยานยนต์
สถาบันเทคโนโลยีพระจอมเกล้าเจ้าคุณทหารลาดกระบัง
ที่มา
บทความฟิสิกส์ล่าสุด
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
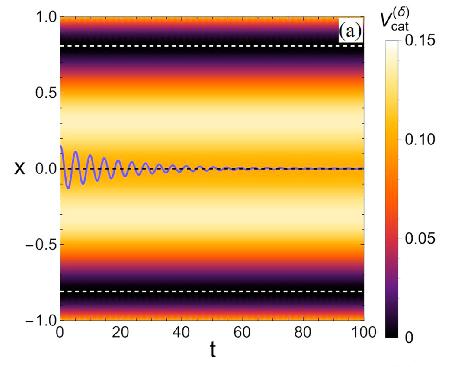 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

