การประยุกต์ทฤษฏีฟิสิกส์ในทฤษฎีเกม
26-10-2020 อ่าน 5,277
เกมในความหมายทั่วไปของคนส่วนใหญ่ มักจะนึกถึงเกมหมากประเภทต่างๆและเกมไพ่รูปแบบต่างๆ ที่ต้องมีผู้ชนะกับผู้แพ้อย่างชัดเจนซึ่งเมื่อเป็นเกม คนส่วนใหญ่มักจะเล่นแบบไม่ได้คิดอะไรมากหรือเล่นเพื่อความสนุกสนาน แต่มุมมองของคำว่าเกมก็เปลี่ยนไป ในปี 1947 โดย จอห์น ฟอน นอยมันน์ (John von Neumann) ที่พิจารณาเกมในรูปแบบปัญหาอย่างง่ายผ่านตัวเลขของผลตอบแทน (payoff) จากการตัดสินใจเลือกแต่ละกลยุทธ์และผลลัพธ์ที่เกิดขึ้นซึ่งเป็นผลมาจากคู่แข่งด้วย ทฤษฎีเกม (Game theory) ก็เริ่มมีการพูดถึงมากขึ้นต่อมา ในปี 1950-51 จอห์น แนช (John Nash) ได้นำเสนอ เกมแบบไม่ร่วมมือกัน (non-cooperative game) ซึ่งผลลัพธ์ของเกมประเภทนี้ ผู้เล่นทุกคนสามารถเสมอกันได้หรือแบ่งตอบแทนเท่าๆ กัน ที่ไม่ใช่ผลตอบแทนสูงสุดแก่ผู้เล่นทุกคน เรียกว่า ดุลยภาพแนช (Nash equilibrium) เพื่อทำความเข้าใจดุลยภาพแนชให้ชัดเจนขึ้น โดยยกตัวอย่างเกมอย่างง่ายที่มักนำมาอธิบาย คือ เกมทวิบทนักโทษ (prison’s dilemma game) เป็นสถานการณ์ที่มีนักโทษ 2 คน คือ นักโทษส้ม กับ นักโทษเขียว ซึ่งนักโทษทั้งสองจะถูกสอบสวนแยกออกจากกันทำให้ไม่สามารถร่วมมือกันได้ โดยนักโทษแต่ละคนสามารถเลือกได้ 2 กลยุทธ์ คือ สารภาพ กับ ไม่สารภาพ ผลลัพธ์จากการตัดสินใจในแต่ละกลยุทธ์ของนักโทษแต่ละคนจะให้ผลออกมาตามตารางผลลัพธ์ ดังรูปที่ 1. โดยจำนวนปี คือ เวลาที่ต้องติดคุก

รูปที่ 1 : ตารางผลลัพธ์ในแต่ละการตัดสินใจของเกมทวิบทนักโทษ โดยจำนวนปี คือ เวลาที่ต้องติดคุก
1. ถ้านักโทษส้มเลือก ไม่สภาพ แต่ถ้าเกิดนักโทษเขียวหักหลังโดยเลือกสารภาพนักโทษส้มก็ต้องติดคุก 10 ปีและนักโทษเขียวจะเป็นอิสระ ซึ่งมีความเสี่ยงสูงเกินไปสำหรับนักโทษส้ม
2. ถ้านักโทษส้มเลือก สภาพ แต่ถ้านักโทษเขียวเลือกสภาพคนทั้งจะติดคุกแค่ 3 ปี และถ้านักโทษเขียวเลือกไม่สภาพนักโทษส้มก็จะเป็นอิสระ
เพราะฉะนั้นผลของทางเลือกที่ดีกับตัวเองที่สุดของนักโทษส้ม คือ สารภาพ ด้วยเหตุผลเช่นเดียวกันนี้ทำให้ผลของทางเลือกที่ดีกับตัวเองที่สุดของนักโทษเขียวจึงเป็นสารภาพเช่นเดียวกัน ซึ่งนักโทษทั้งสองคนเลือกสารภาพทั้งคู่ซึ่งเป็นทางเลือกที่ดีกับตัวเองที่สุดจึงเป็นดุลยภาพแนชในเกมนี้ แต่ถ้านักโทษทั้งสองได้ร่วมกันก็จะเลือก ไม่สภาพ ทั้งคู่ทำให้ติดคุกคนละ 1 ปี ซึ่งให้ผลตอบแทนที่มากกว่าดุลยภาพแนช จากมุมมองของเกมแบบไม่ร่วมมือกันและดุลยภาพแนชได้ถูกนำไปประยุกต์ในการตัดสินใจปัญหาต่างๆในเศรษฐศาสตร์

รูปที่ 2 : ตัวอย่างเมตริกซ์ผลตอบแทน (payoff matrix) ของเกมทวิบทนักโทษแบบควอนตัม (quantum prison’s dilemma game) ที่ติดตัวแปรต่างๆ ตามเงือนไขทางควอนตัม โดย C คือ ร่วมมือ (cooperate), D คือ หักหลัง (defect) และ Q คือ ควอนตัม (quantum) เครดิตรูปภาพจากแหล่งอ้างอิง [3]
ในปี 1999 เริ่มมีการนำสมบัติการซ้อนทับ (superposition) ของกลศาสตร์ควอนตัมมาใช้ในทฤษฎีเกม โดยเฉพาะของ Jens Eisert และทีมงาน ด้วยการดัดแปลงเกมทวิบทนักโทษซึ่งให้นักโทษทั้งสองสามารถเลือกได้สองทางเลือกเปรียบเสมือนการให้รหัสบิต (bit) ที่เป็น 0 หรือ 1 และเปลี่ยนทางเลือกของกลยุทธ์ไปเป็นรูปแบบ ร่วมมือ (cooperate) หรือ หักหลัง (defect) แทน สารภาพ หรือ ไม่สารภาพ เพิ่มเติมด้วยรูปแบบสมบัติของควอนตัมโดยการแทนบิตด้วย คิวบิต (qubit) หรือ ควอนตัมบิต (quantum bit) ที่มีสมบัติการซ้อนทับแบบควอนตัม 2 สถานะ ดังเช่น อิเล็กตรอนที่มีสถานะซ้อนทับของ สปินขึ้น (spin up) และ สปินลง (spin down) จนกว่าจะถูกวัดจึงแสดงได้แค่ 1 สถานะเท่านั้น ซึ่งผู้เล่นแต่ละคนสามารถแสดงทางเลือกได้ทั้ง ร่วมมือ และ หักหลัง พร้อมกับให้ผู้เล่นทั้งสองมีความพัวพันเชิงควอนตัม (quantum entanglement) เงื่อนไขความซับซ้อนในแต่ละเกมขึ้นกับนักฟิสิกส์แต่ละคนกำหนดดังในตัวอย่าง รูปที่ 2. ในปัจจับันการศึกษาแนวคิดนี้เรียกว่า ทฤษฎีเกมควอนตัม (quantum game theory) 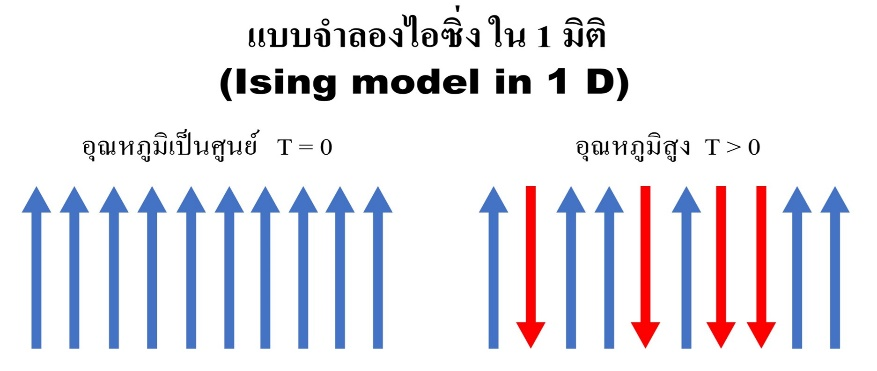
รูปที่ 3. แบบจำลองไอซิ่ง ใน 1 มิติ
นอกจากนี้ ในปี 2020 เดือนสิงหาคม ในวารสาร Chaos เรื่อง Thermodynamic susceptibility as a measure of cooperative behavior in social dilemma โดยเป็นการประยุกต์ สปิน- ½ แบบจำลองไอซิ่งในหนึ่งมิติ (spin-½ Ising model in 1D) เมื่ออุณหภูมิเป็นศูนย์ภายใต้สนามแม่เหล็กภายนอกทิศทางของสปินก็จะไปในทิศทางเดียวกัน แต่เมื่ออุณหภูมิสูงขึ้นสปินเริ่มมีทิศทางต่างกันไปแบบสุ่ม (randomness) ใน 2 แบบ คือ สปินขึ้น และ สปินลง ดังรูปที่ 3. ซึ่งเปรียบเทียบได้กับผู้เล่นแต่ละคนมีการตัดสินใจได้ 2 ทางเลือกแบบสุ่มของผู้เล่นจำนวนมหาศาล (N → ∞) โดยสามารถวิเคราะห์ผ่านค่าสภาพรับไว้ได้ (susceptibility) หรือ ความไวของสปินที่ได้รับผลของสนามแม่เหล็กและอุณหภูมิ ในเกมทวิบทนักโทษ, The hawk-dove game และจัดรูปแบบใหม่ในเกมทวิบทนักโทษแบบควอนตัม (quantum prison’s dilemma game) ถึงแม้ว่าการประยุกต์ทฤษฎีฟิสิกส์ในทฤษฎีเกมจะประยุกต์ใช้ในโลกความเป็นจริงได้ยากเช่นดียวกับดุลยภาพแนชในช่วงแรกแต่ในที่สุดก็มีการประยุกต์ดุลยภาพนี้ในเศรษฐศาสตร์มากมาย จากเหตุนี้จึงมีความเป็นไปได้ที่การประยุกต์ทฤษฎีเกมโดยทฤษฎีฟิสิกส์อาจจะให้ผลประโยชน์ที่เกินจินตนาการในการคำนวณเชิงควอนตัม (quantum computing) ก็เป็นได้บทความโดย
ดร. ธีระวัฒน์ ชัชวาลธีรัตต์
ผู้ช่วยงานวิจัย ภาคฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
ดร. ธีระวัฒน์ ชัชวาลธีรัตต์
ผู้ช่วยงานวิจัย ภาคฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
แหล่งอ้างอิง
- [1] Klarreich, E. Playing by quantum rules. Nature 414, 244–245 (2001). https://doi.org/10.1038/35104702
- [2] Eisert, J., Wilkens, M. & Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 83, 3077 (1999).
- [3] Li, A., Yong, X. Entanglement Guarantees Emergence of Cooperation in Quantum Prisoner's Dilemma Games on Networks. Sci Rep 4, 6286 (2014). https://doi.org/10.1038/srep06286
- [4] Colin Benjamin, Aditya Dash. Thermodynamic susceptibility as a measure of cooperative behavior in social dilemmas. Chaos 30, 093117 (2020); https://doi.org/10.1063/5.0015655
บทความฟิสิกส์ล่าสุด
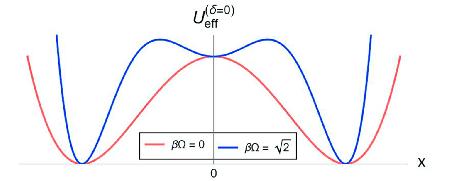 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
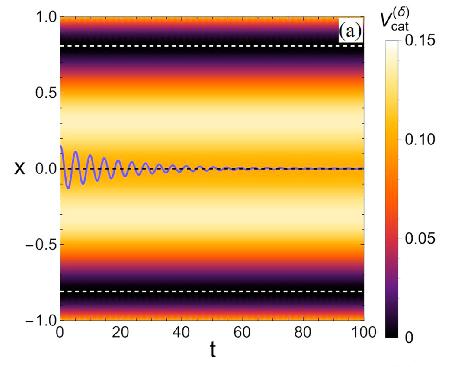 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

