ความต้านทานทางเสียง (Acoustic impedance)

          จากบทความที่ผ่านมาเรื่อง “การวัดค่าสัมประสิทธิ์การดูดซับเสียง” (อ่านและดูภาพประกอบเพิ่มเติมที่ http://www.thaiphysoc.org/article/101/) เราพบเคยว่าในสมการที่ใช้ในการคำนวณหาสัมประสิทธิ์การดูดซับเสียงนั้นตัวแปรหลักๆของทุกวิธีการวัด คือ “ความต้านทานทางเสียง”  ดังนั้นเรามาทำความรู้จัก ความต้านทานทางเสียง กันให้มากยิ่งขึ้นดีกว่า


          ความต้านทาน คือ ตัวชี้วัดความยากลำบากในการเคลื่อนที่ของสิ่งใดสิ่งหนึ่ง ในทางไฟฟ้าความต้านทาน (R) ของวัตถุจะถูกกำหนดให้เป็นอัตราส่วนของ แรงดันไฟฟ้า (Electric voltage, (V)) ต่อกระแส (Electric current, (/))

 

เช่นเดียวกันกับความต้านทานเชิงกลที่มีค่าเท่ากับแรงกระทำภายนอก (External force, (F)) ต่อความเร็ว (Velocity, (v))
 

ในกรณีของเสียงความต้านทานทางเสียง คำนวณได้จาก ความดันเสียง (Sound pressure, (p))  ต่อความเร็วของอนุภาคเสียง (Particle velocity, (v))

 

เมื่อคลื่นเสียงแพร่กระจายในพื้นที่เปิดโล่ง ผ่านตัวกลางที่เป็นอากาศ โดยไม่มีการสูญเสีย ความต้านทานทางเสียง จะเป็นจำนวนจริงเสมอ ซึ่งสามารถคำนวณได้จาก ผลคูณของความหนาแน่นของตัวกลาง (Density, (ρ)) และความเร็วเสียง (Sound speed, (c)) ดังสมการ
 

แล้วค่าความต้านทานเสียงมาเป็นค่าสัมประสิทธิ์การสะท้อน การส่งผ่าน หรือ การดูดซับเสียงได้ยังไง ?

          เมื่อเสียงเดินทางผ่านตัวกลางสองชนิด เกิดความสัมพันธ์ระหว่างการสะท้อนและการส่งผ่านของเสียงดังแสดงในรูปที่ 1 ภายใต้เงื่อนไขสองประการคือ 1) ความดันเสียงต้องมีความต่อเนื่อง และ 2) ความเร็วต้องเท่ากัน แม้ว่าความดันเสียงจะไม่มีทิศทาง แต่ความเร็วเป็นปริมาณเวกเตอร์ด้วยเหตุนี้สามารถเขียนแทนได้ดังสมการ (5.1) และ (5.2)

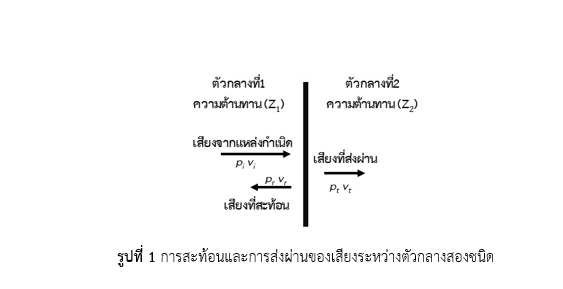
            ดังนั้นค่าสัมประสิทธิ์การดูดซับเสียงจะถูกกำหนดโดยอัตราส่วนความต้านทานทางเสียง (z) ต่อความต้านทานของอากาศ (Z) เราเรียก อัตราส่วนความต้านทานทางเสียงนี้ว่า ความต้านทานทางเสียงปกติของผิววัสดุ (Normalized impedance of the material surface) 


การนำความต้านทานทางเสียงไปใช้จริงทำได้อย่างไร

          มาถึงตรงนี้หลายท่านอาจจะคิดว่ามันไม่ง่ายเลยใช่ไหมครับ กว่าจะมาเป็นค่าสัมประสิทธิ์การสะท้อน การส่งผ่าน หรือ การดูดซับเสียง แต่ทุกท่านไม่ต้องเป็นห่วงครับ เราสามารถนำข้อมูลที่วัดผ่านเครื่องวิเคราะห์การแปลงฟูเรียร์อย่างเร็ว (Fast Fourier transform, (FFT)) เพื่อคำนวณข้อมูลจำนวนมากมายออกมาเป็นชุดข้อมูลสำเร็จรูปหรือเป็นกราฟที่ต้องการ ดังแสดงในรูปที่ 2

            ค่าสัมประสิทธิ์การดูดซับเสียงและค่าความต้านทานเสียงภายหลังการวัดและการคำนวณผ่านเครื่องวิเคราะห์การแปลงฟูเรียร์อย่างเร็วแสดงในรูปที่ 4 รูป 4ก แกนนอนคือ ความถี่ (Frequency) แกนตั้งคือค่าสัมประประสิทธิ์การดูดซับเสียง (Sound abosrption coefficient) โดยค่าที่ได้มาจากการวิเคราะห์การแปลงฟูเรียร์อย่างเร็วในข้อมูล 4ข แกนนอนคือ ความถี่ ส่วนแกนตั้งคืออัตราส่วนความต้านทานทางเสียงที่กล่าวไปในข้างต้น

   

อ้างอิง

• Z. Maekawa, P. Lord, Environmental and Architectural Acoustics, E & FN Spon, London, 1997, pp. 104–105.
• S. Lawanwadeekul, T. Otsuru, R. Tomiku, N. Hi-royasu, I. Eto, D. Matsuoka, and R. Yoshimoto, "Applying the ensemble averaging method with a pressure–velocity sensor to measure sound absorp-tion characteristics of porous clay bricks," Appl. Acoust, 164, 107250, (2020).