จากสมมาตรรูปทรงสู่ moiré exciton ในโครงสร้างผลึก
04-12-2020 อ่าน 3,166
จากการประกาศผลรางวัลโนเบลสาขาฟิสิกส์ในปี 2020 โรเจอร์ เพนโรส (Roger Penrose) ได้ใช้หลักคณิตศาสตร์ทางทอพอโลยี (topology) ช่วยในการศึกษารูปแบบของหลุมดำ แต่น้อยคนนักจะรู้ว่าอีกหนึ่งเรื่องที่เพนโรสโด่งดังในทางคณิตศาสตร์นั้นคือ การหารูปสมมาตรประเภทสมมาตรของการหมุนซึ่งมีความสอดคล้องกับการหมุนให้กลับมาเป็นรูปเดิมได้และมีสมมาตรการสะท้อนด้วย โดยเรียกว่า fold (พับ) หรือ การหมุนด้วยองศาค่าหนึ่ง โดยมีความสัมพันธ์เป็น 1-, 2-, 3-, 4- และ 6-fold ซึ่งแสดงเป็นค่ามุมได้เป็น 360°, 180°, 120°, 90° และ 60° (360°/จำนวน-fold) เช่น เมื่อบิดรูปสามเหลี่ยมด้านเท่าไป 120° จะได้รูปเดิม หรือ เมื่อบิดรูปสี่เหลี่ยมจัตุรัสไป 90° ก็จะเป็นรูปเดิม การศึกษาสามาตรของรูปทรงได้ถูกนำไปประยุกต์ใช้ในการศึกษาโครงสร้างผลึก (lattice) นักวิทยาศาสตร์หลายคนเชื่อว่า ไม่น่าจะมีโครงสร้างผลึกหรือรูปทรงที่สอดคล้องกับ 5-fold (72°)
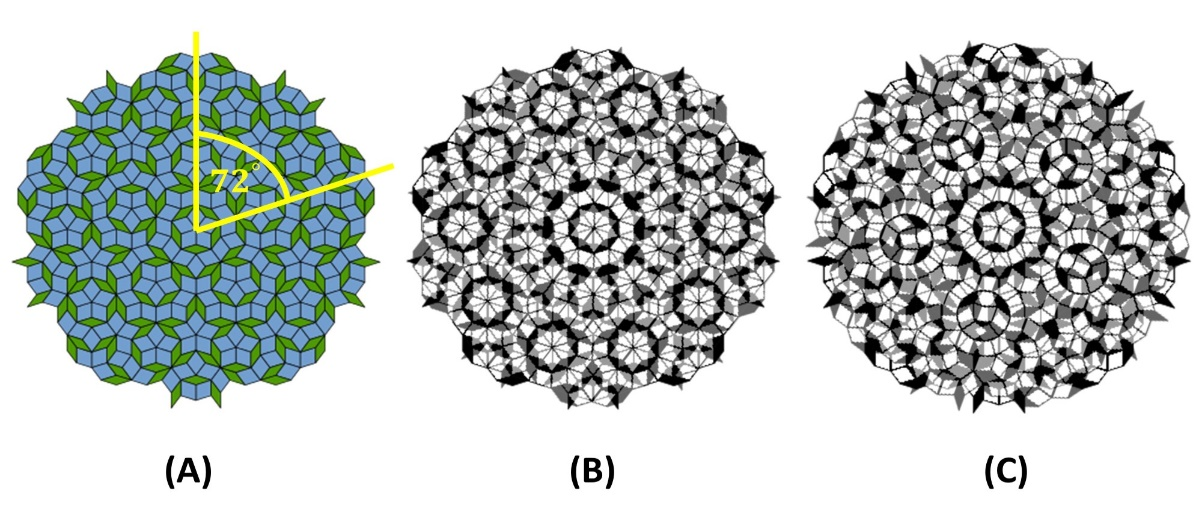
รูปที่ 1: (A) Penrose tiling, (B) และ (C) ลวดลายมัวเรที่เกิดจาก Penrose tiliing 2 แผ่นซ้อนทับกันและบิดด้วยมุมค่าหนึ่ง credit ภาพ: Inductiveload ในแหล่งอ้างอิง [2]
จนกระทั่งในปี 1974 เพนโรส ได้นำเสนอ Penrose tiling ดังรูปที่ 1(A) ซึ่งเมื่อบิดไป 72° (360°/5-fold) จะกับรูปเดิมและมีสมมาตรการสะท้อนด้วย และในปี 1984 มีการค้นพบ quasicrystals ที่เป็นโครงสร้างผลึกที่อยู่รหว่างคริสตัลและของเหลวจากการสังเกต อะตอมแมงกานีส (Mn) ที่ล้อมรอบด้วย อะลูมิเนียม (Al) 12 อะตอมในรูปทรง ทรงยี่สิบหน้า (icosahedron) มี 30 หน้า 12 จุดยอด (vertices) จาก X-ray diffraction ซึ่งแสดงลักษณะใกล้กับสมมาตรแบบ 5-fold ดังรูปที่ 2(A) ในปี 2015 จากวราสาร Scientific report เรื่อง Natural quasicrystal with decagonal symmetry ได้รายงานการค้นพบ quasicrystals ที่มีสมมาตรแบบ 10-fold โดยองค์ประกอบเป็น Al17 Ni24 Fe5 ดังรูปที่ 2(B) ในปัจจุบันการบรรยายของ โรเจอร์ เพนโรสให้กับบุคคลทั่วไป มักจะนำลวดลาย Penrose tilling 2 แผ่นมาซ้อนทับกันแล้วบิดเป็นลวดลายใหม่ๆ ขึ้นมา ดังรูปที่ 1(B) และ 1(C) เพื่อให้ผู้คนทั่วไปตื่นเต้น การที่นำลวดลายสมมาตรมาซ้อนกันให้เกิดลวดลายรูปแบบต่างๆ เรียกว่า ลายมัวเร (moiré)
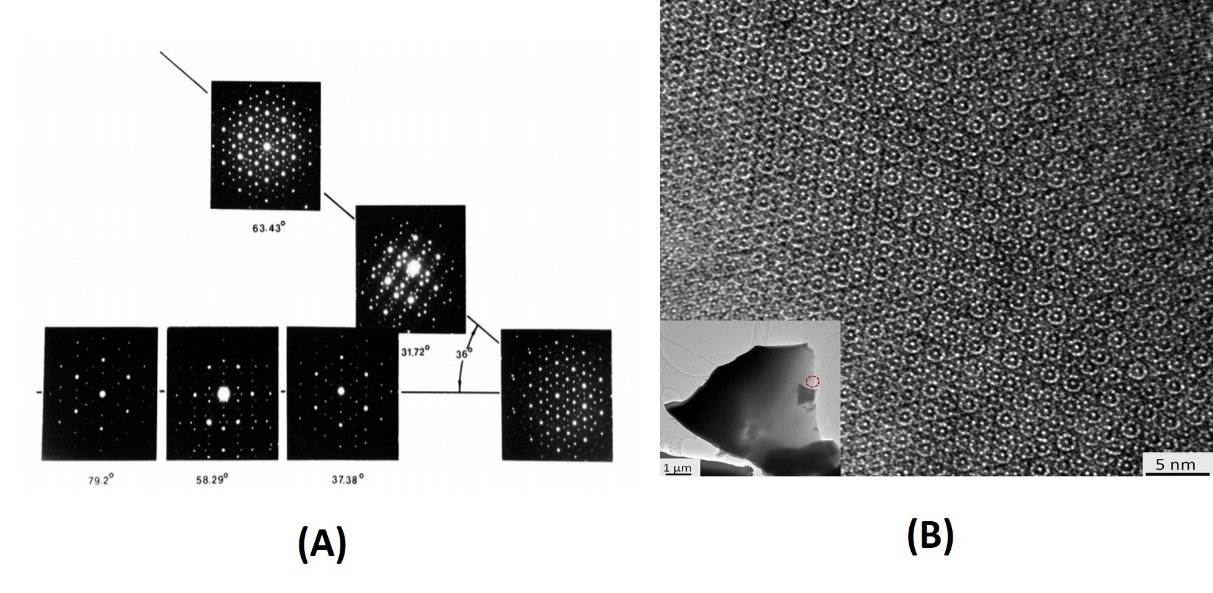
รูปที่ 2: (A) ภาพถ่าย X-ray diffraction ซึ่งแสดงลักษณะใกล้กับสมมาตรแบบ 5-fold จากแหล่งอ้างอิง [4], (B) ภาพ High-resolution transmission electron microscopy (HRTEM) ของ quasicrystals ที่มีสมมาตรแบบ 10-fold จากแหล่งอ้างอิง [3]
จากในปี 2018 กลุ่มนักฟิสิกส์จาก MIT ได้ค้นพบสภาพนำยิ่งยวด (superconductor) จากการนำแผ่นแกรฟีน 2 แผ่นมาบิดกันที่มุม 1.1 องศา ซึ่งแกรฟีนนั้นเป็นวัสดุ 2 มิติ (2 D material) ซึ่งมีความหนาประมาณ 1 ชั้นอะตอม ปรากฏการณ์นี้จึงจุดเรื่มต้นการศึกษานำวัสดุ 2 มิติมาซ้อนกันด้วยพันธะแวนเดอร์วาลส์เป็นโครงสร้างที่เรียกว่า van der Waal (vdW) heterostructures หนึ่งสิ่งสำคัญที่เกี่ยวกับวัสดุคือ การหาช่องว่างระหว่างแถบพลังงาน (energy gap หรือband gap) เพื่อให้ทราบถึงสมบัติต่างๆ เกี่ยวกับการดูดซับคลื่นแม่เหล็กไฟฟ้าในช่วงความถี่เท่าใดและสมบัติการนำไฟฟ้า เมื่อนำมาวัสดุ 2 มิติที่ซับกันและบิดให้เกิดมุมจะทำให้เกิดการเปลี่ยนแปลงโครงสร้างอะตอมของวัสดุที่มีการเลื่อนตำแหน่งไปจากเดิม ดังรูปที่ 3(A) ทำให้สมบัติทางวัสดุเปลี่ยนไปด้วยการศึกษานี้ เรียกว่า moiré excitons ซึ่งผ่านการพิจารณาจากช่องว่างระหว่างแถบพลังงานและอื่นๆ โดยช่องว่างระหว่างแถบพลังงาน Eg อยู่ระหว่างแถบตัวนำ (conductor band) และแถบวาเลนซ์ (valence band) ซึ่งแถบวาเลนซ์เต็มไปด้วยอิเล็กตรอน โดยยกตัวอย่างจากสารกึ่งตัวนำ (semiconductor) เมื่ออุณหภูมิเพิ่มขึ้นอิเล็กตรอนในแถบวาเลนซ์จะถูกกระตุ้นขึ้นไปที่แถบตัวนำ การเกิด excitons นั้น มีสาเหตุหลักๆมาจากเมื่อมีโฟตอน (photon) หรืออนุภาคแสงที่มีพลังงานมากกว่าช่องว่างระหว่างแถบพลังงาน Eg ทำให้เกิดชั้นแถบพลังงานใหม่เรียกว่า excitron level ใต้แถบตัวนำ

รูปที่ 3: (A) วัสดุ 2 มิติ MoS2/WS2 ซ้อนกันและบิดด้วยมุม 3.48° และ 56.52° , (B) ภาพแถบพลังานเมื่อมีมุมต่างกัน และ ภาพความหนาแน่นประจุในแถบตัวนำน้อยสุด (conductor band minimum: CBM) ใช้สีแดง กับ ภาพความหนาแน่นประจุในแถบวาเสนซ์น้อยสุด (valence band minimum: VBM) ใช้สีน้ำเงิน , (C) การเปลี่ยนแปลงเมื่อเปิดสนามไฟฟ้า Credit ภาพ: แหล่งอ้าอิง [5]
ในบทความนี้จะกล่าวเฉพาะ vdw heterostructures แบบ โลหะทรานซิชันไดคาลโคจิไนด์ (Transition metal dichalcogenide, TMD) ซึ่งมีองค์ประกอบทางเคมีเป็น MoX2/WX2 โดย Mo และ W เป็นธาตุโลหะทรานซิชัน ส่วน X เป็นคาลโลเจน ในเดือนตุลาคม ปี 2020 ได้มีงานวิจัยเรื่อง Shedding light on moiré excitons: A first-principles perspective โดยตีพิมพ์ในวราสาร Science advances ซึ่งใช้วัสดุ 2 มิติที่นำมาซ้อนกัน คือ MoS2/WS2 ซึ่งโดยรวมวิเคราะห์ exciton ผ่านคำนวณหาความหนาแน่นประจุ (charge density) ภายในโครงสร้างจาก first-principle เมื่อพบคำว่า first-principle ในงานวิจัยเกี่ยวกับแขนงวัสดุต่างๆ มักหมายถึง Density functional theory (DFT) หรือเรียกอีกชื่อหนึ่งว่า ab initio ซึ่งใช้คอมพิวเตอร์ช่วยการคำนวณและจำลองภาพ ดังรูปที่ 3(B) ในช่วงปี 1970 เทคนิค DFT เป็นที่นิยมในฟิสิกส์สถานะของแข็ง (solid-state physics) แต่ยังไม่พียงพอสำหรับควอนตัมเชิงเคมี (quantum chemistry) จนกระทั่งในปี 1990 ได้เพิ่มการประมาณค่าใหม่ที่เกี่ยวข้องกับอันตรกิริยาแลกเปลี่ยนภายในการประมาณ Hartee-Fock และความสัมพันธ์ระหว่างอิเล็กตรอนซึ่งการปรับแต่งครั้งนี้เป็นการพัฒนาทฤษฏีควอนตัมในระบบหลายอนุภาค (many-body system) หลังจากการปรับ DFT ในแบบใหม่สามารถศึกษาทิศทางของสนามไฟฟ้า(electric field gradient) ในโครงสร้างผลึกดังรูปที่ 3(C) จากการศึกษาเกี่ยวกับสมมาตรทางคณิตศาสตร์ไปสู่โครงสร้างผลึกในฟิสิกส์ แต่สำหรับ moiré exciton ยังคงเป็นเรื่องใหม่ทางฟิสิกส์ ในอนาคตอาจจะมีนักคณิตศาสตร์หรือนักฟิสิกส์ที่เห็นความสอดคล้องกับทฤษฏีทางคณิตศาสตร์ในลายมัวเรมาประยุกต์ใช้อย่างมีประสิทธิภาพต่อการศึกษาโครงสร้างผลึกก็เป็นไปได้
บทความโดย
ดร. ธีระวัฒน์ ชัชวาลธีรัตต์
ผู้ช่วยงานวิจัย
ภาคฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
ผู้ช่วยงานวิจัย
ภาคฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
แหล่งอ้างอิง
- [1] Kittel, C. (2004). Introduction to solid state physics (8th ed.). John Wiley & Sons.
- [2] Penrose tiling: https://en.wikipedia.org/wiki/Penrose_tiling
- [3] Bindi, L., Yao, N., Lin, C. et al. Natural quasicrystal with decagonal symmetry. Sci Rep 5, 9111 (2015). https://doi.org/10.1038/srep09111
- [4] Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J. (1984). "Metallic Phase with Long-Range Orientational Order and No Translational Symmetry". Physical Review Letters. 53 (20): 1951–1953. doi:10.1103/PhysRevLett.53.1951
- [5] Hongli Guo et al, Science Advances 16 Oct 2020: Vol. 6, no. 42, eabc5638 DOI: 10.1126/sciadv.abc5638
- [6] Kittel, C. Quantum Theory of Solids. John Wiley & Sons.
บทความฟิสิกส์ล่าสุด
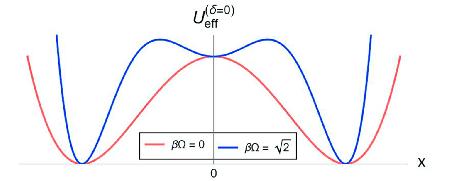 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
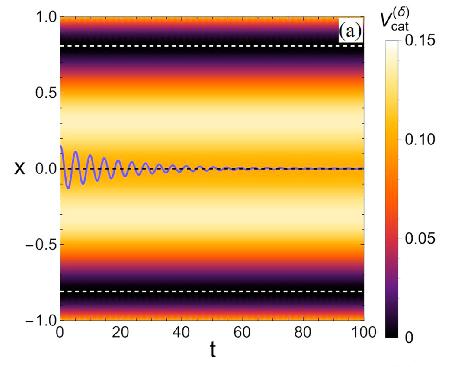 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

