การใช้ลูกตุ้มชนิดบิด (torsion pendulum) ในการช่วยหาโมเมนต์ความเฉื่อย (moment of inertia)
25-01-2021 อ่าน 8,981

τ=-κθ (1)
โดย τ,κ,θ คือ ทอร์กดึงกลับ (restoring torque) ค่าคงที่การบิด (torsion constant) และแอมพลิจูดเชิงมุมของการบิดตามลำดับ

การทำงานของลูกตุ้มชนิดบิด
เครดิต Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of physics. John Wiley & Sons.
เครดิต Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of physics. John Wiley & Sons.
จะสังเกตได้ว่า (1) นี้คล้ายกับกฎของฮุกที่กล่าวว่า เมื่อมีแรงดึงหรือกดวัสดุ ความยาวที่ยืดออกหรือหดเข้าของวัสดุจะเป็นสัดส่วนกับแรงแต่ต่างกันตรงที่ (1) จะเป็นกฎของฮุกในแบบเชิงมุมโดยแทนที่จะมีค่า k คือค่าคงที่ของสปริงใช้วัดความแข็งหรืออ่อนของสปริงใน (1) กลับมีค่า κ มาแทนที่โดยหมายถึงค่าคงที่การบิดซึ่งขึ้นอยู่กับความยาวของลวด ขนาดเส้นผ่านศูนย์กลางของลวดและวัสดุที่ใช้ทำลวดแขวนของลูกตุ้มชนิดบิด
ระบบลูกตุ้มชนิดบิดประกอบด้วยเส้นลวดที่สามารถหมุนบิดได้ที่ด้านบนสุดนั้นถูกยึดติดแน่นแขวนไว้ โดยส่วนล่างสุดนั้นมีแผ่นกลมแขวนอยู่ หรืออาจจะใช้วัสดุที่มีรูปร่างอื่นๆแทนก็ได้ โดยสมมติว่าแผ่นกลมที่แขวนอยู่นั้นถูกบิดเป็นมุมเล็กๆและปล่อยเป็นอิสระ แผ่นกลมมันก็จะบิดไปกลับเรื่อยๆ โดยทอร์กดึงกลับของระบบนั้นจะแปรผันตรงกับมุม θ ที่ถูกบิด นั้นหมายความว่ายิ่งมุม θ มีค่ามาก τ ก็ยิ่งจะมีค่ามากตามไปด้วย ซึ่งจะสอดคล้องกับ (1)
หลายคนอาจสงสัยว่าแล้วลูกตุ้มชนิดบิดมีประโยชน์อะไรบ้าง ทำไมเราถึงสร้างมันขึ้นมา จริงๆแล้วมันมีประโยชน์หลายอย่างเช่นเราสามารถใช้ลูกตุ้มชนิดบิดมาสร้างเป็นนาฬิกาได้ สำหรับผู้สนใจสามารถดูวิดีโอการทำงานได้ที่ https://www.youtube.com/watch?v=sQj5HDKk238&ab_channel=WhatTheHey แต่ในครั้งนี้จะพูดถึงประโยชน์อีกหนึ่งอย่างที่สำคัญของมันคือมันยังสามารถนำไปใช้หาโมเมนต์ความเฉื่อย (moment of inertia) ได้
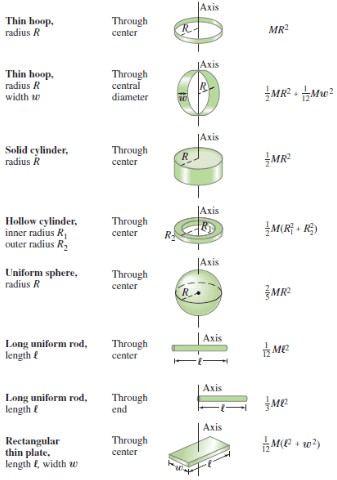
โมเมนต์ความเฉื่อยของวัตถุรูปทรงต่าง ๆ
เครดิต https://physicsabout.com/moment-of-inertia/
เครดิต https://physicsabout.com/moment-of-inertia/
โมเมนต์ความเฉื่อย หมายถึงปริมาณที่บ่งบอกถึงความเฉื่อยต่อการหมุน จะมีบทบาทเหมือนกับมวลในกรณีของการเลื่อนที่ โมเมนต์ความเฉื่อยเป็นปริมาณสเกลาร์ ในตอนเรียนเรื่องโมเมนต์ความเฉื่อย เราจะพบว่าบางรูปทรงที่ไม่ซับซ้อนมากนัก จะมีสูตรการหาโมเมนต์ความเฉื่อยของรูปทรงนั้นอยู่ หรือตอนเรียนเราอาจจะใช้ทฤษฎีบทแกนขนาน (parallel axis theorem) ในการช่วยคำนวณหาโมเมนต์ความเฉื่อยได้ หรือในบางวัตถุรูปทรงที่แปลกๆที่เราไม่มีสูตรในการคำนวณ เราสามารถใช้การทดลองเรื่องลูกตุ้มชนิดบิดช่วยคำนวณได้โดยใช้ความรู้ที่ว่าคาบของลูกตุ้มชนิดบิดสามารถเขียนเป็นความสัมพันธ์ได้คือ
T=2π√(I/k) (2)
โดยที่ T,I,k คือ คาบของลูกตุ้มชนิดบิด โมเมนต์ความเฉื่อยและค่าคงที่การบิดตามลำดับ โดยหลักการคำนวณก็คือนำวัตถุเช่นทรงแผ่นกลมมาแขวนสร้างเป็นลูกตุ้มชนิดบิด โดยเราทราบโมเมนต์ความเฉื่อยของทรงแผ่นกลมนี้ (I_a) ก่อนแล้ว(เพราะเป็นรูปทรงมาตรฐานมีสูตรคำนวณโมเมนต์ความเฉื่อย) และมาทดลองหาคาบของลูกตุ้มชนิดบิดนี้ (T_a) เราก็จะสามารถคำนวณค่าคงที่การบิดของเส้นลวดได้ κ และเมื่อเรานำวัตถุที่เราไม่ทราบโมเมนต์ความเฉื่อยมาแขวนเป็นลูกตุ้มชนิดบิด เพราะว่าลวดที่ใช้แขวนเป็นเส้นลวดเดิมจึงมีค่าคงที่ของการบิดคงเดิม เมื่อเราทดลองหาค่าคาบของลูกตุ้มชนิดบิดที่แขวนโดยวัตถุที่เราไม่ทราบโมเมนต์ความเฉื่อย (T_b) เราก็จะสามารถคำนวณหาโมเมนต์ความเฉื่อยของวัตถุที่เราไม่ทราบค่า (I_b) ได้โดยอาศัย (2) สุดท้ายเราจะได้สมการที่ใช้คำนวณหาโมเมนต์ความเฉื่อยของวัตถุที่เราไม่ทราบค่า
I_b=I_a (T_b^2)/(T_a^2 ) (3)
ซึ่งต้องเน้นย้ำก่อนว่าโมเมนต์ความเฉื่อยที่คำนวณได้นั้นต้องเป็นแบบที่แกนหมุนประมาณจากจุดศูนย์กลางของวัตถุเท่านั้น จะเห็นว่าลูกตุ้มชนิดบิดมีประโยชน์สำหรับใช้คำนวณโมเมนต์ความเฉื่อยของวัตถุที่ไม่ใช่รูปทรงปรกติที่มีสูตรพื้นฐานในการคำนวณหาโมเมนต์ความเฉื่อย
เรียบเรียงโดย
ณัฐพล โชติศรีศุภรัตน์
นักศึกษาระดับปริญญาเอก ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
อ้างอิง
- Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of physics. John Wiley & Sons.
- https://www.slideserve.com/layne/ph0101-unit-1-lecture-2
- http://farside.ph.utexas.edu/teaching/301/lectures/node139.html
- https://phys.libretexts.org/Bookshelves/Classical_Mechanics/Book%3A_Classical_Mechanics_(Tatum)/11%3A_Simple_and_Damped_Oscillatory_Motion/11.03%3A_Torsion_Pendulum
บทความฟิสิกส์ล่าสุด
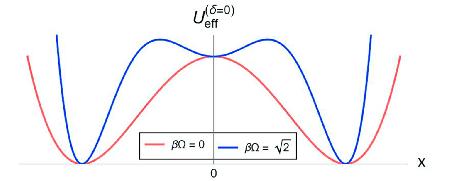 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
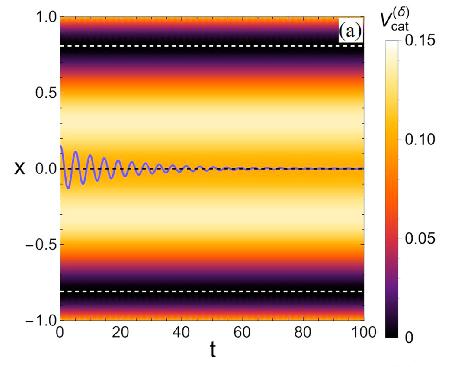 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

