การทดลองเพื่อทำความเข้าใจวิธีมอนติคาร์โล (Monte Carlo method)
24-08-2021 อ่าน 9,041
วิธีมอนติคาร์โล (Monte Carlo method) อธิบายอย่างคร่าวๆคือขั้นตอนวิธีแบบหนึ่งเพื่อประมาณค่าที่เราไม่รู้ โดยอาศัยการสุ่มตัวอย่างแบบง่าย (sample random sampling หมายถึงเป็นการสุ่มตัวอย่างซึ่งหน่วยตัวอย่างประชากรที่เปิดโอกาสให้ประชากรทุกหน่วยมีสิทธิ์ได้รับการเลือกเท่าๆ กัน) วิธีการนี้ตั้งตามชื่อเมืองมอนติคาร์โล ในประเทศโมนาโค เมืองที่มีชื่อเสียงด้านการพนันเสี่ยงโชค เพราะกระบวนการวิธีมอนติคาร์โลเกี่ยวข้องกับการสร้างตัวแปรโอกาสที่จะเกิดเหตุการณ์ขึ้นโดยเกี่ยวข้องกับการสุ่ม เหมือนการเล่นพนันเช่นทอยลูกเต๋าซึ่งมีการสุ่มตัวเลขที่จะออก วิธีมอนติคาร์โลเริ่มมีการใช้ครั้งแรกในช่วงปี ค.ศ. 1944 เพื่อใช้แก้ปัญหาคำนวณการแพร่ของนิวตรอนในระเบิดอะตอมที่ Alamos Scientific Laboratory
ในการแก้ปัญหาในการคำนวณเราอาจะทำได้หลายวิธี ซึ่งแต่ละวิธีก็จะมีข้อดีข้อเสียแตกต่างกันไป กล่าวคือในการแก้แบบเชิงวิเคราะห์ (analytical method) เช่นการแก้สมการเชิงอนุพันธ์ด้วยวิธีนี้ คำตอบที่ออกมาจะสวยงาม ให้คำตอบที่ถูกต้องแต่ข้อเสียคือจำกัดเฉพาะปัญหาที่ค่อนข้างง่ายสามารถแก้แบบเชิงวิเคราะห์ได้ แต่ถ้ามีตัวแปรจำนวนมากวิธีนี้ก็อาจจะไม่เหมาะสม การแก้แบบระเบียบวิธีเชิงตัวเลข (numerical method) เช่น วิธีของออยเลอร์ (Euler method) เพื่อแก้สมการเชิงอนุพันธ์ ผลลัพธ์ที่ได้จะเป็นในรูปแบบของตัวเลขที่มีค่าประมาณ แต่เหมาะสำหรับการแก้ปัญหาที่มีความซับซ้อนของระบบเพิ่มขึ้นมา และการแก้แบบแบบจำลองสถานการณ์ (simulation modeling) เช่นวิธีมอนติคาร์โลเหมาะสำหรับระบบที่มีความซับซ้อนมาก แต่ข้อเสียคือโดยปรกติแล้วต้องพึ่งพาคอมพิวเตอร์เพื่อประมวลผล ในการเรียนขั้นสูงเช่นระดับบัณฑิตศึกษาหรือในการทำงานวิจัย การเลือกวิธีการแก้ปัญหาให้เหมาะสมมีความสำคัญมาก
วิธีมอนติคาร์โลมีประโยชน์อย่างมากในหลายสาขาวิชาเช่น ในวิชาวิศวกรรม ชีววิทยาเชิงคำนวณ สถิติประยุกต์หรือแม้แต่ในทางตลาดหุ้นและการเงิน สำหรับปัญหาในทางฟิสิกส์และคณิตศาสตร์ เราสามารถนำวิธีมอนติคาร์โลมาช่วยแก้ปัญหาที่หลากหลาย เช่น ใช้เป็นแบบจำลองของระบบเพื่อศึกษาในระบบที่มี degrees of freedom สูงๆเช่น ในของไหล หรือใช้เป็นแบบจำลองไอซิง (Ising model) ในกลศาสตร์เชิงสถิติ หรือใช้เป็นแบบจำลอง lattice QCD ในทฤษฎีสนามควอนตัม เป็นต้น
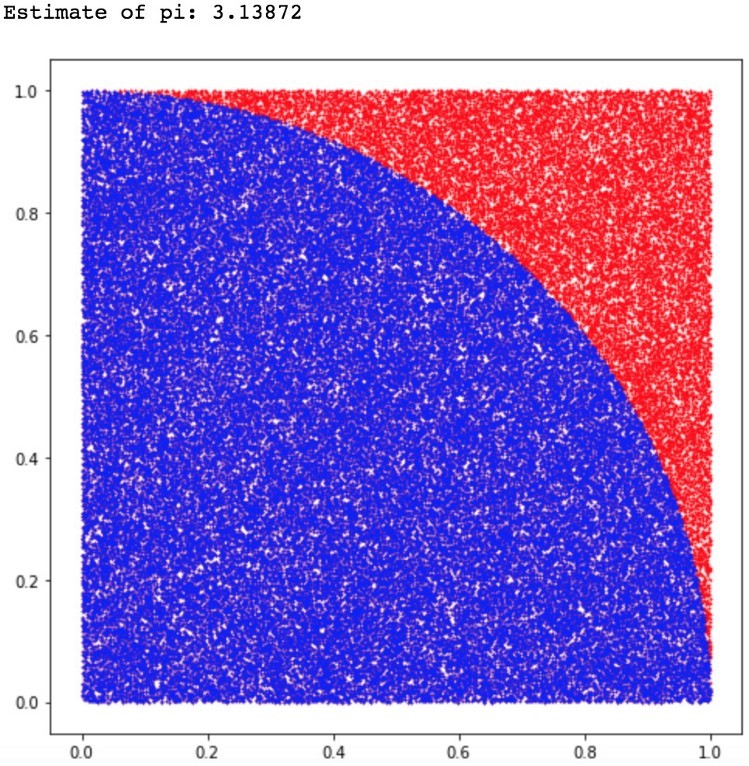
Timothy Williamson ได้ตีพิมพ์บทความเรื่อง “Calculating Pi Using the Monte Carlo Method” ลงในวารสาร The Physics Teacher เมื่อเดือนตุลาคม ค.ศ. 2013 เพื่อทำการทดลองอย่างง่ายในการหาค่าพาย ค่าคงตัวคณิตศาสตร์ที่ใช่บ่อยในการคำนวณทั้งในวิชาคณิตศาสตร์และวิชาฟิสิกส์ โดยใช้การทดลองอย่างง่ายที่ต้องการอุปกรณ์ไม่กี่อย่างคือ แผ่นกระดาษขนาดใหญ่ ดินสอ ไม้บรรทัด วงเวียนเพื่อสร้างวงกลม เครื่องชั่งมวล เมล็ดข้าวสารและเครื่องคิดเลข โดยจะแนะนำเนื้อหาที่เกี่ยวข้องและวิธีการทดลองดังต่อไปนี้
พื้นที่ของสี่เหลี่ยมจัตุรัสคือ
ฉะนั้นอัตราส่วนของพื้นที่จะเท่ากับ
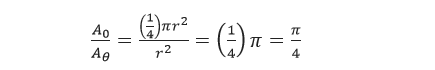(3)
อ้างอิง
ในการแก้ปัญหาในการคำนวณเราอาจะทำได้หลายวิธี ซึ่งแต่ละวิธีก็จะมีข้อดีข้อเสียแตกต่างกันไป กล่าวคือในการแก้แบบเชิงวิเคราะห์ (analytical method) เช่นการแก้สมการเชิงอนุพันธ์ด้วยวิธีนี้ คำตอบที่ออกมาจะสวยงาม ให้คำตอบที่ถูกต้องแต่ข้อเสียคือจำกัดเฉพาะปัญหาที่ค่อนข้างง่ายสามารถแก้แบบเชิงวิเคราะห์ได้ แต่ถ้ามีตัวแปรจำนวนมากวิธีนี้ก็อาจจะไม่เหมาะสม การแก้แบบระเบียบวิธีเชิงตัวเลข (numerical method) เช่น วิธีของออยเลอร์ (Euler method) เพื่อแก้สมการเชิงอนุพันธ์ ผลลัพธ์ที่ได้จะเป็นในรูปแบบของตัวเลขที่มีค่าประมาณ แต่เหมาะสำหรับการแก้ปัญหาที่มีความซับซ้อนของระบบเพิ่มขึ้นมา และการแก้แบบแบบจำลองสถานการณ์ (simulation modeling) เช่นวิธีมอนติคาร์โลเหมาะสำหรับระบบที่มีความซับซ้อนมาก แต่ข้อเสียคือโดยปรกติแล้วต้องพึ่งพาคอมพิวเตอร์เพื่อประมวลผล ในการเรียนขั้นสูงเช่นระดับบัณฑิตศึกษาหรือในการทำงานวิจัย การเลือกวิธีการแก้ปัญหาให้เหมาะสมมีความสำคัญมาก
วิธีมอนติคาร์โลมีประโยชน์อย่างมากในหลายสาขาวิชาเช่น ในวิชาวิศวกรรม ชีววิทยาเชิงคำนวณ สถิติประยุกต์หรือแม้แต่ในทางตลาดหุ้นและการเงิน สำหรับปัญหาในทางฟิสิกส์และคณิตศาสตร์ เราสามารถนำวิธีมอนติคาร์โลมาช่วยแก้ปัญหาที่หลากหลาย เช่น ใช้เป็นแบบจำลองของระบบเพื่อศึกษาในระบบที่มี degrees of freedom สูงๆเช่น ในของไหล หรือใช้เป็นแบบจำลองไอซิง (Ising model) ในกลศาสตร์เชิงสถิติ หรือใช้เป็นแบบจำลอง lattice QCD ในทฤษฎีสนามควอนตัม เป็นต้น
Timothy Williamson ได้ตีพิมพ์บทความเรื่อง “Calculating Pi Using the Monte Carlo Method” ลงในวารสาร The Physics Teacher เมื่อเดือนตุลาคม ค.ศ. 2013 เพื่อทำการทดลองอย่างง่ายในการหาค่าพาย ค่าคงตัวคณิตศาสตร์ที่ใช่บ่อยในการคำนวณทั้งในวิชาคณิตศาสตร์และวิชาฟิสิกส์ โดยใช้การทดลองอย่างง่ายที่ต้องการอุปกรณ์ไม่กี่อย่างคือ แผ่นกระดาษขนาดใหญ่ ดินสอ ไม้บรรทัด วงเวียนเพื่อสร้างวงกลม เครื่องชั่งมวล เมล็ดข้าวสารและเครื่องคิดเลข โดยจะแนะนำเนื้อหาที่เกี่ยวข้องและวิธีการทดลองดังต่อไปนี้
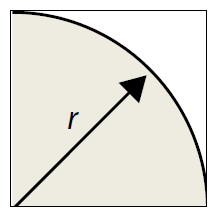
รูปที่ 1 ส่วนโค้งของวงกลมรัศมี r ในสี่เหลี่ยมจัตุรัส
เครดิต Williamson, T. (2013). Calculating Pi Using the Monte Carlo Method. The Physics Teacher, 51(8), 468-469.
พิจารณาส่วนโค้งของวงกลมที่มีรัศมี r ที่อยู่ในพื้นที่สี่เหลี่ยมจัตุรัสซึ่งมีความยาวแต่ละด้านคือ r พื้นที่ในส่วนโค้งของวงกลมสามารถคำนวณได้จากสูตร เครดิต Williamson, T. (2013). Calculating Pi Using the Monte Carlo Method. The Physics Teacher, 51(8), 468-469.
\(A_0= \frac {πr^2}4 \) (1)
โดยที่ A0,r คือพื้นที่ส่วนโค้งของวงกลมและความยาวรัศมีของส่วนโค้งของวงกลมตามลำดับ
พื้นที่ของสี่เหลี่ยมจัตุรัสคือ
\(A_θ= r^2 \) (2)
โดยที่ Aθ,r คือพื้นที่ของสี่เหลี่ยมจัตุรัสและความยาวด้านยาวตามลำดับโดยจะสังเกตว่ามีขนาดความยาวเท่ากับความยาวรัศมีของส่วนโค้งของวงกลม
ฉะนั้นอัตราส่วนของพื้นที่จะเท่ากับ
ค่าของพายจะสามารถหาได้วิธีมอนติคาร์โลโดยสมมติให้ความหนาแน่นของเมล็ดข้าวสารในพื้นที่ทั้งหมดเท่ากัน (ความหนาแน่นของเมล็ดข้าวสารพื้นที่ส่วนโค้งของวงกลมเท่ากับความหนาแน่นของเมล็ดข้าวสารในพื้นที่สี่เหลี่ยมจัตุรัส หรือเขียนได้เป็น σ0=σθ) ฉะนั้น
\(\frac{ m_0}{A_0} =\frac{m_θ}{A_θ} และ \frac{m_0}{m_θ}=\frac{A_0}{A_θ }\) (4)
โดยที่ σ,m,A คือความหนาแน่น มวลและพื้นที่ตามลำดับ แทน (4) ลงใน (3) สุดท้ายจะได้
\(π=4\left(\frac{m_0}{m_θ}\right)\) (5)
การทดลองหาค่าพายด้วยวิธีมอนติคาร์โล (Monte Carlo method)
เครดิต Williamson, T. (2013). Calculating Pi Using the Monte Carlo Method. The Physics Teacher, 51(8), 468-469.
วิธีการทดลองคือนำกระดาษแผ่นใหญ่มาวาดรูปขยายของรูปที่ 1 ลงไปในแผ่นกระดาษ บันทึกค่าความยาวรัศมี r ของรูปที่สร้าง นำเมล็ดข้าวสารมาโรยให้ทั่วแผ่นกระดาษในในช่องสี่เหลี่ยมจัตุรัสให้มีการกระจายของเมล็ดข้าวสารสม่ำเสมอเหมือนกันทั่ว หลังจากนั้นค่อยๆเก็บเมล็ดข้าวสารที่อยู่นอกส่วนโค้งของวงกลม นำมาชั่งหามวลของเมล็ดข้าวสารกลุ่มนี้และบันทึกข้อมูล เมื่อเสร็จแล้วนำเมล็ดข้าวสารที่อยู่ในส่วนโค้งวงกลม นำมาชั่งเพื่อหามวลของเมล็ดข้าวสารกลุ่มนี้ สุดท้ายนำเมล็ดข้าวสารทั้งสองกลุ่มมารวมกันชั่งหามวลอีกครั้ง บันทึกผลข้อมูลลงในตาราง ใช้สมการ (5) เพื่อนำมาคำนวณค่าพาย สุดท้ายนำค่าพายที่แท้จริงมาเปรียบเทียบเพื่อหา % error นี่เป็นการทดลองจริงเพื่อให้เข้าใจหลักการทำงานของวิธีมอนติคาร์โลเพื่อคำนวณหาค่าพาย เครดิต Williamson, T. (2013). Calculating Pi Using the Monte Carlo Method. The Physics Teacher, 51(8), 468-469.
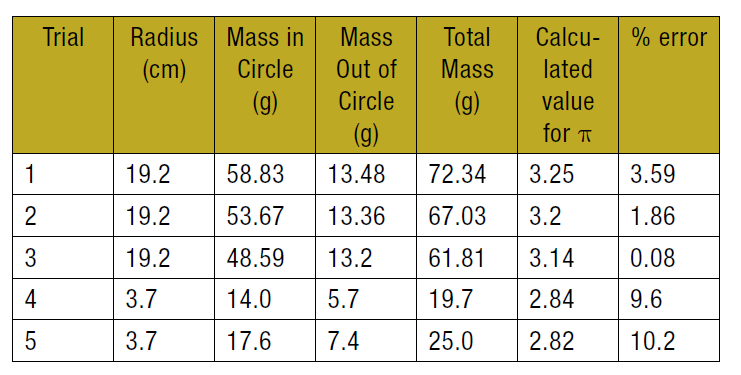
ตารางแสดงผลจากการทดลองและค่าพายที่ได้จากการคำนวณ
เครดิต Williamson, T. (2013). Calculating Pi Using the Monte Carlo Method. The Physics Teacher, 51(8), 468-469.
จากการทดลองตัวอย่างในบทความนี้พบว่าสามารถคำนวณค่าพายเฉลี่ยได้เท่ากับ 3.20 โดยมี % error คือ 1.9 ซึ่งถือได้ว่าน่าประทับใจ ขนาดของเมล็ดข้าวส่งผลต่อความแม่นยำในการคำนวณ การทดลองนี้เหมาะสำหรับการเริ่มเรียนรู้วิธีมอนติคาร์โล เพื่อนำวิธีการนี้ไปใช้ในการคำนวณปัญหาที่ยากขึ้นต่อไปในอนาคต สิ่งที่ต้องเน้นย้ำคือวิธีการนี้คำตอบได้เป็นค่าประมาณจากแก้แบบจำลองสถานการณ์ ซึ่งจะมีประโยชน์มากในการทำวิจัยทางฟิสิกส์ (หรือสาขาอื่นๆ) ที่ปัญหายากมาก มีความซับซ้อนสูง การแก้แบบเชิงวิเคราะห์จะกระทำได้ยากมาก วิธีการนี้จะเหมาะสมกว่าเครดิต Williamson, T. (2013). Calculating Pi Using the Monte Carlo Method. The Physics Teacher, 51(8), 468-469.
เรียบเรียงโดย
ณัฐพล โชติศรีศุภรัตน์
นักศึกษาระดับปริญญาเอก ภาควิชาฟิสิกส์
คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
ณัฐพล โชติศรีศุภรัตน์
นักศึกษาระดับปริญญาเอก ภาควิชาฟิสิกส์
คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
อ้างอิง
- Williamson, T. (2013). Calculating Pi Using the Monte Carlo Method. The Physics Teacher, 51(8), 468-469.
- https://towardsdatascience.com/an-overview-of-monte-carlo-methods-675384eb1694
- https://www.oulu.fi/tf/montecarlo/lectures/mc_notes1.pdf
- https://machinelearningmastery.com/monte-carlo-sampling-for-probability/
บทความฟิสิกส์ล่าสุด
หอสังเกตการณ์นิวทริโนไอซ์คิวบ์ ตอนที่ 2
29-02-2024
หอสังเกตการณ์นิวทริโนไอซ์คิวบ์ ตอนที่ 1
09-02-2024
