การหาจุดศูนย์กลางมวล (center of mass) ด้วยการวิเคราะห์ภาพ
01-09-2021 อ่าน 17,646
ตอนเรียนวิชาฟิสิกส์หลายคนอาจเคยสงสัยว่าจุดศูนย์กลางมวลกับจุดศูนย์ถ่วงต่างกันอย่างไร จุดศูนย์กลางมวล (center of mass, CM) หมายถึงจุดเสมือนเป็นที่รวมของมวลทั้งหมดของวัตถุ เป็นตำแหน่งภายในหรือภายนอกวัตถุเฉพาะสำหรับแต่ละวัตถุแข็งเกร็ง (วัตถุที่มีรูปทรงแน่นอน ระยะห่างระหว่างจุดต่าง ๆ บนวัตถุคงตัว และวัตถุไม่เปลี่ยนแปลงรูปร่างเมื่อเคลื่อนที่หรือมีแรงกระทำ) ซึ่งเมื่อมีแรงภายนอกมากระทำต่อวัตถุแข็งเกร็งนั้นโดยแนวแรงผ่านจุดศูนย์กลางนี้แล้ว จะทำให้วัตถุแข็งเกร็งเลื่อนที่โดยไม่เกิดการหมุน แต่ถ้าแนวแรงไม่ผ่านจุดศูนย์กลางมวลวัตถุจะมีการเคลื่อนที่แบบหมุน ขณะที่จุดศูนย์ถ่วง (center of gravity, CG) คือ เป็นตำแหน่งที่ถือเสมือนว่าแรงดึงดูดโลกที่กระทำต่อวัตถุผ่านตำแหน่งนี้ ในหลายกรณีทั้งสองจุดนี้มักจะเป็นจุดตำแหน่งเดียวกัน แต่อาจจะคนละตำแหน่งก็ได้เช่นกรณีที่สนามโน้มถ่วงไม่สม่ำเสมอ (non-uniform gravitational field) แนวคิดเรื่องจุดศูนย์กลางมวลมีมานานเป็นพันปีแล้วตั้งแต่ยุคกรีก นำเสนอโดยนักปรัชญานามว่าอาร์คิมิดีส
รูปที่ 2 (บน) การทำสัญลักษณ์จุดบนค้อนเพื่อไว้ศึกษาเรื่องการหาจุดศูนย์กลางมวล (ล่าง) ภาพแบบสโตโบสโคปแสดงการโยนค้อนโดยมีอัตราการจับภาพที่ 20 ภาพต่อวินาที
เครดิต Dias, M. A., Carvalho, P. S., & Rodrigues, M. (2016). How to determine the centre of mass of bodies from image modelling. Physics Education, 51(2), 025001.
เครดิต Dias, M. A., Carvalho, P. S., & Rodrigues, M. (2016). How to determine the centre of mass of bodies from image modelling. Physics Education, 51(2), 025001.
Marco Adriano Dias และคณะได้ตีพิมพ์บทความเรื่อง “How to determine the centre of mass of bodies from image modelling” ลงในวารสาร Physics Education เมื่อวันที่ 13 มกราคม ค.ศ. 2016 เพื่อทดลองทำการหาจุดศูนย์กลางมวลจากการหาจุดศูนย์กลางมวล (center of mass) ด้วยการวิเคราะห์ภาพ เทคนิคการทำแบบจำลองด้วยภาพกำลังได้รับความนิยมมากขึ้นในช่วงที่ผ่านมาเช่นการถ่ายภาพดิจิตอลแบบสโตโบสโคป (digital stroboscopic photography) ซอฟต์แวร์วิเคราะห์วิดีโอ เป็นต้น ซึ่งเราสามารถนำสิ่งเหล่านี้มาวิเคราะห์การเคลื่อนที่ของวัตถุในวิชาฟิสิกส์ได้ ซึ่งจะสร้างประโยชน์ได้มาก
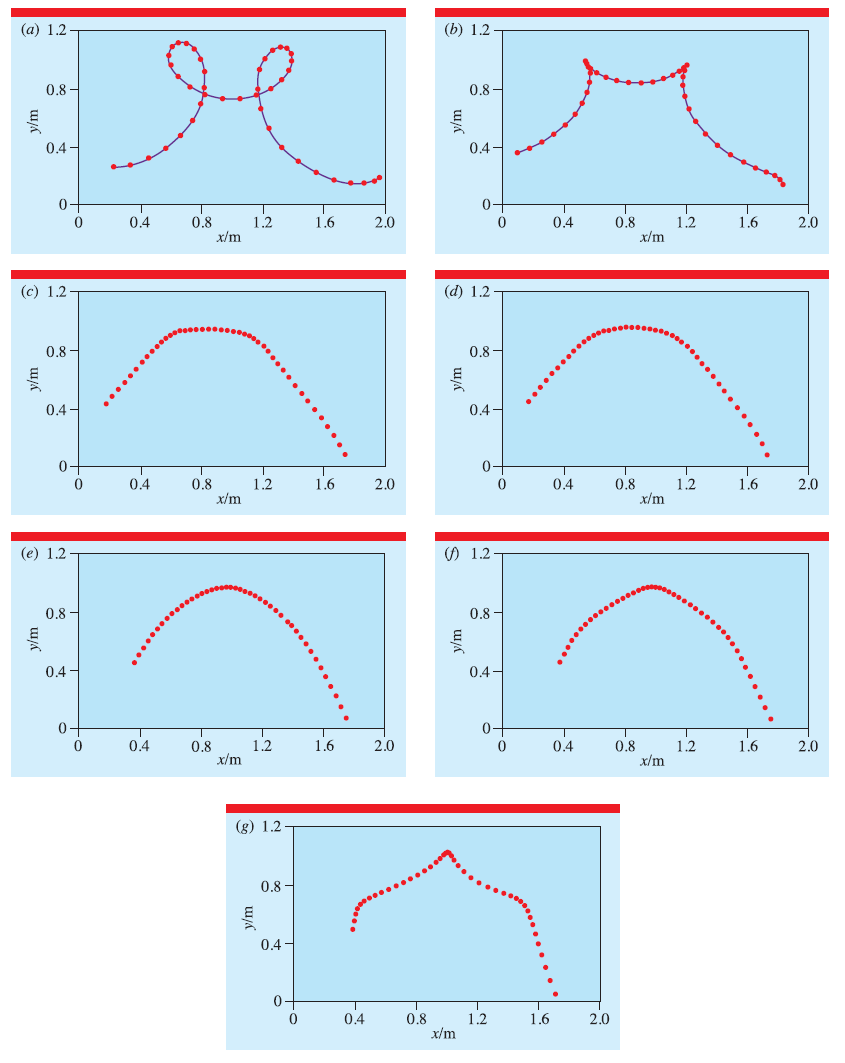
รูปที่ 3 กราฟแสดงวิถีของจุดบนค้อนของจุด A, B, C, D, E, F และ G ตามลำดับ
เครดิต Dias, M. A., Carvalho, P. S., & Rodrigues, M. (2016). How to determine the centre of mass of bodies from image modelling. Physics Education, 51(2), 025001.
เครดิต Dias, M. A., Carvalho, P. S., & Rodrigues, M. (2016). How to determine the centre of mass of bodies from image modelling. Physics Education, 51(2), 025001.
การทดลองหาตำแหน่งของ CM ด้วยวิธีของ Marco Adriano Dias และคณะนี้สามารถใช้ได้ทั้งกับวัตถุที่มีความหนาแน่นแบบสม่ำเสมอดี (isotropic) และแบบความหนาแน่นไม่ค่อยสม่ำเสมอ (anisotropic) โดยในการทดลองที่ใช้การโยนค้อนในแนวเฉียงและถ่ายภาพแบบสโตโบสโคปและถ่ายวิดีโอ การโยนค้อนนี้จะทำให้ค้อนมีทั้งการเคลื่อนที่แบบหมุน (rotation) และเคลื่อนที่แบบเลื่อนที่ (translation) สมมติว่าเราโยนวัตถุแข็งเกร็งทรงกลมขนาดเล็กที่มีความหนาแน่นของมวลสม่ำเสมอดีในแนวเฉียงโดยไม่คิดถึงแรงต้านอากาศ เราจะสังเกตการเคลื่อนที่เป็นวิถีแบบพาราโบลา ในขณะที่สมมติว่าเราโยนวัตถุที่มีความหนาแน่นของมวลไม่ค่อยสม่ำเสมอเช่นค้อน วิถีของมันไม่สามารถอธิบายได้ง่ายนักเพราะแต่ละจุดของวัตถุจะมีวิถีที่แตกต่างกันไป จุดส่วนใหญ่จะไม่ใช่วิถีแบบพาราโบลาเพราะเมื่อค้อนหมุน แต่ละจุดบนค้อนจะหมุนรอบจุดของวัตถุคือ CM นั่นเอง
ตำแหน่งของ CM ของวัตถุสามารถคำนวณได้จาก
\(r ⃗_Cm=\frac1M ∫r ⃗∙dm\) (1)
โดยที่ \(r ⃗_Cm\) คือตำแหน่งของ CM
โดยวัตถุที่มีรูปทรงสมมาตรและมีความหนาแน่นของมวลสม่ำเสมอดี CM จะอยู่ที่จุดศูนย์กลางของวัตถุ แต่ในกรณีที่รูปทรงซับซ้อนเช่นค้อน การหา CM จะค่อนข้างยาก โดย CM จะอยู่ชิดไปทางด้านที่มีมวลมากกว่าอีกด้านหนึ่ง ในแบบจำลองจลศาสตร์ของ CM ในกรณีไม่มีแรงต้านอากาศและวัตถุได้รับอิทธิจากแรงโน้มถ่วงของโลกสมการวิถีของ CM จะเป็น
\(Δy=Δx tanθ_0-\frac{g(Δx)^2}{(2(v_0 cosθ_0 )^2} \) (2)
โดยที่ Δy,Δx,θ0,g,v0 คือตำแหน่งที่เปลี่ยนไปในวิถีเทียบจากระบบพิกัดของแกน y,x มุมเอียงเริ่มต้น ความเร่งเนื่องจากแรงโน้มถ่วงของโลกและความเร็วเริ่มต้น องค์ประกอบในแกนนอนของ CM สามารถอธิบายเป็นฟังก์ชันของเวลาโดยใช้สมการ
\(y=y_0+v_0 t sinθ_0- \frac{g}{2} t^2\) (3)
โดยที่ y_0 เป็นตำแหน่งเริ่มต้นในแกนตั้งของ CM และองค์ประกอบในแกนตั้งของ CM สามารถอธิบายเป็นฟังก์ชันของเวลาโดยใช้สมการ
\(x=x_0+v_0 t cosθ_0 \) (4)
โดยที่ x0 เป็นตำแหน่งเริ่มต้นในแกนนอนของ CM
เพื่อที่จะหา CM ของค้อนก่อนโยนค้อนให้ทำเครื่องหมายจุดต่างๆบนค้อน 7 จุดคือจุด A ถึงจุด G และโยนค้อนในแนวเฉียง บันทึกการเคลื่อนไหวโดยกล้องวิดีโอที่อัตรา 60 เฟรมต่อวินาที ทำเป็นภาพแบบสโตโบสโคปโดยใช้ โปรแกรม VirtualDub และ ImageJ เราจะสามารถสังเกตการเคลื่อนที่แต่ละจุดบนค้อนได้อย่างชัดเจนนำวิถีของจุดต่างๆมาวิเคราะห์เพื่อหา CM โดยจากการวิเคราะห์วิดีโอแต่ละจุดบนค้อนมีวิถีที่แตกต่างกันออกไป จุดที่ยิ่งอยู่ใกล้ CM ยิ่งมีวิถีการเคลื่อนที่คล้ายแบบพาลาโบรามากขึ้น โดยพบว่าวิถีที่มีลักษณะดังกล่าวมากที่สุดคือจุด E โดยพบว่ามีผลการคำนวณดัง (2) และยังพบว่าที่จุดดังกล่าวมีค่าสอดคล้องประมาณใกล้เคียงกับผลการคำนวณทั้งตำแหน่งในแนวตั้งและในแนวนอนตามที่บรรยายไว้ใน (3) และ (4)
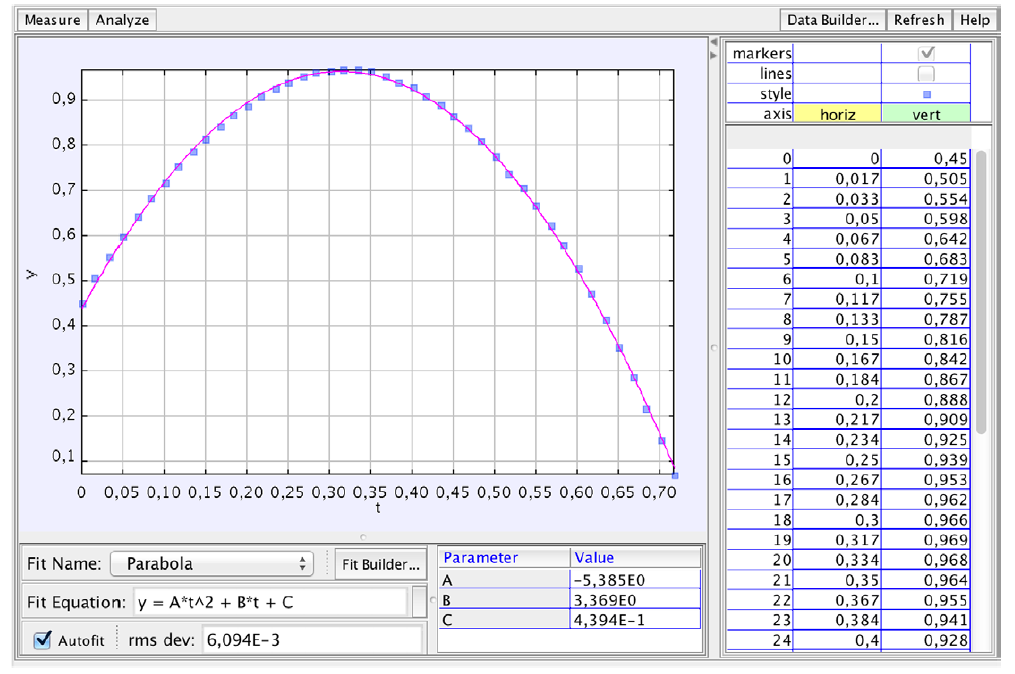
รูปที่ 4 ตำแหน่ง y ของจุด E เป็นฟังก์ชันของเวลาพบว่าเป็นแบบพาราโบลา
เครดิต Dias, M. A., Carvalho, P. S., & Rodrigues, M. (2016). How to determine the centre of mass of bodies from image modelling. Physics Education, 51(2), 025001.
เครดิต Dias, M. A., Carvalho, P. S., & Rodrigues, M. (2016). How to determine the centre of mass of bodies from image modelling. Physics Education, 51(2), 025001.
ในการทดลองเพิ่มเติมเราอาจจะลองเปลี่ยนวัตถุเพื่อหา CM ของวัตถุอื่นๆ ที่เราต้องการทราบ
ณัฐพล โชติศรีศุภรัตน์
นักศึกษาระดับปริญญาเอก
ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
นักศึกษาระดับปริญญาเอก
ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยศรีนครินทรวิโรฒ
อ้างอิง
- Dias, M. A., Carvalho, P. S., & Rodrigues, M. (2016). How to determine the centre of mass of bodies from image modelling. Physics Education, 51(2), 025001.
- http://hyperphysics.phy-astr.gsu.edu/hbase/cm.html
- http://www.neutron.rmutphysics.com/physics-glossary/index.php?option=com_content&task=view&id=1025&Itemid=85
บทความฟิสิกส์ล่าสุด
หอสังเกตการณ์นิวทริโนไอซ์คิวบ์บรรลุความแม่นยำระดับที่ไม่เคยมีมาก่อนในการศึกษาการแกว่งของนิวทริโน
20-08-2024
หอสังเกตการณ์นิวทริโนไอซ์คิวบ์ ตอนที่ 4
19-07-2024
หอสังเกตการณ์นิวทริโนไอซ์คิวบ์ ตอนที่ 3
04-03-2024
หอสังเกตการณ์นิวทริโนไอซ์คิวบ์ ตอนที่ 2
29-02-2024
