การใช้แสงเลเซอร์ความยาวคลื่น 532 nm สาธิตหลักการของฮอยเกนส์ (Huygens' principle)
01-11-2021 อ่าน 5,041
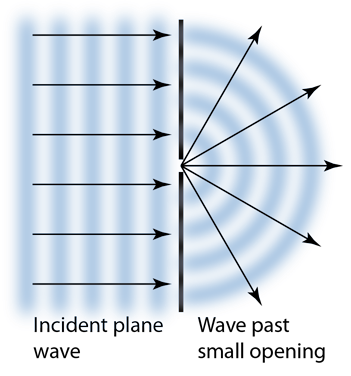
ในศตวรรษที่ 17 ถ้าไม่มีไอแซก นิวตัน นักวิทยาศาสตร์ที่โด่งดังที่สุดในยุคนั้นก็น่าจะเป็นใครไปไม่ได้นอกจากคริสตียาน เฮยเคินส์ (Christiaan Huygens) หรือท่านฮอยเกนส์ที่เราคุ้นชื่อกันนั่นเอง นี่เองคล้ายในตำนานสามก๊กตอนที่จิวยี่แพ้และกระอักเลือดให้แก่ขงเบ้งโดยรำพึงว่า "เมื่อฟ้าส่งข้ามาเกิดแล้ว เหตุไฉนถึงส่งขงเบ้งมาเกิดด้วย" แต่คงไม่ใช่แบบนั้นหรอกเพราะนักวิทยาศาสตร์ทุกคนต่างกันช่วยกันพัฒนาโลกให้ดีขึ้น ส่งเสริมกันไป ฮอยเกนส์มีผลงานด้านวิทยาศาสตร์ที่หลากหลายสาขาทั้งฟิสิกส์ คณิตศาสตร์ ปรัชญา โฮโลโลจี (horology หมายถึงศิลปะหรือวิทยาศาสตร์ในการทำเครื่องบอกเวลาหรือวัดเวลา) และดาราศาสตร์ นับเป็นพหูสูตอย่างแท้จริง เขาเริ่มต้นด้วยอาชีพนักการฑูตแต่แล้วก็ทนกับความเย้ายวนปริศนาของธรรมชาติไม่ไหว จึงเปลี่ยนมาเป็นอาชีพนักวิทยาศาสตร์ในที่สุด ผลงานหนึ่งที่โด่งดังของเขาคือหลักการของฮอยเกนส์ (Huygens' principle) ซึ่งหมายถึงแต่ละจุดบนหน้าคลื่นถือได้ว่าเป็นแหล่งกำเนิดคลื่นวงกลมคลื่นใหม่ที่ส่งออกไปด้วยอัตราเร็วเท่ากับอัตราเร็วคลื่นเดิม ซึ่งหลักการนี้ช่วยอธิบายการเลี้ยวเบนของคลื่นได้
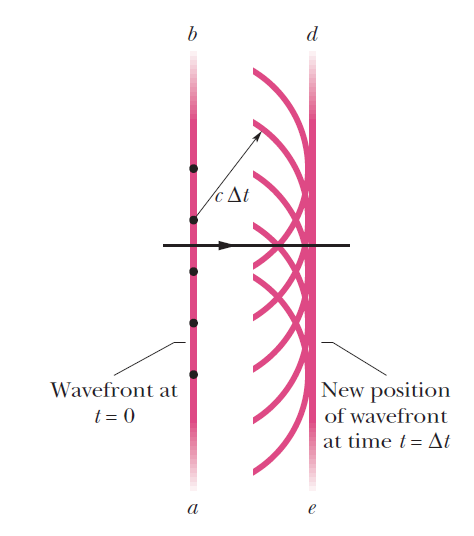
ภาพที่ 1 หลักการของฮอยเกนส์
เครดิต Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of physics. John Wiley & Sons.
เครดิต Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of physics. John Wiley & Sons.
Stephen Hughes และ Som Gurung ได้ตีพิมพ์บทความเรื่อง “A simple method of demonstrating Huygens’ principle in the classroom” ลงในวารสาร Physics Education เมื่อวันที่ 11 กุมภาพันธ์ ค.ศ. 2021 เพื่อใช้แสงเลเซอร์ความยาวคลื่น 532 nm สาธิตหลักการฮอยเกนส์ การทดลองทำได้ไม่ยากนักและอุปกรณ์ราคาไม่แพง เหมาะสำหรับให้นักเรียน นักศึกษาได้รับประสบการณ์จริงโดยตรงเพื่อศึกษาเรื่องนี้ งานวิจัยนี้แสดงให้เห็นว่าคลื่นแสงที่แพร่ไปแต่ละจุดบนหน้าคลื่นถือได้ว่าเป็นแหล่งกำเนิดคลื่นวงกลมคลื่นใหม่ แสงเลเซอร์เมื่อเคลื่อนที่ผ่านแต่ละด้านของเส้นลวด การเลี้ยวเบนไม่สามารถอธิบายได้ด้วยการสะท้อน แสงจะสามารถสะท้อนออกไปทั้งสองด้านของเส้นลวดแต่ไม่สามารถหักเหเข้าและออกในแต่ละด้านของเส้นลวดจนสร้างเป็นริ้วรอยของการแทรกสอดได้ แต่ที่ในการทดลองเราค้นพบริ้วการแทรกสอดได้ เหตุผลการอธิบายที่สมเหตุสมผลก็คือหลักการของฮอยเกนส์ นั่นเอง

ภาพที่ 2 (บน) เรขาคณิตอธิบายการเกิดริ้วการแทรกสอด (ล่าง) การนำเส้นลวดทองแดงขนาดเล็กที่มีเส้นผ่านศูนย์กลาง (d) วัดได้คือ \(0.1±0.01 mm\) มาพันไว้ตรงกลางหน้าแสงเลเซอร์
เครดิต Hughes, S., & Gurung, S. (2021). A simple method of demonstrating Huygens’ principle in the classroom. Physics Education, 56(3), 035005.
เครดิต Hughes, S., & Gurung, S. (2021). A simple method of demonstrating Huygens’ principle in the classroom. Physics Education, 56(3), 035005.
วิธีการทดลองสามารถทำได้โดยนำเส้นลวดทองแดงขนาดเล็กที่มีเส้นผ่านศูนย์กลาง (d) วัดได้คือ \(0.1±0.01 mm\) มาพันไว้ตรงกลางหน้าแสงเลเซอร์ \(<5 mW \) และมีความยาวคลื่น 532 nm สาเหตุก็คือที่ความยาวคลื่นนี้จะได้แสงเลเซอร์สีเขียวซึ่งดวงตาของมนุษย์ไวต่อการกระตุ้นด้วยย่านความยาวคลื่นนี้ที่สุดอีกทั้งสีเขียวยังตัดกับฉากรับสีขาวทำให้สังเกตวัดค่าได้ง่าย ลำแสงเลเซอร์จะถูกชี้ไปยังแท่งดินสอที่ทำหน้าที่เป็นตัวกันลำแสงตรงกลางที่จะตกไปยังฉากรับคือกำแพงสีขาว เพื่อให้ปรับปรุงการเปรียบต่าง (contrast) เมื่อริ้วการแทรกสอดแสดงบนฉากรับ ถ่ายภาพด้วยสมาทโฟนนำริ้วการแทรกสอดนี้แล้วนำมาวิเคราะห์ต่อไป โดยการปิดไฟในห้องทดลองจะช่วยให้สังเกตผลการทดลองได้ง่ายขึ้น ที่ฉากรับมีไม้บรรทัดติดไว้ด้วยเพื่อให้ทราบระยะสิ่งที่ต้องการวัด ระยะทางจากเลเซอร์ไปยังฉากรับคือ (x) = \(3.8±0.2 cm\) เมื่อถ่ายภาพริ้วการแทรกสอดไปวิเคราะห์บนคอมพิวเตอร์พบว่าระยะระหว่างแถบมืด (minima) คือ \(3.8±0.2 cm\) ความยาวคลื่นของแสงเลเซอร์คือ 543 nm เมื่อทราบค่าทั้งหมดแล้วต้องการคำนวณหาขนาดเส้นผ่านศูนย์กลางของเส้นลวด ใช้สมการของแบรกก์ (Bragg's equation)
\(λ=d sinθ\) (1)
ย้ายข้างสมการใหม่ จะได้ \(d=\frac{λ}{sinθ} = \frac{λ}{sin(tan^-1)(y/x))} \) (2)
โดยที่ d คือขนาดเส้นผ่านศูนย์กลางของเส้นลวด

ภาพที่ 3 (บน) ริ้วการแทรกสอดที่ฉากรับที่เกิดขึ้นจากการฉายเลเซอร์ผ่านเส้นลวดทองแดงขนาดเล็กที่มีเส้นผ่านศูนย์กลาง (d) วัดได้คือ \(0.1±0.01 mm\)(ล่าง) ตัวอย่างการทำการทดลอง
เครดิต Hughes, S., & Gurung, S. (2021). A simple method of demonstrating Huygens’ principle in the classroom. Physics Education, 56(3), 035005.
โดยเมื่อแทนค่าต่างๆไปแล้วจะพบว่า \(d=9.5±0.5×10^-5 m = 0.095±0.005 mm\) ซึ่งสอดคล้องกับข้อมูลที่เราทราบอยู่ก่อนแล้วคือ \(0.1±0.01 mm\) จะพบว่าผลที่ได้จากการคำนวณตรงกับผลการวัด
การทดลองนี้สาธิตหลักการของฮอยเกนส์ เลเซอร์ที่ใช้ในการทดลองนี้แม้จะมีกำลังไฟฟ้าไม่มากนักแต่ก็ควรทำการทดลองด้วยความระมัดระวังและไม่มองลำแสงเลเซอร์ตรงๆด้วยตาของเรา
ณัฐพล โชติศรีศุภรัตน์
นักศึกษาระดับปริญญาเอก
ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์
มหาวิทยาลัยศรีนครินทรวิโรฒ
นักศึกษาระดับปริญญาเอก
ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์
มหาวิทยาลัยศรีนครินทรวิโรฒ
อ้างอิง
- Hughes, S., & Gurung, S. (2021). A simple method of demonstrating Huygens’ principle in the classroom. Physics Education, 56(3), 035005.
- https://courses.lumenlearning.com/boundless-physics/chapter/diffraction/
- http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/huygen.html
- https://mgronline.com/science/detail/9540000058818
บทความฟิสิกส์ล่าสุด
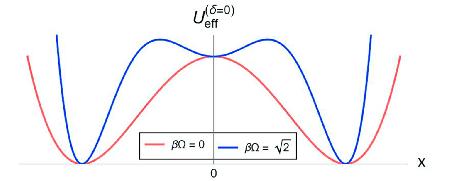 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
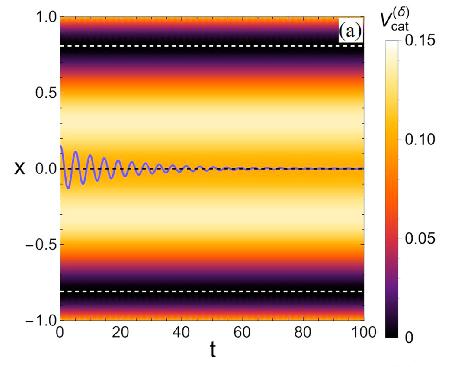 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

