การเคลื่อนที่แบบบราวน์ (Brownian motion) ในมุมมองไอน์สไตน์
22-11-2021 อ่าน 10,516
ทฤษฏีการเคลื่อนที่แบบบราวน์ในปัจจุบันมีการประยุกต์ใช้ในชีววิทยาและฟิสิกส์ด้วยแบบจำลองทางคณิตศาสตร์ นอกจากนี้ยังมีการประยุกต์ในเศรษฐศาสตร์และด้านการเงินการลงทุนโดยมีหัวข้อที่โด่งดังที่สุดนั้น คือ สมการแบล็ก-สโคลล์ (Black-Scholes equation) ซึ่งเกี่ยวกับการลงทุนออปชันที่อ้างอิงกับหุ้นรายตัว (stock options) สำหรับเทรดเดอร์และนักลงทุน เรื่องราวเกี่ยวกับทฤษฏีการเคลื่อนที่แบบบราวน์เริ่มต้น ในปี 1827 โดยนักชีววิทยา โรเบิร์ต บราวน์ (Robert Brown) ได้สังเกตเห็นการเคลื่อนที่แบบสุ่มทิศทางของละอองเรณู (pollen grain) ในน้ำนิ่งจากกล้องจุลทรรศน์ นักวิทยาศาสตร์จึงมีความสงสัยว่าอะไรที่ทำให้ละอองเรณูนั้นเคลื่อนที่แบบสุ่ม เนื่องจากในสมัยนั้น ยังไม่มีความเข้าใจเกี่ยวกับเรื่องอะตอมและโมเลกุลที่เป็นเบื้องหลังของการเคลื่อนที่แบบสุ่มของละอองเรณู โดยน้ำมีความใสเมื่อมองด้วยตาเปล่าคนส่วนใหญ่จึงไม่เชื่อเรื่องการมีอยู่ของอะตอมและโมเลกุล
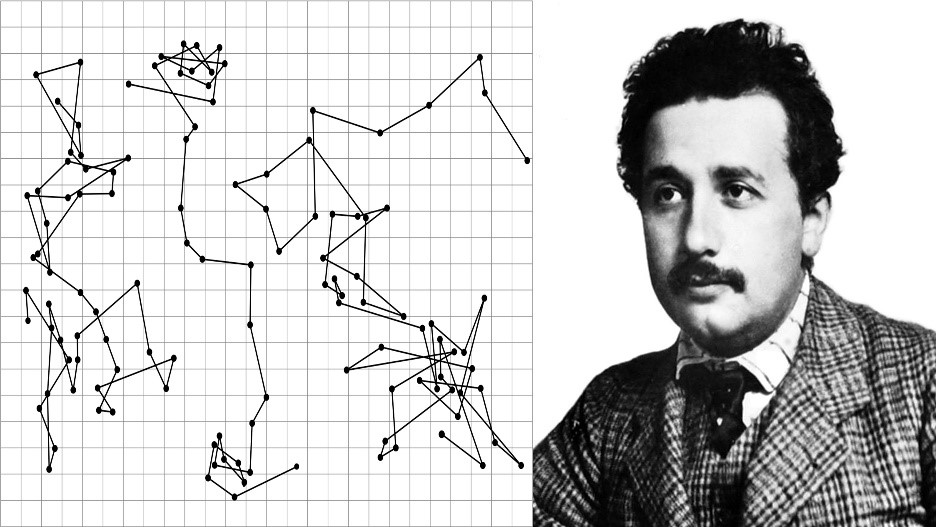
รูปที่ 1: ด้านซ้ายเป็นเส้นทางการเคลื่อนที่ของอนุภาครัศมี 0.53 ไมโครเมตร ของฌอง เพอร์ริน (Jean Perrin)
แม้จนกระทั่งเวลาล่วงเลยมาถึงในต้นศตวรรษที่ 20 นักฟิสิกส์ ลูทวิช บ็อลทซ์มัน (Ludwig Boltzmann) ได้นำเสนอการมีอยู่ของอะตอมด้วยสมการบ็อลทซ์มัน (Boltzmann equation) ที่พัฒนามาจากเรื่องก๊าซอุดมคติ แต่บ็อลทซ์มันก็ถูกนักวิทยาศาสตร์ส่วนใหญ่ต่อต้านแนวคิดของเขาจนทำให้เป็นอีกหนึ่งในสาเหตุสำคัญซึ่งส่งผลกระทบให้บ็อลทซ์มันฆ่าตัวตายในปี 1906 แต่ก่อนหน้านั้นหนึ่งปี ในปีมหัศจรรย์ของไอน์สไตน์ (ปี 1905) หนึ่งในสี่บทความที่ตีพิมพ์ในวารสาร Annalen der Physik ที่มีชื่อว่า “การเคลื่อนที่ของอนุภาคขนาดเล็กที่ลอยอยู่ในของเหลวนิ่งที่เกิดโดยโมเลกุล-จลนศาสตร์ของความร้อน” (“On the movement of small particles suspended in a stationary liquid demanded by the molecule-kinetic of heat”) ซึ่งในบทความนี้ ไอน์สไตน์ได้เสนอแนวคิดการพิสูจน์การมีอยู่ของโมเลกุลที่ทำให้เกิดการเคลื่อนที่แบบบราวน์ โดยพิจารณาการกระจัด (displacement) กำลังสองเฉลี่ย 〈s2〉 ของอนุภาคเคลื่อนที่ในน้ำในแต่ละช่วงเวลา t ตามความสัมพันธ์ของสมการที่ (1)

จากงานวิจัยนี้ของไอน์สไตน์ได้เป็นจุดเริ่มต้นการพัฒนาโดยใช้แบบจำลองทางคณิตศาสตร์อธิบายการเคลื่อนที่แบบบราวน์ ได้แก่ สมการแลงเจวิน (Langevin equation) กระบวนการวิกเนอร์ (Wiener process) และเป็นส่วนหนึ่งใน stochastic process โดยทฤษฏีการเคลื่อนที่แบบบราวน์นั้นยังมีความสำคัญอย่างมากเนื่องจาก เมื่อเราพิจารณาในระดับต่ำกว่านาโนเมตร (10-9 เมตร) หรืออะตอมนั้นต้องใช้กลศาสตร์ควอนตัมที่ใช้คณิตศาสตร์ความน่าจะเป็น ส่วนในชีวิตประจำวันก็ใช้หลักกลศาสตร์แบบนิวตันที่สามารถคำนวณได้ค่าอย่างตรงไปตรงมา แต่ถ้าเป็นระดับโมเลกุลหรือระดับฝุ่นนั้นอยู่ในขนาดระหว่างกลางของสองกลศาสตร์นี้ซึ่งทำให้ทฤษฏีการเคลื่อนที่แบบบราวน์เป็นสิ่งแรกที่นักฟิสิกส์นึกถึงในการอธิบายปราการณ์ในระดับไมโครเมตร (10-6 เมตร) หรือกลุ่มโมเลกุล

รูปที่ 2 : การติดตั้งเครื่องมือวัดการเคลื่อนที่แบบบราวน์ (Credit picture [2])
ในปัจจุบัน เราสามารถทำการทดลองการเคลื่อนที่แบบบราวน์เพื่อพิสูจน์แนวคิดของไอน์สไตน์ตามรูปแบบการสอนที่เผยแพร่วันที่ 27 สิงหาคม 2021 ในวารสาร Physics Education ในชื่อ “การวัดที่นับไม่ถ้วนโดยใช้เทคโนโลยีสารสนเทศในตัวอย่างการเคลื่อนที่แบบบราวน์” (“Measuring the immeasurable using information technologies on the example of Brownian motion”) ซึ่งทีมงานใช้ซอฟแวร์ VirtualDub และ ติดตาม (tracker) การเปลี่ยนแปลงของการกระจัดของอนุภาคเคลื่อนที่ใน 2 มิติ มีขนาดรัศมีของอนุภาคประมาณ r=(0.73±0.01)×10-6 เมตร โดยทีมงานสามารถวัดการกระจัดเฉลี่ยได้ประมาณ s=(0.5±0.006)×10-6เมตร ที่เปลี่ยนแปลงในทุกๆ 0.2 วินาที น้ำมีอุณหภูมิประมาณ 20 องศาเซลเซียส (293 K) โดยที่ R เป็นค่าคงที่แก๊ส และ η=0.001 Pa s เมื่อคำนวณในสมการที่ (3) ซึ่งพิจารณาใน 2 มิติจึงคูณสองในสมการที่ (2) เป็น
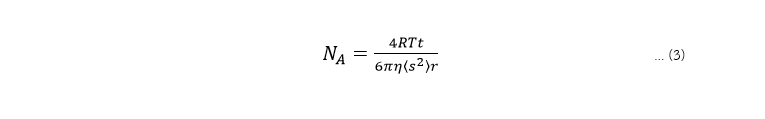
บทความโดย
ดร. ธีระวัฒน์ ชัชวาลธีรัตต์
ผู้ช่วยงานวิจัย ภาคฟิสิกส์ คณะวิทยาศาสตร์
มหาวิทยาลัยศรีนครินทรวิโรฒ
ดร. ธีระวัฒน์ ชัชวาลธีรัตต์
ผู้ช่วยงานวิจัย ภาคฟิสิกส์ คณะวิทยาศาสตร์
มหาวิทยาลัยศรีนครินทรวิโรฒ
Pursuing Certified Information Systems Auditor (CISA) certification can be an excellent investment for information systems and cybersecurity. While exact CISA costs depend on factors like membership status and study materials, its value to your career cannot be overstated. CISA stands as an internationally respected certification that displays your skill in auditing, control, and assurance of information systems - and represents your dedication to upholding high standards of IT governance and security.
learn more about CISA certification cost
Consider the CISA cost as an investment in opening up new possibilities. As organizations look for professionals adept at safeguarding information assets against data breaches and cyber threats, organizations require specialists like you who possess skills such as assessing vulnerabilities, managing risks and assuring compliance - this certification provides this edge over others while increasing job prospects and earning potential. Putting aside its financial cost implications for now - taking this route would open up endless career advancement and job security in an ever-evolving field like information systems makes CISA worth its price in your professional growth!
learn more about CISA exam cost แหล่งอ้างอิง
- [1] Einstein, Albert (May 1905). "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen" Annalen der Physik (in German). 322 (8): 549–560. Bibcode:1905AnP...322..549E. doi:10.1002/andp.19053220806. Retrieved 2008-04-10.
- [2] Halina Falfushynska et al 2021 Phys. Educ. 56 065013
- [3] F. Reif, Fundamentals of statistical and thermal physics, (McGraw-Hill)
บทความฟิสิกส์ล่าสุด
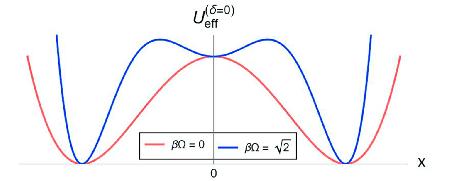 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
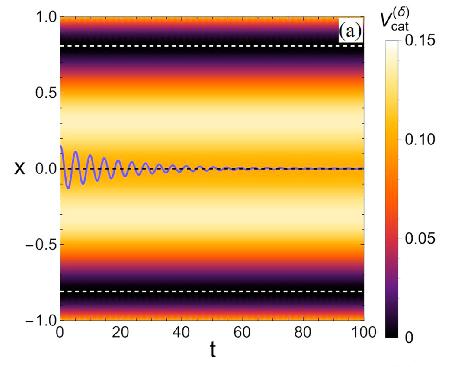 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

