แนะนำโปรแกรม Scilab:Xcos กับการศึกษาฟิสิกส์เรื่องการแกว่งกวัดของระบบมวลติดสปริงในแนวราบ
29-08-2023 อ่าน 1,722
การศึกษาปรากฏการณ์ทางฟิสิกส์บางเรื่องสามารถสังเกตการณ์ได้ด้วยตาเปล่า บางเรื่องต้องใช้เครื่องมือต่างๆเข้ามาช่วย อย่างไรก็ตามปรากฏการณ์ทั้งหมดนี้จะถูกอธิบายในรูปแบบของคณิตศาสตร์ทั้งสิ้น ซึ่งหมายความว่าเรากำลังศึกษาปรากฏการณ์ฟิสิกส์ผ่านคณิตศาสตร์ สำนวนของคณิตศาสตร์ที่ใช้จะมีความง่ายยากต่างกันไปในแต่ละปรากฏการณ์ มนุษย์จึงพยายามสร้างตัวช่วยในการทำความเข้าใจคณิตศาสตร์ เช่น ลูกคิด เครื่องคิดเลข กระดาษกราฟ และอื่นๆอีกมากมาย ปัจจุบันเรามีเทคโนโลยีที่จะเป็นตัวช่วยในการคำนวณ และทำความเข้าใจเกี่ยวกับคณิตศาสตร์เพื่อให้เราได้สามารถอธิบาย และคาดการณ์ผลลัพธ์ของปรากฏการณ์ต่างๆได้อย่างลึกซึ้งและแม่นยำมากขึ้น ไม่ว่าจะเป็น matlab solidwork photomath comsol scilab และอื่นๆ ซอฟต์แวร์เหล่านี้ถูกสร้างขึ้นมาตามความเหมาะสมที่แตกต่างกันออกไป สำหรับบทความนี้จะขอแนะนำโปรแกรมที่ชื่อว่า “Scilab:Xcos”
ในปี ค.ศ. 1990 scilab ถูกสร้างโดยกลุ่มนักวิจัยจาก INRIA และ ENPC ถูกตั้งชื่อในขณะนั้นว่า Psilab หลังจากนั้นถูกพัฒนามาอย่างต่อเนื่องจนกระทั่งปัจจุบันเวอร์ชั่นล่าสุดคือ scilab 6.1.1 มี UI เรียบง่ายสวยงามและใช้งานได้อย่างสะดวกสบาย Scilab เป็นโปรแกรมฟรีสำหรับคำนวณเชิงตัวเลขสามารถใช้งานในด้านการประมวลผลสัญญาณ การวิเคราะห์ทางสถิติ การจำลองพลศาสตร์ของไหล และสร้างแบบจำลองต่างๆ ภาษาที่ใช้ในโปรแกรมจะมีความใกล้เคียงกับ C C++ และ Fortran นอกจากนี้จะมีแพ็คเกจเสริมที่ชื่อว่า Xcos สำหรับสร้างแบบจำลองและจำลองสภาวะของระบบต่างๆ โดยการวาดแผนผังที่มีลักษณะจะคล้ายคลึงกับ Simulink
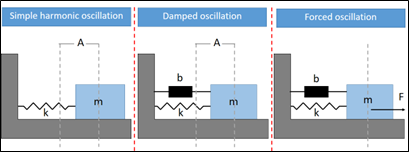
การแกว่งกวัดนับว่าเป็นเรื่องที่น่าสนใจ และสามารถใช้อธิบายเรื่องต่างๆในชิวิตมมนุษย์ได้อย่างกว้างขวาง เริ่มตั้งแต่การแกว่งกวัดของอิเล็กตรอนที่ส่งผลให้เกิดการแผ่คลื่นแม่เหล็กไฟฟ้า การแกว่งกวัดของเส้นเสียงที่ทำให้เกิดเสียงโทนต่างๆ ไปจนถึงการแกว่งกวัดของระบบช่วงล่างรถยนต์ที่ทำให้เกิดความรู้สึกของการขับขี่ที่แตกต่างกันของรถยนต์แต่ละรุ่น ตัวอย่างปรากฏการณ์ที่นำมาศึกษาคือการแกว่งกวัดของระบบมวลติดสปริงในแนวราบทั้ง 3 รูปแบบ ได้แก่ 1) Simple harmonic oscillation 2) Damped oscillation และ 3) Forced oscillation ดังรูปที่1 ระบบทั้ง 3 จะถูกแปลงเป็นสมการอนุพันธ์เพื่อใช้ในการสร้างแผนผังในโปรแกรม Xcos ดังสมการต่อไปนี้ตามลำดับ
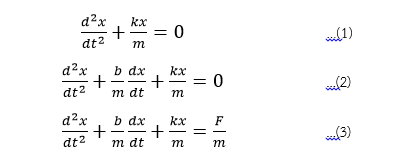
รูปที่ 1 สมการของการแกว่งกวัดของระบบมวลติดสปริงในแนวราบทั้ง 3 รูปแบบ
เริ่มต้นด้วยระบบที่ง่ายที่สุด Simple harmonic oscillation กำหนดให้ แอมพลิจูด (A) เท่ากับ 5 m และอัตราส่วนค่านิจของสปริงต่อมวลปลายสปริง (k/m) เท่ากับ 0.5 s-2 หลังจากนั้นแปลงสมการที่ 1 ให้เป็นแผนผังในโปรแกรม Xcos ดังรูปที่ 2 ทำการตั้งค่าเวลาและใส่เงื่อนไขต่างๆของระบบรวมทั้งสร้างสโคปเพื่อให้โปรแกรมแสดงกราฟของการกระจัดเทียบกับเวลา หรือปริมาณต่างๆที่ต้องการศึกษา เช่น ความเร็ว และความเร่ง ขั้นตอนต่อไปคือเริ่ม simulation หลังจากที่โปรแกรมคำนวณเสร็จจะปรากฏหน้าต่างกราฟที่สร้างโดยสโคป ในกรณีนี้เป็นกราฟแสดงความสัมพันธ์ระหว่างการกระจัด และเวลา ดังรูปที่ 3
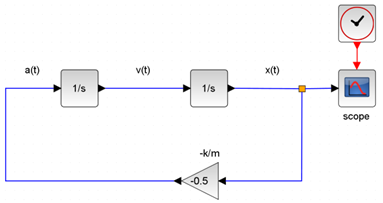
รูปที่ 2 แผนผังระบบ Simple harmonic oscillation ในโปรแกรม Xcos
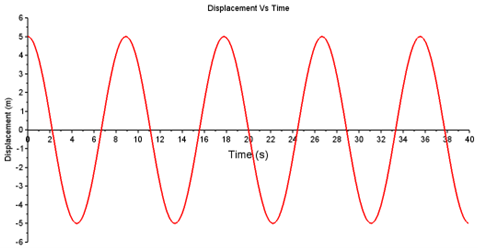
รูปที่ 3 กราฟการกระจัด-เวลาของระบบ Simple harmonic oscillation
ผลที่ได้จากจำลองดังรูปที่ 3 มีลักษณะเป็นกราฟ cosine เนื่องจากตอนเริ่มต้นมวลปลายสปริงอยู่ห่างจากระยะสมดุล 5 m ซึ่งเท่ากับแอมพลิจูด และแอมพลิจูดของการเคลื่อนที่นี้คงตัวอยู่ที่ 5 m มีคาบเวลา (T) ประมาณ 9 s ดั้งนั้นกราฟนี้สามารถอธิบายสั้นๆได้ว่ามวลปลายสปริงจะเกิดการสั่นกลับไปกลับมาเรื่อยๆโดยแอมพลิจูดไม่เปลี่ยนแปลงในรูปแบบฟังก์ชั่น cosine ที่ขึ้นกับเวลา สำหรับระบบต่อไปจะมีความซับซ้อนมากขึ้น เนื่องจากเพิ่มผลกระทบของการหน่วงเข้าไปนั่นคือ Damped oscillation
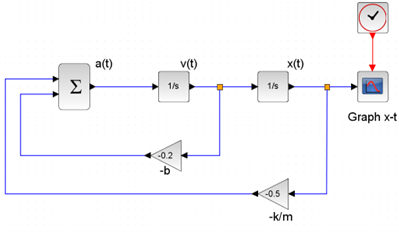
รูปที่ 4 แผนผังระบบ Damped oscillation ในโปรแกรม Xcos
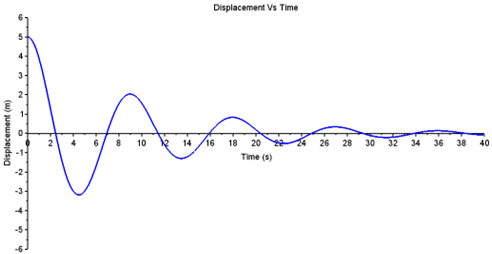
รูปที่ 5 กราฟการกระจัด-เวลาของระบบ Damped oscillation
ระบบที่สองคือ Damped oscillation กำหนดให้ แอมพลิจูด (A) เท่ากับ 5 m อัตราส่วนค่าคงที่ความหน่วงต่อมวลปลายสปริง (b/m) เท่ากับ 0.2 s-1 และอัตราส่วนค่านิจของสปริงต่อมวลปลายสปริง(k/m) เท่ากับ 0.5 s-2 สามารถสร้างแผนผังจากสมการที่ 2 ดังรูปที่ 4 ผลลัพธ์ที่ได้คือกราฟแสดงความสัมพันธ์ระหว่างการกระจัด และเวลา ดังรูปที่ 5 แสดงให้เห็นว่าคาบเวลา(T) ประมาณ 9 s แอมพลิจูดของการสั่นมีค่าลดลงโดยที่ลักษณะของกราฟยังคงเป็นฟังก์ชั่น cosine ที่ขึ้นกับเวลาเช่นเดิม หมายความว่าเมื่อปล่อยให้เวลาผ่านไปเรื่อยๆ มวลปลายสปริงจะสั่นด้วยแอมพลิจูดที่ลดลงจนกระทั่งหยุดนิ่งเมื่อแอมพลิจูดมีค่าเท่ากับศูนย์ ซึ่งต่างจากระบบ Simple harmonic oscillation ที่จะสั่นไปเรื่อยๆ ด้วยแอมพลิจูดคงที่ นอกจากนี้ในระบบ Damped oscillation สามารถวิเคราะห์ศึกษารายละเอียดในกรณีต่างๆ เช่น Underdamped Critical damped และ Overdamped โดยการปรับเปลี่ยนค่านิจของสปริง (k) ค่าคงที่ความหน่วงต่อมวลปลายสปริง (b) และมวลปลายสปริง (m)
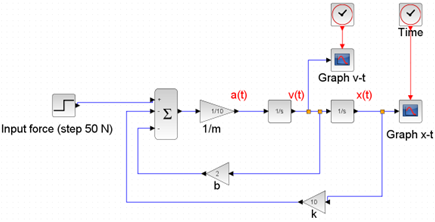
รูปที่ 6 แผนผังระบบ Forced oscillation ในโปรแกรม Xcos
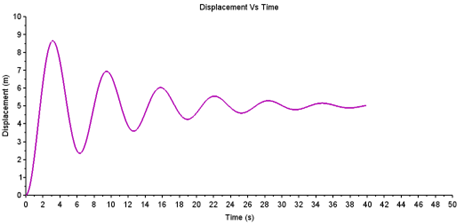
รูปที่ 7 กราฟการกระจัด-เวลาของระบบ Forced oscillation
ระบบสุดท้ายเป็นระบบที่ค่อนข้างซับซ้อน และมีความใกล้เคียงความเป็นจริงมากที่สุดคือ Forced oscillation ภายในระบบประกอบไปด้วยผลกระทบที่เกิดจากความหน่วง พร้อมทั้งแรงภายนอกที่กระทำต่อมวลปลายสปริง กำหนดให้ ค่านิจของสปริง (k) เท่ากับ 10 N•m-1 มวลปลายสปริง (m) เท่ากับ 10 kg ค่าคงที่ความหน่วง (b) เท่ากับ 2 kg•s-1 และแรงที่กระทำคงที่ (F) มีค่า 50 N โดยเริ่มออกแรงเมื่อเวลามากกว่าศูนย์ สมการของระบบนี้คือสมการที่ 3 เขียนเป็นแผนผังได้ดังรูปที่ 6 คำอธิบายที่ได้จากกราฟแสดงความสัมพันธ์ระหว่างระยะกระจัดกับเวลา ดังแสดงในรูปที่ 7 คือ เริ่มต้นมวลปลายสปริงอยู่ในตำแหน่งสมดุล หลังจากนั้นออกแรกยืดคงที่ ระหว่างนั้นจะเกิดการแกว่งกวัดขึ้น และจะค่อยๆลดน้อยลงเนื่องจากผลกระทบของความหน่วง เมื่อเวลาผ่านไปเรื่อยมวลปลายสปริงจะถูกยืดจนมีระยะกระจัดประมาณ 5 m ไปตลอดซึ่งเป็นผลมาจากแรงดึงคงที่นั่นเอง
การศึกษาระบบมวลติดสปริงในแนวนอนด้วยโปรแกรม Xcos พบว่าสามารถอธิบายปรากฏการณ์ออกมาในรูปแบบกราฟของเวลา ซึ่งสะดวกใช้งานง่าย ประหยัดเงินสำหรับซื้อโปรแกรมช่วยคำนวณไปได้มาก นอกจากนี้สามารถใช้งานได้ตั้งแต่ระบบที่เรียบง่าย จนถึงระบบที่มีความซับซ้อน สามารถนำไปประยุกต์ใช้ในการศึกษางานวิจัยในด้านต่างๆ เช่น วงจรไฟฟ้า ระบบควบคุม แบบจำลองของแบตเตอรี่ และแบบจำลองอื่นๆ เพียงทราบสมการและแปลงเป็นแผนผัง สุดท้ายนี้หวังว่าบทความนี้จะเป็นประโยชน์เล็กๆน้อยๆสำหรับพวกเราชาวฟิสิกส์
การศึกษาระบบมวลติดสปริงในแนวนอนด้วยโปรแกรม Xcos พบว่าสามารถอธิบายปรากฏการณ์ออกมาในรูปแบบกราฟของเวลา ซึ่งสะดวกใช้งานง่าย ประหยัดเงินสำหรับซื้อโปรแกรมช่วยคำนวณไปได้มาก นอกจากนี้สามารถใช้งานได้ตั้งแต่ระบบที่เรียบง่าย จนถึงระบบที่มีความซับซ้อน สามารถนำไปประยุกต์ใช้ในการศึกษางานวิจัยในด้านต่างๆ เช่น วงจรไฟฟ้า ระบบควบคุม แบบจำลองของแบตเตอรี่ และแบบจำลองอื่นๆ เพียงทราบสมการและแปลงเป็นแผนผัง สุดท้ายนี้หวังว่าบทความนี้จะเป็นประโยชน์เล็กๆน้อยๆสำหรับพวกเราชาวฟิสิกส์
ชาคริต ปัตตาเวีย
จบปริญญาโทสาขาฟิสิกส์จาก
สถาบันเทคโนโลยีพระจอมเกล้าเจ้าคุณทหารลาดกระบัง
อ้างอิง
- Javier E. H. (2009). Classical Mechanics with MATLAB Applications. Jones and Bartlett publishers.
- King, G. C. (2009). Vibrations and waves. John Wiley & Sons.
- https://www.scilab.org/about/scilab-open-source-software
บทความฟิสิกส์ล่าสุด
หอสังเกตการณ์นิวทริโนไอซ์คิวบ์ ตอนที่ 2
29-02-2024
หอสังเกตการณ์นิวทริโนไอซ์คิวบ์ ตอนที่ 1
09-02-2024
