การหักเหแสงเหนือธรรมชาติ
 (ภาพจาก https://www.mat.ucsb.edu/~g.legrady/academic/courses/10f200a/md/metamaterials.htm)
(ภาพจาก https://www.mat.ucsb.edu/~g.legrady/academic/courses/10f200a/md/metamaterials.htm)
แสงเดินทางเป็นเส้นตรงด้วยอัตราเร็วคงที่ประมาณสามแสนกิโลเมตรต่อวินาทีในสุญญากาศ อัตราเร็วระดับนี้เป็นขีดจำกัดสูงสุดของอัตราเร็วที่เป็นไปได้ในเอกภพ แต่เมื่อแสงวิ่งจากตัวกลางสุญญากาศไปยังตัวกลางอื่นแล้วอัตราเร็วของมันจะลดลง ซึ่งส่งผลให้เส้นทางการเคลื่อนที่ของมันเบี่ยงเบนออกจากเส้นทางเดิม ทั้งนี้ก็เพราะแสงมีเส้นทางเดินใหม่ที่ใช้เวลาน้อยที่สุด นักฟิสิกส์เรียกปรากฏการณ์ที่เส้นทางของแสงเกิดการเบี่ยงเบนไปจากเส้นทางเดิมเมื่อแสงเคลื่อนที่ข้ามพื้นผิวระหว่างสองตัวกลางว่า “การหักเหแสง” (refraction)
อัตราส่วนระหว่างอัตราเร็วแสงในสุญญากาศและอัตราเร็วแสงในตัวกลางใดๆ มีชื่อเรียกว่า “ดัชนีหักเหแสง” (refractive index) ของตัวกลางดังกล่าว สัญลักษณ์ที่ใช้แทนดัชนีหักเหแสงคือ “n” ดัชนีหักเหแสงที่น้อยที่สุดในธรรมชาติคือ n=1 ซึ่งเป็นดัชนีหักเหแสงของสุญญากาศนั่นเอง นอกจากนี้เรายังพบว่าอากาศมีดัชนีหักเหแสงมากกว่าหนึ่งเพียงเล็กน้อย ดังนั้นเราจึงมักจะประมาณให้ดัชนีหักเหแสงของอากาศมีค่าเท่ากับหนึ่งด้วย ส่วนตัวกลางตามธรรมชาติอื่นๆ ที่ไม่ใช่อากาศจะมีค่าดัชนีหักเหแสงมากกว่าหนึ่งเสมอ
อาจกล่าวได้ว่าแผนภาพทางซ้ายมือสุดของรูปที่ 1 เป็นแผนภาพหนึ่งที่โด่งดังที่สุดในทางทัศนศาสตร์ แผนภาพนี้แสดงให้เห็นว่าเส้นรังสี (ซึ่งแทนทิศทางการเคลื่อนที่ของแสง) ที่ตกกระทบลงบนพื้นผิวระหว่างอากาศและตัวกลางอื่นที่มีค่าดัชนีหักเหแสงมากกว่าหนึ่ง (เช่น น้ำ แก้ว เป็นต้น) ด้วย “มุมตกกระทบ” เท่ากับ A จะเกิดการเบี่ยงเบนออกจากแนวเดิมด้วย “มุมหักเห” B ซึ่งไม่เท่ากับ A เส้นรังสีหักเหจะเบนออกจากแนวเดิมมากขึ้นเมื่อค่าดัชนีหักเหแสงของตัวกลางมีค่ามากขึ้น และถ้าสมมติให้ดัชนีหักเหแสงมีค่ามากกว่า 1 มากๆ (n>>1) เส้นรังสีหักเหจะตั้งฉากพอดีกับพื้นผิวระหว่างอากาศและตัวกลางดังกล่าว นั่นคือมุมหักเหจะมีค่าเท่ากับศูนย์พอดี แต่อย่างไรก็ตาม เส้นรังสีหักเหภายในวัสดุตามธรรมชาติจะไม่มีทางเบนออกไปทางฝั่งซ้ายมือของเส้นตั้งฉากโดยเด็ดขาด

รูปที่ 1 การหักเหแสงในตัวกลางที่มีค่าดัชนีหักเหแสงต่างกัน
เส้นรังสีหักเหอาจจะสามารถเบนไปทางด้านซ้ายมือได้ถ้าตัวกลางมีค่าดัชนีหักเหแสงติดลบ ซึ่งจะส่งผลให้มุมหักเหมีค่าติดลบตามไปด้วยดังแสดงในรูปทางด้านขวามือสุดของรูปที่ 1 แต่ธรรมชาติไม่ได้มอบตัวกลางเช่นนี้มาให้เรา ดังนั้นถ้าจะกล่าวว่าวัสดุที่มีค่าดัชนีหักเหแสงติดลบเป็นวัสดุเหนือธรรมชาติก็คงจะไม่ใช่คำกล่าวที่เกินจริงแต่อย่างใด
นักฟิสิกส์คนแรกผู้ศึกษาความเป็นไปได้ของวัสดุที่ไม่น่าจะเป็นไปได้คือนักฟิสิกส์ชาวรัสเซียชื่อวิคเตอร์
เวเซลาโก้ (รูปที่ 2) ในปี ค.ศ. 1968 เวเซลาโก้ได้จินตนาการถึงตัวกลางที่มีค่าดัชนีหักเหแสงติดลบ เวเซลาโก้ได้ตั้งข้อสังเกตว่าค่าดัชนีหักเหแสงของตัวกลางใดๆ ยังขึ้นอยู่กับคุณสมบัติทางไฟฟ้าและคุณสมบัติทางแม่เหล็กของวัสดุอีก 2 ตัวที่เรียกว่าค่าเอพซิลอน (หรือค่าคงที่ไดอิเล็กทริก: dielectric constant) และค่ามิว (หรือสภาพซึมซับแม่เหล็ก: magnetic permeability) ตามลำดับ โดยค่าดัชนีหักเหแสงของตัวกลางใดๆ เป็นรากที่สองของผลคูณระหว่างค่าคงที่ไดอิเล็กทริกและสภาพซึมซับแม่เหล็กของตัวกลางดังกล่าว เช่นอากาศมีค่าคงที่ไดอิเล็กทริกและสภาพซึมซับแม่เหล็กเท่ากับหนึ่งพอดี จึงทำให้ค่าดัชนีหักเหแสงของอากาศมีค่าเท่ากับหนึ่งตามไปด้วย
เวเซลาโก้อ้างเป็นครั้งแรกว่าวัสดุจะทีค่าดัชนีหักเหแสงติดลบได้ก็ต่อเมื่อค่าคงที่ไดอิเล็กทริกและสภาพซึมซับแม่เหล็กของวัสดุมีค่าติดลบพร้อมๆ กัน [1] เขาอธิบายให้เห็นว่าแสงยังสามารถวิ่งผ่านวัสดุที่มีค่าดัชนีหักเหแสงติดลบได้ ข้อกล่าวอ้างของเวเซลาโก้มีพื้นฐานอยู่บนหลักการของเหตุและผล (causality) กล่าวคือเมื่อแสงวิ่งตกกระทบลงบนพื้นผิวของวัสดุใดๆ พลังงานของแสงจะต้องแผ่ขยายออกจากพื้นผิวดังกล่าวด้วยระดับพลังงานที่ลดลง
แต่เป็นที่น่าเสียดายที่เวเซลาโก้ไม่ได้อธิบายวิธีประดิษฐ์วัสดุที่เขากล่าวอ้าง ทำให้งานวิจัยของเขาขึ้นหิ้งอยู่หลายปี แต่ผู้อ่านคงจะพอเดาออกแล้วว่าต่อมาก็ได้มีคนหยิบเอางานของเวเซลาโก้ขึ้นมาปัดฝุ่นใหม่ หาวิธีประดิษฐ์วัสดุนี้ขึ้นในห้องแลบ และที่สำคัญที่สุดคือหาหนทางนำวัสดุเหนือธรรมชาตินี้มาใช้ประโยชน์

รูปที่ 2 วิคเตอร์ เวเซลาโก้ (Victor Veselago) [2]
นักฟิสิกส์คนแรกผู้ชี้ให้เห็นว่าเราสามารถนำเอาวัสดุค่าดัชนีหักเหแสงติดลบมาใช้ให้เกิดประโยชน์ได้คือนักฟิสิกส์ชาวอังกฤษชื่อ จอห์น เพนดรี้ (John Pendry) (รูปที่ 3) นอกจากนี้เพนดรี้ยังถือเป็นบุคคลแรกที่คิดค้นวิธีประดิษฐ์วัสดุค่าดัชนีหักเหแสงติดลบในเชิงทฤษฎีเป็นคนแรก ซึ่งต่อมาไม่นานก็มีทีมวิศวกรและนักฟิสิกส์ซึ่งนำโดย เดวิด สมิทธ์ (David Smith) นำวิธีดังกล่าวไปประดิษฐ์และสาธิตทดลองให้เห็นจริง

รูปที่ 3 จอห์น เพนดรี้ (John Pendry) [2]
ในปี ค.ศ. 2000 เพนดรี้ใช้ทฤษฎีคลื่นแม่เหล็กไฟฟ้าของแสง (นั่นคือแสงประกอบไปด้วยสนามไฟฟ้าและสนามแม่เหล็ก) เพื่ออธิบายการเคลื่อนที่ของแสงภายในแผ่นวัสดุที่มีค่าดัชนีหักเหแสงใกล้เคียง -1 วัสดุนี้จะต้องมีทั้งค่าคงที่ไดอิเล็กทริกและสภาพซึมซับแม่เหล็กใกล้เคียง -1 ด้วยจึงจะทำให้ค่าดัชนีหักเหแสงของมันเข้าใกล้ค่า -1 เพนดรี้ได้ข้อสรุปว่าแผ่นวัสดุเหนือธรรมชาตินี้ประพฤติตัวเหมือน “เลนส์สมบูรณ์แบบ” (perfect lens) คือมันสามารถสร้างภาพของวัตถุที่มีขนาดเล็กกว่าความยาวคลื่นของแสงที่ใช้ถ่ายภาพมากๆ ได้โดยอาศัยการหักเหแสงเชิงลบดังแสดงในรูปที่ 4 [3] คุณสมบัตินี้ไม่มีในเลนส์ธรรมดาทั่วไปที่มีค่าดัชนีหักเหแสงเป็นบวก เลนส์สมบูรณ์แบบจะทำให้เรามีกล้องถ่ายภาพด้วยแสงที่มีความละเอียดสูงซึ่งจะสามารถถ่ายภาพวัตถุเล็กในระดับไม่กี่นาโนเมตรเช่น ไวรัส เป็นต้น แทนที่การใช้กล้องอิเล็กตรอนที่มีราคาแพง

รูปที่ 4 เลนส์สมบูรณ์แบบของเพนดรี้
เพนดรี้ตั้งข้อสังเกตว่า ความยาวคลื่นของแสงที่ตามองเห็น (visible light) มีค่ามากกว่าขนาดของอะตอมมาก อะตอมมีขนาดอยู่ในระดับของ 0.1 นาโนเมตรหรือเล็กกว่าขนาดของเส้นผมคนเราประมาณล้านเท่า แต่แสงที่ตามองเห็นเช่นแสงสีเขียวมีความยาวคลื่น 532 นาโนเมตรหรือเล็กกว่าขนาดของเส้นผมคนเราประมาณ 200 เท่า ดังนั้นความยาวคลื่นแสงที่ตามองเห็นจึงมีค่ามากกว่าขนาดอะตอมอยู่ประมาณ 5,000 เท่า ด้วยเหตุนี้ค่าคงที่ไดอิเล็กทริกและสภาพซึมซับแม่เหล็กจึงเป็น “ค่าเฉลี่ยของการตอบสนองของอะตอมหลายๆ อะตอมต่อแสง” คุณสมบัติทั้งสองตัวนี้จึงมีค่าขึ้นอยู่กับความยาวคลื่นของแสงตกกระทบ ส่งผลให้ค่าดัชนีหักเหแสงมีค่าขึ้นอยู่กับความยาวคลื่นของแสงตกกระทบด้วย ปรากฏการณ์ทางธรรมชาติที่เป็นผลลัพธ์ของคุณสมบัติเช่นนี้คือสายรุ้ง ค่าดัชนีหักเหแสงของหยดน้ำมีค่าขึ้นกับความยาวคลื่นของแสงตกกระทบ ดังนั้นแสงที่ตกกระทบลงบนหยดน้ำจึงเบี่ยงเบนออกจากแนวเดิมด้วยมุมที่ต่างกันซึ่งส่งผลให้แสงที่แต่ละความยาวคลื่นเกิดการแยกออกจากกัน ทำให้เรามองเห็นแถบแสงปรากฏบนทองฟ้า
ดังนั้นเพนดรี้จึงเสนอว่า ทำไมเราไม่สร้างอะตอมประดิษฐ์ (artificial atoms) ขึ้นมา โดยให้อะตอมประดิษฐ์นี้มีขนาดเล็กกว่าความยาวคลื่นแสงอย่างน้อย 2 เท่า เราสามารถใช้ทฤษฎีคลื่นแม่เหล็กไฟฟ้าของแสงเพื่อออกแบบอะตอมประดิษฐ์ให้มันมีการตอบสนองใดๆ ตามที่เราต้องการได้ ค่าคงที่ไดอิเล็กทริกและสภาพซึมซับแม่เหล็กจะเป็นค่าเฉลี่ยของการตอบสนองเชิงไฟฟ้าและเชิงแม่เหล็กตามลำดับของอะตอมประดิษฐ์ที่มีต่อแสง ดังนั้นเราจึงสามารถประดิษฐ์วัสดุที่มีค่าคงที่ไดอิเล็กทริกและสภาพซึมซับแม่เหล็กตามที่เราต้องการได้
ค่าคงที่ไดอิเล็กทริกติดลบจะเกิดขึ้นที่ความยาวคลื่นใกล้เคียงกับความยาวคลื่นของแสงที่ทำให้อะตอมประดิษฐ์เกิดการสั่นพ้องเชิงไฟฟ้ากับสนามไฟฟ้าของแสง ส่วนสภาพซึมซับแม่เหล็กติดลบจะเกิดขึ้นที่ความยาวคลื่นใกล้เคียงกับความยาวคลื่นของแสงที่ทำให้อะตอมเกิดการสั่นพ้องเชิงแม่เหล็กกับสนามแม่เหล็กของแสง เพนดรี้บอกว่าถ้าการสั่นพ้องเชิงไฟฟ้าและการสั่นพ้องเชิงแม่เหล็กเกิดขึ้นที่ความยาวคลื่นแสงใกล้เคียงกันแล้ว วัสดุที่ประกอบขึ้นจากอะตอมประดิษฐ์เหล่านี้จะมีค่าดัชนีหักเหแสงติดลบได้ ปัจจุบันเราเรียกวัสดุประดิษฐ์นี้ว่า “เมต้าแมททีเรียลส์” (metamaterials)
ในปี ค.ศ. 1999 เพนดรี้ได้นำเสนอโครงสร้างแบบใหม่เรียกว่าตัวสั่นพ้องวงแหวนแยก (split ring resonator: SRR) [5] ดังแสดงในรูปที่ 5(ซ้าย) ซึ่งเมื่อนำ SRR มาจัดวางให้เป็นผลึกดังแสดงในรูปที่ 5(ขวา) แล้วจะกลายเป็นวัสดุที่มีสภาพซึมซับแม่เหล็กติดลบ ดังนั้น SRR ของเพนดรี้จึงเป็นเหมือนอะตอมเชิงแม่เหล็กสำหรับแสง โดย SRR ของเพนดรี้ทำมาจากโลหะเช่นเงิน อลูมิเนียม หรือทองแดง มันเป็นวงแหวนสองอันคือวงแหวนอันเล็กวางอยู่ภายในวงแหวนอันใหญ่ แต่ละวงแหวนมีช่องอากาศแคบๆ หนึ่งช่องถูกเจาะเอาไว้ ช่องแคบทั้งสองนี้อยู่ตรงข้ามกัน ตำแหน่งความยาวคลื่นสั่นพ้องเชิงแม่เหล็กของ SRR จะขึ้นอยู่กับตัวแปรทางตรีโกณมิติของมัน เช่น รัศมีภายในของวงแหวน ความหนาของวงแหวน ความกว้างของช่องแยก ความกว้างของช่องว่างระหว่างวงแหวนใหญ่และวงแหวนเล็ก รวมทั้งค่าคงที่ผลึกซึ่งเป็นระยะห่างระหว่างแต่ละ SRR อีกด้วย คุณสมบัติเช่นนี้ทำให้เราสามารถย่อหรือขยายขนาดของ SRR เพื่อปรับการตอบสนองของวัสดุนี้ต่อแสงที่ความยาวคลื่นต่างๆ กัน ตั้งแต่แสงที่ตามองเห็นจนถึงแสงที่ตามองไม่เห็น โดย SRR สามารถมีขนาดเล็กมากๆ เมื่อเปรียบเทียบกับขนาดของความยาวคลื่น

รูปที่ 5 ตัวสั่นพ้องวงแหวนแยกสำหรับใช้เป็นอะตอมเชิงแม่เหล็กสำหรับแสง (ซ้าย)
และโครงสร้างจากการจัดเรียงตัวซ้ำๆ ของตัวสั่นพ้องวงแหวนแยก (ขวา) [6]
นอกจากนี้ โลหะเช่นเงิน อลูมิเนียม และทองแดงมีค่าคงที่ไดอิเล็กทริกติดลบอยู่แล้วสำหรับแสงที่มีค่าพลังงานต่ำกว่ารังสี UV เพราะความยาวคลื่นสั่นพ้องเชิงไฟฟ้าของพวกมันอยู่ในย่านรังสี UV เราสามารถปรับความยาวคลื่นสั่นพ้องเชิงไฟฟ้านี้ไปยังตำแหน่งความยาวคลื่นใดๆ ก็ได้โดยนำเส้นลวดโลหะยาวมาวางจัดเรียงให้เป็นผลึกดังแสดงในรูปที่ 6 โดยความยาวคลื่นของการสั่นพ้องเชิงไฟฟ้าจะขึ้นอยู่กับค่ารัศมีของเส้นลวดโลหะยาวและค่าคงที่ผลึกในการจัดเรียงตัวของเส้นลวด

รูปที่ 6 โครงสร้างจากการจัดเรียงตัวซ้ำๆ ของเส้นลวดโลหะยาว [7]
จากนั้นเราสามารถนำเอาโครงสร้างในรูปที่ 5 และ 6 มาประกอบเข้าด้วยกัน โดยเราสามารถปรับให้ความยาวคลื่นการสั่นพ้องเชิงแม่เหล็กของโครงสร้างในรูปที่ 5 มีค่าใกล้เคียงกับความยาวคลื่นการสั่นพ้องเชิงไฟฟ้าของโครงสร้างในรูปที่ 6 ดังนั้นโครงสร้างใหม่นี้จึงกลายเป็นวัสดุที่สามารถมีสภาพซึมซับแม่เหล็กและค่าคงที่ไดอิเล็กทริกติดลบพร้อมกันได้ ส่งผลให้วัสดุใหม่นี้มีค่าดัชนีหักเหแสงติดลบได้
โครงสร้างนี้ถูกประดิษฐ์ขึ้นในห้องวิจัยเป็นครั้งแรกโดยสมิทธ์และคณะในปี ค.ศ. 2000 เพื่อทดลองพิสูจน์ให้เห็นจริงว่าคลื่นไมโครเวฟ (ซึ่งเป็นแสงประเภทหนึ่งที่มีความยาวคลื่นเยอะกว่าแสงที่ตามองเห็น) หักเหแบบติดลบภายในวัสดุประดิษฐ์นี้ [4] รูปภาพจริงของวัสดุประดิษฐ์นี้แสดงอยู่ในรูปที่ 7 เนื่องจากมันทำงานในแถบความยาวคลื่น 14.0-15.3 เมตรของคลื่นไมโครเวฟทำให้มันมีขนาดไม่เล็กมากและสามารถประดิษฐ์ขึ้นได้ไม่ยากด้วยวิธีการเดียวกันกับการกัดแผ่นวงจรอิเล็กทรอนิกส์ สมิทธ์และทีมวิจัยของเขาได้ทดลองให้เห็นเป็นครั้งแรกว่าพลังงานของคลื่นไมโครเวฟภายในวัสดุประดิษฐ์นี้แผ่ขยายในทิศทางตรงกันข้ามกับการเคลื่อนที่ของคลื่น ผลการทดลองนี้ยืนยันว่าวัสดุประดิษฐ์นี้มีดัชนีหักเหแสงเป็นลบ
งานวิจัยของสมิทธ์และคณะนี้ได้รับการยอมรับว่าเป็นหลักฐานชิ้นแรกที่ยืนยันว่ามนุษย์สามารถประดิษฐ์วัสดุเหนือธรรมชาติขึ้นมาได้

รูปที่ 7 วัสดุประดิษฐ์ค่าดัชนีหักเหแสงติดลบสำหรับคลื่นไมโครเวฟอันแรกของโลก [4]

รูปที่ 8 ปริซึมที่ทำจากวัสดุค่าดัชนีหักเหแสงเป็นบวก (บนซ้าย) ปริซึมที่ทำจากวัสดุค่าดัชนีหักเหแสงเป็นลบ (บนขาว) และค่าการส่งผ่านของแสงที่มุมหักเหต่างกัน (ล่าง) [6],[8]
ต่อมาในปี ค.ศ. 2003 ปาราซโซลิและคณะได้ทำการทดลองสาธิตการหักเหของแสงผ่านปริซึมที่ทำมาจากวัสดุที่มีค่าดัชนีหักเหแสงแบบเดียวกันกับที่สมิทธ์และทีมเคยใช้ก่อนหน้านั้นสามปี [8] ปาราซโซลิยังเตรียมปริซึมขนาดเท่ากันแต่ทำมาจากวัสดุที่มีค่าดัชนีหักเหแสงเป็นบวกเพื่อใช้เป็นตัวเปรียบเทียบให้เห็นความแตกต่าง ผลของการวัดค่าการส่งผ่านแสง ณ มุมหักเหแสงต่างๆ กันแสดงให้เห็นชัดเจนว่าแสงได้หักเหผ่านปริซึมทั้งสองไปคนละฝั่งของเส้นตั้งฉากดังแสดงในรูปที่ 8(ล่าง) การทดลองนี้แสดงให้เห็นอย่างชัดเจนอีกครั้งว่าวัสดุประดิษฐ์ของสมิทธ์และทีมมีค่าดัชนีหักเหแสงเป็นลบ
จะเห็นได้ว่าในช่วงปี ค.ศ. 2000-2003 นับได้ว่าเป็นช่วงเวลาที่งานวิจัยสาขาใหม่ทางทัศนศาสตร์ชื่อเมต้าแมททีเรียลส์ได้ถือกำเนิดขึ้น นักวิจัยทั่วโลกพยายามที่จะย่นย่อขนาดของอะตอมประดิษฐ์ให้เล็กลงไปสู่ระดับนาโนเมตรในขณะที่ยังคงรักษาไว้ซึ่งขนาดของวัสดุโดยรวม เพื่อให้วัสดุประดิษฐ์นี้ที่เรียกว่าเมต้าแมททีเรียลส์สามารถใช้ได้กับแสงในย่านพลังงานสูงขึ้น เช่น รังสีอินฟราเรดและแสงที่ตามองเห็น โครงสร้างใหม่ๆ ของอะตอมประดิษฐ์ยังได้ถูกพัฒนาขึ้นเพื่อลดปัญหาของโครงสร้างแบบเก่า แต่ยิ่งอะตอมประดิษฐ์มีขนาดเล็กลง เครื่องมือที่ใช้เตรียมเมต้าเมททีเรียลส์จากอะตอมประดิษฐ์เหล่านี้ก็ยิ่งมีความซับซ้อนและราคาแพงขึ้น ผู้อ่านที่สนใจการพัฒนาเมต้าแมททีเรียลส์เพื่อใช้งานกับแสงที่ตามองเห็นสามารถศึกษาได้จากเอกสารอ้างอิงด้านท้ายบทความ [9]
ถึงแม้ว่าจะมีการศึกษาเมต้าแมททีเรียลส์มาเกือบ 2 ทศวรรษแล้ว แต่งานวิจัยในสาขานี้ก็ยังคงได้รับความสนใจเป็นอย่างมากในปัจจุบัน การวิจัยทางด้านเมต้าแมททีเรียลส์ได้เจอกับปัญหาสำคัญ นั่นคือปัญหาเรื่องการสูญเสียพลังงานแสงไปเป็นพลังงานความร้อนภายในโลหะที่เป็นส่วนประกอบสำคัญของเมต้าแมททีเรียลส์ ถึงแม้ว่าจะมีการพัฒนาโครงสร้างใหม่ๆ เพื่อให้มีค่าการสูญเสียพลังงานต่ำลง เช่น การเจาะรูแบบผลึกบนแผ่นฟิล์มหลายชั้นของโลหะและฉนวนไฟฟ้า [10] แต่มันก็ยังไม่ดีพอที่จะทำให้เลนส์สมบูรณ์แบบของเพนดรี้เป็นจริงขึ้นมาได้ งานวิจัยในปัจจุบันจึงมุ่งเน้นไปที่การใช้วัสดุฉนวนไฟฟ้าแทนโลหะ [11] แต่มันก็เป็นเรื่องท้าทายมากของนักวัสดุศาสตร์ที่จะหาฉนวนไฟฟ้าที่สามารถสะท้อนแสงได้ดีเหมือนโลหะแต่ไม่ดูดกลืนแสงเลย
นอกจากปัญหาเรื่องการดูดกลืนแสง ก็ยังมีปัญหาเรื่องของปริมาณของวัสดุเมต้าแมททีเรียลส์ที่ประดิษฐ์ได้ การตรียมลวดลายของอะตอมประดิษฐ์สำหรับแสงที่ตามองเห็นต้องใช้เครื่องมือการแกะสลักในระดับนาโนเมตรด้วยลำแสงอิเล็กตรอน (electron beam lithography) แต่เครื่องมือนี้แพงมากและให้ลวดลายครอบคลุมพื้นที่น้อย ดังนั้นมันจึงเป็นไปไม่ได้เลยที่จะใช้เครื่องมือนี้ผลิตอุปกรณ์เมต้าแมททีเรียลส์เพื่อนำออกไปใช้งานจริง เครื่องมือนี้จึงมักจะถูกใช้เตรียมตัวอย่างเพื่อศึกษาคุณสมบัติพื้นฐานเพียงเท่านั้น แต่ปัญหานี้ก็อาจจะพอผ่อนคลายได้บ้างโดยใช้เทคนิคนาโนอิมปริ้น (nanoimprint) [12] โดยเทคนิคนาโนอิมปริ้นจะลอกลวดลายของอะตอมประดิษฐ์ลงไปบนแผ่นฟิล์มโดยใช้รังสี UV หรือความร้อน การลอกลวดลายนี้จะทำติดต่อกันหลายครั้งจนกระทั่งได้ลวดลายครอบคลุมพื้นที่กว้าง ทำให้เราสามารถประดิษฐ์เมต้าแมททีเรียลส์ในระดับขนาดใหญ่ขึ้นได้
เรียบเรียงโดย
ดร. ปิยวัฒน์ ทัพสนิท
อาจารย์คณะวิทยาศาสตร์ พลังงานและสิ่งแวดล้อม มหาวิทยาลัยเทคโนโลยีพระจอมเกล้าพระนครเหนือ (วิทยาเขตระยอง)
อ้างอิง
- [1] V. G. Veselago, Soviet Physics USPEKHI 10, 509, (1968).
- [2] A. Boardman, J. Opt. 13, 020401 (2011).
- [3] J. B. Pendry, Phys. Rev. Lett. 85, 3966-3969 (2000).
- [4] D. R. Smith, Willie J. Padilla, D. C. Vier, S. C. Nemat-Nasser, and S. Schultz, Phys. Rev. Lett. 84, 4184-4187 (2000).
- [5] J. B. Pendry, A. J. Holden, D. J. Robbins, and W. J. Stewart, IEEE Trans. Microwave Theory Tech. 47, 2075 (1999).
- [6] J. B. Pendry, Contemporary Physics, 45, 191-202 (2004).
- [7] W. J. Padilla†, D. N. Basov, D. R. Smith, materialstoday 9,28-35 (2006).
- [8] C. G. Parazzoli, R. B. Greegor, K. Li, B. E. C. Koltenbah, and M. Tanielian, Phys. Rev Lett. 90, 107401 (2003).
- [9] V. M. Shalaev, Nat. Photon. 1, 41-48 (2007).
- [10] Y. Liang, Z. Yu, N. Ruan, Q. Sun, and T. Xu, Opt. Lett. 42, 3239-3242 (2017).
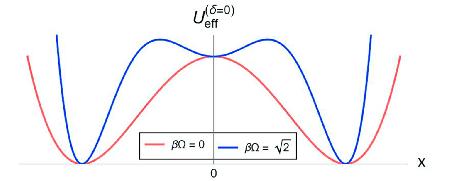 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( พฤติกรรมที่น่าฉงน และบทสรุป )
18-03-2025
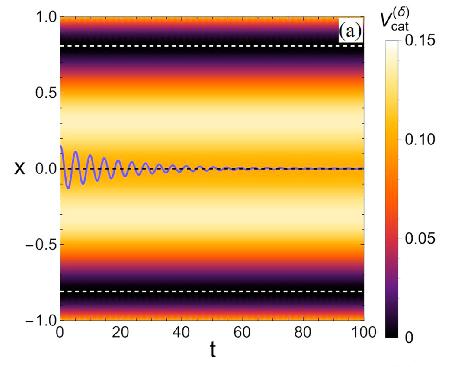 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 2: คำอธิบายพฤติกรรมหลัก )
18-03-2025
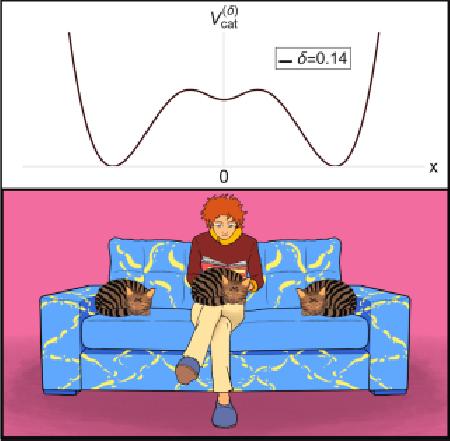 ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
ฟิสิกส์ของปฏิสัมพันธ์ระหว่าง แมว กับคน … เมื่อน้องแมวถูกนำมาช่วยสอนฟิสิกส์ ( ตอนที่ 1: เกริ่นนำ )
17-03-2025
 หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024
หรือว่าเราอาศัยอยู่ในโฮโลแกรม ?
24-10-2024

